**一. 关于boosting算法的起源** boost 算法系列的起源来自于PAC Learnability（直译过来称为：PAC 可学习性）。这套理论主要研究的是什么时候一个问题是可被学习的。 我们知道，**可计算性**在计算理论中已经有定义，而**可学习性**正是PAC Learnability理论所要定义的内容。另外，在计算理论中还有很大一部分精力花在研究问题是可计算的时候，其复杂度又是什么样的。因此，在计算学习理论中，也有研究可学习的问题的复杂度的内容，主要是样本复杂度 (Sample Complexity) 。 最后，在可计算的时候，得到实现计算的具体算法也是计算理论中的一个重要部分；而更多的在“机器学习”这个领域中，我们往往会探讨针对可学习的问题的具体的学习算法。 听起来很复杂，简而言之，就是：**PAC 模型的作用相当于提供了一套严格的形式化语言来陈述以及刻画这里所提及的可学习性 Learnability 以及（样本）复杂度 (Sample) Complexity 问题。** 这套理论是由Valiant提出来的，作者曾获得了2010年的图灵奖。  PAC 定义了学习算法的强弱： 弱学习算法：识别错误率小于1/2（即准确率仅比随机猜测略高的学习算法）；  强学习算法：识别准确率很高并能在多项式时间内完成的学习算法。 更为严格的定义： 弱学习算法：一个概念如果存在一个多项式的学习算法能够学习它，并且学习的正确率仅比随机猜测略好(高于50%)，那么，这个概念是弱可学习的； 强学习算法：一个概念如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么，这个概念是强可学习的。 同时 ,Valiant和Kearns还提出了PAC学习模型中弱学习算法和强学习算法的等价性问题，即**任意给定仅比随机猜测略好的弱学习算法 ,是否可以将其提升为强学习算法 ?** 如果弱学习算法和强学习算法二者等价 ,那么只需找到一个比随机猜测略好的弱学习算法就可以将其提升为强学习算法 ,而不必寻找很难获得的强学习算法。 也就是这种猜测，让无数研究人员去设计算法来验证PAC理论的正确性。 不过很长一段时间都没有一个切实可行的办法来实现这个理想。细节决定成败，再好的理论也需要有效的算法来执行。终于功夫不负有心人， Schapire在1996年提出一个有效的算法真正实现了这个夙愿，它的名字叫AdaBoost。AdaBoost把多个不同的决策树用一种非随机的方式组合起来，表现出惊人的性能和优点： 1. 把决策树的准确率大大提高，可以与SVM媲美； 2. 当使用简单分类器时，计算出的结果是可以理解的。而且弱分类器构造极其简单 3. 速度快，且基本不用调参数； 4. 简单，无需做特征筛选； 5. 不用担心Overfitting。 “我估计当时Breiman和Friedman肯定高兴坏了，因为眼看着他们提出的CART正在被SVM比下去的时候，AdaBoost让决策树起死回生！Breiman情不自禁地在他的论文里赞扬AdaBoost是最好的现货方法（off-the-shelf，即“拿下了就可以用”的意思）。”（这段话摘自统计学习那些事） **二. 基于数据集多重抽样的分类器** 前面我们已经尝试设计多种分类器，如果我们尝试将不同的分类器组合在一起，这种组合的结果就是**集成方法（或称为元算法）**。使用集成方法时会有多种形式，它可以是不同算法的集成，也可以是同一算法在不同设置下的集成，还可以是数据集的不同部分分配给不同分类器后的集成。通常的集成方法有bagging方法和boosting方法。 **1.bagging：基于数据随机重抽样的分类器构建方法** bagging方法，又称为自举汇聚法(bootstrap aggregating)，是在从原始数据集重选择（有放回，可以重复）得到S个新数据集的一种技术，新数据集与原数据集大小相等，每个数据集都是通过在原始数据集中随机选择一个样本来进行替换而得到。 建立好S个新数据集后，将某个学习算法分别作用于每一个数据集，就得到S个分类器。对这S个分类器进行叠加，他们的权重都相等(当然这里S个分类器采用的分类算法不一样的话，可以考虑使用投票)，这样就可以得到一个强学习器。 以下给出bagging方法的主要步骤： 1. 重复地从一个样本集合D中采样n个样本 2. 针对每次采样的子样本集，进行统计学习，获得假设Hi 3. 将若干个假设进行组合，形成最终的假设Hfinal 4. 将最终的假设用于具体的分类任务 **2.boosting方法** 书中给出以下解释：boosting是一种与bagging很类似的技术。不论是在boosting还是bagging方法中，所使用的多个分类器的类型都是一致的。不同的是，bagging方法通过串行训练获得不同的分类器，每个新分类器都根据以训练出的分类器性能来进行训练；**boosting则是通过集中关注被已有分类器错分的那些数据来获得新的分类器。** boosting方法的分类结果是基于所有分类器的加权求和结果，每个分类结果的权重并不相等，每个权重代表的是其对应分类器在上一轮迭代中的成功度。 boosting方法拥有多个版本，Adaboost就是属于其中一种。 **三. Adaboost：基于错误提升分类器的性能** Adaboost是一种迭代算法，其核心思想是针对同一个训练集训练不同的分类器，即弱分类器，然后把这些弱分类器集合起来，构造一个更强的最终分类器，比起弱分类器，这个“强”分类器的错误率会低很多。 Adaboost算法本身是改变数据分布实现的，它根据每次训练集之中的每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改权值的新数据送给下层分类器进行训练，然后将每次训练得到的分类器融合起来，作为最后的决策分类器。以下给出 Adaboost算法的运行过程： 1. 训练数据中的每个样本，并赋予其一个权重，这些权重构成向量D，一开始时权重D初始化为相等的值； 2. 先在训练样本上训练得到第一个弱分类器并计算分类器的**错误率** ； 3. 在同一数据集上再次训练弱分类器，在分类器的二次训练中，会重新调整每个样本的权重，其中第一次分类正确的样本的权重将会降低，而分类错误的样本权重将会提高 ； 4. 为了从所有弱分类器中得到最终的分类结果，Adaboost为每个分类器都分配了一个权重值alpha，这一组值是基于每个弱分类器的**错误率**进行计算的。 其中，**错误率**由以下公式定义：  而alpha的计算公式如下：  Adaboost算法的流程图如下：  图中的左边表示数据集，其中直方图的不同宽度表示每个样例上的不同权重。在经过一个分类器之后，加权的预测结果会通过三角形中的alpha值进行加权，每个三角形中输出的加权结果在圆形中求和，从而得到最终的输出结果。 计算出alpha值后，**可以对权重向量D进行更新，使得那些正确分类的样本的权重降低而错分样本的权重升高。**计算方法如下： 对于正确分类的样本，其权重更改为：  对于错误分类的样本，其权重更改为：  在计算出权重向量D后，Adaboost方法开始进入下一轮的迭代。Adaboost方法会不断地重复训练和调整权重的过程，知道训练错误率为0（或达到用户指定的条件）为止。 **一个博客给出一种容易理解的解释**：Adaboost的训练过程有如一个学生学习的过程：我们把每个训练样例看做一道练习题，所有的训练样本看做一本习题集。第一次做题的时候，由于每道题都没有做过，不知道哪些难哪些简单，所以一视同仁，做完了对照答案，可能会有很多题目做的不对，那么对于做错的题目，我们就重点标记，给予更高的重视程度，这个用权重w来标示，到第二轮做题的时候就重视这些没做对的“难题”，对于第一次就做对的题目，可以认为是比较简单的，那么第二次的时候稍微看下就可以了，可以降低他的权重。并且，对于第一轮做完以后的效果给一个整体的评分，评价这轮做题的能力，这个就是alpha。在第二轮做题的时候，就按照上一轮调整过的权重对不同的题目给予不同的重视程度和时间分配。如此不断练习，几轮下来，难题就逐渐被攻克了。每轮做题都是有收获的，只不过每次收获的知识权重不同（alpha），这样，我们最后就得到m个分类器，综合每个分类器的权重，我们就能得到一个“学习成绩很好”的分类器了。 **四. 基于单层决策树构建分类器** 使用Python实现： ~~~ def loadSimDat(): dataMat = matrix([[1, 2.1], [2.0, 1.1], [1.3, 1.0], [1.0, 1.0], [2.0, 1.0]]) classLabels = [1.0, 1.0, -1.0, -1.0, 1.0] return dataMat, classLabels # 单层决策树生成函数 def stumpClassify(dataMatrix,dimen,threshVal,threshIneq):#just classify the data retArray = ones((shape(dataMatrix)[0],1)) if threshIneq == 'lt': retArray[dataMatrix[:,dimen] <= threshVal] = -1.0 else: retArray[dataMatrix[:,dimen] > threshVal] = -1.0 return retArray def buildStump(dataArr, classLabels, D): dataMatrix = mat(dataArr); labelMat = mat(classLabels).T m,n = shape(dataMatrix) numSteps = 10.0; bestStump = {}; bestClassEst = mat(zeros((m,1))) minError = inf for i in range(n): rangeMin = dataMatrix[:,i].min(); rangeMax = dataMatrix[:,i].max(); stepSize = (rangeMax - rangeMin)/numSteps for j in range(-1, int(numSteps)+1): for inequal in ['lt','gt']: threshVal = (rangeMin + float(j)*stepSize) predictedVals = stumpClassify(dataMatrix, i, threshVal, inequal) errArr = mat(ones((m,1))) errArr[predictedVals == labelMat] = 0 weightedError = D.T * errArr #这里的error是错误向量errArr和权重向量D的相应元素相乘得到的即加权错误率 #print "split: dim %d, thresh %.2f, thresh inequal: %s, the weighted error is %.3f" %(i, threshVal, inequal, weightedError) if weightedError < minError: minError = weightedError bestClassEst = predictedVals.copy() bestStump['dim'] = i bestStump['thresh'] = threshVal bestStump['ineq'] = inequal return bestStump, minError, bestClassEst ~~~ 下一节将应用Adaboost算法，处理非均衡的分类问题。 参考链接：  [http://blog.csdn.net/lu597203933/article/details/38666303](http://blog.csdn.net/lu597203933/article/details/38666303)  [http://blog.csdn.net/lskyne/article/details/8425507](http://blog.csdn.net/lskyne/article/details/8425507)

该节的内容是支持向量机(SVM, support vectormachine)。 这里首先要推荐一下July的SVM三层境界([http://blog.csdn.net/v_july_v/article/details/7624837](http://blog.csdn.net/v_july_v/article/details/7624837))由于《机器学习实战》关于SVM一章的内容很多，本节先简单归纳一下关于支持向量机的基础。 **一.概念描述** 支持向量机，就是通过最大化支持向量到分类超平面之间的分类间隔。分类超平面就是我们想要得到的决策曲面；支持向量就是离分类超平面最近的点，而间隔即为支持向量到分类超平面的距离。 核函数：这是一种将SVM扩展到更多数据集的方式，一般的说法是，核函数的作用是将数据从低维空间映射到高维空间，使得线性不可分变得线性可分。这句话的意思用个简单的例子来说明： 有：`a1 * x1^2 + a2 * x2^2 + a3 * x1x2 = 0` 此时令：`z1=x1^2,` `z2=x2^2`, `z3=x1x2` 这样就由原来的二维映射到三维空间了，而此时问题变成线性可分了。我们知道，在求解SVM时，**所有的运算都可以写成内积的形式**，但是在高维空间中计算内积往往比较复杂，有时可能出现维数灾难，此时我们就可以把内急运算符换成核函数，从而解决这个问题。 设非线性映射`Φ(x)`将全部原始数据 `x` 变换到另一个特征空间，在训练SVM时，需要计算两个样本间的内积，两个样本`xi`和`xj`对应的高维空间的内积为：`<Φ(xi), Φ(xj)>`，该内积可以通过一个核函数`K(xi, xj)`计算得到。而不用知道这个样本映射Φ(x)是怎样。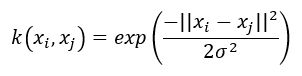径向基函数是SVM中常用的一个核函数：  径向基函数是一个采用向量作为自变量的函数，能够基于向量距离运算输出一个标量。 **二.书中提到的几点** * SVM可能是现成最好的分类器，这里“现成”指的是分类器不加修改即可直接使用。几乎所有的分类问题都可以使用SVM，但是，SVM本身是一个二值分类器，对于多类分类问题，如果需要使用SVM，则需要对代码做一些修改。 * SVM的实现方法有很多，最常用的就是序列最小最优化算法(SMO，Sequential Minimal Optimization) * 支持向量机是一种分类器。之所以称为“机”是因为它会产生一个二值决策结果，即它是一种决策“机”。

**前言：** 生活中，人们经常会遇到各种最优化问题，比如如何在最短时间从一个地点到另外一个地点？如何在投入最少的资金而却能得到最高的受益？如何设计一款芯片使其功耗最低而性能最好？这一节就要学习一种最优化算法——Logistic回归，设计最优化算法的目的依然是用于分类。在这里，**Logistic回归的主要思想是根据现有的数据对分类边界线建立回归公式，达到分类的目的。**假设我们有一堆数据，需要划一条线(最佳直线)对其分类，这就是Logistic回归的目的。 而“Logistic回归”中的“回归”又是代表什么？数学认为，回归是一个拟合过程，回归分析本质上就是一个函数估计的问题，就是找出因变量和自变量之间的因果关系。具体到例子，假设我们有一些数据点，现在使用一条直线对这些点进行拟合，使得这条线尽可能地表示数据点的分布，这个拟合过程就称作“回归”。 在机器学习任务中，训练分类器时就是寻找最佳拟合曲线的过程，因此接下来将使用最优化算法。在实现算法之前，先总结Logistic回归的一些属性： * 优点：计算代价不高，易于理解和实现 * 缺点：容易欠拟合，分类精度可能不高 * 适用的数据类型：数值型和标称型数据 **目录：** 一、基于Sigmoid函数的Logistic回归 1. Sigmoid函数 2. 基于最优化方法的最佳回归系数确定 3. 梯度上升法的实现 4. 随机梯度上升算法的实现 二、一个实例：从疝气病症预测病马的死亡率 1. 准备数据 2. 测试算法，使用Logistic回归进行分类 三、总结 =============================================== **一、基于Sigmoid函数的Logistic回归** **1.Sigmoid函数** Logistic回归想要得到的函数是，能接受所有的输入然后返回预测的类别，比如，在两类情况下函数应输出类别0或1。sigmoid函数可是胜任这一工作，它像是一个阶跃函数。其公式如下：  其中：  向量***w***称为回归系数，也就是我们要找到的最佳参数， ***x***是`n`维的特征向量，是分类器的输入数据。 下面附上书本上的图，该图是函数在不同坐标尺度下的曲线图：  为了实现Logistic回归分类器，我们可以在每个特征上乘以一个回归系数，然后把所有的结果值相加，将这个总和结果代入sigmoid函数中，进而得到一个范围在`0~1`之间的数值。任何大于`0.5`的数据被分入`1`类，小于`0.5`的数据被归入`0`类。所以，Logistic回归也可以被看成是一种概率估计。 **2.基于最优化方法的最佳回归系数确定** 上面提到Sigmoid函数里的一部分：  其中向量***w***称为回归系数，也就是我们要找到的最佳参数， ***x***是`n`维的特征向量，是分类器的输入数据。接下来将介绍几种需找最佳参数的方法： * 梯度上升法：基于的思想是要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻。 * 梯度下降法：与梯度上升的思想相似，但方向相反，即如果要找到某函数的最小值，最好的方法是沿着该函数的梯度方向的反方向寻找。 这里使用梯度上升法，对于一个函数`f(x,y)`，其梯度表示方法如下：  该梯度意味着要沿`x`和`y`的方向分别移动一定的距离，这其实是**确立了算法到达每个点后下一步移动的方向**。其中，函数`f(x,y)` 必须要在待计算的点上有定义并且可微。 **移动方向**确定了，这里我们定义移动的大小为步长，用`α`表示，用向量来表示的话，梯度上升算法的迭代公式如下：  该公式表明，最佳参数***w***的结果收到梯度变化和步长`α`的影响，这个公式将一直被迭代执行，直到满足某个停止条件。 **3.梯度上升法的实现** 以下使用Python实现了梯度上升法，并找到了最佳参数，其中使用的样本数据有`100`个，每个数据包含两个数值型的特征：`X1`和`X2` ，这些数据点可以被绘制成二维散点图。在找出最佳参数***w***后，再编写函数画出不同类别数据之间的分割线，观察最优化算法的效果。 ~~~ # -*- coding: utf-8 -*- """ Created on Sat Sep 12 22:53:07 2015 @author: Herbert """ from numpy import * sys.setrecursionlimit(1500) def loadData(): dataMat = []; labelMat = [] fr = open('testSet.txt') for line in fr.readlines(): lineSplit = line.strip().split() dataMat.append([1.0, float(lineSplit[0]), float(lineSplit[1])]) labelMat.append(int(lineSplit[2])) return dataMat, labelMat def sigmoid(x): return 1.0 / (1 + exp(-x)) def gradAscent(data, label): dataMat = mat(data) labelMat = mat(label).transpose() m, n = shape(dataMat) alpha = 0.001 maxCycles = 500 w = ones((n, 1)) for k in range(maxCycles): p = sigmoid(dataMat * w) error = labelMat - p w = w + alpha * dataMat.transpose() * error return dataMat, labelMat, w data, label = loadData() dataMat, labelMat, w = gradAscent(data, label) print labelMat def plotBestSplit(w): import matplotlib.pyplot as plt dataMat, labelMat = loadData() dataArr = array(dataMat) n = shape(dataArr)[0] xcord1 = []; ycord1 = [] xcord2 = []; ycord2 = [] for i in range(n): if int(labelMat[i]) == 1: xcord1.append(dataArr[i, 1]) # array only ycord1.append(dataArr[i, 2]) else: xcord2.append(dataArr[i, 1]) ycord2.append(dataArr[i, 2]) fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xcord1, ycord1, s = 30, c = 'red', marker = 's') ax.scatter(xcord2, ycord2, s = 30, c = 'blue') x = arange(-3.0, 3.0, 0.1) y = (-w[0] - w[1] * x) / w[2] ax.plot(x, y) plt.xlabel('x1'); plt.ylabel('x2'); plt.show() plotBestSplit(w.getA()) ~~~ 结果如下，可看到使用了Logistic回归的分类结果还是挺不错的，尽管有三四个样本点被错分：  **4.随机梯度上升算法的实现** 梯度上升算法在处理`100`个左右的数据集时尚可，但如果有数十亿样本和成千上万的特征，那么该方法的计算复杂度将变得很恐怖。改进方法为随机梯度上升算法，该方法一次仅用一个样本点来更新回归系数。它占用更少的计算资源，是一种在线算法，可以在数据到来时就完成参数的更新，而不需要重新读取整个数据集来进行批处理运算。一次处理所有的数据被称为批处理。以下代码实现了随机梯度上升算法： ~~~ # 随机梯度上升算法 def stocGradAscent(data, label): m,n = shape(data) alpha = 0.01 w = ones(n) for i in range(m): h = sigmoid(sum(data[i]) * w) error = label[i] - h w = w + alpha * error *data[i] return w wNew = stocGradAscent(data, label) plotBestSplit(wNew) ~~~ 结果：  由上图可以看出，随机梯度上升算法分错了很多样本点，其分类效果并没有原先实现的普通梯度上升算法好。 书中给出的解释是，普通梯度上升算法是在整个数据集上迭代`500`次得到的结果，而随机梯度上升算法只是迭代了`100`次。一个判断算法优劣的可靠方法是看它是否收敛，也就是说求解的参数是否达到了稳定值，是否还会不断变化。 书中给出了一个例子，让随机梯度上升算法在整个数据集上运行`200`次，迭代过程中 **w向量** 的3个参数的变化如下图：  图中，**w**的第二个参数最先达到稳定，而其他两个参数则还需要更多的迭代次数来达到稳定。而我们也发现，在整个迭代过程中，**w**的三个参数都有不同程度的波动。产生这种现象的原因是存在一些被错分的样本点，这些样本在参与每次迭代的过程中都会引起参数的剧烈变化。为了避免这种剧烈波动，并改善算法的性能，采用以下策略对随机梯度上升算法做了改进： * 在每次迭代时更新步长alpha的值，使得alpha的值不断减小，但是不能减少为`0`，这样做的原因是为了保证在多次迭代后新数据仍然具有一定的影响。 * 通过随机采取样本来更新回归参数，这种方法将减少周期性的波动，**每次随机从列表中取一个值，然后该值会从列表中删除。** 实现代码： ~~~ def stocGradAscentAdvanced(data, label, numIter = 150): m,n = shape(data) w = ones(n) for i in range(numIter): dataIndex = range(m) for j in range(m): alpha = 4 / (1.0 + i + j) + 0.01 randIndex = int(random.uniform(0, len(dataIndex))) h = sigmoid(sum(data[randIndex] * w)) error = label[randIndex] - h w = w + alpha * error* array(data[randIndex]) del(dataIndex[randIndex]) return w wNewAdv = stocGradAscentAdvanced(data, label, numIter = 150) plotBestSplit(wNewAdv) ~~~ 在使用了优化策略后，各个回归系数参数的变化情况大幅改善，参数的收敛得更快了：  使用改进后的随机梯度上升算法对样本点进行划分，效果与普通梯度上升算法相当，但其中所用的计算量更少了：  **二、一个实例：从疝气病症预测病马的死亡率** **1.准备数据** 该实例使用Logistic回归来预测患有疝病的马的存活问题。这里的数据来自2010年1月11日的UCI机器学习数据库，其中包含`368`个样本和**28**个特征。**这里的数据集是有`30%`的数据缺失的**。-.- 在实现算法之前，先了解一些关于处理数据中缺失值的方法： * 使用可用特征的均值来填补缺失值； * 使用特殊值来填补缺失值，如-1； * 忽略有缺失值的样本； * 使用相似样本的均值来填补缺失值； * 使用另外的机器学习算法预测缺失值； * 对于类别标签丢失的数据，只能将该数据丢弃。 这里我们使用实数`0`来替换所有缺失的值，这种方法恰好适用于Logistic回归；而对于类别标签丢失的数据，则须将该数据丢弃。 **2.测试算法，使用Logistic回归进行分类** 基于以上工作，以下代码把测试集上的每个特征向量乘以最优化算法得来的回归系数w，再将该乘积结果求和，最后输入到Sigmoid函数，如果对应的Sigmoid函数值大于`0.5`，则将该样本的类别判定为`1`，否则判定为`0`；最后，统计判定结果与实际结果的误差，由于误差具有不确定性，程序最后使用了`10`次分类结果求平均的方法，得出算法的平均分类错误率。 ~~~ def classifyVector(x, w): prob = sigmoid(sum(x * w)) if prob > 0.5: return 1.0 else: return 0.0 def horseColicTest(): frTrain = open('horseColicTraining.txt') frTest = open('horseColicTest.txt') trainingData = []; trainingLabel = [] for line in frTrain.readlines(): currLine = line.strip().split('\t') lineArr = [] for i in range(21): lineArr.append(float(currLine[i])) trainingData.append(lineArr) trainingLabel.append(float(currLine[21])) w = stocGradAscentAdvanced(array(trainingData), trainingLabel, numIter = 500) errorCount = 0.0; numOfTest = 0.0 for line in frTest.readlines(): numOfTest += 1.0 currLine = line.strip().split('\t') lineArr = [] for i in range(21): lineArr.append(float(currLine[i])) if int(classifyVector(array(lineArr), w)) != int(currLine[21]): errorCount += 1 errorRate = float(errorCount) / numOfTest print "The error rate of this test is: %f" % errorRate return errorRate def finalTest(): numOfTest = 10; errorSum = 0.0 for i in range(numOfTest): errorSum += horseColicTest() print "After %d iterations the average error rate is: %f" \ % (numOfTest, errorSum / float(numOfTest)) finalTest() ~~~  分类错误率是`39.4%`，乍一看是挺高的。但如果你知道所使用的数据集是有`30%`的数据缺失的，你就不会这么想了…-.- **三、总结** Logistic回归的目的是寻找一个非线性函数sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。在最优化算法中，最常用的就是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。 随机梯度上升算法和梯度上升算法的效果相当，但占用更少的计算资源。随机梯度上升算法是一种在线算法，可以在数据到来时就完成参数的更新，而不需要重新读取整个数据集来进行批处理运算。

概率是许多机器学习算法的基础，在前面生成决策树的过程中使用了一小部分关于概率的知识，即统计特征在数据集中取某个特定值的次数，然后除以数据集的实例总数，得到特征取该值的概率。 之前的基础实验中简单实现了朴素贝叶斯分类器，并正确执行了文本分类，这一节将贝叶斯运用到实际场景，垃圾邮件过滤这一实际应用。 **实例：使用朴素贝叶斯过滤垃圾邮件** 在上一节：[http://blog.csdn.net/liyuefeilong/article/details/48383175](http://blog.csdn.net/liyuefeilong/article/details/48383175)中，使用了简单的文本文件，并从中提取了字符串列表。这个例子中，我们将了解朴素贝叶斯的一个最著名的应用：电子邮件垃圾过滤。首先看一下如何使用通用框架来解决问题： * 收集数据：提供文本文件，下载地址：[http://download.csdn.net/detail/liyuefeilong/9106481](http://download.csdn.net/detail/liyuefeilong/9106481)，放在工程目录下并解压即可； * 准备数据：将文本文件解析成词条向量； * 分析数据：检查词条确保解析的正确性； * 训练算法：使用我们之前建立的trainNaiveBayes(trainMatrix, classLabel)函数； * 测试算法：使用函数naiveBayesClassify(vec2Classify, p0, p1, pBase)，并且构建一个新的测试函数来计算文档集的错误率； * 使用算法：构建一个完整的程序对一组文档进行分类，将错分的文档输出到屏幕上。 **1.生成贝叶斯分类器** 在上一节已实现，在实现朴素贝叶斯的两个应用前，需要用到之前的分类器训练函数，完整的代码如下： ~~~ # -*- coding: utf-8 -*- """ Created on Tue Sep 08 16:12:55 2015 @author: Administrator """ from numpy import * # 创建实验样本，可能需要对真实样本做一些处理，如去除标点符号 def loadDataSet(): postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']] listClass = [0, 1, 0, 1, 0, 1] # 1代表存在侮辱性的文字，0代表不存在 return postingList, listClass # 将所有文档所有词都存到一个列表中，用set()函数去除重复出现的词 def createNonRepeatedList(data): vocList = set([]) for doc in data: vocList = vocList | set(doc) # 两集合的并集 return list(vocList) def detectInput(vocList, inputStream): returnVec = [0]*len(vocList) # 创建和vocabList一样长度的全0列表 for word in inputStream: if word in vocList: # 针对某段words进行处理 returnVec[vocList.index(word)] = 1 # ? else: print "The word :%s is not in the vocabulary!" % word return returnVec # 贝叶斯分类器训练函数 def trainNaiveBayes(trainMatrix, classLabel): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pBase = sum(classLabel) / float(numTrainDocs) # The following Settings aim at avoiding the probability of 0 p0Num = ones(numWords) p1Num = ones(numWords) p0Denom = 2.0 p1Denom = 2.0 for i in range(numTrainDocs): if classLabel[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p0 = log(p0Num / p0Denom) p1 = log(p1Num / p1Denom) return p0, p1, pBase def trainNaiveBayes(trainMatrix, classLabel): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pBase = sum(classLabel) / float(numTrainDocs) # The following Settings aim at avoiding the probability of 0 p0Num = ones(numWords) p1Num = ones(numWords) p0Denom = 2.0 p1Denom = 2.0 for i in range(numTrainDocs): if classLabel[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p0 = log(p0Num / p0Denom) p1 = log(p1Num / p1Denom) return p0, p1, pBase trainMat = [] for doc in loadData: trainMat.append(detectInput(vocList, doc)) p0,p1,pBase = trainNaiveBayes(trainMat, dataLabel) #print "trainMat : " #print trainMat # test the algorithm def naiveBayesClassify(vec2Classify, p0, p1, pBase): p0res = sum(vec2Classify * p0) + log(1 - pBase) p1res = sum(vec2Classify * p1) + log(pBase) if p1res > p0res: return 1 else: return 0 def testNaiveBayes(): loadData, classLabel = loadDataSet() vocList = createNonRepeatedList(loadData) trainMat = [] for doc in loadData: trainMat.append(detectInput(vocList, doc)) p0, p1, pBase = trainNaiveBayes(array(trainMat), array(classLabel)) testInput = ['love', 'my', 'dalmation'] thisDoc = array(detectInput(vocList, testInput)) print testInput, 'the classified as: ', naiveBayesClassify(thisDoc, p0, p1, pBase) testInput = ['stupid', 'garbage'] thisDoc = array(detectInput(vocList, testInput)) print testInput, 'the classified as: ', naiveBayesClassify(thisDoc, p0, p1, pBase) ~~~ **2.准备数据：切分文本** 首先，编写一个Python函数textSplit()，用来对所有的email文件进行解析并把一篇文章分解为一个个的单词。这里将邮件分为两种，正常的邮件放在路径/email/ham/下，垃圾邮件放在/email/spam/下。以下的代码就是读入文本数据，然后切分，得到词向量，然后将词向量中的词都转换成小写，并把长度大于2的字符串提取出来，写入到文本文件中去，在切分文本的过程中使用了一些技巧，包括正则表达式、将所有字符串转换成小写（.lower()）等等。 ~~~ def textParse(bigString) : # 正则表达式进行文本解析 import re listOfTokens = re.split(r'\W*', bigString) return[tok.lower() for tok in listOfTokens if len(tok) > 2] ~~~ 以下是使用不同的处理对文本进行切分，第一次输出将一些标点符号也划分为单词的一部分；第二部分使用了正则表达式，去除了标点符号，但由于对字符串长度没有限制，因此出现了空字符；第三个输出加入了字符串长度控制，同时将字母全部变成小写。  **3.测试算法：使用朴素贝叶斯进行交叉验证** 该部分将文本解析器集成到一个完整分类器中： ~~~ # 过滤垃圾邮件 def spamTest() : docList = []; classList = []; fullText = [] for i in range(1, 26) : # 导入并解析文本文件，25个普通邮件和25个垃圾邮件 wordList = textParse(open('email/spam/%d.txt' % i).read()) docList.append(wordList) fullText.extend(wordList) classList.append(1) wordList = textParse(open('email/ham/%d.txt' % i).read()) docList.append(wordList) fullText.extend(wordList) classList.append(0) vocabList = createVocabList(docList) trainingSet = range(50); testSet = [] for i in range(10) : # 随机构建训练集，包含10个样本 randIndex = int(random.uniform(0, len(trainingSet))) testSet.append(trainingSet[randIndex]) del(trainingSet[randIndex]) trainMat = []; trainClasses = [] # 用于存放训练集和训练样本的标签 for docIndex in trainingSet : trainMat.append(setOfWords2Vec(vocabList, docList[docIndex])) trainClasses.append(classList[docIndex]) p0V, p1V, pSpam = trainNB0(array(trainMat), array(trainClasses)) errorCount = 0 for docIndex in testSet : # 对测试集进行分类 wordVector = setOfWords2Vec(vocabList, docList[docIndex]) if classifyNB(array(wordVector), p0V, p1V, pSpam) != classList[docIndex]: # 误判 errorCount += 1 print 'the error rate is: ', float(errorCount) / len(testSet) # 输出分类误差 ~~~  **4.小结** 以上代码会对10封随机选择的电子邮件进行分类，并统计分类的错误率。经过多次的运算，平均错误率为6%，这里的错误是指将垃圾邮件误判为正常邮件。相比之下，将垃圾邮件误判为正常邮件要好过将正常邮件误判为垃圾邮件，同时，若提高训练样本个数，可以进一步降低错误率。 算法训练测试的方法是从总的数据集中随机选择数字，将其添加到测试集中，同时将其从训练集中剔除。这种随机选择数据的一部分作为训练集，而剩余部分作为测试集的过程为留存交叉验证（hold-out cross validation）。有时为了更精确地估计分类器的错误率，就应该进行多次迭代后求出平均错误率。

概率是许多机器学习算法的基础，在前面生成决策树的过程中使用了一小部分关于概率的知识，即统计特征在数据集中取某个特定值的次数，然后除以数据集的实例总数，得到特征取该值的概率。 **目录：** * 一.基于贝叶斯理论的分类方法 * 二.关于朴素贝叶斯的应用场景 * 三.基于Python和朴素贝叶斯的文本分类 1.准备数据 2.训练算法 3.测试算法 * 四.小结 **以下进入正文：** **一.基于贝叶斯理论的分类方法** 假设有两类数据组成的数据集如下：  其中，假设两个概率分布的参数已知，并用`p1(x,y)`表示当前数据点`(x,y)`属于类别一的概率；用`p2(x,y)`表示当前数据点`(x,y)`属于类别二的概率。 贝叶斯决策理论的核心思想是：选择高概率所对应的类别，选择具有最高概率的决策。有时也被总结成“多数占优”的原则。 具体到实例，对于一个数据点`(x,y)`，可以用如下规则判定它的类别： 若`p1(x,y)>p2(x,y)`，那么点`(x,y)`被判定为类别一。  若`p1(x,y)<p2(x,y)`，那么点`(x,y)`被判定为类别二。 当然，在实际情况中，单单依靠以上的判定无法解决所有的问题，因为以上准则还不是贝叶斯决策理论的所有内容，使用`p1(x,y)`和`p2(x,y)` 只是为了简化描述。更多的，我们使用`p(ci|x,y)` 来确定给定坐标的点`(x,y)`，该数据点来自类别`ci`的概率是多少。具体地，应用贝叶斯准则可得到，该准则可以通过已知的三个概率值来计算未知的概率值：  则以上判定法则可转化为： 若`p(c1|x,y)>p(c2|x,y)`，那么点`(x,y)`被判定为类别一。  若`p(c1|x,y)<p(c2|x,y)`，那么点`(x,y)`被判定为类别二。 **二.关于朴素贝叶斯的应用场景** 机器学习的一个重要应用就是文档的自动分类，而朴素贝叶斯正是文档分类的常用算法。基本步骤是遍历并记录下文档中出现的词，并把每个词的出现或者不出现作为一个特征。这样便有跟文档中出现过词汇的个数一样多的特征。若有大量特征时，使用直方图效果更好。以下是朴素贝叶斯的一般过程： 1. 收集数据：这里使用RSS源 2. 准备数据：需要数值型&布尔型数据 3. 分析数据：有大量特征时，绘制特征的作用不大，此时使用直方图效果更好 4. 训练算法：计算不同的独立特征的条件概率 5. 测试算法：计算错误率 6. 使用算法：如文档分类 讲到这里，你也许还会带着疑问，为什么贝叶斯前会加上“朴素”，其实，这是基于朴素贝叶斯的一个假设，即：**特征之间相互（统计意义上）独立**，如一个单词出现的可能性与其他单词相邻没有关系，当然这在实际情况中不一定是正确的，但无数实验表明，这种假设是有必要的，而且朴素贝叶斯的实际效果其实很好。 朴素贝叶斯的另外一个假设是：每个特征同等重要。当然，这个假设也有问题（不然就不叫假设了……），但确实有用的假设。 **三.基于Python和朴素贝叶斯的文本分类** 从文本中提取特征，首先需要将文本进行拆分，转化为词向量，某个词存在表示为1，不存在表示为0，这样，原来一大串字符串便转为简单的0，1序列的向量。这种情况下只考虑某个词是否出现，当然，你也可以使用记录词的出现次数作为向量，或者记录不同词出现的频率等等。 1.准备数据：从文本中构建词向量，这里考虑出现在所有文档中的所有单词，并将每一篇文档转化为词汇表上的向量。下面的代码实现了功能，其中： 函数`loadDataSet()` 创建了一些实验样本`postingList`和对应的标签`listClass`，有一些样本被标签为带有侮辱性文字；  函数`createNonRepeatedList()` 统计并保存一个列表`vocList`，该列表包含所有文档中出现的词（不重复），这里使用了Python的`set`函数；  函数`detectInput(vocList, inputStream)`使用了词列表`vocList`， `inputStream`为待检测的word串，输出文档向量，向量的每一元素为`1`或`0`，分别表示词汇表中的单词在输入文档中是否出现。 ~~~ # -*- coding: utf-8 -*- """ Created on Tue Sep 08 16:12:55 2015 @author: Administrator """ from numpy import * # 创建实验样本，可能需要对真实样本做一些处理，如去除标点符号 def loadDataSet(): postingList=[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']] listClass = [0, 1, 0, 1, 0, 1] # 1代表存在侮辱性的文字，0代表不存在 return postingList, listClass # 将所有文档所有词都存到一个列表中，用set()函数去除重复出现的词 def createNonRepeatedList(data): vocList = set([]) for doc in data: vocList = vocList | set(doc) # 两集合的并集 return list(vocList) def detectInput(vocList, inputStream): returnVec = [0]*len(vocList) # 创建和vocabList一样长度的全0列表 for word in inputStream: if word in vocList: # 针对某段words进行处理 returnVec[vocList.index(word)] = 1 # ? else: print "The word :%s is not in the vocabulary!" % word return returnVec ~~~  2.训练算法：从词向量计算概率，将之前的贝叶斯准则中的`(x,y)`改为向量`w`, 其长度为词向量的长度，如以下公式：  计算分为类别`ci`的概率`p(ci)`。通过类别i中的文档数除以总的文档数可计算。及`label_i/sum(label)`。 已知某个类别c，计算w在类别`ci`中的概率`p(w|ci)`。由于朴素贝叶斯假设所有特征相互独立，故有： `p(w|ci) = p(w0,w1,...,wn|ci) = p(w0|ci)*p(w1|ci)*...*p(w0|ci)`计算每个词wj在已知类别i的概率，然后再相乘。 伪代码如下： ~~~ 计算每个类别中的文档数目 对每篇训练文档： 对每个类别： 如果词条出现在文档中 -> 增加该词条的计数值 增加所有词条的计数值 对每个类别： 将该词条的数目除以总词条数目得到条件概率 返回每个类别的条件概率 ~~~ 贝叶斯分类器训练函数代码如下： ~~~ def trainNaiveBayes(trainMatrix, classLabel): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pBase = sum(classLabel) / float(numTrainDocs) # The following Settings aim at avoiding the probability of 0 p0Num = ones(numWords) p1Num = ones(numWords) p0Denom = 2.0 p1Denom = 2.0 for i in range(numTrainDocs): if classLabel[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p0 = log(p0Num / p0Denom) p1 = log(p1Num / p1Denom) return p0, p1, pBase ~~~  3.测试算法：测试分类器的效果 在 `p(w0|ci)*p(w1|ci)*...p(w0|ci)`中，如果某个值为0，则会使得最后的乘积为0，故将所有词初始化为至少出现一次。分母初始化为2，这样不改变实际效果。同时，`p(w0|ci)*p(w1|ci)*...*p(w0|ci)` 取对数，得到：`ln(p(w0|ci))+ln(p(w1|ci))+...+ln(p(w0|ci))`， 由于对数函数`ln(x)`为单调递增函数，因此在计算过程中对乘法取对数对概率曲线的单调性没有影响（高等数学中常用的性质）。修改代码后进行测试： ~~~ def trainNaiveBayes(trainMatrix, classLabel): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pBase = sum(classLabel) / float(numTrainDocs) # The following Settings aim at avoiding the probability of 0 p0Num = ones(numWords) p1Num = ones(numWords) p0Denom = 2.0 p1Denom = 2.0 for i in range(numTrainDocs): if classLabel[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p0 = log(p0Num / p0Denom) p1 = log(p1Num / p1Denom) return p0, p1, pBase trainMat = [] for doc in loadData: trainMat.append(detectInput(vocList, doc)) p0,p1,pBase = trainNaiveBayes(trainMat, dataLabel) #print "trainMat : " #print trainMat # test the algorithm def naiveBayesClassify(vec2Classify, p0, p1, pBase): p0res = sum(vec2Classify * p0) + log(1 - pBase) p1res = sum(vec2Classify * p1) + log(pBase) if p1res > p0res: return 1 else: return 0 def testNaiveBayes(): loadData, classLabel = loadDataSet() vocList = createNonRepeatedList(loadData) trainMat = [] for doc in loadData: trainMat.append(detectInput(vocList, doc)) p0, p1, pBase = trainNaiveBayes(array(trainMat), array(classLabel)) testInput = ['love', 'my', 'dalmation'] thisDoc = array(detectInput(vocList, testInput)) print testInput, 'the classified as: ', naiveBayesClassify(thisDoc, p0, p1, pBase) testInput = ['stupid', 'garbage'] thisDoc = array(detectInput(vocList, testInput)) print testInput, 'the classified as: ', naiveBayesClassify(thisDoc, p0, p1, pBase) testNaiveBayes() ~~~  最后，对两组word串进行检测，第一段被判定为非侮辱性用语，而第二段则被判定为侮辱性用语，分类正确。 **四.小结** 以上实验基本实现了朴素贝叶斯分类器，并正确执行了文本分类，后面要进一步学习，将朴素贝叶斯运用到垃圾邮件过滤、个人广告获取区域倾向等实际应用。

上一节实现了决策树，但只是使用包含树结构信息的嵌套字典来实现，其表示形式较难理解，显然，绘制直观的二叉树图是十分必要的。Python没有提供自带的绘制树工具，需要自己编写函数，结合Matplotlib库创建自己的树形图。这一部分的代码多而复杂，涉及二维坐标运算；书里的代码虽然可用，但函数和各种变量非常多，感觉非常凌乱，同时大量使用递归，因此只能反复研究，反反复复用了一天多时间，才差不多搞懂，因此需要备注一下。 **一.绘制属性图** 这里使用Matplotlib的注解工具annotations实现决策树绘制的各种细节，包括生成节点处的文本框、添加文本注释、提供对文字着色等等。在画一整颗树之前，最好先掌握单个树节点的绘制。一个简单实例如下： ~~~ # -*- coding: utf-8 -*- """ Created on Fri Sep 04 01:15:01 2015 @author: Herbert """ import matplotlib.pyplot as plt nonLeafNodes = dict(boxstyle = "sawtooth", fc = "0.8") leafNodes = dict(boxstyle = "round4", fc = "0.8") line = dict(arrowstyle = "<-") def plotNode(nodeName, targetPt, parentPt, nodeType): createPlot.ax1.annotate(nodeName, xy = parentPt, xycoords = \ 'axes fraction', xytext = targetPt, \ textcoords = 'axes fraction', va = \ "center", ha = "center", bbox = nodeType, \ arrowprops = line) def createPlot(): fig = plt.figure(1, facecolor = 'white') fig.clf() createPlot.ax1 = plt.subplot(111, frameon = False) plotNode('nonLeafNode', (0.2, 0.1), (0.4, 0.8), nonLeafNodes) plotNode('LeafNode', (0.8, 0.1), (0.6, 0.8), leafNodes) plt.show() createPlot() ~~~ 输出结果：  该实例中，`plotNode()`函数用于绘制箭头和节点，该函数每调用一次，将绘制一个箭头和一个节点。后面对于该函数有比较详细的解释。`createPlot()`函数创建了输出图像的对话框并对齐进行一些简单的设置，同时调用了两次`plotNode()`，生成一对节点和指向节点的箭头。 **绘制整颗树** 这部分的函数和变量较多，为方便日后扩展功能，需要给出必要的标注： ~~~ # -*- coding: utf-8 -*- """ Created on Fri Sep 04 01:15:01 2015 @author: Herbert """ import matplotlib.pyplot as plt # 部分代码是对绘制图形的一些定义，主要定义了文本框和剪头的格式 nonLeafNodes = dict(boxstyle = "sawtooth", fc = "0.8") leafNodes = dict(boxstyle = "round4", fc = "0.8") line = dict(arrowstyle = "<-") # 使用递归计算树的叶子节点数目 def getLeafNum(tree): num = 0 firstKey = tree.keys()[0] secondDict = tree[firstKey] for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': num += getLeafNum(secondDict[key]) else: num += 1 return num # 同叶子节点计算函数，使用递归计算决策树的深度 def getTreeDepth(tree): maxDepth = 0 firstKey = tree.keys()[0] secondDict = tree[firstKey] for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': depth = getTreeDepth(secondDict[key]) + 1 else: depth = 1 if depth > maxDepth: maxDepth = depth return maxDepth # 在前面例子已实现的函数，用于注释形式绘制节点和箭头 def plotNode(nodeName, targetPt, parentPt, nodeType): createPlot.ax1.annotate(nodeName, xy = parentPt, xycoords = \ 'axes fraction', xytext = targetPt, \ textcoords = 'axes fraction', va = \ "center", ha = "center", bbox = nodeType, \ arrowprops = line) # 用于绘制剪头线上的标注，涉及坐标计算，其实就是两个点坐标的中心处添加标注 def insertText(targetPt, parentPt, info): xCoord = (parentPt[0] - targetPt[0]) / 2.0 + targetPt[0] yCoord = (parentPt[1] - targetPt[1]) / 2.0 + targetPt[1] createPlot.ax1.text(xCoord, yCoord, info) # 实现整个树的绘制逻辑和坐标运算，使用的递归，重要的函数 # 其中两个全局变量plotTree.xOff和plotTree.yOff # 用于追踪已绘制的节点位置，并放置下个节点的恰当位置 def plotTree(tree, parentPt, info): # 分别调用两个函数算出树的叶子节点数目和树的深度 leafNum = getLeafNum(tree) treeDepth = getTreeDepth(tree) firstKey = tree.keys()[0] # the text label for this node firstPt = (plotTree.xOff + (1.0 + float(leafNum)) / 2.0/plotTree.totalW,\ plotTree.yOff) insertText(firstPt, parentPt, info) plotNode(firstKey, firstPt, parentPt, nonLeafNodes) secondDict = tree[firstKey] plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': plotTree(secondDict[key], firstPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), \ firstPt, leafNodes) insertText((plotTree.xOff, plotTree.yOff), firstPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD # 以下函数执行真正的绘图操作，plotTree()函数只是树的一些逻辑和坐标运算 def createPlot(inTree): fig = plt.figure(1, facecolor = 'white') fig.clf() createPlot.ax1 = plt.subplot(111, frameon = False) #, **axprops) # 全局变量plotTree.totalW和plotTree.totalD # 用于存储树的宽度和树的深度 plotTree.totalW = float(getLeafNum(inTree)) plotTree.totalD = float(getTreeDepth(inTree)) plotTree.xOff = -0.5 / plotTree.totalW plotTree.yOff = 1.0 plotTree(inTree, (0.5, 1.0), ' ') plt.show() # 一个小的测试集 def retrieveTree(i): listOfTrees = [{'no surfacing':{0: 'no', 1:{'flippers':{0:'no', 1:'yes'}}}},\ {'no surfacing':{0: 'no', 1:{'flippers':{0:{'head':{0:'no', \ 1:'yes'}}, 1:'no'}}}}] return listOfTrees[i] createPlot(retrieveTree(1)) # 调用测试集中一棵树进行绘制 ~~~ `retrieveTree()`函数中包含两颗独立的树，分别输入参数即可返回树的参数`tree`，最后执行`createPlot(tree)`即得到画图的结果，如下所示：   书中关于递归计算树的叶子节点和深度这部分十分简单，在编写绘制属性图的函数时，难度在于这本书中一些绘图坐标的取值以及在计算节点坐标所作的处理，书中对于这部分的解释比较散乱。博客：[http://www.cnblogs.com/fantasy01/p/4595902.html](http://www.cnblogs.com/fantasy01/p/4595902.html) 给出了十分详尽的解释，包括坐标的求解和公式的分析，以下只摘取一部分作为了解： 这里说一下具体绘制的时候是利用自定义，如下图： 这里绘图，作者选取了一个很聪明的方式，并不会因为树的节点的增减和深度的增减而导致绘制出来的图形出现问题，当然不能太密集。这里利用整 棵树的叶子节点数作为份数将整个x轴的长度进行平均切分，利用树的深度作为份数将y轴长度作平均切分，并利用plotTree.xOff作为最近绘制的一 个叶子节点的x坐标，当再一次绘制叶子节点坐标的时候才会plotTree.xOff才会发生改变;用plotTree.yOff作为当前绘制的深 度，plotTree.yOff是在每递归一层就会减一份（上边所说的按份平均切分），其他时候是利用这两个坐标点去计算非叶子节点，这两个参数其实就可 以确定一个点坐标，这个坐标确定的时候就是绘制节点的时候 **`plotTree`函数的整体步骤分为以下三步：** 1. 绘制自身 2. 若当前子节点不是叶子节点，递归 3. 若当子节点为叶子节点，绘制该节点 以下是`plotTree`和`createPlot`函数的详细解析，因此把两个函数的代码单独拿出来了： ~~~ # 实现整个树的绘制逻辑和坐标运算，使用的递归，重要的函数 # 其中两个全局变量plotTree.xOff和plotTree.yOff # 用于追踪已绘制的节点位置，并放置下个节点的恰当位置 def plotTree(tree, parentPt, info): # 分别调用两个函数算出树的叶子节点数目和树的深度 leafNum = getLeafNum(tree) treeDepth = getTreeDepth(tree) firstKey = tree.keys()[0] # the text label for this node firstPt = (plotTree.xOff + (1.0 + float(leafNum)) / 2.0/plotTree.totalW,\ plotTree.yOff) insertText(firstPt, parentPt, info) plotNode(firstKey, firstPt, parentPt, nonLeafNodes) secondDict = tree[firstKey] plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD for key in secondDict.keys(): if type(secondDict[key]).__name__ == 'dict': plotTree(secondDict[key], firstPt, str(key)) else: plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), \ firstPt, leafNodes) insertText((plotTree.xOff, plotTree.yOff), firstPt, str(key)) plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD # 以下函数执行真正的绘图操作，plotTree()函数只是树的一些逻辑和坐标运算 def createPlot(inTree): fig = plt.figure(1, facecolor = 'white') fig.clf() createPlot.ax1 = plt.subplot(111, frameon = False) #, **axprops) # 全局变量plotTree.totalW和plotTree.totalD # 用于存储树的宽度和树的深度 plotTree.totalW = float(getLeafNum(inTree)) plotTree.totalD = float(getTreeDepth(inTree)) plotTree.xOff = -0.5 / plotTree.totalW plotTree.yOff = 1.0 plotTree(inTree, (0.5, 1.0), ' ') plt.show() ~~~ 首先代码对整个画图区间根据叶子节点数和深度进行平均切分，并且`x`和`y`轴的总长度均为`1`，如同下图：  **解释如下**： 1.图中的方形为非叶子节点的位置，`@`是叶子节点的位置，因此上图的一个表格的长度应该为： `1/plotTree.totalW`，但是叶子节点的位置应该为`@`所在位置，则在开始的时候 `plotTree.xOff` 的赋值为： `-0.5/plotTree.totalW`，即意为开始`x` 轴位置为第一个表格左边的半个表格距离位置，这样作的好处是在以后确定`@`位置时候可以直接加整数倍的 `1/plotTree.totalW`。 2.plotTree函数中的一句代码如下： ~~~ firstPt = (plotTree.xOff + (1.0 + float(leafNum)) / 2.0/ plotTree.totalW, plotTree.yOff) ~~~ 其中，变量`plotTree.xOff`即为最近绘制的一个叶子节点的`x`轴坐标，在确定当前节点位置时每次只需确定当前节点有几个叶子节点，因此其叶子节点所占的总距离就确定了即为： `float(numLeafs)/plotTree.totalW`，因此当前节点的位置即为其所有叶子节点所占距离的中间即一半为：`float(numLeafs)/2.0/plotTree.totalW`，但是由于开始`plotTree.xOff`赋值并非从`0`开始，而是左移了半个表格，因此还需加上半个表格距离即为：`1/2/plotTree.totalW`，则加起来便为： `(1.0 + float(numLeafs))/2.0/plotTree.totalW`，因此偏移量确定，则`x`轴的位置变为：`plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW` 3.关于`plotTree()`函数的参数 ~~~ plotTree(inTree, (0.5, 1.0), ' ') ~~~ 对`plotTree()`函数的第二个参数赋值为`(0.5, 1.0)`，因为开始的根节点并不用划线，因此父节点和当前节点的位置需要重合，利用2中的确定当前节点的位置为`(0.5, 1.0)`。 **总结**：利用这样的逐渐增加`x` 轴的坐标，以及逐渐降低`y`轴的坐标能能够很好的将树的叶子节点数和深度考虑进去，因此图的逻辑比例就很好的确定了，即使图像尺寸改变，我们仍然可以看到按比例绘制的树形图。 **二.使用决策树预测隐形眼镜类型** 这里实现一个例子，即利用决策树预测一个患者需要佩戴的隐形眼镜类型。以下是整个预测的大体步骤： 1. 收集数据：使用书中提供的小型数据集 2. 准备数据：对文本中的数据进行预处理，如解析数据行 3. 分析数据：快速检查数据，并使用`createPlot()`函数绘制最终的树形图 4. 训练决策树：使用`createTree()`函数训练 5. 测试决策树：编写简单的测试函数验证决策树的输出结果&绘图结果 6. 使用决策树：这部分可选择将训练好的决策树进行存储，以便随时使用 此处新建脚本文件`saveTree.py`，将训练好的决策树保存在磁盘中，这里需要使用Python模块的`pickle`序列化对象。`storeTree()`函数负责把`tree`存放在当前目录下的`filename(.txt)`文件中，而`getTree(filename)`则是在当前目录下的`filename(.txt)`文件中读取决策树的相关数据。 ~~~ # -*- coding: utf-8 -*- """ Created on Sat Sep 05 01:56:04 2015 @author: Herbert """ import pickle def storeTree(tree, filename): fw = open(filename, 'w') pickle.dump(tree, fw) fw.close() def getTree(filename): fr = open(filename) return pickle.load(fr) ~~~ 以下代码实现了决策树预测隐形眼镜模型的实例，使用的数据集是隐形眼镜数据集，它包含很多患者的眼部状况的观察条件以及医生推荐的隐形眼镜类型，其中隐形眼镜类型包括：硬材质`(hard)`、软材质`(soft)`和不适合佩戴隐形眼镜`(no lenses)` ， 数据来源于UCI数据库。代码最后调用了之前准备好的`createPlot()`函数绘制树形图。 ~~~ # -*- coding: utf-8 -*- """ Created on Sat Sep 05 14:21:43 2015 @author: Herbert """ import tree import plotTree import saveTree fr = open('lenses.txt') lensesData = [data.strip().split('\t') for data in fr.readlines()] lensesLabel = ['age', 'prescript', 'astigmatic', 'tearRate'] lensesTree = tree.buildTree(lensesData, lensesLabel) #print lensesData print lensesTree print plotTree.createPlot(lensesTree) ~~~  可以看到，前期实现了决策树的构建和绘制，使用不同的数据集都可以得到很直观的结果，从图中可以看到，沿着决策树的不同分支，可以得到不同患者需要佩戴的隐形眼镜的类型。 **三.关于本章使用的决策树的总结** 回到决策树的算法层面，以上代码的实现基于ID3决策树构造算法，它是一个非常经典的算法，但其实缺点也不少。实际上决策树的使用中常常会遇到一个问题，即**“过度匹配”**。有时候，过多的分支选择或匹配选项会给决策带来负面的效果。为了减少过度匹配的问题，通常算法设计者会在一些实际情况中选择**“剪枝”**。简单说来，如果叶子节点只能增加少许信息，则可以删除该节点。 另外，还有几种目前很流行的决策树构造算法：C4.5、C5.0和CART，后期需继续深入研究。 参考资料：[http://blog.sina.com.cn/s/blog_7399ad1f01014wec.html](http://blog.sina.com.cn/s/blog_7399ad1f01014wec.html)

决策树是个极其易懂的算法，也是最常用的数据挖掘算法，决策树允许机器根据数据集创造规则，其实这就是机器学习的过程。专家系统中经常会使用到决策树及其变种，而且决策树给出的结果往往可以匹敌在当前领域具有几十年工作经验的专家。 * **优点**：决策树的计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据； * **缺点**：可能会产生过度匹配的问题； * **适用数据类型**：数值型和标称型。 这一章节的主要任务是讨论决策树的方法，以及编写构造决策树的python代码，使用递归调用建立分类器，最后可使用Matplotlib绘制决策树图。算法验证部分，对决策树输入一些隐形眼镜的处方数据，并由训练好的分类器预测需要的镜片类型。 以下是决策树的Python实现： 一、首先编写几个函数对数据进行预处理： **1.计算熵函数**：熵代表集合的无序程度，集合越的分布无序，则熵越大； ~~~ from math import log def entropy(sample): log2 = lambda x:log(x)/log(2) results = {} for row in sample: r = row[len(row)-1] results[r] = results.get(r, 0) + 1 ent = 0.0 # entropy for r in results.keys(): p = float(results[r]) / len(sample) ent -= p * log2(p) return ent ~~~ **2.按属性和值获取数据集函数**，可以看到使用python编写的函数十分简洁，该函数的意义是从数据集sample序列中取得第k列的值为v的子集，并从获得的子集中去掉第k列： ~~~ def fetch_subdataset(sample, k, v): return [d[:k] + d[k+1:] for d in sample if d[k] == v] ~~~ **3.计算最大概率属性的相关函数**，在构建决策树时，在处理所有决策属性后，还不能唯一区分数据时，我们采用多数表决的方法来选择最终分类： ~~~ def MaxFeature(classList): classCount = {} for cla in classList: classCount[cla] = classCount.get(cla, 0) + 1 sortedClassCount = sorted(classCount.items(), key=lambda d: d[1], reverse = True) return sortedClassCount[0][0] ~~~ 二.选取最优数据特征划分方式的函数 在构造决策树之前，首先需要评估每个特性的作用，思考以哪一列的值划分集合，从而获得最大的信息增益，以下函数实现了这一功能，输入数据集，输出最优的特征值。 ~~~ def DecisionFeature(sample): ent, feature = 100000000, -1 for i in range(len(sample[0]) - 1): feat_list = [e[i] for e in sample] unq_feat_list = set(feat_list) ent_t = 0.0 for f in unq_feat_list: sub_data = fetch_subdataset(sample, i, f) ent_t += entropy(sub_data) * len(sub_data) / len(sample) if ent_t < ent: ent, feature = ent_t, i return feature ~~~ 三.使用递归构建决策树 ~~~ def buildTree(sample, datalabel): cla = [c[-1] for c in sample] if len(cla) == cla.count(cla[0]): return cla[0] if len(sample[0]) == 1: return MaxFeature(sample) feature = DecisionFeature(sample) featureLabel = datalabel[feature] decisionTree = {featureLabel:{}} del(datalabel[feature]) featValue = [d[feature] for d in sample] UniqueFeatValue = set(featValue) for value in UniqueFeatValue: subLabel = datalabel[:] decisionTree[featureLabel][value] = buildTree( \ fetch_subdataset(sample, feature, value), subLabel) return decisionTree ~~~ 四.使用决策树 ~~~ def classify(decisionTree, featLabels, test): label = decisionTree.keys()[0] next_dict = decisionTree[label] feat_index = featLabels.index(label) for key in next_dict.keys(): if test[feat_index] == key: if type(next_dict[key]).__name__ == 'dict': c_label = classify(next_dict[key], featLabels, test) else: c_label = next_dict[key] return c_label ~~~ 由于时间有限，只能分析到这里，实现结果和实例验证有待进一步讨论。

之前学习了k-近邻算法的实现后，参考《机器学习实战》中的例子进行了k-近邻算法的测验，主要测试了针对约会网站和手写识别系统的数据分类，这两个测试使用的是《机器学习实战》提供的数据集。 在编写函数前，需在.py文件中添加以下内容： ~~~ from numpy import * import numpy as np import operator from os import listdir ~~~ **第一部分是针对约会网站的数据分类**，用于改进约会网站的配对效果。该实例的简介如下： * 海伦一直使用在线约会网站寻找合适自己的约会对象。尽管约会网站会推荐不同的人选，但她没有从中找到喜欢的人。经过一番总结，她发现曾交往过三种类型的人：  1.不喜欢的人（ 以下简称1 ）；  2.魅力一般的人（ 以下简称2 ）；  3.极具魅力的人（ 以下简称3 ） * 尽管发现了上述规律，但海伦依然无法将约会网站推荐的匹配对象归入恰当的分类。她觉得可以在周一到周五约会哪些魅力一般的人，而周末则更喜欢与那些极具魅力的人为伴。海伦希望我们的分类软件可以更好的帮助她将匹配对象划分到确切的分类中。此外海伦还收集了一些约会网站未曾记录的数据信息，她认为这些数据更有助于匹配对象的归类。 * 这里提取一下这个案例的目标：根据一些数据信息，对指定人选进行分类（1或2或3）。为了使用kNN算法达到这个目标，我们需要哪些信息？前面提到过，就是需要样本数据，仔细阅读我们发现，这些样本数据就是“海伦还收集了一些约会网站未曾记录的数据信息 ”。 针对以上的描述，需要进行以下步骤： 1. 收集数据 2. 准备数据 3. 设计算法分析数据 4. 测试算法 **1.收集数据** 海伦收集的数据是记录一个人的三个特征：每年获得的飞行常客里程数；玩视频游戏所消耗的时间百分比；每周消费的冰淇淋公升数。数据是txt格式文件，如下图，前三列依次是三个特征，第四列是分类（1：代表不喜欢的人，2：代表魅力一般的人，3：代表极具魅力的人），每一行数据代表一个人。  **2.准备数据** 计算机需要对数据文件txt读取数据，因此需要把数据进行格式化，对于数学运算，计算机擅长把数据存放在矩阵中。以下代码中`file2matrix(filename)`函数完成了这一工作，该函数输入数据文件名（字符串），输出训练样本矩阵和类标签向量。 这一过程返回两个矩阵：一个矩阵用于存放每个人的三个特征数据，一个矩阵存放每个人对应的分类。 **3.设计算法分析数据** k-近邻算法的思想是寻找测试数据的前k个距离最近的样本，然后根据这k个样本的分类来确定该数据的分类，**遵循“多数占优”原则**。因此，如何寻找样本成为主要的问题，**在信号处理和模式识别领域中，常常使用“距离”来度量信号或特征的相似度**。在这里，我们假定可以使用三个特征数据来代替每个人，比如第一个人的属性我们用[40920， 8.326976， 0.953952]来代替，并且他的分类是3。那么此时的距离就是点的距离。 求出测试样本与训练样本中每个点的距离，然后进行从小到大排序，前k位的就是k-近邻，然后看看这k位近邻中占得最多的分类是什么，也就获得了最终的答案。这一部分是k-近邻算法的核心，代码中`classify()`函数就实现了k-近邻算法的核心部分。 一个优化算法效果的步骤——归一化数据： 打开数据文件我们可用发现第一列代表的特征数值远远大于其他两项特征，这样在求距离的公式中就会占很大的比重，致使两个样本的距离很大程度上取决于这个特征，其他特征的特性变得可有可无，这显然有悖于实际情况。因此通常我们可用使用归一化这一数学工具对数据进行预处理，这一处理过后的各个特征既不影响相对大小又可以不失公平。`Normalize(data)`函数实现了这一功能。 **4.测试算法** 经过了对数据进行预处理后、归一化数值，可用验证kNN算法有效性，测试代码为：`WebClassTest()` 由于数据有1000条，我们设置一个比率`ratio = 0.1`也就是令 `1000 * ratio = 100` 条作为测试样本，其余`900`条作为训练样本，当然，`ratio`的值可用改变，对算法效果是有影响的。 实现代码： ~~~ def classify(data, sample, label, k): SampleSize = sample.shape[0] DataMat = tile(data, (SampleSize, 1)) delta = (DataMat - sample)**2 distance = (delta.sum(axis = 1))**0.5 # sortedDist = distance.argsort() classCount = {} for i in range(k): votedLabel = label[sortedDist[i]] classCount[votedLabel] = classCount.get(votedLabel, 0) + 1 result = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse = True) return result[0][0] #print classify([10,0], sample, label, 3) def file2matrix(filename): fil = open(filename) fileLines = fil.readlines() # Convert the contents of a file into a list lenOfLines = len(fileLines) Mat = zeros((lenOfLines, 3)) classLabel = [] index = 0 for line in fileLines: line = line.strip() listFromLine = line.split('\t') Mat[index,: ] = listFromLine[0:3] classLabel.append(int(listFromLine[-1])) # the last one of listFromLine is Label index += 1 return Mat, classLabel mat,label = file2matrix('datingTestSet2.txt') #print mat # draw import matplotlib import matplotlib.pyplot as plt fil = open('datingTestSet2.txt') fileLines = fil.readlines() # Convert the contents of a file into a list lenOfLines = len(fileLines) figure = plt.figure() axis = figure.add_subplot(111) lab = ['didntLike', 'smallDoses', 'largeDoses'] for i in range(3): n = [] l = [] for j in range(lenOfLines): if label[j] == i + 1: n.append(list(mat[j,0:3])) l.append(label[j]) n = np.array(n) # list to numpy.adarray #reshape(n, (3,k)) axis.scatter(n[:,0], n[:,1], 15.0*array(l), 15.0*array(l), label = lab[i]) print type(mat) print type(n) plt.legend() plt.show() def Normalize(data): minValue = data.min(0) maxValue = data.max(0) ValueRange = maxValue - minValue norm_data = zeros(shape(data)) k = data.shape[0] norm_data = data - tile(minValue, (k, 1)) norm_data = norm_data / tile(ValueRange, (k, 1)) return norm_data, ValueRange, minValue def WebClassTest(): ratio = 0.1 dataMat, dataLabels = file2matrix('datingTestSet2.txt') normMat, ValueRange, minValue = Normalize(dataMat) k = normMat.shape[0] num = int(k * ratio) # test sample : 10% errorCount = 0.0 for i in range(num): result = classify(normMat[i,:], normMat[num:k,:],\ dataLabels[num:k], 7) # k = 3 print "The classifier came back with: %d, the real answer is %d"\ % (result, dataLabels[i]) if (result != dataLabels[i]): errorCount += 1 print "The total error rate is %f " % (errorCount / float(num)) WebClassTest() ~~~ 在程序设计过程中，需要注意list、array、adarray等数据结构的使用，numpy.ndarray和标准Python库类array.array功能是不相同的。以上代码中`print type(mat)`和`print type(n)` 就是为了观察各变量的类型。允许以上代码，可用画出散点图如下：  以上散点使用数据集中第二维和第三维数据绘制而出，当然，你可用选择其他维度的数据画二维散点图，或者使用所有维度的数据画高维图（未实现），如下图所示：  对约会网站分类的测试，由于分类效果依赖于参数k和测试样本占样本数目的比例，开始测试按照书中的参数进行，取`k=3`，测试样本占总样本比例为`0.1`进行测试，结果如下：  理论上来说，增大k的取值可以提高准确率，但实际上若k值太大，也会造成准确率下降，而且运算复杂度增大。 k = 7：  k = 17：  另一方面，降低ratio值（即增大训练样本集的比率）也可以提高算法的准确率，但由于每次算法需要比较更多的样本，因此算法复杂度也会增加。 **第二部分是手写数字识别**： 首先来看看书本给出的数据集： ~~~ def img2vector(filename): returnVect = zeros((1,1024)) fr = open(filename) for i in range(32): lineStr = fr.readline() for j in range(32): returnVect[0,32*i+j] = int(lineStr[j]) return returnVect def handwritingClassTest(): hwLabels = [] trainingFileList = listdir('trainingDigits') #load the training set m = len(trainingFileList) trainingMat = zeros((m,1024)) for i in range(m): fileNameStr = trainingFileList[i] fileStr = fileNameStr.split('.')[0] # take off .txt classNumStr = int(fileStr.split('_')[0]) hwLabels.append(classNumStr) trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr) testFileList = listdir('testDigits') # iterate through the test set errorCount = 0.0 mTest = len(testFileList) for i in range(mTest): fileNameStr = testFileList[i] fileStr = fileNameStr.split('.')[0] # take off .txt classNumStr = int(fileStr.split('_')[0]) vectorUnderTest = img2vector('testDigits/%s' % fileNameStr) classifierResult = classify(vectorUnderTest, trainingMat, hwLabels, 3) # k = 3 print "The classifier came back with: %d, the real answer is: %d"\ % (classifierResult, classNumStr) if (classifierResult != classNumStr): errorCount = errorCount + 1.0 print "\nThe total number of errors is: %d" % errorCount print "\nThe total error rate is: %f" % (errorCount/float(mTest)) handwritingClassTest() ~~~ 一个结果（`k = 3`）：  `k = 7`时的结果，正确率并不比`k = 3`时要好：  在手写数字识别过程中，随着k值得增大，准确率反而降低了。k的取值并不是越大越好。 至此，完成了k-近邻算法的学习和实例验证。比起其他机器学习方法，k-近邻算法是最简单最有效的分类数据算法，使用算法时必须有接近实际数据的训练样本数据。但是如前一节所说的，该算法的缺点也很多，最大的一点是无法给出数据的内在含义。事实上k决策树是k-近邻算法的优化版本，比起前者，决策树有效减少了储存空间和计算空间的开销，后期需继续深入学习！

上一学期主要的学习和研究任务是模式识别、信号理论和图像处理，实际上这些领域都与机器学习有或多或少的交集。因此，仍在继续深入阅读《机器学习》、观看斯坦福大学的机器学习课程。在此过程中因为未来课题组项目的要求，需要接触Python，因此选择了《机器学习实战》这本书，同时参考教材和视频一起学习。事实上该书的理论研究不够深入，只能算是练习Python并验证一些著名的机器学习算法的工具书了。 在介绍k-近邻算法之前，对机器学习算法进行简单的分类和梳理：简单来说，机器学习主要分为两大类，有监督学习(supervised learning)和无监督学习(unsupervised learning)。有监督学习又可分两类：分类（classification.）和回归（regression），分类的任务就是把一个样本划为某个已知类别，每个样本的类别信息在训练时需要给定，比如人脸识别、行为识别、目标检测等都属于分类。回归的任务则是预测一个数值，比如给定房屋市场的数据（面积，位置等样本信息）来预测房价走势。而无监督学习也可以成两类：聚类（clustering）和密度估计（density estimation）,聚类则是把一堆数据聚成弱干组，没有类别信息；密度估计则是估计一堆数据的统计参数信息来描述数据,比如深度学习的RBM。 作为开头章节，作者介绍了简单而容易理解的k-近邻(kNN)算法。该算法在模式识别一书中与Parzen窗估计放在一起讲，属于非参数估计的方法。这类方法用于处理任意形式的概率分布而不必事先考虑概率密度的参数形式。 更多关于非参数估计方法的介绍：[http://blog.csdn.net/liyuefeilong/article/details/45274325](http://blog.csdn.net/liyuefeilong/article/details/45274325) 在使用k-近邻算法前，需要了解算法的优缺点和适用性：  优点：精度高，对异常数据不敏感，无数据输入假定  缺点：时间和空间复杂度均较高  适用的数据类型：数值型和标识型 基本K均值算法的基本思路为：首先你需要有一组训练样本，也称作训练样本集。该集合中每个样本的分类类别都是已知的，也就是我们知道每个数据与所属分类的对应关系。此时，可以输入一个待预测的数据，将新数据的每个特征与训练样本集中每个数据的特征进行比较，根据一种比较结果（如欧氏距离），找出`k` 个与待预测数据最相似的训练样本，看看这些训练样本都是属于哪一类的，最后就是秉承“多数占优”的原则：既然待预测数据与很多个某A类的训练样本都很近，和其他类不是很相近，那就把预测数据判定为A类吧。 在以上描述中提出使用欧氏距离作为待预测数据和训练样本集的比较结果，即假设测试样本为`a`，而`xi`表示训练样本集中的第`i`个样本，测试样本和训练样本均有`n`个特征属性，则测试样本和训练样本之间的欧氏距离定义为：  通常该算法的k是不大于20的正整数。当`k=7` 时，根据上述欧氏距离公式计算出78个与待预测数据最近的训练样本，在这7个实例中，某个分类出现的次数最多，则预测数据就被分到该类。 以下是根据《机器学习实战》一书写的代码，直接实现了k-近邻算法，由于对python不十分熟悉，因此对于kNN的算法实现难度主要存在于Numpy的使用上，但毕竟这是学习python的一个好机会，以下为算法的代码实现： ~~~ # -*- coding: utf-8 -*- """ Created on Sat Aug 29 14:36:02 2015 Input: data: vector of test sample (1xN) sample: size m data set of known vectors (NxM) labels: labels of the sample (1xM vector) k: number of neighbors Output: the class label @author: peng__000 """ from numpy import * import operator from os import listdir # training samples sample = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]]) # the labels of samples label = ['A', 'A', 'B', 'B'] def classify(data, sample, label, k): SampleSize = sample.shape[0] # 训练样本集的行数 DataMat = tile(data, (SampleSize, 1)) #将data扩展到和训练样本集sample一样的行数 delta = (DataMat - sample)**2 distance = (delta.sum(axis = 1))**0.5 # 以上三步计算欧氏距离 sortedDist = distance.argsort() # 对欧氏距离向量进行排序 classCount = {} # 以下操作获取距离最近的k个样本的标签 for i in range(k): votedLabel = label[sortedDist[i]] classCount[votedLabel] = classCount.get(votedLabel, 0) + 1 result = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse = True) return result[0][0] print classify([10,0], sample, label, 3) # test ~~~ 这段简短的代码除了一些矩阵的操作、简单的排序操作外没有复杂的运算。 在简单完成k-近邻算法的实现后，接下来需要将算法的应用到别的场景，根据书本《机器学习实战》上的教程，主要测试了针对约会网站的分类和手写识别系统。 总的来说，k-近邻算法是模式识别和机器学习领域中最简单且最有效的分类算法，缺点是运算速度差强人意，而且在算法执行过程中须保存全部数据集，如果训练数据集非常巨大，必须使用大量的存储空间，此时算法的性能会大大降低。k-近邻算法的另一个缺陷是无法给出任何数据的基础结构信息，因此也无法知晓平均实例样本和典型实例样本具有什么样的特征。通过实验过程也可以发现，对参数的选取和调整要根据实际情况进行多次实验才能达到比较理想的效果。

> 原文出处：[《机器学习实战》笔记专栏文章](http://blog.csdn.net/column/details/machinglearninginact.html) > 作者：[谢浩鹏](http://blog.csdn.net/liyuefeilong) **本系列文章经作者授权在看云整理发布，未经作者允许，请勿转载！** # 《机器学习实战》笔记 > 机器学习是人工智能研究领域中一个极其重要的研究方向，在现今的大数据时代背景下，捕获数据并从中获取有价值的信息或模式，成为各行业求生存、谋发展的决定性手段，这使得这一过去为分析师和数学家所专属的领域越来越为人们所瞩目。