* [How to program a Gaussian Blur without using 3rd party libraries](http://www.swageroo.com/wordpress/how-to-program-a-gaussian-blur-without-using-3rd-party-libraries/)

如果一个点处于边界，周边没有足够的点，怎么办？ 一个变通方法，就是把已有的点拷贝到另一面的对应位置，模拟出完整的矩阵。

有了权重矩阵，就可以计算高斯模糊的值了。 假设现有9个像素点，灰度值（0-255）如下：  每个点乘以自己的权重值：  得到  将这9个值加起来，就是中心点的高斯模糊的值。 对所有点重复这个过程，就得到了高斯模糊后的图像。如果原图是彩色图片，可以对RGB三个通道分别做高斯模糊。

假定中心点的坐标是（0,0），那么距离它最近的8个点的坐标如下：  更远的点以此类推。 为了计算权重矩阵，需要设定σ的值。假定σ=1.5，则模糊半径为1的权重矩阵如下：  这9个点的权重总和等于0.4787147，如果只计算这9个点的加权平均，还必须让它们的权重之和等于1，因此上面9个值还要分别除以0.4787147，得到最终的权重矩阵。 

上面的正态分布是一维的，图像都是二维的，所以我们需要二维的正态分布。  正态分布的密度函数叫做["高斯函数"](http://en.wikipedia.org/wiki/Gaussian_function)（Gaussian function）。它的一维形式是：  其中，μ是x的均值，σ是x的方差。因为计算平均值的时候，中心点就是原点，所以μ等于0。  根据一维高斯函数，可以推导得到二维高斯函数：  有了这个函数 ，就可以计算每个点的权重了。

正态分布显然是一种可取的权重分配模式。  在图形上，正态分布是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。 计算平均值的时候，我们只需要将"中心点"作为原点，其他点按照其在正态曲线上的位置，分配权重，就可以得到一个加权平均值。

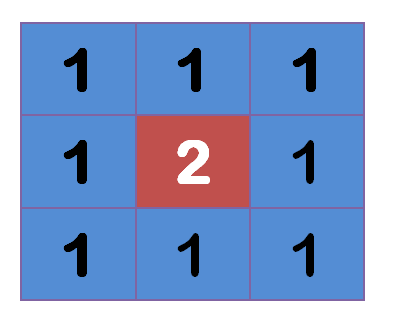
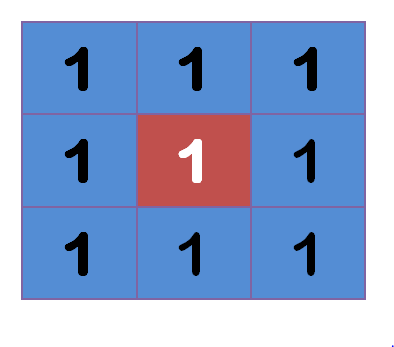
所谓"模糊"，可以理解成每一个像素都取周边像素的平均值。  上图中，2是中间点，周边点都是1。  "中间点"取"周围点"的平均值，就会变成1。在数值上，这是一种"平滑化"。在图形上，就相当于产生"模糊"效果，"中间点"失去细节。  显然，计算平均值时，取值范围越大，"模糊效果"越强烈。  上面分别是原图、模糊半径3像素、模糊半径10像素的效果。模糊半径越大，图像就越模糊。从数值角度看，就是数值越平滑。 接下来的问题就是，既然每个点都要取周边像素的平均值，那么应该如何分配权重呢？ 如果使用简单平均，显然不是很合理，因为图像都是连续的，越靠近的点关系越密切，越远离的点关系越疏远。因此，加权平均更合理，距离越近的点权重越大，距离越远的点权重越小。

> 原文出处：http://www.ruanyifeng.com/blog/2012/11/gaussian_blur.html > 作者：阮一峰 通常，图像处理软件会提供"模糊"（blur）滤镜，使图片产生模糊的效果。  "模糊"的算法有很多种，其中有一种叫做["高斯模糊"](http://en.wikipedia.org/wiki/Gaussian_blur)（Gaussian Blur）。它将[正态分布](http://zh.wikipedia.org/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83)（又名"高斯分布"）用于图像处理。  本文介绍"高斯模糊"的算法，你会看到这是一个非常简单易懂的算法。本质上，它是一种[数据平滑技术](http://en.wikipedia.org/wiki/Smoothing)（data smoothing），适用于多个场合，图像处理恰好提供了一个直观的应用实例。