（5）上下文无关文法，及其语法树

首先我们回顾一下上篇的内容，上篇讲述了四种类型的文法，0型1型2型3型，他们要求的规则越来越严格。 **开始教程**： 本篇着重讲解上下文无关文法及其语法树，因为对于计算机程序来讲，上下文无关文法表达能力足够强，来表达大多数程序语言的语法。 描述一种上下文无关的推导工具：**句型的推导和语法树（推导树）** 给定文法G（VN,VT,P ,S）,对于G的任何句型都能构造与之关联的语法树。**这棵树满足下面四个条件**： ① 每个结点都有一个标记，此标记是V的 一个符号。（说的是节点一定是终结符或非终结符） ② 根的标记是S。（说的是树根的标记是开始符号S） ③ 若一结点标记A,至少有一个从它出发的分枝，则A肯定在VN中（说的是如果一个节点有分支的话，这个节点一定是非终结符） ④ 如果标记为A，有n个从它出发的分枝，并且这些分枝的结点的标记（从左到右）为B1, B2，…，Bn，那么A→B1B2，…，Bn一定是P中的一个产生式。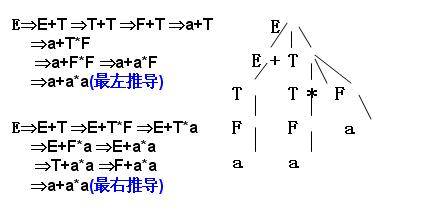（说的是从A出发的叶子节点从左到右排列，一定是P中规则的一个产生式） 例1: 文法G[S]: S→aAS A→SbA A→SS S→a A→ba 写出aabbaa句型的推导过程： （１）Ｓ＝＞aAS=>aAa=>aSbAa=>aSbbaa=>aabbaa(最右推导）（最右推（２）Ｓ＝＞aAS=>aSbAS=>aabAS=>aabbaS=>aabbaa(最左推导）（最左推导，就是从最左侧的非终结符开始） 例2： G[E]：        E→E+T|T                      T→T*F|F                      F→(E)|a                      判断a+a*a         是否是合法的句子,采用最左推导和最右推导 　　　　Ｅ＝＞Ｅ＋Ｔ＝＞Ｔ＋Ｔ＝＞Ｆ＋Ｔ＝＞a＋Ｔ＝＞a+Ｔ*Ｆ                 ＝＞a＋Ｆ＊Ｆ＝＞a＋a＊Ｆ=>a＋a*a(最左推导） 　　　　Ｅ＝＞Ｅ+Ｔ＝＞Ｅ＋Ｔ＊Ｆ＝＞Ｅ＋Ｔ＊a＝＞Ｅ＋Ｆ＊a                 =>Ｅ＋a*a＝＞Ｔ＋a*a＝＞Ｆ＋a*a＝＞a+a*a(最右推导） 书上规定，**最右推导又称为规范推导，规范推导推导出的句型又称为规范句型**。 **构造上述句型的语法树：** 画出a+a*a句型的语法树                              E→E+T|T                   T→T*F|F                  F→(E)|a  注:上面的例子来自网络。 而一个语法树可以表示可能的不同推导过程，包括最右推导和最左推导。但是一个句型是否对应唯一的一颗语法树呢？一个句型是否只有唯一的一个最左推导（最右推导）？答案是否定的，下面我们讲述二义文法。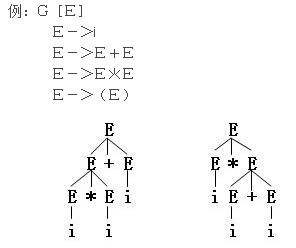 看看下面的文法推导树：  **二义文法的定义**： 若一个文法存在某个句子对应两棵不同的语法树，则称这个文法是二义的，或一个文法有两个不同的最左推导，则称这个文法是二义的。 当然我们不希望程序的某些文法是二义的，希望对程序的每个句子的分析是唯一的。 本篇到此结束，下篇讲述句型的简单分析。 愿开心阅读，一起掌握知识(*^__^*) 。