随机背景

> 原文出处：http://www.w3cplus.com/css3/css-secrets/random-backgrounds.html ## 问题 虽然平铺几何图形很棒，但看起来还是有点乏味。**而在自然界中，万事万物皆有不同。**即使是在相似中，也充满了变化和随机因素。你可以看一看花圃：虽然花朵具有一致的艳丽，但也各有各的亮点。这个世界上没有任何两朵花是相同的。这就是为什么我们要尝试让背景图案接近真实，而且我们也在尝试让平铺的元素之间尽量减少缝隙，让它们显得浑然天成自成一体，但是这也会让样式文件的大小超出我们的预期。 > 当你发现了某些独特的特性——比如木头纹理上特定距离就会出现的结，就会打破随机性这种感觉 — Alex Walker, [The Cicada Principle and Why It Matters to Web Designers](http://sitepoint.com/the-cicada-principle-and-why-it-matters-to-web-designers) 模拟随机是一件非常具有挑战性的事情，因为 CSS 并没有任何创造随机性的能力。让我们重新拿起条纹这个示例，假设我们想要得到拥有各种颜色和宽度的垂直条纹（让我们简化为四种颜色吧），并且还要让它们之间过渡自然。我们的第一个想法可能就是创建一个渐变： ~~~ background: linear-gradient(90deg, #fb3 15%, #655 0, #655 40%, #ab4 0, #ab4 65%, hsl(20, 40%, 90%) 0); background-size: 80px 100%; ~~~ 就像下图看到的那样  *图注：实现伪随机条纹的初次尝试，其中所有的颜色都是由相同的线性渐变生成的* 非常明显就分辨出了重复元素，这主要是因为它只重复了 `80px`（`background-size`）。我们可以做得更好吗？ ## 解决方案 对于这一问题，我的第一个想法就是将整个的条纹分成不同块，然后增加这些块的随机性：一个基色和三个条纹层，在不同的距离上实现平铺。通过硬编码颜色过渡点的位置，我们可以改变条纹的宽度，通过使用 `backgroud-size`，我们可以控制间距，最终就能实现上面的初步设想了： ~~~ background: hsl(20, 40%, 90%); background-image: linear-gradient(90deg, #fb3 10px, transparent 0), linear-gradient(90deg, #ab4 20px, transparent 0), linear-gradient(90deg, #655 20px, transparent 0); background-size: 80px 100%, 60px 100%, 40px 100%; ~~~ 因为最顶层的平铺将会最容易被注意到（因为它覆盖了所有的图层），所以我们对最上面的一层施加最大的间歇性间距（在本例中，就是桔黄色条纹）。  *图注：第二次尝试，通过不同的 `background-size` 让不同的图层发生重叠；虚线框内的图案是用来平铺的图案* 正如上图中所看到的那样，整体看起来随机多了，但如果我们仔细观察，还是能意识到每 `240px` 就会有一次重复。也就是说，在此类组合中，所有重复块的偏移量就是第一个非重复条纹终点位置的一倍或数倍。也许你还记得在学校里我们学过的最小公倍数（LCM，Least Common Multiple），它是一个整数集合中所有整数的一倍或多倍。因此，这里条纹块的大小就是背景大小的最小公倍数，即 `40/60/80`，它们的最小公倍数就是 `240`。 上面的示例就遵循了这一不易察觉的随机性，所以我们需要增大平铺条纹块的大小。感谢数学的存在，无需漫长和痛苦的计算我们就可以实现它，因为我们已经知道了答案。为了达到最大的最小公倍数，那么这些数之间必须互质。在本例中，最小公倍数就是由它们得出来的。比如，`3/4/5` 就互为质数，所以它们的最小公倍数就是 `3 × 4 × 5 = 60`。让数值互为质数的最简单方式就是让它们是质数，在数学上质数和其他任何数都互为质数。质数的列表在网络上随处可见。 为了保持最大的随机性，我们甚至使用质数来设计条纹的宽度。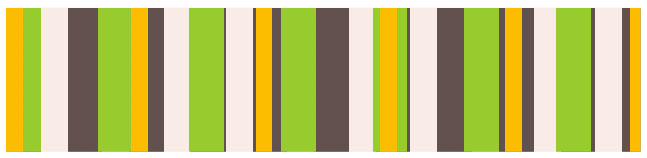这就是我们的代码： ~~~ background: hsl(20, 40%, 90%); background-image: linear-gradient(90deg, #fb3 11px, transparent 0), linear-gradient(90deg, #ab4 23px, transparent 0), linear-gradient(90deg, #655 41px, transparent 0); background-size: 41px 100%, 61px 100%, 83px 100%; ~~~ 是的，代码很难看，但是效果如下图所示：  *图注：最终的条纹，使用质数来增加随机性* 现在我们的条纹至少 `41 × 61 × 83 = 207583px` 才会平铺一次，完全超出了一个屏幕分辨率所能容纳的数量。 上面的技巧（使用质数增加背景平铺时的随机性）被称为 “The Cicada Principle”，由 Alex Walker 第一次提出。值得注意的是，这不仅仅对背景有用，而且对需要平铺的任何事情都有用。其他的应用包括但不限于： * 为一个图库中图片的旋转角度增加一点点随机性，可以使用 `:nth-child(an)` 选择器，其中 `a` 为质数。 * 为动画的运动过程添加一些随机性，那么可以添加多个以质数为时间长度的持续时间（点击这里查看[示例](http://codepen.io/airen/pen/WQoBRR)） > 向提出这一技巧的 Alex Walker 致敬， [The Cicada Principle and Why It Matters to Web Designers](http://www.sitepoint.com/the-cicada-principle-and-why-it-matters-to-web-designers/)。 [Eric Meyer](http://meyerweb.com/) 随后提出了 [Cicadients](http://meyerweb.com/eric/thoughts/2012/06/22/cicadients/) 这一概念, 其中就包含了将该技巧通过 CSS 渐变添加到背景图片上。Dudley Storey 也就该概念发表了[大量非常有价值的文章](http://demosthenes.info/blog/840/Brood-X-Visualizing-The-Cicada-Principle-In-CSS). ## 总结 前面介绍的内容，不管是使用渐变实现的线性渐变还是径向渐变，或者说是复杂的纹理背景，都是具有一定的规律性。在这一节中主要向大家阐述了如何实现随机性的背景图效果。