模式识别:利用MATLAB生成模式类
最后更新于:2022-04-01 06:47:21
最近开始了模式识别的学习,在此之前需要对模式和模式类的概念有一个了解,这里使用MATLAB实现一些模式类的生成。在此之前,引用百科上对于模式识别和模式类的定义,也算加深以下了解:
>模式识别(Pattern Recognition):人类在日常生活的每个环节,从事着模式识别的活动。可以说每个有正常思维的人,在他没有入睡时都在进行模式识别的活动。坐公共汽车找汽车站,骑车判别可行进道路,对观察到的现象作出判断,对听到的声音作出反应,判断东西的好与坏以及水果的成熟与否等等都是人们判断是非,判别事物的过程。但是对模式识别这个词就显得陌生而难以理解了。确切地说,模式识别在这里是针对让计算机来判断事物而提出的,如检测病理切片中是否有癌细胞,文字识别,话语识别,图像中物体识别等等。该学科研究的内容是使机器能做以前只能由人类才能做的事,具备人所具有的、对各种事物与现象进行分析、描述与判断的部分能力。
模式类与模式,或者模式与样本在集合论中是子集与元素之间的关系。当用一定的度量来衡量两个样本,而找不出它们之间的差别时,它们在这种度量条件下属于同一个等价类。这就是说它们属于同一子集,是一个模式,或一个模式类。而不同的模式类之间应该是可以区分的,它们之间应有明确的界线。但是对实际样本来说,有时又往往不能对它们进行确切的划分,即在所使用的度量关系中,分属不同的类别的样本却表现出相同的属性,因而无法确凿无误地对它们进行区分。例如在癌症初期,癌细胞与正常细胞的界线是含糊的,除非医术有>了进一步发展,能找到更准确有效的分类方法。
下面是练习:
在Matlab 中提供了很多产生随机数和随机向量的函数,以及计算随机函数的概率密度值的函数。下面是几个较常用的函数:
rand() 生成均匀分布随机数
randn() 生成高斯分布随机数
mvnrnd() 生成多元高斯分布的随机向量矩阵
mvnpdf() 计算多元高斯分布的概率密度函数值
在阅读了上述函数的MATLAB在线帮助后,完成下面的程序实现,分为三个练习:
练习一:在一维区间[10,70]中,生成1000个均匀分布的随机数,然后统计并绘制这些数的直方图;在二维区间[1,5]☓[20,30]中,生成5000 个均匀分布的二维随机点,并绘制出它们的二维散点图;在三维区间[10,50]☓[30,60]☓[10,15]中,生成10000 个均匀分布的三维随机点量,并绘制出它们的三维散点图。
~~~
% rand()生成区间[10,70]的1000个随机数
% 并显示直方图
for i = 1:1000
a(i) = rand() * 60 + 10;
end
b = hist(a, 10:70);
figure,bar(10:70, b, 'g');
grid on
title('rand()产生1000个[10,70]的随机数直方图');
for k = 1:5000
TwoDimension(k,1) = rand() * 4 + 1;
TwoDimension(k,2) = rand() * 10 + 20;
end
figure,plot(TwoDimension(:,1), TwoDimension(:,2), '*');
xlim([0 6]);
ylim([10 40]);
grid on
title('在[1,5]*[20,30]中产生5000个均匀分布的二维随机点');
for j = 1:10000
ThreeDimension(j,1) = rand() * 40 + 10;
ThreeDimension(j,2) = rand() * 30 + 30;
ThreeDimension(j,3) = rand() * 5 + 10;
end
figure,scatter3(ThreeDimension(:,1),ThreeDimension(:,2),ThreeDimension(:,3),'r');
xlim([0 60]);
ylim([20 70]);
zlim([0 20]);
grid on;
title('产生10000个均匀分布的三维随机点');
~~~
输出一维、二维和三维随机点生成效果(边界限定参照要求):
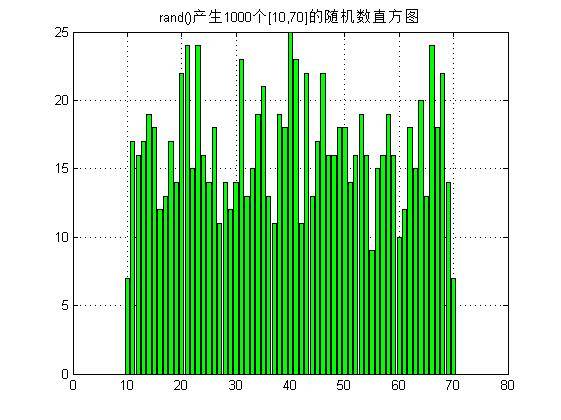
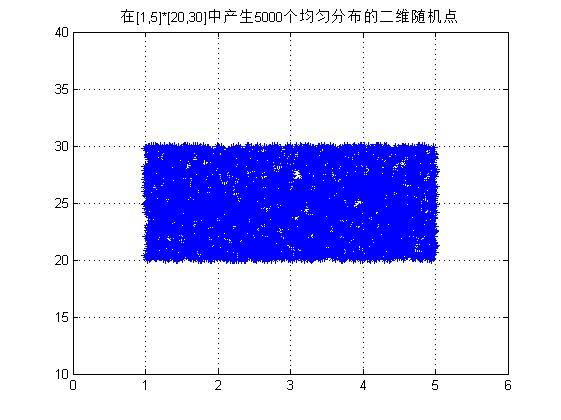
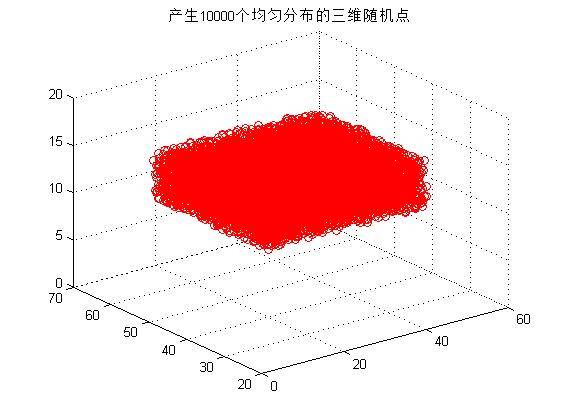
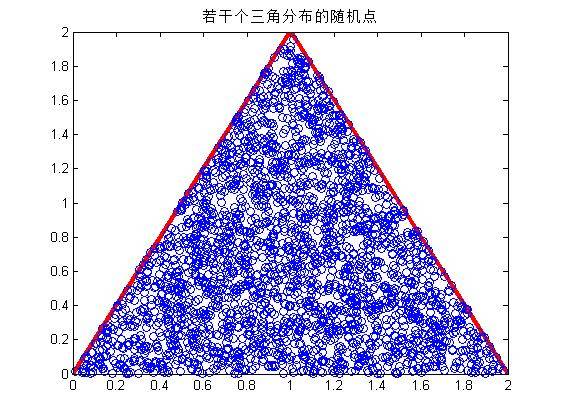
下面是在练习一基础上的扩展:利用均匀分布的随机数函数,编写可以生成具有三角分布、以及梯形分布的随机数的函数。用它们生成一定数量的样本数据,并绘制数据分布图。
~~~
% 产生5000个随机点,然后根据公式剔除三角形外的点
n = 5000;
x = rand(n,2) * 2;
% 变量名 = @(输入参数列表)运算表达式
fx = @(x)(x < 1).*(2*x)+(x >= 1).*(4-2*x);
g=0:0.2:2;
y=fx(g);
% 绘制边界直线,设定直线粗细
figure,plot(g,y,'r-','linewidth',3);
hold on
% 判断元素在y轴上的值是否超出三角形的边界
% 对边界外的点标记为一个值
for t = 1:n
if x(t,2) > fx(x(t,1))
x(t,:) = [0, 0];
end
end
% 扫描标定的值并删除这些元素,剩下边界内的元素
for t = n:-1:1
if x(t,:) == [0, 0]
x(t,:) = [];
end
end
plot(x(:,1),x(:,2),'o');
title('若干个三角分布的随机点');
% 绘制随机点分布直方图
[f, y] = hist(x(:,1), g);
figure,bar(y,f,1);
title('随机点分布直方图');
% 产生5000个随机点,然后根据公式剔除梯形外的点
n = 5000;
x = rand(n,2) * 3;
% 变量名 = @(输入参数列表)运算表达式
fx = @(x)(x <= 1).*(3*x)+( x > 1 & x <= 2).*3 + (x > 2).*(9-3*x);
g=0:0.1:3;
y=fx(g);
% 绘制边界直线,设定直线粗细
figure,plot(g,y,'r-','linewidth',3);
hold on
% 判断元素在y轴上的值是否超出梯形的边界
% 对边界外的点标记为一个值
for t = 1:n
if x(t,2) > fx(x(t,1))
x(t,:) = [0, 0];
end
end
% 扫描标定的值并删除这些元素,剩下边界内的元素
for t = n:-1:1
if x(t,:) == [0, 0]
x(t,:) = [];
end
end
plot(x(:,1),x(:,2),'o');
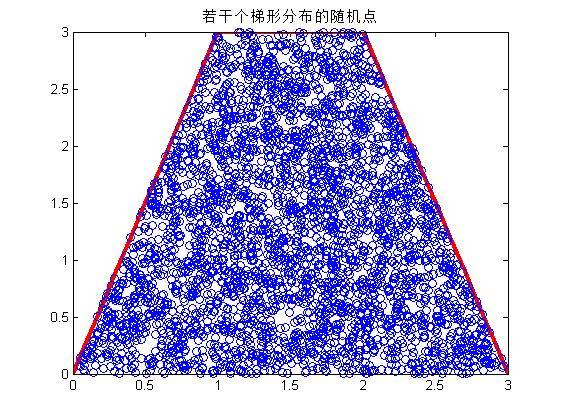
title('若干个梯形分布的随机点');
% 绘制随机点分布直方图
[f, y] = hist(x(:,1), g);
figure,bar(y,f,1);
title('随机点分布直方图');
~~~
输出三角分布和梯形分布的随机点结果、直方图:


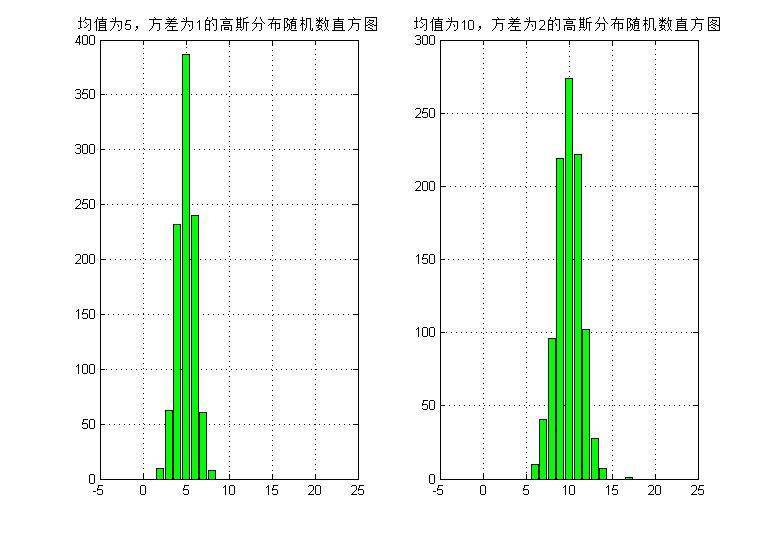
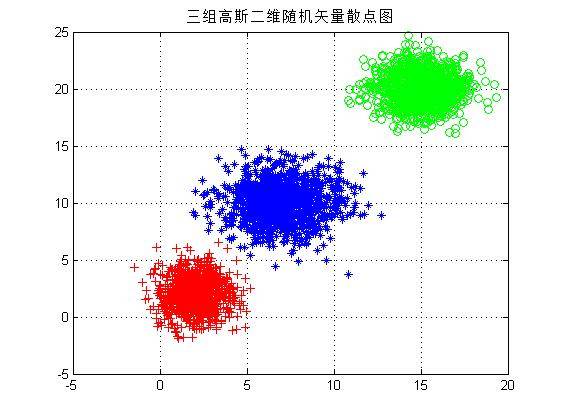
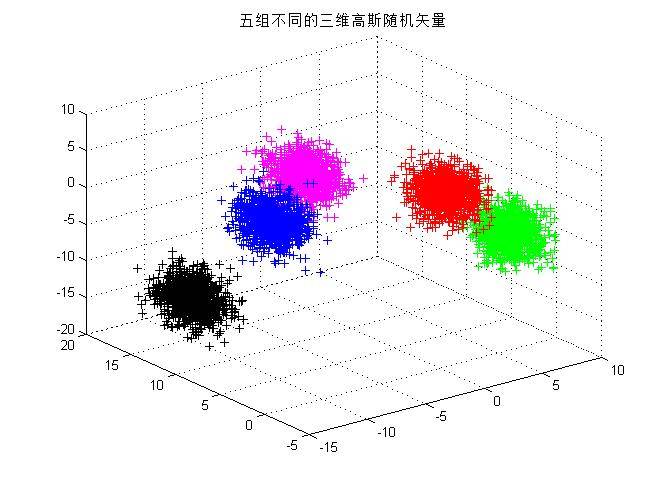
练习二:生成两组各1000个具有不同均值和方差的一维高斯分布的随机数,然后统计并绘制这些点的直方图;生成三组各1000 个具有不同均值矢量和协方差矩阵的二维随机矢量,并绘制出它们的二维散点图;生成五组各1000个具有不同均值矢量和协方差矩阵的三维随机矢量,并绘制出它们的三维散点图。进一步,绘制上述三维随机矢量数据集合的二维投影散点图。可以指定模式向量的其中两个分量,将集合中每个向量的这两个分量提取出来构成一个2维模式子分量的向量集合,然后在二维平面上画出该子分量集合的二维散点图。
~~~
% 使用randn()两组1000个随机数
% 并显示直方图
% 产生一个随机分布的指定均值和方差的矩阵:将randn产生的结果乘以标准差,然后加上期望均值即可。
for i = 1:1000
Gaussian(i,1) = sqrt(1) * randn() + 5;
Gaussian(i,2) = sqrt(2) * randn() + 10;
end
G1 = hist(Gaussian(:,1), 0:20);
G2 = hist(Gaussian(:,2), 0:20);
figure,subplot(1,2,1),bar(0:20, G1, 'g');
grid on
title('均值为5,方差为1的高斯分布随机数直方图');
subplot(1,2,2),bar(0:20, G2, 'g');
grid on
title('均值为10,方差为2的高斯分布随机数直方图');
% mvnrnd(mu,sigma,n)
% 产生二维正态随机数,mu为期望向量,sigma为协方差矩阵,n为规模。
mu = [2 2];
sigma = [1 0; 0 2];
r = mvnrnd(mu,sigma,1000);
figure,plot(r(:,1),r(:,2),'r+');
hold on;
mu = [7 10];
sigma = [ 3 0; 0 3];
r2 = mvnrnd(mu,sigma,1000);
plot(r2(:,1),r2(:,2),'b*')
hold on;
mu = [15 20];
sigma = [ 2 0; 0 2];
r3 = mvnrnd(mu,sigma,1000);
plot(r3(:,1),r3(:,2),'go')
grid on;
title('三组高斯二维随机矢量散点图');
% 产生五组不同的三维高斯随机矢量
mu1 = [2 2 2];
sigma1 = [1 0 0; 0 2 0; 0 0 3];
r1 = mvnrnd(mu1,sigma1,1000);
mu2 = [6 0 -4];
sigma2 = [1 0 0; 0 2 0; 0 0 3];
r2 = mvnrnd(mu2,sigma2,1000);
mu3 = [-9 7 0];
sigma3 = [1 0 0; 0 2 0; 0 0 3];
r3 = mvnrnd(mu3,sigma3,1000);
mu4 = [0 15 -2];
sigma4 = [1 0 0; 0 2 0; 0 0 3];
r4 = mvnrnd(mu4,sigma4,1000);
mu5 = [-12 12 -12];
sigma5 = [1 0 0; 0 2 0; 0 0 3];
r5 = mvnrnd(mu5,sigma5,1000);
figure,plot3(r1(:,1),r1(:,2),r1(:,3),'r+',...
r2(:,1),r2(:,2),r2(:,3),'g+',...
r3(:,1),r3(:,2),r3(:,3),'b+',...
r4(:,1),r4(:,2),r4(:,3),'m+',...
r5(:,1),r5(:,2),r5(:,3),'k+');
grid on
title('五组不同的三维高斯随机矢量');
% 绘制三维随机矢量的二维投影散点图
figure,plot(r1(:,2),r1(:,3),'r+',...
r2(:,2),r2(:,3),'g+',...
r3(:,2),r3(:,3),'b+',...
r4(:,2),r4(:,3),'m+',...
r5(:,2),r5(:,3),'k+');
grid on
title('三维高斯随机矢量的二维投影,取第2、3维');
~~~

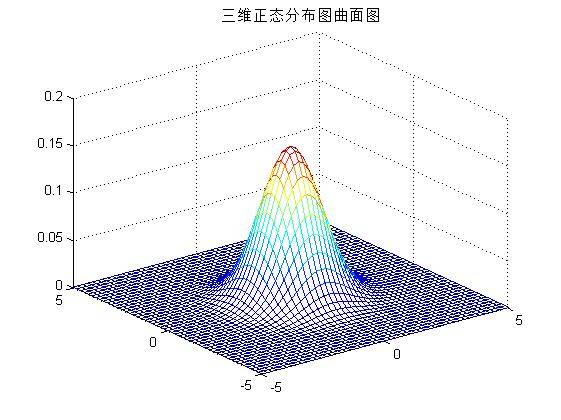
练习三:确定一个二维的均值矢量和协方差矩阵,然后利用matlab 中的meshgrid 函数生成一个二维网格,利用mvnpdf 函数计算在每个网格点上的概率密度函数值,并绘制出这些函数值的三维曲面图。
~~~
% 用meshgird,mvnpdf等函数绘制三维网格图
mu = [0 0];
SIGMA = [1 0; 0 1];
[X,Y] = meshgrid(-5:0.2:5, -5:0.2:5); %在XOY面上,产生网格
p = mvnpdf([X(:),Y(:)],mu,SIGMA); % 求取联合概率密度,相当于Z轴
p = reshape(p,size(X)); % 将Z值对应到相应的坐标上
mesh(X,Y,p); % 绘制
title('三维正态分布图曲面图');
~~~
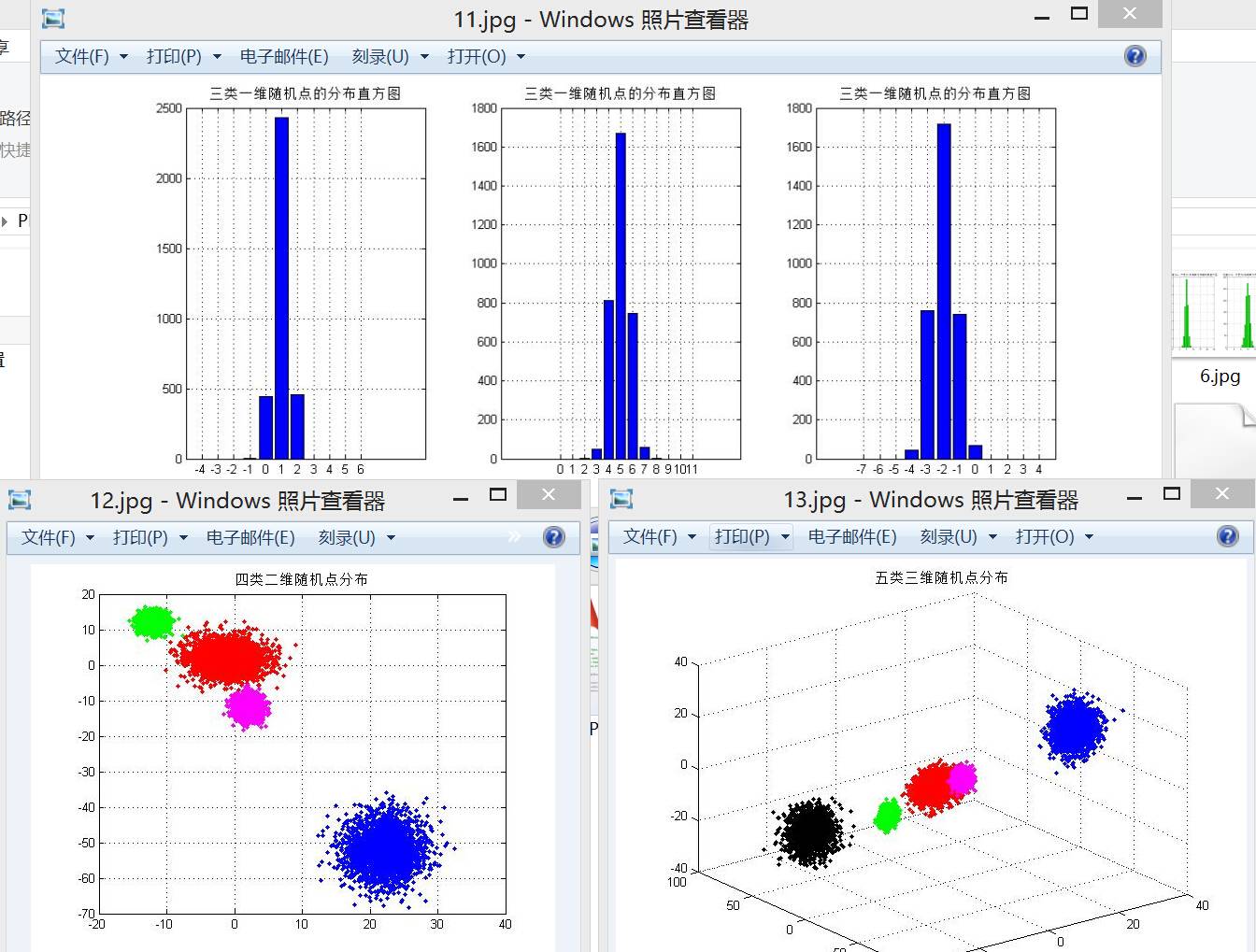
扩展实验2,编写一个生成N 个d 维向量的混合高斯类数据集的函数。其中,生成的数据集中共有N个模式向量,它们分成c 类。各个类对应的样本数分别为Ni,i = 1, 2, …, c,服从N(mi,Si),i = 1, 2, …, c 的高斯分布, mi,Si 分别是第i 类的均值向量和协方差矩阵。取不同的值,在二维空间和三维空间中生成数据,并绘制出散点图进行验证。这里我们创建一个函数实现这个功能MixGaussian():
~~~
% 随机点个数N ,类别C ,维度d ,均值mu, 方差sigma
function result = MixGaussian(N, C, d, mu, sigma)
color = {'r.', 'g.', 'm.', 'b.', 'k.', 'y.'}; % 用于存放不同类数据的颜色
% if nargin <= 3 & N < 0 & C < 1 & d < 1
% error('参数太少或参数错误');
if d == 1
for i = 1 : C
for j = 1 : N/C
r(j,i) = sqrt(sigma(1,i)) * randn() + mu(1,i);
end
X = round(mu(1,i)-5);
Y = round(mu(1,i) + sqrt(sigma(1,i))+5);
b = hist(r(:,i), X:Y);
subplot(1,C,i),bar(X:Y, b,'b');
title('三类一维随机点的分布直方图');
grid on
end
elseif d == 2
for i = 1:C
r(:,:,i) = mvnrnd(mu(:,:,i),sigma(:,:,i),round(N/C));
plot(r(:,1,i),r(:,2,i),char(color(i)));
hold on;
end
elseif d == 3
for i = 1:C
r(:,:,i) = mvnrnd(mu(:,:,i),sigma(:,:,i),round(N/C));
plot3(r(:,1,i),r(:,2,i),r(:,3,i),char(color(i)));
hold on;
end
else disp('维数只能设置为1,2或3');
end
result = r;
~~~
效果如下,根据输入的维度、方差、均值等参数的不同均可以输出模式类:
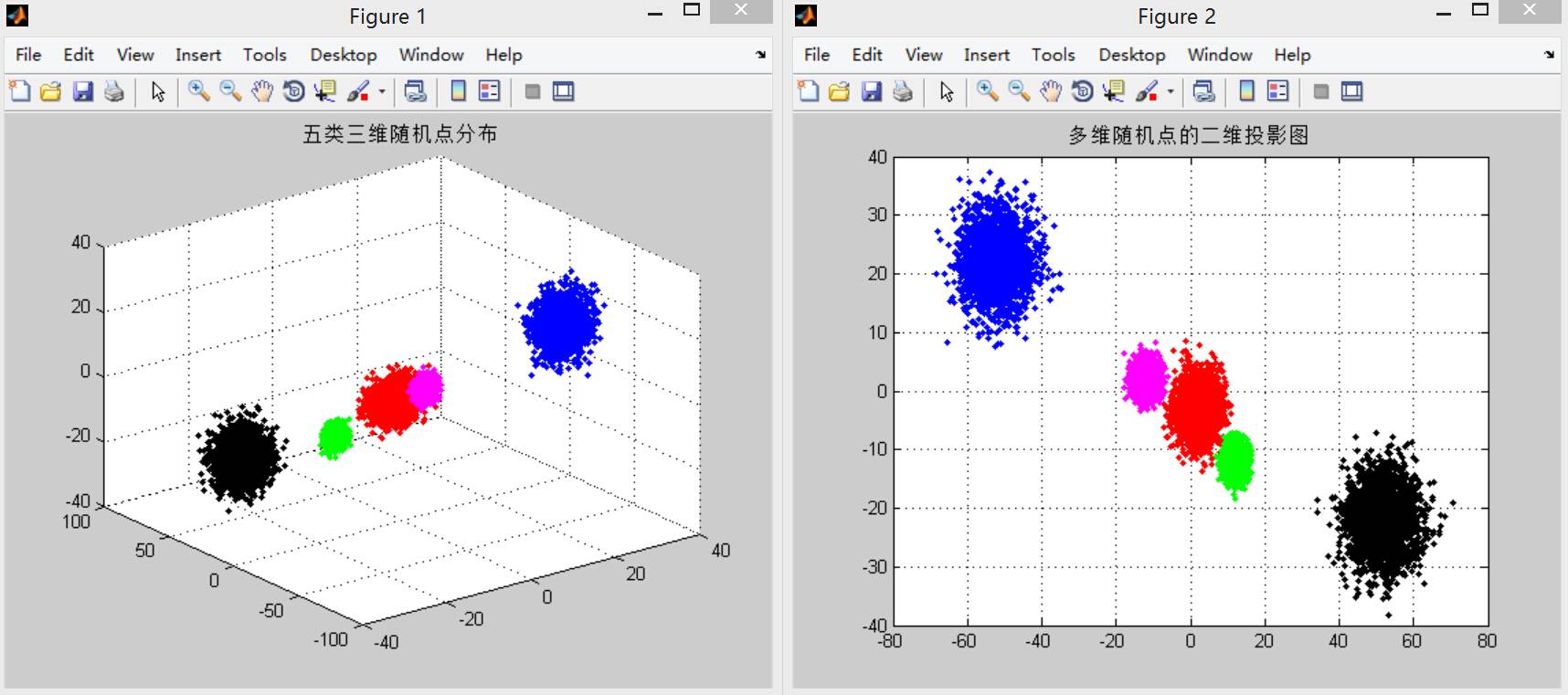
扩展实验3,编写一个绘制由c类共N个d 维模式向量构成的多模式类集合的二维投影绘图函数。其中,模式的类别标记已知,不同类别的模式绘制时用不同的颜色表示。其中,d维模式的2维子空间,简单来说就是由d 维模式矢量中的其中2个分量构成向量空间,在作图时以这两个分量做为坐标量,这里定义一个函数TwoDProject()。
~~~
% 输入数据,输出二维投影,X,Y为坐标轴选择
function TwoDProject(data, X, Y)
color = {'r.', 'g.', 'm.', 'b.', 'k.', 'y.'}; % 用于存放不同类数据的颜色
figure;
[a,b,c] = size(data);
if X == 1 && Y == 2
for i = 1:c
plot(data(:,X,i),data(:,Y,i),char(color(i)));
hold on;
end
elseif X == 1 && Y == 3
for i = 1:c
plot(data(:,X,i),data(:,Y,i),char(color(i)));
hold on;
end
elseif X == 2 && Y == 3
for i = 1:c
plot(data(:,X,i),data(:,Y,i),char(color(i)));
hold on;
end
else
disp('维数设置错误');
end
grid on;
title('多维随机点的二维投影图');
~~~
以上完整代码可在此处下载:[http://download.csdn.net/detail/liyuefeilong/8499915](http://download.csdn.net/detail/liyuefeilong/8499915)