众所周知,递归的实现是通过调用函数本身，函数调用的时候，每次调用时要做地址保存，参数传递等，这是通过一个递归工作栈实现的,同时影响效率的。递归是利用系统的堆栈保存函数当中的局部变量来解决问题的,而递归就是在栈处理栈上一堆的指针指向内存中的对象，这些对象一直不被释放，直到递归执行到最后一次后，才释放空间. ### 循环效率与递归效率 递归与循环是两种不同的解决问题的典型思路。当然也并不是说循环效率就一定比递归高，递归和循环是两码事，递归带有栈操作，循环则不一定，两个概念不是一个层次，不同场景做不同的尝试。  递归通常很直白地描述了一个求解过程，因此也是最容易被想到和实现的算法。循环其实和递归具有相同的特性（即：做重复任务），但有时，使用循环的算法并不会那么清晰地描述解决问题步骤。单从算法设计上看，递归和循环并无优劣之别。然而，在实际开发中，因为函数调用的开销，递归常常会带来性能问题，特别是在求解规模不确定的情况下。而循环因为没有函数调用开销，所以效率会比递归高。除少数编程语言对递归进行了优化外，大部分语言在实现递归算法时还是十分笨拙，由此带来了如何将递归算法转换为循环算法的问题。算法转换应当建立在对求解过程充分理解的基础上，有时甚至需要另辟蹊径。 - 一般递归调用可以处理的算法，也通过循环去解决需要额外的低效处理。 - 现在的编译器在优化后，对于多次调用的函数处理会有非常好的效率优化，效率未必低于循环。 - 递归和循环两者完全可以互换。如果用到递归的地方可以很方便使用循环替换，而不影响程序的阅读，那么替换成递归往往是好的。（例如：求阶乘的递归实现与循环实现。） 要转换成为非递归，两步工作：第一步，可以自己建立一个堆栈保存这些局部变量，替换系统栈；第二步把对递归的调用转变为循环处理就可以了。递归使用的栈布局.首先，看一下系统栈和用户栈的用途。系统栈（也叫核心栈、内核栈）是内存中属于操作系统空间的一块区域，其主要用途为：保存中断现场，对于嵌套中断，被中断程序的现场信息依次压入系统栈，中断返回时逆序弹出；以及保存操作系统子程序间相互调用的参数、返回值、返回点以及子程序(函数)的局部变量。用户栈是用户进程空间中的一块区域，用于保存用户进程的子程序间相互调用的参数、返回值、返回点以及子程序(函数)的局部变量。我们编写的递归程序属于用户程序，因此使用的是用户栈。 ### 循环与迭代 来自<<为之漫笔>>对这几个概念的一段理解："loop、iterate、traversal and recursion".这几个词是计算机技术书中经常会出现的几个词汇,众所周知，这几个词分别翻译为：循环、迭代、遍历和递归。乍一看，这几个词好像都与重复（repeat）有关，但有的又好像不完全是重复的意思。那么这几个词到底各是什么含义，有什么区别和联系呢？即: - 循环（loop），指的是在满足条件的情况下，重复执行同一段代码。比如，while语句。 - 迭代（iterate），指的是按照某种顺序逐个访问列表中的每一项。比如，for语句。 - 遍历（traversal），指的是按照一定的规则访问树形结构中的每个节点，而且每个节点都只访问一次。 - 递归（recursion），指的是一个函数不断调用自身的行为。比如，以编程方式输出著名的斐波纳契数列。 这几个概念之间的区别其实就比较清楚了。至于它们之间的联系，严格来讲，它们似乎都属于算法的范畴。换句话说，它们只不过是解决问题的不同手段和方式，而本质上则都是计算机编程中达成特定目标的途径。 迭代算法是用计算机解决问题的一种基本方法。它利用计算机运算速度快、适合做重复性操作的特点，让计算机对一组指令（或一定步骤）进行重复执行，在每次执行这组指令（或这些步骤）时，都从变量的原值推出它的一个新值。利用迭代算法解决问题，需要三个方面的.**第一**确定迭代变量。在可以用迭代算法解决的问题中，至少存在一个直接或间接地不断由旧值递推出新值的变量，这个变量就是迭代变量;**第二**建立迭代关系式。所谓迭代关系式，指如何从变量的前一个值推出其下一个值的公式(或关系)。迭代关系式的建立是解决迭代问题的关键，通常可以使用递推或倒推的方法来完成。**第三**对迭代过程进行控制。在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。不能让迭代过程无休止地重复执行下去。迭代过程的控制通常可分为两种情况：一种是所需的迭代次数是个确定的值，可以计算出来;另一种是所需的迭代次数无法确定。对于前一种情况，可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况，需要进一步分析出用来结束迭代过程的条件。经典的迭代的算法问题如兔子产子问题和上楼梯的走法问题. 迭代与循环,先从字面上看：迭代：“迭”：轮流，轮番，替换，交替，更换。“代”：代替。所以迭代的意思是：变化的循环，这种变化就是轮番代替，轮流代替。而循环：不变的重复。或者迭代是循环的一种，循环体代码分为固定循环体，和变化的循环体。 固定的循环如： ~~~ for(int i=0; i < 8; i++){ echo 'Welcome to AlgrithemMagic'; } ~~~ 实现迭代： ~~~ int sum = 0; for(int i = 1; i <= 1000; i++ ){ sum += i; } ~~~ 上面的迭代是常见的递增式迭代。类似的还有递减式迭代，递乘式迭代。迭代的好处：迭代减少了冗余代码，提高了代码的利用率和动态性。 ### 循环、迭代与递归 递归算法与迭代算法的设计思路区别在于：函数或算法是否具备收敛性，当且仅当一个算法存在预期的收敛效果时，采用递归算法才是可行的，否则，就不能使用递归算法。当然，从理论上说，所有的递归函数都可以转换为迭代函数，反之亦然，然而代价通常都是比较高的。但从算法结构来说，递归声明的结构并不总能够转换为迭代结构，原因在于结构的引申本身属于递归的概念，用迭代的方法在设计初期根本无法实现，这就像动多态的东西并不总是可以用静多态的方法实现一样。这也是为什么在结构设计时，通常采用递归的方式而不是采用迭代的方式的原因，一个极典型的例子类似于链表，使用递归定义及其简单，但对于内存定义(数组方式)其定义及调用处理说明就变得很晦涩，尤其是在遇到环链、图、网格等问题时，使用迭代方式从描述到实现上都变得很不现实。 递归其实是方便了程序员难为了机器。它只要得到数学公式就能很方便的写出程序。优点就是易理解，容易编程。但递归是用栈机制实现的，每深入一层，都要占去一块栈数据区域，对嵌套层数深的一些算法，递归会力不从心，空间上会以内存崩溃而告终，而且递归也带来了大量的函数调用，这也有许多额外的时间开销。所以在深度大时，它的时空性就不好了。循环其缺点就是不容易理解，编写复杂问题时困难。优点是效率高。运行时间只因循环次数增加而增加，没什么额外开销。空间上没有什么增加。 局部变量占用的内存是一次性的，也就是O(1)的空间复杂度，而对于递归,每次函数调用都要压栈，那么空间复杂度是O(n)，和递归次数呈线性关系。 递归程序改用循环实现的话，一般都是要自己维护一个栈的，以便状态的回溯。如果某个递归程序改用循环的时候根本就不需要维护栈，那其实这个递归程序这样写只是意义明显一些，不一定要写成递归形式。但很多递归程序就是为了利用函数自身在系统栈上的auto变量记录状态，以便回溯。原理上讲，所有递归都是可以消除的，代价就是可能自己要维护一个栈。而且我个人认为，很多情况下用递归还是必要的，它往往能把复杂问题分解成更为简单的步骤，而且很能反映问题的本质。 递归其实就是利用系统堆栈，实现函数自身调用，或者是相互调用的过程。在通往边界的过程中，都会把单步地址保存下来，知道等出边界，再按照先进后出的进行运算，这正如我们装木桶一样，每一次都只能把东西方在最上面，而取得时候，先放进取的反而最后取出。递归的数据传送也类似。但是递归不能无限的进行下去，必须在一定条件下停止自身调用，因此它的边界值应是明确的。就向我们装木桶一样，我们不能总是无限制的往里装，必须在一定的时候把东西取出来。比较简单的递归过程是阶乘函数，你可以去看一下。但是递归的运算方法，往往决定了它的效率很低，因为数据要不断的进栈出栈。但是递归作为比较基础的算法，它的作用不能忽视。 关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

插入排序(Insertion Sort)的基本思想是每次将一个待排序的记录，按其关键字大小插入到前面已经排好序的子文件中的适当位置，直到全部记录插入完成为止。 #### 基本思想与伪代码 经过j-1遍处理后,A[1..j-1]己排好序。第j遍处理仅将A[j]插入L[1..j-1]的适当位置，使得A[1..j]又是排好序的序列。要达到这个目的，我们可以用顺序比较的方法。首先比较A[j]和A[j-1]，如果A[j-1]≤ A[j]，则A[1..j]已排好序，第i遍处理就结束了；否则交换A[j]与A[j-1]的位置，继续比较A[j-1]和A[j-2]，直到找到某一个位置i(1≤i≤j-1)，使得A[j] ≤A[j+1]时为止。用伪码描述如下： ~~~ 算法: InsertSort(A,n) 输入：n个数组A 输出：按照递增顺序的数组A 1. for j ← 2 to n do 2. x←A[j] 3. i ← j-1 //行3到行7把A[j]插入A[1.....j-1]之中 4. while i >0 and x =0 && t_<: ~~~ void InsertionSort(int *ptritems, int count) { int i, j, k; for (i=1; i< count; ++i) { k = ptritems[i]; for ( j=i-1; (j>=0) && (k ';

分治策略(Divide and Conquer)是一种常用的算法技术,使用分治策略设计的算法通常是递归算法.很多时候我们看明白一个复杂的递归都有点费时间，尤其对模型所描述的问题概念不清的时候，想要自己设计一个递归那么就更是有难度了。如果递归仅仅是循环，估计现在我们就看不到递归了。递归之所以现在还存在是因为递归可以产生无限循环体. ### 用归纳法来理解递归 数学都不差的我们，第一反应就是递归在数学上的模型是什么。毕竟我们对于问题进行数学建模比起代码建模拿手多了。 自己观察递归，我们会发现，递归的数学模型其实就是归纳法。即:归纳法适用于想解决一个问题转化为解决他的子问题，而他的子问题又变成子问题的子问题，而且我们发现这些问题其实都是一个模型，也就是说存在相同的逻辑归纳处理项。当然有一个是例外的，也就是递归结束的哪一个处理方法不适用于我们的归纳处理项，当然也不能适用，否则我们就无穷递归了。这里又引出了一个归纳终结点以及直接求解的表达式。如果运用列表来形容归纳法就是： - 步进表达式：问题蜕变成子问题的表达式 - 结束条件：什么时候可以不再是用步进表达式 - 直接求解表达式：在结束条件下能够直接计算返回值的表达式 - 逻辑归纳项：适用于一切非适用于结束条件的子问题的处理，当然上面的步进表达式其实就是包含在这里面了。 ### 分治策略一般性描述 把上面的设计思想加以归纳,可以得到分治算法的一般描述.设P是待求解的问题,|P|代表问题的输入规模,一般的分治算法Divide-and-Conquer伪码描述如下: ~~~ 算法 Divide-and-Conquer(P) 1. if |P| < c or |P| = c then S(P) 2. divide P into P1,P2,P3,...,Pk 3. for i = 1 to k do 4. yi ← Divide-and-Conquer(Pi) 5.Return Merge(y1,y2,y3,....,yk) ~~~ ### 需要满足的两个条件 编程人员还是停留在“自己调用自己”的程度上。这其实这只是递归的表象（PS:严格来说连表象都概括得不全面，因为除了“自己调用自己”的递归外，还有交互调用的递归）。而递归的思想远不止这么简单。递归，并不是简单的“自己调用自己”，也不是简单的“交互调用”。它是一种分析和解决问题的方法和思想。简单来说，递归的思想就是：把问题分解成为规模更小的、具有与原问题有着相同解法的问题。比如二分查找算法，就是不断地把问题的规模变小（变成原问题的一半），而新问题与原问题有着相同的解法。有些问题使用传统的迭代算法是很难求解甚至无解的，而使用递归却可以很容易的解决。比如Hanoi塔问题。但递归的使用也是有它的劣势的，因为它要进行多层函数调用，所以会消耗很多堆栈空间和函数调用时间。 既然递归的思想是把问题分解成为规模更小且与原问题有着相同解法的问题，那么是不是这样的问题都能用递归来解决呢？答案是否定的。并不是所有问题都能用递归来解决。那么什么样的问题可以用递归来解决呢？一般来讲，能用递归来解决的问题必须满足两个条件： - 可以通过递归调用来缩小问题规模，且新问题与原问题有着相同的形式。 - 存在一种简单情境，可以使递归在简单情境下退出。 如果一个问题不满足以上两个条件，那么它就不能用递归来解决。为了方便理解，如斐波那契数列来说下：求斐波那契数列的第N项的值。这是一个经典的问题，说到递归一定要提到这个问题。斐波那契数列这样定义：f(0) = 0, f(1) = 1, 对n > 1, f(n) = f(n-1) + f(n-2) 这是一个明显的可以用递归解决的问题。让我们来看看它是如何满足递归的两个条件的： - 对于一个n>2, 求f(n)只需求出f(n-1)和f(n-2)，也就是说规模为n的问题，转化成了规模更小的问题； - 对于n=0和n=1，存在着简单情境：f(0) = 0, f(1) = 1。 因此，我们可以很容易的写出计算费波纳契数列的第n项的递归程序： ~~~ int fib(n){ if(n == 0) return 0; else if(n == 1) return 1; else return f(n-1) + f(n-2); } ~~~ 在编写递归调用的函数的时候，一定要把对简单情境的判断写在最前面，以保证函数调用在检查到简单情境的时候能够及时地中止递归，否则，你的函数可能会永不停息的在那里递归调用了。 ### 两个熟悉的例子 先看两个熟悉的例子:字符串回文现象的递归判断和二分查找算法 #### 字符串回文现象的递归判断 回文是一种字符串，它正着读和反着读都是一样的。比如level,eye都是回文。用迭代的方法可以很快地判断一个字符串是否为回文。用递归的方法如何来实现呢？首先我们要考虑使用递归的两个条件： - 这个问题是否可以分解为形式相同但规模更小的问题？ - 如果存在这样一种分解，那么这种分解是否存在一种简单情境？ 先来看第一点，是否存在一种符合条件的分解。容易发现，如果一个字符串是回文，那么在它的内部一定存在着更小的回文。 比如level里面的eve也是回文。 而且，我们注意到，一个回文的第一个字符和最后一个字符一定是相同的。所以我们很自然的有这样的方法：先判断给定字符串的首尾字符是否相等，若相等，则判断去掉首尾字符后的字符串是否为回文，若不相等，则该字符串不是回文。注意，我们已经成功地把问题的规模缩小了，去掉首尾字符的字符串当然比原字符串小。 接着再来看第二点， 这种分解是否存在一种简单情境呢？简单情境在使用递归的时候是必须的，否则你的递归程序可能会进入无止境的调用。对于回文问题，我们容易发现，一个只有一个字符的字符串一定是回文，所以，只有一个字符是一个简单情境，但它不是唯一的简单情境，因为空字符串也是回文。这样，我们就得到了回文问题的两个简单情境：字符数为1和字符数为0。 综上两点分析,满足分治策略需要满足的两个条件了.即编写出解决回文问题的递归实现如下代码所示.: ~~~ int is_palindereme(char *str, int n){ printf("Length: %d \n",n); printf("%c ----- %c\n", str[0], str[n-1]); if(n == 0 || n == 1) return 1; else{ return ((str[0] == str[n-1]) ? is_palindereme(str+1, n-2) : 0); } } ~~~ 运行结果[ ](http://www.nowamagic.net/librarys/veda/detail/2317) [ ](http://www.nowamagic.net/librarys/veda/detail/2317) #### 二分查找算法的递归实现 典型的递归例子是对已排序数组的二分查找算法。现在有一个已经排序好的数组，要在这个数组中查找一个元素，以确定它是否在这个数组中，很一般的想法是顺序检查每个元素，看它是否与待查找元素相同。这个方法很容易想到，但它的效率不能让人满意，它的复杂度是O(n)的。现在我们来看看递归在这里能不能更有效。 还是考虑上面的两个条件： - 第一：这个问题是否可以分解为形式相同但规模更小的问题？ - 第二：如果存在这样一种分解，那么这种分解是否存在一种简单情境？ 考虑条件一：我们可以这样想，如果想把问题的规模缩小，我们应该做什么？可以的做法是：我们先确定数组中的某些元素与待查元素不同，然后再在剩下的元素中查找，这样就缩小了问题的规模。那么如何确定数组中的某些元素与待查元素不同呢？ 考虑到我们的数组是已经排序的，我们可以通过比较数组的中值元素和待查元素来确定待查元素是在数组的前半段还是后半段。这样我们就得到了一种把问题规模缩小的方法。 接着考虑条件二：简单情境是什么呢？容易发现，如果中值元素和待查元素相等，就可以确定待查元素是否在数组中了，这是一种简单情境，那么它是不是唯一的简单情境呢？ 考虑元素始终不与中值元素相等，那么我们最终可能得到了一个无法再分的小规模的数组，它只有一个元素，那么我们就可以通过比较这个元素和待查元素来确定最后的结果。这也是一种简单情境。 这个问题可以用递归来解决，二分法的代码如下： ~~~ void selectionSort(int data[], int count){ int i, j, min, temp; for(i = 0; i < count; i ++) { /*find the minimum*/ min = i; for(j = i + 1; j < count; j ++) if(data[j] < data[min]) min = j; temp = data[i]; data[i] = data[min]; data[min] = temp; } } int binary_search(int *data, int n, int key){ int mid; if(n == 1){ return (data[0] == key); } else{ mid = n/2; printf("mid=%d\n", data[mid]); if(data[mid-1] == key) return 1; else if(data[mid-1] > key){ printf("key %d 比 data[mid-1] %d 小，取前半段 \n", key, data[mid-1]); return binary_search(&data[0], mid, key); } else{ printf("key %d 比 data[mid-1] %d 大，取后半段 \n", key, data[mid-1]); return binary_search(&data[mid], n - mid, key); } } } ~~~ 程序运行结果：  这个算法的复杂度是O(logn)的，显然要优于先前提到的朴素的顺序查找法。 ### 小结 递归的基本思想是把规模大的问题转化为规模小的相似的子问题来解决。在函数实现时，因为解决大问题的方法和解决小问题的方法往往是同一个方法，所以就产生了函数调用它自身的情况。另外这个解决问题的函数必须有明显的结束条件，这样就不会产生无限递归的情况了。 关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

**背景：** 假定你有一雄一雌一对刚出生的兔子，它们在长到一个月大小时开始交配，在第二月结束时，雌兔子产下另一对兔子，过了一个月后它们也开始繁殖，如此这般持续下去。每只雌兔在开始繁殖时每月都产下一对兔子，假定没有兔子死亡，在一年后总共会有多少对兔子？ 在一月底，最初的一对兔子交配，但是还只有1对兔子；在二月底，雌兔产下一对兔子，共有2对兔子；在三月底，最老的雌兔产下第二对兔子，共有3对兔子；在四月底，最老的雌兔产下第三对兔子，两个月前生的雌兔产下一对兔子，共有5对兔子；……如此这般计算下去，兔子对数分别是：1, 1, 2, 3, 5, 8, 13, 21, 34, 55,89, 144, ...看出规律了吗？从第3个数目开始，每个数目都是前面两个数目之和。这就是著名的斐波那契（Fibonacci）数列。 **数学表示：** Fibonacci数列的数学表达式就是： **F(n) = F(n-1) + F(n-2)** **F(1) = 1 ,F(2) = 1** **递归程序1：** **Fibonacci数列可以用很直观的二叉递归程序来写，用C++语言的描述如下：** ~~~ long fib1(int n){ if (n <= 2){ return 1;} else{ return fib1(n-1) + fib1(n-2);} } ~~~ 看上去程序的递归使用很恰当，可是在用VC2010的环境下测试n=37的时候用了大约3s，而n=45的时候基本下楼打完饭也看不到结果……显然这种递归的效率太低了！！**递归效率分析：**例如，用下面一个测试函数： ~~~ long fib1(int n, int* arr){ arr[n]++; if (n <= 2){ return 1;} else{return fib1(n-1, arr) + fib1(n-2, arr);} } ~~~ 这时，可以得到每个fib(i)被计算的次数： fib(10) = 1     fib(9) = 1      fib(8) = 2      fib(7) = 3 fib(6) = 5      fib(5) = 8      fib(4) = 13    fib(3) = 21 fib(2) = 34   fib(1) = 55    fib(0) = 34 可见，计算次数呈反向的Fibonacci数列，这显然造成了大量重复计算。我们令T(N)为函数fib(n)的运行时间，当N>=2的时候我们分析可知： ***T(N) = T(N-1) + T(N-2) + 2*** 而fib(n) = fib(n-1) + fib(n-2)，所以有T(N) >= fib(n)，归纳法证明可得： ***fib(N) < (5/3)^N*** ***当N>4时，fib（N）>= (3/2)^N*** ***标准写法： *** 显然这个***O（(3/2)^N）***是以指数增长的算法，基本上是最坏的情况。 **其实，这违反了递归的一个规则：合成效益法则。*合成效益法则（Compound interest rule）：在求解一个问题的同一实例的时候，切勿在不同的递归调用中做重复性的工作。***所以在上面的代码中调用fib(N-1)的时候实际上同时计算了fib(N-2)。这种小的重复计算在递归过程中就会产生巨大的运行时间。 **递归程序2：** 用一叉递归程序就可以得到近似线性的效率，用C++语言的描述如下： ~~~ long fib(int n, long a, long b, int count){ if (count == n) return b; return fib(n, b, a+b, ++count); } long fib2(int n){ return fib(n, 0, 1, 1); } ~~~ **这种方法虽然是递归了，但是并不直观，而且效率上相比下面的迭代循环并没有优势。** **迭代解法：** Fibonacci数列用迭代程序来写也很容易，用C++语言的描述如下： ~~~ //也可以用数组将每次计算的f(n)存储下来，用来下次计算用（空间换时间） long fib3 (int n){ long x = 0, y = 1; for (int j = 1; j < n; j++) { y = x + y; x = y - x; } return y; } ~~~ **这时程序的效率显然为*O（N）*，N = 45的时候<1s就能得到结果。** 我们将数列写成： Fibonacci[0] = 0，Fibonacci[1] = 1 Fibonacci[n] = Fibonacci[n-1] + Fibonacci[n-2] (n >= 2) 可以将它写成矩阵乘法形式：  将右边连续的展开就得到：  下面就是要用O(log(n))的算法计算： 显然用二分法来求，结合一些面向对象的概念，C++代码如下： ~~~ class Matrix{ public: long matr[2][2]; Matrix(const Matrix&rhs); Matrix(long a, long b, long c, long d); Matrix& operator=(const Matrix&); friend Matrix operator*(const Matrix& lhs, const Matrix& rhs){ Matrix ret(0,0,0,0); ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0]; ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1]; ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0]; ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1]; return ret; } }; Matrix::Matrix(long a, long b, long c, long d){ this->matr[0][0] = a; this->matr[0][1] = b; this->matr[1][0] = c; this->matr[1][1] = d; } Matrix::Matrix(const Matrix &rhs){ this->matr[0][0] = rhs.matr[0][0]; this->matr[0][1] = rhs.matr[0][1]; this->matr[1][0] = rhs.matr[1][0]; this->matr[1][1] = rhs.matr[1][1]; } Matrix& Matrix::operator =(const Matrix &rhs){ this->matr[0][0] = rhs.matr[0][0]; this->matr[0][1] = rhs.matr[0][1]; this->matr[1][0] = rhs.matr[1][0]; this->matr[1][1] = rhs.matr[1][1]; return *this; } Matrix power(const Matrix& m, int n){ if (n == 1) return m; if (n%2 == 0) return power(m*m, n/2); else return power(m*m, n/2) * m; } long fib4 (int n){ Matrix matrix0(1, 1, 1, 0); matrix0 = power(matrix0, n-1); return matrix0.matr[0][0]; } ~~~ **这时程序的效率为*O（log(N)）*。公式解法：在*O（1）*的时间就能求得到F(n)了：** *** *** **注意：其中[x]表示取距离x最近的整数。** **用C++写的代码如下：** ~~~ long fib5(int n){ double z = sqrt(5.0); double x = (1 + z)/2; double y = (1 - z)/2; return (pow(x, n) - pow(y, n))/z + 0.5; } ~~~ **这个与数学库实现开方和乘方本身效率有关的，我想应该还是在O(log(n))的效率。** **总结：** 上面给出了5中求解斐波那契数列的方法，用测试程序主函数如下： ~~~ int main(){ cout << fib1(45) << endl; cout << fib2(45) << endl; cout << fib3(45) << endl; cout << fib4(45) << endl; cout << fib5(45) << endl; return 0; } ~~~ 函数fib1会等待好久，其它的都能很快得出结果，并且相同为：1134903170。而后面两种只有在n = 1000000000的时候会显示出优势。由于我的程序都没有涉及到高精度，所以要是求大数据的话，可以通过取模来获得结果的后4位来测试效率与正确性。另外斐波那契数列在实际工作中应该用的很少，尤其是当数据n很大的时候（例如：1000000000），所以综合考虑基本普通的非递归O(n)方法就很好了，没有必要用矩阵乘法。 程序全部源码 ~~~ class Matrix{ public: long matr[2][2]; Matrix(const Matrix&rhs); Matrix(long a, long b, long c, long d); Matrix& operator=(const Matrix&); friend Matrix operator*(const Matrix& lhs, const Matrix& rhs) { Matrix ret(0,0,0,0); ret.matr[0][0] = lhs.matr[0][0]*rhs.matr[0][0] + lhs.matr[0][1]*rhs.matr[1][0]; ret.matr[0][1] = lhs.matr[0][0]*rhs.matr[0][1] + lhs.matr[0][1]*rhs.matr[1][1]; ret.matr[1][0] = lhs.matr[1][0]*rhs.matr[0][0] + lhs.matr[1][1]*rhs.matr[1][0]; ret.matr[1][1] = lhs.matr[1][0]*rhs.matr[0][1] + lhs.matr[1][1]*rhs.matr[1][1]; return ret; } }; Matrix::Matrix(long a, long b, long c, long d){ this->matr[0][0] = a; this->matr[0][1] = b; this->matr[1][0] = c; this->matr[1][1] = d; } Matrix::Matrix(const Matrix &rhs){ this->matr[0][0] = rhs.matr[0][0]; this->matr[0][1] = rhs.matr[0][1]; this->matr[1][0] = rhs.matr[1][0]; this->matr[1][1] = rhs.matr[1][1]; } Matrix& Matrix::operator =(const Matrix &rhs){ this->matr[0][0] = rhs.matr[0][0]; this->matr[0][1] = rhs.matr[0][1]; this->matr[1][0] = rhs.matr[1][0]; this->matr[1][1] = rhs.matr[1][1]; return *this; } Matrix power(const Matrix& m, int n){ if (n == 1) return m; if (n%2 == 0) return power(m*m, n/2); else return power(m*m, n/2) * m; } //普通递归 long fib1(int n){ if (n <= 2) { return 1; } else { return fib1(n-1) + fib1(n-2); } } long fib(int n, long a, long b, int count){ if (count == n) return b; return fib(n, b, a+b, ++count); } //一叉递归 long fib2(int n){ return fib(n, 0, 1, 1); } //非递归方法O(n) long fib3 (int n){ long x = 0, y = 1; for (int j = 1; j < n; j++) { y = x + y; x = y - x; } return y; } //矩阵乘法O(log(n)) long fib4 (int n){ Matrix matrix0(1, 1, 1, 0); matrix0 = power(matrix0, n-1); return matrix0.matr[0][0]; } //公式法O(1) long fib5(int n){ double z = sqrt(5.0); double x = (1 + z)/2; double y = (1 - z)/2; return (pow(x, n) - pow(y, n))/z + 0.5; } int main(){ //n = 45时候fib1()很慢 int n = 10; cout << fib1(n) << endl; cout << fib2(n) << endl; cout << fib3(n) << endl; cout << fib4(n) << endl; cout << fib5(n) << endl; return 0; } ~~~ 关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

**矩阵预备知识** 在数学中，矩阵（Matrix）是指纵横排列的二维数据表格，最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。 矩阵是高等代数学中的常见工具，也常见于统计分析等应用数学学科中。并且在ACM竞赛，有很多涉及到矩阵知识的题。许多算法都会结合矩阵来处理，而比较具有代表性的矩阵算法有：矩阵快速幂、高斯消元等等。例如下面的图片就是一个矩阵：  上述矩阵是一个 4 × 3 矩阵：某矩阵 A 的第 i 行第 j 列，或 I , j位，通常记为 A[i,j] 或 Aij。在上述例子中A[3,3]=37。此外 Aij = (aij)，意为 A[i,j] = aij。①  矩阵相乘的规则：矩阵与矩阵相乘 第一个矩阵的列数必须等于第二个矩阵的行数 假如第一个是m*n的矩阵 第二个是n*p的矩阵 则结果就是m*p的矩阵 且得出来的矩阵中元素具有以下特点：第一行第一列元素为第一个矩阵的第一行的每个元素和第二个矩阵的第一列的每个元素乘积的和 以此类推 第i行第j列的元素就是第一个矩阵的第i行的每个元素与第二个矩阵第j列的每个元素的乘积的和。②  单位矩阵： n*n的矩阵  mat ( i , i )=1;  任何一个矩阵乘以单位矩阵就是它本身 n*单位矩阵=n， 可以把单位矩阵等价为整数1。（单位矩阵用在矩阵快速幂中）例如下图就是一个3*3的单位矩阵：  ### 问题描述: 设A1,A2,…,An为矩阵序列，Ai为Pi-1×Pi阶矩阵，i = 1,2,…,n. 确定乘法顺序使得元素相乘的总次数最少.输入：向量P = **实例： ** P = <10, 100, 5, 50>  A1: 10 × 100, A2: 100 × 5, A3: 5 × 50 **乘法次序：** (A1 A2)A3: 10 × 100 × 5 + 10 ×5 × 50 = 7500       A1(A2 A3): 10 × 100 × 50 + 100 × 5 × 50 = 75000 搜索空间的规模先将矩阵链加括号分为两部分，即P=A1*A2*...*An=（A1*A2...*Ak）*（Ak+1*...An），则有f(n)=f(1)*f(n-1)+f(2)*f(n-2)+...+f(n-1)*f(1)种方法。f(n)为一个[Catalan数](http://baike.baidu.com/view/1163998.htm)，所以一般的方法要计算 种。 ### 动态规划算法 输入P=< P0, P1, …, Pn>，Ai..j 表示乘积 AiAi+1…Aj 的结果，其最后一次相乘是：  m[i,j] 表示得到Ai..j的最少的相乘次数。 递推方程：  为了确定加括号的次序，设计表s[i,j],记录求得最优时最一位置。 ### 算法递归实现 由上面的递归公式，很容易得到算法的递归实现,用一个N=10, P=<30,35,15,5,40,20,10,8,9,60,80>的简单实例.参考代码如下所示： ~~~ int RecurMatrixChain(int *ptrArray,int start,int end){ m[start][end]=100000; s[start][end]=start; if(start==end) m[start][end]=0; else{ for(int k=start;k的简单实例，运行上述代码：  ### HDOJ 4920 Matrix multiplication **Problem Description** Given two matrices A and B of size n×n, find the product of them.bobo hates big integers. So you are only asked to find the result modulo 3. **Input** The input consists of several tests. For each tests: The first line contains n (1≤n≤800). Each of the following n lines contain n integers — the description of the matrix A. The j-th integer in the i-th line equals Aij. The next n lines describe the matrix B in similar format (0≤Aij,Bij≤109). **Output** For each tests: Print n lines. Each of them contain n integers — the matrix A×B in similar format. **Sample Input** 1 0 1 2 0 1 2 3 4 5 6 7 **Sample Output** 0 0 1 2 1 题目大意：求两个矩阵相乘mod3的结果。这道题就是一个赤裸裸的矩阵相乘的题。但是要注意题目的时间复杂度，一定要进行优化。并且，此题还有二个坑点，如果把握不好就会超时。① 就是Mod 3 时，一定不能在矩阵相乘算法的for循环里，如果放在相乘算法里会超时。②在进行相乘之前把所有元素先Mod 3 这样做也会优化一定的时间。因为题目所给数据并不是很大，所以即使把mod 3 放到结束输出语句里面就可以了，不用担心相乘的过程会超出int型。 **源代码参考**： ~~~ int X[MAXN][MAXN]; int Y[MAXN][MAXN]; int t[MAXN][MAXN]; int main() { while(scanf("%d",&N)!=EOF){ for(int i=0;i ';

众所周知,算法所需的时间应当是随着其输入规模增长的，而输入规模与特定具体问题有关。对大多数问题来说其最自然的度量就是输入中的元素个数。算法的运行时间是指在特定输入时所执行的基本操作数。我们可以得到关于一个关于输入规模n的所需时间的函数。然而可以进一步简化算法的时间分析，我们进行进一步抽象，首先，忽略每条语句的真实代价，通过运行时间的增长率来度量一个算法在时间方面的表现。我们只考虑公式的最高次项，并忽略它的常数系数。本博文主要介绍一些相关的数学知识即:函数的渐近的界的定义与性质.常用的证明方法. ### 渐近符号 当输入规模大到使运行时间只和增长的量级有关时，就是在研究算法的 渐近 效率。就是说，从极限角度看，我们只关心算法运行时间如何随着输入规模的无限增长而增长。表示算法的渐近运行时间的记号是用定义域为自然数集 N = {0， 1， 2， …} 的函数来定义的。这些记号便于用来表示最坏情况运行时间 T ( n )。 #### *Θ* 记号(**读音:theta**) 对一个给定的函数 *g* ( *n* )，用 *Θ* ( *g* ( *n* ))来表示函数集合：  对任何一个函数 *f* ( *n* )，若存在正常数 *c1* ， *c2* ，使当 *n* 充分大时， *f* ( *n* )能被夹在 *c1 g* ( *n* )和 *c2 g* ( *n* )之间，则 *f* ( *n* )属于集合 *Θ* ( *g* ( *n* ))。可以写成“ *f* ( *n* ) ∈ *Θ* ( *g* ( *n* ))”表示 *f* ( *n* )是 *Θ* ( *g* ( *n* ))的元素。不过，通常写成“ *f* ( *n* ) = *Θ* ( *g* ( *n* ))”来表示相同的意思。  上图给出了函数 *f* ( *n* )和 *g* ( *n* )的直观图示，其中 *f* ( *n* ) = *Θ* ( *g* ( *n* ))。对所有位于 *n0* 右边的 *n* 值， *f* ( *n* )的值落在 *c1 g* ( *n* )和 *c2 g* ( *n* )之间。换句话说，对所有的 *n* >= *n0* ， *f* ( *n* )在一个常数因子范围内与 *g* ( *n* )相等。我们说 *g* ( *n* )是 *f* ( *n* )的一个 **渐近确界**。*Θ* ( *g* ( *n* ))的定义要求每个成员 *f* ( *n* ) ∈ *Θ* ( *g* ( *n* ))都是 **渐近非负**，就是说当 *n* 足够大时 *f* ( *n* )是非负值。这就要求函数 *g* ( *n* )本身也是渐近非负的，否则集合 *Θ* ( *g* ( *n* ))就是空集。*Θ* 记号的效果相当于舍弃了低阶项和忽略了最高阶项的系数。 #### *O* 符号 *Θ* 记号渐近地给出了一个函数的上界和下界。当只有 **渐近**上界时，使用 *O* 记号。对一个函数 *g* ( *n* )，用 *O* ( *g* ( *n* ))表示一个函数集合：  上图说明了 *O* 记号的直观意义。对所有位于 *n0* 右边的 *n* 值，函数 *f* ( *n* )的值在 *g* ( *n* )下。 [![clip_image002[10]](https://docs.gechiui.com/gc-content/uploads/sites/kancloud/5830ff47f8743bc1ec107f4666226ffb_104x42.png "clip_image002[10]")](http://images.cnblogs.com/cnblogs_com/zabery/201107/201107192011436308.png)， 则可以表示为 f(n) = O(n2)。证明：要使得 0 <= f(n) <= cg(n)      [![clip_image002[12]](https://docs.gechiui.com/gc-content/uploads/sites/kancloud/0bab581d328aa6eb03c99486016c950f_198x42.png "clip_image002[12]")](http://images.cnblogs.com/cnblogs_com/zabery/201107/201107192011542187.png) [](http://images.cnblogs.com/cnblogs_com/zabery/201107/201107192012001003.png) [](http://images.cnblogs.com/cnblogs_com/zabery/201107/201107192012005605.png) 存在c = 9/2 ,n0 = 1,使得对所有的n >= n0都有 0 <= f(n) <= cg(n)。O(g(n) 以及后面讲到的记号表示的都是集合，而f(n) = O(n2)的实际意义 是 f(n) ∈ O(n2)。假设有 [![clip_image002[14]](https://docs.gechiui.com/gc-content/uploads/sites/kancloud/1a837264b2834af446bb6e81a3131268_90x31.png "clip_image002[14]")](http://images.cnblogs.com/cnblogs_com/zabery/201107/201107192012029377.png) ， [![clip_image002[10]](https://docs.gechiui.com/gc-content/uploads/sites/kancloud/5830ff47f8743bc1ec107f4666226ffb_104x42.png "clip_image002[10]")](http://images.cnblogs.com/cnblogs_com/zabery/201107/201107192012055392.png)则 g(n) = O(n2) , f(n) = O(n2) #### **o* 记号* *O* 记号提供的渐近上界可能是也可能不是渐近紧确的。这里用 *o* 记号表示非渐近紧确的上界。 *o* ( *g* ( *n* ))的形式定义为集合：  *O* 记号与 *o* 记号的主要区别在于对 *f* ( *n* ) = *O* ( *g* ( *n* ))，界0 <= *f* ( *n* ) <= *c g* ( *n* )对某个常数 *c* > 0成立；但对 *f* ( *n* ) = *o* ( *g* ( *n* ))，界0 <= *f* ( *n* ) <= *c g* ( *n* )对所有常数 *c* > 0都成立。即  #### **Ω* 记号* *Ω* 记号给出了函数的渐近下界。给定一个函数 *g* ( *n* )，用 *Ω* ( *g* ( *n* ))表示一个函数集合：  上图说明了 *Ω* 记号的直观意义。对所有在 *n0* 右边的 *n* 值，函数 *f* ( *n* )的数值等于或大于 *c g* ( *n* )。 **定理**  对任意两个函数 *f* ( *n* )和 *g* ( *n* )， *f* ( *n* ) = *Θ* ( *g* ( *n* ))当且仅当 *f* ( *n* ) = *O* ( *n* )和 *f* ( *n* ) = *Ω* ( *g* ( *n* ))。 #### *ω* 记号 我们用 *ω* 记号来表示非渐近紧确的下界。 *ω* ( *g* ( *n* ))的形式定义为集合：  关系 *f* ( *n* ) = *ω* ( *g* ( *n* ))意味着  如果这个极限存在。也就是说当 *n* 趋于无穷时， *f* ( *n* )相对 *g* ( *n* )来说变得任意大了。 #### 函数间的比较 设 *f* ( *n* )和 *g* ( *n* )是渐近正值函数。 **传递性：** - *f* ( *n* ) = *Θ* ( *g* ( *n* ))和 *g* ( *n* ) = *Θ* ( *h* ( *n* )) 蕴含 *f* ( *n* ) = *Θ* ( *h* ( *n* )) - *f* ( *n* ) = *O* ( *g* ( *n* ))和 *g* ( *n* ) = *O* ( *h* ( *n* )) 蕴含 *f* ( *n* ) = *O* ( *h* ( *n* )) - *f* ( *n* ) = *Ω* ( *g* ( *n* ))和 *g* ( *n* ) = *Ω* ( *h* ( *n* )) 蕴含 *f* ( *n* ) = *Ω* ( *h* ( *n* )) - *f* ( *n* ) = *o* ( *g* ( *n* ))和 *g* ( *n* ) = *o* ( *h* ( *n* )) 蕴含 *f* ( *n* ) = *o* ( *h* ( *n* )) - *f* ( *n* ) = *ω* ( *g* ( *n* ))和 *g* ( *n* ) = *ω* ( *h* ( *n* )) 蕴含 *f* ( *n* ) = *ω* ( *h* ( *n* )) **自反性：** - *f* ( *n* ) = *Θ* ( *f* ( *n* )) - *f* ( *n* ) = *O* ( *f* ( *n* )) - *f* ( *n* ) = *Ω* ( *f* ( *n* )) **对称性：** - *f* ( *n* ) = *Θ* ( *g* ( *n* ))当且仅当 *g* ( *n* ) = *Θ* ( *f* ( *n* )) **转置对称性：** - *f* ( *n* ) = *O* ( *g* ( *n* ))当且仅当 *g* ( *n* ) = *Ω* ( *f* ( *n* )) - *f* ( *n* ) = *o* ( *g* ( *n* ))当且仅当 *g* ( *n* ) = *ω* ( *f* ( *n* )) ### 求解递归式的方法。 #### 递归树法 递归树法是一种解递归式比较特别的方法，在第一节将归并排序的时候有用到过这个方法。它最棒的一点就是总是能用，它能告诉你一种直觉让你知道答案是多少，只是有些不严谨。所以用这个方法时要特别小心，不然可能会得到错的答案。因为它需要用到点、点、点，使用省略号来得到结论。  #### 主定理方法 主定理方法本质上可以认为是递归树方法的一个应用，但是它更精确。不同于递归树方法有省略号有待证明，主定理方法基于一个定理（主定理）。遗憾的是，主方法限制颇多只能应用到特定的递归式上。主方法是计算时间复杂度的时候用的  那么这里我在取一个不满足主定理的例子~  所以主定理不满足时就利用决策树进行带入吧！如果数学计算能力比较强大还是可以计算出来的，毕竟主定理都是决策树证明的，数学能力不强表示证明有点困难... 不过这里有个偷懒的证明方法，直接假设f（n）是一个nk形式的； T（n）=aT（n/b）+nk T（n/b）=aT（n/b2）+（n/b）k ... 所以T(n)=a（aT（n/b2）+（n/b）k）+nk=nk（1+a/bk+...+(a/bk)h)=(nk-nlogba)/(1-a/bk),接下来讨论a和bk的关系决定了为nk还是nlogba，上面如果为1则为nklogbn了。 简单的证明， 替换法举一个例子如下：  关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

桶排序Bucket Sort从1956年就开始被使用，该算法的基本思想是由E.J.Issac  R.C.Singleton提出来。本博介绍BucketSort算法相关知识。 #### 算法描述与伪代码 假设输入的待排序元素是等可能的落在等间隔的值区间内.一个长度为N的数组使用桶排序, 需要长度为N的辅助数组. 等间隔的区间称为桶, 每个桶内落在该区间的元素. 桶排序是基数排序的一种归纳结果.算法的主要思想: 待排序数组A[1...n]内的元素是随机分布在[0,1)区间内的的浮点数.辅助排序数组B[0....n-1]的每一个元素都连接一个链表.将A内每个元素乘以N(数组规模)取底,并以此为索引插入(插入排序)数组B的对应位置的连表中**.**最后将所有的链表依次连接起来就是排序结果.这个过程可以简单的分步如下: 1. 设置一个定量的数组当作空桶子。 1. 寻访序列，并且把项目一个一个放到对应的桶子去。 1. 对每个不是空的桶子进行排序。 1. 从不是空的桶子里把项目再放回原来的序列中。 注意:1)note: 待排序元素越均匀, 桶排序的效率越高. 均匀意味着每个桶在中间过程中容纳的元素个数都差不多,不会出现特别少或者特别多的情况, 这样在排序子程序进行桶内排序的过程中会达到最优效率.2)note: 将元素通过恰当的映射关系将元素尽量等数量的分到各个桶(值区间)里面, 这个映射关系就是桶排序算法的关键.桶的标记(数组索引Index)的大小也要和值区间有对应关系 ~~~ BUCKET_SORT (A) n ← length [A] For i = 1 to n do Insert A[i] into list B[nA[i]] For i = 0 to n-1 do Sort list B with Insertion sort Concatenate the lists B[0], B[1], . . B[n-1] together in order. ~~~ **映射函数**bindex=f(key)   其中，bindex 为桶数组B的下标(即第bindex个桶), k为待排序列的关键字。桶排序之所以能够高效，其关键在于这个映射函数，它必须做到：如果关键字k1key=0; bucket_table[i]->next=NULL; } for(int j=0;jkey=A[j]; node->next=NULL; int index=A[j]/10; KeyNode *p=bucket_table[index]; if(p->key==0){ bucket_table[index]->next=node; (bucket_table[index]->key)++; } else{ while(p->next!=NULL&&p->next->key<=node->key) p=p->next; node->next=p->next; p->next=node; (bucket_table[index]->key)++; } } } ~~~ 注：上述部分codes采用桶内数据排序，我们使用了基于单链表的直接插入排序算法。可以使用基于双向链表的快排算法提高效率。 关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

对于给定的问题，一个计算机算法就是用计算机求解这个问题的方法。一般来说，算法是由有限条指令构成，每条指令规定了计算机所要行的有限次运算或者操作。对于一个问题，如果可以通过一个计算机程序，在有限的存储空间内运行有限长的时间而得到正确的结果，则称这个问题是算法可解的。但算法不等于程序，也不等于计算方法。当然，程序也可以作为算法的一种描述，但程序通常还需考虑很多与方法和分析无关的细节问题，这是因为在编写程序时要受到计算机系统运行环境的限制。通常，程序的编制不可能优于算法的设计。 算法的基本特征作为一个算法，一般应具有以下几个基本特征。 - 可行性（effectiveness) 针对实际问题设计的算法，人们总是希望能够得到满意的结果。但一个算法又总是在某个特定的计算工具上执行的，因此，算法在执行过程中往往要受到计算工具的 限制，使执行结果产生偏差。例如，在进行数值运算时，如果某计算工具有7位有效数字（如程序设计语言中的单精度运算），则在计算下列三个量A=1012，B=1，C= —1012的和时，如果采用不同的运算顺序，就会得到不同的结果，即：A+B+C=1012+1+（—1012）=0   A+C+B=1012+（—1012）+1=1 而在数学上，A+B+C与A+C+B是完全等价的。因此，算法与计算公式是有差别的。在设计一个算法时，必须考虑它的可行性，否则是不会得到满意结果的。 - 确定性 (definiteness)算 法的确定性，是指算法中的每一个步骤都必须是有明确定义的，不允许有模棱两可的解释，也不允许有多义性。这一性质也反映了算法与数学公式的明显差别。在解 决实际问题时，可能会出现这样的情况：针对某种特殊问题，数学公式是正确的，但按此数学公式设计的计算过程可能会使计算机系统无所适从。这是因为根据数学 公式设计的计算过程只考虑了正常使用的情况，而当出现异常情况时，此计算过程就不能适应了。 - 有穷性 (finiteness) 算法的有穷性，是指算法必须能在有限的时间内做完，即算法必须能在执行有限个步骤之后终止。数学中的无穷级数，在实际计算时只能取有限项，即计算无穷级数值的过程只能是有穷的。因此，一个数的无穷级数表示只是一个计算公式，而根据精度要求确定的计算过程才是有穷的算法。算法的有穷性还应该包括合理的执行时间的含义。因为，如果一个算法需要执行千万年，显然失去了实用价值。 - 拥有足够的情报 一个算法是否有效，还取决于为算法所提供的情报是否足够。通常，算法中的各种运算总是要施加到各个运算对象上，而这些运算对象又可能具有某种初始状态，这 是算法执行的起点或者是依据。因此，一个算法执行的结果总是与输入的初始数据有关，不同的输入将会有不同的结果输出。当输入不够或输入错误时，算法本身也 就无法执行或导致执行有错。一般来说，当算法拥有足够的情报时，此算法才是有效的，而当提供的情报不够时，算法可能无效。 综上所述，所谓算法，是一组严谨的定义运算顺序的规则，并且每一个规则都是有效的，且是明确的，此顺序将在有限的次数下终止。 算法的基本要素 一个算法通常有两种基本要素组成：一是对数据对象的运算和操作，二是算法的控制结构。 1. 算法中对数据的运算和操作: 每个算法实际上是按解题要求从环境能进行的所有操作中选择合适的操作所组成的一组指令序列。因此，计算机算法就是计算机能处理的操作所组成的指令序列。 通常，计算机可以执行的基本操作是以指令的形式描述的。一个计算机系统能执行的所有指令的集合，称为该计算机系统的指令系统。计算机程序就是按解题要求从计算机指令系统中选择合适的指令所组成的指令序列。在一般的计算机系统中，基本的运算和操作有以下四类：①算术运算：主要包括加、减、乘、除等运算。②逻辑运算：主要包括“与”、“或”、“非”等运算。③关系运算：主要包括“大于”、“小于”、“等于”、“不等于”等运算。④数据传输：主要包括赋值、输入、输出等操作。前面提到，计算机程序也可以作为算法的一种描述，但由于在编制计算机程序时通常要考虑很多与方 法和分析无关的细节问题（如语法规则），因此，在设计算法的一开始，通常并不直接用计算机程序来描述算法，而是用别的描述工具（如流程图，专门的算术描述 语言，甚至用自然语言）来描述算法。但不管用哪种工具来描述算法，算法的设计一般都应从上述四种基本操作考虑，按解题要求从这些基本操作中选择合适的操作 组成解题的操作序列。算法的主要特征着重于算法的动态执行，它区别于传统的着重于静态描述或按演绎方式求解问题的过程。传统的演绎数学是以公理系统为基础 的，问题的求解过程是通过有限次推演来完成的，每次推演都将对问题作进一步的描述，如此不断推演，直到直接将解描述出来为止。而计算机算法则是使用一些最 基本的操作，通过对已知条件一步一步的加工和变换，从而实现解题目标。这两种方法的解题思路是不同的。 1. 算法的控制结构 :一个算法的功能不仅取决于所选用的操作，而且还与各操作之间的执行顺序有关。算法中各操作之间的执行顺序称为算法的控制结构。算法的控制结构给出了算法的基本框架，它不仅决定了算法中各操作的执行顺序，而且也直接反映了算法的设计是否符合结构化原则。描述算法的工具通常有传统的流程图、N-S结构化流程图、算法描述语言等。一个算法一般都可以用顺序、选择、循环三种基本控制结构组合而成。 算法复杂度主要包括时间复杂度和空间复杂度。 算法的时间复杂度 所谓算法的时间复杂度，是指执行算法所需要的计算工作量。为了能够较客观的反映出一个算法的效率，在度量一个算法的工作量时，不仅应该与所使用的计算机、程序设计语言以及程序编制者无关，而且还应该与算法实现过程中的许多细节无关。为此，可以用算法在执行过程中所需基本运算的执行次数来度量算法的工作量。基本运算反映了算法运算的主要特征，因此，用基本运算的次数来度量算法工作量是客观的也是实际可行的，有利于比较同一问题的几种算法的优劣。例如，在考虑 两个矩阵相乘时，可以将两个实数之间的乘法运算作为基本运算，而对于所用的加法（或减法）运算忽略不计。又如，当需要在一个表中进行查找时，可以将两个元 素之间的比较作为基本运算。所执行的基本运算次数还与问题的规模有关。综上所述，算法的工作量用算法所执行的基本运算次数来度量，而算法所执行的基本运算次数是问题规模的函数. 算法的空间复杂度 一个算法的空间复杂度，一般是指执行这个算法所需要的内存空间。一 个算法所占用的存储空间包括算法程序所占的空间、输入的初始数据所占的存储空间以及算法执行过程中所需要的额外空间。其中额外空间包括算法程序执行过程中 的工作单元以及某种数据结构所需要的附加存储空间（例如，在链式结构中 ，除了要存储数据本身外，还需要存储链接信息）。如果额外空间量相对于问题规模来说是常数，则称该算法是原地（inplace）工作的。在许多实际问题中，为了减少算法所占的存储空间，通常采用压缩存储技术，以便尽量减少不必要的额外空间。 关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

原本计划在假期中总结完，结果速度太悠哉了，至今没整理完 。 "是否具有算法知识与技术的坚实基础是区分真正熟练的程序员与初学者的一个特征(《算法导论》)".  Charles Leiserson教授在MIT算法导论第一堂课说的：“如果你想成为一个编程高手，只要两年中每天坚持编程，你就能成为编程高手。如果你想成为一名世界级的程序员，你既可以十年如一日每天坚持编程，也可以两年中每天编程，然后上一门算法课”。依然是记忆犹新，同时也在一直提醒着我算法的重要性。 以下是**程序算法艺术与实践**内容博文的索引：***（待定未完待续）*** 1. 预备知识 - [有关算法的基本概念](http://blog.csdn.net/songzitea/article/details/46057403) - [函数的渐近的界 ](http://blog.csdn.net/songzitea/article/details/47668991) 分治/递归策略(Divide and Conquer) - [分治/递归的基本思想](http://blog.csdn.net/songzitea/article/details/48468733) - [递归循环与迭代](http://blog.csdn.net/songzitea/article/details/48498119) - [Fibonacci数列](http://blog.csdn.net/songzitea/article/details/47669689) - [矩阵相乘问题](http://blog.csdn.net/songzitea/article/details/47669533) 动态规划(Dynamic Programming) - DP设计思想 - 经典应用：投资问题 - 经典应用：背包问题(Knapsack Problem) - 经典应用：最长公共子序列LCS 贪心法(Greedy Approach) - GA设计思想 - 关于GA的正确性证明 - 经典应用：哈夫曼Huffman编码问题 - 经典应用：最小生成树（Prme算法与KMP算法） - 经典应用：单源最短路径（Dijkstra算法） NP完全问题 近似算法 随机算法 在线算法 遗传算法 模拟退火算法 蚁群算法 **经典排序算法** 1. [插入排序(Insertion Sort)](http://blog.csdn.net/songzitea/article/details/48498019) 1. [桶排序(Bucket Sort)](http://blog.csdn.net/songzitea/article/details/47124461) 1. 冒泡排序(Bubble Sort**) 1. 快速排序(Quick Sort) 1. 归并排序(Merge Sort) 1. 堆积排序(Heap Sort) 1. 选择排序(Selection sort) **参考资料** 1. Donald E.Knuth 著，苏运霖 译，《计算机程序设计艺术，第1卷基本算法》，国防工业出版社，2002年 1. Donald E.Knuth 著，苏运霖 译，《计算机程序设计艺术，第2卷半数值算法》，国防工业出版社，2002年 1. Donald E.Knuth 著，苏运霖 译，《计算机程序设计艺术，第3卷排序与查找》，国防工业出版社，2002年 1. Thomas H. Cormen, Charles E.Leiserson, etc., Introduction to Algorithms（3rd edition）, McGraw-Hill Book Company,2009 1. Jon Kleinberg, Ėva Tardos, Algorithm Design， Addison Wesley, 2005. 1. Sartaj Sahni ，《数据结构算法与应用：C++语言描述》 ，汪诗林等译，机械工业出版社，2000. 1. 屈婉玲，刘田，张立昂，王捍贫，算法设计与分析，清华大学出版社，2011年版，2013年重印. 1. 张铭，赵海燕，王腾蛟，《数据结构与算法实验教程》，高等教育出版社，2011年 1月 1. 王晓东，《算法设计与分析》 ，清华大学出版社，2003年1月。 **参考网站** 1. MIT 的《算法导论》（有OCW链接）[http://stellar.mit.edu/S/course/6/sp13/6.006/](http://stellar.mit.edu/S/course/6/sp13/6.006/) 1. Stanford 算法[ https://www.coursera.org/course/algo](https://www.coursera.org/course/algo) 1. Princeton 算法课  [https://www.coursera.org/course/algs4partI](https://www.coursera.org/course/algs4partI) 1. Berkeley《数据结构》  [http://www.cs.berkeley.edu/~jrs/61b/](http://www.cs.berkeley.edu/%7Ejrs/61b/) 1. Web 上的术语资源[http://www.nist.gov/dads/](http://www.nist.gov/dads/)   1. Algorithms in the Real World[ http://www.cs.cmu.edu/~guyb/realworld.html](http://www.cs.cmu.edu/%7Eguyb/realworld.html) 1. Advanced Data Structures and Algorithms[ http://theory.stanford.edu/~rajeev/cs361.html](http://theory.stanford.edu/%7Erajeev/cs361.html) 1. Advanced Data Structures[ http://www.cs.biu.ac.il/~moshe/ds1.html](http://www.cs.biu.ac.il/%7Emoshe/ds1.html) 1. CS 2015 Grad Algorithms, Spring [2015 http://people.cs.pitt.edu/~kirk/cs2150/](http://people.cs.pitt.edu/~kirk/cs2150/) 1. 哈工大《算法设计与分析之入门篇》[http://mooc.study.163.com/course/HIT-1000002012#/info](http://mooc.study.163.com/course/HIT-1000002012#/info) 1. 哈工大《算法设计与分析之进阶篇》[http://mooc.study.163.com/course/HIT-1000005000#/info](http://mooc.study.163.com/course/HIT-1000005000#/info) 1. 《数据结构与算法》精品课程  [http://www.jpk.pku.edu.cn/pkujpk/course/sjjg](http://www.jpk.pku.edu.cn/pkujpk/course/sjjg) 关于[程序算法艺术与实践](http://blog.csdn.net/column/details/tac-programalgrithm.html)更多讨论与交流，敬请关注本博客和新浪微博[songzi_tea](http://weibo.com/songzitea).

### B-树 我们知道B-树每个节点上包含着数据和指针，每个指针指向其一个子节点的位置， B-树的查找需要一次对每个节点进行二分查找，直至找到或返回null。通常，可以引入布朗过滤器等方式加速查找。B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点(其搜索性能等价于在关键字全集内做一次二分查找)。 应用场景： - 一般B-树常常作为磁盘的查找的数据结构使用。 - 一般磁盘为了减少寻道时间，往往会进行预读，一次读入1个或多个page的数据。我们只要将B-树的每个节点控制在一个page大小，就可以保证，磁盘一次的查找只需要一次IO。一个page大小一般在4k，可以存储不少的数据， 假设一个节点存储数据量为100**，**深度为3的B-树，即可保存100w数据(100*100*100)，而100的数据一般用不了4k的存储空间。当然，这里节点中存储的东西主要包括data和指针，指针大小是固定的，而数据有大有小。只要控制好每个数据块的大小，就可以提高B-树的性能。另外，一般情况下非叶子节点占用空间一般较小，完全可以缓存至内存中，这点也是在实际数据库实现中常常使用到的优化。 ### B+树  ### 特点 1. 有n棵子树的节点中含有n个关键字。 1. 所有的叶子结点中包含了全部关键字的信息，及所指向含这些关键字记录的指针，且叶子节点本身依关键字的大小而自小到大的顺序链接。 1. 所有非叶子结点可以看成是索引部分，结点中仅含有其子树中的最大(最小)关键字。 ### NOTE 1. B+树通常有两个指针，一个指向根结点，另一个指向关键字最小的叶子结点。因些，对于B+树进行查找两种运算：一种是从最小关键字起顺序查找，另一种是从根结点开始进行随机查找。 1.  在随机查找时，若非终端结点上的数据等于给定值，并不终止，而是继续向下直到叶子结点。因此，在B+树中，不管查找成功与否，每次查找都是走了一条从根到叶子结点的路径 1. B+树的查找与删除都从叶子节点开始 1. B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了 ### 应用场景： 这个结构一般用于数据库的索引，综合效率非常高，像 BerkerlyDB , sqlite , mysql 数据库都使用了这个算法处理索引。如果想自己做个小型数据库，可能参考一下这个算法的实现。索引在数据库中的作用。在数据库系统的使用过程当中，数据的查询是使用最频繁的一种数据操作。当数据库中数据非常多的时候，数据查询的效率就是数据库系统用户最关心的问题。要提高数据查询的效率，最简单、有效的方法就是在数据表相应的列上建立索引。索引是对数据库表中一个或多个列的值进行排序的结构。与在表中搜索所有的行相比，索引用指针指向存储在表中指定列的数据值，然后根据指定的次序排列这些指针，有助于更快地获取信息。通常情况下，只有当经常查询索引列中的数据时，才需要在表上创建索引。索引将占用磁盘空间，并且影响数据更新的速度。但是在多数情况下，索引所带来的数据检索速度优势大大超过它的不足之处。 ### B+树和B-树最大的不同点 1. B-树的关键字和记录是放在一起的，叶子节点可以看作外部节点，不包含任何信息；B+树的非叶子节点中只有关键字和指向下一个节点的索引，记录只放在叶子节点中。 1. 在B-树中，越靠近根节点的记录查找时间越快，只要找到关键字即可确定记录的存在；而B+树中每个记录的查找时间基本是一样的，都需要从根节点走到叶子节点，而且在叶子节点中还要再比较关键字。从这个角度看B-树的性能好像要比B+树好，而在实际应用中却是B+树的性能要好些。因为B+树的非叶子节点不存放实际的数据，这样每个节点可容纳的元素个数比B-树多，树高比B-树小，这样带来的好处是减少磁盘访问次数。尽管B+树找到一个记录所需的比较次数要比B-树多，但是一次磁盘访问的时间相当于成百上千次内存比较的时间，因此实际中B+树的性能可能还会好些，而且B+树的叶子节点使用指针连接在一起，方便顺序遍历(例如查看一个目录下的所有文件，一个表中的所有记录等)，这也是很多数据库和文件系统使用B+树的缘故。 数据库中集中索引方式。比如一个数据库中存储的是：用户信息(id, age, last_name, hometow)这样的四元组 **hash index：**如果要查询”finding all people with a last name of 'Smith.'”, 可以构造hash表，其key为last_name,而其value为指向某行的指针(也就是整条用户信息)。但是如果要查询"Find all people who are younger than 45."则hash表无能为力了，因为Hashes can deal with equality but not inequality. **bitmap index:**采用这种索引的话，查询效率很高，可以在常数时间内查询，但需要很大的存储空间 **B- index:** The main benefit of a B-tree is that it **allows logarithmic selections, insertions, and deletions in the worst case scenario**.**And unlike hash indexes it stores the data in an ordered way, allowing for faster row retrieval when the selection conditions include things like inequalities or prefixes. **Nodes in a B-tree contain**a value **and **a number of pointers to children nodes.**For database indexes the "**value" is really a pair of values: the indexed field and a pointer to a database row.(but in B+ the value is only an indexed field)**That is,rather than storing the row data right in the index, you store a pointer to the row on disk. B-tree indexes are typically designed so that each node takes up one disk block [](http://en.wikipedia.org/wiki/Block_(data_storage)). This allows each node to be read in with a single disk operation. ### 小结 B树：平衡二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点； B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点； 所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中； B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中； 转载请注明出处：[http://blog.csdn.net/songzitea/article/details/8864192](http://blog.csdn.net/songzitea/article/details/8864192)

### Trie树定义 Trie树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计和排序大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：最大限度地减少无谓的字符串比较，查询效率比哈希表高。Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。它有3个基本性质： (1)     根节点不包含字符，除根节点外每一个节点都只包含一个字符。 (2)     从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。 (3)     每个节点的所有子节点包含的字符都不相同。 ### 树的构建 **题目：**给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。**** **分析：**这题当然可以用hash来解决，但是本文重点介绍的是trie树，因为在某些方面它的用途更大。比如说对于某一个单词，我们要询问它的前缀是否出现过。这样hash就不好搞了，而用trie还是很简单。假设我要查询的单词是abcd，那么在他前面的单词中，以b，c，d，f之类开头的我显然不必考虑。而只要找以a开头的中是否存在abcd就可以了。同样的，在以a开头中的单词中，我们只要考虑以b作为第二个字母的，一次次缩小范围和提高针对性，这样一个树的模型就渐渐清晰了。好比假设有b，abc，abd，bcd，abcd，efg，hii 这6个单词，我们构建的树就是如下图这样的：  对于一个单词，只要顺着根走到对应的节点，再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色，就相当于插入了这个单词。这样一来查询和插入可以一起完成（重点体会这个查询和插入是如何一起完成的），所用时间仅仅为单词长度，在本题中因为每个单词的长度不超过10。可以看到，trie树每一层的节点数是26^i(i为层数)级别的。所以为了节省空间。我们用动态链表，或者用数组来模拟动态。空间的花费，不会超过单词数×单词长度。 ### 前缀查询 上文中提到”比如说对于某一个单词，我们要询问它的前缀是否出现过。这样hash就不好搞了，而用trie还是很简单“。下面，咱们来看看这个前缀查询问题： 题目：已知n个由小写字母构成的平均长度为10(len)的单词,判断其中是否存在某个串为另一个串的前缀子串 1)  最容易想到的：即从字符串集中从头往后搜，看每个字符串是否为字符串集中某个字符串的前缀，复杂度为O(n^2)。 2) 使用hash：我们用hash存下所有字符串的所有的前缀子串，建立存有子串hash的复杂度为O(n*len)，而查询的复杂度为O(n)*O(1)= O(n)。**NOTE:**因为是前缀子串，所以一个长度为len的字符串的前缀子串数目为len **例如：**abc的前缀子串为a，ab，abc 3) 使用trie：因为当查询如字符串abc是否为某个字符串的前缀时，显然以b,c,d....等不是以a开头的字符串就不用查找了。所以建立trie的复杂度为O(n*len)，而建立+查询在trie中是可以同时执行的，建立的过程也就可以成为查询的过程，hash就不能实现这个功能。所以总的复杂度为O(n*len)，实际查询的复杂度也只是O(len)。（说白了，就是Trie树的平均高度h为len，所以Trie树的查询复杂度为O（h）=O（len）。好比一棵二叉平衡树的高度为logN，则其查询，插入的平均时间复杂度亦为O（logN））。 下面解释下上述方法3中所说的为什么hash不能将建立与查询同时执行，而Trie树却可以：在hash中，例如现在要输入两个串911，911456，如果要同时查询这两个串，且查询串的同时若hash中没有则存入。那么，这个查询与建立的过程就是先查询其中一个串911，没有，然后存入9、91、911；而后查询第二个串911456，没有然后存入9、91、911、9114、91145、911456。因为程序没有记忆功能，所以并不知道911在输入数据中出现过，只是照常以例行事，存入9、91、911、9114、911...。也就是说用hash必须先存入所有子串，然后for循环查询。而trie树中，存入911后，已经记录911为出现的字符串，在存入911456的过程中就能发现而输出答案；倒过来亦可以，先存入911456，在存入911时，当指针指向最后一个1时，程序会发现这个1已经存在，说明911必定是某个字符串的前缀。 ### 查询 Trie树是简单但实用的数据结构，通常用于实现字典查询。我们做即时响应用户输入的AJAX搜索框时，就是Trie开始。本质上，Trie是一颗存储多个字符串的树。相邻节点间的边代表一个字符，这样树的每条分支代表一则子串，而树的叶节点则代表完整的字符串。和普通树不同的地方是，相同的字符串前缀共享同一条分支。下面，再举一个例子。给出一组单词，inn, int, at, age,adv, ant, 我们可以得到下面的Trie：  搭建Trie的基本算法也很简单，无非是逐一把每个单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在，就共享，否则创建对应的节点和边。 比如要插入单词add，就有下面几步： (1)      考察前缀"a"，发现边a已经存在。于是顺着边a走到节点a。 (2)      考察剩下的字符串"dd"的前缀"d"，发现从节点a出发，已经有边d存在。于是顺着边d走到节点ad (3)      考察最后一个字符"d"，这下从节点ad出发没有边d了，于是创建节点ad的子节点add，并把边ad->add标记为d ### Trie树的应用 除了本文引言处所述的问题能应用Trie树解决之外，Trie树还能解决下述问题： 1) 有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。 2)一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。 转载请注明出处：[http://blog.csdn.net/utimes/article/details/8864150](http://blog.csdn.net/utimes/article/details/8864150)

### 问题描述 二阶马尔可夫链：**例如：of the people, by thepeople, for the people** ### 分析 Prefix(后缀数组)     Suffix of the                       people                                    比如 thepeople后面可以跟by for 空，可根据概率选择一个如果选择for，则过度到状态people for，从 the people                by                                         而可以知道后续为the依次类推，给定一个前缀，可以一直往下找，直到”空”为止 people, by                 the                                        **几种实现方法：(note:C++ stl中可用map>实现)** by  the          people         1)普通的hash表，记录前缀与后缀(比如前缀thepeople的后缀包括by, for,空)，给定前缀可以通过hash the people    for         表很快查找到后缀，然后根据概率选择一个后缀(根据在后缀中出现次数)，过渡到下一个状态 people for the        2)使用后缀数组，数组中每个元素指向一个单词的开始的位置，**先对后缀数组排序**，然后**用二分查找** for the          people        **得到prefix第一次出现的位置 ，**最后往后遍历根据概率选择一个后缀。 the people                        空        3) hash表与后缀数组相结合，使用后缀数组构造hash表 **首先解决一个问题** 当有多个suffix时，如何按照概率选择一个，比如the people by for 空， ~~~ int nmatch=0; for everyone in suffix if( rand()%++nmatch==0 ) select=this_suffix; ~~~ 对每一个后缀都执行上述的判断，可知第一个suffix一定被选中，第二个suffix以1/2的概率替换，第三个以1/3的概率替换 ~~~ #include #include #include #define NHASH 49979 #define MULT 31 #define MAXWORDS 80000 char inputchars[4300000];//存储输入数据 char *word[MAXWORDS];//后缀数组 int nword=0;//记录单词数 int k=2;//2阶 int next[MAXWORDS];//用于构建hash表 int bin[NHASH]; //以k个单词为单位，进行hash unsigned int hash(char* str){ int n; unsigned int h=0; char* p=str; for(n=k;n>0;++p){ h=MULT*h+*p; if(*p=='\0') --n; } return h%NHASH; } //比较前k个单词的大小 int wordncmp(char* p,char *q){ int n; for(n=k;*p==*q;++p,++q){ if(*p=='\0'&&(--n)==0) return 0; } return *p-*q; } //从当前单词出发，跳过前n个单词 char* skip(char* p,int n){ for(;n>0;++p){ if(*p=='\0') --n; } return p; } int main(){ int i,j; //步骤1：构建后缀数组 word[0]=inputchars; //scanf以空格作为分隔符, 并且自动加上'\0' while((scanf("%s",word[nword]))!=EOF){ word[nword+1]=word[nword]+strlen(word[nword])+1; ++nword; } //附加k个空字符,保证wordncmp()正确（感觉不需要这个） for(i=0;inext[5](1)->next[1](0)->next[0](-1) for(i=0;i<=nword-k;++i) { j=hash(word[i]); next[i]=bin[j]; bin[j]=i; } //步骤3：生成随机文本 int wordsleft;//生成单词数 int psofar; char *phrase,*p; phrase=inputchars; for(wordsleft=10000;wordsleft>0;--wordsleft){ psofar=0; for(j=bin[hash(phrase)];j>=0;j=next[j]) //在hash值相同的项中找出字符串值相同的后缀数组表项，根据概率选择一个 if(wordncmp(phrase,word[j])==0&&rand()%(++psofar)==0) p=word[j]; //将phrase重新设置 phrase=skip(p,1); //输出符合要求单词的后面第k个单词 if(strlen(skip(phrase,k-1))==0) break; printf("%s\n",skip(phrase,k-1)); } return 0; } ~~~ **转载请注明出处：**[http://blog.csdn.net/utimes/article/details/8864122](http://blog.csdn.net/utimes/article/details/8864122)

### 引言 本节主要介绍基本的排序算法原理与实现 ，即：插入排序，选择排序，冒泡排序. ### 插入排序算法 #### 基本思想 插入排序首先考虑data中的前两个元素，即data[0]和data[1]。如果它们的次序颠倒了，就交换它们。然后，考虑第三个元素data[2],将其插入到合适的位置上。如果data[2]同时小于data[0]和data[1],那么data[0]和data[1]都要移动一个位置；data[0]放在位置1上，data[1]放在位置2上，而将data[2]放在位置0上。如果data[2]小于data[1]，而不于data[0],那么只须把data[1]移动到位置2上，并由data[2]占据它的位置。最后，如果data[2]不小于前两个元素，它将保留在当前的位置。每一个元素data[i]都要插入到合适的位置j上，使0<=j<=i,所有比data[i]大的元素都要移动一个位置。 插入排序算法的要点如下： ~~~ insertionsort(data[],n){ for(i=1; i void insertionsort(T data[], int n) { for(int i =1, j; i0&&tmp< data[j-1]; j--) data[j] = data[j-1]; data[j] =tmp; } } ~~~ 插入排序的一个优点是只有需要时才对数组排序。如果数组已经排好序了，就不再对数组进行移动；只有变量tmp得到初始化，存储在变量中的值返回值原位置。可以识别出已排序的数组部分，并相应停止，但忽视元素可以已在合适位置上的事实。一个缺点是：如果插入数据项，所有比插入元素大的元素都必须移动。插入操作不是局部的，可能需要移动大量的元素。其中，在博文[【编程珠玑】插入排序](http://blog.csdn.net/songzitea/article/details/8761722)中，介绍了关于插入排序优化代码。 #### 算法分析 为了获取insertionsort()算法执行的移动和比较次数，首先要注意，外层的for语句执行n-1次。但是，比data[i]大的元素移动一个位置的次数并不总是相同的。 **最好的情况是**：数据已排好序。对于每个位置i,只需比较一匀，这样就只需进行n-1次比较(其数量级是o(n))和2(n-1)次移动，所有的移动和比较都是多余的。**最坏的情况是：**数据按相反顺序排序。在这种情况下，对于外层for的每次迭代i,都比较i次，即所有迭代的比较总数是  内层for中的赋值次数可以用相同的公式计算。把tmp在外层for中加载和卸载的次数加起来，得到总的移动次数：  前面我们只考虑了极端情况。如果数据是随机排序的，结果如何呢？假设数据项占用数组单元的概率相等，在外层for的迭代i中，data[i]与其它元素的平均比较次数计算如下：  为了求得所有比较次数的平均值，对于所有的迭代i来说，都必须从1开始一直累加到n-1为止。结果是  它的时间复杂度是O(n^2),大约是最坏情况下的比较次数的1/2。按照相同的方式，可以确定在外层for的迭代i中，data[i]需要移动0,1,..i-1次：即  次，加上一定分会发生的两次移动。因此，在外层for中所有迭代中，平均移动次数为  其中时间复杂度为O(n^2)。 综上所述，对于随机顺序的数组来说，移动和比较的次数是与最好情况接近，还是与最坏情况接近？遗憾的是，它接近于后者，即：当数组的元素加倍时，平均需要付出4倍的努力来排序。 #### 测试输出结果  ### 选择排序算法 #### 基本思想 选择排序先找到时位置不合适的元素，再把它放在其最终的合适位置上，它试图仅在本地交换数组元素。基本思想是：先找出数组中的最小元素，将其与第一个位置上的元素进行交换。然后在剩余元素data[1],...,data[i-1]中找到最小元素，把它放到第二个位置上。这种选择和定位的方法是：在每次迭代中，找出元素data[i],....data[n-1]中的最小元素，然后将其与data[i]交换位置，直到所有的元素都放到了合适位置为止。 如下的伪代码反映出选择排序算法的简单性： ~~~ selectionsort(data[] ,n) for i =0 到n-2 找出元素data[i]....data[n-1]中的最小元素； 将其与data[i]交换； ~~~ 很明显，n-2是最后一个i值，因为寻如果除最后一个元素之外的所有元素都放在合适的位置上，那么第n个元素就是一定是最大的。下面提选择排序的C++代码： ~~~ template void selectionsort (genType data[], int n) { int j,least; for(int i =0; ii;--j) 如果两者逆序，交换位置j和j-1的元素 ~~~ 下面是冒泡排序的实现： ~~~ template void bubblesort( genType data[], int n) { for( int i =0; ii;--j){ if(data[j] ';

### 问题描述 从2开始到n-1都不能整除则为素数。 ### 优化 1. 从2到sqrt(n)不能整除就可以 1.  通过对被2、3和5整除的特殊检验，避免了近3/4的开方运算，其次，只考虑奇数作为可能的因子，在剩余的数中避免了大约一半的整除检验（注意一点，2，3，5本身也是素数）（If( n%2 == 0 ) return (n==2); //能被2整除且不是2本身的不是素数） 1. 用乘法运算代替开方运算 ~~~ int prime(int n) { if(n%2==0)return (n==2); if(n%3==0)return (n==3); if(n%5==0)return (n==5); for(int i=7; i*i<=n; i+=2) if(n%i==0)return 0; return 1; } ~~~ ### 简单的埃氏筛法 实现简单的埃氏筛法（Sieve of Eratosthenes）来计算所有小于n的素数。这个程序的主要数据结构是一个n比特的数组，初始值都为真。每发现一个素数时，数组中所有这个素数的倍数就设置为假。下一个素数就是数组中下一个为真的比特。 ### 解析 下面的C程序实现了埃氏筛法来计算所有小于n的素数。其基本数据结构是n比特数组x，初始值全部为1。每发现一个素数，数组中所有它的倍数都设为0。下一个素数就是数组中的下一个取值为1的比特位。 ~~~ #include using namespace std; int main( ){ int i, p, n; char x[100001];  n = 100000; for (i = 1; i <= n; i++) x[i] = 1; x[1] = 0; //1不是素数 p = 2; //第一个素数 while (p <= n){ cout< ';

### 问题描述 前面有两节提供了不同方法解决关于将一个具有n个元素的一维向量向左旋转i个位置。即：***[旋转交换](http://blog.csdn.net/utimes/article/details/8762497)***和***[J](http://blog.csdn.net/utimes/article/details/8759966)****[uggling算法](http://blog.csdn.net/utimes/article/details/8759966)*。本节，提出另一种方案，块变换解决此问题。 （来源于**《编程珠玑》第2版**的第2章第11页问题B） 请将一个具有n个元素的一维向量向左旋转i个位置。例如，假设n=8，i=3，那么向量abcdefgh旋转之后得到向量defghabc。简单编码使用一个具有n个元素的中间向量分n步即可完成此作业。你可以仅使用几十字节的微小内存，花费与n成比例的时间来旋转该向量吗？ ### 解析 直观的想法：由于要对数组整体向左循环移动k位，那么我们就可以对数组中的每一个元素向左移动k位(超过数组长度的可以取模回到数组中)，此时总是能获得结果的。如原串　01234567结果：34567012。观察结果，直接的想法，我们能不能直接把待移动的串直接后面（0123456789  -- 7893456012）。此时，012是正确的位置了，但是其他元素还需调整。但是我们可以看到，把7893456变成3456789也需要向左循环移3位，这和第一步的变化是一样的，可以用递归做。 **原理：**将待旋转的向量x看成是由向量a和b组成的，那么旋转向量x实际上就是将向量ab的两个部分交换为向量ba **步骤**：假设a比b短(谁长，谁分成两部分) 　　　1)将b分割为bl和br两个部分，使得br的长度和a的长度一样 　　　2)交换a和br，即ablbr转换成了brbla。通过本次变换，序列a就位于它的最终位置了。 　　　3)我们需要集中精力交换b的两个部分了，这个时候就回到了最初的问题上了,我们可以递归地处理b部分。 举例：待旋转字符串"0123456789",向左移动3位 原串：　0123456789结果：3456789012 第一步：　把**b**分成**bl**和**br**两部分 **a     b** **012** 3456789 ->**012**3456789(3456是一部分，789是一部分） 第二步：　把**a**与**br**交换 **br    bl    a** 789  3456  012 (此时，012就是自己的最终的位置) 第三步：　之后可以递归处理　789 3456(**a**代表789,**b**代表3456) ---------------------------------------------------------- 全部过程 待旋转序列：0123456789 结果：3456789012 红色表示已排好，绿色表示分的第一部分，黑色表示分的第二部分 第一步：7893456012 第二步：4563789012 第三步：3564789012 第四步：3465789012 第五步：3456789012 ### 程序代码 ~~~ #include #include using namespace std; // 函数作用：把两块数据互换 // arr:待翻转的字符串,aStart：第一块内容的起始位置,bStart：第二块内容的起始位置,len：交换的长度 void swap(char* arr,int aStart,int bStart,int len){ assert(arr != NULL && aStart >= 0 && bStart >= 0 && len > 0); char tmp; while(len-- > 0){ tmp = arr[aStart]; arr[aStart] = arr[bStart]; arr[bStart] = tmp; aStart++; bStart++; } //cout< rightLen) { swap(str,leftStart,leftStart+leftLen,rightLen); Rotate(str,leftStart +rightLen,len-rightLen,len-2*rightLen); } else { swap(str,leftStart,leftStart+len-leftLen,leftLen); Rotate(str,leftStart,len-leftLen,leftLen); } } void LeftRotateString(char* str,int k){ Rotate(str,0,strlen(str),k); } int main( ){ char str[60] = "abcdefghi"; LeftRotateString(str,3); cout< ';

### 问题描述 （来源于**《编程珠玑》第2版**的第2章第11页问题B） 请将一个具有n个元素的一维向量向左旋转i个位置。例如，假设n=8，i=3，那么向量abcdefgh旋转之后得到向量defghabc。简单编码使用一个具有n个元素的中间向量分n步即可完成此作业。你可以仅使用几十字节的微小内存，花费与n成比例的时间来旋转该向量吗？ ### 解决思路 ### 方案一： 将向量x中的前i个元素复制到一个临时数组中，接着将余下的n-i个元素左移i个位置，然后再将前i个元素从临时数组中复制回x中的后面位置。该方案使用了i个额外的位置，如i足够大，过于浪费空间。 ~~~ #include void Rotate(char *a, int length, int i) { char tmp[10]; int step = i % length; if (step == 0) { return; } int j = 0; for (j = 0; j < step; j++){ tmp[j] = a[j]; } tmp[step] = '\0'; for (j = step; j < length; j++){ a[j -step] = a[j]; } while((a[length - step + j] = tmp[j]) != '\0'){ j++; } } void main() { char a[9] = "abcdefgh"; Rotate(a,8,3); printf("%s",a); } ~~~ ### 方案二： 定义一个函数来将x向左旋转一个位置，然后调用该函数i次。该方案需要将数组移到i将，过于浪费时间。 ### 方案三： 先将x[0]移临时变量t中，然后将x[i]移到x[0]中，x[2i]移到x[i]中，依次类推，直到我们又回到从x[0]中提取元素，不过在这时我们要从t中提取元素，然后结束该过程。当i=3，n=12时，该阶段将以下面的次序移到各个元素。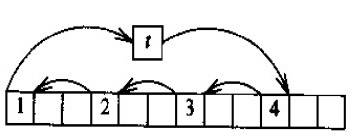  如果该过程不能移动所有的元素，那么我们再从x[1]开始移动，一直依次进行下去，直到移动了所有的元素时为止。 该方案过于精巧，像书中所说的一样堪称巧妙的杂技表演，非常容易出错。 ### 方案四： 旋转向量x实际上就是将向量ab的两个部分交换为向量ba，这里a代表x的前i个元素。假设a比b短。将b分割成bl和br，使br的长度和a的长度一样。交换a和br，将ablbr转换成brbla。因为序列a已在它的最终位置了，所以我们可以集中精力交换b的两个部分了。由于这个新问题和原先的问题是一样的，所以我们以递归的方式进行解决。 该方案要求编码细腻，还需要深思熟虑，以确保程序具有足够的效率。 ### 方案五： [最佳] 将这个问题看作是把数组ab转换成数组ba吧，但同时也假定我们具有在数组中转置指定部分元素的函数。我们先从ab开始，转置a得到arb，再转置b得到arbr，然后再转置整个arbr得到（arbr）r，实际上就是ba。 ~~~ reverse(0, i-1) /*cbadefgh*/ reverse(i, n-1) /*cbahgfed*/ reverse(0, n-1) /*defghabc*/ ~~~ 该转置代码在时间和空间上都很有效，并且是这么简短和简单，想出错都很难。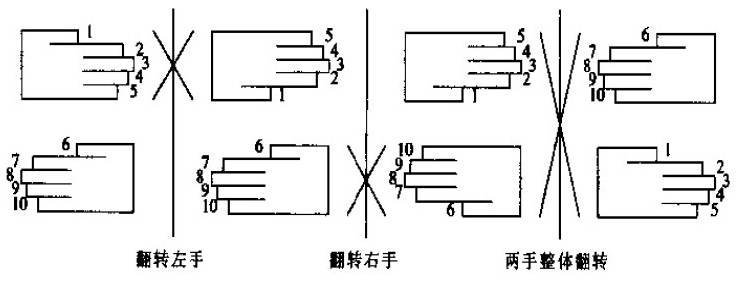 书中还提供了将10个元素的数组向上旋转5个位置的手摇法例子：先是掌心对着你自己，左手在右手上面，如图所示  ### 代码实现 ~~~ #include void swap(int *p, int *q); void reverse(int *vector, int index_begin, int index_end); void revrot(int *vector, int len, int step); int main(int argc, char **argv){ int step = 3; int i = 0; int vector[1024] = {1,2,3,4,5,6,7,8}; revrot(vector, 8, step); printf("after revolve: "); for(i = 0; i < 8; i++){ printf("%d ", vector[i]); } printf("\n"); } void swap(int *p, int *q){ int temp; temp = *p; *p = *q; *q = temp; } void reverse(int *vector, int index_begin, int index_end){ while(index_begin < index_end){ swap(vector + index_begin, vector + index_end); index_begin++; index_end--; } } void revrot(int *vector, int len, int step){ reverse(vector, 0, step - 1); reverse(vector, step, len - 1); reverse(vector, 0, len - 1); } ~~~ **转载请注明出处**：[http://blog.csdn.net/utimes/article/details/8762497](http://blog.csdn.net/utimes/article/details/8762497)

在编程珠玑一书对快速排序讲得较为透彻，最早的快排是单向的，慢慢演化成双向的，也就是目前的版本。从此书能看到这种演化的必要性。我想在这里，对其原理搞懂了就不会忘了（^_^）。 ### 快速排序思想 1962年，由C.A.R.Hoare创造出来。该算法核心思想就一句话：“**排序数组时，将数组分成两个小部分，然后对它们递归排序**”。然而采取什么样的策略将数组分成两个部分是关键，想想看，如果随便将数组A分成A1和A2两个小部分，即便分别将A1和A2排好序，那么A1和A2重新组合成A时仍然是无序的。所以，我们可以在数组中找一个值，称为key值，我们在把数组A分解为A1和A2前先对A做一些处理，让小于key值的元素都移到其左边，所有大于key值的元素都移到其右边。这样递归排序A1和A2，数组A就排好了。 **举例**   我们要排序的数组如下： | 55 | 41 | 59 | 26 | 53 | 58 | 97 | 93 | |-----|-----|-----|-----|-----|-----|-----|-----| 我们选取第一个元素作为key值，即55.（一般都是选取第一个元素）。假如我们有一种办法可以将数组做一步预处理，让小于key值的元素都位于其左边，大于key值的元素都位于其右边，预处理完数组如下： | 41 | 26 | 53 | 55 | 59 | 58 | 97 | 93 | |-----|-----|-----|-----|-----|-----|-----|-----| 这样数组就被key值划分成了两段，A[0...2]小于key，A[4...7]大于key，可见key值本身已排好序，接下来对A[0...2]和A[4...7]分别进行递归排序，那么整个数组就排好序了。预处理做的工作再次澄清下：找一个key值，把key位放到某位置A[p]，使小于key值的元素都位于A[p]左边，大于key值的元素都位于A[p]的右边。到此，我们的快排模型就成型了。 ~~~ //s, u 代表待排序部分的下界和上界 void qsort(s, u){ //递归结束条件是待排序部分的元素个数小于2 if(s >= u) { return; } //此处进行预处理，预处理后key值位于位置p qsort(s, p-1); qsort(p+1, u); } ~~~ 接下来看如何做预处理。我们选取A[0]做为key值, p作为key值的位置。我们从A[1]开始遍历后面的数组，用变量i指示目前的位置，每次找到小于key的值都与A[++p]交换。开始时p=0. | 55 | 41 | 59 | 26 | 53 | 58 | 97 | 93 | |-----|-----|-----|-----|-----|-----|-----|-----| i = 1，A[i]位置为41, 即A[i] < key, swap(++p , i)，即p = 1: | 55 | 41 | 59 | 26 | 53 | 58 | 97 | 93 | |-----|-----|-----|-----|-----|-----|-----|-----| i = 2，A[i]位置为59，A[i] > key，不做任何改变。 i = 3，A[i]位置为26，A[i] < key，swap(++p, i)， 即p = 2: | 55 | 41 | 26 | 59 | 53 | 58 | 97 | 93 | |-----|-----|-----|-----|-----|-----|-----|-----| i = 4，A[i]位置为53，A[i] < key，swap(++p, i)，p = 3: | 55 | 41 | 26 | 53 | 59 | 58 | 97 | 93 | |-----|-----|-----|-----|-----|-----|-----|-----| i = 5，A[i]位置为58，A[i] > key，不做任何改变。 i = 6，A[i]位置为97，A[i] > key，不做任何改变. i = 7，A[i]位置为93，A[i] > key，不做任何改变.结束循环。此时p为key的最终位置。还需一步把key值填入p位置。 最后swap(l, p)即把Key值放到最终位置上了。至于为什么要交换l,p的位置，可以另拿一组数据试一下：55，41，59，26，99，58，97，93。 ~~~ //l, u 代表待排序部分的下界和上界 void qsort(int l, int u){ //递归结束条件是待排序部分的元素个数小于2 if(l >= u) return;  int p = l; for(int i = l+1; i <= u; i++) { if(A[i] < A[l]) swap(++p, i); } swap(l, p); qsort(l, p-1); qsort(p+1, u); } ~~~ 这就是第一代快速排序算法，正常情况下其复杂度为nlogn，但在考虑一种极端情况：n个相同元素组成的数组。在n-1次划分中每次划分都需要O(n)的时间，所以总的时间为O（n^2）。使用双向划分就可以避免这个问题。 ### 双向划分快速排序 ~~~ /*l, u 代表待排序部分的下界和上界*/ void qsort(int l, int u){ /*递归结束条件是待排序部分的元素个数小于2*/ if(l >= u) return; key = A[l] for(int i = l, j = u+1; i <= j; ) { do i++ while(i <= u && A[i] < key)); do j-- while(A[j] > key); if(i > j) break; swap(i, j); } swap(l, j); qsort(l, j-1); qsort(j+1, u); } ~~~ **转载请注明了出处**：[http://blog.csdn.net/utimes/article/details/8762451](http://blog.csdn.net/utimes/article/details/8762451)

### 问题描述 设有n个人围坐一圈并按顺时针方向从1到n编号,从第s个人开始进行1到m的报数, 报数到第m个人, 此人出圈, 再从他的下一个人重新开始1到m的报数,如此进行下去直到所有的人都出圈为止。现要求按出圈次序,给出这n个人的顺序表p。请考生编制函数Josegh()实现此功能并调用函数WriteDat()把编号按照出圈的顺序输出到OUT.DAT文件中。设 n = 100, s = 1, m = 10进行编程。 ### 解析 约瑟夫环有好多种解法，但是大体的可以分为两类：1. 将符合出圈要求的人进行标注，但是不出圈，只是下次再轮到此人时，直接跳过，不参加报数2. 将符合出圈要求的人直接出圈(从环中删除），剩下的人继续报数。这里列的是第二种方法，删除的方法是把该元素放到数组中的最后一个位置上，在出圈元素的后边的元素，都向前移动一位。 ### 实现如下： ~~~ void Josegh(void) { int i; int count;//count当做数数的变量 int people=n;//定义没有出圈的人数 int tem;//存放出圈人的编号 int j; //为这100个人进行编号 for(i=0;i1) { i=i%people;//已经出圈人的下标不再计算之内，也就是说数到数组中最后一个没有出圈的编号的时候，i重新指向0 count=count%m;//count数到9的时候再从零开始数 //count数到10的时候count的值为0，执行下面的if语句 if(count==0){ //下面的循环将出圈的人之后的编号往前移动一位，出圈的人的编号放在p数组中的最后一位，视为出圈，同时人数减少一个 tem=p[i]; for(j=i;j ';

我们在前几节，介绍了一篇三种方案解决**如何生成位于0到n-1之间的k个不同的随机顺序的随机整数？**[[请点击](http://blog.csdn.net/utimes/article/details/8761541)]，本节则基于上述中，拓展如下所示的问题，然后，给出几个方案。 ### 问题描述 产生[0, n) 范围内不重复的随机数。 ### 方案一：Knuth 的S方案 有一个结论：从r中等概率的选出s个，某一个被选中的概率为s/r。证明：从r中选出s个有C(r, s)种情况，其中C(r, s)表示组合。同理，若要选定某项比如t，则需要从生下的(r-1)项中，选择(s-1)项，有C(r-1, s-1)种情况。则从r项中选择s项，t被选中的概率为　P = C(r-1, s - 1) / C(r, s)　；另一方面有排列组合的性质知，C(r,s) = r!/( s! *(r-s)! )　则有 　　C(r - 1, s - 1) = (r-1)!/( (s-1)! * (r-s)! ) = s/r * r/s * (r-1)!/( (s-1)! * (r-s)! )                             = s/r * r*(r-1)! / ( s*(s-1)! * (r-s)!) = s/r * r!/( s! *(r-s)! ) = s/r * C(r, s) 故有P = s/r 伪代码 ~~~ for i = [0, n) if bigrand()%r < s then print i --s; --r; ~~~ 例如n=5, m =2, 那么选第一个元素的概率就是2/5,如果选上了那么选第二个元素概率就是1/4，否则选择第二个元素的概率就是2/4 ~~~ void gen_knuth(int n, int m){ for(int i = 0; i < n; i ++){ if(big_rand()%(n-i) < m){ cout << i; m--; } } cout<< endl; } ~~~ ### 方案二：Knuth 置换方法P 首先用一个数组顺序存储[0, n)的数据，然后随机交换任意两个下标的元素，最终取其最初的m个，记得到m个不同的随机数。 ~~~ for i = [0, n) x[i] = i; for i = [0, m) swap(i, randint(i, n-1)) ~~~ ### 方案三：蓄水池方法 蓄水池方法用以解决n很大或者n实现不可知的情况。将k看成水池容量，n = length(S)看成一个事先未知的集合S的大小 ~~~ array R[k]; // result integer i, j; // fill the reservoir array for each i in 1 to k do R[i] := S[i] done; // replace elements with gradually decreasing probability for each i in k+1 to length(S) do j := random(1, i); // important: inclusive range if j <= k then R[j] := S[i] fi done ~~~ 个人的理解是，若文档非空(至少有一行)，则先记下该行，然后看文档是否读完，若没有(对应着 while more input lines)，当前行是第k行，则以1/k的概率(相当于把1到k行放在一起，等概率选择)决定是否用第k行替换上次的选择的结果。一次类推，最终array R[1] 中存储的一个[0, n)的随机

### 问题描述 （来源于**《编程珠玑》第2版**的第2章第11页问题A） Given a sequential file that contains at most four billion 32-bit integers in random order, find an integer that isn't in the file (and there must be at least one missing -- why?). How would you solve this problem with ample quantities of  main memory ? How would you solve it if you could use several external "scratch" files but only a few hundreds bytes of main memories ?　[译]给定一个包含40亿个随机排列的顺序文件，找到一个不在文件中的32位整数，在有足够内存的情况下应该如何解决该问题？如果有几个外部的临时文件可用，但是仅有几百字节的内存，又该如何解决？如有足够内存，完全可用第一章介绍的位图方法解决。这里关注内存不足时的解决方案。 ### 基本思想 二分搜索（binary search）又称折半查找，它是一种效率较高的查找方法。二分查找要求：1）必须采用顺序存储结构； 2）必须按关键字大小有序排列。优缺点：折半查找法的优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。 因此，折半查找方法适用于不经常变动而查找频繁的有序列表。充分利用了元素间的次序关系，采用分治策略，可在最坏的情况下用O(log n)完成搜索任务。 首先，将表中间位置记录的关键字与查找关键字比较， 如果两者相等，则查找成功； 否则利用中间位置记录将表分成前、后两个子表， 如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。将n个元素分成个数大致相同的两半，取a[n/2]与欲查找的x作比较，如果x=a[n/2]则找到x，算法终止。如果xa[n/2]，则我们只要在数组a的右半部继续搜索x。 二分搜索法的应用极其广泛，而且它的思想易于理解。第一个二分搜索算法早在1946 年就出现了，但是第一个完全正确的二分搜索算法直到1962年才出现。Bentley在他的著作《Writing Correct Programs》中写道，90%的计算机专家不能在2小时内写出完全正确的二分搜索算法。问题的关键在于准确地制定各次查找范围的边界以及终止条件的确定，正确地归纳奇偶数的各种情况，其实整理后可以发现它的具体算法是很直观的。 **分析** 对于32位的整数，可以表示的整数个数为2^32 = 4 294 967 296 > 4e9(40亿)，因此有些数据不在该文件中。部分呼号约定：设存有40亿数据的文件为F，其中每个数据均为32bit，不在该文件中的数据集合为M(just think about the word missing for a while)。F 中的数据和M中的数据一起构成32比特能够表示的所有数据，即|F| + |M| = 2^32。从F中各数据的最高位比特开始，按其为0或者1分为两部分，假设分别为A、B，则A、B的大小有两种情况： 1) A和B中的数据个数相同。[由于|F| < 2^32，则|A| = |B| = |F|/2 < 2^31，]由于最初的数据文件F不包含数据M，则A、B均不包含M中的数据，即A、B中均缺失32比特能够表示的”部分数据“(即M中的数据)，此时随便找一个文件，比如A，设定其为新的F，同时假设A中缺失的数据为新的M(也就是先前M中以0开头的数据，由于A 是以0开头的数据，事实上M当然是未知的)，然后按照次高位比特进行划分。 2) A和B中的数据个数不同。假设A的个数多余B中的个数，即|A| > |B|，不能确定A中是否缺失数据，因为A完全可能包含以0开头的所有数据，这样A就不缺失数据。但是可以确定的是B一定缺失数据，否则|B| = 2^31，总数为40亿(小于2^32)，导致A中的数据小于2^31，进而少于于B中的数据个数，与开始处的假设矛盾。令B为新的F，B中缺失的数据位新的M(即M中以1打头的数据，这也是由于B是以1开始的)。 通过上述最高位比特的分析后，可以得到一个文件F，其数据规模不超过N/2，其中N位F中的所有数据。同时可知有些数据不在文件F中，仅在M中。接着按第二位比特的信心对F进行上述的A、B分类，A是F中第二位比特为0的数据，B是F中第二位比特为1的数据。也能得出A、B中数据个数的信息。 1、若|A| = |B|，即A、B缺失数据，令F为A即可，继续。 2、若|A| != |B|，假设|A| > |B| ，则B缺失数据，令F为B，继续。 可以得到新的F其规模不超过N/4，继续A、B分类 ### 示例模拟： 一大堆的文字描述不好理解，下面以一组4bit数字模拟一下上面的过程：4bit共可表示2^4 = 16个整数，假设初始文件F如下： ~~~ 0 0000 1 0001 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 11 1011 12 1100 13 1101 14 1110 15 1111 ~~~ 前面一列为10进制数，可以看到文件中缺失了0010（2），1010（10）。 ### 第一次分解文件 A文件只包含0xxx的数：（x为未探索的位） ~~~ 0 0000 1 0001 3 0011 4 0100 5 0101 6 0110 7 0111 ~~~ B文件只包含1xxx的数： ~~~ 8 1000 9 1001 11 1011 12 1100 13 1101 14 1110 15 1111 ~~~ 按照上面的分析，|A|=|B|=7 < 2^3 ，都有数据缺失，随机选取A文件为新的文件F。 ### 第二次分解文件 A文件只包含00xx的数： ~~~ 0 0000 1 0001 3 0011 ~~~ B文件只包含01xx的数： ~~~ 4 0100 5 0101 6 0110 7 0111 ~~~ 由于|A| < |B|，选取A为新的F文件。 ### 第三次分解文件 A文件只包含000x的数据： ~~~ 0 0000 1 0001 ~~~ B文件只包含001x的数据： ~~~ 3 0011 ~~~ 由于|B| < |A|，选取B为新的F文件。 ### 第四次分解文件 A文件只包含0010的数据：没有数据。 B文件只包含0011的数据：0011 此时|A| < |B| ，所以缺失的数据必在A中，那么缺失的数据应该为0010，即十进制2。 ### 代码 ~~~ #include #include #define MAX_BIT 32 void file_split(FILE *srcfd, FILE *bit0fd, FILE *bit1fd, unsigned int *bit0_count, unsigned int *bit1_count, int cur_bit); /* binary search(0/1 search). For simplicity, ignore error checking */ int main(int argc, char**argv){ unsigned int mdata = 0; unsigned int bit0_count = 0; unsigned int bit1_count = 0; unsigned int missing_num = 0xFFFFFFFF;   char mdatafn[] = "mdata.txt"; char bit0fn[] = "bit0.txt"; char bit1fn[] = "bit1.txt"; FILE *mdatafn_ptr = NULL; FILE *bit0_ptr = NULL; FILE *bit1_ptr = NULL; int cur_bit = MAX_BIT; mdatafn_ptr = fopen(mdatafn, "w+"); printf("Please input one number or input EOF to stop input:\n"); while(scanf("%u", &mdata) != EOF){ fprintf(mdatafn_ptr, "%u\n", mdata); printf("Please input one number or input EOF to stop input:\n"); } fflush(mdatafn_ptr); rewind(mdatafn_ptr); bit0_ptr = fopen(bit0fn, "w+"); bit1_ptr = fopen(bit1fn, "w+"); while(cur_bit-- > 0){ bit0_count = 0; bit1_count = 0; file_split(mdatafn_ptr, bit0_ptr, bit1_ptr, &bit0_count, &bit1_count, cur_bit); if(bit0_count <= bit1_count){ /* if |A| <= |B|, select A as new metadata */ printf("the missiong data's %d bit is 0.\n", cur_bit+1); missing_num &= (~(1< ';