# 简单计算器 **Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 16351    Accepted Submission(s): 5604** Problem Description 读入一个只包含 +, -, *, / 的非负整数计算表达式，计算该表达式的值。 Input 测试输入包含若干测试用例，每个测试用例占一行，每行不超过200个字符，整数和运算符之间用一个空格分隔。没有非法表达式。当一行中只有0时输入结束，相应的结果不要输出。 Output 对每个测试用例输出1行，即该表达式的值，精确到小数点后2位。 Sample Input ~~~ 1 + 2 4 + 2 * 5 - 7 / 11 0 ~~~ Sample Output ~~~ 3.00 13.36 ~~~ 1.将原表达式转为后缀式在求值 2.代码： ~~~ #include<cstdio> #include<cstring> #include<stack> using namespace std; char s[1000]; int ss[1000]; int a[1000]; char s1[100]; char s2[1000]; int hsh[300]; int e[10]; int main() { hsh['#']=-1; hsh['+']=0; hsh['-']=0; hsh['*']=1; hsh['/']=1; e[0]=1; e[1]=10; e[2]=100; e[3]=1000; e[4]=10000; e[5]=100000; e[6]=1000000; e[7]=10000000; e[8]=100000000; e[9]=1000000000; while(gets(s)) { if(strcmp(s,"0")==0) break; int len=strlen(s); int pos=0; stack<char> S; S.push('#'); s[len]=' '; int j=0; int k=0; int l=0; for(int i=0; i<=len; i++) { if(s[i]>='0'&&s[i]<='9') s1[j++]=s[i]; else if(s[i]==' ') { int x=0; for(int jj=0; jj<j; jj++) { x+=(s1[jj]-'0')*e[j-1-jj]; } if(j!=0) a[l++]=x; j=0; } else s2[k++]=s[i]; } s2[k]='#'; for(int i=0; i<=k+l; i++) { if(i%2==1) { while(!S.empty()&&hsh[S.top()]>=hsh[s2[i/2]]) { if(S.top()!='#') { char cc=S.top(); if(cc=='+') ss[pos++]=-1; if(cc=='-') ss[pos++]=-2; if(cc=='*') ss[pos++]=-3; if(cc=='/') ss[pos++]=-4; }; S.pop(); } S.push(s2[i/2]); } else ss[pos++]=a[i/2]; } stack<double> SS; for(int i=0; i<pos; i++) { if(ss[i]>=0) { double x=(double)ss[i]; SS.push(x); } else { double sec=SS.top(); SS.pop(); double fir=SS.top(); SS.pop(); if(ss[i]==-1) { fir=fir+sec; } if(ss[i]==-2) { fir=fir-sec; } if(ss[i]==-3) { fir=fir*sec; } if(ss[i]==-4) { fir=fir/sec; } SS.push(fir); } } printf("%.2lf\n",SS.top()); } return 0; } ~~~

# Nightmare **Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 9120    Accepted Submission(s): 4389** Problem Description Ignatius had a nightmare last night. He found himself in a labyrinth with a time bomb on him. The labyrinth has an exit, Ignatius should get out of the labyrinth before the bomb explodes. The initial exploding time of the bomb is set to 6 minutes. To prevent the bomb from exploding by shake, Ignatius had to move slowly, that is to move from one area to the nearest area(that is, if Ignatius stands on (x,y) now, he could only on (x+1,y), (x-1,y), (x,y+1), or (x,y-1) in the next minute) takes him 1 minute. Some area in the labyrinth contains a Bomb-Reset-Equipment. They could reset the exploding time to 6 minutes. Given the layout of the labyrinth and Ignatius' start position, please tell Ignatius whether he could get out of the labyrinth, if he could, output the minimum time that he has to use to find the exit of the labyrinth, else output -1. Here are some rules: 1\. We can assume the labyrinth is a 2 array. 2\. Each minute, Ignatius could only get to one of the nearest area, and he should not walk out of the border, of course he could not walk on a wall, too. 3\. If Ignatius get to the exit when the exploding time turns to 0, he can't get out of the labyrinth. 4\. If Ignatius get to the area which contains Bomb-Rest-Equipment when the exploding time turns to 0, he can't use the equipment to reset the bomb. 5\. A Bomb-Reset-Equipment can be used as many times as you wish, if it is needed, Ignatius can get to any areas in the labyrinth as many times as you wish. 6\. The time to reset the exploding time can be ignore, in other words, if Ignatius get to an area which contain Bomb-Rest-Equipment, and the exploding time is larger than 0, the exploding time would be reset to 6. Input The input contains several test cases. The first line of the input is a single integer T which is the number of test cases. T test cases follow. Each test case starts with two integers N and M(1<=N,Mm=8) which indicate the size of the labyrinth. Then N lines follow, each line contains M integers. The array indicates the layout of the labyrinth. There are five integers which indicate the different type of area in the labyrinth: 0: The area is a wall, Ignatius should not walk on it. 1: The area contains nothing, Ignatius can walk on it. 2: Ignatius' start position, Ignatius starts his escape from this position. 3: The exit of the labyrinth, Ignatius' target position. 4: The area contains a Bomb-Reset-Equipment, Ignatius can delay the exploding time by walking to these areas. Output For each test case, if Ignatius can get out of the labyrinth, you should output the minimum time he needs, else you should just output -1. Sample Input ~~~ 3 3 3 2 1 1 1 1 0 1 1 3 4 8 2 1 1 0 1 1 1 0 1 0 4 1 1 0 4 1 1 0 0 0 0 0 0 1 1 1 1 4 1 1 1 3 5 8 1 2 1 1 1 1 1 4 1 0 0 0 1 0 0 1 1 4 1 0 1 1 0 1 1 0 0 0 0 3 0 1 1 1 4 1 1 1 1 1 ~~~ Sample Output ~~~ 4 -1 13 ~~~ 代码： ~~~ #include<cstdio> #include<cstring> #include<queue> using namespace std; struct node { int x,y; int t; int step; node(int a,int b,int c,int d):x(a),y(b),t(c),step(d) {} void Set(int a,int b,int c,int d) { x=a; y=b; t=c; step=d; } }; int n,m; int xs,ys,xe,ye; int mat[10][10]; int vis[10][10]; int dir[4][2]= {-1,0,1,0,0,-1,0,1}; //up down left right void bfs() { memset(vis,0,sizeof(vis)); queue<node> Q; node first=node(xs,ys,6,0); if(first.x==xe&&first.y==ye&&first.t>0) { printf("%d\n",first.step); return; } Q.push(first); vis[first.x][first.y]=first.t; while(!Q.empty()) { //printf("----------------\n"); first=Q.front(); Q.pop(); node next=node(0,0,0,0); for(int i=0; i<4; i++) { int tx=first.x+dir[i][0]; int ty=first.y+dir[i][1]; if(tx>=n||tx<0||ty>=m||ty<0) continue; if(mat[tx][ty]==0) continue; if(vis[tx][ty]+1>=vis[first.x][first.y]) continue; next.Set(tx,ty,first.t-1,first.step+1); if(mat[tx][ty]==4) next.t=6; vis[next.x][next.y]=next.t; //printf("%d %d %d %d\n",next.x,next.y,next.t,next.step); if(next.x==xe&&next.y==ye&&next.t>0) { printf("%d\n",next.step); return; } Q.push(next); } } printf("-1\n"); } int main() { int t; scanf("%d",&t); //printf("%d\n",t); while(t--) { scanf("%d%d",&n,&m); for(int i=0; i<n; i++) { for(int j=0; j<m; j++) { scanf("%d",&mat[i][j]); if(mat[i][j]==2) { xs=i; ys=j; } if(mat[i][j]==3) { xe=i; ye=j; } } } bfs(); } return 0; } ~~~

# Ignatius and the Princess I **Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 15576    Accepted Submission(s): 4937 Special Judge** Problem Description The Princess has been abducted by the BEelzebub feng5166, our hero Ignatius has to rescue our pretty Princess. Now he gets into feng5166's castle. The castle is a large labyrinth. To make the problem simply, we assume the labyrinth is a N*M two-dimensional array which left-top corner is (0,0) and right-bottom corner is (N-1,M-1). Ignatius enters at (0,0), and the door to feng5166's room is at (N-1,M-1), that is our target. There are some monsters in the castle, if Ignatius meet them, he has to kill them. Here is some rules: 1.Ignatius can only move in four directions(up, down, left, right), one step per second. A step is defined as follow: if current position is (x,y), after a step, Ignatius can only stand on (x-1,y), (x+1,y), (x,y-1) or (x,y+1). 2.The array is marked with some characters and numbers. We define them like this: . : The place where Ignatius can walk on. X : The place is a trap, Ignatius should not walk on it. n : Here is a monster with n HP(1<=n<=9), if Ignatius walk on it, it takes him n seconds to kill the monster. Your task is to give out the path which costs minimum seconds for Ignatius to reach target position. You may assume that the start position and the target position will never be a trap, and there will never be a monster at the start position. Input The input contains several test cases. Each test case starts with a line contains two numbers N and M(2<=N<=100,2<=M<=100) which indicate the size of the labyrinth. Then a N*M two-dimensional array follows, which describe the whole labyrinth. The input is terminated by the end of file. More details in the Sample Input. Output For each test case, you should output "God please help our poor hero." if Ignatius can't reach the target position, or you should output "It takes n seconds to reach the target position, let me show you the way."(n is the minimum seconds), and tell our hero the whole path. Output a line contains "FINISH" after each test case. If there are more than one path, any one is OK in this problem. More details in the Sample Output. Sample Input ~~~ 5 6 .XX.1. ..X.2. 2...X. ...XX. XXXXX. 5 6 .XX.1. ..X.2. 2...X. ...XX. XXXXX1 5 6 .XX... ..XX1. 2...X. ...XX. XXXXX. ~~~ Sample Output ~~~ It takes 13 seconds to reach the target position, let me show you the way. 1s:(0,0)->(1,0) 2s:(1,0)->(1,1) 3s:(1,1)->(2,1) 4s:(2,1)->(2,2) 5s:(2,2)->(2,3) 6s:(2,3)->(1,3) 7s:(1,3)->(1,4) 8s:FIGHT AT (1,4) 9s:FIGHT AT (1,4) 10s:(1,4)->(1,5) 11s:(1,5)->(2,5) 12s:(2,5)->(3,5) 13s:(3,5)->(4,5) FINISH It takes 14 seconds to reach the target position, let me show you the way. 1s:(0,0)->(1,0) 2s:(1,0)->(1,1) 3s:(1,1)->(2,1) 4s:(2,1)->(2,2) 5s:(2,2)->(2,3) 6s:(2,3)->(1,3) 7s:(1,3)->(1,4) 8s:FIGHT AT (1,4) 9s:FIGHT AT (1,4) 10s:(1,4)->(1,5) 11s:(1,5)->(2,5) 12s:(2,5)->(3,5) 13s:(3,5)->(4,5) 14s:FIGHT AT (4,5) FINISH God please help our poor hero. FINISH ~~~ 1.abduct：绑架，诱拐，使外展 2.如果结构体中有构造函数，用该结构体类型去定义变量时，必须用构造函数去初始化变量，否则编译通不过 3.代码： ~~~ #include<cstdio> #include<cstring> #include<queue> #include<stack> using namespace std; struct node { int x,y,t; node(int a,int b,int c):x(a),y(b),t(c) {}//构造函数 void Set(int a,int b,int c)//设置函数 { x=a; y=b; t=c; } bool operator <(const node &a)const//让优先队列的优先级：t小的，优先级高 { return a.t<t; } }; struct node1 { int x,y; }; int n,m; char mat[105][105]; bool vis[105][105]; node1 matt[105][105];//记录父亲坐标 int dir[4][2]= {1,0,0,1,-1,0,0,-1}; bool flag; void bfs() { memset(vis,0,sizeof(vis)); priority_queue<node> Q; node first=node(0,0,0); Q.push(first); vis[first.x][first.y]=1; matt[0][0].x=0; matt[0][0].y=0; while(!Q.empty()) { first=Q.top(); Q.pop(); if(first.x==n-1&&first.y==m-1) { flag=1; printf("It takes %d seconds to reach the target position, let me show you the way.\n",first.t); stack<node1> S;//把路径存储在栈里 node1 e; e.x=n-1; e.y=m-1; S.push(e); while(1) { e=S.top(); if(e.x==matt[e.x][e.y].x&&e.y==matt[e.x][e.y].y) { break; } node1 ee; ee.x=matt[e.x][e.y].x; ee.y=matt[e.x][e.y].y; S.push(ee); } for(int i=1; i<=first.t; i++)//输出路径 { printf("%ds:",i); if(mat[S.top().x][S.top().y]!='.') { printf("FIGHT AT (%d,%d)\n",S.top().x,S.top().y); mat[S.top().x][S.top().y]--; if(mat[S.top().x][S.top().y]=='0') { mat[S.top().x][S.top().y]='.'; } } else { printf("(%d,%d)",S.top().x,S.top().y); S.pop(); printf("->(%d,%d)\n",S.top().x,S.top().y); } } printf("FINISH\n"); break; } node next=node(0,0,0); for(int i=0; i<4; i++) { int tx=first.x+dir[i][0]; int ty=first.y+dir[i][1]; if(tx>=n||tx<0||ty>=m||ty<0||vis[tx][ty]==1) { continue; } else if(mat[tx][ty]=='X') { continue; } else if(mat[tx][ty]=='.') { next.Set(tx,ty,first.t+1); matt[tx][ty].x=first.x; matt[tx][ty].y=first.y; vis[tx][ty]=1; Q.push(next); } else { next.Set(tx,ty,first.t+1+mat[tx][ty]-'0'); vis[tx][ty]=1; matt[tx][ty].x=first.x; matt[tx][ty].y=first.y; Q.push(next); } } } if(!flag) printf("God please help our poor hero.\nFINISH\n"); } int main() { while(scanf("%d%d",&n,&m)==2) { for(int i=0; i<n; i++) { scanf("%s",mat[i]); } flag=0; bfs(); } return 0; } ~~~

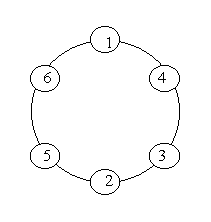
# Prime Ring Problem **Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 37427    Accepted Submission(s): 16521** Problem Description A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime. Note: the number of first circle should always be 1.    Input n (0 < n < 20).   Output The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order. You are to write a program that completes above process. Print a blank line after each case.   Sample Input ~~~ 6 8 ~~~   Sample Output ~~~ Case 1: 1 4 3 2 5 6 1 6 5 2 3 4 Case 2: 1 2 3 8 5 6 7 4 1 2 5 8 3 4 7 6 1 4 7 6 5 8 3 2 1 6 7 4 3 8 5 2 ~~~ 1.自然数（natural number），是非负整数（1, 2, 3, 4……）。认为自然数不包含[零](http://baike.baidu.com/subview/45676/8420704.htm)的其中一个理由是因为人们在开始学习数字的时候是由“一、二、三...”开始，而不是由“零、一、二、三...”开始, 因为这样是非常不自然的。在全球范围内，目前针对0是否属于自然数的争论依旧存在。在中国大陆，2000年左右之前的中小学教材一般不将0列入自然数之内，或称其属于“扩大的自然数列”。在2000年左右之后的新版中小学教材中，普遍将0列入自然数。 2.代码： ~~~ #include<cstdio> #include<cstring> using namespace std; int n; int vis[30]; int a[30]; int p[20]={2,3,5,7,11,13,17,19,23,29,31,37,41}; int c=1; int cnt; bool isPrime(int x) { for(int i=0;i<13;i++) { if(x==p[i]) { return 1; } } return 0; } void dfs(int level,int num) { a[level]=num; vis[num]=1; if(level==n) { if(isPrime(a[n]+a[1])) { if(cnt==0) printf("Case %d:\n",c++); cnt++; for(int i=1;i<=n;i++) { if(i==1) printf("%d",a[i]); else printf(" %d",a[i]); } printf("\n"); } return; } for(int i=1;i<=n;i++) { if(vis[i]==1||isPrime(i+a[level])==0) continue; dfs(++level,i); level--; vis[i]=0; } } int main() { while(scanf("%d",&n)==1) { memset(vis,0,sizeof(vis)); cnt=0; dfs(1,1); printf("\n"); } return 0; } ~~~

# Safecracker ##### Time Limit : 2000/1000ms (Java/Other)   Memory Limit : 65536/32768K (Java/Other) ##### Total Submission(s) : 3   Accepted Submission(s) : 1 Problem Description === Op tech briefing, 2002/11/02 06:42 CST === "The item is locked in a Klein safe behind a painting in the second-floor library. Klein safes are extremely rare; most of them, along with Klein and his factory, were destroyed in World War II. Fortunately old Brumbaugh from research knew Klein's secrets and wrote them down before he died. A Klein safe has two distinguishing features: a combination lock that uses letters instead of numbers, and an engraved quotation on the door. A Klein quotation always contains between five and twelve distinct uppercase letters, usually at the beginning of sentences, and mentions one or more numbers. Five of the uppercase letters form the combination that opens the safe. By combining the digits from all the numbers in the appropriate way you get a numeric target. (The details of constructing the target number are classified.) To find the combination you must select five letters v, w, x, y, and z that satisfy the following equation, where each letter is replaced by its ordinal position in the alphabet (A=1, B=2, ..., Z=26). The combination is then vwxyz. If there is more than one solution then the combination is the one that is lexicographically greatest, i.e., the one that would appear last in a dictionary." v - w^2 + x^3 - y^4 + z^5 = target "For example, given target 1 and letter set ABCDEFGHIJKL, one possible solution is FIECB, since 6 - 9^2 + 5^3 - 3^4 + 2^5 = 1. There are actually several solutions in this case, and the combination turns out to be LKEBA. Klein thought it was safe to encode the combination within the engraving, because it could take months of effort to try all the possibilities even if you knew the secret. But of course computers didn't exist then." === Op tech directive, computer division, 2002/11/02 12:30 CST === "Develop a program to find Klein combinations in preparation for field deployment. Use standard test methodology as per departmental regulations. Input consists of one or more lines containing a positive integer target less than twelve million, a space, then at least five and at most twelve distinct uppercase letters. The last line will contain a target of zero and the letters END; this signals the end of the input. For each line output the Klein combination, break ties with lexicographic order, or 'no solution' if there is no correct combination. Use the exact format shown below."   Sample Input ~~~ 1 ABCDEFGHIJKL 11700519 ZAYEXIWOVU 3072997 SOUGHT 1234567 THEQUICKFROG 0 END ~~~   Sample Output ~~~ LKEBA YOXUZ GHOST no solution ~~~ 1.lexicographical order:cap < card < cat < to < too< two < up 2.其实是个组合问题12*11*10*9*8大约十几万次当然5个循环不超时，用搜索的形式写的时候因为递归和回溯耗时，所以超时 3.代码： ~~~ #include<cstdio> #include<cstring> #include<algorithm> using namespace std; int t; char s[20]; int a[10]; int len; bool flag; int cmp(int a,int b) { return a>b; } void Find() { for(int i=1; i<=len; i++) { a[1]=s[i]-'A'+1; for(int j=1; j<=len; j++) { if(i==j) continue; a[2]=s[j]-'A'+1; for(int k=1; k<=len; k++) { if(j==k||k==i) continue; a[3]=s[k]-'A'+1; for(int l=1; l<=len; l++) { if(l==k||l==j||l==i) continue; a[4]=s[l]-'A'+1; for(int m=1; m<=len; m++) { if(m==l||m==k||m==j||m==i) continue; a[5]=s[m]-'A'+1; if(a[1]-a[2]*a[2]+a[3]*a[3]*a[3]-a[4]*a[4]*a[4]*a[4]+a[5]*a[5]*a[5]*a[5]*a[5]==t) { flag=1; break; } } if(flag) break; } if(flag) break; } if(flag) break; } if(flag) break; } } int main() { while(scanf("%d%s",&t,s+1)==2) { if(t==0&&strcmp("END",s+1)==0) { break; } else { len=strlen(s+1); flag=0; sort(s+1,s+1+len,cmp);//保证答案是字典序上最大 Find(); if(flag) printf("%c%c%c%c%c\n",a[1]+'A'-1,a[2]+'A'-1,a[3]+'A'-1,a[4]+'A'-1,a[5]+'A'-1); else printf("no solution\n"); } } return 0; } ~~~

# Tempter of the Bone **Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 95890    Accepted Submission(s): 25982** Problem Description The doggie found a bone in an ancient maze, which fascinated him a lot. However, when he picked it up, the maze began to shake, and the doggie could feel the ground sinking. He realized that the bone was a trap, and he tried desperately to get out of this maze. The maze was a rectangle with sizes N by M. There was a door in the maze. At the beginning, the door was closed and it would open at the T-th second for a short period of time (less than 1 second). Therefore the doggie had to arrive at the door on exactly the T-th second. In every second, he could move one block to one of the upper, lower, left and right neighboring blocks. Once he entered a block, the ground of this block would start to sink and disappear in the next second. He could not stay at one block for more than one second, nor could he move into a visited block. Can the poor doggie survive? Please help him.   Input The input consists of multiple test cases. The first line of each test case contains three integers N, M, and T (1 < N, M < 7; 0 < T < 50), which denote the sizes of the maze and the time at which the door will open, respectively. The next N lines give the maze layout, with each line containing M characters. A character is one of the following: 'X': a block of wall, which the doggie cannot enter; 'S': the start point of the doggie; 'D': the Door; or '.': an empty block. The input is terminated with three 0's. This test case is not to be processed.   Output For each test case, print in one line "YES" if the doggie can survive, or "NO" otherwise.   Sample Input ~~~ 4 4 5 S.X. ..X. ..XD .... 3 4 5 S.X. ..X. ...D 0 0 0 ~~~   Sample Output ~~~ NO YES ~~~ 1.奇偶剪枝：http://baike.baidu.com/view/7789287.htm 百度百科，假设起点是sx，sy终点是ex,ey那么abs(ex-sx)+abs(ey-ey)为起点到终点的最短步数。起点到终点的步数要么是最短步数（最短步数+0），要么是最短步数+一个偶数（偏移路径）。 2.代码： ~~~ #include<cstdio> #include<cstring> using namespace std; char mat[10][10]; bool vis[10][10]; int n,m,t; int xs,ys,xd,yd; bool flag; int dir[4][2]={1,0,-1,0,0,-1,0,1};//up,lower,left,right int ABS(int a) { if(a<0) return -a; else return a; } void dfs(int x,int y,int time) { if(x<0||x>=n||y<0||y>=m) return; if(mat[x][y]=='X') return; if(vis[x][y]==1) return; vis[x][y]=1; if(x==xd&&y==yd&&time==t) { flag=true; return; } if(time==t&&(x!=xd||y!=yd)) return; if(time>t) return; for(int i=0;i<4;i++) { int xt=x+dir[i][0]; int yt=y+dir[i][1]; if(xt<0||xt>=n||yt<0||yt>=m||mat[xt][yt]=='X'||vis[xt][yt]==1) continue; dfs(xt,yt,++time); vis[xt][yt]=0; time--; if(flag==1) return; } } int main() { while(scanf("%d%d%d",&n,&m,&t)&&(n||m||t)) { for(int i=0;i<n;i++) { scanf("%s",mat[i]); for(int j=0;j<m;j++) { if(mat[i][j]=='S') { xs=i; ys=j; } if(mat[i][j]=='D') { xd=i; yd=j; } } } int ms=ABS(xd-xs)+ABS(yd-ys); if(t<ms) { printf("NO\n"); continue; } if((t-ms)%2) { printf("NO\n"); continue; } flag=false; memset(vis,0,sizeof(vis)); dfs(xs,ys,0); if(flag) printf("YES\n"); else printf("NO\n"); } return 0; } ~~~

1.代码： ~~~ #include<stdio.h> #include<string.h> #include<math.h> #define Max(a,b) ((a)>(b)?(a):(b)) #define Min(a,b) ((a)<(b)?(a):(b)) #define N 100000 int a[N]; int ST1[N][20]; int ST2[N][20]; int n,q; void make_ST() { for(int j=1;(1<<j)<=n;j++) { for(int i=1;(i+(1<<j)-1)<=n;i++) { ST1[i][j]=Max(ST1[i][j-1],ST1[i+(1<<(j-1))][j-1]); ST2[i][j]=Min(ST2[i][j-1],ST2[i+(1<<(j-1))][j-1]); } } } int Query(int l,int r) { int k=floor(log((double)(r-l+1))/log((double)(2))); return Max(ST1[l][k],ST1[r-(1<<k)+1][k])-Min(ST2[l][k],ST2[r-(1<<k)+1][k]); } int main() { while(scanf("%d%d",&n,&q)==2) { for(int i=1;i<=n;i++) { scanf("%d",&a[i]); ST1[i][0]=ST2[i][0]=a[i]; } make_ST(); while(q--) { int l,r; scanf("%d%d",&l,&r); printf("%d\n",Query(l,r)); } } return 0; } ~~~

**1.题目解析可见《训练指南》P198** **2代码：** ~~~ #include<cstdio> #include<cstring> #include<cmath> #define Min(a,b) ((a)<(b)?(a):(b)) #define Max(a,b) ((a)>(b)?(a):(b)) #define N 100005 #define INF 1<<30 using namespace std; int a[N]; int value[N],cnt[N],num[N],L[N],R[N]; int ST[N][20]; int n,q; int k; void make_ST()//对cnt[]预处理 { for(int i=1;i<=k;i++) { ST[i][0]=cnt[i]; } for(int j=1;(1<<j)<=n;j++) { for(int i=1;(i+(1<<j)-1)<=n;i++) { ST[i][j]=Max(ST[i][j-1],ST[i+(1<<(j-1))][j-1]); } } } int Query(int l,int r) { if(l>r) return 0; else { int kk=floor(log2(r-l+1)); return Max(ST[l][kk],ST[r-(1<<kk)+1][kk]); } } int main() { while(scanf("%d",&n)&&n) { scanf("%d",&q); k=0; value[0]=INF; for(int i=1;i<=n;i++) { scanf("%d",&a[i]); if(a[i]!=value[k]) { R[k]=i; value[++k]=a[i]; L[k]=i-1; cnt[k]=1; num[i]=k; } else { cnt[k]++; num[i]=num[i-1]; } } R[k]=n+1; make_ST(); while(q--) { int l,r; scanf("%d%d",&l,&r); if(num[l]==num[r]) { printf("%d\n",r-l+1); } else { int tmp=Max(R[num[l]]-l,r-L[num[r]]); int ans=Max(tmp,Query(num[l]+1,num[r]-1)); printf("%d\n",ans); } } } return 0; } ~~~

代码： ~~~ #include<cstdio> #include<cstring> using namespace std; int LCPS[1000005]; int next[1000005]; char s[1000005]; int n; void GetLCPS() { int j=0; int k=-1; next[0]=-1; while(j<n) { if(k==-1||s[k]==s[j]) { LCPS[j++]=++k; next[j]=k; } else { if(k-1>=0) k=LCPS[k-1]; else k=-1; } } } int main() { int cnt=0; while(scanf("%d",&n)&&n) { printf("Test case #%d\n",++cnt); scanf("%s",s); GetLCPS(); for(int i=1;i<n;i++) { int cir=(i+1)-(next[i+1]); int r=(i+1)%cir; int k=(i+1)/cir; if(r==0&&k>1) { printf("%d %d\n",i+1,k); } } printf("\n"); } return 0; } ~~~

**1.区间是一段的，不是断开的哟** **2.代码是看着标程写的** **3.枚举左端点，二分右端点流程：**  ~~~ #include<cstdio> #include<cstring> #include<cmath> #define LL long long #define Max(a,b) ((a)>(b)?(a):(b)) #define Min(a,b) ((a)<(b)?(a):(b)) using namespace std; const int N=200007; int minn[N][20];//2^18=262144 2^20=1048576 int maxx[N][20]; //----------------------查询O(1)------------- int queryMin(int l,int r) { int k=floor(log2((double)(r-l+1)));//2^k <= (r - l + 1),floor()向下取整函数 return Min(minn[l][k],minn[r-(1<<k)+1][k]); } int queryMax(int l,int r) { int k=floor(log2((double)(r-l+1))); return Max(maxx[l][k],maxx[r-(1<<k)+1][k]); } //------------------------------------------------- int calc(int l,int r) { int k=log2((double)(r-l+1)); int MAX=Max(maxx[l][k],maxx[r-(1<<k)+1][k]); int MIN=Min(minn[l][k],minn[r-(1<<k)+1][k]); return MAX-MIN; } int main() { int T; int n,k,i,j,p; LL ans; scanf("%d",&T); while(T--) { scanf("%d%d",&n,&k); for(i=1; i<=n; ++i) { scanf("%d",&j); minn[i][0]=maxx[i][0]=j; } //------------------------------------------预处理O(nlogn)--------------- for(j=1; (1<<j)<=n; ++j)//1<<j==2^j,枚举区间长度1，2，4，8，16，，，，， for(i=1; i+(1<<j)-1<=n; ++i)//i+(1<<j)-1表示区间右边界，枚举区间左边界 { p=(1<<(j-1)); minn[i][j]=Min(minn[i][j-1],minn[i+p][j-1]); maxx[i][j]=Max(maxx[i][j-1],maxx[i+p][j-1]); } //----------------------------------------------------------------------- //---------------------------枚举左端点，二分右端点--------------------------- int l,r,mid; ans=0; //左端点固定为i，右端点用l,r,mid去确定，最后用l和r中的其中一个，此时l+1==r for(i=1; i<=n; ++i) { l=i,r=n; while(l+1<r) { mid=(l+r)>>1;//(l+r)/2==(l+r)>>1 if(calc(i,mid)<k) { l=mid; } else { r=mid-1;//自己去演示算法流程就知道r可以赋值mid-1 } } if(calc(i,r)<k) { ans=ans+(LL)(r-i+1); } else { ans=ans+(LL)(l-i+1); } } //--------------------------------------------------------------------------- printf("%lld\n",ans); } return 0; } ~~~

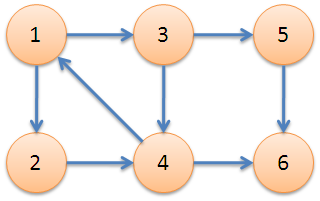
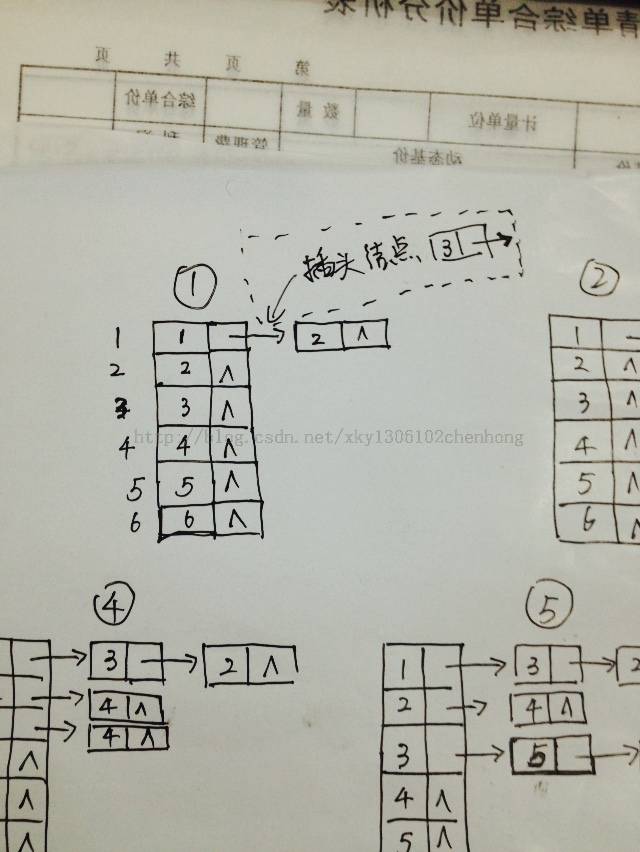
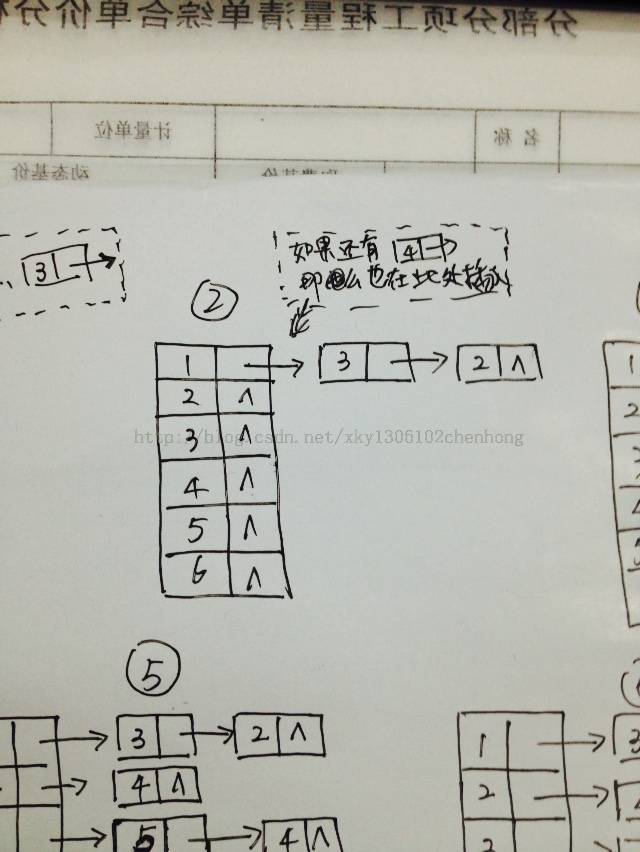
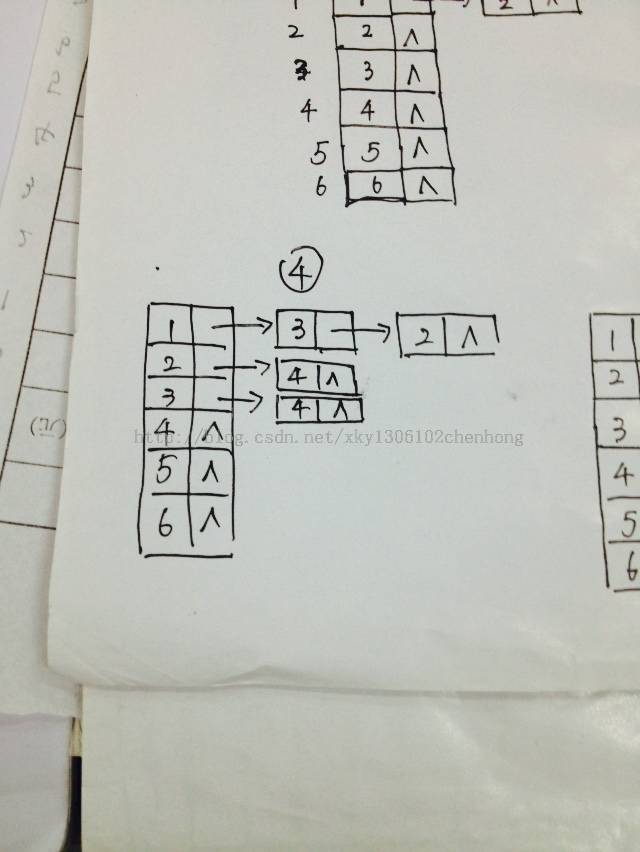
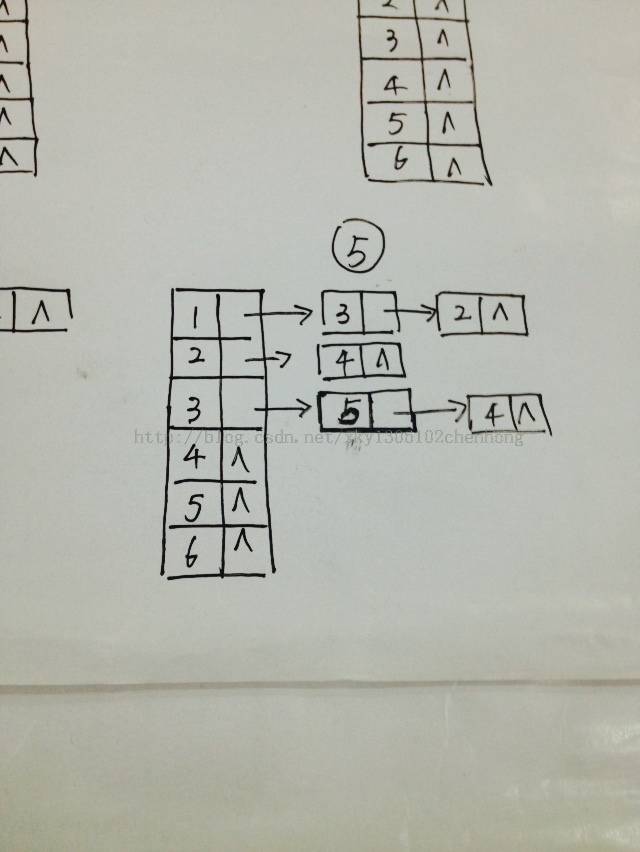
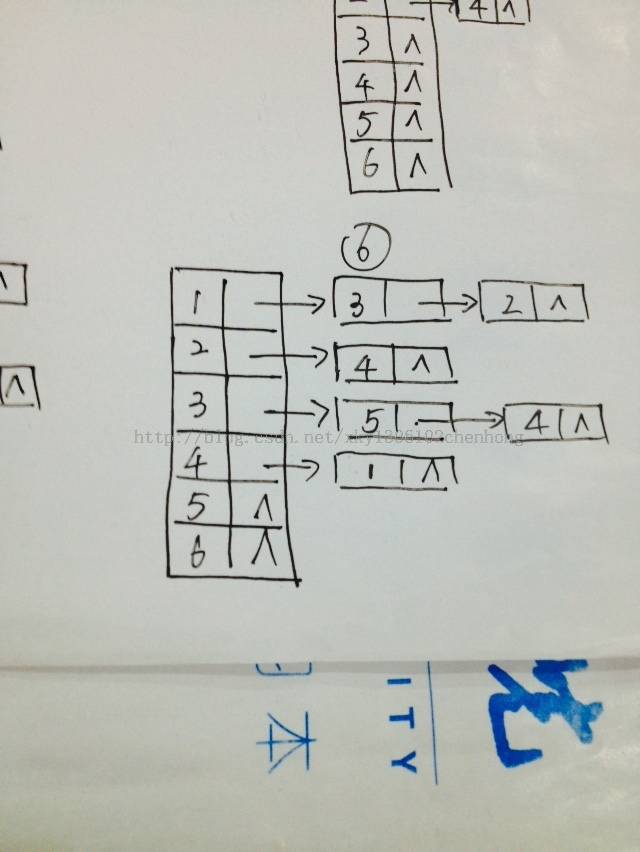
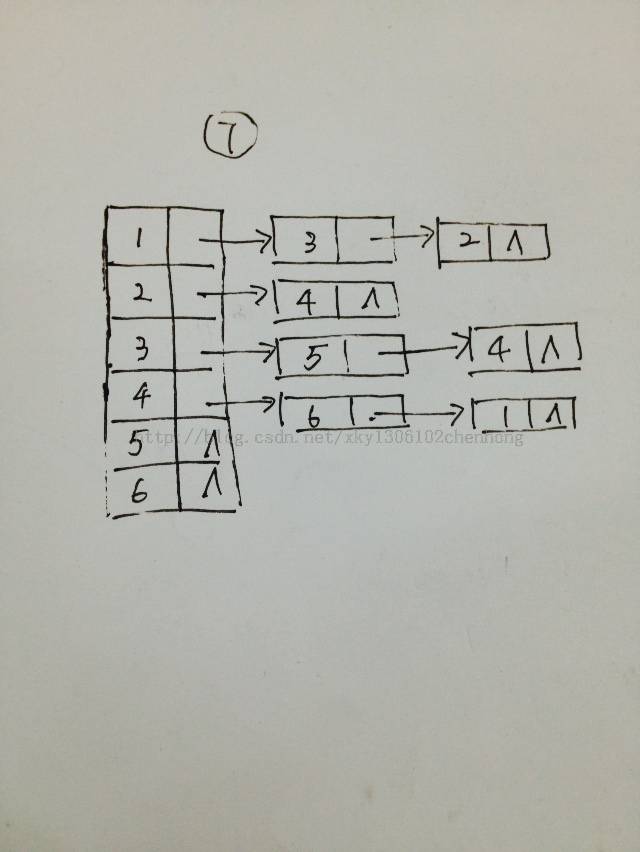
例如要存储一下有向图：  当输入6个顶点，8条弧 1 2 1 3 2 4 3 4 3 5 4 1 4 6 5 6 建立的邻接表的流程图为：         实现代码： ~~~ /* 用邻接表存储n个顶点m条弧的有向图 */ #include<stdio.h> #include<stdlib.h> #define MAX 10005 typedef struct ArcNode { int adjvex; struct ArcNode * nextarc; }ArcNode; typedef struct VNode { int vertex; ArcNode * firstarc; }VNode; int n,m; VNode V[MAX]; void init() { ArcNode * p; for(int i=1;i<=n;i++) { V[i].vertex=i; V[i].firstarc=NULL; } for(int i=0;i<m;i++) { int a,b; scanf("%d%d",&a,&b); p=(ArcNode*)malloc(sizeof(ArcNode)); p->adjvex=b; p->nextarc=V[a].firstarc; V[a].firstarc=p; } } int main() { while(scanf("%d%d",&n,&m)!=EOF&&(n||m)) { init(); ArcNode * p; ArcNode * q; for(int i=1;i<=n;i++) { printf("%d",V[i].vertex); p=V[i].firstarc; while(p!=NULL) { printf(" %d",p->adjvex); q=p; p=p->nextarc; free(q); } printf("\n"); } } return 0; } ~~~  

~~~ #include<cstdio> #include<cstring> using namespace std; long long f[200005]; int vis[200005]; int main() { int t; int n; scanf("%d",&t); while(t--) { scanf("%d",&n); f[0]=0; memset(vis,0,sizeof(vis)); for(int i=1;i<=n;i++) { int x; scanf("%d",&x); f[i]=x+f[i-1]+(i-1-vis[x])*x; vis[x]=i; } long long ans=0; for(int i=1;i<=n;i++) ans+=f[i]; printf("%lld\n",ans); } return 0; } ~~~

> 原文出处：[算法初步](http://blog.csdn.net/column/details/xky1306102chenhong.html) 作者：[xky1306102chenhong](http://blog.csdn.net/xky1306102chenhong) **本系列文章经作者授权在看云整理发布，未经作者允许，请勿转载！** # 算法初步 > 为了acm而刷题