HDU 1016 Prime Ring Problem(DFS)
最后更新于:2022-04-01 16:02:17
# Prime Ring Problem
**Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 37427 Accepted Submission(s): 16521**
Problem Description
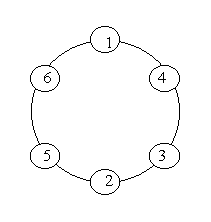
A ring is compose of n circles as shown in diagram. Put natural number 1, 2, ..., n into each circle separately, and the sum of numbers in two adjacent circles should be a prime.
Note: the number of first circle should always be 1.
Input
n (0 < n < 20).
Output
The output format is shown as sample below. Each row represents a series of circle numbers in the ring beginning from 1 clockwisely and anticlockwisely. The order of numbers must satisfy the above requirements. Print solutions in lexicographical order.
You are to write a program that completes above process.
Print a blank line after each case.
Sample Input
~~~
6
8
~~~
Sample Output
~~~
Case 1:
1 4 3 2 5 6
1 6 5 2 3 4
Case 2:
1 2 3 8 5 6 7 4
1 2 5 8 3 4 7 6
1 4 7 6 5 8 3 2
1 6 7 4 3 8 5 2
~~~
1.自然数(natural number),是非负整数(1, 2, 3, 4……)。认为自然数不包含[零](http://baike.baidu.com/subview/45676/8420704.htm)的其中一个理由是因为人们在开始学习数字的时候是由“一、二、三...”开始,而不是由“零、一、二、三...”开始, 因为这样是非常不自然的。在全球范围内,目前针对0是否属于自然数的争论依旧存在。在中国大陆,2000年左右之前的中小学教材一般不将0列入自然数之内,或称其属于“扩大的自然数列”。在2000年左右之后的新版中小学教材中,普遍将0列入自然数。
2.代码:
~~~
#include<cstdio>
#include<cstring>
using namespace std;
int n;
int vis[30];
int a[30];
int p[20]={2,3,5,7,11,13,17,19,23,29,31,37,41};
int c=1;
int cnt;
bool isPrime(int x)
{
for(int i=0;i<13;i++)
{
if(x==p[i])
{
return 1;
}
}
return 0;
}
void dfs(int level,int num)
{
a[level]=num;
vis[num]=1;
if(level==n)
{
if(isPrime(a[n]+a[1]))
{
if(cnt==0)
printf("Case %d:\n",c++);
cnt++;
for(int i=1;i<=n;i++)
{
if(i==1)
printf("%d",a[i]);
else
printf(" %d",a[i]);
}
printf("\n");
}
return;
}
for(int i=1;i<=n;i++)
{
if(vis[i]==1||isPrime(i+a[level])==0)
continue;
dfs(++level,i);
level--;
vis[i]=0;
}
}
int main()
{
while(scanf("%d",&n)==1)
{
memset(vis,0,sizeof(vis));
cnt=0;
dfs(1,1);
printf("\n");
}
return 0;
}
~~~