这一章节主要总结线性表顺序存储结构的优缺点。 在总结之前，我们来讨论一下线性表顺序存储结构的执行方法的时间复杂度： 存储、读取：O（1） 插入、删除：O（n） 优点： 1.无需为表中的逻辑关系增加额外的存储空间 2.可以快速存取表中对象 缺点： 1.插入和删除需要移动大量的对象 2.存储设备的碎片化 3.当线性表过大的时候，很难确定长度

这一章节我们来看一下线性表顺序存储结构删除操作的简单实现 ~~~ package com.ray.testobject; public class Test { private Object[] list; public Object[] getList() { return list; } /** * 初始化list * * @param num * 元素个数 */ private void iniList(int num) { list = new Object[num]; for (int i = 0; i < num; i++) { list[i] = new Object(); } } /** * 删除某个元素 * * @param pos * 元素位置 */ private Object delItemOfList(int pos) { Object delItem = null; if (pos <= 0 || pos > list.length) { System.out.println("输入位置不正确，不能执行删除方法"); return delItem; } delItem = list[pos - 1]; list[pos - 1] = null; if (pos < list.length) { for (int i = pos; i < list.length; i++) { list[i - 1] = list[i]; } list[list.length - 1] = null; } return delItem; } public static void main(String[] args) { Test test = new Test(); test.iniList(5); for (int i = 0; i < test.getList().length; i++) { System.out.println(test.getList()[i]); } System.out.println("--------------------"); System.out.println("被删除的元素：" + test.delItemOfList(3)); for (int i = 0; i < test.getList().length; i++) { System.out.println(test.getList()[i]); } } } ~~~ 输出： java.lang.Object@1fb8ee3 java.lang.Object@61de33 java.lang.Object@14318bb java.lang.Object@ca0b6 java.lang.Object@10b30a7 -------------------- 被删除的元素：java.lang.Object@14318bb java.lang.Object@1fb8ee3 java.lang.Object@61de33 java.lang.Object@ca0b6 java.lang.Object@10b30a7 null 注意：上面的代码只是一个简单的模拟，如果有问题，请指出，谢谢。

今天来说说线性表的实现 这里以List作为例子 ~~~ package com.ray.testobject; public class List { private int length; private Man[] array; public int getLength() { return length; } public void setLength(int length) { this.length = length; } public Man[] getArray() { return array; } public void setArray(Man[] array) { this.array = array; } } ~~~ list只是简单的封装了一个数组和一个整形数的长度 ~~~ package com.ray.testobject; public class Test { // 构造一个不满的线性表出来 private List initList() { List list = new List(); int n = 5; list.setArray(new Man[n + 1]);// 构造多一个元素的线性表 for (int i = 0; i < n; i++) { Man man = new Man(); man.setId(i); list.getArray()[i] = man; list.setLength(i + 1); } return list; } private boolean insertElement(List list, int pos, Man e) { boolean flag = false; Man[] array = list.getArray(); if (list.getLength() == array.length) { return false; } if (pos < 1 || pos > array.length) { return false; } if (pos < array.length) { for (int i = array.length-1; i > pos-1; i--) { array[i] = array[i - 1]; } } array[pos] = e; list.setLength(list.getLength() + 1); return flag; } public static void main(String[] args) { Test test = new Test(); List list = test.initList(); Man man = new Man(); man.setId(10); test.insertElement(list, 3, man); for (int i = 0; i < list.getArray().length; i++) { System.out.println(list.getArray()[i].getId()); } } } ~~~ 在上面的测试类里面，我们实现了List的初始化与插入元素，后面还会继续实现删除等方法

抽象数据类型概念（百度版） 抽象数据类型(Abstract Data Type 简称ADT)是指一个数学模型以及定义在此数学模型上的一组操作。 它包括数据对象、数据关系、操作集合 例子：arraylist ADT ArrayList{        数据对象：D={a1,a2,a3,....an-1,an}        数据关系：R1={<ai-1,ai>|ai-1,ai∈D,i=2,…,n}        基本操作：        Init():void         操作结果：构造一个空的线性表L        Destroy():boolean         初始条件：线性表已存在         操作结果：销毁线性表L        Clear():boolean         初始条件：线性表已存在         操作结果：置线性表L为空表       isListEmpty():boolean         初始条件：线性表已存在         操作结果：若线性表L为空表，则返回TRUE，否则返回FALSE       Lenght():int         初始条件：线性表已存在         操作结果：返回线性表L数据元素个数        GetElementAt(i):e         初始条件：线性表已存在（1≤i≤ListLenght(L)）         操作结果：返回e代表线性表L中第i个数据元素的值        locatElem(e):int         初始条件：线性表已存在,comare()是数据元素判定函数         操作结果：返回线性表L中第1个与e相同的位序，没有返回0        PreElem(e):e         初始条件：线性表已存在         操作结果：若e是线性表L的数据元素，且不是第一个，则返回它的前驱，否则操作失败        NextElem(e):e         初始条件：线性表已存在         操作结果：若e是线性表L的数据元素，且不是第最后一个，则返回它的后继，否则操作失败       Insert(e):boolean         初始条件：线性表已存在（1≤i≤ListLenght(L)+1）         操作结果：在线性表L中第i个数据元素之前插入新元素e，L长度加1       Delete(e):boolean         初始条件：线性表已存在（1≤i≤ListLenght(L)）         操作结果：删除线性表L中第i个数据元素，用e返回其值，L长度减1         }ADT List

1.线性表概念 线性表是由零个或者多个数据元素组成的有序的序列。 图示：  2.特点 2.1 有序 我们可以从上图看见，线性表里面的元素是一个挨着一个顺序排下去的，就像平常小朋友排队等放学的样子 2.2 允许零元素，也就是空表 2.3 第一个元素有且仅有一个后继，最后一个元素有且仅有一个前驱，其他元素有且仅有一个前驱以及有且仅有一个后继 我们可以从上图看见，线性表里面第一个元素a1，他没有前驱，只有一个a2的后继，最后一个元素an，只有一个前驱a（n-1），没有对应的后继，其他某个元素ai，它有且仅有一个前驱a（i-1）以及有且仅有一个后继a(i+1)

今天我们来谈一下如何计算时间复杂度。 时间复杂度概念：（百度版） 同一问题可用不同算法解决，而一个算法的质量优劣将影响到算法乃至程序的效率。算法分析的目的在于选择合适算法和改进算法。 计算机科学中，算法的时间复杂度是一个函数，它定量描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，它考察当输入值大小趋近无穷时的情况。 注意：本文承接上一篇《数据结构与算法-函数的渐近增长》，想详细了解渐近增长，请点击：[数据结构与算法-函数的渐近增长](http://blog.csdn.net/raylee2007/article/details/47022295) 现在先上代码，请大家详细阅读注释，因为整个计算过程都已经在注释里面体现。 ~~~ /** * 计算时间复杂度 * * @author ray * */ public class Test { private void test1(int n) { System.out.println(n);// 操作=1 } private void test2(int n) { int a = 0; for (int i = 0; i < n; i++) {// 操作=n a++;// 操作=1 } // 总操作=n*1=n // 时间复杂度=O(1) } private void test3(int n) { int a = 0; for (int i = 0; i < n; i++) {// 操作=n for (int j = 0; j < n; j++) {// 操作=n a++;// 操作=1 } } // 总操作=n*n*1=n^2 // 时间复杂度=O(n^2) } private void test4(int n) { int a = 0; for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) {// 操作=n,n-1,n-2,n-3......1=(n+1)n/2 a++;// 操作=1 } } // 总操作=(n+1)n/2=n^2/2+n/2 // 由于时间复杂度是一个抽象的概念，当n的规模达到一定程度的时候，时间复杂度只取最高次幂，而且忽略其他次要项和系数 // 时间复杂度=O(n^2) } private void test5(int n) { int a = 0; for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) {// 操作=n,n-1,n-2,n-3......1=(n+1)n/2 a++;// 操作=1 System.out.println(a);// 操作=1 // for循环内总操作=2 } } // 总操作=(n+1)n/2*2=n^2+n // 由于时间复杂度是一个抽象的概念，当n的规模达到一定程度的时候，时间复杂度只取最高次幂，而且忽略其他次要项和系数 // 时间复杂度=O(n^2) } private void test6(int n) { int a = 0; for (int i = 0; i < n; i++) { for (int j = i; j < n; j++) {// 操作=n,n-1,n-2,n-3......1=(n+1)n/2 a++;// 操作=1 System.out.println(a);// 操作=1 System.out.println(i);// 操作=1 // for循环内总操作=3 } } // 总操作=(n+1)n/2*3=n^2*3/2+n*3/2 // 由于时间复杂度是一个抽象的概念，当n的规模达到一定程度的时候，时间复杂度只取最高次幂，而且忽略其他次要项和系数 // 时间复杂度=O(n^2) } private void test7(int n) { int a = 0; int b = 0; for (int i = 0; i < n; i++) {// 操作=n for (int j = 0; j < n; j++) {// 操作=n a++;// 操作=1 System.out.println(a);// 操作=1 // for循环内总操作=2 for (int k = 0; k < n; k++) {// 操作=n b++;// 操作=1 // for循环内总操作=1 } } } // 总操作==n^3+2n^2 // 由于时间复杂度是一个抽象的概念，当n的规模达到一定程度的时候，时间复杂度只取最高次幂，而且忽略其他次要项和系数 // 时间复杂度=O(n^3) } public static void main(String[] args) { int n = 10; Test t = new Test(); t.test1(n); t.test2(n); t.test3(n); t.test4(n); t.test5(n); t.test6(n); t.test7(n); } } ~~~

在说函数的渐近增长的例子前，先说说概念， **  函数的渐近增长：给定两个函数f(n)和g(n)，如果存在一个整数N，使得对于所有的n > N，f(n)总是比g(n)大，那么，我们说f(n)的**渐近**增长快于g(n)。** 文字说明，比较难理解，我们利用下面的表格来说明 注意：n^2代表n 的平方，n^3代表n的立方 | 数值\函数 | n | 2n | 2n+1 | 3n+8 | n^2 | 2n^2 | 2n^2+2n+1 | n^3 | |-----|-----|-----|-----|-----|-----|-----|-----|-----| | 1 | 1 | 2 | 3 | 11 | 1 | 2 | 5 | 1 | | 2 | 2 | 4 | 5 | 14 | 4 | 8 | 13 | 8 | | 3 | 3 | 6 | 7 | 17 | 9 | 18 | 25 | 27 | | 5 | 5 | 10 | 11 | 23 | 25 | 50 | 61 | 125 | | 9 | 9 | 18 | 19 | 35 | 81 | 162 | 181 | 729 | | 10 | 10 | 20 | 21 | 38 | 100 | 200 | 221 | 1000 | | 100 | 100 | 200 | 201 | 308 | 10000 | 20000 | 20201 | 1000000 | | 1000 | 1000 | 2000 | 2001 | 3008 | 1000000 | 2000000 | 2002001 | 1000000000 | | 10000 | 10000 | 20000 | 20001 | 30008 | 100000000 | 200000000 | 200020001 | 1000000000000 | | 100000 | 100000 | 200000 | 200001 | 300008 | 10000000000 | 20000000000 | 20000200001 | 1000000000000000 | | 1000000 | 1000000 | 2000000 | 2000001 | 3000008 | 1000000000000 | 2000000000000 | 2000002000001 | 1000000000000000000 | 例如：f（n）=2n^2+1，g（n）=2n+1 当n=1是f(n)=g(n)，这个时候对应上面的概念，N=1，当n>N，也就是当n>1时，f(n)>g(n)，所以，我们说f（n）的渐近增加快于g（n） 同理，我们可以观察2n与2n^2 由于渐近增长是可以看作是一种抽象，所以他的对比具有一些特点： 1.注意关注函数最高次幂的变化 2.忽略次要项与乘数 为了更好理解这些特点，我做了一些图表，以便更加清楚的知道为什么 1.我们对比2n与2n+1这两个函数  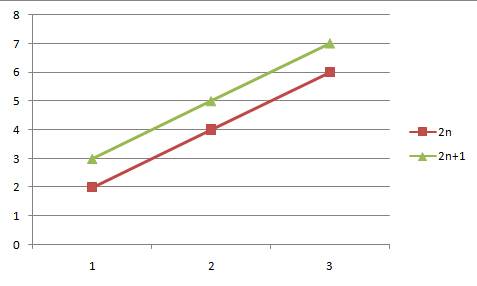当数值比较小的时候，两个函数之间还是存在一定的区别，但是  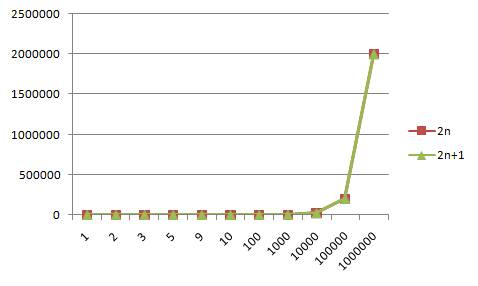当输入数值非常大的时候，两条曲线基本重叠，或者可以说看作重叠，所以得出结论是，2n+1其中里面作为常数的1，在输入数值大到一定程度，他对于函数的影响可以忽略不计，这时候的1就被看作是次要项 同样，我们选择2n^2与2n^2+2n+1   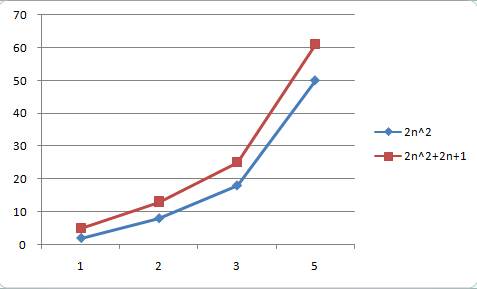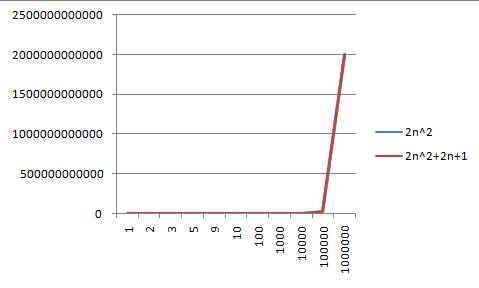从上面两图可以看出，当输入数值比较小的时候，他们直接具有一定差别，但是当输入数量非常大的时候，他们两条曲线可以看作重叠，这个时候2n+1就会被看作是次要项 最后我们来看看关于乘数是次要项的例子，请看3n+8与2n^2   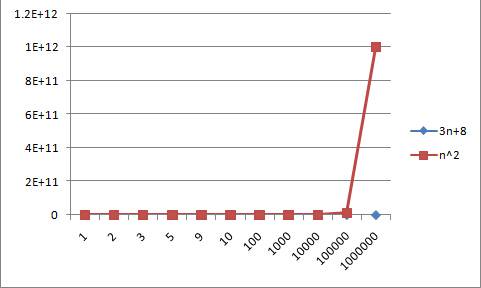从上面的图形得出的结论与之前的一致。

今天来说说为什么需要使用算法？ 算法是什么？算法是：指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。（百度百科版） 说完了算法的概念，我们举个例子说一下为什么需要算法？ ~~~ public class Test { /** * 使用原始的循环计算等差数列 */ private void originalMethod(long n) { System.out.println("**使用原始循环算法**"); long startTime = System.currentTimeMillis(); long sum = 0; for (long i = 0; i <= n; i++) { sum += i; } long endTime = System.currentTimeMillis(); System.out.println("结果：" + sum); System.out.println("用时：" + (endTime - startTime)); } /** * 使用等差数列算法计算 * * @param n */ private void advanceMethod(long n) { System.out.println("**使用等差数列算法**"); long startTime = System.currentTimeMillis(); long sum = 0; long a1 = 1; long an = n; sum = (a1 + an) * n / 2; long endTime = System.currentTimeMillis(); System.out.println("结果：" + sum); System.out.println("用时：" + (endTime - startTime)); } public static void main(String[] args) throws InterruptedException { Test test = new Test(); long n = 1000; System.out.println("-------当n=" + n + "的时候------"); test.originalMethod(n); test.advanceMethod(n); n = 1000000; System.out.println("-------当n=" + n + "的时候------"); test.originalMethod(n); test.advanceMethod(n); n = 1000000000L; System.out.println("-------当n=" + n + "的时候------"); test.originalMethod(n); test.advanceMethod(n); } } ~~~ 输出结果： -------当n=1000的时候------ **使用原始循环算法** 结果：500500 用时：0 **使用等差数列算法** 结果：500500 用时：0 -------当n=1000000的时候------ **使用原始循环算法** 结果：500000500000 用时：3 **使用等差数列算法** 结果：500000500000 用时：0 -------当n=1000000000的时候------ **使用原始循环算法** 结果：500000000500000000 用时：2070 **使用等差数列算法** 结果：500000000500000000 用时：0 从上面的结果可以看见，使用循环算法的所用时间不断的增加，而且达到某个数量级之后（例如10的20次方），估计我们等死也等不到结果出来，而反观使用等差数列算法，使用的实际都是0，当然，其实不是0，只不过太快了，没有显示出来而已，两个计算方式相互比较一下，算法的性能一下子就看出来了。 而且对于现今大数据来说，动不动就是几亿几十亿的数据，计算的过程比我们上面的更加复杂，所需要的时间就更多，这时候如果不使用相应的算法，解决一个问题的时间基本是不可估计的，因此，我们需要算法

> 原文出处：[数据结构与算法](http://blog.csdn.net/column/details/shujujiegouyusuanfa.html) 作者：[李灵晖](http://blog.csdn.net/raylee2007) **本系列文章经作者授权在看云整理发布，未经作者允许，请勿转载！** # 数据结构与算法 > 介绍数据结构与算法