数据结构与算法-函数的渐近增长
最后更新于:2022-04-01 07:04:21
在说函数的渐近增长的例子前,先说说概念,
** 函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n > N,f(n)总是比g(n)大,那么,我们说f(n)的**渐近**增长快于g(n)。**
文字说明,比较难理解,我们利用下面的表格来说明
注意:n^2代表n 的平方,n^3代表n的立方
| 数值\函数 | n | 2n | 2n+1 | 3n+8 | n^2 | 2n^2 | 2n^2+2n+1 | n^3 |
|-----|-----|-----|-----|-----|-----|-----|-----|-----|
| 1 | 1 | 2 | 3 | 11 | 1 | 2 | 5 | 1 |
| 2 | 2 | 4 | 5 | 14 | 4 | 8 | 13 | 8 |
| 3 | 3 | 6 | 7 | 17 | 9 | 18 | 25 | 27 |
| 5 | 5 | 10 | 11 | 23 | 25 | 50 | 61 | 125 |
| 9 | 9 | 18 | 19 | 35 | 81 | 162 | 181 | 729 |
| 10 | 10 | 20 | 21 | 38 | 100 | 200 | 221 | 1000 |
| 100 | 100 | 200 | 201 | 308 | 10000 | 20000 | 20201 | 1000000 |
| 1000 | 1000 | 2000 | 2001 | 3008 | 1000000 | 2000000 | 2002001 | 1000000000 |
| 10000 | 10000 | 20000 | 20001 | 30008 | 100000000 | 200000000 | 200020001 | 1000000000000 |
| 100000 | 100000 | 200000 | 200001 | 300008 | 10000000000 | 20000000000 | 20000200001 | 1000000000000000 |
| 1000000 | 1000000 | 2000000 | 2000001 | 3000008 | 1000000000000 | 2000000000000 | 2000002000001 | 1000000000000000000 |
例如:f(n)=2n^2+1,g(n)=2n+1
当n=1是f(n)=g(n),这个时候对应上面的概念,N=1,当n>N,也就是当n>1时,f(n)>g(n),所以,我们说f(n)的渐近增加快于g(n)
同理,我们可以观察2n与2n^2
由于渐近增长是可以看作是一种抽象,所以他的对比具有一些特点:
1.注意关注函数最高次幂的变化
2.忽略次要项与乘数
为了更好理解这些特点,我做了一些图表,以便更加清楚的知道为什么
1.我们对比2n与2n+1这两个函数
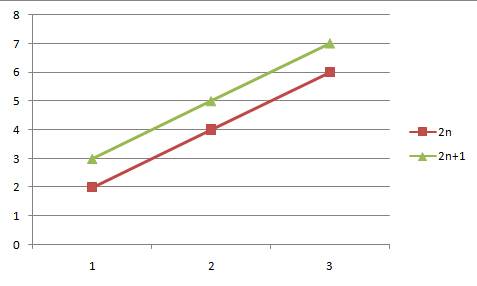
当数值比较小的时候,两个函数之间还是存在一定的区别,但是
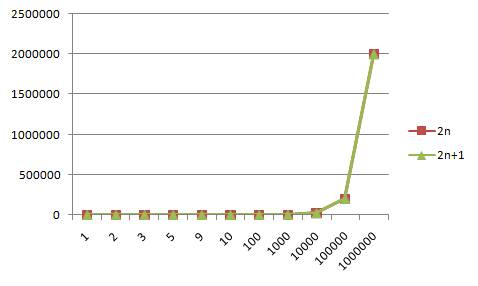
当输入数值非常大的时候,两条曲线基本重叠,或者可以说看作重叠,所以得出结论是,2n+1其中里面作为常数的1,在输入数值大到一定程度,他对于函数的影响可以忽略不计,这时候的1就被看作是次要项
同样,我们选择2n^2与2n^2+2n+1
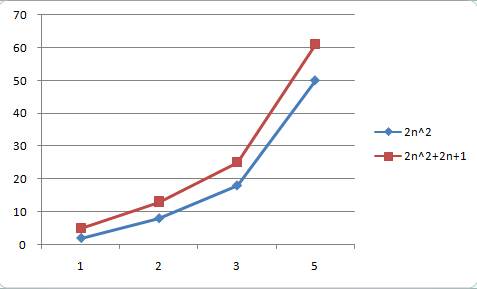
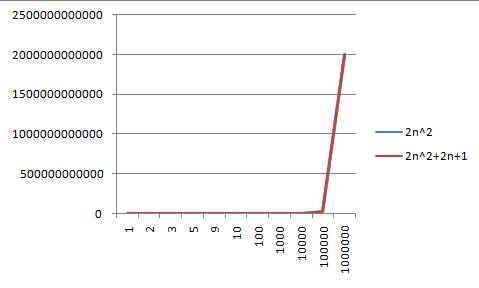
从上面两图可以看出,当输入数值比较小的时候,他们直接具有一定差别,但是当输入数量非常大的时候,他们两条曲线可以看作重叠,这个时候2n+1就会被看作是次要项
最后我们来看看关于乘数是次要项的例子,请看3n+8与2n^2

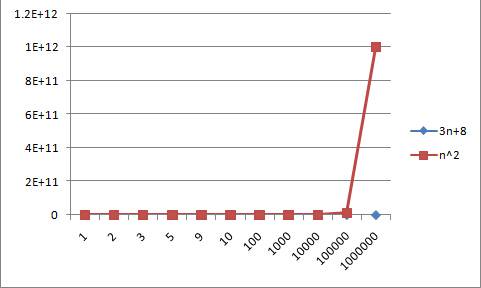
从上面的图形得出的结论与之前的一致。