Julia 数学函数
最后更新于:2022-03-27 03:04:30
Julia 数学函数
Julia 提供了一套高效、可移植的标准数学函数。
数值比较
下表列出了用于数值比较的函数:
| 函数 | 测试是否满足如下性质 |
|---|---|
isequal(x, y) |
x 与 y 值与类型是否完全相同 |
isfinite(x) |
x 是否是有限大的数字 |
isinf(x) |
x 是否是(正/负)无穷大 |
isnan(x) |
x 是否是 NaN |
isequal 认为 NaN 之间是相等的:
实例
true
julia> isequal([1 NaN], [1 NaN])
true
julia> isequal(NaN, NaN32)
true
isequal 也能用来区分带符号的零:
实例
true
julia> isequal(–0.0, 0.0)
false
其他函数实例:
实例
true
julia> isfinite(NaN32)
false
舍入函数
下表列出了 Julia 支持的舍入函数:
| 函数 | 描述 | 返回类型 |
|---|---|---|
round(x) |
x 舍到最接近的整数 |
typeof(x) |
round(T, x) |
x 舍到最接近的整数 |
T |
floor(x) |
x 向 -Inf 舍入 |
typeof(x) |
floor(T, x) |
x 向 -Inf 舍入 |
T |
ceil(x) |
x 向 +Inf 方向取整 |
typeof(x) |
ceil(T, x) |
x 向 +Inf 方向取整 |
T |
trunc(x) |
x 向 0 取整 |
typeof(x) |
trunc(T, x) |
x 向 0 取整 |
T |
实例
4.0
julia> round(Int, 3.8)
4
julia> floor(3.8)
3.0
julia> floor(Int, 3.8)
3
julia> ceil(3.8)
4.0
julia> ceil(Int, 3.8)
4
julia> trunc(3.8)
3.0
julia> trunc(Int, 3.8)
3
除法函数
下表列出了 Julia 支持的除法函数:
| 函数 | 描述 |
|---|---|
div(x,y), x÷y |
截断除法,无论任何类型相除的结果都会省略小数部分,剩下整数部分,商向零近似。 |
fld(x,y) |
向下取整除法;商向 -Inf 近似 |
cld(x,y) |
向上取整除法;商向 +Inf 近似 |
rem(x,y) |
取余;满足 x == div(x,y)*y + rem(x,y);符号与 x 一致 |
mod(x,y) |
取模;满足 x == fld(x,y)*y + mod(x,y);符号与 y 一致 |
mod1(x,y) |
偏移 1 的 mod;若 y>0,则返回 r∈(0,y],若 y<0,则 r∈[y,0) 且满足 mod(r, y) == mod(x, y) |
mod2pi(x) |
对 2pi 取模;0 <= mod2pi(x) < 2pi |
divrem(x,y) |
返回 (div(x,y),rem(x,y)) |
fldmod(x,y) |
返回 (fld(x,y),mod(x,y)) |
gcd(x,y...) |
x, y,… 的最大公约数 |
lcm(x,y...) |
x, y,… 的最小公倍数 |
实例
2
julia> div(7, 4)
1
julia> fld(11, 4)
2
julia> fld(–5,3)
–2
julia> fld(7.5,3.3)
2.0
julia> cld(7.5,3.3)
3.0
julia> mod(5, 0:2)
2
julia> mod(3, 0:2)
0
julia> mod(8.9,2)
0.9000000000000004
julia> rem(8,4)
0
julia> rem(9,4)
1
julia> mod2pi(7*pi/5)
4.39822971502571
julia> divrem(8,3)
(2, 2)
julia> fldmod(12,4)
(3, 0)
julia> fldmod(13,4)
(3, 1)
julia> mod1(5,4)
1
julia> gcd(6,0)
6
julia> gcd(1//3,2//3)
1//3
julia> lcm(1//3,2//3)
2//3
符号和绝对值函数
下表列出了 Julia 支持的符号和绝对值函数:
| 函数 | 描述 |
|---|---|
abs(x) |
x 的模 |
abs2(x) |
x 的模的平方 |
sign(x) |
表示 x 的符号,返回 -1,0,或 +1 |
signbit(x) |
表示符号位是 true 或 false |
copysign(x,y) |
返回一个数,其值等于 x 的模,符号与 y 一致 |
flipsign(x,y) |
返回一个数,其值等于 x 的模,符号与 x*y 一致 |
实例
7
julia> abs(5+3im)
5.830951894845301
julia> abs2(–7)
49
julia> abs2(5+3im)
34
julia> copysign(5,-10)
–5
julia> copysign(–5,10)
5
julia> sign(5)
1
julia> sign(–5)
–1
julia> signbit(–5)
true
julia> signbit(5)
false
julia> flipsign(5,10)
5
julia> flipsign(5,-10)
–5
符号和绝对值函数
下表列出了 Julia 支持的符号和绝对值函数:
| 函数 | 描述 |
|---|---|
sqrt(x), √x |
x 的平方根 |
cbrt(x), ∛x |
x 的立方根 |
hypot(x,y) |
当直角边的长度为 x 和 y时,直角三角形斜边的长度 |
exp(x) |
自然指数函数在 x 处的值 |
expm1(x) |
当 x 接近 0 时的 exp(x)-1 的精确值 |
ldexp(x,n) |
x*2^n 的高效算法,n 为整数 |
log(x) |
x 的自然对数 |
log(b,x) |
以 b 为底 x 的对数 |
log2(x) |
以 2 为底 x 的对数 |
log10(x) |
以 10 为底 x 的对数 |
log1p(x) |
当 x接近 0 时的 log(1+x) 的精确值 |
exponent(x) |
x 的二进制指数 |
significand(x) |
浮点数 x 的二进制有效数(也就是尾数) |
实例
7.0
julia> sqrt(–49)
ERROR: DomainError with –49.0:
sqrt will only return a complex result if called with a complex argument. Try sqrt(Complex(x)).
Stacktrace:
[1] throw_complex_domainerror(::Symbol, ::Float64) at .\math.jl:33
[2] sqrt at .\math.jl:573 [inlined]
[3] sqrt(::Int64) at .\math.jl:599
[4] top-level scope at REPL[43]:1
julia> cbrt(8)
2.0
julia> cbrt(–8)
–2.0
julia> a = Int64(5)^10;
julia> hypot(a, a)
1.3810679320049757e7
julia> exp(5.0)
148.4131591025766
julia> expm1(10)
22025.465794806718
julia> expm1(1.0)
1.718281828459045
julia> ldexp(4.0, 2)
16.0
julia> log(5,2)
0.43067655807339306
julia> log(4,2)
0.5
julia> log(4)
1.3862943611198906
julia> log2(4)
2.0
julia> log10(4)
0.6020599913279624
julia> log1p(4)
1.6094379124341003
julia> log1p(–2)
ERROR: DomainError with –2.0:
log1p will only return a complex result if called with a complex argument. Try log1p(Complex(x)).
Stacktrace:
[1] throw_complex_domainerror(::Symbol, ::Float64) at .\math.jl:33
[2] log1p(::Float64) at .\special\log.jl:356
[3] log1p(::Int64) at .\special\log.jl:395
[4] top-level scope at REPL[65]:1
julia> exponent(6.8)
2
julia> significand(15.2)/10.2
0.18627450980392157
julia> significand(15.2)*8
15.2
三角和双曲函数
Julia 也提供了所有标准的三角和双曲函数:
sin cos tan cot sec csc sinh cosh tanh coth sech csch asin acos atan acot asec acsc asinh acosh atanh acoth asech acsch sinc cosc
下图中以弧度为单位的角度对应于单位圆上的一个点,其坐标定义了角度的正弦和余弦。
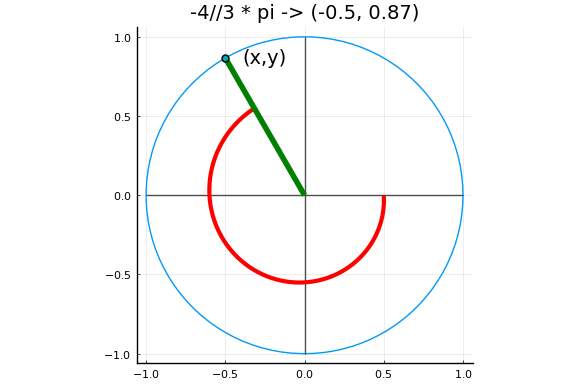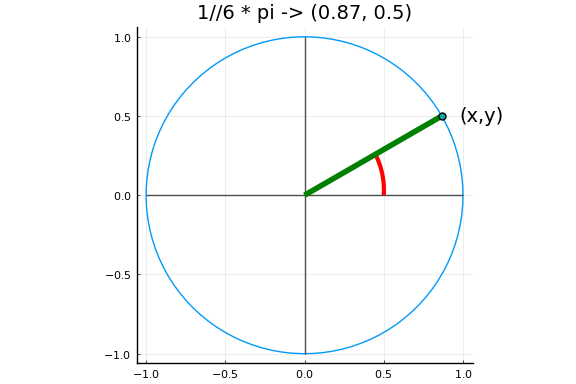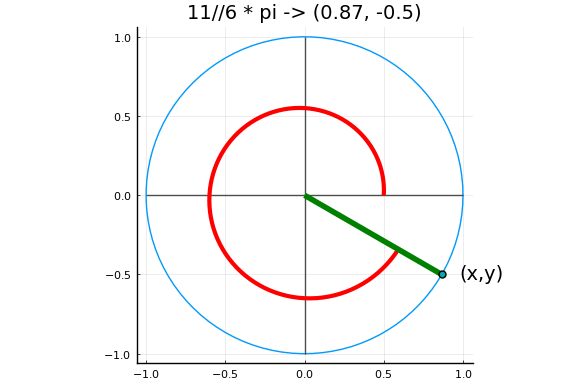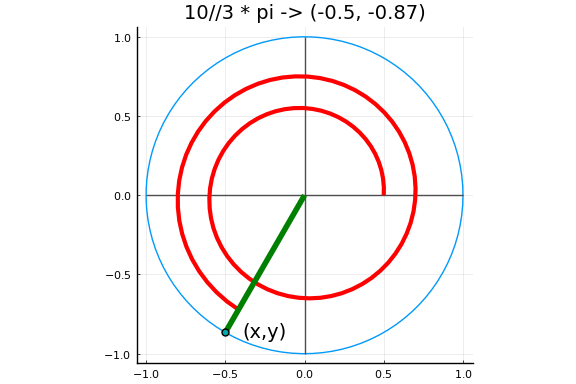
实例
π = 3.1415926535897…
julia> sin(0)
0.0
julia> sin(pi/6)
0.49999999999999994
julia> sin(pi/4)
0.7071067811865475
julia> cos(0)
1.0
julia> cos(pi/6)
0.8660254037844387
julia> cos(pi/3)
0.5000000000000001
以上提供的函数都是单参数函数,不过 atan 也可以接收两个参数 来表示传统的 atan2 函数。
atan(y) atan(y, x)
分别计算 y 或 y/x 的反正切。
实例
2.356194490192345
julia> x,y = (cos(theta), sin(theta))
(–0.7071067811865475, 0.7071067811865476)
julia> atan(y/x)
–0.7853981633974484
julia> atan(y, x)
2.356194490192345
另外,sinpi(x) 和 cospi(x) 分别用来对 sin(pi*x) 和 cos(pi*x) 进行更精确的计算。
要计算角度而非弧度的三角函数,以 d 做后缀。 比如,sind(x) 计算 x 的 sine 值,其中 x 是一个角度值。 下面是角度变量的三角函数完整列表:
sind cosd tand cotd secd cscd asind acosd atand acotd asecd acscd
实例
0.853220107722584
julia> cosd(56)
0.5591929034707468
Julia 基本运算符
最后更新于:2022-03-27 03:04:27
Julia 基本运算符
运算符是一种告诉编译器执行特定的数学或逻辑操作的符号,如: 3+2=5。
Julia 语言内置了丰富的运算符,支持的运算有:
- 算术运算符
- 逻辑运算符
- 关系运算符
- 位运算符
- 赋值运算符
- 向量化 “点” 运算符
算术运算符
下表显示了 Julia 的基本算术运算符,适用于所有的基本数值类型:
| 表达式 | 名称 | 描述 |
|---|---|---|
+x |
一元加法运算符 | 全等操作 |
-x |
一元减法运算符 | 将值变为其相反数 |
x + y |
二元加法运算符 | 两数相加 |
x - y |
二元减法运算符 | 两数相减 |
x * y |
乘法运算符 | 两数相乘 |
x / y |
除法运算符 | 两数相除 |
x ÷ y |
整除 | 取 x / y 的整数部分 |
x \ y |
反向除法 | 等价于 y / x |
x ^ y |
幂操作符 | x 的 y 次幂 |
x % y |
取余 | 等价于 rem(x,y) |
实例
6
julia> 1 – 2
–1
julia> 3*2/12
0.5
julia> 2+20–5
17
julia> 50*2/10
10.0
julia> 23%2
1
julia> 2^4
16
布尔运算符
下表显示了 Julia 的布尔运算符:
| 表达式 | 名称 |
|---|---|
!x |
否定 |
x && y |
短路与,在表达式 x && y 中,子表达式 y 仅当 x 为 true 的时候才会被执行。 |
x || y |
短路或,在表达式 x || y 中,子表达式 y 仅在 x 为 false 的时候才会被执行。 |
实例
false
julia> !false
true
julia> true && (x = (1, 2, 3))
(1, 2, 3)
julia> false && (x = (1, 2, 3))
false
julia> false || (x = (1, 2, 3))
(1, 2, 3)
关系运算符
下表显示了 Julia 的关系运算符:
| 操作符 | 名称 |
|---|---|
== |
相等 |
!=, ≠ |
不等 |
< |
小于 |
<=, ≤ |
小于等于 |
> |
大于 |
>=, ≥ |
大于等于 |
实例
true
julia> 100 == 101
false
julia> 100 != 101
true
julia> 100 == 100.0
true
julia> 100 < 500
true
julia> 100 > 500
false
julia> 100 >= 100.0
true
julia> –100 <= 100
true
julia> –100 <= –100
true
julia> –100 <= –500
false
julia> 100 < –10.0
false
链式比较
链式比较在写数值代码时特别方便,它使用 && 运算符比较标量,数组则用 & 进行按元素比较。比如,0 .< A .< 1 会得到一个 boolean 数组,如果 A 的元素都在 0 和 1 之间则数组元素就都是 true。
Julia 允许链式比较:
实例
true
注意链式比较的执行顺序:
实例
M (generic function with 1 method)
julia> M(1) < M(2) <= M(3)
2
1
3
true
julia> M(1) > M(2) <= M(3)
2
1
false
位运算符
下表显示了 Julia 的位运算符:
| 表达式 | 名称 |
|---|---|
~x |
按位取反 |
x & y |
按位与 |
x | y |
按位或 |
x ⊻ y |
按位异或(逻辑异或) |
x ⊼ y |
按位与(非与) |
x ⊽ y |
按位或(非或) |
x >>> y |
逻辑右移 |
x >> y |
算术右移 |
x << y |
逻辑/算术左移 |
实例
–124
julia> 123 & 234
106
julia> 123 | 234
251
julia> 123 ⊻ 234
145
julia> xor(123, 234)
145
julia> nand(123, 123)
–124
julia> 123 ⊼ 123
–124
julia> nor(123, 124)
–128
julia> 123 ⊽ 124
–128
julia> ~UInt32(123)
0xffffff84
julia> ~UInt8(123)
0x84
赋值运算符
每一个二元运算符和位运算符都可以给左操作数复合赋值,方法是把 = 直接放在二元运算符后面。比如,x += 3 等价于 x = x + 3 。
下表显示了 Julia 的赋值运算符:
| 运算符 | 描述 | 实例 |
|---|---|---|
| = | 简单的赋值运算符,把右边操作数的值赋给左边操作数 | C = A + B 将把 A + B 的值赋给 C |
| += | 加且赋值运算符,把右边操作数加上左边操作数的结果赋值给左边操作数 | C += A 相当于 C = C + A |
| -= | 减且赋值运算符,把左边操作数减去右边操作数的结果赋值给左边操作数 | C -= A 相当于 C = C – A |
| *= | 乘且赋值运算符,把右边操作数乘以左边操作数的结果赋值给左边操作数 | C *= A 相当于 C = C * A |
| /= | 除且赋值运算符,把左边操作数除以右边操作数的结果赋值给左边操作数 | C /= A 相当于 C = C / A |
| %= | 求模且赋值运算符,求两个操作数的模赋值给左边操作数 | C %= A 相当于 C = C % A |
| <<= | 左移且赋值运算符 | C <<= 2 等同于 C = C << 2 |
| >>= | 右移且赋值运算符 | C >>= 2 等同于 C = C >> 2 |
| &= | 按位与且赋值运算符 | C &= 2 等同于 C = C & 2 |
| ^= | 按位异或且赋值运算符 | C ^= 2 等同于 C = C ^ 2 |
| |= | 按位或且赋值运算符 | C |= 2 等同于 C = C | 2 |
| >>>= | 左移且逻辑运算符 | C >>>= 2 等同于 C = C >>>2 |
| ⊻= | 异或(逻辑异或)赋值运算符 | C ⊻= 2 等同于 C = C ⊻= 2 |
实例
1
julia> x += 3
4
julia> x
4
向量化 “点” 运算符
Julia 中,每个二元运算符都有一个 “点” 运算符与之对应,例如 ^ 就有对应的 .^ 存在。这个对应的 .^ 被 Julia 自动地定义为逐元素地执行 ^ 运算。比如 [1,2,3] ^ 3 是非法的,因为数学上没有给(长宽不一样的)数组的立方下过定义。但是 [1,2,3] .^ 3 在 Julia 里是合法的,它会逐元素地执行 ^ 运算(或称向量化运算),得到 [1^3, 2^3, 3^3]。类似地,! 或 √ 这样的一元运算符,也都有一个对应的 .√ 用于执行逐元素运算。
实例
3-element Vector{Int64}:
1
8
27
除了点运算符,我们还有逐点赋值运算符,类似 a .+= b(或者 @. a += b)会被解析成 a .= a .+ b。
运算符的优先级与结合性
运算符的优先级确定表达式中项的组合。这会影响到一个表达式如何计算。某些运算符比其他运算符有更高的优先级,例如,乘除运算符具有比加减运算符更高的优先级。
例如 x = 7 + 3 * 2,在这里,x 被赋值为 13,而不是 20,因为运算符 * 具有比 + 更高的优先级,所以首先计算乘法 3*2,然后再加上 7。
下表将按运算符优先级从高到低列出各个运算符,具有较高优先级的运算符出现在表格的上面,具有较低优先级的运算符出现在表格的下面。在表达式中,较高优先级的运算符会优先被计算。
| 分类 | 运算符 | 结合性 |
|---|---|---|
| 语法 | . followed by :: |
左结合 |
| 幂运算 | ^ |
右结合 |
| 一元运算符 | + - √ |
右结合 |
| 移位运算 | << >> >>> |
左结合 |
| 除法 | // |
左结合 |
| 乘法 | * / % & \ ÷ |
左结合 |
| 加法 | + - | ⊻ |
左结合 |
| 语法 | : .. |
左结合 |
| 语法 | |> |
左结合 |
| 语法 | <| |
右结合 |
| 比较 | > < >= <= == === != !== <: |
无结合性 |
| 流程控制 | && followed by || followed by ? |
右结合 |
| Pair 操作 | => |
右结合 |
| 赋值 | = += -= *= /= //= \= ^= ÷= %= |= &= ⊻= <<= >>= >>>= |
右结合 |
我们也可以通过内置函数 Base.operator_precedence 查看任何给定运算符的优先级数值,数值越大优先级越高:
实例
(11, 12, 17)
julia> Base.operator_precedence(:sin), Base.operator_precedence(:+=), Base.operator_precedence(:(=)) # (注意:等号前后必须有括号 `:(=)`)
(0, 1, 1)
另外,内置函数 Base.operator_associativity 可以返回运算符结合性的符号表示:
实例
(:left, :none, :right)
julia> Base.operator_associativity(:⊗), Base.operator_associativity(:sin), Base.operator_associativity(:→)
(:left, :none, :right)
Julia 复数和有理数
最后更新于:2022-03-27 03:04:25
Julia 复数和有理数
本章节我们主要要来学习 Julia 的复数和有理数。
Julia 语言包含了预定义的复数和有理数类型,并且支持它们的各种标准数学运算和初等函数。
复数
复数,为实数的延伸,它使任一多项式方程都有根。
我们把形如 z=a+bi(a、b均为实数)的数称为复数。其中,a 称为实部,b 称为虚部,i 称为虚数单位,它有着性质
全局常量 im 被绑定到复数 i,表示 -1 的主平方根。
由于 Julia 允许数值字面量作为数值字面量系数,这种绑定就足以为复数提供很方便的语法,类似于传统的数学记法:
实例
1 + 2im
我们也可以对复数进行各种算术操作:
实例
8 + 1im
julia> (1 + 2im)/(1 – 2im)
–0.6 + 0.8im
julia> (1 + 2im) + (1 – 2im)
2 + 0im
julia> (–3 + 2im) – (5 – 1im)
–8 + 3im
julia> (–1 + 2im)^2
–3 – 4im
julia> (–1 + 2im)^2.5
2.729624464784009 – 6.9606644595719im
julia> (–1 + 2im)^(1 + 1im)
–0.27910381075826657 + 0.08708053414102428im
julia> 3(2 – 5im)
6 – 15im
julia> 3(2 – 5im)^2
–63 – 60im
julia> 3(2 – 5im)^-1.0
0.20689655172413796 + 0.5172413793103449im
类型提升机制也确保你可以使用不同类型的操作数的组合:
实例
2 – 2im
julia> (2 + 3im) – 1
1 + 3im
julia> (1 + 2im) + 0.5
1.5 + 2.0im
julia> (2 + 3im) – 0.5im
2.0 + 2.5im
julia> 0.75(1 + 2im)
0.75 + 1.5im
julia> (2 + 3im) / 2
1.0 + 1.5im
julia> (1 – 3im) / (2 + 2im)
–0.5 – 1.0im
julia> 2im^2
–2 + 0im
julia> 1 + 3/4im
1.0 – 0.75im
注意 3/4im == 3/(4*im) == -(3/4*im),因为系数比除法的优先级更高。
Julia 提供了一些操作复数的标准函数:
实例
1 + 2im
julia> real(1 + 2im) # z 的实部
1
julia> imag(1 + 2im) # z 的虚部
2
julia> conj(1 + 2im) # z 的复共轭
1 – 2im
julia> abs(1 + 2im) # z 的绝对值
2.23606797749979
julia> abs2(1 + 2im) # 取平方后的绝对值
5
julia> angle(1 + 2im) # 以弧度为单位的相位角
1.1071487177940904
按照惯例,复数的绝对值(abs)是从零点到它的距离。abs2 给出绝对值的平方,作用于复数上时非常有用,因为它避免了取平方根。angle 返回以弧度为单位的相位角(也被称为辐角函数)。所有其它的初等函数在复数上也都有完整的定义:
实例
0.7071067811865476 + 0.7071067811865475im
julia> sqrt(1 + 2im)
1.272019649514069 + 0.7861513777574233im
julia> cos(1 + 2im)
2.0327230070196656 – 3.0518977991517997im
julia> exp(1 + 2im)
–1.1312043837568135 + 2.4717266720048188im
julia> sinh(1 + 2im)
–0.4890562590412937 + 1.4031192506220405im
注意数学函数通常应用于实数就返回实数值,应用于复数就返回复数值。例如,当 sqrt 应用于 -1 与 -1 + 0im 会有不同的表现,虽然 -1 == -1 + 0im:
实例
ERROR: DomainError with –1.0:
sqrt will only return a complex result if called with a complex argument. Try sqrt(Complex(x)).
Stacktrace:
[…]
julia> sqrt(–1 + 0im)
0.0 + 1.0im
从变量构建复数时,文本型数值系数记法不再适用。相反地,乘法必须显式地写出:
实例
1 + 2im
然而,我们并不推荐这样做,而应改为使用更高效的 complex 函数直接通过实部与虚部构建一个复数值:
实例
1 + 2im
这种构建避免了乘法和加法操作。
Inf 和 NaN 可能出现在复数的实部和虚部,正如特殊的浮点值章节所描述的:
实例
1.0 + Inf*im
julia> 1 + NaN*im
1.0 + NaN*im
有理数
有理数是整数(正整数、0、负整数)和分数的统称,是整数和分数的集合。
数学上,可以表达为两个整数比的数(




Julia 有一个用于表示整数精确比值的分数类型。分数通过 // 运算符构建:
实例
2//3
如果一个分数的分子和分母含有公因子,它们会被约分到最简形式且分母非负:
实例
2//3
julia> –4//8
–1//2
julia> 5//-15
–1//3
julia> –4//-12
1//3
整数比值的这种标准化形式是唯一的,所以分数值的相等性可由校验分子与分母都相等来测试。分数值的标准化分子和分母可以使用 numerator 和 denominator 函数得到:
实例
2
julia> denominator(2//3)
3
分子和分母的直接比较通常是不必要的,因为标准算术和比较操作对分数值也有定义:
实例
true
julia> 2//3 == 9//27
false
julia> 3//7 < 1//2
true
julia> 3//4 > 2//3
true
julia> 2//4 + 1//6
2//3
julia> 5//12 – 1//4
1//6
julia> 5//8 * 3//12
5//32
julia> 6//5 / 10//7
21//25
分数可以很容易地转换成浮点数:
实例
0.75
对任意整数值 a 和 b(除了 a == 0 且 b == 0 时),从分数到浮点数的转换遵从以下的一致性:
实例
julia> isequal(float(a//b), a/b)
true
Julia接受构建无穷分数值:
实例
1//0
julia> x = –3//0
–1//0
julia> typeof(x)
Rational{Int64}
但不接受试图构建一个 NaN 分数值:
实例
ERROR: ArgumentError: invalid rational: zero(Int64)//zero(Int64)
Stacktrace:
[…]
像往常一样,类型提升系统使得分数可以轻松地同其它数值类型进行交互:
实例
8//5
julia> 3//5 – 0.5
0.09999999999999998
julia> 2//7 * (1 + 2im)
2//7 + 4//7*im
julia> 2//7 * (1.5 + 2im)
0.42857142857142855 + 0.5714285714285714im
julia> 3//2 / (1 + 2im)
3//10 – 3//5*im
julia> 1//2 + 2im
1//2 + 2//1*im
julia> 1 + 2//3im
1//1 – 2//3*im
julia> 0.5 == 1//2
true
julia> 0.33 == 1//3
false
julia> 0.33 < 1//3
true
julia> 1//3 – 0.33
0.0033333333333332993
Julia 数据类型
最后更新于:2022-03-27 03:04:22
Julia 数据类型
在编程语言中,都有基本的数学运算和科学计算,它们常用的数据类型为整数和浮点数。
另外还有一个“字面量”的术语,字面量(literal)用于表达源代码中一个固定值的表示法(notation),整数、浮点数以及字符串等等都是字面量。
例如:
a=1 // a 是变量,1 是整型字面量
b=1.0 // b 是变量,1.0 是浮点型字面量
Julia 提供了很丰富的原始数值类型,并基于它们定义了一整套算术运算操作,另外还提供按位运算符以及一些标准数学函数。
整数类型
下表列出来 Julia 支持的整数类型:
| 类型 | 带符号? | 比特数 | 最小值 | 最大值 |
|---|---|---|---|---|
| Int8 | ✓ | 8 | -2^7 | 2^7 – 1 |
| UInt8 | 8 | 0 | 2^8 – 1 | |
| Int16 | ✓ | 16 | -2^15 | 2^15 – 1 |
| UInt16 | 16 | 0 | 2^16 – 1 | |
| Int32 | ✓ | 32 | -2^31 | 2^31 – 1 |
| UInt32 | 32 | 0 | 2^32 – 1 | |
| Int64 | ✓ | 64 | -2^63 | 2^63 – 1 |
| UInt64 | 64 | 0 | 2^64 – 1 | |
| Int128 | ✓ | 128 | -2^127 | 2^127 – 1 |
| UInt128 | 128 | 0 | 2^128 – 1 | |
| Bool | N/A | 8 | false (0) | true (1) |
整数字面量形式:
实例
1
julia> 1234
1234
整型字面量的默认类型取决于目标系统是 32 位还是 64 位架构(目前大部分系统都是 64 位):
实例
julia> typeof(1)
Int32
# 64 位系统:
julia> typeof(1)
Int64
Julia 的内置变量 Sys.WORD_SIZE 表明了目标系统是 32 位还是 64 位架构:
实例
julia> Sys.WORD_SIZE
32
# 64 位系统:
julia> Sys.WORD_SIZE
64
Julia 也定义了 Int 与 UInt 类型,它们分别是系统有符号和无符号的原生整数类型的别名。
实例
julia> Int
Int32
julia> UInt
UInt32
# 64 位系统:
julia> Int
Int64
julia> UInt
UInt64
溢出行为
在 Julia 里,超出一个类型可表示的最大值会导致环绕 (wraparound) 行为:
实例
9223372036854775807
julia> x + 1
–9223372036854775808
julia> x + 1 == typemin(Int64)
true
因此,Julia 的整数算术实际上是模算数的一种形式,它反映了现代计算机实现底层算术的特点。在可能有溢出产生的程序中,对最值边界出现循环进行显式检查是必要的。否则,推荐使用任意精度算术中的 BigInt 类型作为替代。
下面是溢出行为的一个例子以及如何解决溢出:
实例
–8446744073709551616
julia> big(10)^19
10000000000000000000
除法错误
在以下两种例外情况下,整数除法会触发 DivideError 错误:
- 除以零
- 除以最小的负数
rem 取余函数和 mod 取模函数在除零时抛出 DivideError 错误,实例如下:
实例
ERROR: DivideError: integer division error
Stacktrace:
[1] div at .\int.jl:260 [inlined]
[2] div at .\div.jl:217 [inlined]
[3] div at .\div.jl:262 [inlined]
[4] fld at .\div.jl:228 [inlined]
[5] mod(::Int64, ::Int64) at .\int.jl:252
[6] top-level scope at REPL[52]:1
julia> rem(1, 0)
ERROR: DivideError: integer division error
Stacktrace:
[1] rem(::Int64, ::Int64) at .\int.jl:261
[2] top-level scope at REPL[54]:1
浮点类型
下表列出来 Julia 支持的浮点类型:
| 类型 | 精度 | 比特数 |
|---|---|---|
| Float16 | 半精度 | 16 |
| Float32 | 单精度 | 32 |
| Float64 | 双精度 | 64 |
此外,对复数和有理数的完整支持是在这些原始数据类型之上建立起来的。
浮点数字面量格式表示如下,必要时可使用 E 来表示。
实例
1.0
julia> 1.
1.0
julia> 0.5
0.5
julia> .5
0.5
julia> –1.23
–1.23
julia> 1e10
1.0e10
julia> 2.5e-4
0.00025
注:
在科学计数法中,为了使公式简便,可以用带 E 的格式表示。例如 1.03乘10的8次方,可简写为 “1.03E+08” 的形式,其中 “E” 是 exponent(指数) 的缩写。
上面的结果都是 Float64 类型的值。使用 f 替代 e 可以得到 Float32 类型的字面量:
实例
0.5f0
julia> typeof(x)
Float32
julia> 2.5f-4
0.00025f0
数值可以很容易地转换为 Float32 类型:
julia> x = Float32(–1.5)
-1.5f0
julia> typeof(x)
Float32
也存在十六进制的浮点数字面量,但只适用于 Float64 类型的值。一般使用 p 前缀及以 2 为底的指数来表示:
实例
1.0
julia> 0x1.8p3
12.0
julia> x = 0x.4p-1
0.125
julia> typeof(x)
Float64
Julia 也支持半精度浮点数(Float16),但它们是使用 Float32 进行软件模拟实现的。
julia> sizeof(Float16(4.))
2
julia> 2*Float16(4.)
Float16(8.0)
下划线 _ 可用作数字分隔符:
实例
(10000, 5.0e-9, 0xdeadbeef, 0xb2)
浮点数中的零
浮点数有两种零,正零和负零。它们相互相等但有着不同的二进制表示,可以使用 bitstring 函数来查看:
实例
true
julia> bitstring(0.0)
"0000000000000000000000000000000000000000000000000000000000000000"
julia> bitstring(–0.0)
"1000000000000000000000000000000000000000000000000000000000000000"
特殊的浮点值
有三种特定的标准浮点值不和实数轴上任何一点对应:
| Float16 | Float32 | Float64 | 名称 | 描述 |
|---|---|---|---|---|
| Inf16 | Inf32 | Inf | 正无穷 | 一个大于所有有限浮点数的数 |
| -Inf16 | -Inf32 | -Inf | 负无穷 | 一个小于所有有限浮点数的数 |
| NaN16 | NaN32 | NaN | 不是一个数 | 一个不和任何浮点值(包括自己)相等(==)的值 |
以下列举了一些浮点数的运算实例:
实例
0.0
julia> 1/0
Inf
julia> –5/0
-Inf
julia> 0.000001/0
Inf
julia> 0/0
NaN
julia> 500 + Inf
Inf
julia> 500 – Inf
-Inf
julia> Inf + Inf
Inf
julia> Inf – Inf
NaN
julia> Inf * Inf
Inf
julia> Inf / Inf
NaN
julia> 0 * Inf
NaN
julia> NaN == NaN
false
julia> NaN != NaN
true
julia> NaN < NaN
false
julia> NaN > NaN
false
我们还可以使用 typemin 和 typemax 函数:
实例
(-Inf16, Inf16)
julia> (typemin(Float32),typemax(Float32))
(-Inf32, Inf32)
julia> (typemin(Float64),typemax(Float64))
(-Inf, Inf)
机器精度
大多数实数都无法用浮点数准确地表示,因此有必要知道两个相邻可表示的浮点数间的距离,它通常被叫做机器精度。
Julia 提供了 eps 函数,它可以给出 1.0 与下一个 Julia 能表示的浮点数之间的差值:
实例
1.1920929f-7
julia> eps(Float64)
2.220446049250313e-16
julia> eps() # 与 eps(Float64) 相同
2.220446049250313e-16
这些值分别是 Float32 中的 2.0^-23 和 Float64 中的 2.0^-52。eps 函数也可以接受一个浮点值作为参数,然后给出这个值与下一个可表示的浮点数值之间的绝对差。也就是说,eps(x) 产生一个和 x 类型相同的值,并且 x + eps(x) 恰好是比 x 更大的下一个可表示的浮点值:
实例
2.220446049250313e-16
julia> eps(1000.)
1.1368683772161603e-13
julia> eps(1e-27)
1.793662034335766e-43
julia> eps(0.0)
5.0e-324
两个相邻可表示的浮点数之间的距离并不是常数,数值越小,间距越小,数值越大,间距越大。换句话说,可表示的浮点数在实数轴上的零点附近最稠密,并沿着远离零点的方向以指数型的速度变得越来越稀疏。根据定义,eps(1.0) 与 eps(Float64) 相等,因为 1.0 是个 64 位浮点值。
Julia 也提供了 nextfloat 和 prevfloat 两个函数分别返回基于参数的下一个更大或更小的可表示的浮点数:
实例
1.25f0
julia> nextfloat(x)
1.2500001f0
julia> prevfloat(x)
1.2499999f0
julia> bitstring(prevfloat(x))
"00111111100111111111111111111111"
julia> bitstring(x)
"00111111101000000000000000000000"
julia> bitstring(nextfloat(x))
"00111111101000000000000000000001"
这个例子体现了一般原则,即相邻可表示的浮点数也有着相邻的二进制整数表示。
舍入模式
一个数如果没有精确的浮点表示,就必须被舍入到一个合适的可表示的值。
Julia 所使用的默认模式总是 RoundNearest,指舍入到最接近的可表示的值,这个被舍入的值会使用尽量少的有效位数。
实例
1.5
julia> BigFloat("1.550564889",2,RoundNearest)
1.5
julia> BigFloat("1.560564889",2,RoundNearest)
1.5
0 和 1 的字面量
Julia 提供了 0 和 1 的字面量函数,可以返回特定类型或所给变量的类型。
| 函数 | 描述 |
|---|---|
| zero(x) | x 类型或变量 x 的类型的零字面量 |
| one(x) | x 类型或变量 x 的类型的一字面量 |
这些函数在数值比较中可以用来避免不必要的类型转换带来的开销。
例如:
实例
0.0f0
julia> zero(1.0)
0.0
julia> one(Int32)
1
julia> one(BigFloat)
1.0
类型转换
类型转换是把变量从一种类型转换为另一种数据类型。例如,如果您想存储一个 float 类型的值到一个简单的整型中,您需要把 float 类型强制转换为 int 类型。您可以使用强制类型转换运算符来把值显式地从一种类型转换为另一种类型,如下所示:
Julia 支持三种数值转换,它们在处理不精确转换上有所不同。
第一种:
T(x) 或 convert(T,x)
以上都会把 x 转换为 T 类型。
- 如果 T 是浮点类型,转换的结果就是最近的可表示值, 可能会是正负无穷大。
- 如果 T 为整数类型,当 x 不能由 T 类型表示时,会抛出 InexactError。
第二种:
x % T 也可以将整数 x 转换为整型 T,与 x 模 2^n 的结果一致,其中 n 是 T 的位数。
第三种:
舍入函数接收一个 T 类型的可选参数。比如,round(Int,x) 是 Int(round(x)) 的简写版。
实例
127
julia> Int8(128)
ERROR: InexactError: trunc(Int8, 128)
Stacktrace:
[…]
julia> Int8(127.0)
127
julia> Int8(3.14)
ERROR: InexactError: Int8(3.14)
Stacktrace:
[…]
julia> Int8(128.0)
ERROR: InexactError: Int8(128.0)
Stacktrace:
[…]
julia> 127 % Int8
127
julia> 128 % Int8
–128
julia> round(Int8,127.4)
127
julia> round(Int8,127.6)
ERROR: InexactError: trunc(Int8, 128.0)
Stacktrace:
[…]
Julia 元组
最后更新于:2022-03-27 03:04:20
Julia 元组
Python 的元组与数组类似,都是有序的元素集合,不同之处在于元组的元素不能修改。
另外元组使用小括号 (…),数组使用方括号 […]。
元组创建很简单,只需要在括号中添加元素,并使用逗号隔开即可,数组中的很多函数也可以在元组中使用。
如下实例:
实例
(5, 10, 15, 20, 25, 30)
julia> tupl
(5, 10, 15, 20, 25, 30)
julia> tupl[3:end] # 输出第三个到最后一个元素的元组
(15, 20, 25, 30)
julia> tupl = ((1,2),(3,4)) # 创建二维元组
((1, 2), (3, 4))
julia> tupl[1] # 访问二维元组元素,输出第一维元组
(1, 2)
julia> tupl[1][2] # 访问二维元组元素,输出第一维元组的第二个元素
2
元组的元素是不能修改,如果我们尝试修改它就回报错:
实例
(1, 2, 3, 4)
julia> tupl2[2]=0
ERROR: MethodError: no method matching setindex!(::NTuple{4, Int64}, ::Int64, ::Int64)
Stacktrace:
[1] top-level scope
@ REPL[8]:1
元组命名
我们可以为元组命名,从而可以更方便的访问它。
以下列出了几种不同元组的命名方式。
1、元组中的键(key)和值(value)分开命名
元组中的键(key)和值(value)可以分开独立命名,实例如下:
实例
(:corner1, :corner2)
julia> values_shape = ((100, 100), (200, 200))
((100, 100), (200, 200))
julia> shape_item2 = NamedTuple{names_shape}(values_shape)
(corner1 = (100, 100), corner2 = (200, 200))
我们可以使用 . 点号来访问元组:
实例
(100, 100)
julia> shape_item2.corner2
(200, 200)
2、键(key)和值(value)同时在一个元组中
键(key)和值(value)可以同时在一个元组中,实例如下:
实例
(corner1 = (1, 1), corner2 = (–1, –1), center = (0, 0))
我们可以使用 . 点号来访问元组:
实例
(1, 1)
julia> shape_item.corner2
(–1, –1)
julia> shape_item.center
(0, 0)
julia> (shape_item.center,shape_item.corner2)
((0, 0), (–1, –1))
我们还可以像使用普通元组一样访问所有值,如下所示:
实例
(corner1 = (1, 1), corner2 = (–1, –1), center = (0, 0))
julia> c1
(1, 1)
3、合并两个已命名的元组
我们可以使用 merge() 函数来合并两个已命名的元组,实例如下:
实例
(top = "red", bottom = "green")
julia> shape_item = (corner1 = (1, 1), corner2 = (–1, –1), center = (0, 0))
(corner1 = (1, 1), corner2 = (–1, –1), center = (0, 0))
julia> merge(shape_item, colors_shape)
(corner1 = (1, 1), corner2 = (–1, –1), center = (0, 0), top = "red", bottom = "green")
元组作为函数参数
以下实例我们创建一个 testFunc 函数,并将元组 options 作为参数传入:
实例:test.jl 文件代码
function testFunc(x, y, z; a=10, b=20, c=30)
println("x = $x, y = $y, z = $z; a = $a, b = $b, c = $c")
end
# 创建元组
options = (b = 200, c = 300)
# 执行函数,元组作为参数传入
testFunc(1, 2, 3; options…)
使用 julia 命令执行以上文件,输出结果为:
$ julia test.jl x = 1, y = 2, z = 3; a = 10, b = 200, c = 300
如果指定的参数在元组后面,则会覆盖元组中已有的参数:
实例
function testFunc(x, y, z; a=10, b=20, c=30)
println("x = $x, y = $y, z = $z; a = $a, b = $b, c = $c")
end
# 创建元组
options = (b = 200, c = 300)
# 执行函数,元组作为参数传入,指定参数在元组前,不会覆盖
testFunc(1, 2, 3; b = 1000_000, options…)
# 执行函数,元组作为参数传入,指定参数在元组后,会覆盖
testFunc(1, 2, 3; options…, b= 1000_000)
使用 julia 命令执行以上文件,输出结果为:
$ julia test.jl x = 1, y = 2, z = 3; a = 10, b = 200, c = 300 x = 1, y = 2, z = 3; a = 10, b = 1000000, c = 300
Julia 数组
最后更新于:2022-03-27 03:04:18
Julia 数组
数组,就是相同数据类型的元素按一定顺序排列的集合,可以是一维数组和多维数组。
Julia 支持数组数据结构,它可以存储一个大小不是固定的,类型可以相同也可以不同的顺序集合。
Julia 数组是可变类型集合,用于列表、向量、表格和矩阵。
Julia 数组的索引键值可以使用整数表示,数组的大小不是固定的。
Julia 提供了很多函数帮助我们来操作数组,比如数组添加元素,合并数组等。
Julia 数组用方括号 […] 指定,多个元素使用逗号 , 分隔。
创建一个一维数组(即一个向量)语法为:
[A, B, C, ...]
创建一维数组
下面实例创建了一个简单的一维数组:
实例
3-element Vector{Int64}:
1
2
3
上面的实例中我们创建了一个包含 3 个元素的一维数组,每个元素都是一个 64 位整数,这个一维数组绑定到变量 arr 中。
数组元素的类型也可以不一样:
实例
4-element Vector{Any}:
1
"RUNOOB"
2.5
π = 3.1415926535897…
上面的实例中我们创建了一个包含 4 个元素不同类型的一维数组, pi 是常量 π,每个元素都是一个 64 位整数,这个一维数组绑定到变量 arr 中。
当然也可以强制指定类型:
实例
3-element Vector{Int64}:
1
2
3
julia> arr2 = String["Taobao","RUNOOB","GOOGLE"]
3-element Vector{String}:
"Taobao"
"RUNOOB"
"GOOGLE"
以上实例数组 arr 限制只能输入整数,arr2 限制只能输入字符串。
我们也可以创建一个空数组:
实例
Int64[]
julia> arr2 = String[]
String[]
创建的数组可以直接使用索引值来访问,第一个值的索引为 1(不是 0),第二个值索引为 2,以此类推,最后一个可以使用 end 表示:
实例
3-element Vector{Int64}:
1
2
3
julia> arr[2]
2
julia> arr2 = String["Taobao","RUNOOB","GOOGLE"]
3-element Vector{String}:
"Taobao"
"RUNOOB"
"GOOGLE"
julia> arr2[1]
"Taobao"
julia> arr2[end]
"GOOGLE"
指定数组类型及维度
我们还可以使用以下语法指定数组的类型和维度:
Array{type}(undef, dims...)
undef 表示数组未初始化。
dims… 可以是维度的单多元组,也可以是维度作为可变参数时的一组值。
dims… 数字表示元素个数,多个维度使用逗号 , 分隔。
实例
3-element Vector{Int64}:
4834342704
4377305096
0
julia> array = Array{Int64}(undef, 3, 3, 3) # 表示 3 维数组,每个维度数组有 3 个元素
3×3×3 Array{Int64, 3}:
[:, :, 1] =
4562265712 0 0
1 0 0
0 0 0
[:, :, 2] =
0 0 0
0 0 0
0 0 0
[:, :, 3] =
0 0 0
0 0 0
0 0 0
以上实例中,数组的类型我们放在花括号中 {}, undef 用于设置数组未初始化为任何已知值,这就是我们在输出中得到随机数的原因。
创建二维数组和矩阵
我们可以将数组元素中的逗号 , 省略掉或者使用两个冒号 ;;,这样就可以创建一个二维数组了,如下实例:
实例
1×4 Matrix{Int64}:
1 2 3 4
julia> [1;; 2;; 3;; 4]
1×4 Matrix{Int64}:
1 2 3 4
注意:第一行输出的 1×4 Matrix{Int64}:,1×4 表示一行四列的矩阵。
虽然只有一行,也是二维数组,因为 Julia 只认可列向量,而不认可所谓的行向量。
要添加另一行,只需添加分号 ;,看以下实例:
实例
2×2 Matrix{Int64}:
1 2
3 4
也可以使用冒号 : 和空格 来实现,看以下实例:
实例
2×2 Matrix{Int64}:
1 3
2 4
注意:第一行输出的 2×2 Matrix{Int64}:,2×2 表示两行两列的矩阵。
我们也可以在方括号 [] 中嵌入多个长度相同的一维数组,并用空格分隔来创建二维数组:
实例
2×3 Matrix{Int64}:
1 3 5
2 4 6
2×3 表示两行三列的数组。
下面我们通过灵活运用分号 ; 和空格 创建一个两行三列和三行两列的二维数组:
实例
2×3 Matrix{Int64}:
1 3 5
2 4 6
julia> [[1 2]; [3 4]; [5 6]]
3×2 Matrix{Int64}:
1 2
3 4
5 6
使用范围函数来创建数组
省略号 …
可以使用省略号 … 来创建一个数组,实例如下:
实例
11-element Vector{Int64}:
0
1
2
3
4
5
6
7
8
9
10
collect() 函数
collect() 函数语法格式如下:
collect(start:step:stop)
start 为开始值,step 为步长,stop 为结束值。
该函数返回数组。
以下实例值为 1,步长为 2,结束值为 13:
实例
7-element Vector{Int64}:
1
3
5
7
9
11
13
collect() 函数也可以指定类型,语法格式如下:
collect(element_type, start:step:stop)
以下实例创建一个浮点型数组:
实例
3-element Vector{Float64}:
1.0
3.0
5.0
range() 函数
range() 函数可以生存一个区间范围并指定步长,可以方便 collect() 函数 调用。
range() 函数语法格式如下:
range(start, stop, length)
range(start, stop; length, step)
range(start; length, stop, step)
range(;start, length, stop, step)
start 为开始值,step 为步长,stop 为结束值,length 为长度。
实例
1:100
julia> range(1, stop=100)
1:100
julia> range(1, step=5, length=100)
1:5:496
julia> range(1, step=5, stop=100)
1:5:96
julia> range(1, 10, length=101)
1.0:0.09:10.0
julia> range(1, 100, step=5)
1:5:96
julia> range(stop=10, length=5)
6:10
julia> range(stop=10, step=1, length=5)
6:1:10
julia> range(start=1, step=1, stop=10)
1:1:10
如果未指定长度 length,且 stop – start 不是 step 的整数倍,则将生成在 stop 之前结束的范围。
julia> range(1, 3.5, step=2) 1.0:2.0:3.0
使用 range() 和 collect() 创建数组:
实例
10-element Vector{Int64}:
1
2
3
4
5
6
7
8
9
10
julia> collect(range(1, length=15, stop=150))
15-element Vector{Float64}:
1.0
11.642857142857142
22.285714285714285
32.92857142857143
43.57142857142857
54.214285714285715
64.85714285714286
75.5
86.14285714285714
96.78571428571429
107.42857142857143
118.07142857142857
128.71428571428572
139.35714285714286
150.0
使用推导式和生成器创建数组
创建数组的另一种有用方法是使用推导。
数组推导式语法格式如下:
A = [ F(x,y,...) for x=rx, y=ry, ... ]
F(x,y,…) 取其给定列表中变量 x,y 等的每个值进行计算。值可以指定为任何可迭代对象,但通常是 1:n 或 2:(n-1) 之类的范围,或者像 [1.2, 3.4, 5.7] 这样的显式数组值。结果是一个 N 维密集数组,将变量范围 rx,ry 等的维数拼接起来得到其维数,并且每次 F(x,y,…) 计算返回一个标量。
实例
10-element Vector{Int64}:
1
4
9
16
25
36
49
64
81
100
创建二维数组:
实例
10×10 Matrix{Int64}:
1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
3 6 9 12 15 18 21 24 27 30
4 8 12 16 20 24 28 32 36 40
5 10 15 20 25 30 35 40 45 50
6 12 18 24 30 36 42 48 54 60
7 14 21 28 35 42 49 56 63 70
8 16 24 32 40 48 56 64 72 80
9 18 27 36 45 54 63 72 81 90
10 20 30 40 50 60 70 80 90 100
也可以在没有方括号的情况下编写(数组)推导,从而产生称为生成器的对象。
以下实例创建一个数组:
实例
5-element Vector{Int64}:
1
4
9
16
25
以下表达式在不分配内存的情况下对一个序列进行求和:
实例
1.6439345666815615
Julia 数组基本函数
| 函数 | 描述 |
|---|---|
eltype(A) |
A 中元素的类型 |
length(A) |
A 中元素的数量 |
ndims(A) |
A 的维数 |
size(A) |
一个包含 A 各个维度上元素数量的元组 |
size(A,n) |
A 第 n 维中的元素数量 |
axes(A) |
一个包含 A 有效索引的元组 |
axes(A,n) |
第 n 维有效索引的范围 |
eachindex(A) |
一个访问 A 中每一个位置的高效迭代器 |
stride(A,k) |
在第 k 维上的间隔(stride)(相邻元素间的线性索引距离) |
strides(A) |
包含每一维上的间隔(stride)的元组 |
Julia构造和初始化
Julia 提供了许多用于构造和初始化数组的函数。在下列函数中,参数 dims … 可以是一个元组 tuple 来表示维数,也可以是一个可变长度的整数值作为维数。大部分函数的第一个参数都表示数组的元素类型 T 。如果类型 T 被省略,那么将默认为 Float64。
| 函数 | 描述 |
|---|---|
Array{T}(undef, dims...) |
一个没有初始化的密集 Array |
zeros(T, dims...) |
一个全零 Array |
ones(T, dims...) |
一个元素均为 1 的 Array |
trues(dims...) |
一个每个元素都为 true 的 BitArray |
falses(dims...) |
一个每个元素都为 false 的 BitArray |
reshape(A, dims...) |
一个包含跟 A 相同数据但维数不同的数组 |
copy(A) |
拷贝 A |
deepcopy(A) |
深拷贝,即拷贝 A,并递归地拷贝其元素 |
similar(A, T, dims...) |
一个与A具有相同类型(这里指的是密集,稀疏等)的未初始化数组,但具有指定的元素类型和维数。第二个和第三个参数都是可选的,如果省略则默认为元素类型和 A 的维数。 |
reinterpret(T, A) |
与 A 具有相同二进制数据的数组,但元素类型为 T |
rand(T, dims...) |
一个随机 Array,元素值是
半开区间中的均匀分布且服从一阶独立同分布 [1] |
randn(T, dims...) |
一个随机 Array,元素为标准正态分布,服从独立同分布 |
Matrix{T}(I, m, n) |
m 行 n 列的单位矩阵 (需要先执行 using LinearAlgebra 来才能使用 I) |
range(start, stop=stop, length=n) |
从 start 到 stop 的带有 n 个线性间隔元素的范围 |
fill!(A, x) |
用值 x 填充数组 A |
fill(x, dims...) |
一个被值 x 填充的 Array |
zeros() 创建数组实例,元素初始值 都是 0:
实例
2×3 Matrix{Int8}:
0 0 0
0 0 0
julia> zeros(Int8, (2, 3))
2×3 Matrix{Int8}:
0 0 0
0 0 0
julia> zeros((2, 3))
2×3 Matrix{Float64}:
0.0 0.0 0.0
0.0 0.0 0.0
Python3 reload() 函数
最后更新于:2022-03-27 03:04:16
Python3 reload() 函数
描述
reload() 用于重新载入之前载入的模块。
在 Python2.x 版本中 reload() 是内置函数,可以直线使用,参见 Python2.x reload() 函数。在 Python2.x ~ Python3.3 版本移到 imp 包中(Python2.x 也可以导入 imp 包使用),Python3.4 之后到版本移到了 importlib 包中。
语法
Python2.x ~ Python3.3 之前版本:
import imp imp.reload(module)
或
from imp import reload reload(module)
Python3.4 之后到版本:
import importlib importlib.reload(module)
或
from importlib import reload reload(module)
参数
- module — 模块对象。
返回值
返回模块对象。
实例
以下实例展示了 reload() 的使用方法。
实例 1
重新载入 sys 模块
>>> importlib.reload(sys)
<module ‘sys’ (built-in)>
实例 2
首先我们在当前目录下创建一个 runoob.py :
runoob.py 文件
site = "RUNOOB"
在当前目录下启动 Python 交互式命令窗口:
实例
>>> runoob.site
‘RUNOOB‘
然后在另外一个窗口编辑 runoob.py 文件(不要关闭以上的 Python 交互式命令窗口),修改为以下代码:
修改后的 runoob.py 文件
site = "GOOGLE"
然后回到 Python 交互式命令窗口:
实例
‘RUNOOB’
>>> from importlib import reload # Python 3.4+
>>> reload(runoob) # 重新载入修改后的 runoob.py 文件
<module ‘runoob’ from ‘/Users/RUNOOB/runoob-test/runoob.py’>
>>> runoob.site # 输出结果正常了
‘GOOGLE’
Julia 基本语法
最后更新于:2022-03-27 03:04:13
Julia 基本语法
变量
变量来源于数学,是计算机语言中能储存计算结果或能表示值抽象概念。
变量可以通过变量名访问。
Julia 语言变量名由字母、数字、下划线 _ 组成,其中首个字符不能为数字。
变量名是大小写敏感的。
Julia 变量使用很简单,只需赋值即可,如下实例:
实例
x = 10
# 使用 x 的值做计算
x + 1
11
# 将字符串赋值给变量 site_name
site_name = "RUNOOB"
# 浮点型数据
marks_math = 9.5
交互式命令下输出结果如下:
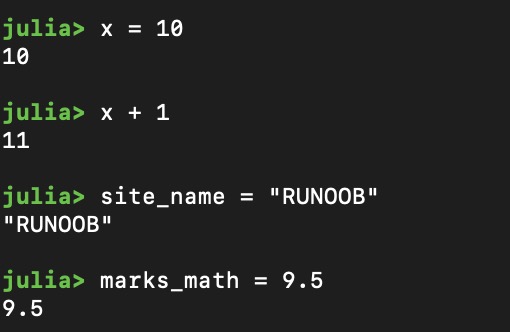
从实例中我们看到,与其他编程语言 C++、Java 等不同的是 Julia 不需要指定变量类型,它可以自动推断等号右侧的对象类型。
命名规范
建议遵循以下这些命名规范:
- 变量名采用小写。
- 使用下划线 _ 来分变量名中的单词。
- 类型 Type 和模块 Module 的名称使用大写字母开头,并且用大写字母而不是用下划线分隔单词。
- 函数(
function)和宏(macro)的名字使用小写,不使用下划线。 - 会对输入参数进行更改的函数要使用
!结尾。这些函数有时叫做 “mutating” 或 “in-place” 函数,因为它们在被调用后会修改他们的输入参数的内容而不仅仅只是返回一个值。
注释
Julia 中的注释有单行注释和多行注释。
Julia 中单行注释以 # 开头,例如:
实例
# 这是另外一行注释
println("Hello World!")
多行注释用 #= 与 =# 将注释括起来,例如:
实例
1、这是一行注释
2、这是另外一行注释
=#
println("Hello World!")
Julia 交互式命令
最后更新于:2022-03-27 03:04:11
Julia 交互式命令窗口
执行 julia 命令可以直接进入交互式命令窗口:
$ julia
_
_ _ _(_)_ | Documentation: https://docs.julialang.org
(_) | (_) (_) |
_ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 1.7.2 (2022-02-06)
_/ |\__'_|_|_|\__'_| | release-1.7/bf53498635 (fork: 461 commits, 259 days)
|__/ |
julia>
执行 exit() 退出交互式命令窗口,也可以通过输入 CTRL-D(同时按 Ctrl 键和 d 键)退出。
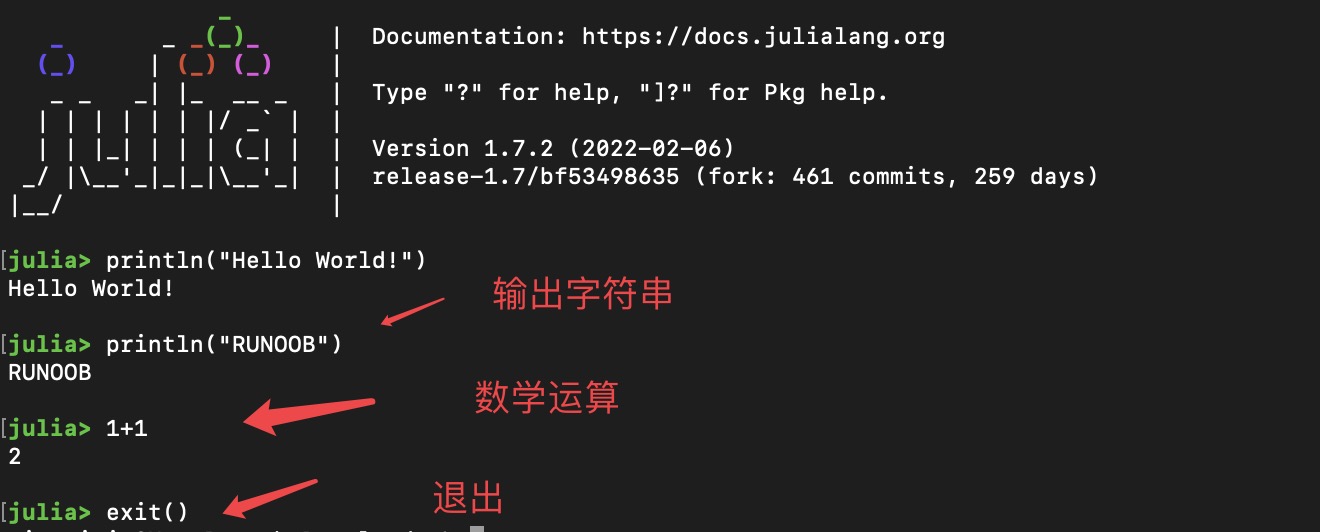
当然我们也可以执行一个 Julia 的代码文件,文件名以 .jl 结尾。
以下是一个名为 runoob_test.jl 的文件:
runoob_test.jl 文件
println("Hello World!")
println("RUNOOB")
println(1+1)
要执行 Julia 语言代码可以使用 julia runoob_test.jl 命令。
执行以上代码输出:
$ julia runoob_test.jl Hello World! RUNOOB 2
Julia 语言环境安装
最后更新于:2022-03-27 03:04:09
Julia 语言环境安装
Julia 语言支持以下系统:
- Linux
- FreeBSD
- macOS
- Windows
- Android
Julia 安装包下载地址为:https://julialang.org/downloads/。
Github 源码地址:https://github.com/JuliaLang/julia。
国内镜像地址:https://mirrors.tuna.tsinghua.edu.cn/julia-releases/bin/
各个系统对应的包名:
| 操作系统 | 包名 |
|---|---|
| Windows | julia-1.7.2-win64.exe |
| Linux | x86_64.tar.gz |
| Mac | julia-1.7.2-mac64.dmg 安装包或 julia-1.7.2-mac64.tar.gz 二进制文件 |
| FreeBSD | julia-1.7.2-freebsd-x86_64.tar.gz |
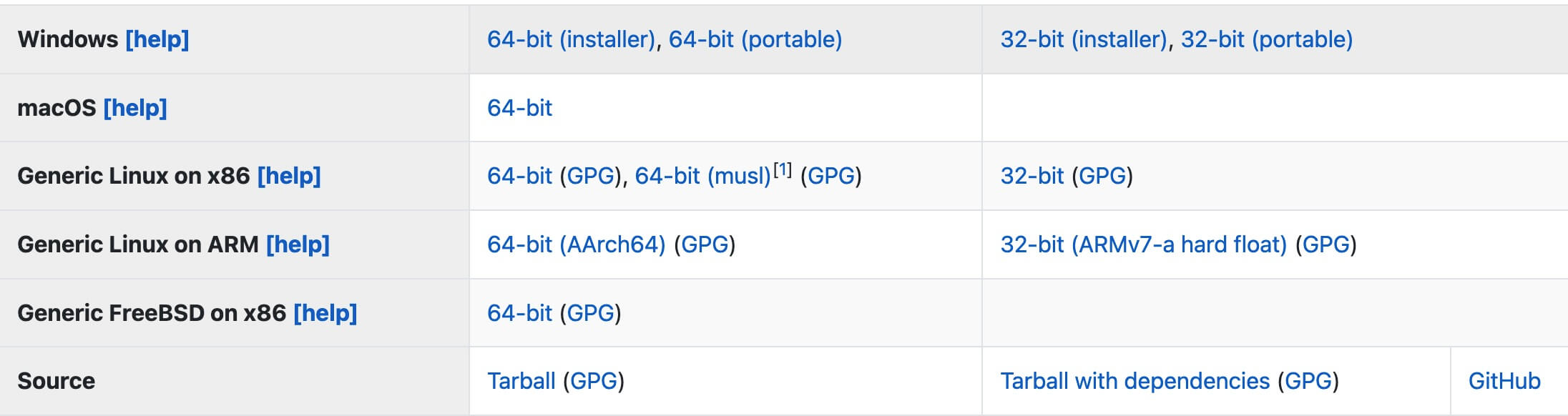
注:CPU 是 X86 还是 ARM 可以通过 uname -m 命令查看:
$ uname -m x86_64
Windows 系统下安装
从 https://julialang.org/downloads/ 下载 Windows Julia 安装程序。
注意:32 位 Julia 二进制文件可在 32 位和 64 位 Windows(x86 和 x86_64)上运行,但 64 位 Julia 二进制文件只能在 64 位 Windows (x86_64) 上运行,现在电脑也基本上是 64 位的。
运行安装程序,安装过程点击 Next 就好了。
勾选 Add Julia To PATH 自动将 Julia 添加到环境变量。
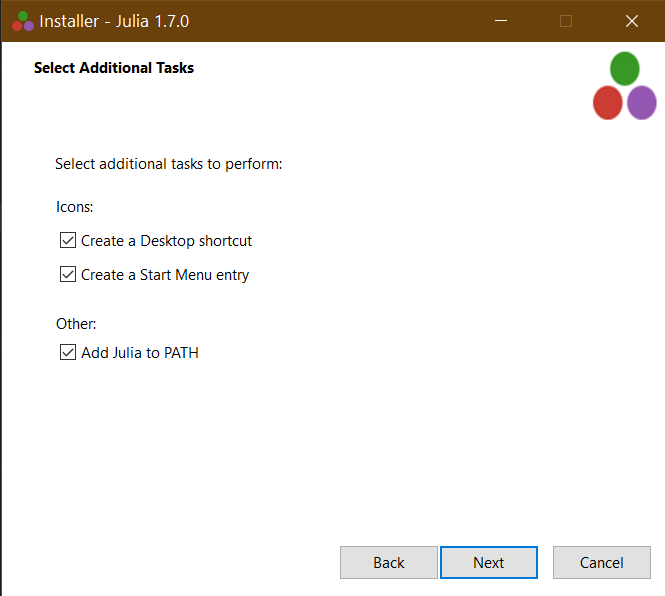
这样我们就可以在终端执行 Julia 命令了。
Julia 默认安装目录应该类似于 C:\Users\RUNOOB\AppData\Local\Programs\Julia 1.7.2。
Linux/FreeBSD 安装
以下介绍了在 Linux/FreeBSD 系统下使用二进制包安装方法,下载二进制包:
wget https://julialang-s3.julialang.org/bin/linux/x64/1.7/julia-1.7.2-linux-x86_64.tar.gz
以上是官网提供的下载地址,如果速度慢,可以采用国内镜像地址下载:
wget https://mirrors.tuna.tsinghua.edu.cn/julia-releases/bin/linux/x86/1.7/julia-1.7.2-linux-i686.tar.gz --no-check-certificate
解压:
tar zxvf julia-1.7.2-linux-i686.tar.gz
Linux/FreeBSD 二进制文件不需要安装,但需要我们的系统可以找到 julia 可执行文件,这就需要将 julia 的目录添加到系统环境中。
解压完成后将 julia 的解压目录移动到 /usr/local 目录下:
mv julia-1.7.2 /usr/local/
移动完成后我们就可以使用 julia 的完整目录执行 Julia 命令:
# /usr/local/julia-1.7.2/bin/julia -v julia version 1.7.2
julia -v 命令用于查看版本号。
julia 使用完整路径调用可执行文件:/usr/local/julia-1.7.2/bin/julia -v
也可以将 julia 命令添加到您的系统 PATH 环境变量中,编辑 ~/.bashrc(或 ~/.bash_profile)文件,在最后一行添加以下代码:
export PATH="$PATH:/usr/local/julia-1.7.2/bin/"
添加后执行以下命令,让环境变量立即生效:
source ~/.bashrc 或 source ~/.bash_profile
# julia -v julia version 1.7.2
macOS 安装
以下介绍了在 macOS 系统下使用二进制包安装方法,下载二进制包:
wget https://julialang-s3.julialang.org/bin/mac/x64/1.7/julia-1.7.2-mac64.tar.gz
以上是官网提供的下载地址,如果速度慢,可以采用国内镜像地址下载:
wget https://mirrors.tuna.tsinghua.edu.cn/julia-releases/bin/mac/x64/1.7/julia-1.7.2-mac64.tar.gz
解压:
tar zxvf julia-1.7.2-mac64.tar.gz
macOS 二进制文件不需要安装,但需要我们的系统可以找到 julia 可执行文件,这就需要将 julia 的目录添加到系统环境中。
解压完成后,可以先把解压包改名为 julia-1.7.2:
mv julia-bf53498635 julia-1.7.2
完成后将 julia-1.7.2目录移动到 /usr/local 目录下:
sudo mv julia-1.7.2 /usr/local/
移动完成后我们就可以使用 julia 的完整目录执行 Julia 命令:
$ /usr/local/julia-1.7.2/bin/julia -v julia version 1.7.2
julia -v 命令用于查看版本号。
julia 使用完整路径调用可执行文件:/usr/local/julia-1.7.2/bin/julia -v
也可以将 julia 命令添加到您的系统 PATH 环境变量中,编辑 ~/.bash_profile文件,在最后一行添加以下代码:
export PATH="$PATH:/usr/local/julia-1.7.2/bin/"
添加后执行以下命令,让环境变量立即生效:
source ~/.bash_profile
$ julia -v julia version 1.7.2
Julia 教程
最后更新于:2022-03-27 03:04:05
Julia 教程

Julia 是一个开源的编程语言,采用 MIT 许可证,每个人都可以免费使用。
Julia 是一个面向科学计算的高性能动态高级程序设计语言。
Julia 最初是为了满足高性能数值分析和计算科学的需要而设计的,不需要解释器,速度快。
Julia 于 2012 年首次发行,支持各种平台:macOS、Windows、Linux、FreeBSD、Android。
Julia 语言特点
- 核心语言非常小,标准库用的是 Julia 语言本身写的。
- 调用许多其它成熟的高性能基础代码,如线性代数、随机数生成、快速傅里叶变换、字符串处理。
- 丰富的用于创建或描述对象的类型语法。
-
高性能,接近于静态编译型语言,包括用户自定义类型等。
- 为并行计算和分布式计算而设计。
- 轻量级协程。
- 优雅的可扩展的类型转换/提升。
- 支持 Unicode,包括但不限于 UTF-8。
- 可直接调用 C 函数(不需要包装或是借助特殊的 API)。
- 有类似 shell 的进程管理能力。
- 有类似 Lisp 的宏以及其它元编程工具。
- 可与 Jupyter notebook 一起使用。
Julia 语言用途
Julia 主要功能是用于数值计算。
第一个 Julia 程序
接下来我们来编写第一个 Julia 程序 hello.jl(Julia 文件扩展名 .jl),代码如下:
hello.jl 文件
println("Hello World!")
要执行 Julia 语言代码可以使用 julia hello.jl 命令。
执行以上代码输出:
$ julia hello.jl Hello, World!
参考链接
Julia 官网:https://julialang.org/
Julia 中文手册:https://docs.juliacn.com/latest/
CSS repeating-conic-gradient() 函数
最后更新于:2022-03-27 03:04:02
CSS repeating-conic-gradient() 函数
定义与用法
repeating-conic-gradient() 函数用于创建一个重复的圆锥渐变。
支持版本:CSS3
浏览器支持
表格中的数字表示支持该函数的第一个浏览器版本号。
| 函数 | |||||
|---|---|---|---|---|---|
| repeating-conic-gradient() | 69.0 | 79.0 | 83.0 | 12.1 | 56.0 |
CSS 语法
background-image: repeating-conic-gradient([from angle] [at position,] color degree, color degree, ...);
| 值 | 描述 |
|---|---|
| from angle | 可选。起始角度。默认值为 0deg。 |
| at position | 可选。中心位置。默认居中。 |
| color degree, …, color degree | 角渐变断点。该值包含一个颜色值,后跟一个可选的停止位置( 0 到 360 之间的度数或 0% 到 100% 之间的百分比)。 |
更多实例
实例
设置开始颜色和停止颜色的重复圆锥渐变::
background-image: repeating-conic-gradient(red 0deg 30deg, yellow 30deg 60deg, blue 60deg 90deg);
}
CSS min() 函数
最后更新于:2022-03-27 03:03:59
CSS min() 函数
实例
使用 min() 函数将 #div1 的宽度设置为最小的值,取 50% 或 300px 的最大值:
background-color: yellow;
height: 100px;
width: min(50%, 300px);
}
定义与用法
min() 函数让你可以从一个逗号分隔的表达式列表中选择最小的值作为属性的值。
min() 函数方法接受一个或多个用逗号分隔的表达式作为他的参数,数值最小的表达式的值将会作为指定的属性的值。
/* 属性: min(expression [, expression]) */ width: min(1vw, 4em, 80px);
在上面的例子中,宽度最多是 80px。如果视口的宽度小于 800px,或者一个 em 的宽度小于 20px,则会更窄。换句话说,最大宽度是 80px,
支持版本:CSS3
浏览器支持
表格中的数字表示支持该函数的第一个浏览器版本号。
| 函数 | |||||
|---|---|---|---|---|---|
| min() | 79.0 | 79.0 | 75.0 | 11.1 | 66.0 |
CSS 语法
min(value1, value2, ...)
| 值 | 描述 |
|---|---|
| value1, value2, … | 必须。逗号分隔值列表,选择最小值。 |
CSS max() 函数
最后更新于:2022-03-27 03:03:57
CSS max() 函数
实例
使用 max() 函数将 #div1 的宽度设置为最大的值,取 50% 或 300px 的最大值:
background-color: yellow;
height: 100px;
width: max(50%, 300px);
}
定义与用法
max() 函数让你可以从一个逗号分隔的表达式列表中选择最大的值作为属性的值。
max() 函数方法接受一个或多个用逗号分隔的表达式作为他的参数,数值最大的表达式的值将会作为指定的属性的值。
/* 属性: max(expression [, expression]) */ width: max(10vw, 4em, 80px);
在上面这个例子中,宽度最小会是 80px,除非视图宽度大于 800px 或者是一个 em 比 20px 宽。简单来说,最小宽度是 80px。你也可以认为 max() 的值提供了一个属性最小可能的值。
支持版本:CSS3
浏览器支持
表格中的数字表示支持该函数的第一个浏览器版本号。
| 函数 | |||||
|---|---|---|---|---|---|
| max() | 79.0 | 79.0 | 75.0 | 11.1 | 66.0 |
CSS 语法
max(value1, value2, ...)
| 值 | 描述 |
|---|---|
| value1, value2, … | 必须。逗号分隔值列表,选择最大值。 |
CSS counter() 函数
最后更新于:2022-03-27 03:03:55
CSS counter() 函数
实例
在页面中创建一个计数器(在 body 选择器中),增加每个 <h3> 元素的计数器值,并在每个 <h3> 元素之前添加文本 “Section 计数器值”:
counter-reset: section; /* 重置计数器成0 */
}
h3:before {
counter-increment: section; /* 增加计数器值 */
content: "Section " counter(section) ": "; /* 显示计数器 */
}
定义与用法
counter() 函数以字符串形式返回当前计数器的值。
计数器的值通过使用 counter-reset 和 counter-increment 操作,在 content 上应用 counter() 函数来显示在页面上。
支持版本:CSS3
浏览器支持
| 函数 | |||||
|---|---|---|---|---|---|
| counter() | 支持 | 支持 | 支持 | 支持 | 支持 |
CSS 语法
counter(countername, counterstyle)
| 值 | 描述 |
|---|---|
| countername | 必需。 计数器的名称(与 counter-reset 和 counter-increment 属性使用的名称相同)。 |
| counterstyle | 可选的。 计数器的样式(可以是 CSS list-style-type 属性值)。 |
更多实例
实例
设置计数器样式:
counter-reset: section;
} h2::before {
counter-increment: section;
content: "Section " counter(section, upper-roman) ": ";
}
实例
设置嵌套计数器:
counter-reset: section; /* 为每个ol元素创建新的计数器实例 */
list-style-type: none;
}
li:before {
counter-increment: section; /* 只增加计数器的当前实例 */
content: counters(section, ".") " "; /* 为所有计数器实例增加以”.”分隔的值 */
}
CSS conic-gradient() 函数
最后更新于:2022-03-27 03:03:53
CSS conic-gradient() 函数
定义与用法
conic-gradient() 函数创建一个由渐变组成的图像。
圆锥渐变是颜色过渡围绕中心点旋转(而不是从中心向外辐射)。
创建圆锥渐变,至少需要设置两个色标。
圆锥渐变实例:
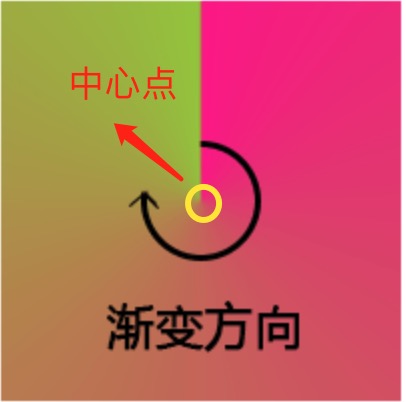
从图中可以看到,圆锥渐变的渐变方向和起始点。起始点是图形中心,然后以顺时针方向绕中心实现渐变效果。
| 版本: | CSS3 |
|---|
浏览器支持
表格中的数字表示支持该函数的第一个浏览器版本号。
| 函数 | |||||
|---|---|---|---|---|---|
| conic-gradient() | 69.0 | 79.0 | 83.0 | 12.1 | 56.0 |
CSS 语法
background-image: conic-gradient([from angle] [at position,] color degree, color degree, ...);
| 值 | 描述 |
|---|---|
| from angle | 可选。起始角度。默认值为 0deg |
| at position | 可选。中心位置。默认居中。 |
| color degree, …, color degree | 角渐变断点。该值包含一个颜色值,后跟一个可选的停止位置( 0 到 360 之间的度数或 0% 到 100% 之间的百分比)。 |
更多实例
实例
三种颜色圆锥渐变,并设置每种渐变度数:
background-image: conic-gradient(red 45deg, yellow 90deg, green 210deg)
}
实例
通过设置 border-radius: 50% 把圆锥渐变变成一个圆:
background-image: conic-gradient(red, yellow, green, blue, black);
border-radius: 50%;
}
实例
设置起始角度:
background-image: conic-gradient(from 90deg, red, yellow, green);
border-radius: 50%;
}
实例
指定中心位置:
background-image: conic-gradient(at 60% 45%, red, yellow, green);
border-radius: 50%;
}
实例
指定一个位置,并且设置一个角度:
background-image: conic-gradient(from 90deg at 60% 45%, red, yellow, green);
border-radius: 50%;
}
实例
一个饼图:
background-image: conic-gradient(red 0deg, red 90deg, yellow 90deg, yellow 180deg, green 180deg);
border-radius: 50%;
}
background-image: conic-gradient(red 0deg, red 90deg, yellow 90deg, yellow 180deg, green 180deg);
代码解析:
- red 0deg, red 90deg 表示 0~90 度区间使用红色 red。
- yellow 90deg, yellow 180deg 表示 90~180 度区间使用黄色 yellow。
- green 180deg 表示 180~360 度区间使用绿色 green。
实例
创建一个取色卡:
background: radial-gradient(closest-side, gray, transparent),
conic-gradient(red, magenta, blue, aqua, lime, yellow, red);
border-radius: 50%;
}
Bootstrap5 表单验证
最后更新于:2022-03-27 03:03:50
Bootstrap5 表单验证
我们可以使用不同的验证类来设置表单的验证功能。
.was-validated 或 .needs-validation 添加到 <form> 元素中,input 输入字段将具有绿色(有效)或红色(无效)边框效果,用于说明表单是否需要输入内容。
.valid-feedback 或 .invalid-feedback 类用来告诉用户缺少什么信息,或者在提交表单之前需要完成什么。
实例
使用 .was-validated 类显示表单在提交之前需要填写的内容:
<div class="form-group">
<label for="uname">Username:</label>
<input type="text" class="form-control" id="uname" placeholder="Enter username" name="uname" required>
<div class="valid-feedback">验证成功!</div>
<div class="invalid-feedback">请输入用户名!</div>
</div>
<div class="form-group">
<label for="pwd">Password:</label>
<input type="password" class="form-control" id="pwd" placeholder="Enter password" name="pswd" required>
<div class="valid-feedback">验证成功!</div>
<div class="invalid-feedback">请输入密码!</div>
</div>
<div class="form-group form-check">
<label class="form-check-label">
<input class="form-check-input" type="checkbox" name="remember" required> 同意协议
<div class="valid-feedback">验证成功!</div>
<div class="invalid-feedback">同意协议才能提交。</div>
</label>
</div>
<button type="submit" class="btn btn-primary">提交</button>
</form>
实例
使用 .needs-validation,它将在表单提交之后验证缺少的内容。这里需要添加一些 JavaScript 代码才能使代码正常工作:
<div class="form-group">
<label for="uname">Username:</label>
<input type="text" class="form-control" id="uname" placeholder="Enter username" name="uname" required>
<div class="valid-feedback">验证成功!</div>
<div class="invalid-feedback">请输入用户名!</div>
</div>
<div class="form-group">
<label for="pwd">Password:</label>
<input type="password" class="form-control" id="pwd" placeholder="Enter password" name="pswd" required>
<div class="valid-feedback">验证成功!</div>
<div class="invalid-feedback">请输入密码!</div>
</div>
<div class="form-group form-check">
<label class="form-check-label">
<input class="form-check-input" type="checkbox" name="remember" required> 同意协议
<div class="valid-feedback">验证成功!</div>
<div class="invalid-feedback">同意协议才能提交。</div>
</label>
</div>
<button type="submit" class="btn btn-primary">提交</button>
</form> <script>
// 如果验证不通过禁止提交表单
(function() {
‘use strict’;
window.addEventListener(‘load’, function() {
// 获取表单验证样式
var forms = document.getElementsByClassName(‘needs-validation’);
// 循环并禁止提交
var validation = Array.prototype.filter.call(forms, function(form) {
form.addEventListener(‘submit’, function(event) {
if (form.checkValidity() === false) {
event.preventDefault();
event.stopPropagation();
}
form.classList.add(‘was-validated’);
}, false);
});
}, false);
})();
</script>
Bootstrap5 表单浮动标签
最后更新于:2022-03-27 03:03:48
Bootstrap5 表单浮动标签
默认情况下,标签内容一般显示在 input 输入框的上方:

使用浮动标签,可以在 input 输入框内插入标签,在单击 input 输入框时使它们浮动到上方

Bootstrap 实例
<input type="text" class="form-control" id="email" placeholder="Enter email" name="email">
<label for="email">Email</label>
</div> <div class="form-floating mt-3 mb-3">
<input type="text" class="form-control" id="pwd" placeholder="Enter password" name="pswd">
<label for="pwd">Password</label>
</div>
注意事项: <label> 元素必须在 <input> 元素之后,并且每个 <input> 元素都需要 placeholder 属性。
文本框
文本框 textarea 也可以有浮动效果:
Bootstrap 实例
<textarea class="form-control" id="comment" name="text" placeholder="Comment goes here"></textarea>
<label for="comment">Comments</label>
</div>
选择框
我们可以在选择菜单上使用浮动标签,它将始终显示在选择菜单的左上角,不会有点击浮动效果:
Bootstrap 实例
<select class="form-select" id="sel1" name="sellist">
<option>1</option>
<option>2</option>
<option>3</option>
<option>4</option>
</select>
<label for="sel1" class="form-label">Select list (select one):</label>
</div>
Bootstrap5 输入框组
最后更新于:2022-03-27 03:03:45
Bootstrap5 输入框组
我们可以使用 .input-group 类来向表单输入框中添加更多的样式,如图标、文本或者按钮。
.input-group-text 类来设置文本的样式。。

Bootstrap 实例
<div class="input-group mb-3">
<span class="input-group-text">@</span>
<input type="text" class="form-control" placeholder="Username">
</div>
<div class="input-group">
<input type="text" class="form-control" placeholder="Your Email">
<span class="input-group-text">@runoob.com</span>
</div>
</form>
输入框大小
使用 .input-group-sm 类来设置小的输入框, .input-group-lg 类设置大的输入框:
Bootstrap 实例
<span class="input-group-text">Small</span>
<input type="text" class="form-control">
</div> <div class="input-group mb-3">
<span class="input-group-text">Default</span>
<input type="text" class="form-control">>
</div> <div class="input-group mb-3 input-group-lg">
<span class="input-group-text">Large</span>
<input type="text" class="form-control">
</div>
多个输入框和文本
Bootstrap 实例
<div class="input-group mb-3">
<span class="input-group-text">Person</span>
<input type="text" class="form-control" placeholder="First Name">
<input type="text" class="form-control" placeholder="Last Name">
</div> <!– 多个文本信息 –>
<div class="input-group mb-3">
<span class="input-group-text">One</span>
<span class="input-group-text">Two</span>
<span class="input-group-text">Three</span>
<input type="text" class="form-control">
</div>
复选框与单选框
文本信息可以使用复选框与单选框替代:

Bootstrap 实例
<div class="input-group-text">
<input type="checkbox">
</div>
<input type="text" class="form-control" placeholder="RUNOOB">
</div> <div class="input-group mb-3">
<div class="input-group-text">
<input type="radio">
</div>
<input type="text" class="form-control" placeholder="GOOGLE">
</div>
输入框添加按钮组
Bootstrap 实例
<button class="btn btn-outline-primary" type="button">Basic Button</button>
<input type="text" class="form-control" placeholder="Some text">
</div> <div class="input-group mb-3">
<input type="text" class="form-control" placeholder="Search">
<button class="btn btn-success" type="submit">Go</button>
</div> <div class="input-group mb-3">
<input type="text" class="form-control" placeholder="Something clever..">
<button class="btn btn-primary" type="button">OK</button>
<button class="btn btn-danger" type="button">Cancel</button>
</div>
设置下拉菜单
输入框中添加下拉菜单不需要使用 .dropdown 类。

Bootstrap 实例
<button type="button" class="btn btn-primary dropdown-toggle" data-bs-toggle="dropdown">
选择网站
</button>
<ul class="dropdown-menu">
<li><a class="dropdown-item" href="https://www.google.com">GOOGLE</a></li>
<li><a class="dropdown-item" href="https://docs.gechiui.com/w3school">RUNOOB</a></li>
<li><a class="dropdown-item" href="https://www.taobao.com">TAOBAO</a></li>
</ul>
<input type="text" class="form-control" placeholder="网站地址">
</div>
输入框组标签
在输入框组通过在输入框组外围的 label 来设置标签,标签的 for 属性需要与输入框组的 id 对应,点击标签后可以聚焦输入框:

Bootstrap 实例
<label for="demo">这里输入您的邮箱:</label>
<div class="input-group mb-3">
<input type="text" class="form-control" placeholder="Email" id="demo" name="email">
<span class="input-group-text">@runoob.com</span>
</div>
</form>
Bootstrap5 选择区间
最后更新于:2022-03-27 03:03:42
Bootstrap5 选择区间
要设置一个选择区间可以在 input 元素中添加 type=”range” 并使用 .form-range 类:
选择区间:

实例
<input type="range" class="form-range" id="customRange">
步长
默认情况下,步长为 1,可以通过 step 属性来设置:
最大最小值
默认情况下,最小值为 0,最大值为 100,可以通过 min(最小) 或 max(最大) 属性来设置:
 Python 内置函数
Python 内置函数