三路排序算法
最后更新于:2022-03-27 02:52:35
三路排序算法
一、概念及其介绍
三路快速排序是双路快速排序的进一步改进版本,三路排序算法把排序的数据分为三部分,分别为小于 v,等于 v,大于 v,v 为标定值,这样三部分的数据中,等于 v 的数据在下次递归中不再需要排序,小于 v 和大于 v 的数据也不会出现某一个特别多的情况),通过此方式三路快速排序算法的性能更优。
二、适用说明
时间和空间复杂度同随机化快速排序。
三路快速排序算法是使用三路划分策略对数组进行划分,对处理大量重复元素的数组非常有效提高快速排序的过程。它添加处理等于划分元素值的逻辑,将所有等于划分元素的值集中在一起。
三、过程图示
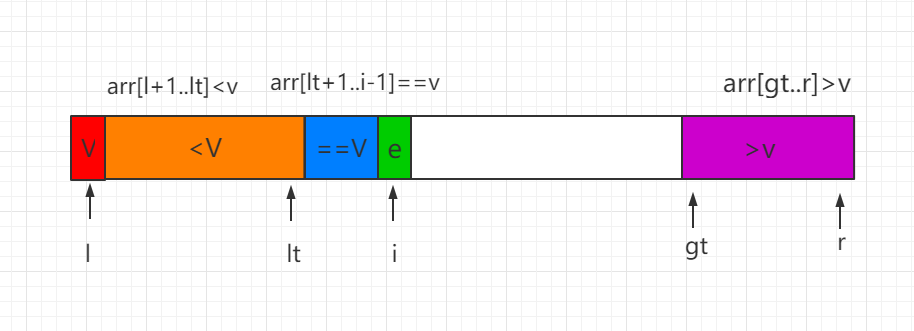
我们分三种情况进行讨论 partiton 过程,i 表示遍历的当前索引位置:
(1)当前处理的元素 e=V,元素 e 直接纳入蓝色区间,同时i向后移一位。
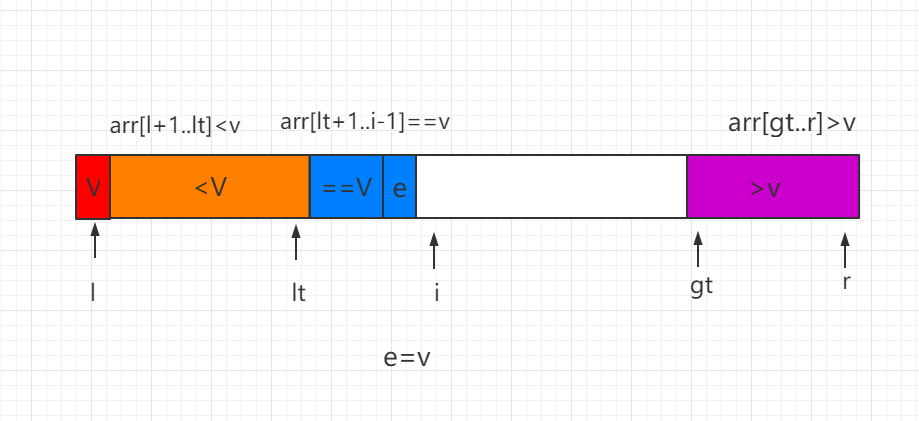
(2)当前处理元素 e<v,e 和等于 V 区间的第一个位置数值进行交换,同时索引 lt 和 i 都向后移动一位
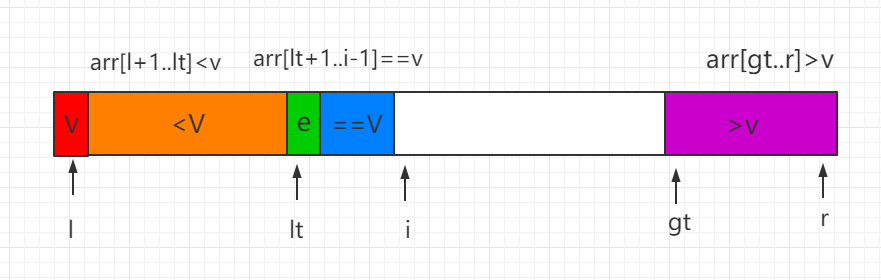
(3)当前处理元素 e>v,e 和 gt-1 索引位置的数值进行交换,同时 gt 索引向前移动一位。
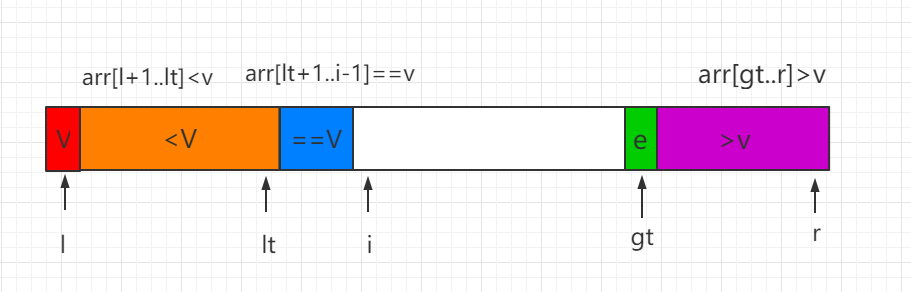
最后当 i=gt 时,结束遍历,同时需要把 v 和索引 lt 指向的数值进行交换,这样这个排序过程就完成了,然后对 <V 和 >V 的数组部分用同样的方法再进行递归排序。
四、Java 实例代码
源码包下载:Download
QuickSort3Ways.java 文件代码:
/**
* 三路快速排序
*/
public class QuickSort3Ways {
//核心代码—开始
// 递归使用快速排序,对arr[l…r]的范围进行排序
private static void sort(Comparable[] arr, int l, int r){
if (l >= r) {
return;
}
// 随机在arr[l…r]的范围中, 选择一个数值作为标定点pivot
swap( arr, l, (int)(Math.random()*(r–l+1)) + l );
Comparable v = arr[l];
int lt = l; // arr[l+1…lt] < v
int gt = r + 1; // arr[gt…r] > v
int i = l+1; // arr[lt+1…i) == v
while( i < gt ){
if( arr[i].compareTo(v) < 0 ){
swap( arr, i, lt+1);
i ++;
lt ++;
}
else if( arr[i].compareTo(v) > 0 ){
swap( arr, i, gt–1);
gt –;
}
else{ // arr[i] == v
i ++;
}
}
swap( arr, l, lt );
sort(arr, l, lt–1);
sort(arr, gt, r);
}
//核心代码—结束
public static void sort(Comparable[] arr){
int n = arr.length;
sort(arr, 0, n–1);
}
private static void swap(Object[] arr, int i, int j) {
Object t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
// 测试 QuickSort3Ways
public static void main(String[] args) {
// 三路快速排序算法也是一个O(nlogn)复杂度的算法
// 可以在1秒之内轻松处理100万数量级的数据
int N = 1000000;
Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
sort(arr);
SortTestHelper.printArray(arr);
}
}