第 26 章 链表、二叉树和哈希表
最后更新于:2022-04-01 22:01:56
# 第 26 章 链表、二叉树和哈希表
**目录**
+ [1\. 链表](ch26s01.html)
+ [1.1\. 单链表](ch26s01.html#id2844144)
+ [1.2\. 双向链表](ch26s01.html#id2845376)
+ [1.3\. 静态链表](ch26s01.html#id2845707)
+ [1.4\. 本节综合练习](ch26s01.html#id2845773)
+ [2\. 二叉树](ch26s02.html)
+ [2.1\. 二叉树的基本概念](ch26s02.html#id2845875)
+ [2.2\. 排序二叉树](ch26s02.html#id2846120)
+ [3\. 哈希表](ch26s03.html)
## 1. 链表
### 1.1. 单链表
[图 23.6 “链表”](ch23s09.html#pointer.linkedlist)所示的链表即单链表(Single Linked List),本节我们学习如何创建和操作这种链表。每个链表有一个头指针,通过头指针可以找到第一个节点,每个节点都可以通过指针域找到它的后继,最后一个节点的指针域为`NULL`,表示没有后继。数组在内存中是连续存放的,而链表在内存中的布局是不规则的,我们知道访问某个数组元素`b[n]`时可以通过`基地址+n×每个元素的字节数`得到它地址,或者说数组支持随机访问,而链表是不支持随机访问的,只能通过前一个元素的指针域得知后一个元素的地址,因此只能从头指针开始顺序访问各节点。以下代码实现了单链表的基本操作。
**例 26.1. 单链表**
```
/* linkedlist.h */
#ifndef LINKEDLIST_H
#define LINKEDLIST_H
typedef struct node *link;
struct node {
unsigned char item;
link next;
};
link make_node(unsigned char item);
void free_node(link p);
link search(unsigned char key);
void insert(link p);
void delete(link p);
void traverse(void (*visit)(link));
void destroy(void);
void push(link p);
link pop(void);
#endif
```
```
/* linkedlist.c */
#include
#include "linkedlist.h"
static link head = NULL;
link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->next = NULL;
return p;
}
void free_node(link p)
{
free(p);
}
link search(unsigned char key)
{
link p;
for (p = head; p; p = p->next)
if (p->item == key)
return p;
return NULL;
}
void insert(link p)
{
p->next = head;
head = p;
}
void delete(link p)
{
link pre;
if (p == head) {
head = p->next;
return;
}
for (pre = head; pre; pre = pre->next)
if (pre->next == p) {
pre->next = p->next;
return;
}
}
void traverse(void (*visit)(link))
{
link p;
for (p = head; p; p = p->next)
visit(p);
}
void destroy(void)
{
link q, p = head;
head = NULL;
while (p) {
q = p;
p = p->next;
free_node(q);
}
}
void push(link p)
{
insert(p);
}
link pop(void)
{
if (head == NULL)
return NULL;
else {
link p = head;
head = head->next;
return p;
}
}
```
```
/* main.c */
#include
#include "linkedlist.h"
void print_item(link p)
{
printf("%d\n", p->item);
}
int main(void)
{
link p = make_node(10);
insert(p);
p = make_node(5);
insert(p);
p = make_node(90);
insert(p);
p = search(5);
delete(p);
free_node(p);
traverse(print_item);
destroy();
p = make_node(100);
push(p);
p = make_node(200);
push(p);
p = make_node(250);
push(p);
while (p = pop()) {
print_item(p);
free_node(p);
}
return 0;
}
```
在初始化时把头指针`head`初始化为`NULL`,表示空链表。然后`main`函数调用`make_node`创建几个节点,分别调用`insert`插入到链表中。
```
void insert(link p)
{
p->next = head;
head = p;
}
```
**图 26.1. 链表的插入操作**
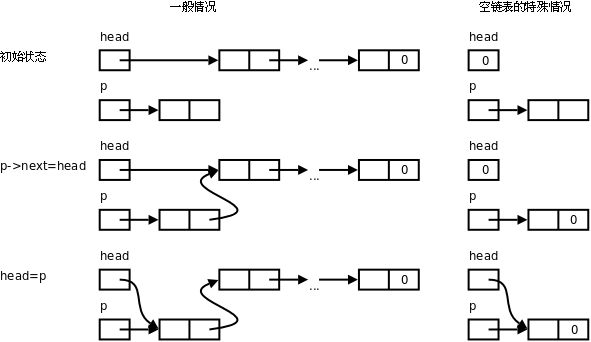
正如上图所示,`insert`函数虽然简单,其中也隐含了一种特殊情况(Special Case)的处理,当`head`为`NULL`时,执行`insert`操作插入第一个节点之后,`head`指向第一个节点,而第一个节点的`next`指针域成为`NULL`,这很合理,因为它也是最后一个节点。所以空链表虽然是一种特殊情况,却不需要特殊的代码来处理,和一般情况用同样的代码处理即可,这样写出来的代码更简洁,但是在读代码时要想到可能存在的特殊情况。当然,`insert`函数传进来的参数`p`也可能有特殊情况,传进来的`p`可能是`NULL`,甚至是野指针,本章的函数代码都假定调用者的传进来的参数是合法的,不对参数做特别检查。事实上,对指针参数做检查是不现实的,如果传进来的是`NULL`还可以检查一下,如果传进来的是野指针,根本无法检查它指向的内存单元是不是合法的,C标准库的函数通常也不做这种检查,例如`strcpy(p, NULL)`就会引起段错误。
接下来`main`函数调用`search`在链表中查找某个节点,如果找到就返回指向该节点的指针,找不到就返回`NULL`。
```
link search(unsigned char key)
{
link p;
for (p = head; p; p = p->next)
if (p->item == key)
return p;
return NULL;
}
```
`search`函数其实也隐含了对于空链表这种特殊情况的处理,如果是空链表则循环体一次都不执行,直接返回`NULL`。
然后`main`函数调用`delete`从链表中摘除用`search`找到的节点,最后调用`free_node`释放它的存储空间。
```
void delete(link p)
{
link pre;
if (p == head) {
head = p->next;
return;
}
for (pre = head; pre; pre = pre->next)
if (pre->next == p) {
pre->next = p->next;
return;
}
}
```
**图 26.2. 链表的删除操作**

从上图可以看出,要摘除一个节点需要首先找到它的前趋然后才能做摘除操作,而在单链表中通过某个节点只能找到它的后继而不能找到它的前趋,所以删除操作要麻烦一些,需要从第一个节点开始依次查找要摘除的节点的前趋。`delete`操作也要处理一种特殊情况,如果要摘除的节点是链表的第一个节点,它是没有前趋的,这种情况要用特殊的代码处理,而不能和一般情况用同样的代码处理。这样很不爽,能不能把这种特殊情况转化为一般情况呢?可以把`delete`函数改成这样:
```
void delete(link p)
{
link *pnext;
for (pnext = &head; *pnext; pnext = &(*pnext)->next)
if (*pnext == p) {
*pnext = p->next;
return;
}
}
```
**图 26.3. 消除特殊情况的链表删除操作**
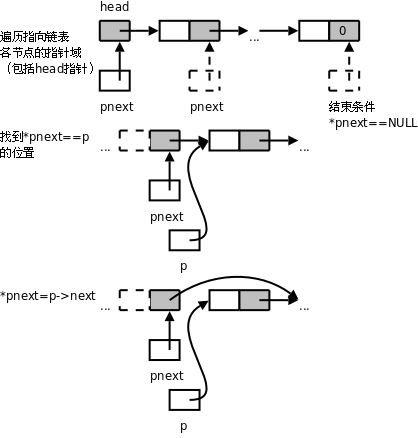
定义一个指向指针的指针`pnext`,在`for`循环中`pnext`遍历的是指向链表中各节点的指针域,这样就把`head`指针和各节点的`next`指针统一起来了,可以在一个循环中处理。
然后`main`函数调用`traverse`函数遍历整个链表,调用`destroy`函数销毁整个链表。请读者自己阅读这两个函数的代码。
如果限定每次只在链表的头部插入和删除元素,就形成一个LIFO的访问序列,所以在链表头部插入和删除元素的操作实现了堆栈的`push`和`pop`操作,`main`函数的最后几步把链表当成堆栈来操作,从打印的结果可以看到出栈的顺序和入栈是相反的。想一想,用链表实现的堆栈和[第 2 节 “堆栈”](ch12s02.html#stackqueue.stack)中用数组实现的堆栈相比有什么优点和缺点?
#### 习题
1、修改`insert`函数实现插入排序的功能,链表中的数据按从小到大排列,每次插入数据都要在链表中找到合适的位置再插入。在[第 6 节 “折半查找”](ch11s06.html#sortsearch.binary)中我们看到,如果数组中的元素是有序排列的,可以用折半查找算法更快地找到某个元素,想一想如果链表中的节点是有序排列的,是否适用折半查找算法?为什么?
2、基于单链表实现队列的`enqueue`和`dequeue`操作。在链表的末尾再维护一个指针`tail`,在`tail`处`enqueue`,在`head`处`dequeue`。想一想能不能反过来,在`head`处`enqueue`而在`tail`处`dequeue`?
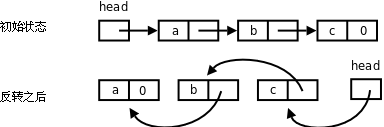
3、实现函数`void reverse(void);`将单链表反转。如下图所示。
**图 26.4. 单链表的反转**
### 1.2. 双向链表
链表的`delete`操作需要首先找到要摘除的节点的前趋,而在单链表中找某个节点的前趋需要从表头开始依次查找,对于n个节点的链表,删除操作的时间复杂度为O(n)。可以想像得到,如果每个节点再维护一个指向前趋的指针,删除操作就像插入操作一样容易了,时间复杂度为O(1),这称为双向链表(Doubly Linked List)。要实现双向链表只需在上一节代码的基础上改动两个地方。
在`linkedlist.h`中修改链表节点的结构体定义:
```
struct node {
unsigned char item;
link prev, next;
};
```
在`linkedlist.c`中修改`insert`和`delete`函数:
```
void insert(link p)
{
p->next = head;
if (head)
head->prev = p;
head = p;
p->prev = NULL;
}
void delete(link p)
{
if (p->prev)
p->prev->next = p->next;
else
head = p->next;
if (p->next)
p->next->prev = p->prev;
}
```
**图 26.5. 双向链表**

由于引入了`prev`指针,`insert`和`delete`函数中都有一些特殊情况需要用特殊的代码处理,不能和一般情况用同样的代码处理,这非常不爽,如果在表头和表尾各添加一个Sentinel节点(这两个节点只用于界定表头和表尾,不保存数据),就可以把这些特殊情况都转化为一般情况了。
**例 26.2. 带Sentinel的双向链表**
```
/* doublylinkedlist.h */
#ifndef DOUBLYLINKEDLIST_H
#define DOUBLYLINKEDLIST_H
typedef struct node *link;
struct node {
unsigned char item;
link prev, next;
};
link make_node(unsigned char item);
void free_node(link p);
link search(unsigned char key);
void insert(link p);
void delete(link p);
void traverse(void (*visit)(link));
void destroy(void);
void enqueue(link p);
link dequeue(void);
#endif
```
```
/* doublylinkedlist.c */
#include
#include "doublylinkedlist.h"
struct node tailsentinel;
struct node headsentinel = {0, NULL, &tailsentinel};
struct node tailsentinel = {0, &headsentinel, NULL};
static link head = &headsentinel;
static link tail = &tailsentinel;
link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->prev = p->next = NULL;
return p;
}
void free_node(link p)
{
free(p);
}
link search(unsigned char key)
{
link p;
for (p = head->next; p != tail; p = p->next)
if (p->item == key)
return p;
return NULL;
}
void insert(link p)
{
p->next = head->next;
head->next->prev = p;
head->next = p;
p->prev = head;
}
void delete(link p)
{
p->prev->next = p->next;
p->next->prev = p->prev;
}
void traverse(void (*visit)(link))
{
link p;
for (p = head->next; p != tail; p = p->next)
visit(p);
}
void destroy(void)
{
link q, p = head->next;
head->next = tail;
tail->prev = head;
while (p != tail) {
q = p;
p = p->next;
free_node(q);
}
}
void enqueue(link p)
{
insert(p);
}
link dequeue(void)
{
if (tail->prev == head)
return NULL;
else {
link p = tail->prev;
delete(p);
return p;
}
}
```
```
/* main.c */
#include
#include "doublylinkedlist.h"
void print_item(link p)
{
printf("%d\n", p->item);
}
int main(void)
{
link p = make_node(10);
insert(p);
p = make_node(5);
insert(p);
p = make_node(90);
insert(p);
p = search(5);
delete(p);
free_node(p);
traverse(print_item);
destroy();
p = make_node(100);
enqueue(p);
p = make_node(200);
enqueue(p);
p = make_node(250);
enqueue(p);
while (p = dequeue()) {
print_item(p);
free_node(p);
}
return 0;
}
```
**图 26.6. 带Sentinel的双向链表**

这个例子也实现了队列的`enqueue`和`dequeue`操作,现在每个节点有了`prev`指针,可以反过来在`head`处`enqueue`而在`tail`处`dequeue`了。
现在结合[第 5 节 “环形队列”](ch12s05.html#stackqueue.circular)想一想,其实用链表实现环形队列是最自然的,以前基于数组实现环形队列,我们还需要“假想”它是首尾相接的,而如果基于链表实现环形队列,我们本来就可以用指针串成首尾相接的。把上面的程序改成环形链表(Circular Linked List)也非常简单,只需要把`doublylinkedlist.c`中的
```
struct node tailsentinel;
struct node headsentinel = {0, NULL, &tailsentinel};
struct node tailsentinel = {0, &headsentinel, NULL};
static link head = &headsentinel;
static link tail = &tailsentinel;
```
改成:
```
struct node sentinel = {0, &sentinel, &sentinel};
static link head = &sentinel;
```
再把`doublylinkedlist.c`中所有的`tail`替换成`head`即可,相当于把`head`和`tail`合二为一了。
**图 26.7. 环形链表**
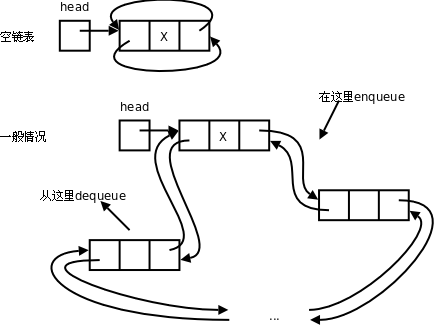
### 1.3. 静态链表
回想一下我们在[例 12.4 “用广度优先搜索解迷宫问题”](ch12s04.html#stackqueue.bfs)中使用的数据结构,我把图重新画在下面。
**图 26.8. 广度优先搜索的队列数据结构**

这是一个静态分配的数组,每个数组元素都有`row`、`col`和`predecessor`三个成员,`predecessor`成员保存一个数组下标,指向数组中的另一个元素,这其实也是链表的一种形式,称为静态链表,例如上图中的第6、4、2、1、0个元素串成一条链表。
### 1.4. 本节综合练习
1、Josephus是公元1世纪的著名历史学家,相传在一次战役中他和另外几个人被围困在山洞里,他们宁死不屈,决定站成一圈,每次数到三个人就杀一个,直到全部死光为止。Josephus和他的一个朋友不想死,于是串通好了站在适当的位置上,最后只剩下他们俩的时候这个游戏就停止了。如果一开始的人数为`N`,每次数到`M`个人就杀一个,那么要想不死应该站在什么位置呢?这个问题比较复杂,[[具体数学]](bi01.html#bibli.concrete "Concrete Mathematics")的1.3节研究了Josephus问题的解,有兴趣的读者可以参考。现在我们做个比较简单的练习,用链表模拟Josephus他们玩的这个游戏,`N`和`M`作为命令行参数传入,每个人的编号依次是1~N,打印每次被杀者的编号,打印最后一个幸存者的编号。
2、在[第 2.11 节 “本节综合练习”](ch25s02.html#stdlib.ioproblem)的习题1中规定了一种日志文件的格式,每行是一条记录,由行号、日期、时间三个字段组成,由于记录是按时间先后顺序写入的,可以看作所有记录是按日期排序的,对于日期相同的记录再按时间排序。现在要求从这样的一个日志文件中读出所有记录组成一个链表,在链表中首先按时间排序,对于时间相同的记录再按日期排序,最后写回文件中。比如原文件的内容是:
```
1 2009-7-30 15:16:42
2 2009-7-30 15:16:43
3 2009-7-31 15:16:41
4 2009-7-31 15:16:42
5 2009-7-31 15:16:43
6 2009-7-31 15:16:44
```
重新排序输出的文件内容是:
```
1 2009-7-31 15:16:41
2 2009-7-30 15:16:42
3 2009-7-31 15:16:42
4 2009-7-30 15:16:43
5 2009-7-31 15:16:43
6 2009-7-31 15:16:44
```
## 2. 二叉树
### 2.1. 二叉树的基本概念
链表的每个节点可以有一个后继,而二叉树(Binary Tree)的每个节点可以有两个后继。比如这样定义二叉树的节点:
```
typedef struct node *link;
struct node {
unsigned char item;
link l, r;
};
```
这样的节点可以组织成下图所示的各种形态。
**图 26.9. 二叉树的定义和举例**
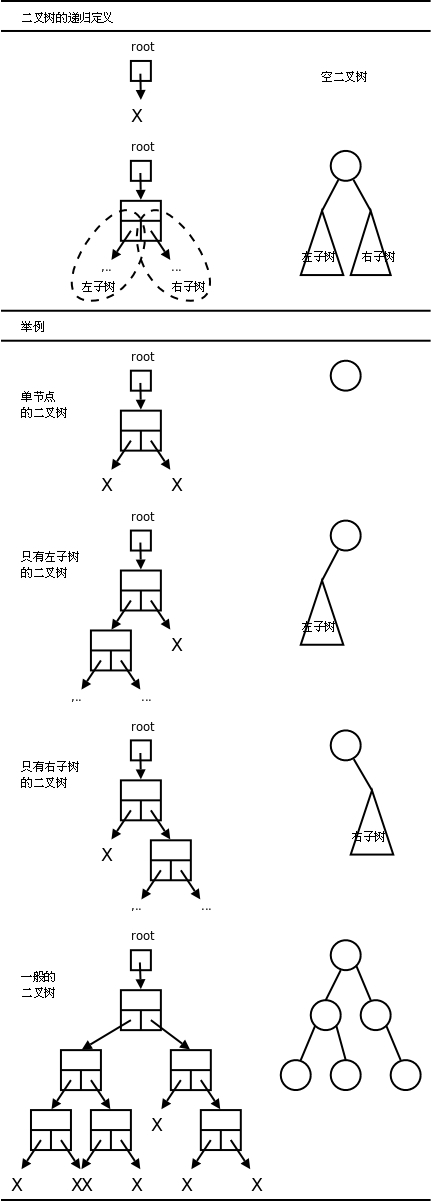
二叉树可以这样递归地定义:
1. 就像链表有头指针一样,每个二叉树都有一个根指针(上图中的`root`指针)指向它。根指针可以是`NULL`,表示空二叉树,或者
2. 根指针可以指向一个节点,这个节点除了有数据成员之外还有两个指针域,这两个指针域又分别是另外两个二叉树(左子树和右子树)的根指针。
上图举例示意了几种情况。
* 单节点的二叉树:左子树和右子树都是空二叉树。
* 只有左子树的二叉树:右子树是空二叉树。
* 只有右子树的二叉树:左子树是空二叉树。
* 一般的二叉树:左右子树都不为空。注意右侧由圈和线段组成的简化图示,以后我们都采用这种简化图示法,在圈中标上该节点数据成员的值。
链表的遍历方法是显而易见的:从前到后遍历即可。二叉树是一种树状结构,如何做到把所有节点都走一遍不重不漏呢?有以下几种方法:
**图 26.10. 二叉树的遍历**
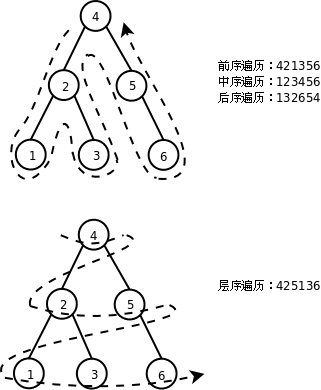
前序(Pre-order Traversal)、中序(In-order Traversal)、后序遍历(Post-order Traversal)和深度优先搜索的顺序类似,层序遍历(Level-order Traversal)和广度优先搜索的顺序类似。
前序和中序遍历的结果合在一起可以唯一确定二叉树的形态,也就是说根据遍历结果可以构造出二叉树。过程如下图所示:
**图 26.11. 根据前序和中序遍历结果构造二叉树**
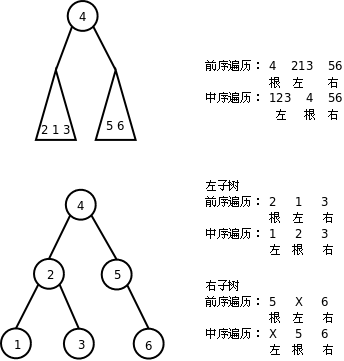
想一想,根据中序和后序遍历结果能否构造二叉树?根据前序和后序遍历结果能否构造二叉树?
**例 26.3. 二叉树**
```
/* binarytree.h */
#ifndef BINARYTREE_H
#define BINARYTREE_H
typedef struct node *link;
struct node {
unsigned char item;
link l, r;
};
link init(unsigned char VLR[], unsigned char LVR[], int n);
void pre_order(link t, void (*visit)(link));
void in_order(link t, void (*visit)(link));
void post_order(link t, void (*visit)(link));
int count(link t);
int depth(link t);
void destroy(link t);
#endif
```
```
/* binarytree.c */
#include
#include "binarytree.h"
static link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->l = p->r = NULL;
return p;
}
static void free_node(link p)
{
free(p);
}
link init(unsigned char VLR[], unsigned char LVR[], int n)
{
link t;
int k;
if (n <= 0)
return NULL;
for (k = 0; VLR[0] != LVR[k]; k++);
t = make_node(VLR[0]);
t->l = init(VLR+1, LVR, k);
t->r = init(VLR+1+k, LVR+1+k, n-k-1);
return t;
}
void pre_order(link t, void (*visit)(link))
{
if (!t)
return;
visit(t);
pre_order(t->l, visit);
pre_order(t->r, visit);
}
void in_order(link t, void (*visit)(link))
{
if (!t)
return;
in_order(t->l, visit);
visit(t);
in_order(t->r, visit);
}
void post_order(link t, void (*visit)(link))
{
if (!t)
return;
post_order(t->l, visit);
post_order(t->r, visit);
visit(t);
}
int count(link t)
{
if (!t)
return 0;
return 1 + count(t->l) + count(t->r);
}
int depth(link t)
{
int dl, dr;
if (!t)
return 0;
dl = depth(t->l);
dr = depth(t->r);
return 1 + (dl > dr ? dl : dr);
}
void destroy(link t)
{
post_order(t, free_node);
}
```
```
/* main.c */
#include
#include "binarytree.h"
void print_item(link p)
{
printf("%d", p->item);
}
int main()
{
unsigned char pre_seq[] = { 4, 2, 1, 3, 6, 5, 7 };
unsigned char in_seq[] = { 1, 2, 3, 4, 5, 6, 7 };
link root = init(pre_seq, in_seq, 7);
pre_order(root, print_item);
putchar('\n');
in_order(root, print_item);
putchar('\n');
post_order(root, print_item);
putchar('\n');
printf("count=%d depth=%d\n", count(root), depth(root));
destroy(root);
return 0;
}
```
#### 习题
1、本节描述了二叉树的递归定义,想一想单链表的递归定义应该怎么表述?请仿照本节的例子用递归实现单链表的各种操作函数:
```
link init(unsigned char elements[], int n);
void pre_order(link t, void (*visit)(link));
void post_order(link t, void (*visit)(link));
int count(link t);
void destroy(link t);
```
### 2.2. 排序二叉树
排序二叉树(BST,Binary Search Tree)具有这样的性质:对于二叉树中的任意节点,如果它有左子树或右子树,则该节点的数据成员大于左子树所有节点的数据成员,且小于右子树所有节点的数据成员。排序二叉树的中序遍历结果是从小到大排列的,其实上一节的[图 26.10 “二叉树的遍历”](ch26s02.html#linkedlist.binarytraverse)就是排序二叉树。
**例 26.4. 排序二叉树**
```
/* bst.h */
#ifndef BST_H
#define BST_H
typedef struct node *link;
struct node {
unsigned char item;
link l, r;
};
link search(link t, unsigned char key);
link insert(link t, unsigned char key);
link delete(link t, unsigned char key);
void print_tree(link t);
#endif
```
```
/* bst.c */
#include
#include
#include "bst.h"
static link make_node(unsigned char item)
{
link p = malloc(sizeof *p);
p->item = item;
p->l = p->r = NULL;
return p;
}
static void free_node(link p)
{
free(p);
}
link search(link t, unsigned char key)
{
if (!t)
return NULL;
if (t->item > key)
return search(t->l, key);
if (t->item < key)
return search(t->r, key);
/* if (t->item == key) */
return t;
}
link insert(link t, unsigned char key)
{
if (!t)
return make_node(key);
if (t->item > key) /* insert to left subtree */
t->l = insert(t->l, key);
else /* if (t->item <= key), insert to right subtree */
t->r = insert(t->r, key);
return t;
}
link delete(link t, unsigned char key)
{
link p;
if (!t)
return NULL;
if (t->item > key) /* delete from left subtree */
t->l = delete(t->l, key);
else if (t->item < key) /* delete from right subtree */
t->r = delete(t->r, key);
else { /* if (t->item == key) */
if (t->l == NULL && t->r == NULL) { /* if t is leaf node */
free_node(t);
t = NULL;
} else if (t->l) { /* if t has left subtree */
/* replace t with the rightmost node in left subtree */
for (p = t->l; p->r; p = p->r);
t->item = p->item;
t->l = delete(t->l, t->item);
} else { /* if t has right subtree */
/* replace t with the leftmost node in right subtree */
for (p = t->r; p->l; p = p->l);
t->item = p->item;
t->r = delete(t->r, t->item);
}
}
return t;
}
void print_tree(link t)
{
if (t) {
printf("(");
printf("%d", t->item);
print_tree(t->l);
print_tree(t->r);
printf(")");
} else
printf("()");
}
```
```
/* main.c */
#include
#include
#include
#include "bst.h"
#define RANGE 100
#define N 6
void print_item(link p)
{
printf("%d", p->item);
}
int main()
{
int i, key;
link root = NULL;
srand(time(NULL));
for (i = 0; i < N; i++)
root = insert(root, rand() % RANGE);
printf("\t\\tree");
print_tree(root);
printf("\n\n");
while (root) {
key = rand() % RANGE;
if (search(root, key)) {
printf("delete %d in tree\n", key);
root = delete(root, key);
printf("\t\\tree");
print_tree(root);
printf("\n\n");
}
}
}
```
```
$ ./a.out
\tree(83(77(15()(35()()))())(86()(93()())))
delete 86 in tree
\tree(83(77(15()(35()()))())(93()()))
delete 35 in tree
\tree(83(77(15()())())(93()()))
delete 93 in tree
\tree(83(77(15()())())())
delete 15 in tree
\tree(83(77()())())
delete 83 in tree
\tree(77()())
delete 77 in tree
\tree()
```
程序的运行结果可以用Greg Lee编写的The Tree Preprocessor([http://www.essex.ac.uk/linguistics/clmt/latex4ling/trees/tree/](http://www.essex.ac.uk/linguistics/clmt/latex4ling/trees/tree/))转换成树形:
```
$ ./a.out | ./tree/tree
83
___|___
| |
77 86
_|__ _|__
| | | |
15 93
_|__ _|__
| | | |
35
_|__
| |
delete 86 in tree
83
___|___
| |
77 93
_|__ _|__
| | | |
15
_|__
| |
35
_|__
| |
delete 35 in tree
83
___|___
| |
77 93
_|__ _|__
| | | |
15
_|__
| |
delete 93 in tree
83
_|__
| |
77
_|__
| |
15
_|__
| |
delete 15 in tree
83
_|__
| |
77
_|__
| |
delete 83 in tree
77
_|__
| |
delete 77 in tree
```
## 3. 哈希表
下图示意了哈希表(Hash Table)这种数据结构。
**图 26.12. 哈希表**

如上图所示,首先分配一个指针数组,数组的每个元素是一个链表的头指针,每个链表称为一个槽(Slot)。哪个数据应该放入哪个槽中由哈希函数决定,在这个例子中我们简单地选取哈希函数h(x) = x % 11,这样任意数据x都可以映射成0~10之间的一个数,就是槽的编号,将数据放入某个槽的操作就是链表的插入操作。
如果每个槽里至多只有一个数据,可以想像这种情况下`search`、`insert`和`delete`操作的时间复杂度都是O(1),但有时会有多个数据被哈希函数映射到同一个槽中,这称为碰撞(Collision),设计一个好的哈希函数可以把数据比较均匀地分布到各个槽中,尽量避免碰撞。如果能把n个数据比较均匀地分布到m个槽中,每个糟里约有n/m个数据,则`search`、`insert`和`delete`和操作的时间复杂度都是O(n/m),如果n和m的比是常数,则时间复杂度仍然是O(1)。一般来说,要处理的数据越多,构造哈希表时分配的槽也应该越多,所以n和m成正比这个假设是成立的。
请读者自己编写程序构造这样一个哈希表,并实现`search`、`insert`和`delete`操作。
如果用我们学过的各种数据结构来表示n个数据的集合,下表是`search`、`insert`和`delete`操作在平均情况下的时间复杂度比较。
**表 26.1. 各种数据结构的search、insert和delete操作在平均情况下的时间复杂度比较**
| 数据结构 | search | insert | delete |
| --- | --- | --- | --- |
| 数组 | O(n),有序数组折半查找是O(lgn) | O(n) | O(n) |
| 双向链表 | O(n) | O(1) | O(1) |
| 排序二叉树 | O(lgn) | O(lgn) | O(lgn) |
| 哈希表(n与槽数m成正比) | O(1) | O(1) | O(1) |
### 习题
1、统计一个文本文件中每个单词的出现次数,然后按出现次数排序并打印输出。单词由连续的英文字母组成,不区分大小写。
2、实现一个函数求两个数组的交集:`size_t intersect(const int a[], size_t nmema, const int b[], size_t nmemb, int c[], size_t nmemc);`。数组元素是32位`int`型的。数组`a`有`nmema`个元素且各不相同,数组`b`有`nmemb`个元素且各不相同。要求找出数组`a`和数组`b`的交集保存到数组`c`中,`nmemc`是数组`c`的最大长度,返回值表示交集中实际有多少个元素,如果交集中实际的元素数量超过了`nmemc`则返回`nmemc`个元素。数组`a`和数组`b`的元素数量可能会很大(比如上百万个),需要设计尽可能快的算法。
';