3.6 scikit-learn:Python中的机器学习
最后更新于:2022-04-01 11:22:08
# 3.6 scikit-learn:Python中的机器学习
In [5]:
```
%matplotlib inline
import numpy as np
```
> 作者: Fabian Pedregosa, Gael Varoquaux
**先决条件**
Numpy, Scipy
IPython
matplotlib
scikit-learn ([http://scikit-learn.org](http://scikit-learn.org)) 
**章节内容**
```
加载样例数据集
- 学习与预测
分类
- KNN分类器
- 分类的支持向量机(SVMs)
聚类:将观察值聚集在一起
- K-means聚类
使用主成分分析的降维
把所有都放在一起:面孔识别
线性模型:从回归到简约
- 简约模型
模型选择:选择预测器和参数
- 网格搜索和交叉验证预测器
```
**警告**:从版本0.9(在2011年9月发布)起,scikit-learn导入路径从scikits.learn 改为 sklearn
## 3.5.1 加载样例数据集

首先,我们将加载一些数据来玩玩。我们将使用的数据是知名的非常简单的花数据鸢尾花数据集。
我们有150个鸢尾花观察值指定了一些测量:花萼宽带、花萼长度、花瓣宽度和花瓣长度,以及对应的子类:Iris setosa、Iris versicolor和Iris virginica。
将数据集加载为Python对象:
In [1]:
```
from sklearn import datasets
iris = datasets.load_iris()
```
这个数据存储在`.data`成员中,是一个 (n_samples, n_features) 数组。
In [2]:
```
iris.data.shape
```
Out[2]:
```
(150, 4)
```
每个观察的类别存储在数据集的`.target`属性中。这是长度是n_samples的1D整型数组 :
In [3]:
```
iris.target.shape
```
Out[3]:
```
(150,)
```
In [4]:
```
import numpy as np
np.unique(iris.target)
```
Out[4]:
```
array([0, 1, 2])
```
数据重排的例子:digits 数据集 
digits 数据集包含1797 图像,每一个是8X8像素的图片,代表一个手写的数字
In [15]:
```
digits = datasets.load_digits()
digits.images.shape
```
Out[15]:
```
(1797, 8, 8)
```
In [8]:
```
import pylab as pl
pl.imshow(digits.images[0], cmap=pl.cm.gray_r)
```
Out[8]:
```
<matplotlib.image.AxesImage at 0x109abd990>
```

要在scikit使用这个数据集,我们将每个8X8图片转化为一个长度为64的向量
In [9]:
```
data = digits.images.reshape((digits.images.shape[0], -1))
```
### 3.5.1.1 学习和预测
现在我们有了一些数据,我们想要从上面学习并且在新的数据做预测。在scikit-learn中,我们通过创建一个预测器,并调用他的 fit(X, Y) 方法从现有数据上学习。
In [11]:
```
from sklearn import svm
clf = svm.LinearSVC()
clf.fit(iris.data, iris.target) # 从数据学习
```
Out[11]:
```
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)
```
一旦我们从数据中学习,我们可以用我们的模型来预测未见过的数据的最可能输出:
In [12]:
```
clf.predict([[ 5.0, 3.6, 1.3, 0.25]])
```
Out[12]:
```
array([0])
```
**注意**:我们可以通过由下滑线结尾的属性来访问模型的参数:
In [13]:
```
clf.coef_
```
Out[13]:
```
array([[ 0.18424728, 0.45122657, -0.80794162, -0.45070597],
[ 0.05691797, -0.89245895, 0.39682582, -0.92882381],
[-0.85072494, -0.98678239, 1.38091241, 1.86550868]])
```
## 3.5.2 分类
### 3.5.2.1 KNN分类器

可能最简单的分类器是最接近的邻居: 给定一个观察,使用在N维空间中训练样例中最接近它标签,这里N是每个样例的特征数。
K个最临近的邻居分类器内部使用基于ball tree的算法,用来代表训练的样例。
**KNN (K个最临近邻居) 分类的例子:**
In [14]:
```
# 创建并拟合一个最临近邻居分类器
from sklearn import neighbors
knn = neighbors.KNeighborsClassifier()
knn.fit(iris.data, iris.target)
```
Out[14]:
```
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_neighbors=5, p=2, weights='uniform')
```
In [15]:
```
knn.predict([[0.1, 0.2, 0.3, 0.4]])
```
Out[15]:
```
array([0])
```
**训练集和测试集**
当用学习算法进行实验时,重要的一点是不要用拟合预测器的数据来测试预测器的预测力。实际上,我们通常会在测试集上得到准确的预测。
In [16]:
```
perm = np.random.permutation(iris.target.size)
iris.data = iris.data[perm]
iris.target = iris.target[perm]
knn.fit(iris.data[:100], iris.target[:100])
```
Out[16]:
```
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_neighbors=5, p=2, weights='uniform')
```
In [17]:
```
knn.score(iris.data[100:], iris.target[100:])
```
Out[17]:
```
0.95999999999999996
```
额外的问题: 为什么我们使用随机排列?
### 3.5.2.2 分类的支持向量机 (SVMs))
#### 3.5.2.2.1 线性支持向量机

SVMs试图构建一个最大化两个类的间距的超平面。它选取输入的一个子集,称为支持向量,这个子集中的观察距离分隔超平面最近。
In [18]:
```
from sklearn import svm
svc = svm.SVC(kernel='linear')
svc.fit(iris.data, iris.target)
```
Out[18]:
```
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)
```
在scikit-learn实现了几种支持向量机。最常用的是`svm.SVC`、`svm.NuSVC` 和 `svm.LinearSVC`; “SVC” 代表支持向量分类器 (也存在用于回归的SVMs, 在scikit-learn被称为“SVR”)。
**练习**
在digits数据集上训练`svm.SVC`。留下最后的10%,在这些观察上测试预测的效果。
#### 3.5.2.2.2 使用核 (kernel))
类通常并不是都能用超平面分隔,因此,有一个不仅仅是线性也可能是多项式或者幂的决策函数是明智的 :
**线性核 (kernel)** 
In [19]:
```
svc = svm.SVC(kernel='linear')
```
**多项式核 (kernel)** 
In [20]:
```
svc = svm.SVC(kernel='poly', degree=3)
# degree: 多项式的阶
```
**RBF核 (kernel) (径向基核函数)** 
In [21]:
```
svc = svm.SVC(kernel='rbf')
# gamma: 径向基核大小的倒数
```
**练习** 以上列出的核哪一个在digits数据集上有较好的预测表现?
## 3.5.3 聚类 : 将观察值分组
以鸢尾花 (iris) 数据集为例,如果有三类鸢尾花,但是并不能访问他们标签,我们可以尝试**非观察学习** : 通过一些标准将观察**聚类**分入一些组。
### 3.5.3.1 K-means 聚类
最简单的聚类算法是k-means。这个算法将集合分成k个组,将每个观察值分配给一个组,以便使观察值 (在n维空间) 到组平均值的距离最小;然后重新计算平均数。循环进行这个操作直到组收敛,比如达到最大的`max_iter`循环次数。
(k-means的另一个实现在SciPy的`cluster`包中。`scikit-learn`实现的不同在于提供了一个对象API和一些额外的功能,包括智能初始化。)
In [2]:
```
from sklearn import cluster, datasets
iris = datasets.load_iris()
k_means = cluster.KMeans(n_clusters=3)
k_means.fit(iris.data)
```
Out[2]:
```
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=3, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001,
verbose=0)
```
In [25]:
```
print k_means.labels_[::10]
```
```
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]
```
In [26]:
```
print iris.target[::10]
```
```
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]
```
**真实情况**
 **K-means (3 组)**
 **K-means (8 组)**

**在图像压缩中的应用**
聚类可以看做从信息中选取一组观察的方式。例如,这个技术可以被用来posterize一个图像 (将连续渐变色调转换为更少色调的一些区域):
In [5]:
```
from scipy import misc
lena = misc.lena().astype(np.float32)
X = lena.reshape((-1, 1)) # We need an (n_sample, n_feature) array
k_means = cluster.KMeans(n_clusters=5)
k_means.fit(X)
```
Out[5]:
```
KMeans(copy_x=True, init='k-means++', max_iter=300, n_clusters=5, n_init=10,
n_jobs=1, precompute_distances='auto', random_state=None, tol=0.0001,
verbose=0)
```
In [6]:
```
values = k_means.cluster_centers_.squeeze()
labels = k_means.labels_
lena_compressed = np.choose(labels, values)
lena_compressed.shape = lena.shape
```
源图片

K-means quantization

## 3.5.4 使用主成分分析的降维


上面观察展开的云点在一个方向非常平坦,因此,一个特征几乎可以准确用另两个特征来计算。PCA找到数据并不平坦的方向,并且可以通过投影到一个子空间中来减少维度。
**警告**: 根据你的scikit-learn版本,PCA将在模块`decomposition`或`pca`中。
In [3]:
```
from sklearn import decomposition
pca = decomposition.PCA(n_components=2)
pca.fit(iris.data)
```
Out[3]:
```
PCA(copy=True, n_components=2, whiten=False)
```
In [4]:
```
X = pca.transform(iris.data)
```
现在我们可视化(转换的)鸢尾花数据集:
In [6]:
```
import pylab as pl
pl.scatter(X[:, 0], X[:, 1], c=iris.target)
```
Out[6]:
```
<matplotlib.collections.PathCollection at 0x107502b90>
```
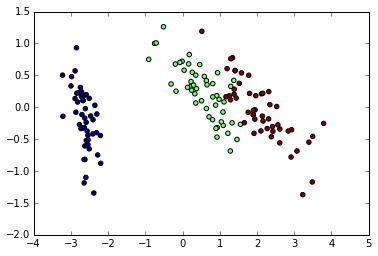
PCA并不仅仅在高纬度数据集的可视化上有用。它也可以用于帮助加速对高维不太高效的有监督方法的预处理步骤。
## 3.5.5 把所有的东西放在一起: 面孔识别
展示使用主成分分析来降维和用执行向量机分类的面孔识别的例子。

In [ ]:
```
"""
Stripped-down version of the face recognition example by Olivier Grisel
http://scikit-learn.org/dev/auto_examples/applications/face_recognition.html
## original shape of images: 50, 37
"""
import numpy as np
import pylab as pl
from sklearn import cross_val, datasets, decomposition, svm
# ..
# .. load data ..
lfw_people = datasets.fetch_lfw_people(min_faces_per_person=70, resize=0.4)
perm = np.random.permutation(lfw_people.target.size)
lfw_people.data = lfw_people.data[perm]
lfw_people.target = lfw_people.target[perm]
faces = np.reshape(lfw_people.data, (lfw_people.target.shape[0], -1))
train, test = iter(cross_val.StratifiedKFold(lfw_people.target, k=4)).next()
X_train, X_test = faces[train], faces[test]
y_train, y_test = lfw_people.target[train], lfw_people.target[test]
# ..
# .. dimension reduction ..
pca = decomposition.RandomizedPCA(n_components=150, whiten=True)
pca.fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
# ..
# .. classification ..
clf = svm.SVC(C=5., gamma=0.001)
clf.fit(X_train_pca, y_train)
# ..
# .. predict on new images ..
for i in range(10):
print lfw_people.target_names[clf.predict(X_test_pca[i])[0]]
_ = pl.imshow(X_test[i].reshape(50, 37), cmap=pl.cm.gray)
_ = raw_input()
```
完整代码: [faces.py](http://scipy-lectures.github.io/_downloads/faces.py)
## 3.5.6 线性模型: 从回归到简约
**糖尿病数据集** 糖尿病数据集包含442个病人测量的10个生理学变量 (年龄、性别、体重、血压),以及一个一年后病情发展的标记:
In [8]:
```
diabetes = datasets.load_diabetes()
diabetes_X_train = diabetes.data[:-20]
diabetes_X_test = diabetes.data[-20:]
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
```
目前的任务是从生理学变量中预测疾病发生。
### 3.5.6.1 简约模型
要改善问题的条件 (信息量小的变量、减少高纬度的诅咒、作为一个特征预处理等等), 仅选择信息量大的特征,并且将没有信息量的特征设置为0将非常有趣。这种惩罚手段,称为**Lasso**, 可以将一些系数设置为0。这个方法称为**简约方法**,简约性可以看做是Occam剃刀的一个应用: 相比于复杂的模型更偏好简单的模型。
In [9]:
```
from sklearn import linear_model
regr = linear_model.Lasso(alpha=.3)
regr.fit(diabetes_X_train, diabetes_y_train)
```
Out[9]:
```
Lasso(alpha=0.3, copy_X=True, fit_intercept=True, max_iter=1000,
normalize=False, positive=False, precompute=False, random_state=None,
selection='cyclic', tol=0.0001, warm_start=False)
```
In [10]:
```
regr.coef_ # 非常简约的系数
```
Out[10]:
```
array([ 0\. , -0\. , 497.34075682, 199.17441034,
-0\. , -0\. , -118.89291545, 0\. ,
430.9379595 , 0\. ])
```
In [11]:
```
regr.score(diabetes_X_test, diabetes_y_test)
```
Out[11]:
```
0.55108354530029779
```
分数与线性回归 (最小二乘) 很相似:
In [12]:
```
lin = linear_model.LinearRegression()
lin.fit(diabetes_X_train, diabetes_y_train)
```
Out[12]:
```
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
```
In [13]:
```
lin.score(diabetes_X_test, diabetes_y_test)
```
Out[13]:
```
0.58507530226905713
```
**相同问题的不同算法** 不同的算法可以用于解决相同的数学问题。例如,_sklearn_中的Lasso对象用_坐标下降法_来解lasso回归,这种方法在大数据集上有效。但是,_sklearn_也提供了_LassoLARS_对象,使用_LARS_,一种在权重向量估计非常稀疏的问题上非常高效的方法,即有很少观察值的问题。
## 3.5.7 模型选择: 选择预测器及其参数
### 3.5.7.1 网格搜索和交叉验证预测器
#### 3.5.7.1.1 网格搜索
scikit-learn提供了一个对象,给定数据,计算预测器在一个参数网格的分数,并且选择可以最大化交叉验证分数的参数。这个对象用一个构建中的预测器并且暴露了一个预测器的探索集API:
In [16]:
```
from sklearn import svm, grid_search
gammas = np.logspace(-6, -1, 10)
svc = svm.SVC()
clf = grid_search.GridSearchCV(estimator=svc, param_grid=dict(gamma=gammas), n_jobs=-1)
clf.fit(digits.data[:1000], digits.target[:1000])
```
Out[16]:
```
GridSearchCV(cv=None, error_score='raise',
estimator=SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,
kernel='rbf', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False),
fit_params={}, iid=True, loss_func=None, n_jobs=-1,
param_grid={'gamma': array([ 1.00000e-06, 3.59381e-06, 1.29155e-05, 4.64159e-05,
1.66810e-04, 5.99484e-04, 2.15443e-03, 7.74264e-03,
2.78256e-02, 1.00000e-01])},
pre_dispatch='2*n_jobs', refit=True, score_func=None, scoring=None,
verbose=0)
```
In [20]:
```
clf.best_score_
```
Out[20]:
```
0.93200000000000005
```
In [22]:
```
clf.best_estimator_.gamma
```
Out[22]:
```
0.00059948425031894088
```
默认,_GridSearchCV_使用三折交叉验证。但是,如果识别传递了一个分类器都不是一个回归器,它将使用一个分层三折。
#### 3.5.7.1.2 交叉验证预测器
一个算法一个算法为基础的设置参数来进行交叉验证更有效。这也就是为什么,对于一些预测器,scikit-learn暴露一个“CV”预测器, 这个预测器通过交叉验证自动设置他们的参数:
In [23]:
```
from sklearn import linear_model, datasets
lasso = linear_model.LassoCV()
diabetes = datasets.load_diabetes()
X_diabetes = diabetes.data
y_diabetes = diabetes.target
lasso.fit(X_diabetes, y_diabetes)
```
Out[23]:
```
LassoCV(alphas=None, copy_X=True, cv=None, eps=0.001, fit_intercept=True,
max_iter=1000, n_alphas=100, n_jobs=1, normalize=False, positive=False,
precompute='auto', random_state=None, selection='cyclic', tol=0.0001,
verbose=False)
```
In [26]:
```
# 预测器自动选择他的lambda:
lasso.alpha_
```
Out[26]:
```
0.012291895087486173
```
这些预测器与他们的对等物调用方式类似,只是在名字后面增加了‘CV’。
**练习** 在糖尿病数据集中,找到最优化的正则化参数alpha。