附录： 包(packages) 包(packages)，是 Common Lisp 把代码组织成模块的方式。早期的 Lisp 方言有一张符号表，即`oblist`【注1】。在这张表里列出了系统中所有已经读取到的符号。借助 oblist 里的符号表项，系统得以存取数据，诸如对象的值，以及属性列表等。保存在 oblist 里的符号被称为 interned。 新一些的 Lisp 方言把 `oblist` 的概念放到了一个个包里面。现在，符号不仅仅是被 `intern` 了，而是被 `intern` 在某个包里。包之所以支持模块化是因为在一个包里的 `intern` 的符号只有在其被显式声明为能被其它包访问的时候，它才能为外部访问(除非用一些歪门邪道的招数)。 包是一种 Lisp 对象。当前包常常被保存在一个名为 `\*package\*` 的全局变量里面。当 Common Lisp 启动时，当前包就是用户包：或者叫 user (**CLTL1** 实现)，或者叫 `common-lisp-user` (**CLTL2**实现)。 包一般用自己的名字相互区别，而这些名字采用的是字符串的形式。要知道当前包的包名，可以试试： ~~~ > (package-name *package*) "COMMON-LISP-USER" ~~~ 通常，当读入一个符号时，它就被 `intern` 到当前的包里了。要弄清给定符号所 `intern` 的是哪个包，我们可以 用 `symbol-package` ： ~~~ > (symbol-package 'foo) #<Package "COMMON-LISP-USER" 4CD15E> ~~~ 这个返回值是实际的包对象。为便于将来使用，我们给 `foo` 赋一个值： ~~~ > (setq foo 99) 99 ~~~ 使用 `in-package` ，我们就可以切换到另一个新的包，若有需要的话这个包会被创建出来【注2】： ~~~ > (in-package 'mine :use 'common-lisp) #<Package "MINE" 63390E> ~~~ 此时此刻应该会响起诡异的背景音乐，因为我们已经身处另一个世界：在这里 `foo` 已经不似从前了： ~~~ MINE> foo >>Error: FOO has no global value. ~~~ 为什么会这样？因为之前被我们设置成 `99` 的那个 `foo` 和现在 `mine` 里面的这个 foo 是两码事。【注3】要从用户包之外引用原来的这个 `foo` ，我们必须把包名和两个冒号作为它的前缀： ~~~ MINE> common-lisp-user::foo 99 ~~~ 因此，具有相同打印名称的不同符号得以在不同包中共存。这样就可以在名为 `common-lisp-user` 的包里有一个 `foo` ，同时在 `mine` 包里也有一个 `foo` ，并且它们两个是不一样的符号。实际上，这就是 `package` 的一部分用意所在，即：你在为你的函数和变量取名字的同时，就不用担心别人会把一样的名字用在其它东西上。现在，就算有重名的情况，重名的符号之间也是互不相干的。 与此同时，包也提供了一种信息隐藏的手段。对程序来说，它必须使用名字来引用不同的函数和变量。如果你不让一个名字在你的包之外可见的话，那么另一个包中的代码就无法使用或者修改这个名字所引用的对象。 在写程序的时候，把包的名字带上两个冒号做为前缀并不是个好习惯。你要是这样做的话，就违背了模块化设计的初衷，而这正是包机制的本意。如果你不得不使用双冒号来引用一个符号，这应该就是有人根本就不希望你引用它。 一般来说，你只应该引用那些被 export 了的符号。把符号从它所属的包 export 出来，我们就能让这个符号对其它包变得可见。要导出一个符号，我们可以调用(你肯定已经猜到了) export ： ~~~ MINE> (in-package 'common-lisp-user) #<Package "COMMON-LISP-USER" 4CD15E> > (export 'bar) T > (setq bar 5) 5 ~~~ 现在，如果回到了 `mine` 包，那么就可以用一个冒号引用 `bar` ，因为这个名字是外部可见的： ~~~ > (in-package 'mine) #<Package "MINE" 63390E> MINE> common-lisp-user:bar 5 ~~~ 如果把 `bar` `import` 到 `mine` 里面，我们就能更进一步，让 `mine` 能和 `user` 包共享 `bar` 这个符号： ~~~ MINE> (import 'common-lisp-user:bar) T MINE> bar 5 ~~~ 在导入 `bar` 之后，我们可以根本不用加任何包的限定符，就能引用它了。现在，这两个包共享了同一个符号 -- 再没有一个独立的 `mine:bar` 了。 万一已经有了一个会怎么样呢？在这种情况下，`import` 调用会导致一个错误，就像下面我们试着`import` `foo` 时造成的错误一样： ~~~ MINE> (import 'common-lisp-user::foo) >>Error: FOO is already present in MINE. ~~~ 之前，我们在 `mine` 里对 `foo` 进行了一次不成功的求值，这次求值顺带着使得一个名为 foo 的符号被加入了 `mine` 。由于这个符号在全局范围内还没有值，因此产生了一个错误，但是输入符号名字的直接后果就是使它被 intern 进了这个包。所以，当我们现在想把 `foo` 引进 `mine` 的时候，`mine`里面已经有一个相同名字的符号了。 通过让一个包使用 (use) 另一个包，我们也能批量的引入符号： ~~~ MINE> (use-package 'common-lisp-user) T ~~~ 这样，所有 `user` `package` 引出的符号就会自动地被引进到 `mine` 里面去了。(要是 `user``package` 已经引出了 `foo` 的话，这个函数调用也会出一个错。) 根据 CLTL2，包含内建操作符和变量名字的包被称为 `common-lisp` 而不是 `lisp` ，因此新一些的包在缺省情况下已不再使用 `lisp` 包了。由于我们通过调用`in-package` 创建了 `mine` ，而在这次调用中也 `use` 了这个包，所以所有 `Common Lisp` 的名字在 `mine` 中都是可见的： ~~~ MINE> #'cons #<Compiled-Function CONS 462A3E> ~~~ 在实际的编程中，你不得不让所有新编写的包使用 common-lisp (或者其他某个含 Lisp 操作符的包)。否则你甚至会没办法跳出这个新的包。【注4】 一般来说，在编译后的代码中，不会像刚才这样在顶层进行包的操作。更多的时候，这些关于包的函数调用会被包含在源文件中。通常，只要把 in-package 和 defpackage 放在源文件的开头就可以了。 (defpackage 宏是 **CLTL2** 里新引进的，但是有些较老的实现也提供了它。) 如果你要编写一个独立的包，下面列出了你可能会放在对应的源文件最开始地方的代码： ~~~ (in-package 'my-application :use 'common-lisp) (defpackage my-application (:use common-lisp my-utilities) (:nicknames app) (:export win lose draw)) ~~~ 这会使得该文件里所有的代码，或者更准确地说，文件里所有的名字，都纳入了 `my-application` 这个包。 `my-application` 同时使用了 `common-lisp` 和 `my-utilities` ，因此，不用加任何包名作为前缀，所有被引出的符号都可以直接使用。 `my-application` 本身仅仅引出了三个符号，它们分别是：`win`、`lose` 和 `draw` 。由于在调用`in-package` 的时候，我们给 `my-application` 取了一个绰号 `app` ，在其它包里面的代码可以用类似 `app:win` 的名字来引用这些符号。 像这样的用包来提供的模块化的确有点不自然。我们的包里面不是对象，而是一堆名字。每个使用`common-lisp` 的包都引入了 `cons` 这个名字，原因在于 `common-lisp` 包含了一个叫这个名字的函数。但是，这样会导致一个名字叫 `cons` 的变量也在每个使用 `common-lisp` 的程序里可见。这样的事情同样也会在 `Common Lisp` 的其他名字空间重演。如果包(package) 这个机制让你头痛，那么这就是一个最主要的原因 -- 包不是基于对象而是基于名字。 和包相关的操作会发生在读取时（read-time），而非运行时。这可能会造成一些困扰。我们输入的第二个表达式： ~~~ (symbol-package 'foo) ~~~ 之所以会返回它返回的那个值是因为：读取这个查询语句的同时，答案就被生成了。为了求值这个表达式，`Lisp` 必须先读入它，这意味着要 `intern` `foo`。 再来个例子，看看下面把两个表达式交换顺序的结果，这两个表达式前面曾出现过： ~~~ MINE> (in-package 'common-lisp-user) #<Package "COMMON-LISP-USER" 4CD15E> > (export 'bar) ~~~ 通常来说，在顶层输入两个表达式的效果等价于把这两个表达式放在一个progn 里面。不过这次有些不同。如果我们这样说 ~~~ MINE> (progn (in-package 'common-lisp-user) (export 'bar)) >>Error: MINE::BAR is not accessible in COMMON-LISP-USER. ~~~ 则会得到个错误提示。错误的原因在于 `progn` 表达式在求值之前就已经被 read 处理过了。当调用 read 时，当前包还是 mine ，因而 bar 被认为是 mine:bar 。运行这个表达式的效果就好像我们想要从 user 包 export 出 mine:bar ，而不是从 `common-lisp-user` export 出 `common-lisp-user:bar` 一样。 `package` 被如此定义，使得编写那些把符号当作数据的程序成为一桩麻烦事。举个例子，要是像下面那样定义 noise ： ~~~ (in-package 'other :use 'common-lisp) (defpackage other (:use common-lisp) (:export noise)) (defun noise (animal) (case animal (dog 'woof) (cat 'meow) (pig 'oink))) ~~~ 这样的话，如果我们从另外一个包调用 noise ，同时传进去的参数是不认识的符号，noise 会走到 case 语句的末尾，并返回 nil ： ~~~ OTHER> (in-package 'common-lisp-user) #<Package "COMMON-LISP-USER" 4CD15E> > (other:noise 'pig) NIL ~~~ 这是因为传进去的参数是 `common-lisp-user:pig` (这没有冒犯阁下的意思)，然而 `case` 接受 `key`是 `other:pig` 。为了让 `noise` 像我们期望的那样工作，就必须把里面用到的所有六个符号都引出来，再在调用 noise 的包里面引入它们。 在此例中，我们也可以通过使用关键字而不是常规的符号，来绕过这个问题。倘若 noise 像下面这样定义: ~~~ (defun noise (animal) (case animal (:dog :woof) (:cat :meow) (:pig :oink))) ~~~ 的话，我们就能从任意一个包安全地调用这个函数了： ~~~ OTHER> (in-package 'common-lisp-user) #<Package "COMMON-LISP-USER" 4CD15E> > (other:noise :pig) :OINK ~~~ 关键字就像金子：普适而且自身就能表明其价值。不论在哪里它们都是可见的，而且它们从不需要被引用。 在编写类似 `defanaph` ( 16.3 节) 的符号驱动的函数时，基本上应该总是用关键字参数。 包里面有很多地方让人不解。这里对这一主题的介绍不过是冰山一角。要知道所有的细节，请参考**CLTL2** 的第 11 章。 备注： 【注1】译者注：GNU Emacs 和 XEmacs 使用的是一张名为 obarray 的哈希表。 【注2】在较早期的 Common Lisp 实现下，请省略掉 :use 参数 【注3】有的 Common Lisp 实现会在 toplevel 提示符的前面显示包的名字。这个特性不是必须的，但的确是比较贴心的设计。 【注4】译者注：即你不仅没有办法使用cons ，更糟糕的是，你也不能用in-package 切换到其它包。

## 第 25 章 面向对象的 Lisp 本章讨论了 Lisp 中的面向对象编程。Common Lisp 提供了一组操作符可供编写面向对象的程序时使用。 这些操作符和起来，并称为 Common Lisp Object System，或者叫 **CLOS** 。在这里我们不把 **CLOS**仅仅看作一种编写面向对象程序的手段，而把它本身就当成一个 Lisp 程序。从这个角度来看待 **CLOS**是理解 Lisp 和面向对象编程之间关系的关键。 ### 25.1 万变不离其宗 面向对象的编程意味着程序组织方式的一次变革。历史上的另一个变化与这个变革有几分类似，即发生在处理器计算能力分配方式上的变化。在 1970 年代，多用户计算机系统指的就是联接到大量哑终端的一两个大型机。时至今日，这个词更有可能说的是大量用网络互相联接的工作站。现在，系统的处理能力散布于多个独立用户中，而不是集中在一台大型计算机上。 这与面向对象编程有很大程度上的相似，后者把传统的程序结构拆分开来：它不再让单一的程序逻辑去操纵那些被动的数据，而是让数据自己知道该做些什么，程序逻辑就隐含在这些新的数据 "对象" 间的交互过程之中。 举例来说，假设我们要算出一个二维图形的面积。解决这个问题的一个办法就是写一个单独的函数，让它检查参数的类型，然后分情况处理： ~~~ (defun area (x) (cond ((rectangle-p x) (* (height x) (width x))) ((circle-p x) (* pi (expt (radius x) 2))))) ~~~ 面向对象的方法则是让每种对象自己就能够计算出自身的面积。area 这个函数就被拆开，同时每条语句都被分到对象的对应类型中去，比如rectangle 类可能就会看起来像这样： ~~~ #'(lambda (x) (* (height x) (width x))) ~~~ 至于 circle 则会是这样： ~~~ #'(lambda (x) (* pi (expt (radius x) 2))) ~~~ 在这种模式下，我们向对象询问该对象的面积，然后对象则根据所属类型所提供的方法来作出回应。 **CLOS** 的到来似乎意味着 Lisp 正在改变自己，以拥抱面向对象的编程方式。与其这样说，不如改成：Lisp 还在墨守成规，用老样子来拥抱面向对象编程，这样还确切一些。不过 Lisp 中的那些基本概念没有名字，面向对象编程却有，所以时下有种趋势要把 Lisp 算成面向对象的语言。另一种说法：Lisp 是一门可扩展的语言，在这种语言里，面向对象编程的机制和结构可以轻松实现，这种说法恐怕更接近真相。 由于 **CLOS** 是原来就有的，所以把 Lisp 说成面向对象的编程语言并没有误导。然而，如果就这样看待 Lisp 未免太小觑它了。诚然，Lisp 是一种面向对象的编程语言，但是原因并不是它采纳了面向对象的编程模式。 事实在于，这种编程模式只是 Lisp 的抽象系统提供的又一种可能性而已。为了证明这种可能性，我们有了 **CLOS** 一个Lisp 程序，它让Lisp 成为了一门面向对象的语言。 本章的主旨在于：通过把 **CLOS** 作为一个嵌入式语言的实例来研究，进而揭示 Lisp 和面向对象编程之间的联系。这同时也是了解 **CLOS** 本身的一个很好的手段，要学习一个编程语言的特性，没什么方法能比了解这个特性的实现更有效的了。在第 7.6 节，那些宏就是用这种方式来讲解的。下一节将会有一个类似的对面向对象抽象是如何建立在 Lisp 之上的一个粗略的介绍。其中提到的程序将被第 25.3 节到第 25.5 节作为一个基准实现来参考。 ### 25.2 阳春版 Lisp 中的对象 我们可以用 Lisp 来模拟各种各样不同种类的语言。有一种特别直接的办法可以把面向对象编程的理念对应到Lisp 的基本抽象机制上。不过， **CLOS** 的庞大规模让我们难以认清这个事实。因此，在我们开始了解 **CLOS** 能让我们做什么之前，不妨先看看我们用最原始的Lisp 都能干些什么。 我们在面向对象编程中想要的大多数特性，其实在Lisp 里面已经有了。我们可以用少得出奇的代码来得 到剩下的那部分。在本节中，我们将会用两页纸的代码实现一个对象系统，这个系统对于相当多真实的应 用已经够用了。面向对象编程，简而言之，就是： 1. 具有属性的对象 2. 它能对各种消息作出反应， 3. 而且对象能从它的父对象继承相应的属性和方法。 在 Lisp 里面已经有好几种存放成组属性的方法。其中一种就是把对象实现成哈希表，把对象的属性作为哈希表里的表项。这样我们就可以用 gethash 来访问指定的属性： ~~~ (gethash 'color obj) ~~~ 由于函数是数据对象，我们同样可以把它们当作属性保存起来。这就是说，我们的对象系统也可以有方法了，要调用对象的特定方法就 funcall 一下哈希表里的同名属性： ~~~ (funcall (gethash 'move obj) obj 10) ~~~ 据此，我们可以定义一种 Smalltalk 风格的消息传递语法： ~~~ (defun tell (obj message &rest args) (apply (gethash message obj) obj args)) ~~~ 这样的话，要告诉 (tell) obj 移动 10 个单位，就可以说 ~~~ (tell obj 'move 10) ~~~ 事实上，阳春版 Lisp 唯一缺少的要素就是继承机制，不过我们可以用六行代码来实现一个初步的版本，这个版本用一个递归版的 gethash 来完成这个功能： ~~~ (defun rget (obj prop) (multiple-value-bind (val win) (gethash prop obj) (if win (values val win) (let ((par (gethash 'parent obj))) (and par (rget par prop)))))) ~~~ 如果我们在原本用 gethash 的地方用 rget ，就会得到继承而来的属性和方法。如此这般，就可以指定对象的父类： ~~~ (setf (gethash 'parent obj) obj2) ~~~ 到现在为止，我们只是有了单继承 即一个对象只能有一个父类。不过我们可以把 parent 属性改成一个列表，这样就能有多继承了，如 [示例代码 25.1] 中定义的 rget 。 * * * **[示例代码 25.1] 多继承** ~~~ (defun rget (obj prop) (some2 #'(lambda (a) (gethash prop a)) (get-ancestors obj))) (defun get-ancestors (obj) (labels ((getall (x) (append (list x) (mapcan #'getall (gethash 'parent x))))) (stable-sort (delete-duplicates (getall obj)) #'(lambda (x y) (member y (gethash 'parents x)))))) (defun some2 (fn lst) (if (atom lst) nil (multiple-value-bind (val win) (funcall fn (car lst)) (if (or val win) (values val win) (some2 fn (cdr lst)))))) ~~~ * * * 在单继承体系里面，当我们需要得到对象的某个属性时，只需要递归地在对象的祖先中向上搜索。如果在对象本身里面没有我们想要的属性信息时，就检查它的父类，如此这般直到找到。在多继承体系里，我们一样会需要做这样的搜索，但是这次的搜索会有点复杂，因为对象的多个祖先会构成一个图，而不再只是个简单列表了。我们不能用深度优先来搜索这个图。如果允许有多个父类，我们有如 [示例代码 25.2] 中所示的继承树： a 继承自 b 和 c ，而 b 和 c 均继承于 d 。深度优先（或叫高度优先） 的遍历会依次走过 a、b、|d|、c 和d 。倘若想要的属性同时存在于在 d 和 c 里，那么我们将会得到 d 中的属性，而非 c 中的。这种情况会违反一个原则：即子类应当会覆盖基类中提供的缺省值。 ~~~ d b c a ~~~ [示例代码 25.2]： 到同一基类的多条路径 如果需要实现继承系统的基本理念，我们就绝不能在检查一个对象的子类之前，提前检查该对象。在本例中，正确的搜索顺序应该是a、b、c、d 。那怎么样才能保证搜索的顺序是先尝试子孙再祖先呢？最简单的办法是构造一个列表，列表由原始对象的所有祖先构成，然后对列表排序，让列表中没有一个对象出现在它的子孙之前，最后再依次查看每个元素。 get-ancestors 采用了这种策略，它会返回一个按照上面规则排序的列表，列表中的元素是对象和它的祖先们。为了避免在排序时把同一层次的祖先顺序打乱，get-ancestors 使用的是 stable-sort 而非 sort。 一旦排序完毕，rget 只要找到第一个具有期望属性的对象就可以了。（实用工具 some2 是 some 的一个修改版，它能适用于 gethash 这类用第二个返回值表示成功或失败的函数。） 对象的祖先列表中元素的顺序是先从最具体的开始，最后到最一般的类型。如果 orange 是citrus 的子类型，后者又是 fruit 的子类型，那么列表的顺序就会像这样：（orange citrus fruit）。 倘若有个对象，它具有多个父类，那么这些前辈的座次会是从左到右排列的。也就是，如果我们说 ~~~ (setf (gethash 'parents x) (list y z)) ~~~ 那么当我们在搜索一个继承得来的属性时，y 就会优先于z 被考虑。举个例子，我们可以说爱国的无赖首先是一个无赖，然后才是爱国者： ~~~ > (setq scoundrel (make-hash-table) patriot (make-hash-table) patriotic-scoundrel (make-hash-table)) #<Hash-Table C4219E> > (setf (gethash 'serves scoundrel) 'self (gethash 'serves patriot) 'country (gethash 'parents patriotic-scoundrel) (list scoundrel patriot)) (#<Hash-Table C41C7E> #<Hash-Table C41F0E>) > (rget patriotic-scoundrel 'serves) SELF T ~~~ 现在让我们对这个简陋的系统加以改进。可以从对象创建函数着手。这个函数将会在新建对象时，构造一个该对象祖先的列表。虽然当前的版本是在进行查询的时候构造这种表的，但是我们没有理由不把这件事情提前完成。[示例代码 25.3] 中定义了一个名为 obj 的函数，这个函数被用于生成新的对象，对象的祖先列表被保存在对象本身里。为了用上保存的祖先列表，我们同时重新定义了 rget 。 * * * **[示例代码 25.3] 用来新建对象的函数** ~~~ (defun obj (&rest parents) (let ((obj (make-hash-table))) (setf (gethash 'parents obj) parents) (ancestors obj) obj)) (defun ancestors (obj) (or (gethash 'ancestors obj) (setf (gethash 'ancestors obj) (get-ancestors obj)))) (defun rget (obj prop) (some2 #'(lambda (a) (gethash prop a)) (ancestors obj))) ~~~ * * * 另一个可以改进的地方是消息调用的语法。tell 本身是多余的东西，并且由于它的原因，动词被排到了第二位。这意味着我们的程序读起来不再像是熟悉的Lisp 前缀表达式了： ~~~ (tell (tell obj 'find-owner) 'find-owner) ~~~ 我们可以通过把每个属性定义成函数来去掉tell 这种语法，如[示例代码 25.4] 所示。可选参数meth? 的值如果是真的话，那表示这个属性应该被当作方法来处理，否则它应该被当成一个slot，并径直返回rget 所取到的值。一旦我们把这两种属性中任一种，像这样定义好了： ~~~ (defprop find-owner t) ~~~ 我们就可以用函数调用的方式来引用它，同时代码读起来又有 Lisp 的样子了： * * * **[示例代码 25.4] 函数式的语法** ~~~ (find-owner (find-owner obj)) (defmacro defprop (name &optional meth?) '(progn (defun ,name (obj &rest args) ,(if meth? '(run-methods obj ',name args) '(rget obj ',name))) (defsetf ,name (obj) (val) '(setf (gethash ',',name ,obj) ,val)))) (defun run-methods (obj name args) (let ((meth (rget obj name))) (if meth (apply meth obj args) (error "No ~A method for ~A." name obj)))) ~~~ * * * 现在，原先的例子也变得更有可读性了： ~~~ > (progn (setq scoundrel (obj)) (setq patriot (obj)) (setq patriotic-scoundrel (obj scoundrel patriot)) (defprop serves) (setf (serves scoundrel) 'self) (setf (serves patriot) 'country) (serves patriotic-scoundrel)) SELF T ~~~ 在当前的实现里，对象中每个名字最多对应一个方法。这个方法要么是对象自己的，要么是通过继承得来的。要是能在这个问题上有更多的灵活性，允许把本地的方法和继承来的方法组合起来，那肯定会方便很多。比如说，我们会希望某个对象的 move 方法沿用其父类的 move 方法，但是除此之外还要在调用之前或者之后运行一些其它的代码。 为了让这个设想变成现实，我们将修改程序，加上 before、 after 和around 方法。before 方法让我们能吩咐程序，"先别急，把这事做完再说"。这些方法会在该方法中其余部分运行前，作为前奏，被先行调用。 after 方法让我们可以要求程序说，"还有，把这事也给办了"。而这些方法会作为收场在最后调用。在两者之间，我们会执行曾经自己就是整个方法的函数，现在被称为主方法（primarymethod）。它的返回值将被作为整个方法的返回值，即使 after 方法在其后调用。 before 和 after 方法让我们能用新的行为把主方法包起来。around 方法则以一种更奇妙的方法实现了这个功能。如果存在around 方法，那么被调用的就不再是主方法，而是around 方法。并且，around 方法有办法调用主方法（用call-next ，该函数在[示例代码 25.7] 中提供），至于调不调则是它的自由。 如[示例代码 25.5] 和[示例代码 25.6] 所示，为了让这些辅助的方法生效，我们对run-methods 和rget 加以了改进。在之前的版本里，当我们调用对象的某个方法时，运行的仅是一个函数：即最匹配的那个主函数。我们将会运行搜索祖先列表时找到的第一个方法。加上辅助方法的支持，调用的顺序将变成这样： 1. 倘若有的话，先是最匹配的around 方法 2. 否则的话，依次是： (a) 所有的before 方法,从最匹配的到最不匹配的。 (b) 最匹配的主方法(这是我们以前会调用的)。 (c) 所有的 after 方法,从最不匹配的到最匹配的。 (defstruct meth around before primary after) (defmacro meth- (field obj) (let ((gobj (gensym))) '(let ((,gobj ,obj)) (and (meth-p ,gobj) (,(symb 'meth- field) ,gobj))))) (defun run-methods (obj name args) (let ((pri (rget obj name :primary))) (if pri (let ((ar (rget obj name :around))) (if ar (apply ar obj args) (run-core-methods obj name args pri))) (error "No primary ~A method for ~A." name obj)))) (defun run-core-methods (obj name args &optional pri) (multiple-value-prog1 (progn (run-befores obj name args) (apply (or pri (rget obj name :primary)) obj args)) (run-afters obj name args))) (defun rget (obj prop &optional meth (skip 0)) (some2 #'(lambda (a) (multiple-value-bind (val win) (gethash prop a) (if win (case meth (:around (meth- around val)) (:primary (meth- primary val)) (t (values val win)))))) (nthcdr skip (ancestors obj)))) [示例代码 25.5]： 辅助的方法 ~~~ (defun run-befores (obj prop args) (dolist (a (ancestors obj)) (let ((bm (meth- before (gethash prop a)))) (if bm (apply bm obj args))))) (defun run-afters (obj prop args) (labels ((rec (lst) (when lst (rec (cdr lst)) (let ((am (meth- after (gethash prop (car lst))))) (if am (apply am (car lst) args)))))) (rec (ancestors obj)))) ~~~ [示例代码 25.6]： 辅助的方法（续） 同时也注意到，方法不再作为单个的函数出现，它成了有四个成员的结构。现在要定义一个（主） 方法，不能再像这样说了： ~~~ (setf (gethash 'move obj) #'(lambda ...)) ~~~ 我们改口说： ~~~ (setf (meth-primary (gethash 'move obj)) #'(lambda ...)) ~~~ 基于上面、还有其它一些原因，我们下一步将会定义一个宏，让它帮我们定义方法。 * * * **[示例代码 25.7] 定义方法** ~~~ (defmacro defmeth ((name &optional (type :primary)) obj parms &body body) (let ((gobj (gensym))) '(let ((,gobj ,obj)) (defprop ,name t) (unless (meth-p (gethash ',name ,gobj)) (setf (gethash ',name ,gobj) (make-meth))) (setf (,(symb 'meth- type) (gethash ',name ,gobj)) ,(build-meth name type gobj parms body))))) (defun build-meth (name type gobj parms body) (let ((gargs (gensym))) '#'(lambda (&rest ,gargs) (labels ((call-next () ,(if (or (eq type :primary) (eq type :around)) '(cnm ,gobj ',name (cdr ,gargs) ,type) '(error "Illegal call-next."))) (next-p () ,(case type (:around '(or (rget ,gobj ',name :around 1) (rget ,gobj ',name :primary))) (:primary '(rget ,gobj ',name :primary 1)) (t nil)))) (apply #'(lambda ,parms ,@body) ,gargs))))) (defun cnm (obj name args type) (case type (:around (let ((ar (rget obj name :around 1))) (if ar (apply ar obj args) (run-core-methods obj name args)))) (:primary (let ((pri (rget obj name :primary 1))) (if pri (apply pri obj args) (error "No next method.")))))) ~~~ * * * [示例代码 25.7] 定义的就是这样的一个宏。代码中有很大篇幅被用来实现两个函数，这两个函数让方法能引用其它的方法。`around` 和主方法可以使用 `call-next` 来调用下一个方法，所谓下一个方法，指的是倘若当前方法不存在，就会被调用的方法。举个例子，如果当前运行的方法是唯一的一个`around` 方法，那么下一个方法就是常见的由 `before` 方法、最匹配的主方法和 `after` 方法三者合体而成的夹心饼干。在最匹配的主方法里， 下一个方法则会是第二匹配的主方法。由于 `call-next`的行为取决于它被调用的地方，因此 `call-next` 绝对不会用一个 `defun` 来在全局定义，不过它可以在每个由 `defmeth` 定义的方法里局部定义。 around 方法或者主方法可以用 `next-p` 来获知下一个方法是否存在。如果当前的方法是个主方法，而且主方法所属的对象是没有父类的，那么就不会有下一个方法。由于当没有下个方法时，`call-next` 会报错， 因此应该经常调用 `next-p` 试试深浅。像 `call-next` ，`next-p` 也是在方法里面单独地局部定义的。 下面将介绍新宏 `defmeth` 的使用方法。如果我们只是希望定义 `rectangle` 对象的 `area` 方法，我们会说 ~~~ (setq rectangle (obj)) (defprop height) (defprop width) (defmeth (area) rectangle (r) (* (height r) (width r))) ~~~ 现在，一个 `rectangle` 实例的面积就会由类型中对应方法计算得出： ~~~ > (let ((myrec (obj rectangle))) (setf (height myrec) 2 (width myrec) 3) (area myrec)) 6 ~~~ 这里有个复杂一些的例子，假设我们为 `filesystem` 对象定义了一个 `backup` 方法： ~~~ (setq filesystem (obj)) (defmeth (backup :before) filesystem (fs) (format t "Remember to mount the tape.~%")) (defmeth (backup) filesystem (fs) (format t "Oops, deleted all your files.~%") 'done) (defmeth (backup :after) filesystem (fs) (format t "Well, that was easy.~%")) ~~~ 正常的调用次序如下： ~~~ > （backup （obj filesystem）） Remember to mount the tape. Oops， deleted all your files. Well， that was easy. DONE ~~~ 接下来，我们想要知道备份一次会花费多少时间，所以可以定义下面的 `around` 方法： ~~~ (defmeth (backup :around) filesystem (fs) (time (call-next))) ~~~ 现在只要调用 `filesystem` 子类的 `backup` （除非有更匹配的 around 方法介入），那么我们的around 方法就会执行。它会运行平常时候在 backup 里运行的那些代码，不同之处是把它们放到了一个 time 的调用里执行。time 的返回值则会被作为 backup 方法调用的值返回。 ~~~ > (backup (obj filesystem)) Remember to mount the tape. Oops, deleted all your files. Well, that was easy. Elapsed Time = .01 seconds DONE ~~~ 一旦知道了备份操作需要的时间，我们就会想要去掉这个around 方法。调用undefmeth 可达到这个目的（如[示例代码 25.8]），它的参数和defmeth 的前两个参数相同： * * * **[示例代码 25.8]** 去掉方法 ~~~ (undefmeth (backup :around) filesystem) (defmacro undefmeth ((name &optional (type :primary)) obj) '(setf (,(symb 'meth- type) (gethash ',name ,obj)) nil)) ~~~ * * * **[示例代码 25.9]** 维护父类和子类的联系 ~~~ (defmacro children (obj) '(gethash 'children ,obj)) (defun parents (obj) (gethash 'parents obj)) (defun set-parents (obj pars) (dolist (p (parents obj)) (setf (children p) (delete obj (children p)))) (setf (gethash 'parents obj) pars) (dolist (p pars) (pushnew obj (children p))) (maphier #'(lambda (obj) (setf (gethash 'ancestors obj) (get-ancestors obj))) obj) pars) (defsetf parents set-parents) (defun maphier (fn obj) (funcall fn obj) (dolist (c (children obj)) (maphier fn c))) (defun obj (&rest parents) (let ((obj (make-hash-table))) (setf (parents obj) parents) obj)) ~~~ * * * 另外一个我们可能需要修改的是对象的父类列表。但是进行了这种修改之后，我们还应该相应地更新该对象以及其所有子类的的祖先列表。到目前为止，还没有办法从对象那里获知它的子类信息，所以我们必须另加一个 children 属性。 [示例代码 25.9] 中的代码被用来操作对象的父类和子类。这里不再用 gethash 来获得父类和子类信息，而是分别改用操作符 parents 和children。其中后者是个宏，因而它对于 setf 是透明的。前者是一个函数，它的逆操作被 defsetf 定义为 set-parents ，这个函数包揽了所有的相关工作，让新的双向链接系统能保持其一致性。 为了更新一颗子树里所有对象的祖先，set-parents 调用了 maphier ，这个函数的作用相当于继承树里的mapc 。mapc 对列表里每个元素运行一个函数，同样的，maphier 也会对对象和它所有的后代应用指定的函数。除非这些节点构成没有公共子节点的树，否则有的对象会被传入这个函数一次以上。在这里，这不会导致问题，因为调用多次get-ancestors 和调用一次的效果是相同的。 现在，要修改继承层次结构的话，我们只要在对象的 parents 上调用 setf 就可以了： ~~~ > (progn (pop (parents patriotic-scoundrel)) (serves patriotic-scoundrel)) COUNTRY T ~~~ 当这个层次结构被修改的时候，受到影响的子孙列表和祖先列表会同时自动地更新。（children 本不是让人直接修改的，但是这也不是不可以。只要我们定义一个和 set-parents 对应的 set-children 就可以了。） 为了配合新代码，我们在[示例代码 25.9] 的最后重新定义了 obj 函数。 这次我们要开发一个新的手段来组合方法，作为对这个系统的最后一项改进。现在，会被调用的唯一主方法将是最匹配的那个（虽然它可以用 call-next 来调用其它的主方法）。要是我们希望能把对象所有祖先的主方法的结果组合起来呢？比如说，假设 my-orange 是 orange 的子类，而 orange 又是 citrus 的子类。如果props 方法用在 citrus 上的返回值是 （round acidic），相应的，orange 的返回值是（orange sweet） ，my-orange 的结果是（dented）。要是能让 （props my-orange） 能返回这些值的并集就好办多了：（dented orange sweet round acidic）。 ~~~ (defmacro defcomb (name op) '(progn (defprop ,name t) (setf (get ',name 'mcombine) ,(case op (:standard nil) (:progn '#'(lambda (&rest args) (car (last args)))) (t op))))) (defun run-core-methods (obj name args &optional pri) (let ((comb (get name 'mcombine))) (if comb (if (symbolp comb) (funcall (case comb (:and #'comb-and) (:or #'comb-or)) obj name args (ancestors obj)) (comb-normal comb obj name args)) (multiple-value-prog1 (progn (run-befores obj name args) (apply (or pri (rget obj name :primary)) obj args)) (run-afters obj name args))))) (defun comb-normal (comb obj name args) (apply comb (mapcan #'(lambda (a) (let* ((pm (meth- primary (gethash name a))) (val (if pm (apply pm obj args)))) (if val (list val)))) (ancestors obj)))) ~~~ [示例代码 25.10]： 方法的组合 假如能让方法对所有主方法的返回值应用某个函数，而不是仅仅返回最匹配的那个主函数的返回值，那就能解决这个问题了。[示例代码 25.10] 中定义有一个宏，这个宏让我们能指定方法的组合手段，图中还定义了新版本的 run-core-methods ，它允许我们把方法组合在一起使用。我们用 defcomb 定义方法的组合形式，它把方法名作为第一个参数，第二个参数描述了期望的组合方式。通常，这第二个参数应该是一个函数。不过，它也可以是 :progn :and :or 和 :standard 中的一个。如果使用前三个，系统就会用相应的操作符来组合主方法，用 :standard 的话，就表示我们想用以前的办法来执行方法。 [示例代码 25.10] 中的核心函数是新的run-core-methods 。如果被调用的方法没有名为mcombine 的属性，那么一切如常。否则，mcombine 应该是个函数（比如+），或是个关键字（比如：or）。前面一种情况，所有主方法返回值构成的列表会被送进这个函数。如果是后者的情况，我们会用和这个关键字对应的函数对主方法一一进行操作。 如果代码写得更讲究一些，可以考虑用 reduce ，这样可以避免手动 cons。 * * * ~~~ (defun comb-and (obj name args ancs &optional (last t)) (if (null ancs) last (let ((pm (meth- primary (gethash name (car ancs))))) (if pm (let ((new (apply pm obj args))) (and new (comb-and obj name args (cdr ancs) new))) (comb-and obj name args (cdr ancs) last))))) (defun comb-or (obj name args ancs) (and ancs (let ((pm (meth- primary (gethash name (car ancs))))) (or (and pm (apply pm obj args)) (comb-or obj name args (cdr ancs)))))) ~~~ [示例代码 25.11]： 方法的组合（续） * * * 如[示例代码 25.11] 所示，and 和 or 这两个操作符必须要特殊处理。它们被特殊对待的原因不是因为它们是special form，而是因为它们的短路（short-circuit） 求值方式： ~~~ > (or 1 (princ "wahoo")) 1 ~~~ 这里，什么都不会被打印出来，因为or 一看到非nil 的参数就会立即返回。与之类似，如果有一个更匹配的方法返回真的话，那么剩下的用or 组合的主方法将不会被调用。为了实现 and 和 or 的这种短路求值，我们用了两个专门的函数：comb-and 和 comb-or。 为了实现我们之前的例子，可以这样写： ~~~ (setq citrus (obj)) (setq orange (obj citrus)) (setq my-orange (obj orange)) (defmeth (props) citrus (c) '(round acidic)) (defmeth (props) orange (c) '(orange sweet)) (defmeth (props) my-orange (m) '(dented)) (defcomb props #'(lambda (&rest args) (reduce #'union args))) ~~~ 这样定义之后，props 就能返回所有主方法返回值的并集了：⁴ ~~~ > (props my-orange) (DENTED ORANGE SWEET ROUND ACIDIC) ~~~ 这个例子恰巧显示了一个只有在 Lisp 里用面向对象编程才会面临的选择：是把信息保存在slot 里，还是保存在方法里。 以后，如果想要 props 方法恢复到缺省的行为，只要把方法的组合方式改回标准模式（standard） 即可： ~~~ > (defcomb props :standard) NIL > (props my-orange) (DENTED) ~~~ 要注意，before 和 after 方法只是在标准的组合模式下才会有效。而 around 方法会像以前那样工作。 本节中展示的程序只是作为一个演示模型，而不是想以它为基础，进行面向对象编程。写这个模型的着眼点是简洁而非效率。不管如何，这至少是一个可以工作的模型，因此也可以被用在试验性质的开发和原型【注4】由于 props 里用的组合函数是 union ，因此列表里的元素不一定会按照原来的顺序排列。 开发中。如果你有意这样用它的话，有一个小改动可以让它的效率有相当的改进：如果对象只有一个父类的话，就不要计算或者保存它的祖先列表。 ### 25.3 类和实例 上一节中写了一个尽可能短小的程序来重新实现 **CLOS** 。理解它为我们进而理解 **CLOS** 铺平了道路。在下面几节中，我们会仔细考察 **CLOS** 本身。 在我们的这个简单实现里，没有把类和实例作语法上的区分，也没有把 slot 和方法分开。在 **CLOS**里，我们用defclass 定义类，同时把各slot 组成列表一并声明： ~~~ (defclass circle () (radius center)) ~~~ 这个表达式的意思是，circle 类没有父类，但是有两个slot：radius 和center。我们用下面的语句可以新建一个 circle 类的实例： ~~~ (make-instance 'circle) ~~~ 不幸的是，我们还没有定义读取circle 中slot 的方式，因此我们创建的任何实例都只是个摆设。为了访问特定的slot，我们需要为它定义一个访问（accessor） 函数： ~~~ (defclass circle () ((radius :accessor circle-radius) (center :accessor circle-center))) ~~~ 现在，如果我们建立了一个circle 的实例，就可以用setf 和与之对应的访问函数来设置它的radius 和center slot： ~~~ > (setf (circle-radius (make-instance 'circle)) 2) 2 ~~~ 如果像下面那样定义slot，那么我们也可以在make-instance 里直接完成这种初始化的工作： ~~~ (defclass circle () ((radius :accessor circle-radius :initarg :radius) (center :accessor circle-center :initarg :center))) ~~~ 在slot 定义中出现的 ：initarg 关键字表示：接下来的实参将要在make-instance 中成为一个关键字形参。这个关键字实参的值将会被作为该slot 的初始值： ~~~ > (circle-radius (make-instance 'circle :radius 2 :center '(0 . 0))) 2 ~~~ 使用：initform，我们也可以定义一些slot，让它们能初始化自己。shape 类中的visible ~~~ (defclass shape () ((color :accessor shape-color :initarg :color) (visible :accessor shape-visible :initarg :visible :initform t))) ~~~ 会缺省地被设置成t ： ~~~ > (shape-visible (make-instance 'shape)) T ~~~ 如果一个slot 同时具有initarg 和initform，那么当initarg 被指定的时候，它享有优先权： ~~~ > (shape-visible (make-instance 'shape :visible nil)) NIL ~~~ slot 会被实例和子类继承下来。如果一个类有多个父类，那么它会继承得到这些父类slot 的并集。因此，如果我们把screen-circle 类同时定义成circle 和shape 两个类的子类， ~~~ (defclass screen-circle (circle shape) nil) ~~~ 那么 screen-circle 会具有四个 slot，每个父类继承两个 slot。注意到，一个类并不一定要自己新建一些新的 slot，screen-circle 的意义就在于提供了一个可以实例化的类型，它同时继承自 circle 和 shape。 以前可以用在 circle 和 shape 实例的那些访问函数和 initarg 会对 screen-circle 类型的实例继续生效： ~~~ > (shape-color (make-instance 'screen-circle :color 'red :radius 3)) RED ~~~ 如果在 `defclass` 里给 `color` 指定一个 `initform`，我们就可以让所有的 `screen-circle` 的对应`slot` 都有个缺省值： ~~~ (defclass screen-circle (circle shape) ((color :initform 'purple))) ~~~ 这样，`screen-circle` 类型的实例在缺省情况下就会是紫色的了： ~~~ > (shape-color (make-instance 'screen-circle)) PURPLE ~~~ 不过我们还是可以通过显式地指定一个：`colorinitarg`，来把这个 `slot` 初始化成其他颜色。 在我们之前实现的简装版面向对象编程框架里，实例的值可以直接从父类的slot 继承得到。在 **CLOS**中， 实例包含 slot 的方式却和类不一样。我们通过在父类里定义 initform 来为实例定义可被继承的缺省值。 在某种程度上，这样处理更有灵活性。因为initform 不仅可以是一个常量，它还可以是一个每次都返回不同值的表达式： ~~~ (defclass random-dot () ((x :accessor dot-x :initform (random 100)) (y :accessor dot-y :initform (random 100)))) ~~~ 每创建一个random-dot 实例，它在x 和y 轴上的坐标都会是从0 到99 之间的一个随机整数： ~~~ > (mapcar #'(lambda (name) (let ((rd (make-instance 'random-dot))) (list name (dot-x rd) (dot-y rd)))) '(first second third)) ((FIRST 25 8) (SECOND 26 15) (THIRD 75 59)) ~~~ 在我们的简装版实现里，我们对两种slot 不加区别：一种是实例自己具有的slot，这种slot 实例和实例之间可以不同；另一种slot 应该是在整个类里面都相同的。在 **CLOS** 中，我们可以指定某些slot 是共享的，换句话说，就是让这些slot 的值在每个实例里都是相同的。为了达到这个效果，我们可以把slot 声明成 ：allocation ：class 的。（另一个选项是 ：allocation ：instance。不过由于这是缺省的设置，因此就没有必要再显式地指定了。） 比如说，如果所有的猫头鹰都是夜间生活的动物，那么我们可以让nocturnal 这个slot 作为owl 类的共享slot，同时让它的初始值为t ： ~~~ (defclass owl () ((nocturnal :accessor owl-nocturnal :initform t :allocation :class))) ~~~ 现在，所有的owl 实例都会继承这个slot 了： ~~~ > (owl-nocturnal (make-instance 'owl)) T ~~~ 如果我们改动了这个slot 的"局部" 值，那么我们实际上修改的是保存在这个类里面的值： ~~~ > (setf (owl-nocturnal (make-instance 'owl)) 'maybe) MAYBE > (owl-nocturnal (make-instance 'owl)) MAYBE ~~~ 这种机制或许会造成一些困扰，所以我们可能会希望让这个slot 成为只读的。在我们为一个slot 定义访问函数的同时，也是在为这个slot 的值定义一个读和写的方法。如果我们需要让这个值可读，但是不可写，那么我们可以给这个slot 仅仅设置一个reader 函数，而不是全功能的访问函数： ~~~ (defclass owl () ((nocturnal :reader owl-nocturnal :initform t :allocation :class))) ~~~ 现在如果尝试修改owl 实例的nocturnal slot 的话，就会产生一个错误： ~~~ > (setf (owl-nocturnal (make-instance 'owl)) nil) >> Error: The function (SETF OWL-NOCTURNAL) is undefined. ~~~ ### 25.4 方法 在我们的简装版实现中，强调了这样一个思想，即在具有词法作用域的语言里，其slot 和方法间是有其相似性的。在实现的时候，保存和继承主方法的方式和对slot 值的处理方式没有什么不同。slot 和方法区别只在于：把一个名字定义成slot，是通过 ~~~ (defprop area) ~~~ 把area 作为一个函数实现的，这个函数得到并返回一个值。而把这个名字定义成一个方法，则是通过 ~~~ (defprop area t) ~~~ 把area 实现成一个函数，这个函数在得到值之后，会funcall 这个值，同时把函数的参数传给它。 在 **CLOS** 中，实现这个功能的单元仍然被称为"方法"，同时也可以定义这些方法，让它们看上去就像类的属性一样。这里，我们为circle 类定义一个名为area 的方法： ~~~ (defmethod area ((c circle)) (* pi (expt (circle-radius c) 2))) ~~~ 这个方法的参数列表表示，这是个接受一个参数的函数，参数应该是circle 类型的实例。 和简单实现里一样，我们像调用一个函数那样调用这个方法： ~~~ > (area (make-instance 'circle :radius 1)) 3.14... ~~~ 我们同样可以让方法接受更多的参数： ~~~ (defmethod move ((c circle) dx dy) (incf (car (circle-center c)) dx) (incf (cdr (circle-center c)) dy) (circle-center c)) ~~~ 如果我们对一个circle 的实例调用这个方法，circle 实例的中心会移动⟨dx，dy⟩ ： ~~~ > (move (make-instance 'circle :center '(1 . 1)) 2 3) (3 . 4) ~~~ 方法的返回值表明了圆形的新位置。 和我们的简装版实现一样，如果一个实例对应的类及其父类有个方法，那么调用这个方法会使最匹配的方法被调用。因此，如果unit-circle 是 circle 的子类，同时具有如下所示的area 方法： ~~~ (defmethod area ((c unit-circle)) pi) ~~~ 那么当我们对一个unit-circle 的实例调用area 方法的时候，将被调用的不是更一般的那个方法，而是在上面定义area。 当一个类有多个父类时，它们的优先级从左到右依次降低。patriotic-scoundrel 类的定义如下： ~~~ (defclass scoundrel nil nil) (defclass patriot nil nil) (defclass patriotic-scoundrel (scoundrel patriot) nil) ~~~ 我们认为爱国的无赖，他首先是一个无赖，然后才是一个爱国者。当两个父类都有合适的方法时， ~~~ (defmethod self-or-country? ((s scoundrel)) 'self) (defmethod self-or-country? ((p patriot)) 'country) ~~~ scoundrel 类的方法会这样被执行： ~~~ > (self-or-country? (make-instance 'patriotic-scoundrel)) SELF ~~~ 到目前为止，所以的例子都让人觉得 **CLOS** 中的方法只针对某一个类。实际上， **CLOS** 中的方法是更为通用的一个概念。在move 方法的参数列表中，我们称 （c circle） 为特化（specialized） 参数，它表示，如果move 的第一个参数是circle 类的一个实例的话，就适用这个方法。对于 **CLOS** 方法，不止一个参数可以被特化。下面的方法就有两个特化参数和一个可选的非特化参数： ~~~ (defmethod combine ((ic ice-cream) (top topping) &optional (where :here)) (append (list (name ic) 'ice-cream) (list 'with (name top) 'topping) (list 'in 'a (case where (:here 'glass) (:to-go 'styrofoam)) 'dish))) ~~~ 如果combine 的前两个参数分别是ice-cream 和topping 的实例的话，上面定义的方法就会被调用。如果我们定义几个最简单类以便构造实例 ~~~ (defclass stuff () ((name :accessor name :initarg :name))) (defclass ice-cream (stuff) nil) (defclass topping (stuff) nil) ~~~ 那么我们就能定义并运行这个方法了： ~~~ > (combine (make-instance 'ice-cream :name 'fig) (make-instance 'topping :name 'olive) :here) (FIG ICE-CREAM WITH OLIVE TOPPING IN A GLASS DISH) ~~~ 倘若方法特化了一个以上的参数，这时就没有办法再把方法当成类的属性了。我们的combine 方法是属于ice-cream 类还是属于topping 类呢？在 **CLOS** 里，所谓"对象响应消息" 的模型不复存在。如果我们像下面那样调用函数，这种模型似乎还是顺理成章的： ~~~ (tell obj 'move 2 3) ~~~ 显而易见，在这里我们调用的是obj 的move 方法。但是一旦我们废弃这种语法，而改用函数风格的等价操作： ~~~ (move obj 2 3) ~~~ 我们就需要定义move ，让它能根据它的第一个参数dispatch 操作，即按照第一个参数的类型来调用适合的方法。 走出这一步，于是有个问题浮出了水面：为什么只能根据第一个参数来进行dispatch 呢？ **CLOS** 的回答是： 就是呀，为什么非得这样呢？在 **CLOS** 中，方法能够指定任意个数的参数进行特化，而且这并不限于用户自定义的类，Common Lisp 类型⁵也一样可以，甚至能针对单个的特定对象特化。下面是一个名为combine 的方法，它被用于字符串： ~~~ (defmethod combine ((s1 string) (s2 string) &optional int?) (let ((str (concatenate 'string s1 s2))) (if int? (intern str) str))) ~~~ 这不仅意味着方法不再是类的属性，而且还表明，我们可以根本不用定义类就能使用方法了。 ~~~ > (combine "I am not a " "cook.") "I am not a cook." ~~~ 下面，第二个参数将对符号palindrome 进行特化： ~~~ (defmethod combine ((s1 sequence) (x (eql 'palindrome)) &optional (length :odd)) (concatenate (type-of s1) s1 (subseq (reverse s1) (case length (:odd 1) (:even 0))))) ~~~ 上面的这个方法能生成任意元素序列的回文：⁶ ~~~ > (combine '(able was i ere) 'palindrome) (ABLE WAS I ERE I WAS ABLE) ~~~ 到现在，我们讲述的内容已经不仅仅局限于面向对象的范畴，它有着更普遍的意义。 **CLOS** 在设计的时候就已经认识到，在对象方法的背后，更深层次的思想是分派（dispatch） 的概念，即选择合适方法的依据可以不仅仅是单独的一个参数，还可以基于多个参数的类型。当我们基于这种更通用的表示手段来构造方法时， 方法就可以脱离特定的类而存在了。方法不再在逻辑上从属于类，它现在和其它的同名方法成为了一体。 **CLOS** 把这样的一组方法称为generic 函数。所有的combine 方法隐式地定义了名为combine 的generic 函数。 我们可以显式地用defgeneric 宏定义generic 函数。虽然没有必要专门调用defgeneric 来定义一个generic 函数，但是这个定义却是一个安置文档，或者为一些错误加入保护措施的好地方。我们在下面的定义中两样都用上了： ~~~ (defgeneric combine (x y &optional z) (:method (x y &optional z) "I can't combine these arguments.") (:documentation "Combines things.")) ~~~ 由于这里为combine 定义的方法没有特化任何参数，所以如果没有其它方法适用的话，这个方法就会被调用。 ~~~ > (combine #'expt "chocolate") "I can't combine these arguments." ~~~ 倘若没有显式定义上面的generic 函数，这个调用就会报错。 ⁵或者更准确地说，是 **CLOS** 定义的一系列形似类型的类，这些类的定义和Common Lisp 的内建类型体系是平行对应的。 ⁶在一个Common Lisp 实现中（否则这个实现就完美了），concatenate 不会接受cons 作为它的第一个参数，因此这个方法调用在这种情况下将无法正常工作。 generic 函数也加入了一个我们把方法当成对象属性时没有的限制：当所有的同名方法加盟一个generic 方法时，这些同名方法的参数列表必须一致。这就是为什么我们所有的combine 方法都另有一个可选参数的原因。如果让第一个定义的combine 方法接受三个参数，那么当我们试着去定义另一个只有两个参数的方法时，就会出错。 **CLOS** 要求所有同名方法的参数列表必须是一致的。两个参数列表取得一致的前提是：它们必须具有相同数量的必选参数，相同数量的可选参数，并且&rest 和&key 的使用也要相互兼容。不同方法最后用的关键字参数（keywordparameter） 可以不一样，不过defgeneric 会坚持要求让它的所有方法接受一个特定的最小集。下面每对参数列表，两两之间是相互一致的： ~~~ (x) (a) (x &optional y) (a &optional b) (x y &rest z) (a b &rest c) (x y &rest z) (a b &key c d) ~~~ 而下列的每组都不一致： ~~~ (x) (a b) (x &optional y) (a &optional b c) (x &optional y) (a &rest b) (x &key x y) (a) ~~~ 重新定义方法就像重定义函数一样。由于只有必选参数才能被特化，每个方法都唯一地对应着它的generic function 及其必选参数的类型。如果我们定义另一个有着相同特化参数的方法，那么新的方法就会覆盖原来的方法。因而，如果我们这样写道： ~~~ (defmethod combine ((x string) (y string) &optional ignore) (concatenate 'string x " + " y)) ~~~ 那么就会重新定义头两个参数都是string 时，combine 方法的行为。 ~~~ (defmacro undefmethod (name &rest args) (if (consp (car args)) (udm name nil (car args)) (udm name (list (car args)) (cadr args)))) (defun udm (name qual specs) (let ((classes (mapcar #'(lambda (s) '(find-class ',s)) specs))) '(remove-method (symbol-function ',name) (find-method (symbol-function ',name) ',qual (list ,@classes))))) ~~~ [示例代码 25.12]： 用于删除方法的宏 不幸的是，如果我们不希望重新定义方法，而是想删除它， **CLOS** 中并没有一个内建的defmethod 的逆操作。万幸的是，这是Lisp，所以我们可以自己写一个。[示例代码 25.12] 中的undefmethod 记录了手动删除一个方法的具体细节。就像调用defmethod 时一样，我们在使用这个宏的时候，把参数传入它，不过不同之处在于，这次我们并没有把整个的参数列表作为第二个或者第三个参数传进去，只是把必选参数的类名送入这个宏。所以，如果要删除两个string 的combine 方法，可以这样写： ~~~ (undefmethod combine (string string)) ~~~ 没有特化的参数被缺省指定为类t ，所以，如果我们之前定义了一个方法，而且这个方法有必选参数，但是这些参数没有特化的话： ~~~ (defmethod combine ((fn function) &optional y) (funcall fn x y)) ~~~ 我们可以用下面的语句把它去掉 ~~~ (undefmethod combine (function t)) ~~~ 如果希望删除整个的genericfunction，那么我们可以用和删除任意函数相同的方法来达到这个目的，即调用fmakunbound ： ~~~ (fmakunbound 'combine) ~~~ ### 25.5 辅助方法和组合 在 **CLOS** 里，辅助函数还是和我们的精简版实现一样的运作。到现在，我们只看到了主方法，但是我们一样可以用before、 after 和around 方法。可以通过在方法的名字后面加上限定关键字（qualifyingkeyword），来定义这些辅助函数。假如我们为speaker 类定义一个主方法speak 如下： ~~~ (defclass speaker nil nil) (defmethod speak ((s speak) string) (format t "~A" string) ~~~ 那么，对一个speaker 的实例调用speak 方法，就会把方法的第二个参数打印出来： ~~~ > (speak (make-instance 'speaker) "life is not what it used to be") life is not what it used to be NIL ~~~ 现在定义一个名为intellectual 的子类，让它把主方法speak 用before 和 after 方法包装起来， ~~~ (defclass intellectual (speaker) nil) (defmethod speak :before ((i intellectual) string) (princ "Perhaps ")) (defmethod speak :after ((i intellectual) string) (princ " in some sense")) ~~~ 然后，我们就能新建一个speaker 的子类，让这个子类总是会自己加上最后一个（以及第一个） 词： ~~~ > (speak (make-instance 'intellectual) "life is not what it used to be") Perhaps life is not what it used to be in some sense NIL ~~~ 在标准的方法组合方式中，方法调用的顺序和我们精简版实现中规定的顺序是一样的：所有的before 方法是从最匹配的开始，然后是最匹配的主方法，接着是 after 方法， after 方法是最匹配的最后才调用。因此，如果我们像下面这样为父类speaker 定义before 或者 after 方法， ~~~ (defmethod speak :before ((s speaker) string) (princ "I think ")) ~~~ 这些方法会在夹心饼干的中间被调用： ~~~ > (speak (make-instance 'intellectual) "life is not what it used to be") Perhaps I think life is not what it used to be in some sense NIL ~~~ 无论被调用的是什么before 或 after 方法，generic 函数的返回值总是最匹配的主方法的值，在本例中，返回的值就是format 返回的nil 。 如果有around 方法的话，这个论断就要稍加改动。倘若一个对象的继承树中有一个类具有around 方法， 或者更准确地说，如果有around 方法特化了generic 函数的某些参数，那么这个around 方法会被首先调用， 然后其余的这些方法是否会被运行将取决于这个around 方法。在我们的精简版实现中，一个around 方法或者主方法能够通过运行一个函数，调用下一个方法：我们以前定义的名为call-next 的函数在 **CLOS** 中叫做call-next-method。与我们的next-p 相对应， **CLOS** 中同样也有一个叫next-method-p 的函数。有了around 方法，我们可以定义speaker 的另一个子类，这个子类说话会更慎重一些： ~~~ (defclass courtier (speaker) nil) (defmethod speak :around ((c courtier) string) (format t "Does the King believe that ~A? " string) (if (eq (read) 'yes) (if (next-method-p) (call-next-method)) (format t "Indeed, it is a preposterous idea.~%")) 'bow) ~~~ 当speak 的第一个参数是个courtier 实例时，这个around 方法会帮弄臣把话说得更四平八稳： ~~~ > (speak (make-instance 'courtier) "kings will last") Does the King believe that kings will last? yes I think kings will last BOW > (speak (make-instance 'courtier) "the world is round") Does the King believe that the world is round? no Indeed, it is a preposterous idea. BOW ~~~ 可以注意到，和 before 和 after 方法不同，around 方法的返回值被作为 generic 函数的返回值返回了。 一般来说，方法调用的顺序如下所列，这些内容是从第 25.2 节里摘抄下来的： 1. 倘若有的话，先是最匹配的 around 方法 2. 否则的话，依次是： (a) 所有的before 方法,从最匹配的到最不匹配的。 (b) 最匹配的主方法(这是我们以前会调用的)。 (c) 所有的 after 方法,从最不匹配的到最匹配的。 这种组合方法的方式被称为标准的方法组合。和我们之前的简装版一样，这里一样有办法以其它的方式组合方法。比如说，让一个 generic 函数返回所有可用的主方法返回值之和。 在我们的程序里，我们通过调用 defcomb 来指定组合方法的方式。缺省情况下，方法是以上面列出的规则调用的，不过如果我们像这样写的话： ~~~ (defcomb price #'+) ~~~ 就能让 price 这个函数返回所有适用主方法的和。 在 **CLOS** 中这被称为操作符方法组合。在我们的程序里，这个方法组合的效果就好像对这样一个Lisp 表达式求值：该表达式中的第一个元素是某个操作符，传给操作符的参数是对所有适用主方法的调用，而调用的顺序是按照匹配程度从高到低的。如果我们定义 price 的 generic 函数，让它使用+ 来组合返回值，同时假设 price 没有适用的 around 方法，那么调用 price 的效果就如同它是用下面的语句定义的： ~~~ (defun price (&rest args) (+ (apply ⟨most specific primary method⟩ args) . . . (apply ⟨most specific primary method⟩ args))) ~~~ 如果有适用的around 方法的话，它们有更高的优先级，这和标准方法组合是一样的。在操作符方法组合里， around 方法仍然可以通过 call-next-method 来调用下一个方法。不过在这里主方法就不能调用 call-next-method 了。（这一点是和精简版的不同之处，在精简版里，我们是允许主方法调用 call-next 的。） 在 **CLOS** 里，我们可以对一个 generic 函数指定它所使用的方法组合类型，传给 defgeneric 的缺省参数 ： method-combination 就是用来实现这一功能的。如下所示： ~~~ (defgeneric price (x) (:method-combination +)) ~~~ 现在这个price 方法就会用+ 这种方法组合了。如果我们定义几种有价格的类， ~~~ (defclass jacket nil nil) (defclass trousers nil nil) (defclass suit (jacet trousers) nil) (defmethod price + ((jk jacket)) 350) (defmethod price + ((tr trousers)) 200) ~~~ 那么当我们要知道一个 suit 实例的价格时，就会得到各个适用的 price 方法之和： ~~~ > (price (make-instance 'suit)) 550 ~~~ 下面所列的符号可以被用作 defmethod 的第二个参数，同时它们也可以用在 defgeneric 的：method-combination 选项上： ~~~ + and append list max min nconc or progn ~~~ 用 define-method-combination ，你可以自己定义其它的方法组合方式：参见 CLTL2，第830 页。 你一旦定义了一个 generic 函数要使用的方法组合方式，那么所有这个函数对应的方法就必须使用和你所指定的方式相同类型的方法组合。如果我们试图把其它操作符（或 :before 和 :after） 用作 price 的 defmethod 方法里的第二个参数，就会导致错误。倘若我们一定要改变 price 的方法组合方式的话，我们只能通过 fmakunbound 来删除整个 price 的 generic 函数. ### 25.6 **CLOS** 与 Lisp **CLOS** 为嵌入式语言树立了一个好榜样。这种编程方式有两大好处： 1. 嵌入式语言在概念上可以很好地与它们所处的领域很好融合在一起，因此在嵌入式语言中，我们得以继续以原来的术语来思考程序代码。 2. 嵌入式语言可以是非常强大的，因为它们能利用被作为基础的那门语言已有的所有功能。 **CLOS** 把这两点都占全了。它和 Lisp 集成得天衣无缝，同时灵活运用了 Lisp 中已有的抽象机制。事实上， 我们可以透 过 **CLOS** 可以看出 Lisp 的神韵。就像物件上虽然蒙着薄布，其形状仍然清晰可辨一样。 我们与 **CLOS** 沟通交互的渠道是一层宏，这并不是巧合。宏是用来转换程序的，而从本质上说，**CLOS** 就是一个程序，它把用面向对象的抽象形式编写而成的程序翻译转换成为 用Lisp 的抽象形式构造而成的程序。 正如本章前两节所展示的，由于面向对象编程的抽象形式能被如此清晰简洁地实现成基于 Lisp 的抽象形式，我们几乎可以把前者说成后者的一个特殊形式了。我们能毫不费力地把面向对象编程里的对象实现成 Lisp 对象，把对象的方法实现为词法闭包。利用这种同构性，我们得以用区区几行代码实现了一个面向对象编程的初步框架，用寥寥几页篇幅就容下了一个 **CLOS** 的简单实现。 虽然 **CLOS** 和我们的简单实现相比，其规模要大很多，功能也强了很多，但是它还没有大到能把其根基伪装成一门嵌入式语言。以defmethod 为例。虽然 CLTL2 没有明确地提出，但是 **CLOS** 的方法具有词法闭包的所有能力。如果我们在某个变量的作用域内定义几个方法： ~~~ (let ((transactions 0)) (defmethod withdraw ((a account) amt) (incf transactions) (decf (balance a) amt)) (defmethod deposit ((a account) amt) (incf transactions) (incf (balance a) amt)) (defun transactions () transactions)) ~~~ 那么在运行时，它们就会像闭包一样，共享这个变量。这些方法之所以会这样是因为，在语法带来的表象之下，它们就是闭包。如果观察一下 defmethod 的展开式，可以发现它的程序体被原封不动地保存在了井号–引号里的 lambda 表达式中。 第 7.6 节中曾提到，思忖宏的运行方式比考虑它们是什么意思要容易些。与之相似，理解 **CLOS** 的法门在于弄清 **CLOS** 是如何映射到 Lisp 基本的抽象形式中的。 ### 25.7 何时用对象 面向对象的风格有几个明显的好处。不同的程序希望在不同程度上从中受益。这些情况有两种趋势。一种情况，有的程序，比如说一些模拟程序，如果用面向对象编程的抽象形式来表达它们是最为自然的。而另外一种程序之所以选用面向对象的风格来编写，主要原因是希望提高程序的可扩展性。 可扩展性的确是面向对象编程带来的巨大好处之一。程序不再被写成囫囵的一团，而是分成小块，每个部分都以自己的功用命名。所以如果事后有其他人需要修改这个程序的话，他就能很方便地找到需要改动的那部分代码。 倘若我们希望 ob 类型的对象显示在屏幕上的样子有所改变的话，我们可以修改 ob 类的 display 方法。要是我们希望创建一个类，让这个类的实例与 ob 的实例大体一样，只在某些方面有些差异，那么我们可以从 ob 派生一个子类，在这个子类里面，我们仅仅修改我们想要的那些属性，其它所有的东西都会从 ob 类缺省地继承得到。 如果我们只是想让某一个 ob 对象的行为和其它 ob 对象有些不一样，可以就新建一个 ob 对象，然后直接修改这个对象的属性。 倘若要修改的程序原来写得很认真，那么我们就可以在完成上述各种修改的同时，甚至不用看程序中其它的代码一眼。从这个角度上来说，以面向对象的思想写出的程序就像被组织成表格一样：只要找到对应的单元格，我们就可以迅速安全地修改程序。 对于扩展性来说，它从面向对象风格得到的东西是最少的。实际上，为了要实现可扩展性，基本上不需要什么外部的支持，所以，一个可扩展的程序完全可以不写成面向对象的。如果要说前面的几章说明了什么道理的话，那就是 Lisp 程序是可以不用写为囫囵一团的。 Lisp 给出了全系列的实现扩展性的方案。比如说， 你可以把程序实现成一张表格：即一个由保存在数组里的闭包构成的程序。 假如你想要的就是可扩展性，那么你大可不必在 "面向对象" 编程和 "传统" 形式的编程中两者取其一。你常常可以不依赖面向对象的技术，就能赋予一个 Lisp 程序它所需要的可扩展性，不多也不少。属于类的slot 是一种全局变量。在本可以用使用参数的地方，却要用全局变量，我们知道这样做有些不合适。和这种情形有几分相似，如果本来可以用原始的Lisp 就轻松完成的程序，偏要写成一堆类和实例，这样做或许也不是很妥当。有了 **CLOS** ，Common Lisp 已经成为了被广泛使用的最强大的面向对象语言。具有讽刺意味的是，对 Common Lisp 来说，面向对象编程是它最无足轻重的特性。 备注： 【注1】译者注：在原文中，本节的标题是 "PlusçaChange" 。它源自法国谚语 "plusçachange，plusc'estlamêmechose" ，字面意思是：变化得越多，越是原来的事物。平时使用中常常略作前半句。 【注2】译者注：指和常用的工作站相比，功能较有限的计算机终端。

## 第 24 章 Prolog 本章将介绍如何编写嵌入式的 Prolog 解释器。第 19 章中已经展示了编写数据库查询语句编译器的方法，这里我们再加入一个新的元素：规则。有了规则，就可以根据已有的知识通过推理得到新知。一组规则定义了表明事实之间相互蕴含关系的一棵树。由于这棵树可能包含无限多的事实，所以我们必须使用非确定性的搜索。 Prolog 是嵌入式语言的一个极好的例子。它融合了三个元素：模式匹配，非确定性，规则。其中，前两个元素在第 18 章和第 22 章曾分别介绍过。把 Prolog 建立在模式匹配和非确定性选择操作的基础之上，我们可以得到一个真正的，多层的，自底向上的系统。图 (24.1) 展示了有关几个抽象层的结构。 ~~~ ![enter image description here][1] ~~~ 本章的第二个目标是学习Prolog。对于经验丰富的程序员来说，简要地说明一下其实现方式可能会更有助于讲解这门语言。而用Lisp 实现Prolog 非常有趣，因为在这过程中能够发掘出这两者间的共同点。 ### 24.1 概念 第19章介绍了如何写一个能接受复杂查询语句的数据库系统，这个系统能自动生成所有满足查询条件的绑定。在下例中，(调用 clear-db 之后)，我们声明两个事实，然后对数据库进行查询： ~~~ > (fact painter reynolds) (REYNOLDS) > (fact painter gainsborough) (GAINSBOROUGH) > (with-answer (painter ?x) (print ?x)) GAINSBOROUGH REYNOLDS NIL ~~~ 从概念上说，Prolog 是一个 "附有规则的数据库程序"。它不仅仅能够直接从数据库中查找匹配的数据来满足查询语句，还能够从已知的事实(数据) 中推导出匹配的数据。例如，若有如下的规则： ~~~ If (hungry ?x) and (smells-of ?x turpentine) en (painter ?x) ~~~ 则，只要数据库中存在 (hungry raoul) 和 (smells-of raoul turpentine) 这两个事实，那么 ?x = raoul 就能满足查询语句 (painter ?x)，即使数据库中没有 (painter raoul) 这个事实。 在 Prolog 中，规则的 "if" 部分被称作 body，"then" 部分被称作 head。(在逻辑中，它们分别叫做前提 (an-tecedent) 和推论 (consequent)，不过用不同的名字也好，能强调 Prolog 的推导不同于逻辑的推导)。在我们试图生成查询的绑定时，程序首先检查规则的 head，如果 head 能满足查询，那么程序会做出响应，为 body 建立各种绑定。根据定义，如果绑定满足 body，那么它也满足 head。 在规则的 body 中用到的各种事实可能会转而由其他规则中推演得出。例如： ~~~ If (gaunt ?x) or (eats-ravenously ?x) en (hungry ?x) ~~~ 规则也可以是递归的，例如： ~~~ If (surname ?f ?n) and (father ?f ?c) en (surname ?c ?n) ~~~ 如果 Prolog 能在种种规则中找到一条通往已知事实的路径，它便会为该查询建立各种绑定。因而，它实质上是一个搜索引擎：它遍历由各种规则形成的逻辑蕴含树，寻找一条通往事实的成功之路。 虽然规则和事实听上去像两回事，其实它们在概念上是可以互换的 规则可以被看作虚拟事实。如果我们希望我们的数据库能够反映出 "凶猛的大型动物是稀有的" 这个发现，我们可以寻找所有的 x ，令 x 满足 (species)，(big) 和 (fierce) 这些事实，找到的话就加上一个新的事实 (rare )。如果定义下面的规则： ~~~ If (species ?x)and (big ?x) and (fierce ?x) en (rare ?x) ~~~ 就会得到相同的效果，而无需在数据库中加入所有的 (rare x) 事实。我们甚至可以定义能推出无穷个事实的规则。因此，在回应查询的时候，我们通过使用规则，用额外的数据处理作为代价，缩小了数据库的规模。 另一方面，事实则是规则的一种退化形式。任一事实 F 的效用，都可以用一个 body 恒为真的规则来达到，如下： ~~~ If true en F ~~~ 为了简化实现,我们将利用这个性质,并用body less rules 来表达事实。 ### 24.2 解释器 第 18.4 节展示了两种定义 if-match 的方式，前一种简洁但效率低下，后来者由于在编译期完成了大量工作，因而速度有很大的提高。这里，我们将沿用这个策略。为了便于引出相关的几个话题，我们先从一个简单的解释器开始，然后再介绍如何把同一程序写得更加高效。 [示例代码 24.2]–24.4 包含了一个简单的 Prolog 解释器。它能接受与第 19.3 节查询解释器相同的输入，但使用的是规则而非数据库来生成绑定。查询解释器是通过宏 with-answer 来调用的，我们的 Prolog 解释器的接口也打算采用一个类似的宏，称其为 with-inference 。犹如 with-answer ，with-inference 的输入是一个查询语句和一组 Lisp 表达式。查询语句中的变量是以问号开头的符号，例如： ~~~ (with-inference (painter ?x) (print ?x)) ~~~ with-inference 的一个调用会展开成一段代码，该代码则将Lisp 表达式应用于生成的绑定并求值。比如上面那段代码，会把所有能导出 (painter ) 的x 打印出来。 这章的许多概念，比如 binding 的含义，在第 18.4 节已经说明。 * * * **[示例代码 24.2]** Toplevel 宏 ~~~ (defmacro with-inference (query &body body) '(progn (setq *paths* nil) (=bind (binds) (prove-query ',(rep_ query) nil) (let ,(mapcar #'(lambda (v) '(,v (fullbind ',v binds))) (vars-in query #'atom)) ，@body (fail))))) (defun rep_ (x) (if (atom x) (if (eq x '_) (gensym "?") x) (cons (rep_ (car x)) (rep_ (cdr x))))) (defun fullbind (x b) (cond ((varsym? x) (aif2 (binding x b) (fullbind it b) (gensym))) ((atom x) x) (t (cons (fullbind (car x) b) (fullbind (cdr x) b))))) (defun varsym? (x) (and (symbolp x) (eq (char (symbol-name x) 0) #\?))) ~~~ * * * [示例代码 24.2] 给出了 with-inference 的定义，及其生成绑定所需的函数。with-answer 和 with-inference 有个显著的区别：前者只是简单地收集所有的有效绑定，而后者则进行非确定性的搜索。我们可以在 with-inference 的定义里注意到这一点：它没有展开成循环，而是展开成了一段能返回一组绑定的代码，紧接着是一个 fail 用来重启下个搜索。这无形中给我们带来了迭代结构。比如： ~~~ > (choose-bind x '(0 1 2 3 4 5 6 7 8 9) (princ x) (if (= x 6) x (fail))) 0123456 6 ~~~ 函数 fullbind 则点出了 with-answer 和 with-inference 的又一不同之处，沿着规则往回跟踪，我们可以建立一系列绑定 变量的绑定是其他变量组成的列表。要使用该查询语句的结果，我们需要一个递归函数来帮我们找到相应的绑定。这就是fullbind 的目的，例如： ~~~ > (setq b '((?x . (?y . ?z)) (?y . foo) (?z . nil))) ((?X ?Y . ?Z) (?Y . FOO) (?Z)) > (values (binding '?x b)) (?Y . ?Z) > (fullbind '?x b) (FOO) ~~~ 查询语句的绑定的是由 with-inference 展开式中的 prove-query 生成的。[示例代码 24.3] 给出了这个函数的定义及其组成部分。这段代码和第 19.3 节中描述的查询解释器结构相同。两者都用相同的函数用于匹配，只不过查询解释器用mapping 和迭代，而 Prolog 解释器则用等价的 choose。 不过，使用非确定性搜索替代迭代的方式确实让解释否定的查询语句变得更难了。例如下面的查询语句： * * * [示例代码 24.3]： 查询语句的解释 ~~~ (not (painter ?x)) (=defun prove-query (expr binds) (case (car expr) (and (prove-and (cdr expr) binds)) (or (prove-or (cdr expr) binds)) (not (prove-not (cadr expr) binds)) (t (prove-simple expr binds)))) (=defun prove-and (clauses binds) (if (null clauses) (=values binds) (=bind (binds) (prove-query (car clauses) binds) (prove-and (cdr clauses) binds)))) (=defun prove-or (clauses binds) (choose-bind c clauses (prove-query c binds))) (=defun prove-not (expr binds) (let ((save-paths *paths*)) (setq *paths* nil) (choose (=bind (b) (prove-query expr binds) (setq *paths* save-paths) (fail)) (progn (setq *paths* save-paths) (=values binds))))) (=defun prove-simple (query binds) (choose-bind r *rlist* (implies r query binds))) ~~~ * * * 查询解释器只需要为 (painter ?x) 建立绑定，如果找到任意的绑定则返回 nil 。而使用非确定性搜索的话，就必须更加小心，因为我们不希望 (painter ?x) 在 not 的作用域之外 fail，同时(如果 (painter ?x) 为真) 我们也不希望保留其剩下还未探索的路径。所以，(painter ?x) 的判断被应用在一个临时的空的搜索路径的环境中。当判断结束时，会恢复原先的路径。 它们之间的另一区别在于对简单模板的解释 类似于 (painter ?x) 的仅仅由一个谓词和几个参数组成的表达式。当查询解释器对简单模板生成绑定时，它调用 lookup (第 19.3 节)。在 Prolog 解释器中，我们必须找到所有规则所能推导出的绑定，因此 lookup 已不适用。 [示例代码 24.4] 中给出了定义和使用规则的代码。规则被放在全局列表 *rlist* 中。每个规则由 body 和 head 所组成的点对(dottedpair) 表达。当一个规则被定义后，任一下划线会被替换为一个唯一的变量。 <- 的定义遵循了三个惯例，一般来说，编写这类程序时通常都会采纳这些习惯做法： 1. 加入新规则的时候，应当把规则放到列表末尾，而不是最前面，这样应用规则时的顺序就和定义规则的顺序一致了。 2. 在表示规则的时候，要把head 放在前面，因为程序查看规则的顺序就是如此。 3. 如果 body 里有多个表达式的话，它们事实上被放在了看不见的 and 里面。 在 <- 的展开式最外层调用了 length ，其目的是为了避免在 toplevel 调用 <- 时，打印出巨大的列表。 规则的语法如 [示例代码 24.5] 所示。规则的 head 必须是一种事实的模式：一个列表，列表的每个元素都由一个谓 ~~~ (defvar *rlist* nil) (defmacro <- (con &rest ant) (let ((ant (if (= (length ant) 1) (car ant) '(and ,@ant)))) '(length (conc1f *rlist* (rep_ (cons ',ant ',con)))))) (=defun implies (r query binds) (let ((r2 (change-vars r))) (aif2 (match query (cdr r2) binds) (prove-query (car r2) it) (fail)))) (defun change-vars (r) (sublis (mapcar #'(lambda (v) (cons v (symb '? (gensym)))) (vars-in r #'atom)) r)) ~~~ ## [示例代码 24.4]： 包含规则的代码 ~~~ ⟨rule⟩ : (<- ⟨sentence⟩ ⟨query⟩) ⟨query⟩ : (not ⟨query⟩) : (and ⟨query⟩*) : (or ⟨query⟩*) : ⟨sentence⟩ ⟨sentence⟩ : (⟨symbol⟩ ⟨argument⟩*) ⟨argument⟩ : ⟨variable⟩ : ⟨symbol⟩ : ⟨number⟩ ⟨variable⟩ : ?⟨symbol⟩ ~~~ [示例代码 24.5]： 规则的语法 * * * 词，跟着任意数量的参数。body 可以是任何查询语句，只要第19章的查询解释器能读懂它就行。下面是本章前面曾用过的一个规则： ~~~ (<- (painter ?x) (and (hungry ?x) (smells-of ?x turpentine))) ~~~ 或直接 ~~~ (<- (painter ?x) (hungry ?x) (smells-of ?x turpentine)) ~~~ 和查询解释器一样，类似turpentine 的参数不会被求值，所以它们没有必要被quoted。 当我们让prove-simple 为某个查询生成绑定时，它的非确定地选择一条规则，并把该规则和查询一同送给implies。下一个函数则试图把查询和规则的head 匹配起来。一旦匹配成功，implies 将会调用prove-query ，让它帮助为body 建立绑定。用这种方法，我们递归搜索逻辑蕴含树。 change-vars 函数把规则中所有的变量换成新生成的。如果在某个规则里使用了?x ，那么这个?x 是和其它规则里面的?x 是没有关系的。为了避免现有绑定之间发生冲突，每应用一条规则，都会调用change-vars 。 为了给用户提供方便，这里可以把_ (下划线) 用作规则里的通配符变量。在定义规则的时候，会调用函数rep_ ，它把每个下划线都替换成真正的变量。下划线也可以用在传给with-inference 的查询里面。 ### 24.3 规则 本节将介绍如何为我们的Prolog 编制规则。先以第24.1 节中的两条规则为例： ~~~ (<- (painter ?x) (hungry ?x) (smells-of ?x turpentine)) (<- (hungry ?x) (or (gaunt ?x) (eats-ravenously ?x))) ~~~ 倘若我们同样也断言了(assert) 下面几个事实： ~~~ (<- (gaunt raoul)) (<- (smells-of raoul turpentine)) (<- (painter rubens)) ~~~ 它们将根据其定义的顺序，来决定要生成的绑定： ~~~ > (with-inference (painter ?x) (print ?x)) RAOUL RUBENS @ ~~~ with-inference 宏和with-answer 一样，对变量绑定有着相同限制(见第19.1节)。 我们能写出这样一种规则，它意味着：对所有可能的绑定，都可以令给定形式的事实为真。这并非不可能。 比如说，如果有变量出现在规则的head 里，但却在body 里销声匿迹。这种规则就能满足要求。下面的规则 ~~~ (<- (eats ?x ?f) (glutton ?x)) ~~~ 说道：如果?x 是个吃货(glutton)，那么?x 就来者不据，照单全收。因为?f 在body 里没有出现，所以，只消为?x 设立一个绑定，就能证明任意形如 (eats ?x ) 的事实。如果我们用一个字面值作为eats 的第二个参数，进行查询， ~~~ > (<- (glutton hubert)) 7 > (with-inference (eats ?x spinach) (print ?x)) HUBERT @ ~~~ 那么任何字面值都能满足要求。如果把一个变量作为第二个参数的话： ~~~ > (with-inference (eats ?x ?y) (print (list ?x ?y))) (HUBERT #:G229) @ ~~~ 我们会得到一个gensym。在查询中把gensym 作为变量的绑定返回，这表示任意值都能令事实为真。在编程序的时候，可以显式地利用这一惯例： ~~~ > (progn (<- (eats monster bad-children)) (<- (eats warhol candy))) 9 > (with-inference (eats ?x ?y) (format t "~A eats ~A.~%" ?x (if (gensym? ?y) 'everything ?y))) HUBERT eats EVERYTHING. MONSTER eats BAD-CHILDREN. WARHOL eats CANDY. @ ~~~ 最后，如果我们想要指定一个特定形式的事实对任意参数都为真，那么可以令其body 为无参数的合取式。 (and) 表达式和永真式的事实，其行为表现是一样的。由于在<- 宏中([示例代码 24.4])，body 的缺省设置就是 (and)，所以对于这种规则，我们可以直接略去其body ： ~~~ > (<- (identical ?x ?x)) 10 > (with-inference (identical a ?x) (print ?x)) A @ ~~~ 若是读者已经粗通Prolog，就可以看出[示例代码 24.6] 展示了把Prolog 语法转换到我们程序语法的过程。照老习惯，第一个Prolog 程序往往是append ，它可以写成[示例代码 24.6] 结尾的那样。在一次append 中，两个较短的列表被并成一个更长的列表。Lisp 的函数append 把两个短列表作为参数，而将长列表当成返回值。Prolog 的append 更通用一些。[示例代码 24.6] 中的两条规则定义了一个程序，只要传入任意两个相关的列表，这个程序就能找到第三个。 我们的语法和传统的Prolog 语法间有如下几点区别： 1. 使用以问号开头的符号，而非大写字母来表示变量。因为Common Lisp 缺省是不区分大小写的， 所以用大写字母的话可能会得不偿失。 1. [ ]变成了nil 。 2. 形如 [x | y] 的表达式成了(x . y)。 3. 形如 [x，y，...] 的表达式成了(x y...)。 4. 断言被挪到了括弧里面，而且用来分隔参数的逗号也被去掉了： ( ，，...) 成了 ( ...)。 于是乎，Prolog 对append 的定义： ~~~ append([ ], Xs, Xs). append([X | Xs], Ys, [X | Zs]) <- append(Xs, Ys, Zs). ~~~ 就成了下面的模样： ~~~ (<- (append nil ?xs ?xs)) (<- (append (?x . ?xs) ?ys (?x . ?zs)) (append ?xs ?ys ?zs)) ~~~ [示例代码 24.6]： 和Prolog 语法的对应关系 ~~~ > (with-inference (append ?x (c d) (a b c d)) (format t "Left: ~A~%" ?x)) Left: (A B) @ > (with-inference (append (a b) ?x (a b c d)) (format t "Right: ~A~%" ?x)) Right: (C D) @ > (with-inference (append (a b) (c d) ?x) (format t "Whole: ~A~%" ?x)) Whole: (ABCD) @ ~~~ 不仅如此，如果给出了最后一个列表，它还能找出前两个列表所有可能的组合： ~~~ > (with-inference (append ?x ?y (a b c)) (format t "Left: ~A Right: ~A~%" ?x ?y)) Left: NIL Right: (A B C) Left: (A) Right: (B C) Left: (A B) Right: (C) Left: (A B C) Right: NIL @ ~~~ append 这个例子揭示出了Prolog 和其它语言之间的天差地别。一组Prolog 规则不一定非要推出某个特定的值。这些规则也可以给出一些约束(constraints)，而这些约束和由程序其他部分生成的约束一同，将能得出一个特定的值。举例来说，如果这样定义member ： ~~~ (<- (member ?x (?x . ?rest))) (<- (member ?x (_ . ?rest)) (member ?x ?rest)) ~~~ 就能用它判断列表的成员关系，和Lisp 的函数member 的用法一模一样： ~~~ > (with-inference (member a (a b)) (print t)) T @ ~~~ 不过，我们也可以用它新建一个成员关系的约束，这个约束和其他约束一起，同样可以得出一个特定的列表。如果我们手里还有个谓词叫cara ~~~ (<- (cara (a _))) ~~~ 任意一个有两个元素的列表，只要其car 为a ，那么这个事实就为真。这样，有了这个谓词和member ，就有了充足的约束条件，可以让Prolog 为我们想出一个确定的答案了： ~~~ > (with-inference (and (cara ?lst) (member b ?lst)) (print ?lst)) (A B) @ ~~~ 例子很简单，但是其中的道理在编写更大规模的程序时也一样适用。无论何时，只要我们想通过把部分结果组合到一起的方式来编写程序，那么就能用上Prolog。事实上借助这种方式可以表达很多类型的问题： 比如说，[示例代码 24.14] 就展示了一个排序算法，这个排序算法是由一组对计算结果的约束来表示的。 ### 24.4 对于非确定性的需求 第22 章解释了确定性和非确定性搜索的区别所在。使用确定性搜索的程序能接受一个查询，并生成所有满足这个查询的结果。而用非确定性搜索的程序则会借助choose，每次生成一个结果，如果用户需要更多的结果，那么它会调用fail ，来重新启动这个搜索过程。 如果我们手中的规则得出的都是有限大小的绑定集合，而且我们希望一次性的得到所有这些绑定，那么就没有理由用非确定性搜索。倘若我们的查询会产生无穷多的绑定，而我们要的只是其中的一个有限子集，那么这两种搜索策略的区别就一目了然了。比如说，下面的规则 ~~~ (<- (all-elements ?x nil)) (<- (all-elements ?x (?x . ?rest)) (all-elements ?x ?rest)) ~~~ 蕴含所有形如 (all-elements x y) 的事实，的每一个成员都等于 。不用回溯的话，我们有能力处理类似下面的查询： ~~~ (all-elements a (a a a)) (all-elements a (a a b)) (all-elements ?x (a a a)) ~~~ 然而，有无数多的?x 可以满足 (all-elements a ?x) 这个查询，比如：nil、(a)、(a a)，等等。要是想用迭代的方式为这个查询生成答案，那么这个迭代就会永不休止，一直运行下去。就算我们弱水三千只取一瓢饮，在这无穷多的答案中仅仅要一个，如果算法的实现在走到下一个Lisp 表达式之前，必须为查询准备好所有的绑定，那么我们永远等不到那一天，更不用说得到答案了。 这就是为什么with-inference 把绑定的产生过程和其body 的求值过程交错进行的原因。由于查询可能会对应无穷多的答案，所以唯一的办法只能是每次产生一个答案，并通过重启前被暂停的搜索来取得新的答案。因为我们的程序使用了choose 和fail ，所以它能够解决下面的问题： ~~~ > (block nil (with-inference (all-elements a ?x) (if (= (length ?x) 3) (return ?x) (princ ?x)))) NIL(A)(A A) (A A A) ~~~ 和所有的Prolog 实现一样，我们也是借助带回溯的深度优先搜索来模拟非确定性的。从理论上而言，"逻辑程序" 是由真正的非确定性驱动的。而实际上，各家Prolog 实现却常常用的是深度优先搜索。这个选择非但没有造成不便，相反，深度优先版的非确定性是标准的Prolog 程序赖以正常工作的基础。在使用真实非确定性的世界里，下面的查询 ~~~ (and (all-elements a ?x) (length ?x 3)) ~~~ 是有答案的，但是在得到这个答案之前，你必须先等到海枯石烂。 Prolog 使用深度优先搜索实现非确定性，不仅如此，它使用的深度优先还和第 22.3 节中定义的版本等价。正如我们在那里提到的，这个实现是不能保证终止的。所以 Prolog 程序员必须采取专门的措施，避免在搜索空间里面产生环。举例来说，如果我们以相反的顺序定义member ~~~ (<- (member ?x (_ . ?rest)) (member ?x ?rest)) (<- (member ?x (?x . ?rest))) ~~~ 那么照道理来说，其意义应该保持不变，但是作为Prolog 程序的话，效果就完全不同了。如果使用member 原来的定义，那么查询 (member 'a ?x)，会得到一系列连绵不绝，无穷多的答案。但是如果把定义的顺序反过来，则会产生一个无穷递归，一个答案都得不到。 ### 24.5 新的实现 在这一节，我们会故友重逢，碰到一个熟悉模式的另一实例。在第18.4 节，在编完if-match 的最初版本之后，我们发现其实可以把它实现得更快。通过利用编译期的已知信息，我们本可以写一个新的版本，让它在运行期做更少的事情。后来，在第19章，我们经历了同样的问题，不过这一次程序的规模更大。我们把查询解释器换成了一个与之等价，但更高效的版本。历史将会在我们的Prolog 解释器上重演。 [示例代码 24.7]，24.8，24.10 一起以另一种方式定义了Prolog。宏with-inference 以前只是Prolog 解释器的接口。 它现在成了程序的主要的组成部分。新程序的结构和原来基本一致，不过在[示例代码 24.8] 中定义的函数里面，只有prove 是在运行期调用的。其他函数则由with-inference 调用，被用来生成其展开式。 [示例代码 24.7] 中是with-inference 的新定义。和if-match 以及 with-answer 中一样，模式匹配变量在开始的时候会被绑定到gensym 上，表示它们还没有被匹配过程赋予真正的值。因而，被match 和fullbind 用来辨别变量的函数varsym? ，就需要修改一下，转而检查是否是gensym。 with-inference 调用gen-query ([示例代码 24.8]) 的目的是为了生成一部分代码，这些代码将为查询建立绑定。 gen-query 要做的的一件事是检查它的第一个参数是不是那种以and 或者or 开头的复杂查询。这个过程会递归地进行，直至遇到简单查询，这些简单查询会被展开成对prove 的调用。在原来的实现中，这种逻辑结构是在运行期完成解析的。以前，每次使用规则时，都必须重新分析body 中的复杂查询。显然，这毫无必要。因为规则和查询的逻辑结构是事先已知的。针对这个问题，新版的实现把复杂表达式的解析工作移到了编译期。 和原来的实现一样，with-inference 表达式展开出的代码会先进行一次查询，查询中的模式变量所绑定到的值是由规则一一设定的，然后再迭代执行Lisp 代码。with-inference 的展开式以一个fail 作结，后者会重启之前保存的状态。 [示例代码 24.8] 中其他函数会为复杂查询生成对应的展开式 即由诸如and、or 和not 的操作符结合起来的查询。倘若有如下的查询 ~~~ (and (big ?x) (red ?x)) ~~~ 并且，我们希望只有那些能同时prove 两个合取式的?x ，才被带入Lisp 代码求值。因此，为了生成and 的展开式，我们把第二个合取式的展开式嵌入到第一个合取式的展开式中。要是 (big ?x) 成功了，就继续尝试 (red ?x)，如果后者也成功的话，则对这个Lisp 表达式进行求值。如此，整个表达式展开后如[示例代码 24.9] 所示。 ~~~ (defmacro with-inference (query &rest body) (let ((vars (vars-in query #'simple?)) (gb (gensym))) '(with-gensyms ,vars (setq *paths* nil) (=bind (,gb) ,(gen-query (rep_ query)) (let ,(mapcar #'(lambda (v) '(,v (fullbind ,v ,gb))) vars) ,@body) (fail))))) (defun varsym? (x) (and (symbolp x) (not (symbol-package x)))) ~~~ [示例代码 24.7]： 新的toplevel 宏 and 意味着嵌入；而or 则意味着choose。有下列查询 ~~~ (or (big ?x) (red ?x)) ~~~ 两个子查询，如果其中任意一个能建立?x 的绑定，我们将希望Lisp 表达式使用这些?x 来进行求值。 函数gen-or 会展开成choose ，后者会在诸参数的gen-query 中选择一个。至于not ，gen-not 基本上和prove-not 同出一辙(见[示例代码 24.3])。 [示例代码 24.10] 中是定义规则的代码。规则被直接转换成Lisp 代码，而后者是由 rule-fn 生成的。因为现在<- 把规则展开成了Lisp 代码，所以如果把一个写满了规则定义的文件编译了的话，就会让这些规则变成编译过的函数。 当一个rule-function 收到一个模式时，它会试图把自己所表示规则的head 与之匹配。如果匹配成功，这个rule-function 就会试图为其body 设立绑定。这个过程和with-inference 的功能基本一致，而且，事实上rule-fn 会在结束的时候调用gen-query 。rule-function 最终会返回一些绑定，它们是为规则的head 中出现的变量而设立的。 ### 24.6 增添Prolog 特性 233 ~~~ (defun gen-query (expr &optional binds) (case (car expr) (and (gen-and (cdr expr) binds)) (or (gen-or (cdr expr) binds)) (not (gen-not (cadr expr) binds)) (t '(prove (list ',(car expr) ,@(mapcar #'form (cdr expr))) ,binds)))) (defun gen-and (clauses binds) (if (null clauses) '(=values ,binds) (let ((gb (gensym))) '(=bind (,gb) ,(gen-query (car clauses) binds) ,(gen-and (cdr clauses) gb))))) (defun gen-or (clauses binds) '(choose ,@(mapcar #'(lambda (c) (gen-query c binds)) clauses))) (defun gen-not (expr binds) (let ((gpaths (gensym))) '(let ((,gpaths *paths*)) (setq *paths* nil) (choose (=bind (b) ,(gen-query expr binds) (setq *paths* ,gpaths) (fail)) (progn (setq *paths* ,gpaths) (=values ,binds)))))) (=defun prove (query binds) (choose-bind r *rules* (=funcall r query binds))) (defun form (pat) (if (simple? pat) pat '(cons ,(form (car pat)) ,(form (cdr pat))))) ~~~ [示例代码 24.8]： 对查询进行的编译处理 ### 24.6 增添Prolog 特性 现有的代码已足以运行绝大多数的"纯"Prolog 程序。最后一步是再加入一些特性，诸如：减枝(cut)，数学计算，还有I/O。 在Prolog 规则中加入cut，就能对搜索树进行剪枝了。通常，当我们的程序碰到fail 的时候，它会回溯到最后一个选择点。在第22.4 节实现的 choose 中，把历史上的选择点都放到了全局变量*paths*里。调用fail ，会在最新近的一个选择点重新启动搜索过程，而这个选择点就是*paths* 的car。cut 让问题更复杂了。当程序遇到cut 时，它会放弃保存在 *paths* 里的一部分最新选择点，具体说，就是在最后一次调用prove 之后保存的选择点。 其结果就是让规则之间互斥。我们可以用cut 来在Prolog 程序中达到case 语句的效果。举例来说，如果像下面这样定义minimum ： ~~~ (with-inference (and (big ?x) (red ?x)) (print ?x)) expandsinto: (with-gensyms (?x) (setq *paths* nil) (=bind (#:g1) (=bind (#:g2) (prove (list 'big ?x) nil) (=bind (#:g3) (prove (list 'red ?x) #:g2) (=values #:g3))) (let ((?x (fullbind ?x #:g1))) (print ?x)) (fail))) ~~~ [示例代码 24.9]： 合取式的展开 ~~~ (defvar *rules* nil) (defmacro <- (con &rest ant) (let ((ant (if (= (length ant) 1) (car ant) '(and ,@ant)))) '(length (conc1f *rules* ,(rule-fn (rep_ ant) (rep_ con)))))) (defun rule-fn (ant con) (with-gensyms (val win fact binds) '(=lambda (,fact ,binds) (with-gensyms ,(vars-in (list ant con) #'simple?) (multiple-value-bind (,val ,win) (match ,fact (list ',(car con) ,@(mapcar #'form (cdr con))) ,binds) (if ,win ,(gen-query ant val) (fail))))))) ~~~ [示例代码 24.10]： 定义规则的代码 ~~~ (<- (minimum ?x ?y ?x) (lisp (<= ?x ?y))) (<- (minimum ?x ?y ?y) (lisp (> ?x ?y))) ~~~ 它会工作正常，但是比较没有效率。若有下列查询 ~~~ (minimum 1 2 ?x) ~~~ 根据第一条规则，Prolog 将会立即建立?x = 1。倘若是人的话，就会到此为止，但是程序会虚掷光阴，继续从第二条规则那里找寻答案，因为没人告诉它这两条规则是互斥的。平均情况下，这个版本的minimum 会多做50% 的无用功。如果在第一个测试后面加个cut 就能解决这一问题： ~~~ (<- (minimum ?x ?y ?x) (lisp (<= ?x ?y)) (cut)) (<- (minimum ?x ?y ?y)) ~~~ 现在，一旦Prolog 完成了第一条规则，它就会一路掠过剩下的规则，完成查询，而不是继续处理下一条规则。 要让我们的程序支持减枝，简直易如反掌。每次在调用 prove 时，当前*paths* 的状态都会被当作参数传进去。如果程序碰到了 cut，它就把*paths* 设置回上一次当作参数传入的值。[示例代码 24.11] 和24.12 显示了为了支持减枝，必须改动的部分代码。(修改过的代码行后面有分号以示区别。并非所有的改动都是由于减枝而造成的。) 仅仅提高程序效率的cut 叫做greencuts 。minimum 中的cut 就是个greencut。那种会改变程序行为的cut 则被称为redcuts。比如说，如果我们像下面那样定义谓词artist ： ~~~ (<- (artist ?x) (sculptor ?x) (cut)) (<- (artist ?x) (painter ?x)) ~~~ 结果就是：如果有雕塑家，那么查询到此结束。如果一个雕塑家都找不到，那么就把画家认作艺术家： ~~~ > (progn (<- (painter 'klee)) (<- (painter 'soutine))) 4 > (with-inference (artist ?x) (print ?x)) KLEE SOUTINE @ ~~~ 但如果存在雕塑家的话，减枝机制使得推理在处理第一条规则时就会停止： ~~~ > (<- (sculptor 'hepworth)) 5 > (with-inference (artist ?x) (print ?x)) HEPWORTH @ ~~~ 有时，cut 会和Prolog 的fail 操作符一起搭配使用。我们的fail 函数也是如此。把cut 放到规则里，就如同把这条规则变成了单行道：一旦你驶上这条路，你就只能用这条规则，不能回头。把cut-fail 组合加到规则里，则意味着治安堪忧的单行道：只要开上这条路，就只能凶多吉少。not-equal 的实现里就有个典型的例子： ~~~ (<- (not-equal ?x ?x) (cut) (fail)) (<- (not-equal ?x ?y)) ~~~ 这里的第一条规则是为冒牌货设下的陷阱。如果我们试图证明形如 (not-equal 1 1) 的事实，它会先和第一条规则的head 匹配，然后就自取灭亡了。而(not-equal 1 2) 的查询则不会和第一条规则的head 匹配，因此会继续与第二条规则匹配，在这里它会匹配成功： ~~~ > (with-inference (not-equal 'a 'a) (print t)) @ > (with-inference (not-equal '(a a) '(a b)) (print t)) T @ ~~~ [示例代码 24.11] 和24.12 中的代码同样也为我们的程序带来了数学计算、I/O 和Prolog 的is 操作符。[示例代码 24.13] 列出了规则和查询的所有语法。 我们为Lisp 开了个后门，通过这种方式加入了数学计算(及其他功能) 的支持。现在，除了诸如and 和or 的操作符，我们又有了lisp 操作符。这个操作符可以跟任意Lisp 表达式，对表达式求值时，将会用查询产生的变量绑定，作为表达式中变量的值。如果表达式求值的结果是nil ，那么整个lisp 表达式会被视为与 (fail) 等价；否则它就和 (and) 等价。 下面举个应用lisp 操作符的例子。试想一下ordered 的Prolog 实现，只有当列表中元素以升序排列的时候，它才是真： ~~~ (defun rule-fn (ant con) (with-gensyms (val win fact binds paths) ; '(=lambda (,fact ,binds ,paths) ; (with-gensyms ,(vars-in (list ant con) #'simple?) (multiple-value-bind (,val ,win) (match ,fact (list ',(car con) ,@(mapcar #'form (cdr con))) ,binds) (if ,win ,(gen-query ant val paths) ; (fail))))))) (defmacro with-inference (query &rest body) (let ((vars (vars-in query #'simple?)) (gb (gensym))) '(with-gensyms ,vars (setq *paths* nil) (=bind (,gb) ,(gen-query (rep_ query) nil '*paths*) ; (let ,(mapcar #'(lambda (v) '(,v (fullbind ,v ,gb))) vars) ,@body) (fail))))) (defun gen-query (expr binds paths) ; (case (car expr) (and (gen-and (cdr expr) binds paths)) ; (or (gen-or (cdr expr) binds paths)) ; (not (gen-not (cadr expr) binds paths)) ; (lisp (gen-lisp (cadr expr) binds)) ; (is (gen-is (cadr expr) (third expr) binds)) ; (cut '(progn (setq *paths* ,paths) ; (=values ,binds))) ; (t '(prove (list ',(car expr) ,@(mapcar #'form (cdr expr))) ,binds *paths*)))) ; (=defun prove (query binds paths) ; (choose-bind r *rules* (=funcall r query binds paths))) ; ~~~ [示例代码 24.11]： 加入对新操作符的支持 ~~~ (<- (ordered (?x))) (<- (ordered (?x ?y . ?ys)) (lisp (<= ?x ?y)) (ordered (?y . ?ys))) ~~~ 用汉语来表述，就是说，单元素的列表是有序的；如果列表中有两个或更多元素，那么只有当第一个元素小于或等于第二个元素，而且从第二个元素开始的列表也是有序的，那么才能说该列表是有序的。 ~~~ > (with-inference (ordered '(1 2 3)) (print t)) T @ > (with-inference (ordered '(1 3 2)) (defun gen-and (clauses binds paths) ; (if (null clauses) '(=values ,binds) (let ((gb (gensym))) '(=bind (,gb) ,(gen-query (car clauses) binds paths) ; ,(gen-and (cdr clauses) gb paths))))) ; (defun gen-or (clauses binds paths) ; '(choose ,@(mapcar #'(lambda (c) (gen-query c binds paths)) ; clauses))) (defun gen-not (expr binds paths) ; (let ((gpaths (gensym))) '(let ((,gpaths *paths*)) (setq *paths* nil) (choose (=bind (b) ,(gen-query expr binds paths) ; (setq *paths* ,gpaths) (fail)) (progn (setq *paths* ,gpaths) (=values ,binds)))))) (defmacro with-binds (binds expr) '(let ,(mapcar #'(lambda (v) '(,v (fullbind ,v ,binds))) (vars-in expr)) ,expr)) (defun gen-lisp (expr binds) '(if (with-binds ,binds ,expr) (=values ,binds) (fail))) (defun gen-is (expr1 expr2 binds) '(aif2 (match ,expr1 (with-binds ,binds ,expr2) ,binds) (=values it) (fail))) ~~~ [示例代码 24.12]： 加入对新操作符的支持 ~~~ (print t)) ~~~ @ 借助lisp 操作符，我们得以提供典型Prolog 实现具有的一些其他特性。要实现Prolog 的I/O 谓词，可以把Lisp 的I/O 调用放到lisp 表达式里。而Prolog 的assert ，它有个副作用，会顺带着定义一些规则。它可以通过在lisp 表达式里调用<- 宏来实现一样的功能。 is 操作符提供了一种赋值的形式。它有两个参数：一个是匹配模式，一个是个Lisp 表达式。它会试图把模式和表达式的返回结果匹配起来。如果匹配失败，那么程序就会调用fail ；否则它会使用新的绑定继续运行。因而，表达式 (is ?x 1) 的作用就是把?x 设置成1，或者更准确地说，程序会认为?x 应该是1。我们希望能让is 进行计算。比如说，计算阶乘： ~~~ (<- (factorial 0 1)) (<- (factorial ?n ?f) (lisp (> ?n 0)) (is ?n1 (- ?n 1)) (factorial ?n1 ?f1) (is ?f (* ?n ?f1))) ~~~ ⟨rule⟩ ： (<- ⟨sentence⟩ ⟨query⟩) ⟨query⟩ ： (not ⟨query⟩) ： (and ⟨query⟩*) ： (lisp ⟨lisp expression⟩) ： (is ⟨variable⟩ ⟨lisp expression⟩) ： (cut) ： (fail) ： ⟨sentence⟩ ⟨sentence⟩ ： (⟨symbol⟩ ⟨argument⟩*) ⟨argument⟩ ： ⟨variable⟩ ： ⟨lisp expression⟩ ⟨variable⟩ ： ?⟨symbol⟩ [示例代码 24.13]： 规则的新语法 我们构造一个查询，让数字 作为它的首个参数，让一个变量作为第二个参数，用这个办法来使用这个定义： ~~~ > (with-inference (factorial 8 ?x) (print ?x)) 40320 @ ~~~ 注意到，lisp 表达式中用到的变量，以及is 的第二个参数，都必须有已建立的绑定与其对应，这样，表达式才能返回值。所有Prolog 都存在这个限制。比如说，下面的查询： ~~~ (with-inference (factorial ?x 120) ; wrong (print ?x)) ~~~ 就不能和这个factorial 的定义一同工作，因为在求值lisp 表达式的时候，?n 还是个未知数。因此，不是所有的Prolog 程序都和append 一样：它们中有许多都要求某些参数应该是真实的值，比如factorial。 ### 24.7 例子 这一节会展示几个Prolog 例程，介绍如何编写能在我们的Prolog 实现中运行的程序。[示例代码 24.14] 的规则一齐定义了快速排序算法。这些规则蕴含了形如 (quicksort ) 的事实，其中 是一个列表，而 是由前一列表中的相同元素构成的另一个列表，不过其中的元素以增序排列。变量可以出现在第二个参数的位置上： ~~~ > (with-inference (quicksort '(3 2 1) ?x) (print ?x)) (1 2 3) @ ~~~ 这里之所以用I/O 循环来测试我们的Prolog 实现，原因是它同时利用了cut，lisp，以及is 这几个操作符。 代码如[示例代码 24.15] 所示。在试图证明 (echo) 的时候，会不带参数地调用这些规则。查询会先和第一个规则匹配，后者会把?x 绑定到read 返回的结果上，并试图建立 (echo ?x)。而新的查询则会与后两条规则之一匹配。如果?x = done ，那么查询就会在第二条规则停下来。否则，查询将匹配第三条规则，打印出读到的值，然后重新开始处理。 这些规则共同定义了一个程序，它会一直回显输入的字串，直到你打done ： 译者注：原文为"isnalsectionshows..."，译文根据实情去掉了"最后"。 ~~~ (setq *rules* nil) (<- (append nil ?ys ?ys)) (<- (append (?x . ?xs) ?ys (?x . ?zs)) (append ?xs ?ys ?zs)) (<- (quicksort (?x . ?xs) ?ys) (partition ?xs ?x ?littles ?bigs) (quicksort ?littles ?ls) (quicksort ?bigs ?bs) (append ?ls (?x . ?bs) ?ys)) (<- (quicksort nil nil)) (<- (partition (?x . ?xs) ?y (?x . ?ls) ?bs) (lisp (<= ?x ?y)) (partition ?xs ?y ?ls ?bs)) (<- (partition (?x . ?xs) ?y ?ls (?x . ?bs)) (lisp (> ?x ?y)) (partition ?xs ?y ?ls ?bs)) (<- (partition nil ?y nil nil)) ~~~ [示例代码 24.14]： Quicksort ~~~ (<- (echo) (is ?x (read)) (echo ?x)) (<- (echo 'done) (cut)) (<- (echo ?x) (lisp (prog1 t (format t "~A~%" ?x))) (is ?y (read)) (cut) (echo ?y)) ~~~ [示例代码 24.15]： Prolog 编写的I/O 循环 ~~~ > (with-inference (echo)) hi HI ho HO done @ ~~~ 像这样的程序很难懂，因为它背离了Prolog 的抽象模型。如果把它在字面上翻译成Lisp 的话，可能就容易懂些了 ~~~ (defun echo (&rest args) (cond ((null args) (echo (read))) ((eq (car args) 'done) nil) (t (format t "~A~%" (car args)) (echo (read))))) ~~~ 如果用地道的Common Lisp 来说，就是： ~~~ (defun echo (&optional (arg (read))) (unless (eq arg 'done) (format t "~A~%" arg) (echo))) ~~~ ### 24.8 编译的含义 "编译" 这个词有好几层意思。通常，它指：把一个程序的某种抽象表述转换成更底层的代码。当然，如果用这个含义的话，本章介绍的程序就是个编译器，因为它会把规则翻译成Lisp 函数。 比较狭义地说，编译是指把程序转换成机器语言的过程。良好的Common Lisp 实现会把函数编译成机器语言。正如第 2.9 节上提到的，如果一段产生闭包的代码是编译过的，那么这段代码产生的闭包也会是 编译过的。因此，在更严格的意义上，这里所说的程序同样也是编译器。如果使用实现良好的Lisp，我们的Prolog 程序就会被转换成为机器语言。 然而，文中描述的程序仍然不能称为Prolog 编译器。对程序设计语言而言，"编译" 的意思要更进一步，单单生成机器代码还不够。一门编程语言的编译器在转换源程序的同时，还必须能优化产生的代码。比如说，如果让一个Lisp 的编译器编译下列表达式 ~~~ (+ x (+ 2 5)) ~~~ 它必须足够智能，能意识到没有必要等到运行期才去对(+ 2 5)进行求值。我们可以用7 取而代之，以此优化程序，这样就变成编译下面的表达式了 ~~~ (+ x 7) ~~~ 在我们的程序中，所有的编译工作都是由Lisp 编译器完成的，而且，它追求的优化是在Lisp 上做文章，而不是在Prolog 上动脑筋。这些优化的确能提升性能，但是它们都太底层了。Lisp 编译器并不知道它正在编译的代码是用来表示规则的。真正的Prolog 编译器会找出那些能转换成循环的规则，而我们的程序寻找的却是能产生常量的表达式，以及能直接在栈上分配的闭包。 嵌入式语言让你从现有的抽象机制中获益良多，但是这些语言也不是一揽子的解决方案。如果你希望把程序从非常抽象的表达方式一路转化成高效的机器代码，还是需要有人教会计算机如何做。在本章，我们用少得惊人的代码完成了这个工作中的相当一部分，但是这和编写一个真正意义上的Prolog 编译器相比还差得很远。

## 第 23 章 使用 ATN 分析句子 这一章将介绍这样一种技术，它把非确定性分析器(parser) 实现成一种嵌入式的语言。其中，第一部分将会解释什么是 ATN 分析器，以及它们是如何表示语法规则的。第二部分会给出一个 ATN 编译器，这个编译器将会使用在前一章定义的非确定性操作符。最后的几个小节则会展示一个小型的 ATN 语法，然后看看它在实际中是如何分析一段样本代码的。 ### 23.1 背景知识 扩充转移网络(ATN)，是 Bill Woods 在 1970 年提出的一种分析器。在那之后，ATN 在自然语言分析领域中作为一种形式化方法，被广为使用。只消一个小时，你就能写出一个能分析有意义的英语句子的 ATN 语法。出于这个原因，人们常常在初次见识 ATN 之后，就会为之着迷。 在 1970 年代，一部分研究者认为 ATN 有朝一日有可能会成为真正感觉有智能的程序的一部分。尽管时至今日，还持有这一观点的人寥寥可数，不过 ATN 的地位是不可磨灭的。它虽然没有你分析英语句子那么在行，但是它仍然能分析数量可观的各种句子。 如果你恪守下面的四个限制条件，ATN 就能大显神通： 1. 仅限用于语义上有限制的领域，比如说作为某个特定的数据库前端。 2. 不能给它过于困难的输入。比如说，请不要认为它们能像人一样能理解非常没有语法的句子。 3. 它们仅仅适用于英语，或者其他单词的顺序决定其语法结构的语言。比如说，ATN 就很可能无法被用来分析那种有屈折变化的语言，如拉丁语。 > 译者注：屈折语言(inected language)，是语言学中的概念，指因为单词的变格造成语句本身结构和意思的变化。汉语和英语主要依靠单词的顺序来确定其语法结构，而屈折语言则主要根据单词的屈折变化(inection) 来表现句子中的语法关系，比如说拉丁语和德语。虽然英语不是屈折语言，但是它里面还是保留着一些形式的屈折变化。比如我们常见的人称代词的"格" 的变化，主格的he 和宾格的him，属格的his。它们的词根相同，但是词尾的变化导致了词性和意思的变化，但是其在句子中的位置仍是决定其意义的主要因素。 1. 不要认为它们总是能正常工作。如果一个应用程序里，只要求它在 90% 的情况下正常工作就足够了，那么 ATN 是可以胜任的。倘若要求它不能出丝毫的差错，那么就不应该考虑用它。 尽管有种种限制，ATN 还是能在很多地方派上用场。最典型的应用案例是用做数据库的前端。如果你给这种数据库系统配备一个用ATN 驱动的接口，用户查询的时候就不用再构造特定格式的请求，只要用一种形式受限的英语提问就可以了。 ### 23.2 形式化 要理解 ATN 的工作机制，我们首先要回忆一下它的全名： > 扩充转移网络(Augmented Transition Network)。 所谓转移网络，是指由有向路径连接起来的一组节点，从根本上可以把它看作一种流程图。其中一个节点被指定为起始节点，而部分其他节点则被作为终结节点。每条路径上都带有测试条件，只有对应的条件被满足的时候，状态才能经由这条路径转移到新的节点。首先，输入是一个序列，并有一个指向当前单词的指针。根据路径进行状态转移会使指针相应地前进。使用转移网络分析句子的过程，就是找到从起始节点走到某个终止节点的路径的过程，在这个过程中，所有的转移条件都要满足。 ATN 在这个模型的基础上另加入了两个特性： 1. ATN 带有寄存器。寄存器是有名字的 slot，它可以被用来保存分析过程中所需的有关信息。转移路径除了能进行条件判断之外，还会设置和修改寄存器中的内容。 2. ATN 的结构可以是递归的。转移路径可以这样要求： > 如果要通过这条路径，分析过程必须能通过某个子网络。 而终结节点则使用寄存器中累积得到信息来建立列表结构并返回它，这种返回结果的方式和函数返回值的方式非常像。实际上，除了它具有的非确定性之外，ATN 的行为方式和函数式编程语言很相似。 [示例代码 23.1] 中定义的 ATN 几乎是最简单的ATN 了。它能分析形如 "Spotruns"("电视广告插播中") 的名词--动词型句子。这种 ATN 的网络表示如[示例代码 23.2] 所示。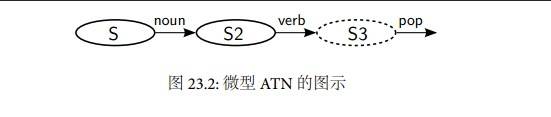 ~~~ (defnode s (cat noun s2 (setr subj *))) (defnode s2 (cat verb s3 (setr v *))) (defnode s3 (up '(sentence (subject ,(getr subj)) (verb ,(getr v))))) ~~~ [示例代码 23.1]： 一个微型ATN ~~~ noun verb pop S S2 S3 ~~~ [示例代码 23.2]： 微型ATN 的图示  当 ATN 分析输入序列 (spot runs) 时，它是如何工作的呢？ 第一个节点有一条出路径(outgoingarc)，或者说一条类型路径(cat)，这条路径指向节点s2。这事实上是表示：如果当前单词是个名词的话，你就可以通过我；如果你通过我的话，你必须把当前单词(即*) 保存在subj 寄存器中。因而，当离开这个节点时，subj 的内容就变成了spot。 总是有个指针指向当前的单词。在开始的时候，它指向句子的第一个单词。在经过cat 路径的时候，指针会往前移动一个单词。因此，在我们到达s2 节点的时候，当前节点会变成第二个单词，即runs 。第二条路径线和第一条一样，不同之处在于它要求的是个动词。它发现了runs ，并把它保存在寄存器v 里面，然后状态就走到了s3。 在最后一个节点s3 上，只有一个pop 路径(或称为终止路径)。(有pop 路径的节点的外围线是虚线)。由于我们正好在把输入序列读完的时候通过了pop 路径，所以我们进行的句子分析是成功的。Pop 路径返回的是一个反引用表达式： ~~~ (sentence (subject spot) (verb runs)) ~~~ 一个 ATN 是与它所要分析语言的语法相对应的。一个用来分析英语的 ATN，如果规模适中的话，那么它会有一个用来分析句子的主网络，以及用来分析名词短语、介词短语，以及修饰词组等语法元素的多个子网络。让我们想一想含有介词短语的名词短语，其中，介词短语也是有可能含有名词短语的，并且这种结构可能会无穷无尽地延续下去。显而易见，要处理下面这种结构的句子，必须要能支持递归： ~~~ "the key on the table in the hall of the house on the hill" ~~~ ### 23.3 非确定性 尽管我们在这个简单的例子里面没有看出来，但是 ATN 的确是非确定性的。一个节点可以有多个出路径，而特定的输入可以同时满足一个以上的出路径的条件。举个例子，一个像样的 ATN 应该既能分析祈使句也能分析陈述句。所以第一个节点要有向外的 cat 路径，与名词(用于陈述句)和动词(用于祈使句)。 要是句子开头的单词是 "time" 呢？"time" 既是名词又是动词。分析器如何知道该选哪条路径呢？如果 ATN 是以不确定的方式运行的，那就意味着用户可以认为分析器总是会猜到正确的那条路径线。如果有路径线会让分析过程走进死胡同，那么它们是不会被选中的。 实际上，分析器是无法预见未来的。它只是在无路可走，或者读完了输入还没能结束分析时，通过回溯的方式来表现出老是猜中的表象。不过所有这些回溯的机制是自动嵌入在 ATN 编译器产生的代码里面的。所以，在编写 ATN 时，我们可以认为分析器能够猜出来应该选择哪一条路径通过。 就像许多 (也许是绝大多数) 使用非确定性算法的程序所做的那样，ATN 一样，使用的也是深度优先搜索。 如果曾有过分析英语的经验，就能很快了解到，任何句子都有大把的合法分析结果，但是它们中的绝大多数都是没有意义的。在传统的单处理器电脑上，一样可以迅速得到较好的分析结果。我们不是一下子算出所有的分析结果，而只是得出最有可能的那个。如果分析结果是合理的，那么我们就用不着再去搜索其他的分析方式了；否则我们还可以调用 fail 继续搜寻更多其它的方式。 为了控制生成分析结果的先后顺序，程序员需要借助某种办法来控 制choose 尝试各待选项的顺序。深度优先实现并不是唯一一种控制搜索顺序的办法。除非选择是随机的，否则任意一种实现都会按照其特定的顺序进行选择。不过，ATN 和 Prolog 一样，深度优先实现是其内化了的实现方式。在 ATN 中，出路径被选中的顺序就是它们当初被定义的顺序。使用这样的设计，程序员就可以根据优先级来排列转换路径线的定义了。 ### 23.4 一个ATN 编译器 一般来说，一个基于 ATN 的分析器由三个部分组成：ATN 本身，用来遍历这个ATN 的解释器，还有一个可以用于查询的词典。 举个例子，借助词典我们就可以知道 "run" 是个动词。说到词典，那是另一个话题了，我们在这里会使用一个比较初级的手工编制的词典。我们也不用在网络解释器上费心，因为我们会把 ATN 直接翻译成 Lisp 代码。在这里要介绍的程序被称为 ATN 编译器的原因是，这个程序能把整个的 ATN 变成对应的代码。节点会成为函数，而转换路径则会变成函数里的代码块。 第 6 章介绍了把函数作为表达方式的用法。这种编程习惯常常能让程序的运行速度更快。在这里，这意味着会免去在运行时解析网络的开销。而这样处理的缺点在于，如果出了问题的话，分析原因的线索就会更少了，特别是如果你用的 Common Lisp 实现没有提 供function-lambda-expression 的时候。 [示例代码 23.3] 中包含了所有用来把 ATN 节点转换为 Lisp 代码的源程序。其中 defnode 宏被用来定义节点。它本身生成的代码很有限，就是一个 choose ，用来在每个转换路径产生的表达式中进行选择。节点函数有两个参数，分别是 pos 和 regs： > pos 的值是当前的输入指针(一个整数)，而regs 是当前的寄存器组(为一个关联表的列表)。 宏 defnode 定义了一个宏，这个宏的名字和对应的节点相同。节点s 将会被定义成宏 s 。这种习惯做法让转换路径知道如何引用它们的目标节点 它们只要调用和节点同名的宏就可以了。这同时也意味着，你在给节点取名的时候应该避免和已有的函数或者宏重名，否则这些函数或宏会被重定义。 译者注：见CLHS 中 FunctionFUNCTION-LAMBDA-EXPRESSION 一节。 ~~~ (defmacro defnode (name &rest arcs) '(=defun ,name (pos regs) (choose ,@arcs))) (defmacro down (sub next &rest cmds) '(=bind (* pos regs) (,sub pos (cons nil regs)) (,next pos ,(compile-cmds cmds)))) (defmacro cat (cat next &rest cmds) '(if (= (length *sent*) pos) (fail) (let ((* (nth pos *sent*))) (if (member ',cat (types *)) (,next (1+ pos) ,(compile-cmds cmds)) (fail))))) (defmacro jump (next &rest cmds) '(,next pos ,(compile-cmds cmds))) (defun compile-cmds (cmds) (if (null cmds) 'regs '(,@(car cmds) ,(compile-cmds (cdr cmds))))) (defmacro up (expr) '(let ((* (nth pos *sent*))) (=values ,expr pos (cdr regs)))) (defmacro getr (key &optional (regs 'regs)) '(let ((result (cdr (assoc ',key (car ,regs))))) (if (cdr result) result (car result)))) (defmacro set-register (key val regs) '(cons (cons (cons ,key ,val) (car ,regs)) (cdr ,regs))) (defmacro setr (key val regs) '(set-register ',key (list ,val) ,regs)) (defmacro pushr (key val regs) '(set-register ',key (cons ,val (cdr (assoc ',key (car ,regs)))) ,regs)) ~~~ [示例代码 23.3]： 节点和路径的编译 调试ATN 时，需要借助某种 trace 工具。由于节点成为了函数，所以就用不着自己实现 trace 了。我们可以利用内建的 Lisp 函数 trace 。如同第 20.2 节提到的，只要用 =defun 定义节点，就意味着我们可以通过告诉 Lisp (trace =mods)来对节点 mods 的分析过程进行 trace。 节点函数体里面的转移路径就是宏调用，而宏调用返回的代码被嵌入在 defnode 生成的节点函数中。因此，每个节点的出路径都被表示为对应的代码，分析器每碰到一个节点，都会通过执行 choose 使用非确定性的机制来对这些代码择一执行。比如下面这个有几条出路径的节点 ~~~ (defnode foo <arc 1> <arc 2>) ~~~ 就会被变换成如下形式的函数定义： ~~~ (=defun foo (pos regs) (choose <translation of arc 1> <translation of arc 2>)) (defnode s (down np s/subj (setr mood 'decl) (setr subj *)) (cat v v (setr mood 'imp) (setr subj '(np (pron you))) (setr aux nil) (setr v *))) ~~~ 被宏展开成： ~~~ (=defun s(pos regs) (choose (=bind (* pos regs) (np pos (cons nil regs)) (s/subj pos (setr mood 'decl (setr subj * regs)))) (if (= (length *sent*) pos) (fail) (let ((* (nth pos *sent*))) (if (member 'v (types *)) (v (1+ pos) (setr mood 'imp (setr subj '(np (pron you)) (setr aux nil (setr v * regs))))) (fail)))))) ~~~ [示例代码 23.4]： 节点函数的宏展开 [示例代码 23.4] 显示了[示例代码 23.11] 中作为 ATN 例子里第一个节点的宏展开前后的模样。当节点函数(如s) 在运行时被调用时，会非确定性地选择一条转移路径通过。pos 参数将会是在输入句子中的当前位置，而regs 则是现有的寄存器数据。 就像在我们最初的那个例子中见到的，cat 路径要求当前的输入单词在语法上属于某个类型。在cat 路径的函数体中，符号* 将会被绑定到当前的输入单词上。 由down 定义的 push 路径，则要求对子网络的调用能成功返回。这些路径函数接受两个目标节点作为参数，它们分别是：子网络目标节点sub ，和当前网络的下个节点，即next 。注意到，虽然为cat 路径生成的代码只是调用了网络中的下一个节点，但是为push 路径生成的代码使用的是=bind 。在继续转移到push 路径指向的节点前，程序必须成功地从子网络返回。在regs 被传入子网络前，一组新的空寄存器(nil) 被cons 到它的前面。在其他类型的转移路径的函数体中，符号* 将会被绑定到输入的当前单词上，不过在push 路径中，* 则是被绑定到从子网络返回的表达式上。 jump 路径就像发生了短路一样。分析器直接跳到了目标节点，不需要进行条件测试，同时输入指针没有向前移动。 最后一种转移路径是pop 路径，这种转移路径由up 定义。pop 路径是比较不常见的，原因在于它们没有目标节点。 就像Lisp 的return 类似，return 把程序带到的不是一个子函数，而是主调函数，而pop 路径指向的不是一个新节点，而是把程序带回"调用方" 的push 路径。pop 路径的=values "返回" 的是最近的一个push 路径的=bind 。 但是如第23.2 节所述，这产生的结果和一个普通的Lisp return 还不一样，=bind 的函数体已经被包在一个续延里了，并且被作为参数顺着之后的转移路径一直传下去，直到pop 路径的=values 把"返回" 值作为参数调用这个续延。 第22 章描述的两个版本的非确定性choose，分别是：一个快速的choose (第 22.3 节)，虽然它无法保证在搜索空间里有环的情况下能正常终止；以及一个较慢的true-choose (第 22.6 节)，它能在有环的情况下仍然正常工作。当然，在一个ATN 同样有可能存在环，不过只要在每个环里至少有一个转移路径能推进输入指针，那么分析器迟早都会走到句子末尾。问题是出在那种不会推进输入指针的那种环上。这里我们有两个方案： 1. 使用较慢的、真正的非确定性选择操作符(**附注**给出了其深度优先版本)。 2. 使用快速的 choose ，同时指出：如果定义的网络含有只需要顺着 jump 路径就能遍历的环，那么这个定义是错误的。 在[示例代码 23.3] 采用的是第二个方案。 [示例代码 23.3] 中的最后四个定义定义了用来读取和设置转移路径函数体中寄存器的宏。在这个程序里，寄存器组是用关联表来表示的。ATN 所使用的并不是寄存器组，而是一系列寄存器组。当分析器进入一个子网络时，它获得了一组新的空寄存器，这组寄存器被压在了已有寄存器组的上面。因此，无论何时，所有寄存器构成的集合都是作为一个关联表的列表存在的。 这些预先定义好的寄存器操作符的操作对象都是当前，或者说是最上面的那一组寄存器：getr 读一个寄存器；setr 设置寄存器；而 pushr 把一个值加入寄存器。setr和pushr 都使用了更基本的寄存器操作宏：set-register。注意到，寄存器不需要事先声明。不管传给 set-register 的是什么名字，它都会用这个名字新建一个寄存器。 这些寄存器操作符都是完全非破坏性的。"Cons，cons，cons"，set-register 念念有词。这拖慢了操作符运行的速度，同时也产生了大量无用的垃圾。不过，正如第20.1 节解释的，如果程序某一部分构造了一个续延，那么就不应该破坏性地修改在这个部分用到的对象。一个正在运行的线程中的对象有可能被另一个正被挂起的线程共享。在本例中，在一个分析过程中发现的寄存器会与许多其他分析过程共享数据结构。如果速度成了问题，我们可以把寄存器保存在vector 里面，而不是关联表里，并且把用过的vector 回收到一个公用的vector 池中。 push、cat 和jump 路径都可以包含表达式体。通常情况下，这些表达式只不过会是一些setr 罢了。通过对它们的表达式体调用compile-cmds ，这些几类转移路径的展开函数会把一系列setr 串在一起，成为一个单独的表达式： ~~~ > (compile-cmds '((setr a b) (setr c d))) (SETR A B (SETR C D REGS)) ~~~ 每个表达式把它后面的那个表达式作为它的最后一个参数安插到自己的参数列表中，不过最后一个表达式除外，它就是regs 。因此转移路径的函数体中的一系列表达式就会被转换成一个单独的表达式，这个表达式将会返回新的那些寄存器。 这个办法让用户能在转移路径的函数体里安插任意的Lisp 代码，只要把这些Lisp 代码用一个progn 包起来就可以了。举例来说： ~~~ > (compile-cmds '((setr a b) (progn (princ "ek!")) (setr c d))) (SETR A B (PROGN (PRINC "ek!") (SETR C D REGS))) ~~~ 我们有意让转移路径的函数体中的代码能访问到部分变量。被分析的句子将被放到全局的*sent* 里。还有两个词法变量也将是可见的，它们是：pos ，它保存着当前的输入指针；以及regs ，它被用来存放当前的所有寄存器。这是又一个有意地利用变量捕捉的实例。如果期望让用户不能引用这些变量，可以考虑把它们换成生成符号。 译者注：原文为 getr ，根据上下文应为setr。 宏 with-parses 是在[示例代码 23.5] 中定义的，它让我们有个办法能调用ATN。要调用它，我们应该传给它起始节点的名字、一个需要分析的表达式，以及一个代码体。这段代码告诉with-parses 应该如何处理返回的分析结果。表面上，with-parses 的功能和dolist 这种操作符差不多。实际上，在它内部进行的并不是简单的叠代操作，而是回溯搜索。每次成功的分析动作都会引起对with-parses 表达式中的代码体的一次求值。在代码体中，符号parse 将会绑定到当前的分析结果上。with-parses 表达式会返回@ ，因为这正是fail 在穷途末路时的返回值。 ~~~ (defmacro with-parses (node sent &body body) (with-gensyms (pos regs) '(progn (setq *sent* ,sent) (setq *paths* nil) (=bind (parse ,pos ,regs) (,node 0 '(nil)) (if (= ,pos (length *sent*)) (progn ,@body (fail)) (fail)))))) ~~~ [示例代码 23.5]： toplevel 宏 在进一步研究表达能力更强的ATN 之前，让我们先看一下之前定义的一个微型ATN 产生的分析结果。 ATN 编译器([示例代码 23.3]) 产生的代码会调用types ，通过它了解单词的在语法上所担当的角色，所以我们需要先给它下个定义： ~~~ (defun types (w) (cdr (assoc w '((spot noun) (runs verb))))) ~~~ 现在我们只要把起始节点作为第一个参数传给with-parses ，并调用它： ~~~ > (with-parses s '(spot runs) (format t "Parsing: ~A~%" parse)) Parsing: (SENTENCE (SUBJECT SPOT) (VERB RUNS)) @ ~~~ ### 23.5 一个 ATN 的例子 既然我们把ATN 编译器从头到尾都说清楚了，接下来可以找个例子小试牛刀了。为了让 ATN 的分析器能处理的句子的类型更多些，你需要把 ATN 网络，而不是 ATN 编译器弄得更复杂一些。这里展示的编译器之所以还只是个玩具，其原因是因为它的速度比较慢，而不是它在处理能力上的局限性。 分析器的处理能力(与处理速度相区别) 源自于它的语法，由于这里篇幅的限制，所以我们不得不用一个玩具版本来说明问题。从[示例代码 23.8] 到[示例代码 23.11] 定义了[示例代码 23.6] 中所示的ATN(或者说一组ATN)。这个网络的规模正好足够大，使得它能在分析那句经典的分析素材"Timeieslikeanarrow" 时，能够得出多种分析结果。 如果要分析更复杂的输入的话，我们就需要一个稍大的词典。函数types ([示例代码 23.7]) 提供了一个最基本的词典。它里面定义了一个由22 个词组成的词汇库，同时把每个词都和一个列表相关联，列表由一个或多个单词对应的语法角色构成。 ATN 也是由ATN 本身连接而成的。在本例中，我们的ATN 部件中最小的一个是[示例代码 23.8] 中的ATN。它分析的是修饰语的字符串，在这里，指的就是名词的字符串。mods 是第一个节点，它接受一个名词。第二个节点是mods/n ，它会去寻找更多的名词或者返回一个分析结果。 第2.4 节介绍了把程序写成函数式风格能让程序更易于测试的缘由： 1. 在函数式程序中，可以单独地测试程序的组成部件。 2. 在Lisp 中，可以在toplevel 的循环里交互地测试函数。 s/subj NP v v NP s v s/obj ~~~ pron pron det MODS noun NP np np/det np/mod np/n np/pp prep NP pp pp/prep pp/np noun mods mods/n noun ~~~ [示例代码 23.6]： 一个规模更大的ATN ~~~ (defun types (word) (case word ((do does did) '(aux v)) ((time times) '(n v)) ((fly flies) '(n v)) ((like) '(v prep)) ((liked likes) '(v)) ((a an the) '(det)) ((arrow arrows) '(n)) ((i you he she him her it) '(pron)))) ~~~ [示例代码 23.7]： 象征性的词典 ~~~ (defnode mods (cat n mods/n (setr mods *))) (defnode mods/n (cat n mods/n (pushr mods *)) (up '(n-group ,(getr mods)))) ~~~ [示例代码 23.8]： 修饰词字符串的子网络 这两条原因合在一起，成为了我们能进行交互式开发的理由：当我们用Lisp 写函数式程序的时候，我们就 可以每写一部分代码，就测试它们。 ATN 和函数式程序非常相像，从它的实现上看，ATN 宏展开成了函数式的程序。这个相似点使得交互式的开发方式也一样适用于ATN 的开发。我们可以把任意一个节点作为起点来测试ATN，只要把节点的名字作为with-parses 的第一个参数传入： ~~~ > (with-parses mods '(time arrow) (format t "Parsing: ~A~%" parse)) Parsing: (N-GROUP (ARROW TIME)) (defnode np (cat det np/det (setr det *)) (jump np/det (setr det nil)) (cat pron pron (setr n *))) (defnode pron (up '(np (pronoun ,(getr n))))) (defnode np/det (down mods np/mods (setr mods *)) (jump np/mods (setr mods nil))) (defnode np/mods (cat n np/n (setr n *))) (defnode np/n (up '(np (det ,(getr det)) (modifiers ,(getr mods)) (noun ,(getr n)))) (down pp np/pp (setr pp *))) (defnode np/pp (up '(np (det ,(getr det)) (modifiers ,(getr mods)) (noun ,(getr n)) ,(getr pp)))) ~~~ [示例代码 23.9]： 名词短语子网络 接下来的两个网络需要放在一起讨论，因为它们之间是互相递归调用的。[示例代码 23.9] 中定义的网络被用来分析名词短语，它从节点np 开始。在[示例代码 23.10] 中定义的网络则被用来分析介词短语。名词短语有可能含有介词短语，反之亦然。所以它们两个各自有一个push 路径，分别调用另一个网络。 名词短语网络中有六个节点。其中，第一个节点np 有三个选择。如果它读到了一个代词，那么它就可以转移到节点pron ，这会让它弹出这个网络： ~~~ > (with-parses np '(it) (format t "Parsing: ~A~%" parse)) Parsing: (NP (PRONOUN IT)) @ ~~~ 另外两个转移路径都指向了节点np/det ：一条路径读入一个限定词(比如说"the")，而另一条路径则直接跳转，不从输入读取任何词。在节点np/det ，两条出路径都通向np/mods ；np/det 可以选择push 到子网络mods ，以此来找出修饰词的字串，或者直接jump。节点np/mods 读入一个名词，然后转移到np/n 。这个节点要么弹出结果，要么进入介词短语网络，看看能不能碰到个介词短语。最后的节点，即np/pp ，弹出结果。 分析不同类型的名词短语所走过分析路径也各不相同。下面是两个名词短语网络的分析结果： ~~~ > (with-parses np '(arrows) (pprint parse)) (NP (DET NIL) (MODIFIERS NIL) ~~~ 220 第23 章 使用ATN 分析句子 ~~~ (NOUN ARROWS)) ~~~ @ > (with-parses np '(a time fly like him) (pprint parse)) (NP (DET A) (MODIFIERS (N-GROUP TIME)) (NOUN FLY) (PP (PREP LIKE) (OBJ (NP (PRONOUN HIM))))) @ 第一次分析在最后jump 到np/det ，再jump 到np/mods 读入一个名词，然后pop 到np/n ，从而成功结束。 第二次的尝试过程中没有jump 过，它首先为了匹配一个修饰词字符串push 进一个子网络，然后为了介词短语也进入了一个子网络。这应该是分析器的通病，我们的分析器也不例外：有些在句法上没有问题的表述在语义上却毫无意义，以致于人都没有办法看出它们的句法结构。这里，名词短语"atimeylikehim" 和"aLisphackerlikehim" 的形式就是一样的。 ~~~ (defnode pp (cat prep pp/prep (setr prep *))) (defnode pp/prep (down np pp/np (setr op *))) (defnode pp/np (up '(pp (prep ,(getr prep)) (obj ,(getr op))))) ~~~ [示例代码 23.10]： 介词短语子网络 万事俱备，只欠东风。现在我们缺的就是一个能识别整句结构的网络了。[示例代码 23.11] 中的网络同时能分析祈使句和陈述句。按照习惯，起始节点被叫做s。第一个节点首先从一个名词短语开始。第二条出路径读入一个动词。当句子在句法结构上有歧义时，两条转移路径都可能被满足，最终得到两个或更多的分析结果，如[示例代码 23.12] 所示。第一个分析结果和"Island nations like a navy" 类似，而第二个和"Find someone like a policeman" 是同一种。对于"Timeieslikeanarrow"，更复杂的ATN 能找出六种以上的分析结果。 在这一章给出ATN 编译器的目的更多的在于展示如何提炼出一个ATN 思路的精髓，而不是实现一个产品级的软件。如果进行一些很明显的改进，代码的效率就能显著提升。当速度很重要的时候，用闭包来模拟非确定性这个思路从整体上说，也许就太慢了。但是如果速度不是关键问题，用本章介绍的这种编程技术可以写出十分简洁明了的程序。 ~~~ (defnode s (down np s/subj (setr mood 'decl) (setr subj *)) (cat v v (setr mood 'imp) (setr subj '(np (pron you))) (setr aux nil) (setr v *))) (defnode s/subj (cat v v (setr aux nil) (setr v *))) (defnode v (up '(s (mood ,(getr mood)) (subj ,(getr subj)) (vcl (aux ,(getr aux)) (v ,(getr v))))) (down np s/obj (setr obj *))) (defnode s/obj (up '(s (mood ,(getr mood)) (subj ,(getr subj)) (vcl (aux ,(getr aux)) (v ,(getr v))) (obj ,(getr obj))))) ~~~ [示例代码 23.11]： 句子网络 ~~~ > (with-parses s '(time flies like an arrow) (pprint parse)) (S (MOOD DECL) (SUBJ (NP (DET NIL) (MODIFIERS (N-GROUP TIME)) (NOUN FLIES))) (VCL (AUX NIL) (V LIKE)) (OBJ (NP (DET AN) (MODIFIERS NIL) (NOUN ARROW)))) (MOOD IMP) (SUBJ (NP (PRON YOU))) (VCL (AUX NIL) (V TIME)) (OBJ (NP (DET NIL) (MODIFIERS NIL) (NOUN FLIES) (PP (PREP LIKE) (OBJ (NP (DET AN) (MODIFIERS NIL) (NOUN ARROW))))))) ~~~ @ [示例代码 23.12]： 一个句子的两种分析方式

## 第 22 章 非确定性 程序设计语言让我们得以从烦冗的细节中脱身而出。Lisp 是一门优秀的语言，其原因在于它本身就帮我们处理如此之多的细枝末节，同时程序员对复杂问题的容忍是有限度的，而 Lisp 让程序员能从他们有限的耐受度中发掘出最大的潜力。 本章将会解说宏是怎么样帮助 Lisp 解决另一类重要的细节问题的：即，将非确定性算法转换为确定性算法的问题。 本章共分为五个部分。 第一部分 阐述了什么是非确定性。 第二部分 介绍了非确定性 choose 和 fail 的一个 Scheme 实现，这个实现使用了续延。 第三部分 呈现了 choose 和 fail 的 Common Lisp 实现，这个版本的实现基于第 20 章提到的 continuation-passing 宏。 第四部分 展示了如何在脱离 Prolog 的情况下，来理解 cut 操作符。 最后一部分 提出了一些改进最初版本的非确定性操作符的建议。 在本章定义的非确定性选择操作符，将会在第 23 章里，被用来编写一个 ATN 编译器，而在第 24 章里，这些操作符会被用在一个嵌入式的 Prolog 实现里面。 ### 22.1 概念 非确定性算法的运行有赖于某种超自然的预见能力。那么，既然我们没有办法用到那种有超能力的电脑，为什么还要讨论这种算法呢？因为非确定性算法可以用确定性的算法来模拟。对于纯函数式程序，即那种没有副作用的程序，要模拟非确定性简直就是小菜一碟。在纯函数式程序里面，非确定性可以用带回溯（backtracking） 的搜索过程来实现。 本章会展示在函数式程序里模拟非确定性的方法。如果我们有了一个能模拟非确定性的模拟器，那么只要是真正的非确定机器能够处理的问题，照理说这个模拟器应该也能得出答案。很多时候，写一个有超自然的洞察力助阵的程序，肯定会比写缺乏这种能力的程序要轻松。所以如果手里能有这样一个模拟器，写起程序来一定会如虎添翼。 在本节中，我们将会界定非确定性将赋予我们什么样的能力。下一节里，会用一些示例程序展示这些能力的用处。本章开始的这两节中的例子将会使用 Scheme 编写。( Scheme 和 Common Lisp 之间的区别已经在第 20.1 节总结过了。) 非确定性算法和确定性算法之所以不一样，其原因在于前者能使用两种特殊的操作符 choose 和 fail 。Choose 是一个函数，它能接受一个有限的集合，并返回其中一个元素。要解释清楚 choose 是如何做选择的，我们必须首先介绍一下计算过程中所谓的未来的概念。 这里，我们令 choose 为一个函数 choose ，它接受一个列表，并返回一个元素。对每个元素来说，如果这个元素被选中，那么这个计算过程就会因为它而导致有一组可能的未来情况与之对应。在下列表达式中 ~~~ (let ((x (choose '(1 2 3)))) (if (odd? x) (+ x 1) x)) ~~~ 接下来，当这个运算过程运行到 choose 这里时，将会有三个可能的结果： 1. 如果 choose 返回 1，那么这个运算过程将会经过 if 的 then 语句，然后返回 2。 2. 如果 choose 返回 2 ，那么这个运算过程将会经过 if 的 else 语句，然后返回 2。 3. 如果 choose 返回 3 ，那么这个运算过程将会经过 if 的 then 语句，然后返回 4 。 本例中，一旦知道 choose 的返回值，我们就能非常清楚这个运算过程下一步将会是什么样子。在普遍情况下，每个选择都会和一组将来的情形相关联，因为在未来的某些情况下，会出现更多的选择。举个例子，如下： ~~~ (let ((x (choose '(2 3)))) (if (odd? x) (choose '(a b)) x)) ~~~ 在这里，在运行到第一个 choose 的时候，接下来会有两个可能性： 1. 如果 choose 返回 2 ，那么这个运算过程将会经过 if 的 else 语句，然后返回 2。 2. 如果 choose 返回 3 ，那么这个运算过程将会经过 if 的 then 语句。走到这里，运算过程到了一个岔路口，面临着两种可能，一个是返回 a ，另一个则返回 b 。 第一个集合有一个可能性，而第二个集合有两个。因而这个计算过程总共有三个可能的去向。 这里要记住的是，如果 choose 有几个选项可供选择，那么每个选项都会牵涉到一组可能的去向（可能性）。 Choose 会返回哪一项呢？我们可以像下面那样假设 choose 的工作方式： 1. 如果将来的可能性中存在有情况，在这种情况下没有调用 fail ，那么 choose 将只会返回一个选择。 2. 如果要在零个选项里作选择，那么这个 choose 就等价于 fail 。 下面用个例子来解释， ~~~ (let ((x (choose '(1 2)))) (if (odd? x) (fail) x)) ~~~ 在上面的例子里面，每个可能的选项都有其确定的将来。既然选择 1 的那个选项的将来调用了fail ，那么只有 2 能被选择。所以，总的来说，这个表达式是确定性的：它总是返回 2。 不过，接下来的表达式就不是确定性的了： ~~~ (let ((x (choose '(1 2)))) (if (odd? x) (let ((y (choose '(a b)))) (if (eq? y 'a) (fail) y)) x)) ~~~ 第一个 choose 那里，有两个可能的将来与 1 这个选择对应，与 2 对应的有一个。对于前者，这个将来是确定的，因为如果选 a 的话，会导致调用 fail。因此，这个表达式总的来说，要么返回 b ，要么返回 2 。最后一个例子，下面的表达式只有一个可能的值: ~~~ (let ((x (choose '(1 2)))) (if (odd? x) (choose '()) x)) ~~~ 因为，如果被选择的是 1，那么接下来会走到一个没有待选项的 choose。这个例子因而也就和上个以及另一个例子等价。 也许从上面举的几个例子，我们还不是很清楚非确定性到底意味着什么，但是我们已经开始感受到了这种动人心魄的力量。在非确定性算法中，我们得以这样表述 "选择一个元素，使得无论我们接下来做什么决定，都不会导致对 fail 调用。" 下面的例子是一个非常典型的非确定性算法，它能弄清楚你祖上是不是有人名叫 Igor： ~~~ function Ig(n) if name(n) = 'Igor' then return n else if parrents(n) then return Ig(choose(parents(n)) else fail ~~~ fail 操作符被用来对 choose 的返回值施加影响。如果我们碰到一个 fail ，那么可以推断 choose 在此之前肯定做了错误的选择。按照定义，choose 的猜测总是正确的。所以，如果我们希望确保计算过程永远不会走到一条特定的路径，那么我们所要做的就是把一个 fail 放到这条路径上的某个地方，那样的话，我们就不会误入歧途。所以，由于这个算法一代一代地递归检查，函数 Ig 就能够在路径上的每一步上作出选择，或者顺着父亲这条线索，或者顺着母亲这条线索，最终让这条路通向 Igor。 这个过程就好像，一个程序能够这样要求：它让 choose 从一组选项中找出某个元素，只要需要的话，就使用 choose 的返回值作为判断的依据，只要 fail 出现，就一票否决，用这个机制倒推出程序希望 choose 在此之前作出的选择。接着，一眨眼功夫，choose 的返回值就是我们想要的结果。在这个模型中，choose 体现出了它预知未来的能力。 实际上，choose 并没有什么超自然的神力。choose 的任意一个实现都必须能通过在发现错误的时候进行回溯，来模拟准确无误的猜测，这个过程就像小老鼠能在迷宫里找到出路一样。但是回溯可以不动声色地发生于无形之间。一旦你有某种形式的 choose 和 fail ，就可以写出像上面例子那样的算法了，感觉就像这个算法真的知道应该选择哪一个祖先一样。借助 choose，只要写一个遍历问题空间的算法，就能搜索这个问题空间了。 ### 22.2 搜索 有许多经典的问题都可以归结为搜索问题，对于这类问题，非确定性常常被证明是一种行之有效的抽象方式。假设 nodes 被绑定到一棵树上节点组成的列表，而 (kids n) 是一个能返回节点 n 的子节点的函数，如果 n 没有子节点的话，就返回 #f 。我们打算写一个函数，即 (descent n1 n2)，让它返回从节点 n1 到其子孙节点 n2 (如果有的话) 所经过的某条路径上所有节点构成的列表。[示例代码 22.1] 中就是这个函数的一个确定性版本。 * * * **[示例代码 22.1] 确定性的树搜索** ~~~ (define (descent n1 n2) (if (eq? n1 n2) (list n2) (let ((p (try-paths (kids n1) n2))) (if p (cons n1 p) #f)))) (define (try-paths ns n2) (if (null? ns) #f (or (descent (car ns) n2) (try-paths (cdr ns) n2)))) ~~~ * * * 非确定性让程序员不用再操心路径寻找的细节。而只要告诉 choose ，让它找到一个节点 n ，使得从 n 到我们的目标节点存在一条路径。用非确定性的办法，我们可以写出更简单的 descent 版本，如 [示例代码 22.2] 所示。 [示例代码 22.2] 中的版本并没有显式地去搜索正确的路径所在的节点。能这样写，是基于这样的假设：即 choose 已经找到了一个具有期望特性的 n 。如果我们习惯于阅读确定性的程序，可能就很难认识到这一点，即：choose 毫无疑问是能完成工作的，就好像它能猜出来到底是哪个 n 能让自己指引整个计算过程一帆风顺、正确无误（fail）地走到终点。 * * * **[示例代码 22.2] 非确定性的树搜索** ~~~ (define (descent n1 n2) (cond ((eq? n1 n2) (list n2)) ((null? (kids n1)) (fail)) (else (cons n1 (descent (choose (kids n1)) n2))))) ~~~ * * * 对于choose 的能力，大概更有说服力的实例要算：即使在函数调用的时候，它的预见力也能奏效。[示例代码 22.3] 里有一对函数，它们能猜出两个数字，让两个数字之和等于调用者给出的数字。在第一个函数two-numbers 里面，非确定性帮助选择出两个数字，并把它们作为一个列表返回。当我们调用parlor-trick 的时候，它会通过调用two-numbers 来得到这两个数字。请注意，在two-numbers 在做决定的时候，它根本就无从得知用户给出的那个数字到底是多少。 * * * ~~~ ;; [示例代码 22.3] 在子函数里的选择非确定性的树搜索 (define (two-numbers) (list (choose '(0 1 2 3 4 5)) (choose '(0 1 2 3 4 5)))) (define (parlor-trick sum) (let ((nums (two-numbers))) (if (= (apply + nums) sum) '(the sum of ,@nums) (fail)))) ~~~ * * * 要是choose 猜的两个数字加起来不等于用户输入的数字，那么这个计算过程会以失败告终。由于我们可以信赖choose ，相信只要存在路径不通向失败的话，choose 选择的路径上就不会有失败存在。因此我们才能假定一旦调用方给出的数字在合适的区间内，choose 就肯定会作出正确的猜测，实际上它就是能做到这一点： ~~~ > (parlor-trick 7) (THE SUM OF 2 5) ~~~ 在简单的搜索问题中，Common Lisp 内置的find-if 函数一样能完成任务。那么非确定性选择到底有什么优越性呢？为什么不在待选项的列表里面一个一个找过来，搜索那些具有期望特性的元素呢？choose 和传统的迭代搜索最根本的区别在于：choose 对于失败到底能看到多远是没有止境的。非确定性choose 可以知道未来任意远的事情。如果将来在某一点会发生导致choose 做出无效选择的事件，我们可以确信choose 自己知道如何避免作出这样猜测。正如我们在parlor-trick 一例中所见到的，甚至在我们从choose 发生的函数中返回之后，fail 操作符仍然能正常工作。 举例来说，这种失败机制常发生在Prolog 进行的搜索中，非确定性之所以在Prolog 里能大显神通的原因在于，这门语言的一个核心特性是它能每次只返回所有查询结果中的一个。倘若使用非确定性的方法，而不是一次返回所有的有效结果，Prolog 就有能力处理递归的规则和条件，否则它就会得出一个大小为无穷大的结果集合。 看到descent 的第一反应，可能就和看到归并排序算法的第一反应差不多：它到底是在哪里完成的工作的呢？就像归并排序一样，工作是在不知不觉中完成的，但是的确是完成了。第22.3 节会介绍一个choose 实现，迄今为止在这个实现里，所有的代码示例都是实际使用的程序。 这些例子体现了非确定性作为一种抽象手段的价值所在。最优秀的编程语言抽象手段不仅仅是让你省下由于Scheme 没有指定参数求值的顺序(正相反，Common Lisp 要求求值的顺序为从左至右)，这次调用也可能会返回(THE SUM OF 5 2)。 了打字的时间，更重要的是让你更省心。在自动机理论里面，要是没有非确定性的话，有些证明简直就难以想象，无法完成。一门允许非确定性的语言也能给程序员创造类似的有利条件。 ### 22.3 Scheme 实现 这一节将会解释续延(continuation) 是如何模拟非确定性的。[示例代码 22.4] 是choose 和fail 的Scheme 实现。在表象之下，choose 和fail 利用回溯来模拟非确定性。然而，一个使用回溯的搜索程序必须保留足够的信息才能在先前选中的选择失败后，继续使用其他的选项搜索。这些信息就以续延的形式保存在全局变量*paths* 里面。 * * * ~~~ ;; [示例代码 22.4] choose 和fail 的Scheme 实现 (define *paths* ()) (define failsym '@) (define (choose choices) (if (null? choices) (fail) (call-with-current-continuation (lambda (cc) (set! *paths* (cons (lambda () (cc (choose (cdr choices)))) *paths*)) (car choices))))) (define fail) (call-with-current-continuation (lambda (cc) (set! fail (lambda () (if (null? *paths*) (cc failsym) (let ((p1 (car *paths*))) (set! *paths* (cdr *paths*)) (p1))))))) ~~~ * * * 传给函数choose 的是一个名为choices 的列表，它由一系列选项构成。如果choice 是空的，那么choose 就会调用fail ，后者会把计算过程打回之前的choose。如果choices 是 ( . ) 的形式，那么choose 会首先把它调用 时的续延压入*paths* ，然后再返回。 相比之下，函数fail 就简单一些。它直接从*paths* 弹出一个续延，然后调用它。如果之前保存的路径都被用完了，fail 就返回符号@。不过，它不会简简单单地像普通的函数返回值那样返回这个符号，也不会把它作为最近的一次choose 的返回值来返回。我们真正想要做的是把@ 直接返回到toplevel 。这个目的 是这样达到的：通过把cc 绑定到定义fail 时所处的那个续延，而定义fail 的地方可以被认为是toplevel。 通过调用cc ，fail 可以直接返回到那里。 [示例代码 22.4] 的实现把*paths* 当成栈来用。在这个实现里面，每当失败的时候就会转而从最新近的抉择点重新开始。这种策略被称为按时间回溯(chrnonologicalbacktracking)，其结果就是在问题空间中的深度优先搜索。"非确定性" 这个词常会被滥用，就好像它是深度优先实现的代名词。Floyd 关于非确定性算法的那篇经典的论文中提到的术语"非确定性"，取的就是这个意思，而且我们看到的一些非确定性解析器(parser) 和Prolog 里面，非确定性算法的实现都是用的深度优先搜索。不过，也要注意到，[示例代码 22.4] 并非唯一的实现， 甚至算不上一个正确的实现。照道理来说，choose 应该能根据任意可计算的指标来选择对象。但是，如果一个图里面有环的话，程序使用这些版本的choose 和fail 来搜索这个图就无法终止了。 在实际应用中，非确定性常常意味着使用和[示例代码 22.4] 中等价的的深度优先实现，同时把避免在搜索空间里面绕圈子的问题留给用户去解决。不过，对这一主题有兴趣的读者，在本章的最后一节将会解释如何实现真正的choose 和fail 。 ### 22.4 Common Lisp 实现 这一节将阐述如何用 Common Lisp 来实现 choose 和 fail 一种表现形式。正如我们在上节所看到的，call/cc 使得在 Scheme 里面能轻而易举地实现非确定性机制。之前，我们对计算过程的未来定义了一个理论中的概念，续延把它给具体化了。在 Common Lisp 中，我们可以用在第20 章中给出的 continuation-passing 宏来实现它。借助这些宏，我们就能给出仅仅比上一节中的 Scheme 版本稍微难看一些的 choose，但是它们在实际使用中的效果是一样的。 * * * ~~~ ;; [示例代码 22.5] 非确定性操作符的Common Lisp 实现 (defparameter *paths* nil) (defconstant failsym '@) (defmacro choose (&rest choices) (if choices '(progn ,@(mapcar #'(lambda (c) '(push #'(lambda () ,c) *paths*)) (reverse (cdr choices))) ,(car choices)) '(fail))) (defmacro choose-bind (var choices &body body) '(cb #'(lambda (,var) ,@body) ,choices)) (defun cb (fn choices) (if choices (progn (if (cdr choices) (push #'(lambda () (cb fn (cdr choices))) *paths*)) (funcall fn (car choices))) (fail))) (defun fail () (if *paths* (funcall (pop *paths*)) failsym)) ~~~ * * * [示例代码 22.5] 中是一个fail 的Common Lisp 实现，以及两个版本的choose。其中一个choose 的Common Lisp 版本 和它的Scheme 版本有些微小的区别。Scheme 的choose 接受一个参数，即：一个待选项的列表，以备选择作为返回值。而Common Lisp 版本采用了progn 的语法。它后面可以跟任意多个表达式，choose 会从里面选出一个进行求值： ~~~ > (defun do2 (x) (choose (+ x 2) (* x 2) (expt x 2))) DO2 > (do2 3) 5 > (fail) 6 ~~~ 在toplevel，我们可以把回溯算法看得更清楚一些，它运行在非确定性搜索的幕后。变量*paths* 被用来保存还没有走过的路径。当计算过程到达一个有多个可选项的choose 表达式的时候，第一个可选项会被求值，而其它几个选项则会被保存在*paths* 里。如果程序在这之后碰到了fail ，那么最后一个被保存的选项会从*paths* 弹出来，然后重新开始计算。要是没有更多的路径可供重启计算的话，fail 会返回一个特殊的值： ~~~ > (fail) 9 > (fail) @ ~~~ 在[示例代码 22.5] 中，用来表示失败的常量failsym ，被定义成了符号@。如果你希望把@ 作为一个普通的返回值，那么可以把failsym 改成用gensym。 另一个非确定性的选择操作符choose-bind 的实现用了一个稍微不一样的形式。它接受的是一个符号、一个待选项的列表，还有一个代码体。choose-bind 会对这个待选项的列表运行choose，然后把被选中的值绑定到符号上，最后对代码体求值： ~~~ > (choose-bind x '(marrakesh strasbourg vegas) (format nil "Let's go to ~A." x)) "Let's go to MARRAKESH." > (fail) "Let's go to STRASBOURG." ~~~ Common Lisp 的实现中提供两个选择操作符的原因只是为了方便。你可以用choose-bind 达到和choose 一样的效果，只要把： ~~~ (choose (foo) (bar)) ~~~ 翻译成 ~~~ (choose-bind x '(1 2) (case x (1 (foo)) (2 (bar)))) ~~~ 就可以了。但是如果在这个情况下我们有一个单独的操作符的话，程序的可读性就会更好些。 Common Lisp 的选择操作符通过闭包和变量捕捉保存了几个相关变量的绑定。choose 和choose-bind 作为宏，在它们所在的表达式的词法环境中展开。注意到，这两个宏加入*paths* 的是一个闭包，在这个闭包保存了将要用到的待选项，还有被引用到的词法变量的所有绑定。举例来说，在下面的表达式里 ~~~ (let ((x 2)) (choose (+ x 1) (+ x 100))) ~~~ 当启用之前保存的选项重新开始计算时，就会用到x 。这就是为什么让choose 把它的参数包装在一个lambda 表达式的原因所在。上面的表达式展开后的结果如下： ~~~ (let ((x 2)) (progn (push #'(lambda () (+ x 100)) *paths*) (+ x 1))) ~~~ 如果需要的话，对外的接口可以只提供单独一个操作符，因为 (fail) 和 (choose)是等价的。 保存在*path* 上的对象是一个含有指向x 指针的闭包。这是由于要闭包里存放变量的需要使然，可以从这一点看出Scheme 和Common Lisp 两者的选择操作符在语义上的不同之处。 倘若我们把choose 和fail 和第20 章的continuation-passing 宏一起用，那么指向我们的续延变量*cont* 的一个指针也会一样被保存下来。如果用=defun 来定义函数，同时用=bind 来调用它们，而且用=values 来获取函数的返回值，我们就可以在任意一个Common Lisp 程序里使用这套非确定性的机制了。 * * * ~~~ ;; [示例代码 22.6]： Common Lisp 版的 "在子函数里作选择" (=defun two-numbers () (choose-bind n1 '(0 1 2 3 4 5) (choose-bind n2 '(0 1 2 3 4 5) (=values n1 n2)))) (=defun parlor-trick (sum) (=bind (n1 n2) (two-numbers) (if (= (+ n1 n2) sum) '(the sum of ,n1 ,n2) (fail)))) ~~~ * * * 在这些宏的帮助下，我们可以毫无问题地运行那个非确定性的选择发生在子函数里的那个例子了。[示例代码 22.6] 中展示了Common Lisp 版本的parlor-trick ，就像之前它在Scheme 里一样，它运行正常： ~~~ > (parlor-trick 7) (THE SUM OF 2 5) ~~~ 这个函数之所以能正常工作，是因为表达式 ~~~ (=values n1 n2) ~~~ 在两个choose-bind 中被展开成了 ~~~ (funcall *cont* n1 n2) ~~~ 而每个choose-bind 则都被展开成了一个闭包，每个闭包都保存有指向body 中引用过的变量的指针，这些变量中包括 *cont*。 在使用choose、choose-bind 和fail 过程中存在的种种限制和[示例代码 20.5] 中所展示的限制是一样的，后者代码中所使用的技术是continuation-passing 宏。只要是选择表达式，它就一定是最后一个被求值的。所以如果我们想要在Common Lisp 里做一系列的选择的话，这些选择就必须以嵌套的形式出现： ~~~ > (choose-bind first-name '(henry william) (choose-bind last-name '(james higgins) (=values (list first-name last-name)))) (HENRY JAMES) > (fail) (HENRY HIGGINS) > (fail) (WILLIAM JAMES) ~~~ 和平时一样，这样做的结果就是深度优先搜索。 在第20 章定义的操作符能让表达式享有最后求值的权利。这个权利由新的宏抽象层接管了，一个=values 表达式必须出现在choose 表达式里面，反过来就行不通。也就是说 ~~~ (choose (=values 1) (=values 2)) ~~~ 是可以的，但是 ~~~ (=values (choose 1 2)) ; wrong ~~~ 却不行。(在后面的例子中，choose 的展开式是无法在=values 的展开式里捕获*cont* 的变量实例的。) 只要我们注意不要超越这里列出的以及[示例代码 20.5] 所示的那些限制，Common Lisp 的非确定选择机制就将会和它在Scheme 中一样，正常工作。与[示例代码 22.2] 中的Scheme 版的非确定性树搜索算法相对应，[示例代码 22.7] 中所示的是它的Common Lisp 版本。Common Lisp 版的descent 是从它的Scheme 版本直译过来的，尽管它显得有点罗嗦，同时也没那么漂亮。 * * * ~~~ ;; [示例代码 22.7]： 在Common Lisp 里做非确定性搜索 > (=defun descent (n1 n2) (cond ((eq n1 n2) (=values (list n2))) ((kids n1) (choose-bind n (kids n1) (=bind (p) (descent n n2) (=values (cons n1 p))))) (t (fail)))) DESCENT > (defun kids (n) (case n (a '(b c)) (b '(d e)) (c '(d f)) (f '(g)))) KIDS > (descent 'a 'g) (A C F G) > (fail) @ > (descent 'a 'd) (A B D) > (fail) (A C D) > (fail) @ > (descent 'a 'h) @ ~~~ * * * 现在有了Common Lisp 版的实用工具，就能做非确定性的搜索，而不用显式地去做回溯了。虽然劳心费力写了这些代码，但可以从此把本会写得冗长拖沓、一团乱麻的代码用寥寥几行就说得清楚明白，这个回报还是值得的。在现有的宏基础上再构造另一层宏，我们就能够用一页纸的篇幅写出一个ATN 编译器(第23 章)，或是在两页纸上初步实现Prolog(第24 章)。 使用了choose 的Common Lisp 程序在编译的时候必须打开尾递归优化，这不只是为了加快程序的运行速度，更重要的是为了避免发生栈溢出。虽然程序是通过调用续延函数来"返回" 值的，但是它真正的返回却是等碰到了最后的fail 才发生的。要是不进行尾递归优化，程序占用的栈空间只会越来越大。 ### 22.5 减枝 本节将会告诉我们如何在进行非确定性选择的Scheme 程序里使用减枝(cut)。虽然cut 一词来自于Prolog， 但是对非确定性来说，它所代表的概念却是普适的。你可以在任意一个作非确定性选择的程序里使用减枝技术。 如果不把Prolog 牵扯进来，可以更容易地理解减枝。让我们先设想一个现实生活中的例子。假设花生糖的生产厂商决定进行一次促销活动。出厂时，一小部分的花生糖盒子里会装有可以用来领奖的兑奖币。为了确保公平，发货的时候不会同时把两个有奖品的盒子送往一个城市。 译者注：原文为"Chocoblob"，是一种巧克力糖。但为了更通顺，译者自作主张把它改为"花生糖"。 促销开始后，糖厂发现由于兑奖币太小了，很容易被小孩误吞下去。这个发现让糖厂的律师预见到了由此导致的索赔和诉讼，别无他法，他们只得发起紧急搜索，想要召回全部有奖的盒子。每个城市都有多家门店销售花生糖，而每个店都会有不止一个盒子。但是律师们用不着打开每一个包装盒，因为只要他们一旦在某个城市发现有硬币的盒子，就不用再在这个城市里检查其他盒子了，因为每个城市最多只有一个有奖的盒子。要实现这个算法，可以做个减枝操作。 减枝指的是排除搜索树里的一部分。对于花生糖问题来说，搜索树是实实在在存在的：根节点是公司的总部，这个节点的子节点是奖盒所发往的城市，而这些子节点的子节点则是每个城市里面的门店，每个门店的子节点则代表了相应门店里的包装盒。当律师们搜索这棵树时，如果找到了有硬币的盒子时，他们会裁减掉当前城市下，还未检查过的分支。 减枝操作实际上含有两个步骤：当你知道那一部分的搜索树已经没有价值了，你就可以进行一次减枝，但是首先你必须在树上你认为可以减枝的地方作上标记。在花生糖的例子里，我们从常识可以推知，我们一搜索到城市的时候，这棵树的标记就做好了。很难用抽象的术语说清楚Prolog 的cut 是干什么的，因为这种标记是隐式的。不过用显式的标记操作符的话，减枝的意思就比较容易理解了。 * * * ~~~ (define (find-boxes) (set! *paths* ()) (let ((city (choose '(la ny bos)))) (newline) (let* ((store (choose '(1 2))) (box (choose '(1 2)))) (let ((triple (list city store box))) (display triple) (if (coin? triple) (display 'c)) (fail))))) (define (coin? x) (member x '((la 1 2) (ny 1 1) (bos 2 2)))) ~~~ [示例代码 22.8]： 穷尽的花生糖搜索 * * * [示例代码 22.8] 中的程序用非确定性的方法搜索了一个规模更小的花生糖树。每当一个盒子被打开，程序就会显示一个( ) 的列表。如果盒子里面有硬币的话，在其后会再打印一个c ： ~~~ > (find-boxes) (LA 1 1)(LA 1 2)C(LA 2 1)(LA 2 2) (NY 1 1)C(NY 1 2)(NY 2 1)(NY 2 2) (BOS 1 1)(BOS 1 2)(BOS 2 1)(BOS 2 2)C @ ~~~ 要实现花生糖的律师们想出的优化搜索算法，我们需要两个新的操作符：mark 和cut。[示例代码 22.9] 展示了一种定义它们的方法。虽然非确定性本身和特定的实现没什么关系，我们可以通过任意一个实现来理解它，但是搜索树的剪枝作为一种优化技术却高度依赖 choose 的实现细节。[示例代码 22.9] 中所示的mark 和cut 适用于深度优先搜索类型choose 实现([示例代码 22.4])。 要做mark ，通常的思路是把标记存到*paths* 里，后者是个列表，被用来保存还没有检查过的选择点。调用cut 会让*paths* 一直退栈，直到弹出最新近压入的标记。但是，我们应该把什么作为标记呢？我们有几个选择，比如说，也许我们可以用符号m ，但是这样的话，我们就需要重写fail ，让它在碰到m 的时候忽略它。幸亏函数也是一种对象，至少还有一种标记让我们能用fail ，它就是：函数fail 本身。这样的话，如果在一个标记上发生了fail ，让它调用自己就可以了。 [示例代码 22.10] 中显示了如何使用这些操作符来对花生糖的例子中的搜索树进行剪枝。(被修改过代码所在的行被用分号注明) 每当选择一个城市的时候，我们都会调用mark 。在那时，*paths* 里有一个续延，它保存着对剩余城市的搜索状态。 * * * ~~~ ;; [示例代码 22.9]： 对搜索树进行标记和剪枝 (define (mark) (set! *paths* (cons fail *paths*))) (define (cut) (cond ((null? *paths*)) ((eq? (car *paths*) fail) (set! *paths* (cdr *paths*))) (else (set! *paths* (cdr *paths*)) (cut)))) ~~~ * * * ~~~ ;; [示例代码 22.10]： 剪枝的花生糖搜索 (define (find-boxes) (set! *paths* ()) (let ((city (choose '(la ny bos)))) (mark) ; (newline) (let* ((store (choose '(1 2))) (box (choose '(1 2)))) (let ((triple (list city store box))) (display triple) (if (coin? triple) (begin (cut) (display 'c))) ; (fail))))) ~~~ * * * 如果我们找到一个有硬币的盒子，就调用cut ，它会让*path* 恢复到之前做标记的状态。执行减枝的效果直到下次调用fail 的时候才能看出来。但是到了那个时候，在display 之后，下一个fail 会把搜索过程 直接带到最外层的choose 那里，就算在搜索树中更下层的地方还有一些没有碰过的选择点，也是这样。结果就是：一旦找到了有硬币的盒子，我们就会从下一个城市继续我们的搜索，如下： ~~~ > (find-boxes) (LA 1 1)(LA 1 2)C (NY 1 1)C (BOS 1 1)(BOS 1 2)(BOS 2 1)(BOS 2 2)C @ ~~~ 在本例中，我们只检查了七个盒子，而不是十二个。 ### 22.6 真正的非确定性 确定性的图搜索程序应该采取专门的措施，以免在循环路径上无法脱身。[示例代码 22.11] 中所示是一个包含环路的有向图。当程序在一条从节点a 通向节点e 的路径上搜索时，就有可能陷入由⟨a，b，c⟩ 构成的环状路径。 除非这个确定性搜索使用了随机算法，广度优先搜索，或者显式地检测循环路径，否则是无法避免死循环的。如[示例代码 22.12] 所示，是path 的实现，其中使用了广度优先搜索，避免了环路。 从理论上说，非确定性应该可以让我们不用考虑环路带来的问题。22.3 中给出的 choose 和 fail 的深度优先实现是无法解决环路问题的，但倘若我们当初要求更严格一些的话，那么应该会要求非确定性的 choose 能够依据任意可计算的指标来选择对象，所以这次的例子照道理也应该不在话下。如果能用上正确版本的choose 的话，我们就能像[示例代码 22.13] 中那样，写出更简短、更清晰的path 。 本节会给出一个环路安全的choose 和fail 的实现。[示例代码 22.14] 中真正的非确定性choose 和fail 的Scheme 实现 * * * ~~~ ;; [示例代码 22.11]： 带环的有向图 a c e b d ~~~ * * * ~~~ ;; [示例代码 22.12]： 确定性搜索 (define (path node1 node2) (bf-path node2 (list (list node1)))) (define (bf-path dest queue) (if (null? queue) '@ (let* ((path (car queue)) (node (car path))) (if (eq? node dest) (cdr (reverse path)) (bf-path dest (append (cdr queue) (map (lambda (n) (cons n path)) (neighbors node)))))))) ~~~ * * * ~~~ ;; [示例代码 22.13]： 非确定性搜索 (define (path node1 node2) (cond ((null? (neighbors node1)) (fail)) ((memq node2 (neighbors node1)) (list node2)) (else (let ((n (true-choose (neighbors node1)))) (cons n (path n node2)))))) ~~~ * * * ~~~ 对于环路也能正常工作。只要是等价的非确定性算法能处理的问题,使用了这个版本的choose 和fail 的程序也一定能找到答案,不过这一点还会受到硬件的限制。 ~~~ [示例代码 22.14] 中定义的true-choose 把用来保存路径的列表当成一个队列来操作。因此，使用true-choose 的程序对状态空间进行的搜索将是广度优先的。每当程序到达选择点的时候，与每一个选择相对应的续延都会被加入到用来保存路径的列表后面。(Scheme 的map 的返回值和Common Lisp 的mapcar 的返回值是一样的。) 然后，和之前一样，还是调用fail。 如果用了这个版本的choose，[示例代码 22.13] 里定义的path 就能找到一条路径了，事实上，它找到的是最短路径，即[示例代码 22.11] 中所示的从a 到e 的那条路径。 虽然为了内容的完整性，本章给出了正确版本的choose 和fail ，其实最初的版本就够用了。我们不能仅仅因为其实现不是形式上正确的，就低估编程语言所提供抽象机制的价值。在用一些语言编程的时候，感觉上似乎我们能使用任意一个整数，其实能操作的最大一个整数可能只是32767。其实只要清楚幻象的限度，那么它所带来的危险就微不足道了，至少我们的抽象是有保证的。下两章中程序的简洁明了，很大程度上就归功于它们对非确定性choose 和fail 的善用。 * * * ~~~ ;; [示例代码 22.14] choose 的 Scheme 版正确实现 (define *paths* ()) (define failsym '@) (define (true-choose choices) (call-with-current-continuation (lambda (cc) (set! *paths* (append *paths* (map (lambda (choice) (lambda () (cc choice))) choices))) (fail)))) (define fail) (call-with-current-continuation (lambda (cc) (set! fail (lambda () (if (null? *paths*) (cc failsym) (let ((p1 (car *paths*))) (set! *paths* (cdr *paths*)) (p1))))))) ~~~

## 第 21 章 多进程 上一章展示了续延是如何使运行中的程序获知自己的状态，并且把它保存起来以便之后重新执行的。这一章将讨论一种计算模型，在这种模型中，计算机运行的不是单个程序，而是一组独立的进程。进程的概念和程序状态这一概念相当接近。通过在前一章的宏的基础上再写一层宏，我们就可以把多进程的机制融入到 Common Lisp 程序中。 ### 21.1 进程抽象 多进程这种表现形式，可以很方便地表示并行处理多个任务的程序。传统的处理器同时只能执行一条指令。我们称多进程能同时处理多件事情，并不是说它通过某种方式克服了硬件的限制，它真正的含义是：它使得我们可以在一个新的抽象层面上进行思考，在这个层面上我们不需要明确地指定计算机在任何给定的时间在做什么。就像虚拟内存给我们制造了一个错觉，似乎计算机的可用内存比它的物理内存还要大，同样的道理，多进程的概念使得我们可以假设计算机可以一次运行多个程序。 从传统上说，对进程的研究属于操作系统领域的范畴。但进程抽象带来的进步并不局限于操作系统。它们在其他实时的应用程序和计算机仿真中一样能大展身手。 有很多对于多进程的研究，它们的目的都是为了避免出现某些特定类型的问题。死锁是多进程的一个经典问题：两个进程同时停下等待另一个做某些事情，就像两个人都拒绝在另一个人之前跨过门槛。另一个问题是查询有可能碰到系统中数据不一致的状态 例如，一个余额查询正好在系统将资金从一个账户转移到另一个账户时发生。这一章只讨论进程抽象本身；这里展示的代码可以用来测试避免死锁和不一致状态的算法，但代码本身没有对这些问题提供任何保护。 这一章中的实现遵循了本书所有程序默默恪守的一条准则：尽可能少的扰乱Lisp。在本质上来说，程序应该尽可能多的让自己像是对语言的修改，而不是用语言写就的一个独立的应用程序。使程序与Lisp 协调一致可以使得程序更为健壮，好比部件配合良好的机器。这样做也能事半功倍；有时你可以让Lisp 为你代劳数量惊人的工作。 这一章的目标是构建一个支持多进程的的语言。我们的策略是通过添加一些操作符，将Lisp 变成这样的语言。我们语言的基本构成元素如下： > **函数** 由前一章的 =defun 或者 =lambda 宏定义。 > > **进程** 由函数调用实例化。活动进程的数量和一个函数能够实例化的进程数量都没有限制。每个进程有一个优先级，初始值由创建时给出的参数指定。 > > **等待表达式(Waitexpressions)** 等待表达式接受一个变量，一个测试表达式和一段代码体。如果进程遇到等待表达式，进程将在这一点被挂起，直到测试表达式返回真。一旦进程重新开始执行，代码体会被求值，变量则被绑定到测试表达式的值。测试表达式通常不应该有副作用，因为它被求值的时间和频率没有任何保证。 > > **调度** 通过优先级来完成。在所有能够重新开始执行的进程中，系统会运行优先级最高的进程。 > > **默认进程** 在其他进程都不能执行时运行。它是一个 read-eval-print 循环。 > > **创建和删除** 绝大多数对象的操作可以即时进行。正在运行中的进程可以定义新的函数，实例化或者杀死进程。 续延使得保存 Lisp 程序的状态成为可能。能够同时保存多个状态离实现多进程也不太远了。有了前一章定义的宏做基础，我们只要不到 60 行的代码就可以实现多进程。 ### 21.2 实现 * * * **[示例代码 21.1] 进程结构及实例化** ~~~ (defstruct proc pri state wait) (proclaim '(special *procs* *proc*)) (defvar *halt* (gensym)) (defvar *default-proc* (make-proc :state #'(lambda (x) (format t "~%>> ") (princ (eval (read))) (pick-process)))) (defmacro fork (expr pri) '(prog1 ',expr (push (make-proc :state #'(lambda (,(gensym)) ,expr (pick-process)) :pri ,pri) *procs*))) (defmacro program (name args &body body) '(=defun ,name ,args (setq *procs* nil) ,@body (catch *halt* (loop (pick-process))))) ~~~ * * * [示例代码 21.1] 和图 21.2 包含了所有用来支持多进程的代码。[示例代码 21.1] 包含了基本数据结构、默认进程、初始化、进程实例化的代码。进程，或者说procs，具有如下结构： pri : 进程的优先级，它应该是一个正数。 state : 是一个续延，它用来表示一个挂起进程的状态。我们可以 funcall 一个进程的 state 来重新启动它。 wait : 通常是一个函数，如果要让进程重新执行，它必须返回真，但刚创建的进程的 wait 为 nil 。wait 为空的进程总是可以被重新执行。 程序使用三个全局变量：*procs* ，当前被挂起的进程列表；*proc* ，正在运行的进程；还有 *default-proc* ，默认进程。 默认进程仅当没有其他进程可以运行时才会运行。它模拟 Lisp 的 toplevel 循环。在这个循环中，用户可以终止程序，或者输入让挂起进程恢复执行的表达式。请注意，默认进程显式地调用了 eval。这是少数几个合理使用 eval 的情形之一。一般来说，我们不赞成在运行时调用 eval ，这有两个原因： 1. 效率低下：eval 直接处理原始列表，要么当场进行编译，要么在解释器中进行求值。不管哪种方式都比先编译再调用来得慢。 2. 功能不够强大，因为表达式不在词法上下文中进行求值。举个例子，这就意味着你不能引用在被求值表达式之外可见的普通变量。 通常来说，显式调用eval 就像在机场礼品店买东西一样。已经是最后关头，你只得高价购买选择有限的劣质商品。 像本例这样两条理由都不适用的情况是很少见的。我们没法提前将表达式编译好。直到读取它们的时候才知道表达式是什么，所以没法事先知道。同样的，表达式无法引用它周遭的词法环境，因为在toplevel 输入的表达式处于空的词法环境中。事实上，这个函数的定义直接反映了它的英语描述：它读取并求值用户的输入。 宏 fork 使用一个函数调用来实例化进程。函数像平时一样由 =defun 定义： ~~~ (=defun foo (x) (format t "Foo was called with ~A.~%" x) (=values (1+ x))) ~~~ 现在当我们以一个函数调用和优先级数值作为参数调用 fork 时： ~~~ (fork (foo 2) 25) ~~~ 一个新进程被加入到了 *procs* 里面。新进程的优先级为 25，因为它还没有执行，所以 proc-wait 为 nil ，而 proc-state 包含了以 2 为参数的对 foo 的调用。 宏 program 使我们可以创建一组进程并一起执行它们。下面的定义： ~~~ (program two-foos (a b) (fork (foo a) 99) (fork (foo b) 99)) ~~~ 宏展开成了两个 fork 表达式，被夹在负责清除挂起进程的代码，以及不断选择进程来运行的代码中间。在这个循环外面，program 宏设置了一个 tag，把控制流抛(throw) 到这个 tag 的话，就会终止这个程序(program)。因为这个 tag 是个生成符号，所以它不会与用户设置的 tag 冲突。定义成 program 的一组进程不返回任何值，而且它们只应该在 toplevel 被调用。 进程实例化之后，进程调度代码开始执行。它的代码见 [示例代码 21.2]。函数 pick-process 在可以继续执行的进程中，选出优先级最高的一个，然后运行它。把这个进程找出来是 most-urgent-process 的工作。如果一个挂起的进程没有 wait 函数或者它的 wait 函数返回真，那么它就被允许运行。在所有被允许运行的进程中，具有最高优先级的被选中。胜出的进程和它的 wait 函数(如果有的话) 返回的值被返回给 pick-process 。获胜进程总是存在，因为默认进程总是想要执行。 [示例代码 21.2] 中其余的代码定义了用于在进程间切换控制权的操作符。标准的等待表达式是wait ，就像[示例代码 21.3] 中函数 pedestrian 使用的那样。在这个例子中，进程一直等到列表 *open-doors* 中有东西为止，然后打印一条消息： ~~~ > (ped) >> (push 'door2 *open-doors*) Entering DOOR2 >> (halt) NIL ~~~ 一个 wait 在实质上来说与 =bind (第 20.2 节) 相似，而且有着一样的限制，那就是它必须在最后被求值。任何我们希望在wait 之后执行的东西必须被放在它的代码体中。因此如果我们想要让一个进程等待多次，那等待表达式必须被嵌套。通过声明互相针对的事实，进程可以相互配合以达到某个目标，就像在 [示例代码 21.4] 中一样。 【】译者注：即 (eval (read)) 【】译者注：catch 操作符的用法可见CLHS 中的Special Operator CATCH 一节。 * * * **[示例代码 21.2] 进程调度** ~~~ (defun pick-process () (multiple-value-bind (p val) (most-urgent-process) (setq *proc* p *procs* (delete p *procs*)) (funcall (proc-state p) val))) (defun most-urgent-process () (let ((proc1 *default-proc*) (max -1) (val1 t)) (dolist (p *procs*) (let ((pri (proc-pri p))) (if (> pri max) (let ((val (or (not (proc-wait p)) (funcall (proc-wait p))))) (when val (setq proc1 p max pri val1 val)))))) (values proc1 val1))) (defun arbitrator (test cont) (setf (proc-state *proc*) cont (proc-wait *proc*) test) (push *proc* *procs*) (pick-process)) (defmacro wait (parm test &body body) '(arbitrator #'(lambda () ,test) #'(lambda (,parm) ,@body))) (defmacro yield (&body body) '(arbitrator nil #'(lambda (,(gensym)) ,@body))) (defun setpri (n) (setf (proc-pri *proc*) n)) (defun halt (&optional val) (throw *halt* val)) (defun kill (&optional obj &rest args) (if obj (setq *procs* (apply #'delete obj *procs* args)) (pick-process))) ~~~ * * * **[示例代码 21.3] 有一个等待的进程** ~~~ (defvar *open-doors* nil) (=defun pedestrian () (wait d (car *open-doors*) (format t "Entering ~A~%" d))) (program ped () (fork (pedestrian) 1)) ~~~ * * * 如果被给予相同的 door ，从 visitor 和 host 实例化的进程会通过黑板上的消息互相交换控制权： ~~~ > (ballet) ~~~ * * * **[示例代码 21.4]： 利用黑板进行同步** ~~~ (defvar *bboard* nil) (defun claim (&rest f) (push f *bboard*)) (defun unclaim (&rest f) (pull f *bboard* :test #'equal)) (defun check (&rest f) (find f *bboard* :test #'equal)) (=defun visitor (door) (format t "Approach ~A. " door) (claim 'knock door) (wait d (check 'open door) (format t "Enter ~A. " door) (unclaim 'knock door) (claim 'inside door))) (=defun host (door) (wait k (check 'knock door) (format t "Open ~A. " door) (claim 'open door) (wait g (check 'inside door) (format t "Close ~A.~%" door) (unclaim 'open door)))) (program ballet () (fork (visitor 'door1) 1) (fork (host 'door1) 1) (fork (visitor 'door2) 1) (fork (host 'door2) 1)) ~~~ * * * ~~~ Approach DOOR2. Open DOOR2. Enter DOOR2. Close DOOR2. Approach DOOR1. Open DOOR1. Enter DOOR1. Close DOOR1. >> ~~~ 还有另外一类更简单的等待表达式：yield ，它的唯一目的是让其他更高优先级的进程有机会运行。 setpri 重置当前进程的优先级，一个进程可能在执行 setpri 表达式后想要让出控制权。就像 wait 一样，在 yield 之后执行的代码都必须被放在它的代码体中。 [示例代码 21.5] 中的程序说明了这两个操作符如何相互工作。开始时，野蛮人有两个目的：占领罗马和掠夺它。占领城市有着(稍微) 高一些的优先级，因此会先执行。然而，在城市沦陷之后，capture 进程的优先级减小到 1 。之后会有一次投票，而 plunder ，作为最高优先级的进程开始运行。 ~~~ > (barbarians) Liberating ROME. Nationalizing ROME. Refinancing ROME. Rebuilding ROME. >> ~~~ 只有在蛮族掠夺了罗马的宫殿，并勒索了贵族之后，capture 进程才会恢复执行，此时他们开始为其领地建筑防御工事。 等待表达式的背后是一个更通用的 arbitrator。这个函数保存当前进程，然后调用 pick-process 来再次执行某个进程(有可能与当前进程为同一个)。它有两个参数：一个测试函数和一个续延。前者会被存储为挂起进程的 proc-wait ，在以后被调用来检查它是否可以被重新执行。 宏 wait 和 yield 通过简单的把它们的代码体包在 --表达式中来建立这个续延函数。例如： * * * **[示例代码 21.5] 改变进程优先级的效果** ~~~ (=defun capture (city) (take city) (setpri 1) (yield (fortify city))) (=defun plunder (city) (loot city) (ransom city)) (defun take (c) (format t "Liberating ~A.~%" c)) (defun fortify (c) (format t "Rebuilding ~A.~%" c)) (defun loot (c) (format t "Nationalizing ~A.~%" c)) (defun ransom (c) (format t "Refinancing ~A.~%" c)) (program barbarians () (fork (capture 'rome) 100) (fork (plunder 'rome) 98)) ~~~ * * * ~~~ (wait d (car *bboard*) (=values d)) ~~~ 被展开成： ~~~ (arbitrator #'(lambda () (car *bboard*)) #'(lambda (d) (=values d))) ~~~ 如果代码遵循了 [示例代码 20.5] 列出的限制，构造一个 wait 代码体的闭包就可以保存当前的整个续延。随着它的 =values 被展开，第二个参数变成： ~~~ #'(lambda (d) (funcall *cont* d)) ~~~ 由于这个闭包中有一个指向 *cont* 的引用，被这个等待函数挂起的进程将会拥有一个句柄(handle)，通过它，这个进程就能回到它当初被挂起的那一刻。 halt 操作符通过将控制权抛回program 展开式建立的标签终止整个进程组。它接受一个可选参数，该参数的值会被作为这个进程组的值返回。因为默认进程始终想要执行，所以终止整个程序的唯一的方法是显式的调用halt 。halt 后面是什么代码并没有关系，因为这些代码不会被求值。 单个进程可以通过调用 kill 来杀死。如果没有参数，这个操作符杀死当前进程。这种情况下，kill 就像是一个不保存当前进程的等待表达式。如果 kill 给定了参数，它们将成为进程列表上的 delete 操作的参数。在现在的代码中，kill 表达式没有什么好说的，因为进程没有许多的属性来被引用。然而，更复杂的系统会为它的进程附加更多的信息 时间戳、拥有者等等。默认进程不能被杀死，因为它并没有被保存在*procs* 中。 ### 21.3 不那么快速的原型 通过续延模拟的进程，其性能远不及真实操作系统的进程。那么，这一章中的程序又有什么用处呢？ 这些程序的用处类似于草图。不管在探索式编程还是快速原型开发中，这些程序其自身并不是最终目的，更多的是作为实现人们想法的手段。在许多其他领域，为这个目的服务的东西被称为草图。在理论上，建译者注：可以认为宏program 建立的由一组同时执行的进程组成的程序，但为与 "程序" 相区别，这里把 program 翻译成 "进程组"。 筑师可以在他的脑海里构思出整栋大楼。但多数建筑师似乎在手里握着笔的时候能想得更周详一些：一栋大楼的设计通常在一系列草图中成型。 快速原型开发就是给软件作草图。就像建筑师的第一张草图，软件原型往往也会由草草几笔一挥而就。在最初把想法付诸实现的时候，开销和效率的问题根本就没有纳入考量。结果是，在这一阶段得到的往往就是无法施工的设计图，或是低效得不可救药的软件。但无论如何，草图依然有它的价值，因为 1. 它们简明的传达了信息 2. 它们提供了试验的机会 像后续章节中的程序一样，这一章描述的程序还只是初步的设计。它仅用寥寥几笔就勾勒出了多进程大略 的模样。而且，尽管它可能因为不够高效，不能使用在产品软件中，但是它对于在多进程的其他方面作一些尝试还是很有用的，比如用来进行调度算法方面的试验。 第 22--24 章展示了其他使用续延的例子。它们都不够高效而不能使用在产品级的软件中。因为Lisp 和快速原型开发一同演化，Lisp 包含了很多专为原型开发打造的特性：低效但是方便的功能如属性列表，关键字参数；推而广之，列表也是这类特性之一。续延可以说属于这一类特性。它们保存了程序通常所需要的更多的状态。所以我们基于续延的Prolog 实现就是一个例子，通过这个实现我们能很好地理解这门语言，但是它的实现方式却是低效的。 本书更多的关注使用 Lisp 可以建立的抽象而不是效率问题。重要的是要意识到，Lisp 既是一个适合写产品软件的语言也是一个适合写原型的语言。如果 Lisp 有着低效的名声，那大部分是因为程序员止步于原型。 用Lisp 写出快速的程序很容易。不幸的是，用它写出低效的程序更是容易。最初版本的 Lisp 程序可以像钻石一样：娇小玲珑，清澈透明，而又笨重昂贵。也许有很大的诱惑使人们就让它保留原状。 在其他的语言中，一旦你大功告成，程序能够运行，那时程序的效率可能就已经可以接受了。如果你用指甲盖大小的瓷砖来铺地板，自然是不会浪费多少的。习惯用这种原则来开发软件的人可能会发现，克服 "程序能工作就完工" 这样的思维有些困难。"虽然用 Lisp 你轻而易举就能把程序写出来，" 他可能会想，"但哥们，这些程序跑得太慢了。" 事实上，两种看法都有问题。你可以写出快速的程序，但你得为此付出努力。 从这角度上说，使用 Lisp 就像生活在一个富裕而非贫穷的国度：似乎人们不得不通过工作来保持身材是种不幸，但这肯定比为了活下去而工作，自然只得消瘦下来要好。 在使用抽象能力较差的语言的时候，你想方设法实现的是功能。而在用 Lisp 的时候，你努力改进的则是程序的运行速度。幸运的是，提升速度更容易一些；大多数程序只在少数几个关键的地方才会关心速度。

## 第 20 章 续延(continuation) 续延是在运行中被暂停了的程序：即含有计算状态的单个函数型对象。当这个对象被求值时，就会在它上次停下来的地方重新启动之前保存下来的计算。对于求解特定类型的问题，能够保存程序的状态并在之后重启是非常有用的。例如在多进程中，续延可以很方便地表示挂起的进程。而在非确定性的搜索问题里，续延可以用来表示搜索树中的节点。 要一下子理解续延或许会有些困难。本章分两步来探讨这个主题。本章的第一部分会先分析续延在 Scheme 中的应用，这门语言内置了对续延的支持。一旦说清楚了续延的行为，第二部分将展示如何使用宏在 Common Lisp 程序里实现续延。第 21-24 章都将用到这里定义的宏。 ### 20.1 Scheme 续延 Scheme 和 Common Lisp 在几个主要方面存在着不同，其中之一就是：前者拥有显式的续延支持。本节展示的是续延在Scheme 中的工作方式。([示例代码 20.1] 列出了 Scheme 和 Common Lisp 间一些其他的区别。) 续延是一个代表着计算的将来的函数。不管是哪一个表达式被求值，总会有谁在翘首以待它将要返回的值。例如，在 ~~~ (/ (- x 1) 2) ~~~ 中，当求值 (- x 1) 时，外面的 / 表达式就在等着这个值，同时，还有另外一个式子也在等着它的值，依此类推下去，最后总是回到 toplevel 上 print 正等在那里。 无论何时，我们都可以把续延视为带一个参数的函数。如果上面的表达式被输入到 toplevel，那么当子表达式 (- x 1) 被求值时，续延将是： ~~~ (lambda (val) (/ val 2)) ~~~ 也就是说，接下来的计算可以通过在返回值上调用这个函数来重现。如果该表达式在下面的上下文中出现 ~~~ (define (f1 w) (let ((y (f2 w))) (if (integer? y) (list 'a y) 'b))) (define (f2 x) (/ (- x 1) 2)) ~~~ 并且 f1 在toplevel 下被调用，那么当 (- x 1) 被求值时，续延将等价于 ~~~ (lambda (val) (let ((y (/ val 2))) (if (integer? y) (list 'a y) 'b))) ~~~ 在 Scheme 中，续延和函数同样是第一类对象。你可以要求 Scheme 返回当前的续延，然后它将为你生成一个只有单个参数的函数，以表示未来的计算。你可以任意长时间地保存这个对象，然后在你调用它时，它将重启当它被创建时所发生的计算。 1. 在 Common Lisp 眼中，一个符号的 symbol-value 和 symbol-function 是不一样的，而 Scheme 对两者不作区分。在 Scheme 里面，变量只有唯一对应的值，它可以是个函数，也可以是另一种对象。因此，在 Scheme 中就不需要 #' 或者 funcall 了。Common Lisp 的： (let ((f #'(lambda (x) (1+ x)))) (funcall f 2)) 在 Scheme 中将变成： ~~~ (let ((f (lambda (x) (1+ x)))) (f 2)) ~~~ 1. 由于 Scheme 只有一个名字空间，因而它没有必要为各个名字空间专门设置对应的赋值操作符(例如 defun 和 setq )。取而代之，它使用 define ，define 的作用和 defvar 大致相当，同时用 set! 替代了 setq 。在用 set! 为全局变量赋值前，必须先用 define 创建这个变量。 2. 在 Scheme 中，通常用 define 定义有名函数，它行使着 defun 和 defvar 在 Common Lisp 中的功能。Common Lisp 的： (defun foo (x) (1+ x)) 有两种可能的 Scheme 翻译： ~~~ (define foo (lambda (x) (1+ x))) (define (foo x) (1+ x)) ~~~ 1. 在 Common Lisp 中，函数的参数按从左到右的顺序求值。而在 Scheme 中，有意地不对求值顺序加以规定。(并且语言的实现者对于忘记这点的人幸灾乐祸。) 2. Scheme 不用 t 和 nil ，相应的，它有 #t 和 #f 。空列表，()，在某些实现里为真，而在另一些实现里为假。 3. cond 和 case 表达式里的默认子句在 Scheme 中带有 else 关键字，而不是 Common Lisp 中的 t 。 4. 某些内置操作符的名字被改掉了：consp 成了 pair? ，而 null 则是 null? ，mapcar (几乎) 是 map ，等等。通常根据上下文，应该能看出这些操作符的意思。 [示例代码 20.1]： Scheme 和 Common Lisp 之间的一些区别 续延可以理解成是一种广义的闭包。闭包就是一个函数加上一些指向闭包创建时可见的词法变量的指针。续延则是一个函数加上一个指向其创建时所在的整个栈的指针。当续延被求值时，它返回的是使用自己的栈拷贝算出的结果，而没有用当前栈。如果某个续延是在 T1 时刻创建的，而在 T2 时刻被求值，那么它求值时使用的将是 T1 时刻的栈。 Scheme 程序通过内置操作符 call-with-current-continuation (缩写为 call/cc) 来访问当前续延。当一个程序在一个单个参数的函数上调用 call/cc 时： ~~~ (call-with-current-continuation (lambda (cc) ...)) ~~~ 这个函数将被传进另一个代表当前续延的函数。通过将 cc 的值存放在某个地方，我们就可以保存在 call/cc 那一点上的计算状态。 在这个例子里，我们 append 出一个列表，列表的最后一个元素是一个 call/cc 表达式的返回值： ~~~ > (define frozen) FROZEN > (append '(the call/cc returned) (list (call-with-current-continuation (lambda (cc) (set! frozen cc) 'a)))) (THE CALL/CC RETURNED A) ~~~ 这个 call/cc 返回了 a ，但它首先将续延保存在了全局变量 frozen 中。 调用 frozen 会导致在 call/cc 那一点上的旧的计算重新开始。无论我们传给 frozen 什么值，这个值都将作为 call/cc 的值返回： ~~~ > (frozen 'again) (THE CALL/CC RETURNED AGAIN) ~~~ 续延不会因为被求值而用完。它们可以被重复调用，就像任何其他的函数型对象一样： ~~~ > (frozen 'thrice) (THE CALL/CC RETURNED THRICE) ~~~ 当我们在某些其他的计算里调用一个续延时，我们可以更清楚地看到所谓返回到原先的栈上是什么意思： ~~~ > (+ 1 (frozen 'safely)) (THE CALL/CC RETURNED SAFELY) ~~~ 这里，紧接着的 + 当 frozen 调用时被忽略掉了。后者返回到了它首次被创建时的栈上：先经过 list ，然后是 append ，直到 toplevel。如果 frozen 像正常函数调用那样返回了一个值，那么上面的表达式将在试图给一个列表加 1 时产生一个错误。 各续延并不会每人都分到自己的一份栈的拷贝。它们可能跟其他续延或者当前正在进行的计算共享一些变量。在下面这个例子里，两个续延共享了同一个栈： ~~~ > (define froz1) FROZ1 > (define froz2) FROZ2 > (let ((x 0)) (call-with-current-continuation (lambda (cc) (set! froz1 cc) (set! froz2 cc))) (set! x (1+ x)) x) 1 ~~~ 因此调用任何一个都将返回后继的整数： ~~~ > (froz2 ()) 2 > (froz1 ()) 3 ~~~ 由于 call/cc 表达式的值将被丢弃，所以无论我们给 froz1 和 froz2 什么参数都无关紧要。 现在能保存计算的状态了，我们可以用它做什么呢？第 21-24 章致力于使用续延的应用。这里将要考察一个比较简单的例子，它能够体现出使用保存状态编程的特色：假设有一组树，我们想从每棵树都取出一个元 素，组成一个列表，直到获得一个满足某种条件的组合。 树可以用嵌套列表来表示。第 5.6 节上描述了一种将一类树表示成列表的方法。这里我们采用另一种方法，允许内部节点带有(原子的) 值，以及任意数量的孩子。在这种表示方法里，内部节点变成了一个列表；其 car 包含保存在这个节点上的值，其 cdr 包含该节点孩子的表示。例如，[示例代码 20.2] 里显示的两棵树可以被表示成： ~~~ (define t1 '(a (b (d h)) (c e (f i) g))) (define t2 '(1 (2 (3 6 7) 4 5))) a 1 b c 2 d e f g 3 4 5 h i 6 7 (a) t1 (b) t2 ~~~ ## [示例代码 20.2]： 两棵树 [示例代码 20.3]： 用续延来遍历树 ~~~ (define (dft tree) (cond ((null? tree) ()) ((not (pair? tree)) (write tree)) (else (dft (car tree)) (dft (cdr tree))))) (define *saved* ()) (define (dft-node tree) (cond ((null? tree) (restart)) ((not (pair? tree)) tree) (else (call-with-current-continuation (lambda (cc) (set! *saved* (cons (lambda () (cc (dft-node (cdr tree)))) *saved*)) (dft-node (car tree))))))) (define (restart) (if (null? *saved*) 'done (let ((cont (car *saved*))) (set! *saved* (cdr *saved*)) (cont)))) (define (dft2 tree) (set! *saved* ()) (let ((node (dft-node tree))) (cond ((eq? node 'done) ()) (else (write node) (restart))))) ~~~ * * * [示例代码 20.3] 中的函数能在这样的树上做深度优先搜索。在实际的程序里，我们可能想要在遇到节点时用它们做一些事。这里只是打印它们。为了便于比较，这里给出的函数 dft 实现了通常的深度优先遍历： ~~~ > (dft t1) ABDHCEFIG() ~~~ 函数 dft-node 按照同样的路径遍历这棵树，但每次只处理一个节点。当 dft-node 到达一个节点时，它跟着节点的 car 走，并且在 *saved* 里压入一个续延来浏览其 cdr 部分。 ~~~ > (dft-node t1) A ~~~ 调用 restart 可以继续遍历，作法是弹出最近保存的续延并调用它。 ~~~ > (restart) B ~~~ 最后，所有之前保存的状态都用完了，restart 通过返回 done 来通告这一事实： ~~~ . . . > (restart) G > (restart) DONE ~~~ 最后，函数 dft2 把我们刚刚手工完成的工作干净漂亮地一笔带过： ~~~ > (dft2 t1) ABDHCEFIG() ~~~ 注意到在dft2 的定义里没有显式的递归或迭代：后继的节点被打印出来，是因为由 restart 引入的续延总是返回到 dft-node 中同样的 cond 子句那里。 这种程序的工作方式就跟采矿差不多。它先调用 dft-node 初步挖出一个矿坑。一旦返回值不是 done ，dft-node 后面的代码将调用 restart 将控制权发回到栈上。这个过程会一直持续，直到到返回值表明矿被采空。这时，dft2 将不再打印返回值，而是返回 #f 。使用续延的搜索方式带来了一种编写程序的新思路：将合适的代码放在栈上，然后不断地返回到那里来获得结果。 如果我们只是想同时遍历一棵树，就像 dft2 里那样，那么实在没有必要使用这种技术。dft-node 的优势在于，可以同时运行它的多个实例。假设有两棵树，并且我们想要以深度优先的顺序生成其中元素的叉积。 ~~~ > (set! *saved* ()) () > (let ((node1 (dft-node t1))) (if (eq? node1 'done) 'done (list node1 (dft-node t2)))) (A 1) > (restart) (A 2) . . . > (restart) (B 1) . . . ~~~ 借助常规技术，我们必须采取显式的措施来保存我们在两棵树中的位置。而通过续延，则能非常自然地维护两个正在进行的遍历操作的状态。对于诸如本例的简单情形，要保存我们在树中的位置还不算太难。树是持久性的数据结构，所以我们至少有办法找到 "我们在树中的位置"。续延的过人之处在于，即使没有持久性的数据结构与之关联，它同样可以在任何的计算过程中轻松保存我们的位置。这一计算甚至也不需要具有有限数量的状态，只要重启它们有限次就行了。 正如第24 章将要展示的，这两种考虑被证实在 Prolog 的实现中至关重要。在 Prolog 程序里，"搜索树" 并非真正的数据结构，而只是程序生成结果的一种隐式方式。而且这些树经常是无穷大的，这种情况下，我们不能指望在搜索下一棵树之前把整棵树都搜完，所以只得想个办法保存我们的位置，除此之外别无选择。 ### 20.2 续延传递宏 虽然 Common Lisp 没有提供 call/cc ，但是再加把劲，我们就可以像在 Scheme 里那样做到同样的事情了。 本节展示如何用宏在 Common Lisp 程序中构造续延。Scheme 的续延给了我们两样东西： 1. 续延被创建时所有变量的绑定。 2. 计算的状态 从那时起将要发生什么。 在一个词法作用域的 Lisp 里，闭包给了我们前者。可以看出我们也能使用闭包来获得后者，办法是把计算的状态同样也保存在变量绑定里。 * * * **[示例代码 20.4] 续延传递宏** ~~~ (defvar *actual-cont* #'values) (define-symbol-macro \*cont\* *actual-cont*) (defmacro =lambda (parms &body body) '#'(lambda (\*cont\* ,@parms) ,@body)) (defmacro =defun (name parms &body body) (let ((f (intern (concatenate 'string "=" (symbol-name name))))) '(progn (defmacro ,name ,parms '(,',f \*cont\* ,,@parms)) (defun ,f (\*cont\* ,@parms) ,@body)))) (defmacro =bind (parms expr &body body) '(let ((\*cont\* #'(lambda ,parms ,@body))) ,expr)) (defmacro =values (&rest retvals) '(funcall \*cont\* ,@retvals)) (defmacro =funcall (fn &rest args) '(funcall ,fn \*cont\* ,@args)) (defmacro =apply (fn &rest args) '(apply ,fn \*cont\* ,@args)) ~~~ * * * [示例代码 20.4] 给出的宏让我们能在保留续延的情况下，进行函数调用。这些宏取代了几个内置的 Common Lisp form，它们被用来定义函数，进行函数调用，以及返回函数值。 如果有函数需要使用续延，或者这个函数所调用的函数要用到续延，那么该函数就该用=defun 而不是 defun 定义。=defun 的语法和 defun 相同，但其效果有些微妙的差别。=defun 定义的并不是单单一个函数，它实际上定义了一个函数和一个宏，这个宏会展开成对该函数的调用。(宏定义必须在先，原因是被定义的函数有可能会调用自己。) 函数的主体就是传给=defun 的那个，但还另有一个形参，即 *cont* ，它被连接在原有的形参列表上。在宏展开式里，*cont* 会和其他参数一同传给这个函数。所以 ~~~ (=defun add1 (x) (=values (1+ x))) ~~~ 宏展开成 ~~~ (progn (defmacro add1 (x) '(=add1 \*cont\* ,x)) (defun =add1 (\*cont\* x) (=values (1+ x)))) ~~~ 当调用add1 时，实际被调用的不是函数而是个宏。这个宏会展开成一个函数调用，但是另外带了一个参数：*cont*。所以，在调用 =defun 定义的操作符的时候，*cont* 的当前值总是被默默地传递着。 那 *cont* 有什么用呢？它将被绑定到当前的续延。=values 的定义显示了这个续延的用场。只要是用 =defun 定义的函数，都必须通过 =values 来返回值，或者调用另一个使用 =values 的函数。=values 的语法与 Common Lisp 的values 相同。如果有个带有相同数量参数的 =bind 等着它的话，它可以返回多值， 但它不能返回多值到 toplevel。 参数 *cont* 告诉那个由 =defun 定义的函数对其返回值做什么。当 =values 被宏展开时，它将捕捉 *cont* ，并用它模拟从函数返回值的过程。表达式 ~~~ (=values (1+ n)) ~~~ 会展开成 ~~~ (funcall \*cont\* (1+ n)) ~~~ 在 toplevel 下，*cont* 的值是 #'values，这就相当于一个真正的 values 多值返回。当我们在 toplevel 下调用 (add1 2) 时，这个调用的宏展开式与下式等价 ~~~ (funcall #'(lambda (\*cont\* n) (=values (1+ n))) \*cont\* 2) ~~~ *cont* 的引用在这种情况下将得到全局绑定。因而，=values 表达式在宏展开后将等价于下式 ~~~ (funcall #'values (1+ n)) ~~~ 即把在 n 上加 1，并返回结果。 在类似 add1 的函数里，我们克服了重重困难，不过是为了模拟 Lisp 进行函数调用和返回值的过程： ~~~ > (=defun bar (x) (=values (list 'a (add1 x)))) BAR > (bar 5) (A 6) ~~~ 关键在于，现在有了 "函数调用" 和 "函数返回" 可供差遣，而且如果愿意的话，我们还可以把它们用在其他地方。 我们之所以能获得续延的效果，要归功于对 *cont* 的操控。虽然 *cont* 的值是全局的，但这个全局变量很少用到：*cont* 几乎总是一个形参，它被 =values 以及用 =defun 定义的宏所捕捉。例如在 add1 的函数体里，*cont* 就是一个形参而非全局变量。这个区别是很重要的，因为如果 *cont* 不是一个局部变量的话这些宏将无法工作。 [示例代码 20.4] 中的第三个宏，=bind ，其用法和 multiple-value-bind 相同。它接受一个参数列表，一个表达式，以及一个代码体：参数将被绑定到表达式返回的值上，而代码体在这些绑定下被求值。倘若一个由 =defun 定义的函数，在被调用之后，需要对另一个表达式进行求值，那么就应该使用=bind 宏。 ~~~ > (=defun message () (=values 'hello 'there)) MESSAGE > (=defun baz () (=bind (m n) (message) (=values (list m n)))) BAZ > (baz) (HELLO THERE) ~~~ 注意到 =bind 的展开式会创建一个称为 *cont* 的新变量。baz 的主体展开成： ~~~ (let ((\*cont\* #'(lambda (m n) (=values (list m n))))) (message)) ~~~ 然后会变成： ~~~ (let ((\*cont\* #'(lambda (m n) (funcall \*cont\* (list m n))))) (=message \*cont\*)) ~~~ 由于 *cont* 的新值是 =bind 表达式的代码体，所以当 message 通过函数调用 *cont* 来 "返回" 时，结果将是去求值这个代码体。尽管如此(并且这里是关键)，在=bind 的主体里： ~~~ #'(lambda (m n) (funcall \*cont\* (list m n))) ~~~ 作为参数传递给=baz 的*cont* 仍然是可见的，所以当代码的主体求值到一个=values 时，它将能够返回到最初的主调函数那里。所有闭包环环相扣：每个*cont* 的绑定都包含了上一个*cont* 绑定的闭包，它们串成一条锁链，锁链的尽头指向那个全局的值。 在这里，我们也可以观察到更小规模的同样现象： ~~~ > (let ((f #'values)) (let ((g #'(lambda (x) (funcall f (list 'a x))))) #'(lambda (x) (funcall g (list 'b x))))) #<Interpreted-Function BF6326> > (funcall * 2) (A (B 2)) ~~~ 本例创建了一个函数，它是含有指向g 的引用的闭包，而g 本身也是一个含有到f 的引用的闭包。第 6.3 节上的网络编译器中曾构造过类似的闭包链。 剩下两个宏，分别是=apply 和=funcall ，它们适用于由=lambda 定义的函数。注意那些用=defun 定义出来的"函数"，因为它们的真实身份是宏，所以不能作为参数传给apply 或funcall。解决这个问题的方法类似于第 8.2 节上提到的技巧。也就是把调用包装在另一个=lambda 里面： ~~~ > (=defun add1 (x) (=values (1+ x))) ADD1 > (let ((fn (=lambda (n) (add1 n)))) (=bind (y) (=funcall fn 9) (format nil "9 + 1 = ~A" y))) "9 + 1 = 10" ~~~ [示例代码 20.5] 总结了所有因续延传递宏而引入的限制。如果有函数既不保存续延，也不调用其他保存续延的函数，那它就没有必要使用这些特殊的宏。比如像list 这样的内置函数就没有这个需要。 [示例代码 20.6] 中把来自[示例代码 20.3] 的代码⁴ 从Scheme 翻译成了Common Lisp，并且用续延传递宏代替了Scheme 续延。以同一棵树为例，dft2 和之前一样工作正常： ⁴译者注：这段代码与原书有一些出入：首先 (setq *saved* nil) 被改为 (defvar *saved* nil)；其次将restart 改为re-start 以避免和Common Lisp 已有的符号冲突，并且将re-start 的定义放在dft-node 的定义之前以确保后者在编译时可以找到re-start 的定义。 1. 一个用=defun 定义的函数的参数列表必须完全由参数名组成。 2. 使用续延，或者调用其他做这件事的函数的函数，必须用=lambda 或=defun 来定义。 3. 这些函数必须终结于用=values 来返回值，或者调用其他遵守该约束的函数。 4. 如果一个=bind ，=values ，或者=funcall 表达式出现在一段代码里，它必须是一个尾调用。任何在=bind 之后求值的代码必须放在其代码体里。所以如果我们想要依次有几个=bind ，它们必须被嵌套： * * * **[示例代码 20.5] 续延传递宏的限制** ~~~ (=defun foo (x) (=bind (y) (bar x) (format t "Ho ") (=bind (z) (baz x) (format t "Hum.") (=values x y z)))) ~~~ * * * **[示例代码 20.6] 使用续延传递宏的树遍历** ~~~ (defun dft (tree) (cond ((null tree) nil) ((atom tree) (princ tree)) (t (dft (car tree)) (dft (cdr tree))))) (defvar *saved* nil) (=defun re-start () (if *saved* (funcall (pop *saved*)) (=values 'done))) (=defun dft-node (tree) (cond ((null tree) (re-start)) ((atom tree) (=values tree)) (t (push #'(lambda () (dft-node (cdr tree))) *saved*) (dft-node (car tree))))) (=defun dft2 (tree) (setq *saved* nil) (=bind (node) (dft-node tree) (cond ((eq node 'done) (=values nil)) (t (princ node) (re-start))))) ~~~ * * * ~~~ > (setq t1 '(a (b (d h)) (c e (f i) g)) t2 '(1 (2 (3 6 7) 4 5))) (1 (2 (3 6 7) 4 5)) > (dft2 t1) ABDHCEFIG NIL ~~~ 和 Scheme 里一样，我们仍然可以保存多路遍历的状态，尽管这个例子会显得有些冗长： ~~~ > (=bind (node1) (dft-node t1) (if (eq node1 'done) 'done (=bind (node2) (dft-node t2) (list node1 node2)))) (A 1) > (re-start) (A 2) . . . > (re-start) (B 1) . . . ~~~ 通过把词法闭包编结成串，Common Lisp 程序得以构造自己的续延。幸运的是，这些闭包是由 [示例代码 20.4] 中血汗工厂给出的宏编织而成的，用户可以不用关心它们的出处，而直接享用劳动成果。 第21–24 章都以某种方式依赖于续延。这些章节将显示续延是一种能力非凡的抽象。它可能不会很快，如果是在语言层面之上，用宏实现的话，其性能可能会更会大打折扣。但是，我们基于续延构造的抽象层可以大大加快某些程序的编写速度，而且提高编程效率也有着其实际意义。 ### 20.3 Code-Walker 和 CPS Conversion 从前一节里描述的宏，我们看到了一种折衷。只有用特定的方式编写程序，我们才能施展续延的威力。 [示例代码 20.5] 的第 4 条规则意味着我们必须把代码写成 ~~~ (=bind (x) (fn y) (list 'a x)) ~~~ 而不能是 ~~~ (list 'a ; wrong (=bind (x) (fn y) x)) ~~~ 真正的 call/cc 就不会把这种限制强加于程序员。call/cc 可以捕捉到所有程序中任意地方的续延。尽管我们也能实现具有 call/cc 所有功能的操作符，但那还要做很多工作。本节会大略提一下，如果真要这样做的话，还有哪些事有待完成。 Lisp 程序可以转换成一种称为 "continuation-passingstyle" (续延传递风格) 的形式。经过完全的  转换的程序是不可读的，但我们可以通过观察被部分转换了的代码来体会这个过程的思想。下面这个用于求逆列表的函数： ~~~ (defun rev (x) (if (null x) nil (append (rev (cdr x)) (list (car x))))) ~~~ 产生的等价续延传递版本： ~~~ (defun rev2 (x) (revc x #'identity)) (defun revc (x k) (if (null x) (funcall k nil) (revc (cdr x) #'(lambda (w) (funcall k (append w (list (car x)))))))) ~~~ 在 continuation-passingstyle 里，函数得到了一个附加的形参(这里是k)，其值将是当前的续延。这个续延是个闭包，它代表了对函数的当前值应该做些什么。在第一次递归时，续延是 identity；此时函数的任务就是返回其当前的值。在第二次递归时，续延将等价于 ~~~ #'(lambda (w) (identity (append w (list (car x))))) ~~~ 也就是说要做的事就是追加一个列表的 car 到当前的值上，然后返回它。 一旦可以进行 CPS 转换，实现 call/cc 就易如反掌了。在带有  转换的程序里，当前的整个续延总是存在的，这样 call/cc 就可以实现成一个简单的宏，将一些函数作为一个参数来和它一起调用就好了。 为了做 CPS 转换，我们需要 code-walker，它是一种能够遍历程序源代码树的程序。为 Common Lisp 编写 code-walker 并非易事。要真正能有用，code-walker 的功能不能仅限于简单地遍历表达式。它还需要相当了解表达式的作用。例如，code-walker 不能只是在符号的层面上思考。比如，符号至少可以代表，它本身，一个函数，变量，代码块名称，或是一个 go 标签。code-walker 必须根据上下文，分辨出符号的种类，并进行相应的操作。 由于编写code-walker 超出了本书的范围，所以本章里描述的宏只是最现实的替代品。本章中的宏将用户跟构建续延的工作分离开了。如果有用户编写了相当接近于  的程序，这些宏可以做其余的事情。第4 条规则实际上说的是：如果紧接着=bind 表达式的每样东西都在其代码体里，那么在 *cont* 的值和=bind 主体中的代码之间，程序有足够的信息用来构造当前的续延。 =bind 宏故意写成这样以使得这种编程风格看起来自然些。在实践中由续延传递宏所引入的各种限制还是可以容忍的。 备注： 【注2】由=defun 产生的函数被有意地赋予了intern 了的名字，好让这些函数能够被 trace 。如果没有必要做trace 的话，用gensym 来作为它们的名字应该会更安全些。 【注3】译者注：原文是 "*cont* 的值是 identity"，这是错误的。并且原书勘误修正了[示例代码 20.4] 中对应的 *cont* 定义，这里译文也随之做了修改。 【注4】译者注：原书中在这里还有一句话："at's why *cont* is given its initial value in a setq instead of a defvar： the latter would also proclaim it to be special." 原作者假设*cont* 全局变量是词法作用域的，但这违反了Common Lisp 标准。为了能在现代Common Lisp 实现上运行这些代码，译文采纳了C 上给出的一个解决方案，使用符号宏来模拟词法变量。具体参见[示例代码 20.4] 中修改过的代码。

## 第 19 章 一个查询编译器 在前面章节里定义的有些宏很长。为了生成展开式，`if-match` 需要用到图 18.7 和18.8 中的所有代码，以及 [示例代码 18.1] 中的 `destruc` 。如此之长的宏自然而然地将我们带入最后一个主题：嵌入式语言。如果说短小的宏是Lisp 的扩展，那么大的宏就是在其中定义子语言 可能带有它们自己的语法或者控制结构。我们在 `if-match` 中看出了些端倪，在这个宏里，它有自己的一套表达变量的方式。 我们把实现在 Lisp 中的语言称为嵌入式语言。和 "实用工具" 一样，这个术语并没有严格的定义；`if-match` 可能仍算是实用工具，但它已经开始有一点嵌入式语言的意思了。 嵌入式语言和那些用传统的编译器或解释器实现的语言截然不同。它是用某种现有的语言实现的，实现的方式通常是采用转换。没有必要在基语言和它的扩展之间制造人为的隔阂：可以将两者自由地混用在一起。对于实现者来说，这意味着可以省下大量精力。你可以让你想要的部分实现成嵌入的，而让其余的部分使用基语言。 转换，在 Lisp 里，意味着使用宏。在某种程度上，你可以用预处理器来实现嵌入式语言。但预处理器通常只能操作文本，而宏却可以利用 Lisp 的一个独一无二的特性：在读取器和编译器之间，你的 Lisp 程序被表达成 Lisp 对象的列表。在这个阶段进行转换要更自如一些。 最著名的嵌入式语言例子是 CLOS，即 Common Lisp Object System。如果你想要把一个普通的语言改造成面向对象的版本，那只能写一个新的编译器。在Lisp 里就不是这样了。调整编译器将使  跑得更快，而在理论上，编译器不需要有丝毫改变。这一整套系统都可以用Lisp 写出来。 接下来的章节会给出几个嵌入式语言的例子。本章将描述如何将一个回答数据库查询的程序嵌入到 Lisp 中。(你将会注意到这个程序和 `if-match` 有一系列相通的地方。) 第一节将介绍如何写一个系统，该系统用于解释查询语句。之后，这个程序被重新实现成一个查询编译器，实质上，是实现成了一个巨大的宏, 这既使程序更加高效，也让它能更好地与 Lisp 集成。 ### 19.1 数据库 鉴于当前的目的，数据库的形式并不是关键。所以，这里出于方便起见把信息保存在列表里。例如，我们将 "Joshua Reynolds 是一位生活于 1723 至 1792 年的英国画家" 这个事实表示成： ~~~ (painter reynolds joshua english) (dates reynolds 1723 1792) ~~~ 把信息压缩表示成列表，并无标准办法可循。我们可以依法炮制，也干脆用一个大列表： ~~~ (painter reynolds joshua 1723 1792 english) ~~~ 组织数据库表项的方式由用户来决定。唯一的限制是这些项目(事实) 将用其第一个元素(谓词) 来索引。 在这些约束下，任何一致的形式都可以工作，尽管某些形式的查询速度更快些。 任何数据库系统都至少要支持两种操作：修改数据库，和查询数据库。[示例代码 19.1] 中给出的代码以一个基本的形式提供了这些操作。数据库由一张哈希表表示，表项则是一个个事实，事实的谓词作为哈希表的键值。 尽管图 19.1 中定义的数据库函数支持多个数据库，但它们默认的操作对象都是 `\*default-db\*`。作为 Common Lisp 里的包，那些不需要操作多个数据库的程序甚至不需要关心它们。在本章所有的例子将 只用到 `\*default-db\*`。 * * * **[示例代码 19.1]：基本的数据库函数** ~~~ (defun make-db (&optional (size 100)) (make-hash-table :size size)) (defvar *default-db* (make-db)) (defun clear-db (&optional (db *default-db*)) (clrhash db)) (defmacro db-query (key &optional (db '*default-db*)) '(gethash ,key ,db)) (defun db-push (key val &optional (db *default-db*)) (push val (db-query key db))) (defmacro fact (pred &rest args) '(progn (db-push ',pred ',args) ',args)) ~~~ * * * 我们调用 `clear-db` ，初始化系统，这个命令会清空当前数据库。我们通过给db-query 一个谓词来查询事实，并用 `db-push` 将新事实插入到一个数据库项里。正如第 12.1 节里解释的那样，一个展开成可逆引用的宏其自身也将是可逆的。由于 `db-query` 就是以这种方式定义的，所以我们可以简单地在谓词的 `db-query` 上 `push` 新事实。在 Common Lisp 里，除非特别指定，哈希表中的项被初始化为 `nil` ，这样任何key 在初始时都会有一个空列表与之关联。最后，`fact` 宏用来给数据库加入新事实。 ~~~ > (fact painter reynolds joshua english) (REYNOLDS JOSHUA ENGLISH) > (fact painter canale antonio venetian) (CANALE ANTONIO VENETIAN) > (db-query 'painter) ((CANALE ANTONIO VENETIAN) (REYNOLDS JOSHUA ENGLISH)) T ~~~ 其中，`t` 是 `db-query` 返回的第二个值。而 `db-query` 会展开成 `gethash` ，后者则把它返回的第二个值作为标记，以区别两种情况：即没有发现项目，和发现了一个值为 `nil` 的项目。 ### 19.2 模式匹配查询 之前用 `db-query` 来查询数据库中的数据，其实这种方式不是很灵活。通常用户会想要问的问题不会单单依赖事实的第一个元素。所谓查询语言就是一种用来表达更复杂查询的语言。在一个典型的查询语言里， 用户可以询问所有满足某些约束组合的值 例如，所有生于 `1697` 年的画家的姓氏。 我们的程序将提供一种声明式的查询语言。在这种查询语言中，由用户指定答案必须满足的约束，而把如何生成答案的麻烦事留给系统。这样表达查询和人们日常会话中的方式很类似。对于我们的程序，我们可 以要求系统找出所有这样的：存在一个 `(painter ...)` 形式的事实，以及一个 `(dates 1697 ...)`形式的事实，以此来表达这个例子查询。如此，就能通过下面这个查询来引用所有生于 1697 年的画家： ~~~ (and (painter ?x ?y ?z) (dates ?x 1697 ?w)) ~~~ 我们的程序不但接受由谓词和一些参数组成的简单查询，还将能够回答由 `and` 和 `or` 这些逻辑操作符连接而成的任意复杂查询。图 19.2 中给出了查询语言的语法。 * * * **[示例代码 19.2] 查询语法** ~~~ <query> : (<symbol> <argument>*) : (not <query>) : (and <query>*) : (or <query>*) <argument> : ?<symbol> : <symbol> : <number> ~~~ * * * 由于事实是用它们的谓词来索引的，所以变量不能出现在谓词的位置上。如果你愿意放弃索引带来的好处，你可以通过总是使用相同的谓词，并且使第一个参数成为事实上的标准谓词来绕过这个限制。 和许多类似的系统一样，这个程序对于真值采取怀疑论的观点：除了已知的事实之外，其他所有陈述都是错误的。如果问题中的事实不在数据库里，`not` 操作符就会成功。某种程度上，你可以使用`Wayne's World`【注1】 的方式显式地表达逻辑假： ~~~ (edible motor-oil not) ~~~ 就算这样，`not` 操作符也不会对这些事实另眼相待。 在编程语言里，解释性和编译性的程序之间有着根本的区别。在本章实现查询的时候，我们也将体会到这一点。查询解释器接受查询，并根据它从数据库里生成答案。而查询编译器接受查询，然后生成一个程序，当这个程序运行时，会得出相同的结果。接下来几节里，会先描述一个查询解释器，然后再实现一个查询编译器。 ### 19.3 一个查询解释器 为了实现一个声明式的查询语言，我们将使用在第 18.4 节定义的模式匹配工具。[示例代码 19.3] 中的函数可以解释 [示例代码 19.2] 那种形式的查询。这段代码里的核心函数是 `interpret-query`，它递归地对复杂查询的数据结构进行处理，在这个过程中生成绑定。复杂查询的求值按从左到右的顺序进行，就像 Common Lisp 本身那样。 当递归进行到代表事实的模式上时，`interpret-query` 调用 `lookup`。这里正是模式匹配发生的地方。函数 `lookup` 接受一个由谓词及其参数列表所组成的模式，然后返回一个能够使模式匹配到数据库中某个事实的所有绑定的列表。它首先获取所有该谓词的数据库表项，然后调用match (18.5 节) 把它们和模式逐一比较。每当匹配成功，就返回一个绑定列表，然后 lookup 返回一个含有所有这些列表的列表。 ~~~ > (lookup 'painter '(?x ?y english)) (((?Y . JOSHUA) (?X . REYNOLDS))) ~~~ 然后，这些结果会根据旁边的逻辑操作符或被滤除，或被组合。最终的结果将以列表的形式返回，其中，列表的元素是绑定的集合。如果用[示例代码 19.4] 中所给出的断言，那么下面是本章先前例子对应的结果： ~~~ > (interpret-query '(and (painter ?x ?y ?z) (dates ?x 1697 ?w))) (((?W . 1768) (?Z . VENETIAN) (?Y . ANTONIO) (?X . CANALE)) ((?W . 1772) (?Z . ENGLISH) (?Y . WILLIAM) (?X . HOGARTH))) ~~~ 这是一个普适的原则，即查询可以无限制地组合和嵌套。在少数情况下，查询语法会有一些细微的限制，但分析完一些例子，了解了这部分代码的用法之后，我们就能很从容地处理这些问题了。 * * * **[示例代码 19.3]：查询解释器** ~~~ (defmacro with-answer (query &body body) (let ((binds (gensym))) '(dolist (,binds (interpret-query ',query)) (let ,(mapcar #'(lambda (v) '(,v (binding ',v ,binds))) (vars-in query #'atom)) ,@body)))) (defun interpret-query (expr &optional binds) (case (car expr) (and (interpret-and (reverse (cdr expr)) binds)) (or (interpret-or (cdr expr) binds)) (not (interpret-not (cadr expr) binds)) (t (lookup (car expr) (cdr expr) binds)))) (defun interpret-and (clauses binds) (if (null clauses) (list binds) (mapcan #'(lambda (b) (interpret-query (car clauses) b)) (interpret-and (cdr clauses) binds)))) (defun interpret-or (clauses binds) (mapcan #'(lambda (c) (interpret-query c binds)) clauses)) (defun interpret-not (clause binds) (if (interpret-query clause binds) nil (list binds))) (defun lookup (pred args &optional binds) (mapcan #'(lambda (x) (aif2 (match x args binds) (list it))) (db-query pred))) ~~~ * * * **[示例代码 19.4]：一些作为示例的事实断言** ~~~ (clear-db) (fact painter hogarth william english) (fact painter canale antonio venetian) (fact painter reynolds joshua english) (fact dates hogarth 1697 1772) (fact dates canale 1697 1768) (fact dates reynolds 1723 1792) ~~~ * * * 宏 `with-answer` 提供了一个在 Lisp 程序里使用这个查询解释器的清爽简洁的方法。它的第一个参数可以是任意合法的查询；其余参数被视为一个代码体。`with-answer` 会展开成这样的代码，它收集由查询生成的所有绑定的集合，然后用每个绑定集合所指定的变量来迭代整个代码体。出现在一个`with-answer` 的查询里的变量(通常) 可以在其代码体里使用。当查询成功但却不含有变量时，`with-answer` 只求值代码体一次。 每一个名字叫 Hogarth 的画家的姓氏和国籍。 ~~~ > (with-answer (painter hogarth ?x ?y) (princ (list ?x ?y))) (WILLIAM ENGLISH) NIL ~~~ 每一个生于 1697 年的画家的姓氏。(我们最初的例子) ~~~ > (with-answer (and (painter ?x _ _) (dates ?x 1697 _)) (princ (list ?x))) (CANALE)(HOGARTH) NIL ~~~ 每一个卒于 1772 年或者 1792 年的人的姓氏和出生年份。 ~~~ > (with-answer (or (dates ?x ?y 1772) (dates ?x ?y 1792)) (princ (list ?x ?y))) (HOGARTH 1697)(REYNOLDS 1723) NIL ~~~ 每一个不和某个威尼斯画家生于同年的英国画家的姓氏。 * * * **[示例代码 19.5] 使用查询解释器** > (with-answer (and (painter ?x _ english) (dates ?x ?b _) (not (and (painter ?x2 _ venetian) (dates ?x2 ?b _)))) (princ ?x)) REYNOLDS NIL * * * 根据定义在 [示例代码 19.4] 中的数据库，[示例代码 19.5] 中罗列了一些带中文翻译的查询作例子。因为模式匹配是由 `match` 完成的，因此在模式中可以使用下划线作为通配符。 为了让这些例子不至于太长，查询的代码体中的代码仅仅打印了查询结果。一般而言，`with-answer`的代码体中可以由任何 Lisp 表达式构成。 ### 19.4 绑定上的限制 对于哪些变量将会被一个查询所绑定这个问题上存在一些限制。例如，为什么下列查询 ~~~ (not (painter ?x ?y ?z)) ~~~ 应该将任何绑定赋值给 `?x` 和 `?y` 呢？存在无限多种不是某个画家名字的 `?x` 和 `?y` 的组合。因此我们加了一个限制：`not` 操作符将过滤掉那些已生成的绑定，例如这里 ~~~ (and (painter ?x ?y ?z) (not (dates ?x 1772 ?d))) ~~~ 但你不能指望它会全自动地生成绑定。我们在生成绑定集合的时候，必须先找出所有的画家，然后再排除那些没有生于 1772 年的。要是我们写子句的顺序相反： ~~~ (and (not (dates ?x 1772 ?d)) (painter ?x ?y ?z)) ; wrong ~~~ 那么，只要存在任何生于 1772 年的画家，结果将是 `nil` 。即使在第一个例子里，我们也不该认为可以在 `with-answer` 表达式的代码体里使用 `?d` 的值。 同样，形如 `(or )` 的表达式只保证可以实际生成那些出现在所有 里的变量的绑定。如果一个 `with-answer` 包含了查询 ~~~ (or (painter ?x ?y ?z) (dates ?x ?b ?d)) ~~~ 你可以预期?x 的绑定是可用的，因为无论哪一个子查询成功了，它都会生成一个 ?x 的绑定。但不管是 ?y 还是 ?b 都不保证可以从查询中得到绑定，尽管它其中一个子查询可以。没有被查询绑定的模式变量在迭代时将是 nil 。 ### 19.5 一个查询编译器 [示例代码 19.3] 中的代码实现了我们想要的功能，但效率不彰。首先，尽管查询结构在编译期就是已知的，程序还是把分析工作放在了运行期完成。其次，程序通过构造列表来保存变量绑定，其实，本可以用变量来保存它们自己的值的。我们不妨换一种方式定义 with-answer ，同时解决这两个问题。 [示例代码 19.6] 定义了一个新版的 `with-answer` 。这个新的实现秉承了一个传统，它始于 `avg`(13.1 节)，在 `if-match` (18.4 节) 继承了下来：新的实现在编译期完成了原来旧版本在运行期的大部分工作。[示例代码 19.6] 和 [示例代码 19.3] 中的代码貌似一模一样，但前者中的函数无一是在运行期调用的。这些函数不再生成绑定，它们直接生成代码，而这些生成的代码将成为 `with-answer`展开式的一部分。在运行期，这些代码将根据当前数据库的状态，产生满足查询要求的绑定。 从效果上来看，这个程序是一个巨大的宏。[示例代码 19.7] 中显示了 `with-answer` 宏展开后的模样。大多数的工作是由 `pat-match` (18.4 节) 完成的，它本身也是一个宏。现在，运行期需要的新函数就只有[示例代码 19.1] 中给出的基本的数据库函数了。 虽然在 `toplevel` 下调用 `with-answer` ，对查询进行编译处理几乎没什么好处。表示查询的代码被生成，求值，然后就被扔在一边。但是当with-answer 表达式出现在Lisp 程序里的时候，表示查询的代码就成为了其宏展开的一部分。这样，当编译包含查询的程序时，所有的查询代码都将在这个过程中被内联(inline) 编译。 尽管这个新方法的主要优势是性能，但它也让 `with-answer` 表达式更好地融入了它所在的代码。这具体表现在两个改进上。首先，查询中的参数现在被求值了，所以我们可以说： ~~~ > (setq my-favorite-year 1723) 1723 > (with-answer (dates ?x my-favorite-year ?d) (format t "~A was born in my favorite year.~%" ?x)) REYNOLDS was born in my favorite year. NIL ~~~ 虽然在查询解释器里同样可以做到这点，但代价是必须显式调用 `eval`。而且即便如此，在查询参数中还是无法引用词法变量。 由于现在查询中的参数都会被求值，所以任何不会求值到其自身的字面参数(例如 english ) 都应该被引用起来。(见[示例代码 19.8]) 新方法的第二个优点是：它现在可以更容易地在查询中包含普通的 Lisp 表达式。查询编译器增加了一个 lisp 操作符，它可以跟任意 Lisp 表达式。就像 not 操作符那样，它不会生成任何绑定，但它将排除那些使表达式返回nil 的绑定。在需要使用诸如> 的内置谓词时，lisp 操作符就能帮上忙： ~~~ > (with-answer (and (dates ?x ?b ?d) (lisp (> (- ?d ?b) 70))) (format t "~A lived over 70 years.~%" ?x)) CANALE lived over 70 years. HOGARTH lived over 70 years. ~~~ 一个实现良好的嵌入式语言可以跟基语言在这两方面都结合得天衣无缝。 除了这两个附加特性以外 参数的求值以及新的 lisp 操作符 查询编译器和查询解释器支持的查询语言是完全相同的。[示例代码 19.8]显示了有查询编译器用 [示例代码 19.4] 中定义的数据库所生成的示例结果。 * * * **[示例代码 19.6] 查询编译器** ~~~ (defmacro with-answer (query &body body) '(with-gensyms ,(vars-in query #'simple?) ,(compile-query query '(progn ,@body)))) (defun compile-query (q body) (case (car q) (and (compile-and (cdr q) body)) (or (compile-or (cdr q) body)) (not (compile-not (cadr q) body)) (lisp '(if ,(cadr q) ,body)) (t (compile-simple q body)))) (defun compile-simple (q body) (let ((fact (gensym))) '(dolist (,fact (db-query ',(car q))) (pat-match ,(cdr q) ,fact ,body nil)))) (defun compile-and (clauses body) (if (null clauses) body (compile-query (car clauses) (compile-and (cdr clauses) body)))) (defun compile-or (clauses body) (if (null clauses) nil (let ((gbod (gensym)) (vars (vars-in body #'simple?))) '(labels ((,gbod ,vars ,body)) ,@(mapcar #'(lambda (cl) (compile-query cl '(,gbod ,@vars))) clauses))))) (defun compile-not (q body) (let ((tag (gensym))) '(if (block ,tag ,(compile-query q '(return-from ,tag nil)) t) ,body))) ~~~ * * * 我们曾提到，把表达式编译后再求值，比将其作为列表送给 `eval` 更胜一筹。第 17.2 节对个中原委解释了两点。前者更快，而且允许表达式在外围的词法上下文中进行求值。对查询加以编译的优点与之非常相似。通常要在运行期做的事现在在编译期就完成了。而且因为这些查询在编译后和周围的 Lisp 代码成为了一体，所以它们得以利用词法上下文。 * * * **[示例代码 19.7] 同一查询的两个展开式** ~~~ (with-answer (painter ?x ?y ?z) (format t "~A ~A is a painter.~%" ?y ?x)) ~~~ 被解释器展开成： ~~~ (dolist (#:g1 (interpret-query '(painter ?x ?y ?z))) (let ((?x (binding '?x #:g1)) (?y (binding '?y #:g1)) (?z (binding '?z #:g1))) (format t "~A ~A is a painter.~%" ?y ?x))) ~~~ 而被编译器展开成： ~~~ (with-gensyms (?x ?y ?z) (dolist (#:g1 (db-query 'painter)) (pat-match (?x ?y ?z) #:g1 (progn (format t "~A ~A is a painter.~%" ?y ?x)) nil))) ~~~ * * * 每一个名字叫 **Hogarth** 的画家的姓氏和国籍。 ~~~ > (with-answer (painter 'hogarth ?x ?y) (princ (list ?x ?y))) (WILLIAM ENGLISH) NIL ~~~ 每一个不跟某个威尼斯画家生于同年的英国画家的姓氏。 ~~~ > (with-answer (and (painter ?x _ 'english) (dates ?x ?b _) (not (and (painter ?x2 _ 'venetian) (dates ?x2 ?b _)))) (princ ?x)) REYNOLDS NIL ~~~ 每一个死于 1770 年到 1800 年开区间的画家的姓氏和死亡年份。 备注： 【注1】译者注：Wayne's World 是上世纪 90 年代 NBC 拍摄的系列短剧，后被改编为电影，中文名为《反斗智多星》。其中的角色经常用类似"这是历史的巧合，才怪！" 的方式表达否定和挖苦的情绪。该剧让这种故意搞怪的表达方式在北美变得流行起来。

## 第 18 章 解构 解构(destructuring) 是赋值的一般形式。操作符 `setq` 和 `setf` 的赋值对象只是独立的变量。而解构把赋值和访问操作合二为一：在这里，我们不再只是把单个变量作为第一个参数，而是给出一个关于变量的模式，在这个模式中，赋给每个变量的值将来自某个结构中对应的位置。 ### 18.1 列表上的解构 从 **CLTL2** 开始，Common Lisp 包括了一个名为 destructuring-bind 的新宏。这个宏在第 7 章里简单介绍过。这里将更仔细地了解它。假设 lst 是一个三元素列表，而我们想要绑定 `x` 到第一个元素，`y` 到第二个，`z` 到第三个。在原始 ****CLTL1**** 的 Common Lisp 里，只能这样表达： ~~~ (let ((x (first lst)) (y (second lst)) (z (third lst))) ...) ~~~ 借助新宏我们只需说： ~~~ (destructuring-bind (x y z) lst ...) ~~~ 这样处理，既短小，又清楚。读者对于视觉形象的感受力比单纯的文字要敏锐很多。使用后一种形式，`x` ，`y` 和 `z` 之间的关系可以一览无余；而在前一种形式下，我们必须稍作思考才看得出来。 如果这样简单的情形都能通过使用解构而变得更清晰，试想一下它在更复杂情况下会带来什么样的改观吧。`destrucuring-bind` 的第一个参数可以是任意复杂的一棵树。想象 ~~~ (destructuring-bind ((first last) (month day year) . notes) birthday ...) ~~~ 如果用 `let` 和列表访问函数来写将会是什么样子。这引出了另一个要点：解构使得程序更容易写也更容易读。 解构在 **CLTL1** 的 Common Lisp 里确实也有过。如果上例中的模式看起来眼熟的话，那是因为它们和宏的参数列表具有相同的形式。事实上，`destructuring` 就是就是用来处理宏参数列表的代码，只不过现在拿出来单卖了。任何可以放进宏参数列表里的东西，你都可以把它置于这个匹配模式中，不过有个无关紧要的例外(那个 `&environment` 关键字)。 建立各种绑定总的来说是一个很有吸引力的想法。接下来的几个小节会介绍这个主题的几个变化。 ### 18.2 其他结构 没有理由把解构仅限于列表。解构同样适用于各种复杂对象。本节展示如何编写用于其他类型对象的类似 destructuring-bind 的宏。 下一步，自然是去处理一般性的序列。[示例代码 18.1] 中定义了一个名为 `dbind` 的宏，它和`destrucuring-bind` 类似，不过可以用在任何种类的序列上。第二个参数可以是列表，向量或者它们的任意组合： * * * **[示例代码 18.1]：通用序列解构操作符** ~~~ (defmacro dbind (pat seq &body body) (let ((gseq (gensym))) '(let ((,gseq ,seq)) ,(dbind-ex (destruc pat gseq #'atom) body)))) (defun destruc (pat seq &optional (atom? #'atom) (n 0)) (if (null pat) nil (let ((rest (cond ((funcall atom? pat) pat) ((eq (car pat) '&rest) (cadr pat)) ((eq (car pat) '&body) (cadr pat)) (t nil)))) (if rest '((,rest (subseq ,seq ,n))) (let ((p (car pat)) (rec (destruc (cdr pat) seq atom? (1+ n)))) (if (funcall atom? p) (cons '(,p (elt ,seq ,n)) rec) (let ((var (gensym))) (cons (cons '(,var (elt ,seq ,n)) (destruc p var atom?)) rec)))))))) (defun dbind-ex (binds body) (if (null binds) '(progn ,@body) '(let ,(mapcar #'(lambda (b) (if (consp (car b)) (car b) b)) binds) ,(dbind-ex (mapcan #'(lambda (b) (if (consp (car b)) (cdr b))) binds) body)))) ~~~ * * * ~~~ > (dbind (a b c) #(1 2 3) (list a b c)) (1 2 3) > (dbind (a (b c) d) '(1 #(2 3) 4) (list a b c d)) (1 2 3 4) > (dbind (a (b . c) &rest d) '(1 "fribble" 2 3 4) (list a b c d)) (1 #\f "ribble" (2 3 4)) ~~~ `#(` 读取宏用于表示向量，而 `#\` 则用于表示字符。由于 `"abc" = #(#\a #\b #\c)`，所以 "fribble" 的第一个元素是字符 `#f` 。为了简单起见，`dbind` 只支持 `&rest` 和 `&body` 关键字。 和迄今为止见过的大多数宏相比，`dbind` 俨然是个庞然大物。这个宏的实现之所以值得好好研究一番，原因不仅仅是为了理解它的工作方式，更是为了它能给我们上一课，课的内容对于 Lisp 编程是通用的。正如第 3.4 节提到的，我们在编写 Lisp 程序时，可以有意识地让它们更易于测试。在多数代码里，我们必须要权衡这一诉求和代码速度上的需求。幸运的是，如第 7.8 节所述，速度对于展开器代码来说不是那么要紧。当编写用来生成宏展开式的代码时，我们可以让自己放轻松一些。`dbind`的展开式由两个函数生成，`destruc` 和 `dbind-ex` 。也许它们两个可以被合并成一个函数，一步到位。但是何苦呢？作为两个独立的函数，它们将更容易测试。为什么要牺牲这个优势，换来我们并不需要的速度呢？ 第一个函数是 `destruc` ，它遍历匹配模式，将每个变量和运行期对应对象的位置关联在一起： > (destruc '(a b c) 'seq #'atom) ((A (ELT SEQ 0)) (B (ELT SEQ 1)) (C (ELT SEQ 2))) 可选的第三个参数是个谓词，它用来把模式的结构和模式的内容区分开。 为了使访问更有效率，一个新的变量(生成符号) 将被绑定到每个子序列上： ~~~ > (destruc '(a (b . c) &rest d) 'seq) ((A (ELT SEQ 0)) ((#:G2 (ELT SEQ 1)) (B (ELT #:G2 0)) (C (SUBSEQ #:G2 1))) (D (SUBSEQ SEQ 2))) ~~~ `destruc` 的输出被发送给 `dbind-ex` ，后者被用来生成宏展开代码。它将 `destruc` 产生的树转化成一系列嵌套的 `let` ： ~~~ > (dbind-ex (destruc '(a (b . c) &rest d) 'seq) '(body)) (LET ((A (ELT SEQ 0)) (#:G4 (ELT SEQ 1)) (D (SUBSEQ SEQ 2))) (LET ((B (ELT #:G4 0)) (C (SUBSEQ #:G4 1))) (PROGN BODY))) ~~~ 注意到 `dbind` ，和 `destructuring-bind` 一样，假设它将发现所有它寻找的列表结构。最后剩下的变量并不是简单地绑定到nil ，就像 `multiple-value-bind` 那样。如果运行期给出的序列里没有包含所有期待的元素，解构操作符将产生一个错误： ~~~ > (dbind (a b c) (list 1 2)) >>Error: 2 is not a valid index for the sequence (1 2) ~~~ 其他有内部结构的对象该怎么处理呢？通常还有数组，它和向量的区别在于其维数可以大于一。如果我们为数组定义解构宏，我们怎样表达匹配模式呢？对于两维数组，用列表还是比较实际的。[示例代码 18.2] 含有一个宏【注1】，`with-matrix` ，用于解构两维数组。 ~~~ > (setq ar (make-array '(3 3))) #<Simple-Array T (3 3) C2D39E> > (for (r 0 2) (for (c 0 2) (setf (aref ar r c) (+ (* r 10) c)))) NIL > (with-matrix ((a b c) (d e f) (g h i)) ar (list a b c d e f g h i)) (0 1 2 10 11 12 20 21 22) ~~~ 对于大型数组，或者维数是3 或更高的数组来说，我们就需要另辟奚径。我们不大可能把一个大数组里的每一个元素都绑定到变量上。将匹配模式做成数组的稀疏表达将会更实际一些 只包含用于少数元素的变量，加上用来标识它们的坐标。[示例代码 18.2] 中的第二个宏就采用了这个思路。这里我们用它来得到前一个数组在对角线上的元素： * * * ~~~ ;; [示例代码 18.2]：数组上的解构 (defmacro with-matrix (pats ar &body body) (let ((gar (gensym))) '(let ((,gar ,ar)) (let ,(let ((row -1)) (mapcan #'(lambda (pat) (incf row) (let ((col -1)) (mapcar #'(lambda (p) '(,p (aref ,gar ,row ,(incf col)))) pat))) pats)) ,@body)))) (defmacro with-array (pat ar &body body) (let ((gar (gensym))) '(let ((,gar ,ar)) (let ,(mapcar #'(lambda (p) '(,(car p) (aref ,gar ,@(cdr p)))) pat) ,@body)))) ~~~ * * * ~~~ > (with-array ((a 0 0) (d 1 1) (i 2 2)) ar (values a d i)) 0 11 22 ~~~ * * * **[示例代码 18.3]：结构体上的解构** ~~~ (defmacro with-struct ((name . fields) struct &body body) (let ((gs (gensym))) '(let ((,gs ,struct)) (let ,(mapcar #'(lambda (f) '(,f (,(symb name f) ,gs))) fields) ,@body)))) ~~~ * * * 通过这个新宏，我们开始逐渐跳出那些认为元素必须以固定顺序出现的思维模式。我们可以做出一个类似形式的宏，用它来绑定变量到 `defstruct` 所建立的结构体字段上。[示例代码 18.3] 中就这样定义一个宏。模式中的第一个参数被接受为与结构体相关联的前缀，其余的都是字段名。为了建立访问调用，这个宏使用了 `symb` (第 4.7 节)。 ~~~ > (defstruct visitor name title firm) VISITOR > (setq theo (make-visitor :name "Theodebert" :title 'king :firm 'franks)) #S(VISITOR NAME "Theodebert" TITLE KING FIRM FRANKS) > (with-struct (visitor- name firm title) theo (list name firm title)) ("Theodebert" FRANKS KING) ~~~ ### 18.3 引用 **CLTL** 自带了一个用于解构实例的宏。假设 `tree` 是一个带有三个 `slot` 的类：`species`、`age` 和`height` ，而 `my-tree` 是一 个 `tree` 的实例。在 ~~~ (with-slots (species age height) my-tree ...) ~~~ 的里面我们可以像常规变量那样引用 `my-tree` 的这些 `slot`。在 `with-slots` 的主体中，符号`height` 指向 `height slot`。`height` 并不是简单地绑定到了对应 `slot` 里的变量，而是直接引用到那个 `slot` 上。所以，如果我们写： ~~~ (setq height 72) ~~~ 那么也将给 `my-tree` 的 `height` 这个 `slot` 一个 `72` 的值。这个宏的工作原理是将 `height` 定义为一个展开到 `slot` 引用的符号宏(第 7.11 节)。事实上，`symbol-macrolet` 就是为了支持像 `with-slots` 这样的宏才被加入到 Common Lisp 中的。 无论 `with-slots` 事实上是不是一个解构宏，它在实际编程中所起的作用和d estructuring-bind 是一样的。虽然通常的解构都是按值调用(call-by-value)，这种新型解构却是按名调用(call-by-name)。无论我们如何调用它，它对我们都是有用的。还有其他什么宏，我们可以依法炮制呢？ * * * **[示例代码 18.4] 序列上的引用解构** ~~~ (defmacro with-places (pat seq &body body) (let ((gseq (gensym))) '(let ((,gseq ,seq)) ,(wplac-ex (destruc pat gseq #'atom) body)))) (defun wplac-ex (binds body) (if (null binds) '(progn ,@body) '(symbol-macrolet ,(mapcar #'(lambda (b) (if (consp (car b)) (car b) b)) binds) ,(wplac-ex (mapcan #'(lambda (b) (if (consp (car b)) (cdr b))) binds) body)))) ~~~ * * * 我们可以这样做：将解构宏展开成 `symbol-macrolet` 而不是 `let` ，这样，就可以为任何解构宏创建出与之对应的按名调用版本。[示例代码 18.4] 给出了一个被修改成与 `with-slots` 行为类似的`dbind` 版本。我们可以像使用 dbind 一样来使用 `with-places` ： ~~~ > (with-places (a b c) #(1 2 3) (list a b c)) (1 2 3) ~~~ 但这个新宏还给我们 `setf` 序列位置的选项，就像我们在 `with-slots` 里所做的那样： ~~~ > (let ((lst '(1 (2 3) 4))) (with-places (a (b . c) d) lst (setf a 'uno) (setf c '(tre))) lst) (UNO (2 TRE) 4) ~~~ 就像在 `with-slots` 里那样，这些变量现在都指向了序列中的对应位置。尽管如此，这里还有一个重要的区别：你必须使用 `setf` 而不是 `setq` 来设置这些伪变量。`with-slots` 宏必须引入一个`code-walker`(第 20.3 节) 来将其体内的 `setq` 转化成 `setf`。这里，写一个 `code-walker` 将需要写很多代码，但是带来的好处却不大。 如果 `with-places` 比 `dbind` 更通用，为什么不干脆只用它呢？`dbind` 将一个变量关联一个值上，而 `with-places` 却是将变量关联到一组用来找到一个值的指令集合上。每一个引用都需要进行一次查询。 当 `dbind` 把 `c` 绑定到 `(elt x 2)` 的值上时，`with-places` 将使 `c` 成为一个展开成 `(elt x 2)`的符号宏。 所以如果c 在宏体中被求值了 次，那将会产生 次对elt 的调用。除非你真的想要 setf 那些由解构创建的变量，否则dbind 将会更快一些。 `with-places` 的定义和 `dbind` ([示例代码 18.1]) 相比仅有轻微的变化。在 `wplac-ex` (之前的dbind-ex) 中那些 `let` 变成了 `symbol-macrolet` 。通过类似的改动，我们也可以为任何正常的解构宏做出一个按名调用的版本。 ### 18.4 匹配 正如解构是赋值的泛化，模式匹配是解构的泛化。"模式匹配" 这个术语有许多含义。在这里的语境中，它指的是这样的操作：比较两个结构，结构中可能含有变量，判断是否存在某种给变量赋值的方式使得它们俩相等。例如，如果 `?x` 和 `?y` 是变量，那么这两个列表 ~~~ (p ?x ?y c ?x) (p a b c a) ~~~ 当 `?x = a` 并且 `?y = b` 时匹配。而列表 ~~~ (p ?x b ?y a) (p ?y b c a) ~~~ 当 `?x = ?y = c` 时匹配。 假设一个程序通过跟外部数据源交换信息的方式工作。为了回复一个消息，程序必须首先知道消息的类型，并且还要取出它的特定内容。通过一个匹配操作符我们可以将这两步并成一步。 要写出这种操作符，必须先想出一种区分变量的办法。我们不能直接把所有符号都当成变量，因为需要让符号在模式中以参数的形式出现。这里我们规定：模式变量是以问号开始的符号。如果将来觉得不方便了，只要重定义谓词var? 就可以改变这个约定。 [示例代码 18.5] 包含一个模式匹配的函数，它跟一些 Lisp 入门读物里的匹配函数样子差不多。我们传给 `match` 两个列表，如果它们可以匹配，将得到另一个列表，该列表会显示它们是如何匹配的： ~~~ > (match '(p a b c a) '(p ?x ?y c ?x)) ((?Y . B) (?X . A)) T > (match '(p ?x b ?y a) '(p ?y b c a)) ((?Y . C) (?X . ?Y)) T > (match '(a b c) '(a a a)) NIL NIL ~~~ 在 `match` 逐个元素地比较它的参数时，它建立起来了一系列值和变量之间的赋值关系，这种关系被称为绑定。这些变量是由参数 `binds` 给出的。若匹配成功，`match` 返回其生成的绑定，否则返回`nil` 。由于并非所有成功的匹配都能生成绑定，所以和 gethash 一样，`match` 用第二个返回值来表示匹配成功与否： ~~~ > (match '(p ?x) '(p ?x)) NIL T ~~~ * * * **[示例代码 18.5] 匹配函数** ~~~ (defun match (x y &optional binds) (acond2 ((or (eql x y) (eql x '_) (eql y '_)) (values binds t)) ((binding x binds) (match it y binds)) ((binding y binds) (match x it binds)) ((varsym? x) (values (cons (cons x y) binds) t)) ((varsym? y) (values (cons (cons y x) binds) t)) ((and (consp x) (consp y) (match (car x) (car y) binds)) (match (cdr x) (cdr y) it)) (t (values nil nil)))) (defun varsym? (x) (and (symbolp x) (eq (char (symbol-name x) 0) #\?))) (defun binding (x binds) (labels ((recbind (x binds) (aif (assoc x binds) (or (recbind (cdr it) binds) it)))) (let ((b (recbind x binds))) (values (cdr b) b)))) ~~~ * * * 当 `match` 像上面那样返回 `nil` 和 `t` 时，它表示一个没有产生任何绑定的成功的匹配。 和 `Prolog` 一样，`match` 也把 `_` (下划线) 用作通配符。它可以匹配任何东西，并且对绑定没有任何影响： * * * **[示例代码 18.6]：慢的匹配操作符** ~~~ > (match '(a ?x b) '(_ 1 _)) ((?X . 1)) T (defmacro if-match (pat seq then &optional else) '(aif2 (match ',pat ,seq) (let ,(mapcar #'(lambda (v) '(,v (binding ',v it))) (vars-in then #'atom)) ,then) ,else)) (defun vars-in (expr &optional (atom? #'atom)) (if (funcall atom? expr) (if (var? expr) (list expr)) (union (vars-in (car expr) atom?) (vars-in (cdr expr) atom?)))) (defun var? (x) (and (symbolp x) (eq (char (symbol-name x) 0) #\?))) ~~~ * * * 有了 `match` ，可以很容易地写出一个模式匹配版本的 `dbind` 。[示例代码 18.6] 中含有一个称为`if-match` 的宏。 像 `dbind` 那样，它的前两个参数是一个模式和一个序列，然后它通过比较模式跟序列来建立绑定。不过，它用另外两个参数取代了代码主体：一个 `then` 子句，在新绑定下被求值，如果匹配成功的话；以及一个 `else` 子句在匹配失败时被求值。这里有一个简单的使用 `if-match` 的函数： ~~~ (defun abab (seq) (if-match (?x ?y ?x ?y) seq (values ?x ?y) nil)) ~~~ 如果匹配成功了，它将建立 `?x` 和 `?y` 的值，然后返回它们： ~~~ > (abab '(hi ho hi ho) HI HO ~~~ 函数 `vars-in` 返回一个表达式中的所有匹配变量。它调用 `var?` 来测试是否某个东西是一个变量。目前，`var?` 和用来检测绑定列表中变量的 `varsym?` ([示例代码 18.5]) 是相同的，之所以使用独立的两个函数是考虑到我们可能想要给这两类变量采用不同的表示方法。 像在 [示例代码 18.6] 里定义的那样，`if-match` 很短，但并不是非常高效。它在运行期做的事情太多了。我们在运行期把两个序列都遍历了，尽管第一个序列在编译期就是已知的。更糟糕的是，在进行匹配的过程中，我们构造列表来存放变量绑定。如果充分利用编译期已知的信息，就能写出一个既不做任何不必要的比较，也不做任何 `cons` 的 `if-match` 版本来。 如果其中一个序列在编译期已知，并且只有这个序列里含有变量，那么就要另做打算了。在一次对 match 的调用中，两个参数都可能含有变量。通过将变量限制在 if-match 的第一个参数上，就有可能在编译期知道哪些变量将会参与匹配。这里，我们不再创建变量绑定的列表，而是将变量的值保存进这些变量本身。 * * * **[示例代码 18.7] 快速匹配操作符** ~~~ (defmacro if-match (pat seq then &optional else) '(let ,(mapcar #'(lambda (v) '(,v ',(gensym))) (vars-in pat #'simple?)) (pat-match ,pat ,seq ,then ,else))) (defmacro pat-match (pat seq then else) (if (simple? pat) (match1 '((,pat ,seq)) then else) (with-gensyms (gseq gelse) '(labels ((,gelse () ,else)) ,(gen-match (cons (list gseq seq) (destruc pat gseq #'simple?)) then '(,gelse)))))) (defun simple? (x) (or (atom x) (eq (car x) 'quote))) (defun gen-match (refs then else) (if (null refs) then (let ((then (gen-match (cdr refs) then else))) (if (simple? (caar refs)) (match1 refs then else) (gen-match (car refs) then else))))) ~~~ * * * 在 [示例代码 18.7] 和 18.8 中是 `if-match` 的新版本。如果能预见到哪部分代码会在运行期求值，我们不妨就直接在编译期生成它。这里，我们生成的代码仅仅完成需要的那些比较操作，而不是展开成对 `match` 的调用。 如果我们打算使用变量 `?x` 来包含 `?x` 的绑定的话，怎样表达一个尚未被匹配过程建立绑定的变量呢？这里，我们将通过将一个模式变量绑定到一个生成符号以表明其未绑定。所以 `if-match` 一开始会生成代码将所有模式中的变量绑定到生成符号上。在这种情况下，代替了展开成一个 `with-gensyms` ，在编译期做一次符号生成，然后将它们直接插入进展开式是安全的。 * * * **[示例代码 18.8] 快速匹配操作符(续)** ~~~ (defun match1 (refs then else) (dbind ((pat expr) . rest) refs (cond ((gensym? pat) '(let ((,pat ,expr)) (if (and (typep ,pat 'sequence) ,(length-test pat rest)) ,then ,else))) ((eq pat '_) then) ((var? pat) (let ((ge (gensym))) '(let ((,ge ,expr)) (if (or (gensym? ,pat) (equal ,pat ,ge)) (let ((,pat ,ge)) ,then) ,else)))) (t '(if (equal ,pat ,expr) ,then ,else))))) (defun gensym? (s) (and (symbolp s) (not (symbol-package s)))) (defun length-test (pat rest) (let ((fin (caadar (last rest)))) (if (or (consp fin) (eq fin 'elt)) '(= (length ,pat) ,(length rest)) '(> (length ,pat) ,(- (length rest) 2))))) ~~~ * * * 其余的展开由 `pat-match` 完成。这个宏接受和 `if-match` 相同的参数；唯一的区别是它不为模式变量建立任何新绑定。在某些情况下这是一个优点，第 19 章将把 `pat-match` 作为一个独立的操作符来使用。 在新的匹配操作符里，模式内容和模式结构之间的差别将用函数 `simple?` 定义。如果我们想要在模式里使用字面引用，那么解构代码(以及 `vars-in`) 必须被告知不要进入那些第一个元素是 `quote` 的列表。在新的匹配操作符下，我们将可以使用列表作为模式元素，只需简单地将它们引用起来。 与 `dbind` 相似，`pat-match` 调用 `destruc` 来得到一个将要在运行期参与其参数调用的列表。这个列表被传给 `gen-match` 来为嵌套的模式递归生成匹配代码，然后再传给 `match1` ，以生成模式树上每个叶子的匹配代码。 最后出现在一个 `if-match` 展开式中的多数代码都来自 `match1` ，如 [示例代码 18.8], 这个函数分四种情况处理。如果模式参数是一个生成符号，那么它是一个由 `destruc` 创建用于保存子列表的不可见变量，并且所有我们需要在运行期做的就是测试它是否具有正确的长度。如果模式元素是一个通配符 (_)，那么不需要生成任何代码。如果模式元素是一个变量，那么 `match1` 会生成代码去匹配，或者将其设置成，运行期给出的序列的对应部分。否则，模式元素被看作一个字面上的值，而 match1 会生成代码去比较它和序列中的对应部分。 让我们通过例子来了解一下展开式中的某些部分的生成过程。假设我们从下面的表达式开始 ~~~ (if-match (?x 'a) seq (print ?x) nil) ~~~ 这个模式将被传给 `destruc` ，同时带着一些生成符号(不妨简称为 `g` ) 来代表那个序列： ~~~ (destruc '(?x 'a) 'g #'simple?) ~~~ 得到： ~~~ ((?x (elt g 0)) ((quote a) (elt g 1))) ~~~ 在这个列表的开头我们接上 `(g seq)`： ~~~ ((g seq) (?x (elt g 0)) ((quote a) (elt g 1))) ~~~ 然后把结果整个地发给 `gen-match` 。就像 `length` (第 2.8 节) 的原生实现那样，`gen-match` 首先一路递归到列表的结尾，然后在回来的路上构造其返回值。当gen-match 走完所有元素时，它就返回其 `then` 参数，也就是 `(print ?x)`【注2】。在递归回来的路上，这个返回值将作为 `then` 参数传给 `match1` 。现在我们将得到一个像这样的调用： ~~~ (match1 '(((quote a) (elt g 1))) '(print ?x) '<else function>) ~~~ 得到： ~~~ (if (equal (quote a) (elt g 1)) (print ?x) <else function>) ~~~ 然后这些将成为另一个 `match1` 调用的 `then` 参数，得到的值将成为最后的 `match1` 调用的 `then`参数。这个 `if-match` 的完整展开式显示在[示例代码 18.9] 【注3】中。 * * * **[示例代码 18.9] 一个 `if-match` 的展开式** ~~~ (if-match (?x 'a) seq (print ?x)) ~~~ 展开成： ~~~ (let ((?x '#:g1)) (labels ((#:g3 nil nil)) (let ((#:g2 seq)) (if (and (typep #:g2 'sequence) (= (length #:g2) 2)) (let ((#:g5 (elt #:g2 0))) (if (or (gensym? ?x) (equal ?x #:g5)) (let ((?x #:g5)) (if (equal 'a (elt #:g2 1)) (print ?x) (#:g3))) (#:g3))) (#:g3))))) ~~~ * * * 在这个展开式里有两个地方用到了 `gensym` (生成符号)，这两个地方的用意各不相同。在运行时，一些变量被用来保存树的一部分，这些变量的名字是用 `gensym` 生成的，目的是为了避免捕捉。而变量`?x` 在开始的◦ 时候被绑定到了一个 `gensym`，以表明它尚未被匹配操作赋给一个值。 在新的 `if-match` 中，模式元素现在是被求值而不再是被隐式引用了。这意味着 Lisp 变量可以被用于模式中，和被引用的表达式一样： ~~~ > (let ((n 3)) (if-match (?x n 'n '(a b)) '(1 3 n (a b)) ?x)) 1 ~~~ 还有两个进一步的改进，是因为新版本调用了 `destruc` ([示例代码 18.1]) 而出现。现在模式中可以包含 `&rest` 或者 `&body` 关键字(`match` 是不管这一套的)。并且因为 `destruc` 使用了一般的序列操作符 `elt` 和 `subseq` ， 新的 `if-match` 将工作在任何类型的序列上。如果 `abab` 采用新版本来定义，它也可以被用于向量和字符串： ~~~ > (abab "abab") #\a #\b > (abab #(1 2 1 2)) 1 2 ~~~ 事实上，模式可以像 dbind 的模式那样复杂： ~~~ > (if-match (?x (1 . ?y) . ?x) '((a b) #(1 2 3) a b) (values ?x ?y)) (A B) #(2 3) ~~~ 注意到，在第二个返回值里，向量的元素被显示出来了。要想使向量以这种方式被输出，需要将`\*print-array\*` 设置为 `t` 。 在本章，我们开始逐步走进一个崭新的编程领域。以一个简单的用于解构的宏作开端。在 `if-match`的最终版本中，我们有了某种看起来更像是它自己的语言的东西。接下来的章节将要介绍一整类程序，它们秉承的都是相同的理念。 备注: 【注1】译者注：这里稍微修改了一下原书的代码，原书中没有定义 `col` 变量就直接使用了 `(setq col -1)`，这里仿照 `row` 的处理方法用 `let` 建立了一个 `col` 的局部绑定。 【注2】译者注：原文中说返回的 `then` 参数是 `?x` ，这应该是个笔误。 【注3】译者注：原书里有一个笔误，展开式代码中的 `(gensym? x)` 应为 `(gensym? ?x)`。

## 第 17 章 读取宏（read-macro） 在 Lisp 表达式的一生中，有三个最重要的时刻，分别是读取期（read-time），编译期（compile-time） 和运行期（runtime）。运行期由函数左右。宏给了我们在编译期对程序做转换的机会。本章讨论读取宏（read-macro），它们在读取期发挥作用。 ### 17.1 宏字符 按照 Lisp 的一般哲学，你可以在很大程度上控制 `reader` 。它的行为是由那些可随时改变的属性和变量控制的。Reader 可以在几个层面上编程。若要改变其行为，最简单的方式就是定义新的宏字符。 宏字符（macro character） 是一种被 Lisp `reader` 特殊对待的字符。举个例子，小写字母 `a` 的处理方式和小写字母 `b` 是一样的，它们都由常规的处理方式处理。但左括号就有些不同：它告诉 Lisp 开始读取一个列表。 每个这样的字符都有一个与之关联的函数，告诉 Lisp `reader` 当遇到该字符的时候做什么。你可以改变一个已有的宏字符的关联函数，或者定义你自己的新的宏字符。 内置函数 `set-macro-character` 提供了一种定义读取宏的方式。它接受一个字符和一个函数，以后当 `read` 遇到这个字符时，它就返回调用该函数的结果。 * * * **[示例代码 17.1] '(引号)的可能定义** ~~~ (set-macro-character #\' #'(lambda (stream char) (declare (ignore char)) (list 'quote (read stream t nil t)))) ~~~ * * * Lisp 中最古老的读取宏之一是单引号 `'` ，即引用。你也可以不用 `'`，而总是将 `'a` 写成 `(quote a)`，但这将会非常烦人, 而且会降低代码的可读性。引用读取宏使 `(quote a)` 可以简写成 `'a`。我们可以用 [示例代码 17.1] 中的方法实现它。当 `read` 在一个普通的上下文中（例如，不在 `"a'b"`或 `|a'b|` 中） 遇到 `'` 时，它将返回在当前流和字符上调用这个函数的结果。（该函数忽略了它的第二个形参，因为它总是那个引用字符。） 所以当 `read` 看到 `'a` 时，它将返回 `(quote a)`。 `read` 的最后三个参数分别控制：是否在碰到 `end-of-file` 时报错，如果不报错的话返回什么值，以及这个 `read` 调用是否是发生在 `read` 调用中的（译者注：关于 `read` 的最后一个参数（recursive-p），详见 **CLTL** 中对 `read` 的解释。) 。在几乎所有的读取宏里，第二和第四个参数都应该是 `t` ，所以第三个参数也就无关紧要了。 读取宏和常规宏一样，其实质都是函数。和生成宏展开的函数一样，和宏字符相关的函数，除了作用于它读取的流以外，不应该再有其他副作用。Common Lisp 明确声明：一个与宏字符相关联的函数何时被执行，或者被执行几次 Common Lisp 对其将不给予保证。（见 **CLTL2** 的 543 页。） 宏和读取宏在不同的阶段分析和观察你的程序。宏在程序中发生作用时，它已经被 reader 解析成了 Lisp 对象，而读取宏在程序还是文本的阶段时，就对它施加影响了。尽管如此，通过在这些文本上调用 read ，一个读取宏，如果它愿意的话，同样可以得到解析后的 Lisp 对象。这样说来，读取宏至少和常规宏一样强有力。 事实上，读取宏至少在两方面比常规宏更为强大。读取宏可以影响 Lisp 读取的每一样东西，而宏只是在代码里被展开。并且，由于读取宏通常递归地调用 read，一个类似： ~~~ ''a ~~~ 的表达式将变成： ~~~ (quote (quote a)) ~~~ 而如果我们试图用一个普通的宏来为 `quote` 定义缩略语的话： ~~~ (defmacro q (obj) '(quote ,obj)) ~~~ 它在某些情况下可以正常工作： ~~~ > (eq 'a (q a)) T ~~~ 但在被嵌套使用时就不行了。例如： ~~~ (q (q a)) ~~~ 将展开成： ~~~ (quote (q a)) ~~~ 译者注：解决这个问题的正确方法是定义一个编译器宏（compiler-macro）。Common Lisp 内置的 `define-compiler-macro` 用于定义编译器宏，详见 **CLTL** 中关于此操作符的说明。 ### 17.2 `dispatching` 宏字符 `#'` 和其他 `#` 开头的读取宏一样，是一种称为 `dispatching` 读取宏的实例。这些读取宏以两个字符出现，其中第一个字符称为 `dispatch` 字符。这类宏的目的，简单说就是尽可能地充分利用  字符集；如果只有单字符读取宏的话，那么读取宏的数量就会受限于字符集的大小。 你可以（通过使用 `make-dispatch-macro-character`） 来定义你自己的 `dispatching` 宏字符，但由于 `#` 已经定义了，所以你也可以直接用它。一些 `#` 打头的组合就是特意为你保留的；其他的那些，如果 Common Lisp 还没有给它们赋予含义的话，也可以拿来用。完整的列表可见 **CLTL2** 的第 531 页。 * * * **[示例代码17.2] 一个用于常数函数的读取宏** ~~~ (set-dispatch-macro-character #\# #\? #'(lambda (stream char1 char2) (declare (ignore char1 char2)) '#'(lambda (&rest ,(gensym)) ,(read stream t nil t)))) ~~~ * * * 新的 `dispatching` 宏字符组合可以通过调用 `set-dispatch-macro-character` 函数定义，除了接受两个字符参数以外和 `set-macro-character` 的用法差不多。一个预留给程序员的组合是 `#?` 。[示例代码 17.2] 显示了如何将这个组合定义成一个用于常数函数的读取宏。现在 `#?2` 将被读取为一个函数，其接受任意数量的参数，并且返回 `2`。例如： ~~~ > (mapcar #?2 '(a b c)) (2 2 2) ~~~ 这个例子里定义的新操作符看起来相当无聊，但在使用了很多函数型参数的程序里，常常会用到常数函数。 事实上，有些方言提供了一个名叫 `always` 的内置函数，专门用来定义它们。 注意到在这个宏字符的定义中使用宏字符是完全没有问题的：和任何 Lisp 表达式一样，当这个定义被读取以后这些宏字符就都消失了。在 `#?` 的后面使用宏字符也是可以的。因为 `#?` 的定义调用了`read` ，所以诸如 `'` 和 `#'` 此类宏字符也可以正常使用： ~~~ > (eq (funcall #?'a) 'a) T > (eq (funcall #?#'oddp) (symbol-function 'oddp)) T ~~~ ### 17.3 定界符 * * * **[示例代码 17.3] 一个定义定界符的读取宏** ~~~ (set-macro-character #\] (get-macro-character #\))) (set-dispatch-macro-character #\# #\[ #'(lambda (stream char1 char2) (declare (ignore char1 char2)) (let ((accum nil) (pair (read-delimited-list #\] stream t))) (do ((i (ceiling (car pair)) (1+ i))) ((> i (floor (cadr pair))) (list 'quote (nreverse accum))) (push i accum))))) ~~~ * * * 除了简单的宏字符，定义得最多的宏字符要算列表定界符了。另一个为用户预留的组合字符是 `#[` 。[示例代码 17.3] 给出的例子，显示了把这个字符定义成一个更复杂的左括号的方法。它定义形如 `#[x y]` 的表达式，使得这样的表达式被读取为在 `x` 到 `y` 的闭区间上所有整数的列表： ~~~ > #[2 7] (2 3 4 5 6 7) ~~~ 这个读取宏里，唯一的新东西是对 `read-delimited-list` 的调用，这个函数是一个完全为这种情况度身定制的内置函数。它的第一个参数是那个被当作列表结尾的字符。有其名才能行其实，为了把`]` 识别成定界符，程序在开始的地方调用了 `set-macro-character`。 * * * **[示例代码17.4] 一个用于定义定界符读取宏的宏** ~~~ (defmacro defdelim (left right parms &body body) '(ddfn ,left ,right #'(lambda ,parms ,@body))) (let ((rpar (get-macro-character #\)))) (defun ddfn (left right fn) (set-macro-character right rpar) (set-dispatch-macro-character #\# left #'(lambda (stream char1 char2) (declare (ignore char1 char2)) (apply fn (read-delimited-list right stream t)))))) ~~~ * * * 多数潜在的定界符读取宏都将在很大程度上重复 [示例代码 17.3] 中的代码。或许可以写个宏，让它从这些机制中提炼出更抽象的接口，以简化代码。[ 示例代码 17.4] 就是一个实现，我们可以像它那样定义一个实用工具，用其定义定界符读取宏。宏 `defdelim` 接受两个字符，一个参数列表，以及一个代码主体。参数列表和代码主体隐式地定义了一个函数。一个对 defdelim 的调用将首个字符定义为 `dispatching` 读取宏，它读取到第二个字符为止，然后将这个函数应用到它读到的东西，并返回其结果。 无独有偶，[示例代码 17.3] 中的函数体也迫切需要一个实用工具，事实上，这个实用工具已经定义过了：见 4.5 节的 `mapa-b` 。使用 `defdelim` 和 `mapa-b` ，[示例代码 17.3] 中定义的读取宏现在只需写成： ~~~ (defdelim #\[ #\] (x y) (list 'quote (mapa-b #'identity (ceiling x) (floor y)))) ~~~ 定界符读取宏也可以用来做函数复合。第5.4 节定义了一个用于函数复合的操作符： ~~~ > (let ((f1 (compose #'list #'1+)) (f2 #'(lambda (x) (list (1+ x))))) (equal (funcall f1 7) (funcall f2 7))) T ~~~ 当我们复合像 `list` 和 `1+` 这样的内置函数时，没有理由等到运行期才去对 compose 的调用求值。第 5.7 节建议一个替代方案；通过给一个 `compose` 表达式前缀 `sharp-dot` 读取宏: ~~~ #.(compose #'list #'1+) ~~~ 我们可以令其在读取期就被求值。 * * * **[示例代码 17.5]：一个用于函数型复合的读取宏** ~~~ (defdelim #\{ #\} (&rest args) '(fn (compose ,@args))) ~~~ * * * 这里我们给出一个与之类似但更清晰的解决方案。[示例代码 17.5] 中定义的读取宏定义了一个 `#{ }`形式的表达式，这个表达式将被读取成 的复合。这样： ~~~ > (funcall #{list 1+} 7) (8) ~~~ 它生成一个对 `fn` （15.1 节） 的调用，该调用在编译期创建函数。 ### 17.4 这些发生于何时 最后，澄清一个可能造成困惑的问题应该会有所帮助。如果读取宏是在常规宏之前作用的话，那么宏是怎样展开成含有读取宏的表达式的呢？例如，这个宏： ~~~ (defmacro quotable () '(list 'able)) ~~~ 会生成一个带有引用的展开式。还是说它没有生成？事实上，真相是：这个宏定义中的两个引用在这个 `defmacro` 表达式被读取时，就都被展开了，展开结果如下 ~~~ (defmacro quotable () (quote (list (quote able)))) ~~~ 通常，在宏展开式里包含读取宏是没有什么问题的。因为一个读取宏的定义在读取期和编译期之间将不会（或者说不应该） 发生变化。

## 第 16 章 定义宏的宏 代码中的模式通常预示着需要新的抽象。这一规则对于宏代码本身也一样适用。如果几个宏的定义在形式上比较相似，我们就可能写一个编写宏的宏来产生它们。本章展示三个宏定义宏的例子：一个用来定义缩略语，另一个用来定义访问宏，第三个则用来定义在 14.1 节中介绍的那种指代宏。 ### 16.1 缩略语 宏最简单的用法就是作为缩略语。一些 Common Lisp 操作符的名字相当之长。它们中最典型的 (尽管不是最长的) 是 destructuring-bind ，长达 18 个字符。Steele 原则(4.3 节) 的一个直接推论是，常用的操作符应该取个简短的名字。("我们认为加法的成本较低，部分原因是由于我们只要用一个字符 '+' 就可以表示它。") 内置的 destructuring-bind 宏引入了一个新的抽象层，但它在简洁上作出的贡献被它的长名字抹杀了： ~~~ (let ((a (car x)) (b (cdr x))) ...) (destructuring-bind (a . b) x ...) ~~~ 和打印出来的文本相似，程序在每行的字符数不超过 70 的时候，是最容易阅读的。当单个名字的长度达到这个长度的四分之一时，我们就开始觉得不便了。 幸运的是，在像 Lisp 这样的语言里你完全没有必要逆来顺受设计者的每个决定。只要定义了: ~~~ (defmacro dbind (&rest args) '(destructuring-bind ,@args)) ~~~ 你就再也不没必要用那个长长的名字了。对于名字更长也更常用的multiple-value-bind 也是一样的道理。 ~~~ (defmacro mvbind (&rest args) '(multiple-value-bind ,@args)) ~~~ 注意到 dbind 和 mvbind 的定义是何等的相似。确实，使用这种 rest 和逗号-at 的惯用法，就已经能为任意一个函数【注1】、宏，或者 `special form` 定义其缩略语了。既然我们可以让一个宏帮我们代劳，为什么还老是照着 `mvbind` 的模样写出一个又一个的定义呢？ 为了定义一个定义宏的宏，我们通常会要用到嵌套的反引用。嵌套反引用的难以理解是出了名的。尽管最终我们会对那些常见的情况了如指掌，但你不能指望随便挑一个反引用表达式，都能看一眼，就能立即说出它可以产生什么。这不能归罪于 Lisp。就像一个复杂的积分，没人能看一眼就得出积分的结果，但是我们不能因为这个就把问题归咎于积分的表示方法。道理是一样的。难点在于问题本身，而非表示问题的方法。 尽管如此，正如在我们在做积分的时候，我们同样也可以把对反引用的分析拆成多个小一些的步骤，让每一步都可以很容易地完成。假设我们想要写一个 abbrev 宏，它允许我们仅用: ~~~ (abbrev mvbind multiple-value-bind) ~~~ * * * **[示例代码 16.1] 自动定义缩略语** ~~~ (defmacro abbrev (short long) '(defmacro ,short (&rest args) '(,',long ,@args))) (defmacro abbrevs (&rest names) '(progn ,@(mapcar #'(lambda (pair) '(abbrev ,@pair)) (group names 2)))) ~~~ * * * 来定义 mvbind 。[示例代码 16.1] 给出了一个这个宏的定义。它是怎样写出来的呢？这个宏的定义可以从一个示例展开式开始。一个展开式是： ~~~ (defmacro mvbind (&rest args) '(multiple-value-bind ,@args)) ~~~ 如果我们把 multiple-value-bind 从反引用里拉出来的话，就会让推导变得更容易些，因为我们知道它将成为最终要得到的那个宏的参数。这样就得到了等价的定义: ~~~ (defmacro mvbind (&rest args) (let ((name 'multiple-value-bind)) '(,name ,@args))) ~~~ 现在我们将这个展开式转化成一个模板。我们先把反引用放在前面，然后把可变的表达式替换成变量。 ~~~ '(defmacro ,short (&rest args) (let ((name ',long)) '(,name ,@args))) ~~~ 最后一步是通过把代表 name 的 ',long 从内层反引用中消去，来简化表达式： ~~~ '(defmacro ,short (&rest args) '(,',long ,@args)) ~~~ 这就得到了 [示例代码 16.1] 中定义的宏的主体。 [示例代码 16.1] 中还有一个 abbrevs ，它用于我们想要一次性定义多个缩略语的场合. ~~~ (abbrevs dbind destructuring-bind mvbind multiple-value-bind mvsetq multiple-value-setq) ~~~ abbrevs 的用户无需插入多余的括号，因为 abbrevs 通过调用 group (4.3 节) 来将其参数两两分组。对于宏来说，为用户节省逻辑上不必要的括号是件好事，而 group 对于多数这样的宏来说都是有用的。 ### 16.2 属性 Lisp 提供多种方式将属性和对象关联在一起。如果问题中的对象可以表示成符号，那么最便利(尽管可能最低效) 的方式之一是使用符号的属性表。为了描述对象 -- 具有值为 的属性 -- 的这一事实，我们修改的属性表： ~~~ (setf (get o p) v) ~~~ 所以如果说 ball1 的 color 为 red ，我们用： ~~~ (setf (get 'ball1 'color) 'red) ~~~ 如果我们打算经常引用对象的某些属性，我们可以定义一个宏来得到它： ~~~ (defmacro color (obj) '(get ,obj 'color)) ~~~ 然后在 get 的位置上使用 color 就可以了： ~~~ > (color 'ball1) RED ~~~ 由于宏调用对 setf 是透明的(见第 12 章)，我们也可以用： ~~~ > (setf (color 'ball1) 'green) GREEN ~~~ 这种宏会有如下优势：它能把程序表示对象颜色的方式隐藏起来。属性表的访问速度比较慢；程序在将来的版本里，可能会出于速度考虑，将颜色表示成结构体的一个字段，或者哈希表中的一个表项。如果通过类似 color 宏这样的外部接口访问数据，我们可以很轻易地对底层代码做翻天覆地的改动，就算是已经成形的程序也不在话下。如果一个程序从属性表改成用结构体，那么在访问宏的外部接口以上的程序可以原封不动；甚至使用这个接口的代码可以根本就对背后的重构过程毫无察觉。 对于重量这个属性，我们可以定义一个宏，它和为 color 写的那个宏差不多： ~~~ (defmacro weight (obj) '(get ,obj 'weight)) ~~~ 和上节的情况相似，color 和 weight 的定义几乎一模一样。在这里 propmacro ([示例代码 16.2]) 扮演了和 abbrev 相同的角色。 * * * **[示例代码 16.2] 自动定义访问宏** ~~~ (defmacro propmacro (propname) '(defmacro ,propname (obj) '(get ,obj ',',propname))) (defmacro propmacros (&rest props) '(progn ,@(mapcar #'(lambda (p) '(propmacro ,p) props)))) ~~~ * * * 一个用来定义宏的宏可以采用和任何其他宏相同的设计过程：先理解宏调用，然后分析预期的展开式，再想出来如何将前者转化成后者。我们想要 ~~~ (propmacro color) ~~~ 被展开成 ~~~ (defmacro color (obj) '(get ,obj 'color)) ~~~ 尽管这个展开式本身也是一个 defmacro ，我们仍然能够为它做一个模板，先把它放到反引用里，然后把加了逗号的参数名放在color 的实例的位置上。如同前一节那样，我们首先通过转化，让展开式已有的反引 用里面没有 color 实例： ~~~ (defmacro color (obj) (let ((p 'color)) '(get ,obj ',p))) ~~~ 然后我们接下来构造这个模板： ~~~ '(defmacro ,propname (obj) (let ((p ',propname)) '(get ,obj ',p))) ~~~ 再简化成： ~~~ '(defmacro ,propname (obj) '(get ,obj ',',propname)) ~~~ 对于需要把一组属性名全部定义成宏的场合，还有 propmacros ([示例代码 16.2])，它展开到一系列单独的对 propmacro 的调用。就像 abbrevs ，这段不长的代码事实上是一个定义定义宏的宏的宏。 虽然本章针对的是属性表，但这里的技术是通用的。对于以任何形式保存的数据，我们都可以用它定义适用的数据访问宏。 ### 16.3 指代宏 第14.1节已经给出了几种指代宏的定义。当你使用类似 aif 或者 aand 这样的宏时，在一些参数求值的过程中，符号 it 将被绑定到其他参数返回的值上。所以，无需再用: ~~~ (let ((res (complicated-query))) (if res (foo res))) ~~~ 只要说 ~~~ (aif (complicated-query) (foo it)) ~~~ 就可以了，而: ~~~ (let ((o (owner x))) (and o (let ((a (address o))) (and a (city a))))) ~~~ 则可以简化成: ~~~ (aand (owner x) (address it) (city it)) ~~~ 第 14.1 节给出了七个指代宏：aif ，awhen ，awhile ，acond ，alambda ，ablock 和 aand。这七个绝不是唯一有用的这种类型的指代宏。事实上，我们可以为任何 Common Lisp 函数或宏定义出对应的指代变形。这些宏中有许多的情况会和 mapcon 很像：很少用到，可一旦需要就是不可替代的。 例如，我们可以定义 a+ ，让它和 aand 一样，使 it 总是绑定到上个参数返回的值上。下面的函数用来计算 在Massachusetts 的晚餐开销： ~~~ (defun mass-cost (menu-price) (a+ menu-price (* it .05) (* it 3))) ~~~ Massachusetts 的餐饮税是 5%，而顾客经常按照这个税的三倍来计算小费。按照这个公式计算的话， 在 Dolphin 海鲜餐厅吃烤鳕鱼的费用共计： ~~~ > (mass-cost 7.95) 9.54 ~~~ 不过这里还包括了沙拉和一份烤土豆。 * * * **[示例代码 16.3] a+ 和 alist 的定义** ~~~ (defmacro a+ (&rest args) (a+expand args nil)) (defun a+expand (args syms) (if args (let ((sym (gensym))) '(let* ((,sym ,(car args)) (it ,sym)) ,(a+expand (cdr args) (append syms (list sym))))) '(+ ,@syms))) (defmacro alist (&rest args) (alist-expand args nil)) (defun alist-expand (args syms) (if args (let ((sym (gensym))) '(let* ((,sym ,(car args)) (it ,sym)) ,(alist-expand (cdr args) (append syms (list sym))))) '(list ,@syms))) ~~~ * * * [示例代码 16.3] 中定义的 a+ ，依赖于一个递归函数 a+expand ，来生成其展开式。a+expand 的一般策略是对宏调用中的参数列表不断地求 cdr，同时生成一系列嵌套的 let 表达式；每一个 let 都将 it 绑定到不同的参数上，但同时也把每个参数绑定到一个不同的生成符号上。展开函数聚集出一个这些生成符号的列表，并且当到达参数列表的结尾时，它就返回一个以这些生成符号作为参数的+ 表达式。所以表达式: ~~~ (a+ menu-price (* it .05) (* it 3)) ~~~ 得到了展开式： ~~~ (let* ((#:g2 menu-price) (it #:g2)) (let* ((#:g3 (* it 0.05)) (it #:g3)) (let* ((#:g4 (* it 3)) (it #:g4)) (+ #:g2 #:g3 #:g4)))) ~~~ [示例代码 16.3] 中还定义了一个类似的 alist ： ~~~ > (alist 1 (+ 2 it) (+ 2 it)) (1 3 5) ~~~ 历史重演了，a+ 和 alist 的定义几乎完全一样。如果我们想要定义更多像它们那样的宏，这些宏也将在很大程度上大同小异。为什么不写一个程序，让它帮助我们产生这些宏呢？[示例代码 16.4] 中的 defanaph 将达到这个目的。借助defanaph ，宏 a+ 和alist 的定义过程可以简化成: ~~~ (defanaph a+) (defanaph alist) ~~~ 这样定义出的 a+ 和 alist 展开式将和 [示例代码 16.3] 中的代码产生的展开式相同。这个用来定义宏的defanaph 宏将为任何其参数按照正常函数求值规则来求值的东西创建出指代变形来。这就是说，defanaph 将适用于任何参数全部被求值，并且是从左到右求值的东西上。所以你不能用这个版本的 defanaph 来定义 aand 或 awhile ，但你可以用它给任何函数定义出其指代版本。 正如 a+ 调用 a+expand 来生成其展开式，defanaph 所定义的宏也调用 anaphex 来做这个事情。通用展开器 anaphex 跟 a+expand 的唯一不同之处在于其接受作为参数的函数名使其出现在最终的展开式里。事实上，a+ 现在可以定义成： * * * **[示例代码 16.4] 自动定义指代宏** ~~~ (defmacro a+ (&rest args) (anaphex args '(+))) (defmacro defanaph (name &optional calls) (let ((calls (or calls (pop-symbol name)))) '(defmacro ,name (&rest args) (anaphex args (list ',calls))))) (defun anaphex (args expr) (if args (let ((sym (gensym))) '(let* ((,sym ,(car args)) (it ,sym)) ,(anaphex (cdr args) (append expr (list sym))))) expr)) (defun pop-symbol (sym) (intern (subseq (symbol-name sym) 1))) ~~~ * * * 无论 anaphex 还是 a+expand 都不需要被定义成单独的函数：anaphex 可以用 labels 或 alambda 定义在 defanaph 里面。这里把展开式生成器拆成分开的函数只是出于澄清的理由。 默认情况下，defanaph 通过将其参数前面的第一个字母(假设是一个 a ) 拉出来以决定在最后的展开式里调用什么。(这个操作是由 pop-symbol 完成的。) 如果用户更喜欢另外指定一个名字，它可以作为一个可选参数。尽管defanaph 可以为所有函数和某些宏定义出其 anaphoric 变形，但它有一些令人讨厌的局限： > 1. 它只能工作在其参数全部求值的操作符上。 > > > 2. 在宏展开中，it 总被绑定在前一个参数上。在某些场合, 例如 awhen 我们想要 it 始终绑在第一个参数的值上。 > > > 3. 它无法工作在像 setf 这种期望其第一个参数是广义变量的宏上。 让我们考虑一下如何在一定程度上打破这些局限。第一个问题的一部分可以通过解决第二个问题来解决。 为了给类似 aif 的宏生成展开式，我们需要对 anaphex 加以修改，让它在宏调用中只替换第一个参数： ~~~ (defun anaphex2 (op args) '(let ((it ,(car args))) (,op it ,@(cdr args)))) ~~~ 这个非递归版本的 anaphex 不需要确保宏展开式将 it 绑定到当前参数前面的那个参数上，所以它可以生成的展开式没有必要对宏调用中的所有参数求值。只有第一个参数是必须被求值的，以便将 it 绑定到它的值上。所以 aif 可以被定义成： ~~~ (defmacro aif (&rest args) (anaphex2 'if args)) ~~~ 这个定义和 14.1 节上原来的定义相比，唯一的区别在于: 之前那个版本里，如果你传给 aif 参数的个数不对的话，那程序会报错；如果调用宏的方法是正确的话，这两个版本将生成相同的展开式。 至于第三个问题，也就是 defanaph 无法工作在广义变量上的问题，可以通过在展开式中使用 _f (12.4 节) 来解决。像 setf 这样的操作符可以被下面定义的 anaphex2 的变种来处理： ~~~ (defun anaphex3 (op args) '(_f (lambda (it) (,op it ,@(cdr args))) ,(car args))) ~~~ 这个展开器假设宏调用必须带有一个以上的参数，其中第一个参数将是一个广义变量。使用它我们可以这样定义 asetf：【注2】【注3】 * * * **[示例代码 16.5] 更一般的 defanaph** ~~~ (defmacro asetf (&rest args) (anaphex3 '(lambda (x y) (declare (ignore x)) y) args)) (defmacro defanaph (name &key calls (rule :all)) (let* ((opname (or calls (pop-symbol name))) (body (case rule (:all '(anaphex1 args '(,opname))) (:first '(anaphex2 ',opname args)) (:place '(anaphex3 ',opname args))))) '(defmacro ,name (&rest args) ,body))) (defun anaphex1 (args call) (if args (let ((sym (gensym))) '(let* ((,sym ,(car args)) (it ,sym)) ,(anaphex1 (cdr args) (append call (list sym))))) call)) (defun anaphex2 (op args) '(let ((it ,(car args))) (,op it ,@(cdr args)))) (defun anaphex3 (op args) '(_f (lambda (it) (,op it ,@(cdr args))) ,(car args))) ~~~ * * * [示例代码 16.5] 显示了所有三个展开器函数在单独一个宏 defanaph 的控制下拼接在一起的结果。用户可以通过可选的 rule 关键字参数来设置目标宏展开的类型，这个参数指定了在宏调用中参数所采用的求值规则。如果这个参数是： ：all (默认值) 宏展开将采用alist 模型。宏调用中所有参数都将被求值，同时it 总是被绑定在前一个参数的值上。 ：first 宏展开将采用aif 模型。只有第一个参数是必须求值的，并且it 将被绑定在这个值上。 ：place 宏展开将采用asetf 模型。第一个参数被按照广义变量来对待，而it 将被绑定在它的初始值上。 使用新的 defanaph ，前面的一些例子将被定义成下面这样： ~~~ (defanaph alist) (defanaph aif :rule first) (defanaph asetf :rule :place) ~~~ asetf 的一大优势是它可以定义出一大类基于广义变量而不必担心多重求值问题的宏。例如，我们可以将incf 定义成： ~~~ (defmacro incf (place &optional (val 1)) '(asetf ,place (+ it ,val))) ~~~ 再比如说 pull ( 12.4 节)： ~~~ (defmacro pull (obj place &rest args) '(asetf ,place (delete ,obj it ,@args))) ~~~ 备注： 【注1】尽管这种缩略语不能传递给 apply 或者funcall。 【注2】译者注：这里给出的 asetf 采用了原书勘误中给出的形式。未勘误的版本里用 'setf 代替了 '(lambda (x y) (declare (ignore x) y))。这个版本也是有效的,但其中的 setf 是不必要的,真正的广义变量赋值操作是由背后的 _f 宏完成的。比较一下后面给出 incf 宏在一个普通调用 (incf a 1) 下两种 asetf 产生的展开式就可以了解这点了。 【注3】译者注：本书中所有忽略了某些形参的函数定义都由译者添加了类似 (declare (ignore char)) 的声明以免编译器报警。

## 第 15 章 返回函数的宏 第五章已经介绍了如何编写返回函数的函数。宏的应用使得组合操作符这项工作的难度大幅降低。本章将说明如何用宏来构造抽象结构，这些结构和第 5 章里定义的那些抽象是等价的，但是用宏会更清晰和高效。 ### 15.1 函数的构造 若 `f` 和 `g` 均为函数，则 `f ○g(x) = f(g(x))`。 第 5.4 节曾介绍过 把 `○` 实现为 Lisp 函数的方法，这个函数名叫 `compose`： * * * **[示例代码 15.1] 通用的用于构造函数的宏** ~~~ > (funcall (compose #'list #'1+) 2) (3) (defmacro fn (expr) '#',(rbuild expr)) (defun rbuild (expr) (if (or (atom expr) (eq (car expr) 'lambda)) expr (if (eq (car expr) 'compose) (build-compose (cdr expr)) (build-call (car expr) (cdr expr))))) (defun build-call (op fns) (let ((g (gensym))) '(lambda (,g) (,op ,@(mapcar #'(lambda (f) '(,(rbuild f) ,g)) fns))))) (defun build-compose (fns) (let ((g (gensym))) '(lambda (,g) ,(labels ((rec (fns) (if fns '(,(rbuild (car fns)) ,(rec (cdr fns))) g))) (rec fns))))) ~~~ * * * 在本节中，我们将思考如何用宏来定义更好的函数构造器。[示例代码 15.1] 中是一个名为 `fn` 的通用函数构造器，它能够根据复合函数的描述来构造它们。它的参数应该是一个形如`(operator . arguments)` 的表达式。 `operator` 可以是一个函数或宏的名字，也可以是会被区别对待的 `compose .Arguments` 可以是接受一个参数的函数或宏的名字，或者是可作为 `fn` 参数的表达式。例如， ~~~ (fn (and integerp oddp)) ~~~ 产生一个等价于: ~~~ #'(lambda (x) (and (integerp x) (oddp x))) ~~~ 的函数。 如果把 `compose` 用作操作符(operator)，我们就得到一个所有参数复合后得到的函数，但不需要像 compose 被定义为函数时那样的显式 `funcall` 调用。例如， ~~~ (fn (compose list 1+ truncate)) ~~~ 展开成： ~~~ #'(lambda (#:g1) (list (1+ (truncate #:g1)))) ~~~ 后者允许对 `list` 和 `1+` 这种简单函数进行内联编译。`fn` 宏接受一般意义上的操作符名称；`-` 表达式也是允许的，就像: ~~~ (fn (compose (lambda (x) (+ x 3)) truncate)) ~~~ 可以展开成: ~~~ #'(lambda (#:g2) ((lambda (x) (+ x 3)) (truncate #:g2))) ~~~ 毫无疑问，这里由`λ`–表达式表示的函数会被内联编译，要是换成用 `sharp-quoted` 的`λ`–表达式作为参数，传给 `compose` ，那就只得通过 `funcall` 调用了。 第 5.4 节还展示了另外三个函数构造器的定义：`fif` ，`fint` ，以及 `fun`。这些函数现在被统一到了通用的 `fn` 宏。使用 `and` 操作符将产生一个参数操作符的交集： ~~~ > (mapcar (fn (and integerp oddp)) '(c 3 p 0)) (NIL T NIL NIL) ~~~ 而 `or` 操作符则产生并集： ~~~ > (mapcar (fn (or integerp symbolp)) '(c 3 p 0.2)) (T T T NIL) ~~~ 并且 `if` 产生的函数，其函数体是条件执行的： ~~~ > (map1-n (fn (if oddp 1+ identity)) 6) (2 2 4 4 6 6) ~~~ 不过，我们可用的函数不仅仅限于上面三个： ~~~ > (mapcar (fn (list 1- identity 1+)) '(1 2 3)) ((0 1 2) (1 2 3) (2 3 4)) ~~~ 并且 `fn` 表达式里的参数本身也可以是表达式： ~~~ > (remove-if (fn (or (and integerp oddp) (and consp cdr))) '(1 (a b) c (d) 2 3.4 (e f g))) (C (D) 2 3.4) ~~~ 这里虽然 `fn` 把 `compose` 作为一种特殊情况单独处理，但是这样做并没有增加这个宏的功能。如果你把嵌套的参数传给 `fn` ，那就可以得到函数的复合。例如， ~~~ (fn (list (1+ truncate))) ~~~ 展开成： ~~~ #'(lambda (#:g1) (list ((lambda (#:g2) (1+ (truncate #:g2))) #:g1))) ~~~ 这相当于： ~~~ (compose #'list #'1+ #'truncate) ~~~ `fn` 宏把 `compose` 单独处理的目的，只是为了提高这种调用的可读性。 ### 15.2 在 `cdr` 上做递归 第 5.5 和 5.6 节显示了如何编写构造递归函数的函数。接下来两节将介绍指代宏是如何给我们在那里定义的函数提供一个更清晰的接口的。 第 5.5 节显示了如何定义一个称为 `lrec` 的扁平列表递归器。通过 `lrec` ，我们可以将下面这个函数： ~~~ (defun our-every (fn lst) (if (null lst) t (and (funcall fn (car lst)) (our-every fn (cdr lst))))) ~~~ 而把 oddp 的调用表示成： ~~~ (lrec #'(lambda (x f) (and (oddp x) (funcall f))) t) ~~~ 在这里，宏可以让我们事半功倍。为了表达一个递归函数，最起码应该说清楚哪几件事情呢？如果用 it 来指代当前列表的 car，并用 rec 指代递归调用，那么我们就可以把它表示成： ~~~ (alrec (and (oddp it) rec) t) ~~~ [示例代码 15.2] 中定义的宏，就允许我们这样做。 ~~~ > (funcall (alrec (and (oddp it) rec) t) '(1 3 5)) T ~~~ 这个新宏把第二个参数给出的表达式转化成传递给 lrec 的函数，用这种方式实现其功能。由于第二个参数可能会通过指代引用 it 或 rec ，因此，在宏展开式里，函数的主体所处的作用域必须含有为这些符号建立的绑定。 事实上，[示例代码 15.2] 中有两个不同版本的 alrec。前例中使用的版本需要用到符号宏(symbol macro，见第7.11 节)。由于只有较新的 Common Lisp 版本才支持符号宏【注1】，所以[示例代码 15.2] 里也提供了一个相形之下不那么方便的 `alrec` 版本，其中 `rec` 被定义成一个局部函数。代价是，rec 作为函数将不得不被包在括号里： ~~~ (alrec (and (oddp it) (rec)) t) ~~~ 在支持 `symbol-macrolet` 的 Common Lisp 实现里，推荐用最初的版本。 Common Lisp 有独立的函数名字空间，这使得通过这些递归构造器定义有名函数略有不便： ~~~ (setf (symbol-function 'our-length) (alrec (1+ rec) 0)) ~~~ [示例代码 15.2] 中最后一个宏的目的就是为了把这一过程变得更抽象一些。借助 `on-cdrs` ，我们可以只需这样写： * * * **[示例代码 15.2] 递归列表的宏** ~~~ (defun our-length (lst) (on-cdrs (1+ rec) 0 lst)) (defun our-every (fn lst) (on-cdrs (and (funcall fn it) rec) t lst)) (defmacro alrec (rec &optional base) "cltl2 version" (let ((gfn (gensym))) '(lrec #'(lambda (it ,gfn) (symbol-macrolet ((rec (funcall ,gfn))) ,rec)) ,base))) (defmacro alrec (rec &optional base) "cltl1 version" (let ((gfn (gensym))) '(lrec #'(lambda (it ,gfn) (labels ((rec () (funcall ,gfn))) ,rec)) ,base))) (defmacro on-cdrs (rec base &rest lsts) '(funcall (alrec ,rec #'(lambda () ,base)) ,@lsts)) ~~~ * * * **[示例代码 15.3] 用 on-cdrs 定义的 Common Lisp 函数** ~~~ (defun our-copy-list (lst) (on-cdrs (cons it rec) nil lst)) (defun our-remove-duplicates (lst) (on-cdrs (adjoin it rec) nil lst)) (defun our-find-if (fn lst) (on-cdrs (if (funcall fn it) it rec) nil lst)) (defun our-some (fn lst) (on-cdrs (or (funcall fn it) rec) nil lst)) ~~~ * * * [示例代码 15.3] 用这个新宏定义了几个已有的 Common Lisp 函数。通过使用 `on-cdrs` 的表达方式，这些函数化简成了它们最根本的形式，同时，若非这样处理，我们恐怕很难注意到它们间的共同点。 [示例代码 15.4] 中有一些新的实用工具，我们可以很方便地用 `on-cdrs` 来定义它们。前三个分别是：`unions` ，`intersections`，和 `differences` ，它们分别实现了集合的并、交、以及差的操作。虽然 Common Lisp 的内置函数已经实现了这些操作，但它们每次只能用于两个列表。这样的话，如果我们想要找到三个列表的并集就必须这样写： ~~~ > (union '(a b) (union '(b c) '(c d))) (A B C D) ~~~ 新的 `unions` 的行为和 `union` 相似，但前者能接受任意数量的参数，这样我们只需说： ~~~ > (unions '(a b) '(b c) '(c d)) (D C A B) ~~~ 和 union 一样，unions 并不保持初始列表中的元素顺序。 在 Common Lisp 的 `intersection` 和更通用的 `intersections` 之间也有着同样的关系。在这个函数的定义里，为了改善效率，在最开始的地方加入了对于宏参数的 `null` 测试；如果集合中存在空集，它将短路掉整个计算过程。 ~~~ (defun unions (&rest sets) (on-cdrs (union it rec) (car sets) (cdr sets))) ~~~ * * * **[示例代码 15.4] 用 on-cdrs 定义的新实用工具** ~~~ (defun intersections (&rest sets) (unless (some #'null sets) (on-cdrs (intersection it rec) (car sets) (cdr sets)))) (defun differences (set &rest outs) (on-cdrs (set-difference rec it) set outs)) (defun maxmin (args) (when args (on-cdrs (multiple-value-bind (mx mn) rec (values (max mx it) (min mn it))) (values (car args) (car args)) (cdr args)))) ~~~ * * * Common Lisp 也有一个称为 `set-difference` 的函数，它接受两个列表，并返回属于第一个集合但不属于第二个集合的元素： ~~~ > (set-difference '(a b c d) '(a c)) (D B) ~~~ 我们的新版本处理多重参数的方式和 `-` 同出一辙。例如，`(differences x y z)` 就等价于 `(set-difference x (unions y z))` ，只是不像后者那样需要做 `cons`。 ~~~ > (differences '(a b c d e) '(a f) '(d)) (B C E) ~~~ 这些集合操作符仅仅是作为例子。对于它们没有实际的需要，因为内置的 `reduce` 已经能处理上面这些例子所示的列表递归的简单情况。例如，不用: ~~~ (unions ...) ~~~ 的话，你也可以说: ~~~ ((lambda (&rest args) (reduce #'union args)) ...) ~~~ 虽然如此，在一般情况下 `on-cdrs` 比 `reduce` 的功能更强。 因为 `rec` 指向的是一个调用而非一个值，所以我们可以用 `on-cdrs` 来创建返回多值的函数。[示例代码 15.4] 中最后一个函数，`maxmin` ，利用这种可能性在一次列表遍历中同时找出最大和最小的元素： ~~~ > (maxmin '(3 4 2 8 5 1 6 7)) 8 1 ~~~ 后面章节中的代码也可以用上 `on-cdrs` 。例如，`compile-cmds` (第 23.4 节) ~~~ (defun compile-cmds (cmds) (if (null cmds) 'regs '(,@(car cmds) ,(compile-cmds (cdr cmds))))) ~~~ 可以简单地定义成： ~~~ (defun compile-cmds (cmds) (on-cdrs '(,@it ,rec) 'regs cmds)) ~~~ ### 15.3 在子树上递归 宏在列表上进行的递归操作，在子树上也一样可以用递归的方式完成。本节里，我们用宏来给 5.6 节里定义的树递归器定义更加清晰的接口。 在5.6 节里我们定义了两个树递归构造器，分别名为 `ttrav` 和 `trec` 。前者总是遍历完整棵树；后者功能更为复杂，但它允许你控制递归停止的时机。借助这些函数，我们可以把 `our-copy-tree` : ~~~ (defun our-copy-tree (tree) (if (atom tree) tree (cons (our-copy-tree (car tree)) (if (cdr tree) (our-copy-tree (cdr tree)))))) ~~~ 表达成 ~~~ (ttrav #'cons) ~~~ 而一个对 `rfind-if`: ~~~ (defun rfind-if (fn tree) (if (atom tree) (and (funcall fn tree) tree) (or (rfind-if fn (car tree)) (and (cdr tree) (rfind-if fn (cdr tree)))))) ~~~ 的调用，例如 `oddp` ，可以表达成： ~~~ (trec #'(lambda (o l r) (or (funcall l) (funcall r))) #'(lambda (tree) (and (oddp tree) tree))) ~~~ `Anaphoric` 宏可以为 `trec` 做出一个更好的接口，就像前一节中它们对 `lrec` 所做的那样。要满足一般的需求，这个宏将必须能够同时指代引用到三个东西：当前所在树，我们称之为 it；递归下降左子树，我们称之为 `left` ；以及递归下降右子树，我们称之为 `right` 。有了这些约定以后，我们就应该可以像下面这样，用新宏来表达前面的函数： ~~~ (atrec (cons left right)) (atrec (or left right) (and (oddp it) it)) ~~~ [示例代码 15.5] 包含有这个宏的定义。 在没有 `symbol-macrolet` 的 `Lisp` 版本中，我们可以用 [示例代码 15.5] 中的第二个定义来定义`atrec`。这个版本将 `left` 和 `right` 定义成局部函数，所以 `our-copy-tree` 就必须写成： ~~~ (atrec (cons (left) (right))) ~~~ 出于便利，我们也定义了一个 `on-trees` 宏，跟前一节里的 `on-cdrs` 相似。[示例代码 15.6] 显示了用 `on-trees` 定义的四个在 5.6 节里定义的函数。 正如第 5 章里提到的，那一章里的递归生成器构造的函数将不是尾递归的。用 `on-cdrs` 或 `on-trees` 定义出的函数不一定是最高效的实现。和底层的 `trec` 和 `lrec` 一样，这些宏主要用于原型设计以及效率不是关键的那部分程序里面。尽管如此，本章和第 5 章的核心思路是：我们可以先编写函数生成器，然后为它们设计出简洁清爽的宏接口。同样的技术也一样可以用在构造那些能够产生特别高效代码的函数生成器上。 ### 15.4 惰性求值 惰性求值就是说，只有当你需要表达式值的时候，才去求值它。使用惰性求值的方式之一是构造一种叫 `delay` 的对象。`Delay` 是某个表达式的值的替代物。它代表着一个承诺，即：如果今后需要的话，就要给出表达式的值。同时，由于这个承诺本身是个 Lisp 对象，因而它代表的值所有的功用，它都责无旁贷，一肩挑起。所以，一旦有需要，`delay` 就能返回表达式的值。 * * * **[示例代码 15.5] 在树上做递归的宏** ~~~ (defmacro atrec (rec &optional (base 'it)) "cltl2 version" (let ((lfn (gensym)) (rfn (gensym))) '(trec #'(lambda (it ,lfn ,rfn) (symbol-macrolet ((left (funcall ,lfn)) (right (funcall ,rfn))) ,rec)) #'(lambda (it) ,base)))) (defmacro atrec (rec &optional (base 'it)) "cltl1 version" (let ((lfn (gensym)) (rfn (gensym))) '(trec #'(lambda (it ,lfn ,rfn) (labels ((left () (funcall ,lfn)) (right () (funcall ,rfn))) ,rec)) #'(lambda (it) ,base)))) (defmacro on-trees (rec base &rest trees) '(funcall (atrec ,rec ,base) ,@trees)) ~~~ * * * **[示例代码 15.6] 用 on-trees 定义的函数** ~~~ (defun our-copy-tree (tree) (on-trees (cons left right) it tree)) (defun count-leaves (tree) (on-trees (+ left (or right 1)) 1 tree)) (defun flatten (tree) (on-trees (nconc left right) (mklist it) tree)) (defun rfind-if (fn tree) (on-trees (or left right) (and (funcall fn it) it) tree)) ~~~ * * * Scheme 内置了对 delay 的支持。Scheme 的操作符 force 和 delay 就是为此服务的。用 Common Lisp 的话，可以用 [示例代码 15.7] 中的方法来实现这两个操作符。其中，把 delay 表示成了一个由两部分构成的结构体。第一个字段代表 delay 是否已经被求值了，如果是的话就被赋予这个值。第二个字段则是一个闭包，调用它就能得到该 delay 所代表的值。宏 delay 接受一个表达式，并返回一个代表该表达式值的 delay： ~~~ > (let ((x 2)) (setq d (delay (1+ x)))) #S(DELAY ...) ~~~ 若要调用 delay 里的闭包，就得 force 这个 delay。函数 force 接受任意对象：对于普通对象它就是 identity 函数，但对于 delay，它是对 delay 所代表的值的请求。 * * * **[示例代码 15.7] force 和 delay 的实现** ~~~ > (force 'a) A (defconstant unforced (gensym)) (defstruct delay forced closure) (defmacro delay (expr) (let ((self (gensym))) '(let ((,self (make-delay :forced unforced))) (setf (delay-closure ,self) #'(lambda () (setf (delay-forced ,self) ,expr))) ,self))) (defun force (x) (if (delay-p x) (if (eq (delay-forced x) unforced) (funcall (delay-closure x)) (delay-forced x)) x)) ~~~ * * * ~~~ > (force d) 3 ~~~ 无论何时，只要需要处理的对象有可能是 delay ，就应该用 force 对付它。例如，如果我们正在排序的列表可能含有 delay ，那么就要用： ~~~ (sort lst #'(lambda (x y) (> (force x) (force y)))) ~~~ 像这样直接用 delay 显得有些笨拙。要是在实际应用中，它们可能会藏身于另一个抽象层之下。 备注： 【注1】 译者注：这些问题现在已经不复存在，几乎所有的现行 Common Lisp 实现(除了GCL，GNU Common Lisp) 都支持 ANSI Common Lisp 标准。和 CLTL2 相比，几乎没有变化。

## 第 14 章 指代宏 第 9 章只是把变量捕捉视为一种问题 某种意料之外，并且只会捣乱的负面因素。本章将显示变量捕捉 也可以被有建设性地使用。如果没有这个特性，一些有用的宏就无法写出来。 在 Lisp 程序里，下面这种需求并不鲜见：希望检查一个表达式的返回值是否为非空，如果是的话，使用这个值做某些事。倘若求值表达式的代价比较大，那么通常必须这样做： ~~~ (let ((result (big-long-calculation))) (if result (foo result))) ~~~ 难道就不能简单一些，让我们像英语里那样，只要说： ~~~ (if (big-long-calculation) (foo it)) ~~~ 通过利用变量捕捉，我们可以写一个 `if`，让它以这种方式工作。 ### 14.1 指代的种种变形 在自然语言里，指代(anaphor) 是一种引用对话中曾提及事物的表达方式。英语中最常用的代词可能要 算 "it" 了，就像在 "Get the wrench and put it on the table(拿个扳手，然后把它放在桌上)" 里那样。指代给日常语言带来了极大的便利 试想一下没有它会发生什么 但它在编程语言里却很少见。这在很大程度上是为了语言着想。指代表达式常会产生歧义，而当今的编程语言从设计上就无法处理这种二义性。 尽管如此，在 Lisp 程序中引入一种形式非常有限的代词，同时避免歧义，还是有可能的。代词，实际上是一种可捕捉的符号。我们可以通过指定某些符号，让它们充当代词，然后再编写宏有意地捕捉这些符号，用这种方式来使用代词。 在新版的 `if` 里，符号 `it` 就是那个我们想要捕捉的对象。`Anaphoricif`，简称 `aif` ，其定义如下： ~~~ (defmacro aif (test-form then-form &optional else-form) '(let ((it ,test-form)) (if it ,then-form ,else-form))) ~~~ 并如前例中那样使用它： ~~~ (aif (big-long-calculation) (foo it)) ~~~ 当你使用 `aif` 时，符号 `it` 会被绑定到测试表达式返回的结果。在宏调用中，`it` 看起来是自由的，但事实上，在 `aif` 展开时，表达式 `(foo it)` 会被插入到一个上下文中，而 `it` 的绑定就位于该上下文： ~~~ (let ((it (big-long-calculation))) (if it (foo it) nil)) ~~~ 这样一个在源代码中貌似自由的符号就被宏展开绑定了。本章里所有的指代宏都使用了这种技术，并加以变化。 [示例代码 14.1] 包含了一些 Common Lisp 操作符的指代变形。`aif` 下面是 `awhen` ，很明显它是`when` 的指代版本： 原书勘误：(acond (3))将返回 nil 而不是 3。后面的 acond2 也有同样的问题。 * * * **[示例代码 14.1] Common Lisp 操作符的指代变形** ~~~ (defmacro aif (test-form then-form &optional else-form) '(let ((it ,test-form)) (if it ,then-form ,else-form))) (defmacro awhen (test-form &body body) '(aif ,test-form (progn ,@body))) (defmacro awhile (expr &body body) '(do ((it ,expr ,expr)) ((not it)) ,@body)) (defmacro aand (&rest args) (cond ((null args) t) ((null (cdr args)) (car args)) (t '(aif ,(car args) (aand ,@(cdr args)))))) (defmacro acond (&rest clauses) (if (null clauses) nil (let ((cl1 (car clauses)) (sym (gensym))) '(let ((,sym ,(car cl1))) (if ,sym (let ((it ,sym)) ,@(cdr cl1)) (acond ,@(cdr clauses))))))) (awhen (big-long-calculation) (foo it) (bar it)) ~~~ * * * `aif` 和 `awhen` 都是经常会用到的，但 `awhile` 可能是这些指代宏中的唯一一个，被用到的机会比它的正常版的同胞兄弟 `while` (定义于 7.4 节) 更多的宏。一般来说，如果一个程序需要等待(poll) 某个外部数据源的话，类似 `while` 和 `awhile` 这样的宏就可以派上用场了。而且，如果你在等待一个数据源，除非你想做的仅是静待它改变状态，否则你肯定会想用从数据源那里获得的数据做些什么： ~~~ (awhile (poll *fridge*) (eat it)) ~~~ aand 的定义和前面的几个宏相比之下更复杂一些。它提供了一个 `and` 的指代版本；每次求值它的实参，it 都将被绑定到前一个参数返回的值上。 在实践中，`aand` 倾向于在那些做条件查询的程序中使用，例如这里： ~~~ (aand (owner x) (address it) (town it)) ~~~ 它返回 `x` 的拥有者(如果有的话) 的地址(如果有的话) 所属的城镇(如果有的话)。如果不使用 `aand`，该表达式就只能写成: ~~~ (let ((own (owner x))) (if own (let ((adr (address own))) (if adr (town adr))))) ~~~ 尽管人们喜欢把 `and` 和 `or` 相提并论，但实现指代版本的 `or` 没有什么意义。一个 `or` 表达式中的实参只有当它前面的实参求值到 `nil` 才会被求值，所以 `aor` 中的代词将毫无用处。 从 `aand` 的定义可以看出，它的展开式将随宏调用中的实参的数量而变。如果没有实参，那么`aand`，将像正常的 `and` 那样，应该直接返回 `t` 。否则会递归地生成展开式，每一步都会在嵌套的`aif` 链中产生一层： ~~~ (aif <first argument> <expansion for rest of arguments>) ~~~ `aand` 的展开必须在只剩下一个实参时终止，而不是像大多数递归函数那样继续展开，直到 `nil` 才停下来。 倘若递归过程一直进行下去，直到消去所有的合取式，那么最终的展开式将总是下面的模样： ~~~ (aif <C> . . . (aif <Cn> t)...) ~~~ 这样的表达式会一直返回 `t` 或者 `nil` ，因而上面的示例将无法正常工作。 第 10.4 节曾警告过：如果一个宏总是产生包含对其自身调用的展开式，那么展开过程将永不终止。虽然 `aand` 是递归的，但是它却没有这个问题，因为在基本情形里它的展开式没有引用 `aand`。 最后一个例子是 `acond` ，它用于 `cond` 子句的其余部分想使用测试表达式的返回值的场合。(这种需求非常普遍，以至于 Scheme 专门提供了一种方式来使用 `cond` 子句中测试表达式的返回值。) 在 `acond` 子句的展开式里，测试结果一开始时将被保存在一个由 `gensym` 生成的变量里，目的是为了让符号 `it` 的绑定只在子句的其余部分有效。当宏创建这些绑定时，它们应该总是在尽可能小的作用域里完成这些工作。这里，要是我们省掉了这个 `gensym`，同时直接把 `it` 绑定到测试表达式的结果上，就像这样： ~~~ (defmacro acond (&rest clauses) ; wrong (if (null clauses) nil (let ((cl1 (car clauses))) '(let ((it ,(car cl1))) (if it (progn ,@(cdr cl1)) (acond ,@(cdr clauses))))))) ~~~ 那么it 绑定的作用域也将包括后续的测试表达式。 * * * **[示例代码 14.2] 更多的指代变形** ~~~ (defmacro alambda (parms &body body) '(labels ((self ,parms ,@body)) #'self)) (defmacro ablock (tag &rest args) '(block ,tag ,(funcall (alambda (args) (case (length args) (0 nil) (1 (car args)) (t '(let ((it ,(car args))) ,(self (cdr args)))))) args))) ~~~ * * * [示例代码 14.2] 有一些更复杂的指代变形。宏 `alambda` 是用来字面引用递归函数的。不过什么时候会需要字面引用递归函数呢？我们可以通过带 `#'` 的 λ表达式来字面引用一个函数： ~~~ #'(lambda (x) (* x 2)) ~~~ 但正如第 2 章里解释的那样，你不能直接用λ–表达式来表达递归函数。代替的方法是，你必须借助`labels` 定义一个局部函数。下面这个函数(来自 2.8 节) ~~~ (defun count-instances (obj lsts) (labels ((instances-in (lst) (if (consp lst) (+ (if (eq (car lst) obj) 1 0) (instances-in (cdr lst))) 0))) (mapcar #'instances-in lsts))) ~~~ 接受一个对象和列表，并返回一个由列表中每个元素里含有的对象个数所组成的数列： ~~~ > (count-instances 'a '((a b c) (d a r p a) (d a r) (a a))) (1 2 1 2) ~~~ 通过代词，我们可以将这些代码变成字面递归函数。`alambda` 宏使用 `labels` 来创建函数，例如，这样就可以用它来表达阶乘函数： ~~~ (alambda (x) (if (= x 0) 1 (* x (self (1- x))))) ~~~ 使用 `alambda` 我们可以定义一个等价版本的 `count-instances` ，如下： ~~~ (defun count-instances (obj lists) (mapcar (alambda (list) (if list (+ (if (eq (car list) obj) 1 0) (self (cdr list))) 0)) lists)) ~~~ `alambda` 与 [示例代码 14.1] 和 14.2 节里的其他宏不一样，后者捕捉的是 it，而 `alambda` 则捕捉`self`。`alambda` 实例会展开进一个 `labels` 表达式，在这个表达式中，`self` 被绑定到正在定义的函数上。`alambda` 表达式不但更短小，而且看起来很像我们熟悉的 `lambda` 表达式，这让使用`alambda` 表达式的代码更容易阅读。 这个新宏被用了在 `ablock` 的定义里，它是内置的 `block special form` 的一个指代版本。在`block` 里面，参数从左到右求值。在 `ablock` 里也是一样，只是在这里，每次求值时变量 `it` 都会被绑定到前一个表达式的值上。 这个宏应谨慎使用。尽管很多时候 `ablock` 用起来很方便，但是它很可能会把本可以被写得优雅漂亮的函数式程序弄成命令式程序的样子。下面就是一个很不幸的反面教材： ~~~ > (ablock north-pole (princ "ho ") (princ it) (princ it) (return-from north-pole)) ho ho ho NIL ~~~ 如果一个宏，它有意地使用了变量捕捉，那么无论何时这个宏被导出到另一个包的时候，都必须同时导出那些被捕捉了的符号。例如，无论 `aif` 被导出到哪里，`it` 也应该同样被导出到同样的地方。否则出现在宏定义里的it 和宏调用里使用的 `it` 将会是不同的符号。 ### 14.2 失败 在 Common Lisp 中符号 `nil` 身兼三职。它首先是一个空列表，也就是 ~~~ > (cdr '(a)) NIL ~~~ 除了空列表以外，nil 被用来表示逻辑假，例如这里 ~~~ > (= 1 0) NIL ~~~ 最后，函数返回 nil 以示失败。例如，内置 `find-if` 的任务是返回列表中第一个满足给定测试条件的元素。 如果没有发现这样的元素，find-if 将返回 nil ： ~~~ > (find-if #'oddp '(2 4 6)) NIL ~~~ 不幸的是，我们无法分辨出这种情形：即 find-if 成功返回，而成功的原因是它发现了 nil ： ~~~ > (find-if #'null '(2 nil 6)) NIL ~~~ 在实践中，用 nil 来同时表示假和空列表并没有招致太多的麻烦。事实上，这样可能相当方便。然而，用nil 来表示失败却是一个痛处。因为它意味着一个像 find-if 这样的函数，其返回的结果可能是有歧义的。 对于所有进行查找操作的函数，都会遇到如何区分失败和 nil 返回值的问题。为了解决这个问题，Common Lisp 至少提供了三种方案。在多重返回值出现之前，最常用的方法是专门返回一个列表结构。例如，区分 assoc 的失败就没有任何麻烦；当执行成功时它返回成对的问题和答案： ~~~ > (setq synonyms '((yes . t) (no . nil))) ((YES . T) (NO)) > (assoc 'no synonyms) (NO) ~~~ 按照这个思路，如果担心 find-if 带来的歧义，我们可以用 member-if ，它不单单返回满足测试的元素，而是返回以该元素开始的整个 cdr： > (member-if #'null '(2 nil 6)) (NIL 6) 自从多重返回值诞生之后，这个问题就有了另一个解决方案：用一个值代表数据，而用第二个值指出成功还是失败。内置的gethash 就以这种方式工作。它总是返回两个值，第二个值代表是否找到了什么东西： ~~~ > (setf edible (make-hash-table) (gethash 'olive-oil edible) t (gethash 'motor-oil edible) nil) NIL > (gethash 'motor-oil edible) NIL T ~~~ 如果你想要检测所有三种可能的情况，可以用类似下面的写法： ~~~ (defun edible? (x) (multiple-value-bind (val found?) (gethash x edible) (if found? (if val 'yes 'no) 'maybe))) ~~~ 这样就可以把失败和逻辑假区分开了： ~~~ > (mapcar #'edible? '(motor-oil olive-oil iguana)) (NO YES MAYBE) ~~~ Common Lisp 还支持第三种表示失败的方法：让访问函数接受一个特殊对象作为参数，一般是用个 gensym，然后在失败的时候返回这个对象。这种方法被用于 get ，它接受一个可选参数来表示当特定属性没有找到时返回的东西： ~~~ > (get 'life 'meaning (gensym)) #:G618 ~~~ 如果可以用多重返回值，那么 gethash 用的方法是最清楚的。我们不愿意像调用 get 那样，为每个访问函数都再传入一个参数。并且和另外两种替代方法相比，使用多重返回值更通用；可以让 find-if 返回两个值，而 gethash 却不可能在不做 consing 的情况下被重写成返回无歧义的列表。这样在编写新的用于查询的函数，或者对于其他可能失败的任务时，通常采用gethash 的方式会更好一些。 * * * **[示例代码 14.3] 多值指代宏** ~~~ (defmacro aif2 (test &optional then else) (let ((win (gensym))) '(multiple-value-bind (it ,win) ,test (if (or it ,win) ,then ,else)))) (defmacro awhen2 (test &body body) '(aif2 ,test (progn ,@body))) (defmacro awhile2 (test &body body) (let ((flag (gensym))) '(let ((,flag t)) (while ,flag (aif2 ,test (progn ,@body) (setq ,flag nil)))))) (defmacro acond2 (&rest clauses) (if (null clauses) nil (let ((cl1 (car clauses)) (val (gensym)) (win (gensym))) '(multiple-value-bind (,val ,win) ,(car cl1) (if (or ,val ,win) (let ((it ,val)) ,@(cdr cl1)) (acond2 ,@(cdr clauses))))))) ~~~ * * * 在 edible? 里的写法不过相当于一种记帐的操作，它被宏很好地隐藏了起来。对于类似 gethash 这样的访问函数，我们会需要一个新版本的 aif ，它绑定和测试的对象不再是同一个值，而是绑定第一个值，并测试第二个值。这个新版本的 aif ，称为 aif2 ，由 [示例代码 14.3] 给出。使用它，我们可以将 edible? 写成： ~~~ (defun edible? (x) (aif2 (gethash x edible) (if it 'yes 'no) 'maybe)) ~~~ [示例代码 14.3] 还包含有 awhen ，awhile ，和 acond 的类似替代版本。作为一个使用a cond2 的例子，见 18.4 节上 match 的定义。通过使用这个宏，我们可以用一个 cond 的形式来表达，否则函数将变得更长并且缺少对称性。 内置的 read 指示错误的方式和 get 同出一辙。它接受一个可选参数来说明在遇到eof 时是否报错，如果不报错的话，将返回何值。[示例代码 14.4] 中给出了另一个版本的 read ，它用第二个返回值指示失败。read2 返回两个值，分别是输入表达式和一个标志，如果碰到eof 的话，这个标志就是nil 。它把一个 gensym 传给 read ，万一遇到 eof 就返回它，这免去了每次调用 read2 时构造 gensym 的麻烦，这个函数被定义成一个闭包，闭包中带有一个编译期生成的 gensym 的私有拷贝。 * * * **[示例代码 14.4] 文件实用工具** ~~~ (let ((g (gensym))) (defun read2 (&optional (str *standard-input*)) (let ((val (read str nil g))) (unless (equal val g) (values val t))))) (defmacro do-file (filename &body body) (let ((str (gensym))) '(with-open-file (,str ,filename) (awhile2 (read2 ,str) ,@body)))) ~~~ * * * [示例代码 14.4] 中还有一个宏，它可以方便地遍历一个文件里的所有表达式，这个宏是用 awhile2 和 read2 写成的。举个例子，借助 do-file ，我们可以这样实现 load ： ~~~ (defun our-load (filename) (do-file filename (eval it))) ~~~ ### 14.3 引用透明(Referential Transparency) 有时认为是指代宏破坏了引用透明，Gelernter 和Jagannathan 是这样定义引用透明的： 一个语言是引用透明的，如果 (a) 任意一个子表达式都可以替换成另一个子表达式，只要后者和前者的值相等，并且 (b) 在给定的上下文中，出现不同地方的同一表达式其取值都相同。 注意到这个标准针对的是语言，而不是程序。没有一个带赋值的语言是引用透明的。在下面的表达式中: ~~~ (list x (setq x (not x)) x) ~~~ 第一个和最后一个 x 带有不同的值，因为被一个 setq 干预了。必须承认，这是丑陋的代码。这一事实意味着 Lisp 不是引用透明的。 Norvig 提到，倘若把 if 重新定义成下面这样将会很方便： ~~~ (defmacro if (test then &optional else) '(let ((that ,test)) (if that ,then ,else))) ~~~ 但 Norvig 否定它的理由，也正是因为这个宏破坏了引用透明。 尽管如此，这里的问题在于：上面的宏重定义了内置操作符，而不是因为它使用了代词。上面定义中的 (b) 条款要求一个表达式 "在给定的上下文中" 必须总是返回相同的值。如果是在这个 let 表达式中就没问题了， ~~~ (let ((that 'which)) ...) ~~~ 符号 that 表示一个新变量，因为 let 就是被用于创建一个新的上下文。 上面那个宏的错误在于，它重定义了 if，而 if 的本意并非是被用来创建新的上下文的。如果我们给指代宏取个自己的名字，问题就迎刃而解。(根据 **CLTL2**，重定义 if 总是非法的。) 由于 aif 定义的一部分就是建立一个新的上下文，并且在这个上下文中，it 是一个新变量，所以这样一个宏并没有破坏引用透明。 现在，aif 确实违背了另一个原则，它和引用透明无关：即，不管用什么办法，新建立的变量都应该在源代码里能很容易地分辨出来。前面的那个 let 表达式就清楚地表明 that 将指向一个新变量。可能会有反对意见，说：一个 aif 里面的 it 绑定就没有那么明显。尽管如此，这里有一个不大站得住脚的理由：aif 只创 建了一个变量，并且创建这个变量是我们使用 aif 的唯一理由。 Common Lisp 自己并没有把这个原则奉为不可违背的金科玉律。**CLOS** 函数 call-next-method 的绑定依赖上下文的方式和 aif 函数体中符号 it 的绑定方式是一样的。(关于 call-next-method 应如何实现的一个建议方案，可见 25.2 节上的 defmeth 宏。) 在任何情况下，这类原则的最终目的只有一个：提高程序的可读性。并且代词确实让程序更容易阅读，正如它们让英语更容易阅读那样。

## 第 13 章 编译期计算 前面的章节描述了几类只能用宏实现的操作符。本章将介绍用函数可以解决，但用宏能更高效的一类问题。第 8.2 节列出了在给定情形下使用宏的利弊。有利的一面包括 "在编译期完成计算"。有时，如果把操作符实现成宏，就可以在展开时完成部分工作。本章会着眼于那些充分利用这种可能性的宏。 ### 13.1 新的实用工具 * * * **[示例代码 13.1] 求平均值时转移计算** ~~~ (defun avg (&rest args) (/ (apply #'+ args) (length args))) (defmacro avg (&rest args) '(/ (+ ,@args) ,(length args))) ~~~ * * * 第 8.2 节里提出，通过宏就可能把计算转移到编译期完成。在那里，我们曾经把宏 `avg` 作为例子，它会返回其参数的平均值： ~~~ > (avg pi 4 5) 4.047... ~~~ 在 [示例代码 13.1] 中先把 `avg` 定义成函数，然后又用宏实现它。当把 `avg` 定义成宏时，对`length` 的调用可以在编译期完成。在宏版本里我们也避免了在运行期处理 `&rest` 参数的开销。所以在许多实现里，写成宏的 `avg` 会更快。 * * * **[示例代码 13.2] 转移和避开计算** ~~~ (defun most-of (&rest args) (let ((all 0) (hits 0)) (dolist (a args) (incf all) (if a (incf hits))) (> hits (/ all 2)))) (defmacro most-of (&rest args) (let ((need (floor (/ (length args) 2))) (hits (gensym))) '(let ((,hits 0)) (or ,@(mapcar #'(lambda (a) '(and ,a (> (incf ,hits) ,need))) args))))) ~~~ * * * 这种优化省去了不必要的计算，它的实现归功于在展开期就知道参数的数量。它还可以和我们在 `in`(11.3 节) 中进行的另一类优化结合起来，后者甚至可以避免求值一些参数。[示例代码 13.2] 中有两个版本的 `most-of` ，它在多数参数都为真的时候返回真： ~~~ > (most-of t t t nil) T ~~~ 和 `in` 一样，宏版本展开成的代码只求值它需要数量的参数。例如: ~~~ (most-of (a) (b) (c)) ~~~ 展开的等价代码： ~~~ (let ((count 0)) (or (and (a) (> (incf count) 1)) (and (b) (> (incf count) 1)) (and (c) (> (incf count) 1)))) ~~~ 在最理想的情况下，只对刚过半的参数求值。 * * * **[示例代码 13.3] 使用编译期知道的参数** ~~~ (defun nthmost (n lst) (nth n (sort (copy-list lst) #'>))) (defmacro nthmost (n lst) (if (and (integerp n) (< n 20)) (with-gensyms (glst gi) (let ((syms (map0-n #'(lambda (x) (gensym)) n))) '(let ((,glst ,lst)) (unless (< (length ,glst) ,(1+ n)) ,@(gen-start glst syms) (dolist (,gi ,glst) ,(nthmost-gen gi syms t)) ,(car (last syms)))))) '(nth ,n (sort (copy-list ,lst) #'>)))) (defun gen-start (glst syms) (reverse (maplist #'(lambda (syms) (let ((var (gensym))) '(let ((,var (pop ,glst))) ,(nthmost-gen var (reverse syms))))) (reverse syms)))) (defun nthmost-gen (var vars &optional long?) (if (null vars) nil (let ((else (nthmost-gen var (cdr vars) long?))) (if (and (not long?) (null else)) '(setq ,(car vars) ,var) '(if (> ,var ,(car vars)) (setq ,@(mapcan #'list (reverse vars) (cdr (reverse vars))) ,(car vars) ,var) ,else))))) ~~~ * * * 如果仅仅知道宏的部分参数值，也一样有可能把计算工作转移到编译期进行。图 13.3 就给出了这样的一个宏。函数 `nthmost` 接受一个数 `n` 以及一个数列，并返回数列中第 `n` 大的数；和其他序列函数一样，它是从零开始索引的： ~~~ > (nthmost 2 '(2 6 1 5 3 4)) 4 ~~~ 函数版本写得非常简单。它对列表排序，然后对排序的结果调用 `nth` 。由于 `sort` 是破坏性的，`nthmost` 在排序之前先复制列表。这样实现，使得 `nthmost` 在两方面影响效率：它构造新的点对，而且对整个参数列表排序，尽管我们只关心前 个。 如果我们在编译期知道 `n` 的值，就可以从另一个角度分析这个问题了。[示例代码 13.3] 中的其余代码定义了一个宏版本的 `nthmost` 。这个宏做的第一件事是去检查它的第一个参数。如果第一个参数字面上不是一个数，它就被展开成和我们上面看到的相同的代码。如果第一个参数是一个数的话，我们可以采用另一个办法。 比方说，如果你想要找到一个盘子里第三大的那块饼干，那么你可以依次查看每一块饼干同时保持手里总是拿着已知最大的三块，用这个办法达到目的。当你检查完所有的饼干之后，你手里最小的那块饼干就是你要找的了。如果 是一个小常数，并且这个数字远小于饼干的总数，那么和 "先对它们的全部进行排序" 的方法相比，用这种技术可以让你更方便地得到想找的那块饼干。 * * * **[示例代码 13.4] nthmost 的展开式** ~~~ (nthmost 2 nums) ~~~ 展开成： ~~~ (let ((#:g7 nums)) (unless (< (length #:g7) 3) (let ((#:g6 (pop #:g7))) (setq #:g1 #:g6)) (let ((#:g5 (pop #:g7))) (if (> #:g5 #:g1) (setq #:g2 #:g1 #:g1 #:g5) (setq #:g2 #:g5))) (let ((#:g4 (pop #:g7))) (if (> #:g4 #:g1) (setq #:g3 #:g2 #:g2 #:g1 #:g1 #:g4) (if (> #:g4 #:g2) (setq #:g3 #:g2 #:g2 #:g4) (setq #:g3 #:g4)))) (dolist (#:g8 #:g7) (if (> #:g8 #:g1) (setq #:g3 #:g2 #:g2 #:g1 #:g1 #:g8) (if (> #:g8 #:g2) (setq #:g3 #:g2 #:g2 #:g8) (if (> #:g8 #:g3) (setq #:g3 #:g8) nil)))) #:g3)) ~~~ * * * 这是一种当在编译期已知时采取的策略。在它的展开式里，宏创建了 个变量，然后调用 `nthmost-gen` 来生成那些求值成查看每一块饼干的代码。[ 示例代码 13.4] 给出了一个示例的宏展开。除了不能作为 apply 的参数传递以外，宏 `nthmost` 在行为上和原来的函数一样。这里使用宏的理由完全是出于效率：宏版本不在运行期构造新点对，并且如果是一个小的常数，那么比较的次数可以更少。 难道为了写出高效的程序，就必须兴师动众，编这么长的宏么？对于本例来说，答案可能是否定的。这里之所以给出两个版本的 `nthmost` ，主要的原因是想举个例子，它揭示了一个普遍的原则：当某些参数在编译期已知时，你可以用宏来生成更高效的代码。是否利用这种可能性取决于你想获得多少好处，以及你可以另外付出多少努力来编写一个高效的宏版本。由于 `nthmost` 的宏版本既长又繁，它可能只有在极端场合才值得去写。尽管如此，就算你宁愿不利用它，编译期已知的信息总还是一个值得考虑的因素。 ### 13.2 举例：贝塞尔曲线 就像 `with-` 宏(第 11.2 节)，用于编译期计算的宏更像是为特定应用而写的，而不是为通用目的设计的实用工具。通用的实用工具在编译期能了解多少信息？它的参数个数，可能还有某些参数的值。但如果我们想要利用其他的约束条件，这些条件也许就只能是程序自己才懂得使用的信息了。 本节将作为一个实例，展示宏是如何加速贝塞尔曲线的生成的。如果对曲线的操作是交互式的话，那么它们的生成速度必须得非常快才行。可以看出，如果曲线的分段数是已知的，那么大多数计算就可以在编译期完成。把曲线生成器写成一个宏，我们就可以将预先算好的值嵌入到代码中。这应该比把它们保存在数组里，这种更常规的优化方式甚至还要快。 一条贝塞尔曲线由四个点确定 — 两个端点和两个控制点。在两维平面上，这些点定义了曲线上所有点的 和 坐标的参数方程。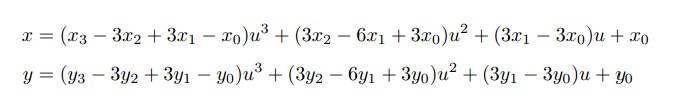如果两个端点是 (x0, y0) 和 (x3, y3)，以及两个控制点 (x1, y1) 和 (x2, y2)，那么曲线上点的方程就是：  如果我们用 `u` 在 `0` 和 `1` 之间的 `n` 个值来求值这个方程，我们就得到曲线上的 `n` 个点。举个例子，如果我们想把曲线画成 `20` 条线段，那么我们将用 `u = .05, .1, ..., .95` 来求值方程。对于`u` 在 `0` 或 `1` 上的求值是不需要的，因为如果 `u = 0` 它们将生成第一个端点 `(x0, y0)`，而当 `u = 1` 时它们将生成第二个端点 。 有个显而易见的优化方法是令 `n` 为定值，并提前计算 `n` 的指数，然后将它们存在一个 `(n - 1) x 3` 的数组里。通过把曲线生成器定义成一个宏，我们甚至可以做得更好。如果 `n` 在展开时已知，程序可以简单地展开成 `n` 条画线指令。那些预先计算好的 `n` 的指数，可以直接作为字面上的值插入到宏展开式里，而不必再保存在数组里了。 [示例代码 13.5] 中有一个实现了这一策略的曲线生成宏。它抛弃了立即画线的策略，而是将生成的点保存在数组里。当交互式地移动一条曲线时，每一个实例必须画两次：一次显示它，还有一次是在画下一个实例之前清除它。在两次画线之间，这些点必须保存在某个地方。 当 `n = 20` 时，`genbez` 展开成 21 个 `setf`。由于 的指数直接出现在代码里，我们省下了在运行期查找它们的开销，以及在启动时计算它们的开销。和 `u` 的指数一样，数组的索引以常量的形式出现在展开式中，所以对那些 `(setf aref)` 的边界检查也可以在编译期完成。 ### 13.3 应用 后面的章节将会提到其它一些宏，它们也使用了编译期的已知信息。其中一个很好的例子是 `if-match` (第 18.4 节)。在这个例子里，模式匹配器会比较两个序列，序列中可能含有变量，在比较的过程中，模式匹配器会分析是否存在某种给这些变量赋值的方式，可以让两个序列相等。`if-match`的设计显示：如果序列中的一个在编译期已知，并且只有这个序列里含有变量，那么匹配可以做得更高效。一个办法是在运行期比较两个序列，并构造列表来保存这个过程中建立的变量绑定，不过我们可以改成用宏，让宏生成的代码严格按照已知的序列来一一对照比较，同时可以在真正的 Lisp 变量里保存绑定。 第 19-24 章里描述的嵌入式语言，也在很大程度上利用了这些可在编译期获得的信息。由于嵌入式语言就是编译器，利用这些信息是其唯一自然的工作方式。这是一个普遍规律：越是精心设计的宏，它对其参数的约束也就越多，并且你利用这些约束来产生高效的代码的机会也就越好。 * * * **[示例代码 13.5] 生成贝塞尔曲线的宏** ~~~ (defconstant *segs* 20) (defconstant *du* (/ 1.0 *segs*)) (defconstant *pts* (make-array (list (1+ *segs*) 2))) (defmacro genbez (x0 y0 x1 y1 x2 y2 x3 y3) (with-gensyms (gx0 gx1 gy0 gy1 gx3 gy3) '(let ((,gx0 ,x0) (,gy0 ,y0) (,gx1 ,x1) (,gy1 ,y1) (,gx3 ,x3) (,gy3 ,y3)) (let ((cx (* (- ,gx1 ,gx0) 3)) (cy (* (- ,gy1 ,gy0) 3)) (px (* (- ,x2 ,gx1) 3)) (py (* (- ,y2 ,gy1) 3))) (let ((bx (- px cx)) (by (- py cy)) (ax (- ,gx3 px ,gx0)) (ay (- ,gy3 py ,gy0))) (setf (aref *pts* 0 0) ,gx0 (aref *pts* 0 1) ,gy0) ,@(map1-n #'(lambda (n) (let* ((u (* n *du*)) (u2 (* u u)) (u3 (expt u 3))) '(setf (aref *pts* ,n 0) (+ (* ax ,u3) (* bx ,u2) (* cx ,u) ,gx0) (aref *pts* ,n 1) (+ (* ay ,u3) (* by ,u2) (* cy ,u) ,gy0)))) (1- *segs*)) (setf (aref *pts* *segs* 0) ,gx3 (aref *pts* *segs* 1) ,gy3)))))) ~~~ `<span class="str" style="color: rgb(128, 0, 0);"> </span>`

## 第 12 章 广义变量 第 8 章曾提到，宏的长处之一是其变换参数的能力。`setf` 就是这类宏中的一员。本章将着重分析`setf` 的内涵，然后以几个宏为例，它们将建立在 `setf` 的基础之上。 要在 `setf` 上编写正确无误的宏并非易事，其难度让人咋舌。为了介绍这个主题，第一节会先给出一个有点小问题的简单例子。接下来的小节将解释该宏的错误之处，然后展示如何改正它。第三和第四节会介绍一些基于 `setf` 的实用工具的例子，而最后一节则会说明如何定义你自己的 `setf` 逆变换。 ### 12.1 概念 内置宏 `setf` 是 `setq` 的推广形式。`setf` 的第一个参数可以是个函数调用而非简单的变量： ~~~ > (setq lst '(a b c)) (A B C) > (setf (car lst) 480) 480 > lst (480 B C) ~~~ 一般而言，`(setf x y)` 可以理解成 "务必让 x 的求值结果为 y"。作为一个宏，`setf` 得以深入到参数内部，弄清需要做哪些工作，才能满足这个要求。如果第一个参数(在宏展开以后) 是个符号，那么`setf` 就只会展开成 setq。但如果第一个参数是个查询语句，那么 `setf` 则会展开到对应的断言上。由于第二个参数是常量，所以前面的例子可以展开成： ~~~ (progn (rplaca lst 480) 480) ~~~ 这种从查询到断言的变换被称为逆变换。Common Lisp 中所有最常用的访问函数都有预定义的逆，包括 `car`、`cdr`、`nth`、`aref`、`get`、`gethash`，以及那些由 `defstruct` 创建的访问函数。( 完整的名单见 **CLTL2** 的第 125 页。) 能充当 `setf` 第一个参数的表达式被称为广义变量。广义变量已经成为了一种强有力的抽象机制。宏调用和广义变量的相似之处在于：一个宏调用，只要能展开成可逆引用，那么其本身就一定是可逆的。 当我们也加入这个行列，基于 `setf` 编写自己的宏时，这种组合可以产生显而易见更清爽的程序。我们可以在 `setf` 上面定义的宏有很多，其中一个是 `toggle`：【注1】 ~~~ (defmacro toggle (obj) '(setf ,obj (not ,obj))) ~~~ 它可以反转一个广义变量的值： ~~~ > (let ((lst '(a b c))) (toggle (car lst)) lst) (NIL B C) ~~~ 现在考虑下面的应用。假设有个人，他可能是个肥皂剧作者、精力充沛的好事者，或是居委会大妈，想要维护一个数据库。其中记录着小镇上所有居民之间的种种恩怨情仇。在数据库里的表里，其中有一张便是用来保存朋友关系的： ~~~ (defvar *friends* (make-hash-table)) ~~~ 这个哈希表的表项本身也是哈希表，其中，潜在的朋友被映射到 `t` 或者 `nil` ： ~~~ (setf (gethash 'mary *friends*) (make-hash-table)) ~~~ 为了使 John 成为 Mary 的朋友，我们可以说： ~~~ (setf (gethash 'john (gethash 'mary *friends*)) t) ~~~ 这个镇被分为两派。正如帮派的传统，每个人都声称 "凡人非友即敌"，所以镇上所有人都被迫加入一方或者另一方。这样当某人转变立场时，他所有的朋友都变成敌人，而所有的敌人则变成朋友。 如果只用内置的操作符来切换 `x` 和 `y` 的敌友关系，我们必须这样说： ~~~ (setf (gethash x (gethash y *friends*)) (not (gethash x (gethash y *friends*)))) ~~~ 尽管去掉 `setf` 后要简单许多，这个表达式还是相当复杂。倘若我们为数据库定义了一个访问宏，如下： ~~~ (defmacro friend-of (p q) '(gethash ,p (gethash ,q *friends*))) ~~~ 那么在这个宏和 `toggle` 的协助下，我们就得以更方便地修改数据库的数据。前面那个更新数据库的语句可以简化成： ~~~ (toggle (friend-of x y)) ~~~ 广义变量就像是美味的健康食品。它们能让你的程序良好地模块化，同时变得更为优雅。如果你给出宏或者可逆函数，用来访问你的数据结构，那么其他模块就可以使用 `setf` 来修改你的数据结构而无需了解其内部细节。 ### 12.2 多重求值问题 上一节曾警告说，我们最初的 `toggle` 定义是不正确的： ~~~ (defmacro toggle (obj) ; wrong '(setf ,obj (not ,obj))) ~~~ 它会碰到第 10.1 节里提到的多重求值问题。如果它的参数有副作用，那麻烦就来了。比如说，若`lst` 是一个对象列表，我们这样写： ~~~ (toggle (nth (incf i) lst)) ~~~ 并期待它能反转第 `(i+1)` 个元素。事与愿违，如果使用 `toggle` 现在的定义，这个调用将展开成： ~~~ (setf (nth (incf i) lst) (not (nth (incf i) lst))) ~~~ 这会使 i 递增两次，并且将第 `(i+1)` 个元素设置成第 `(i+2)` 个元素的反。所以在本例中: ~~~ > (let ((lst '(t nil t)) (i -1)) (toggle (nth (incf i) lst)) lst) (T NIL T) ~~~ 调用 `toggle` 毫无效果。 仅仅把作为 `toggle` 参数给出的表达式插入到 `setf` 的第一个参数的位置上还不够。我们必须深入到表达式内部，看看它到底做了什么：如果它含有 `subform` ，而且这些 `subform` 有副作用的话，我们就需要把它们分开，并单独求值。一般而言，这件事情并不那么简单。 为了让问题容易些，Common Lisp 提供了一个宏，它可以帮助我们自动定义一些基于 `setf` 的宏，不过适用范围有限。宏的名字叫 `define-modify-macro` ，它接受三个参数：被定义宏的宏名，它的附加参数（出现在广义变量之后），以及一个函数名，这个函数将为广义变量产生新值。【注2】【注3】 使用 `define-modify-macro` ，我们可以像下面这样定义 `toggle` ： ~~~ (define-modify-macro toggle () not) ~~~ 具体说，就是 "若要求值形如 (toggle place) 的表达式，应该先找到 `place` 指定的位置，并且，如果保存在那里的值是 `val`，将其替换成 `(not val)` 的值"。下面把这个新宏用在原来的例子里： ~~~ > (let ((lst '(t nil t)) (i -1)) (toggle (nth (incf i) lst)) lst) (NIL NIL T) ~~~ 虽然这个版本正确无误地给出了结果，但它本可以写得更通用些。由于 `setf` 和 `setq` 两者对其参数数量都没有限制，`toggle` 也应如此。我们可以通过在修改宏 (modify-macro) 的基础上定义另一个宏，来赋予它这种能力，如 [示例代码 12.1]所示。 * * * **[示例代码 12.1]：操作在广义变量上的宏** ~~~ (defmacro allf (val &rest args) (with-gensyms (gval) '(let ((,gval ,val)) (setf ,@(mapcan #'(lambda (a) (list a gval)) args))))) (defmacro nilf (&rest args) '(allf nil ,@args)) (defmacro tf (&rest args) '(allf t ,@args)) (defmacro toggle (&rest args) '(progn ,@(mapcar #'(lambda (a) '(toggle2 ,a)) args))) (define-modify-macro toggle2 () not) ~~~ * * * ### 12.3 新的实用工具 本节将给出一些新的实用工具为例，我们用它们对广义变量进行操作。这些实用工具必须是宏，以便将参数原封不动地传给 `setf`。 [示例代码 12.1] 中有四个基于 `setf` 的新宏。第一个是 `allf` ，它被用来将同一值赋给多个广义变量。`nilf` 和 `tf` 就是基于它实现的，它们分别将参数设置 为 `nil` 和 `t` 。虽然这些宏很简单，但是方便实用。 和 `setq` 一样，`setf` 也可以接受多个参数 -- 即交替出现的变量和对应的值： ~~~ (setf x 1 y 2) ~~~ 这些新的实用工具同样有这个能力，而且只用传原来一半的参数就可以了。如果你想要把多个变量初始化为 `nil` ，那么可以不再使用： ~~~ (setf x nil y nil z nil) ~~~ 而改成说： ~~~ (nilf x y z) ~~~ 就行了。最后一个宏是前一节曾介绍过的 `toggle` ：它和 `nilf` 差不多，但给每个参数设置的是真值的反。 这四个宏说明了关于赋值操作符的一个要点。就算我们只需要对普通变量使用一个操作符，而把这个操作符号展开成 `setf` 而非 `setq` ，这样做，有百利而无一害。如果第一个参数是符号，`setf` 将直接展开到 `setq`。由于不费吹灰之力，就能拥有 `setf` 的一般性，所以很少有必要在展开式里使用`setq`。 * * * **[示例代码 12.2] 广义变量上的列表操作** ~~~ (define-modify-macro concf (obj) nconc) (defun conc1f/function (place obj) (nconc place (list obj))) (define-modify-macro conc1f (obj) conc1f/function) (defun concnew/function (place obj &rest args) (unless (apply #'member obj place args) (nconc place (list obj)))) (define-modify-macro concnew (obj &rest args) concnew/function) ~~~ * * * [示例代码 12.2] 【注4】包含三个破坏性修改列表结尾的宏。第 3.1 节提到依赖 ~~~ (nconc x y) ~~~ 的副作用是不可靠的，并且必须改成：【注5】 ~~~ (setq x (nconc x y)) ~~~ 这一习惯用法被嵌入在 `concf` 中了。更特殊的 `conc1f` 和 `concnew` 就像是用于列表另一端的`push` 和 `pushnew`，`conc1f` 在列表结尾追加一个元素，而 `concnew` 的功能相同，但只有当这个元素不在列表中时才会动作。 第 2.2 节曾提到，函数的名字既可以是符号，也可以是–表达式。因此，把整个λ表达式作为第三个参数传给 `define-modify-macro` 也是可行的，正如 `conc1f` 的定义。【注6】 如果用第 4.3 节上的`conc1` 的话，这个宏也可以写成： ~~~ (define-modify-macro conc1f (obj) conc1) ~~~ 在一种情况下，[示例代码 12.2] 中的宏应该限制使用。如果你正准备通过在结尾处追加元素的方式来构造列表，那么最好用 `push` ，最后再 `nreverse` 这个列表。在列表的开头处理数据比在结尾要方便些，因为在结尾处处理数据的话，你首先得到那里。Common Lisp 有许多用于前者的操作符，而适用于后者的操作符则屈指可数，这很可能是为了鼓励程序员设计更高效率的程序。 ### 12.4 更复杂的实用工具 并非所有基于 setf 的宏都可以用 define-modify-macro 定义。比如说，假设我们想要定义一个宏 _f ，让它破坏性把函数应用于一个广义变量。内置宏 incf 就相当于使用了 + 的 setf 的缩写。把： ~~~ (setf x (+ x y)) ~~~ 取而代之，我们只需说： ~~~ (incf x y) ~~~ 新的宏 `_f` 就是上述思路的推广：`incf` 能展开成对 `+` 的调用，而 `_f` 则会展开成对由第一个参数给出操作符的调用。例如，在第 8.3 节 scale-objs 的定义里，我们必须这样写： ~~~ (setf (obj-dx o) (* (obj-dx o) factor)) ~~~ 改用 `_f` 的话，将变成： ~~~ (_f * (obj-dx o) factor) ~~~ `_f` 可能会被错写成： ~~~ (defmacro _f (op place &rest args) ; wrong '(setf ,place (,op ,place ,@args))) ~~~ 不幸的是，我们无法用 `define-modify-macro` 正确无误地定义 `_f` ，因为应用到广义变量上的操作符是由参数给定的。 这类更复杂的宏必须由手工编写。为了让这种宏的编写方便些，`Common Lisp` 提供了函数 `get-setf-expansion` 【注7】，它接受一个广义变量并返回所有用于获取和设置其值的必要信息。通过为下面表达式手工生成展开式，我们将了解如何使用这些信息： `(incf (aref a (incf i)))` 当我们对广义变量调用 `get-setf-expansion` 时，可以得到五个值用作宏展开式的原材料： ~~~ > (get-setf-expansion '(aref a (incf i))) (#:G4 #:G5) (A (INCF I)) (#:G6) (SYSTEM:SET-AREF #:G6 #:G4 #:G5) (AREF #:G4 #:G5) ~~~ 最开始的两个值分别是临时变量列表，以及应该给它们赋的值。因此，我们可以这样开始展开式： ~~~ (let* ((#:g4 a) (#:g5 (incf i))) ...) ~~~ 这些绑定应该在 `let*` 里创建。因为一般来说，这些值 `form` 可能会引用到前面的变量。第三【注8】和第五个值是另一个临时变量和将返回广义变量初值的 `form`。由于我们想要在这个值上加 `1`，所以把后者包在对 `1+` 的调用里： ~~~ (let* ((#:g4 a) (#:g5 (incf i)) (#:g6 (1+ (aref #:g4 #:g5)))) ...) ~~~ 最后，`get-setf-expansion` 返回的第四个值是一个赋值的表达式，该赋值必须在新绑定环境下进行： ~~~ (let* ((#:g4 a) (#:g5 (incf i)) (#:g6 (1+ (aref #:g4 #:g5)))) (system:set-aref #:g6 #:g4 #:g5)) ~~~ 不过，这个 `form` 多半会引用一些内部函数，而这些内部函数不属于 Common Lisp 标准。通常`setf` 掩盖了这些函数的存在，但它们必须存在于某处。因为关于它们的所有东西都依赖于具体的实现，所以注重可移植性的代码应该使用由 `get-setf-expansion` 返回的这些 `form`，而不是直接引用诸如 `system:set-aref` 这样的函数。 现在为实现 `_f` 而编写的宏，所要完成的工作，几乎和我们刚才手工展开 `incf` 时做的事情完全一样。唯一的区别就是，不再把 `let*` 里的最后一个 `form` 包装在 `1+` 调用里，而是将它包装在来自`_f` 参数的一个表达式里。[示例代码 12.3] 给出了 `_f` 的定义。 * * * **[示例代码 12.3] setf 上更复杂的宏** ~~~ (defmacro _f (op place &rest args) (multiple-value-bind (vars forms var set access) (get-setf-expansion place) '(let* (,@(mapcar #'list vars forms) (,(car var) (,op ,access ,@args))) ,set))) (defmethod pull (obj place &rest args) (multiple-value-bind (vars forms var set access) (get-setf-expansion place) (let ((g (gensym))) '(let* ((,g ,obj) ,@(mapcar #'list vars forms) (,(car var) (delete ,g ,access ,@args))) ,set)))) (defmacro pull-if (test place &rest args) (multiple-value-bind (vars forms var set access) (get-setf-expansion place) (let ((g (gensym))) '(let* ((,g ,test) ,@(mapcar #'list vars forms) (,(car var) (delete-if ,g ,access ,@args))) ,set)))) (defmacro popn (n place) (multiple-value-bind (vars forms var set access) (get-setf-expansion place) (with-gensyms (gn glst) '(let* ((,gn ,n) ,@(mapcar #'list vars forms) (,glst ,access) (,(car var) (nthcdr ,gn ,glst))) (prog1 (subseq ,glst 0 ,gn) ,set))))) ~~~ * * * 这是个很有用的实用工具。举个例子，现在在它的帮助下，我们就可以轻易地将任意有名函数替换成其记忆化（第5.3 节）的等价函数。【注9】要对 `foo` 进行记忆化的处理，可以用： ~~~ (_f memoize (symbol-function 'foo)) ~~~ 使用 `_f` ，也有助于简化其他基于 `setf` 的宏的定义。例如，我们现在可以把 `conc1f` （[示例代码 12.2]）定义成： ~~~ (defmacro conc1f (lst obj) '(_f nconc ,lst (list ,obj))) ~~~ [示例代码 12.3] 中还有其他一些有用的宏，它们同样基于 `setf`。下一个是 `pull` ，它是内置的`pushnew` 的逆操作。 这对操作符，就像是给 `push` 和 `pop` 赋予了一定的鉴别能力。如果给定的新元素不是列表的成员，`pushnew` 就把它加入到这个列表里面，而 `pull` 则是破坏性地从列表里删除给定的元素。`pull` 定义中的 `&rest` 参数使 `pull` 可以接受和 `delete` 相同的关键字参数： ~~~ > (setq x '(1 2 (a b) 3)) (1 2 (A B) 3) > (pull 2 x) (1 (A B) 3) > (pull '(a b) x :test #'equal) (1 3) > x (1 3) ~~~ 你几乎可以把这个宏当成这样定义的： ~~~ (defmacro pull (obj seq &rest args) ; wrong '(setf ,seq (delete ,obj ,seq ,@args))) ~~~ 不过，如果它真的这样定义，它将同时碰到求值顺序和求值次数方面的问题。我们也可以把 `pull` 定义成简单的修改宏： ~~~ (define-modify-macro pull (obj &rest args) (lambda (seq obj &rest args) (apply #'delete obj seq args))) ~~~ 但由于修改宏必须将广义变量作为第一个参数，所以我们只得以相反的次序给出前两个参数，这样显得有些不自然。 更通用的 `pull-if` 接受一个初始的函数参数，并且会展开成 `delete-if` 而非 `delete` ： ~~~ > (let ((lst '(1 2 3 4 5 6))) (pull-if #'oddp lst) lst) (2 4 6) ~~~ 这两个宏说明了另一个有普遍意义的要点。如果下层函数接受可选参数，建立在其上的宏也应该这样做。 `pull` 和 `pull-if` 都把可选参数传给了它们的 `delete` 。 [示例代码 12.3] 中最后一个宏是 `popn` ，它是 `pop` 的推广形式。其功能不再是仅仅从列表里弹出一个元素，而是能弹出并返回任意长度的子序列： ~~~ > (setq x '(a b c d e f)) (A B C D E F) > (popn 3 x) (A B C) > x (D E F) ~~~ [示例代码 12.4] 中的宏能对它的参数排序。如果 `x` 和 `y` 是变量，而且我们想要确保x 的值不是两个值中较小的那个，那么我们可以写： ~~~ (if (> y x) (rotatef x y)) ~~~ 但如果我们想对三个或者数量更多的变量做这个操作，所需的代码量就会迅速膨胀。与其手工编写这样的代码，不妨让 `sortf` 来为我们代劳。这个宏接受一个比较操作符，还有任意数量的广义变量，然后不断交换它们的值，直到这些广义变量的顺序符合操作符的要求。在最简单的情形，参数可以是普通变量： * * * **[示例代码 12.4] 一个排序其参数的宏** ~~~ (defmacro sortf (op &rest places) (let* ((meths (mapcar #'(lambda (p) (multiple-value-list (get-setf-expansion p))) places)) (temps (apply #'append (mapcar #'third meths)))) '(let* ,(mapcar #'list (mapcan #'(lambda (m) (append (first m) (third m))) meths) (mapcan #'(lambda (m) (append (second m) (list (fifth m)))) meths)) ,@(mapcon #'(lambda (rest) (mapcar #'(lambda (arg) '(unless (,op ,(car rest) ,arg) (rotated ,(car rest) ,arg))) (cdr rest))) temps) ,@(mapcar #'fourth meths)))) ~~~ * * * ~~~ > (setq x 1 y 2 z 3) 3 > (sortf > x y z) 3 > (list x y z) (3 2 1) ~~~ 一般情况下，它们可以是任何可逆的表达式。假设 `cake` 是一个可逆函数，它能返回某人的蛋糕，而`bigger` 是个针对蛋糕的比较函数。如果我们想要推行一个规定，要求 `moe` 的 `cake` 不得小于`larry` 的 `cake` ，而后者的 `cake` 也不得小于 `curly` 的，我们写成： ~~~ (sortf bigger (cake 'moe) (cake 'larry) (cake 'curly)) ~~~ `sortf` 的定义的大致结构和 `_f` 差不多。它以一个 `let*` 开始，在这个 `let*` 表达式中，由 `get-setf-expansion` 返回的临时变量被绑定到广义变量的初始值上。`sortf` 的核心是中间的 `mapcon`表达式，该表达式生成的代码将被用来对这些临时变量进行排序。宏的这部分生成的代码量会随着参数个数以指数速度增长。在排序之后，广义变量会被用那些由 `get-setf-expansion` 返回的 `form`重新赋值。这里使用的算法是 的冒泡排序，但如果调用的时候参数非常多的话，这个宏就不适用了。 [示例代码 12.5] 给出的是对 sortf 调用的展开式。在最前面的 let* 中，参数和它们的 subform 按照从左到右的顺序小心地求值。之后出现的三个表达式分别比较几个临时变量的值，有可能还会交换它们：先是比较第一个和第二个，接着是第一个和第三个，然后第二个和第三个。最后广义变量从左到右被重新赋值。尽管很少需要注意这个问题，但还是提一下：通常，宏参数应该按从左到右的顺序进行赋值，这和它们求值的顺序是一致的。 有些操作符，如 `_f` 和 `sortf` ，它们与接受函数型参数的函数之间确实有相似之处。不过也应该认识到它们是完全不同的东西。类似 `find-if` 的函数接受一个函数并调用它；而类似 `_f` 的宏接受的则是一个名字，这些宏会让它成为一个表达式的 `car`。让 `_f` 和 `sortf` 都接受函数型参数也不无可能。例如，`_f` 可以这样实现： ~~~ (sortf > x (aref ar (incf i)) (car lst)) ~~~ 展开(在某个可能的实现里) 成： * * * **[示例代码 12.5] 一个 sortf 调用的展开式** ~~~ (let* ((#:g1 x) (#:g4 ar) (#:g3 (incf i)) (#:g2 (aref #:g4 #:g3)) (#:g6 lst) (#:g5 (car #:g6))) (unless (> #:g1 #:g2) (rotatef #:g1 #:g2)) (unless (> #:g1 #:g5) (rotatef #:g1 #:g5)) (unless (> #:g2 #:g5) (rotatef #:g2 #:g5)) (setq x #:g1) (system:set-aref #:g2 #:g4 #:g3) (system:set-car #:g6 #:g5)) ~~~ * * * ~~~ (defmacro _f (op place &rest args) (let ((g (gensym))) (multiple-value-bind (vars forms var set access) (get-setf-expansion place) '(let* ((,g ,op) ,@(mapcar #'list vars forms) (,(car var) (funcall ,g ,access ,@args))) ,set)))) ~~~ 然后调用 `(_f #'+ x 1)`。但是 `_f` 原来的版本不但拥有这个版本的所有功能，而且由于它处理的是名字，所以它还可以接受宏或者 `special form` 的名字。就像 `+` 那样，比如说，你还可以调用`nif` （102页）： ~~~ > (let ((x 2)) (_f nif x 'p 'z 'n) x) P ~~~ ### 12.5 定义逆 12.1 节说明了一个道理：如果一个宏调用能展开成可逆引用，那么它本身应该也是可逆的。不过，你也用不着只是为了可逆，就把操作符定义成宏。通过使用 `defsetf` ，你可以告诉 `Lisp` 如何对任意的函数或宏调用求逆。 使用这个宏的方法有两种。在最简单的情况下，它的参数是两个符号： ~~~ (defsetf symbol-value set) ~~~ 如果用更复杂的方法，那么 `defsetf` 的调用和 `defmacro` 调用会有几分相似，它另外带有一个参数用于更新值 `form`。例如，下式可以为 `car` 定义一种可能的逆： ~~~ (defsetf car (lst) (new-car) '(progn (rplaca ,lst ,new-car) ,new-car)) ~~~ `defmacro` 和 `defsetf` 之间有一个重要的区别：后者会自动为其参数创建生成符号(gensym)。通过上面给出的定义，`(setf (car x) y)` 将展开成： ~~~ (let* ((#:g2 x) (#:g1 y)) (progn (rplaca #:g2 #:g1) #:g1)) ~~~ 这样，我们写 `defsetf` 展开器时就没有后顾之忧，不用担心诸如变量捕捉，或者求值的次数和顺序之类的问题了。 在 **CLTL2** 的 Common Lisp 中，也可以直接用 `defun` 定义 `setf` 的逆。因而前面的示例也可以写成： ~~~ (defun (setf car) (new-car lst) (rplaca lst new-car) new-car) ~~~ 新的值应该作为这个函数的第一个参数。同样按照习惯，也应该把这个值作为函数的返回值。 目前为止的示例都认为，广义变量应该指向数据结构中的某个位置。不法之徒把人质带进地牢，而见义勇为之士则让她重见天日；他们移动的路径相同，但方向相反。所以，如果人们觉得 `setf` 的工作方式也只能是这样，那不足为奇，因为所有预定义的逆看上去都是如此；确实，习惯上，将被求逆的参数也常会使用 `place` 作为其参数名。 从理论上说，`setf` 可以更一般化：`accessform` 和它的逆的操作对象甚至可以不是同种数据结构。假设在某个应用里，我们想要把数据库的更新缓存起来。这可能是迫不得已的，举例来说，倘若每次修改数据，都即时完成真正的更新操作，就有可能会降低效率，或者，如果要求所有的更新都必须在提交之前验证一致性，那就必须引入缓存的机制。 * * * **[示例代码 12.6] 一个非对称的逆转换** ~~~ (defvar *cache* (make-hash-table)) (defun retrieve (key) (multiple-value-bind (x y) (gethash key *cache*) (if y (values x y) (cdr (assoc key *world*))))) (defsetf retrieve (key) (val) '(setf (gethash ,key *cache*) ,val)) ~~~ * * * 假设 `\*world\*` 是实际的数据库。为简单起见，我们将它做成一个元素为 `(key . val)` 形式的关联表（assoc-list）。[示例代码 12.6] 显示了一个称为 `retrieve` 的查询函数。如果 `\*world\*` 是: ~~~ ((a . 2) (b . 16) (c . 50) (d . 20) (f . 12)) ~~~ 那么: ~~~ > (retrieve 'c) 50 ~~~ 和 `car` 的调用不同，`retrieve` 调用并不指向一个数据结构中的特定位置。返回值可能来自两个位置里的 一个。而 `retrieve` 的逆，同样定义在 [示例代码 12.6] 中，仅指向它们中的一个： ~~~ > (setf (retrieve 'n) 77) 77 > (retrieve 'n) 77 T ~~~ 该查询返回第二个值 `t` ，以表明在缓存中找到了答案。 就像宏一样，广义变量是一种威力非凡的抽象机制。这里肯定还有更多的东西有待发掘。当然，有的用户很可能已经发现了一些使用广义变量的方法，使用这些方法能得到更优雅和强大的程序。但也不排除以全新的方式使用 `setf` 逆的可能性，或者发现其它类似的有用的变换技术。 备注： 【注1】这个定义是错误的，下一节将给出解释。 【注2】一般意义上的函数名：`1+` 或者 `(lambda (x) (+ x 1))` 都可以。 【注3】译者注：现行 Common Lisp 标准 (CLHS) 事实上要求 `define-modify-macro` 和 `define-compiler-macro` 的第三个参数的类型必须是符号。 【注4】译者注：这里根据现行 Common Lisp 标准对源代码加以修改，我们额外定义了两个辅助函数以确保 `define-modify-macro` 的第三个参数只能是符号。 【注5】译者注：当作为 `nconc` 第一个参数的变量为空列表，也就是 `nil` 时，该变量在 `nconc` 执行之后将仍是 `nil` ，而不是整个 `nconc` 表达式的那个相当于其第二个参数的值。 【注6】译者注：正如前面两个脚注里提到的那样，Common Lisp 标准并没有定义 `define-modify-macro` 的第三个参数可以是符号之外的其他东西，尽管λ表达式出现在一个函数调用形式的函数位置上确实是合法的。原书作者试图通过类比来说明 λ表达式用在 `define-modify-macro` 中的合法性，这是不恰当的，请读者注意。 【注7】译者注：原书中给出的函数实际上是 `get-setf-method` ，但这个函数已经不在现行 Common Lisp 标准中了，参见 `X3J13 Issue 308`：`SETF-METHOD-VS-SETF-METHOD` 取代它的是`get-setf-expansion` ，这个函数接受两个参数，`place` 以及可选的 `environment` 环境参数。本书后面对于所有采用 `get-setf-method` 的地方一律直接改用 `get-setf-expansion` ，不再另行说明。 【注8】第三个值当前总是一个单元素列表。它被返回成一个列表来提供（目前为止还不可能）在广义变量中保存多值的可能性。 【注9】然而，内置函数是个例外，它们不应该以这种方式被记忆化。Common Lisp 禁止重定义内置函数。

## 第 11 章 经典宏 本章介绍如何定义几种最常用的宏。它们可以大致归为三类 带有一定重叠。第一组宏创建上下文(context)。任何令其参数在一个新的上下文环境里求值的操作符都必须被定义成宏。本章的前两节描述两种基本类型的上下文，并且展示如何定义它们。 接下来的三个小节将描述带有条件和重复求值的宏。一个操作符，如果其参数求值的次数少于一次或者多于一次，那么也同样必须被定义成宏。在做条件求值和重复求值的操作符之间没有明显区别：在本章中，有些例子兼具这两项功能(绑定操作也是如此)。最后一节解释了条件求值和重复求值之间的另一种相似性： 在某些场合，它们都可以用函数来完成。 ### 11.1 创建上下文 这里的上下文有两层意思。一类上下文指的是词法环境。`special form let` 创建一个新的词法环境；`let` 主体中的表达式将在一个可能包含新变量的环境中被求值。如果在 `toplevel` 下，把 `x`设置成 `a` ，那么: ~~~ (let ((x 'b)) (list x)) ~~~ 将必定返回 `(b)` ，因为对 `list` 的调用被放在一个新环境里，它包含一个新的 `x` ，其值为 `b` 。 通常会把带有表达式体的操作符定义成宏。除了类似 `prog1` 和 `progn` 的情况外，这类操作符的目地通常都是让它的主体在某个新的上下文环境中被求值。如果要用创建上下文的代码把主体包裹起来，就需要用到宏，即使这个上下文环境里不包含新的词法变量。 * * * **[示例代码 11.1] let 的宏实现** ~~~ (defmacro our-let (binds &body body) '((lambda ,(mapcar #'(lambda (x) (if (consp x) (car x) x)) binds) ,@body) ,@(mapcar #'(lambda (x) (if (consp x) (cadr x) nil)) binds))) ~~~ * * * [示例代码 11.1] 显示了如何通过 `lambda` 将 `let` 定义为一个宏。一个 `our-let` 展开到一个函数应用: ~~~ (our-let ((x 1) (y 2)) (+ x y)) ~~~ 展开成: ~~~ ((lambda (x y) (+ x y)) 1 2) ~~~ [示例代码 11.2] 包含三个新的创建词法环境的宏。第 7.5 节使用了 `when-bind` 作为参数列表解构的示例，所以这个宏已经在第 7.5 节介绍过了。更一般的 `when-bind*` 接受一个由成对的 (symbol expression) `form` 所组成的列表 就和 `let 的第一个参数的形式相同。如果任何`expression`返回`nil`，那么整个`when-bind*`表达式就返回`nil`。同样，它的主体在每个符号像在`let*` 里那样被绑定的情况下求值： * * * **[示例代码 11.2] 绑定变量的宏** ~~~ (defmacro when-bind ((var expr) &body body) '(let ((,var ,expr)) (when ,var ,@body))) (defmacro when-bind* (binds &body body) (if (null binds) '(progn ,@body) '(let (,(car binds)) (if ,(caar binds) (when-bind* ,(cdr binds) ,@body))))) (defmacro with-gensyms (syms &body body) '(let ,(mapcar #'(lambda (s) '(,s (gensym))) syms) ,@body)) ~~~ * * * ~~~ > (when-bind* ((x (find-if #'consp '(a (1 2) b))) (y (find-if #'oddp x))) (+ y 10)) 11 ~~~ 最后，宏 `with-gensyms` 本身就是用来编写宏的。许多宏在定义的开头就会用 `gensym` 生成一些符号，有时需要生成符号的数量还比较多。宏 `with-redraw` (第 8.3 节) 就必须生成五个： ~~~ (defmacro with-redraw ((var objs) &body body) (let ((gob (gensym)) (x0 (gensym)) (y0 (gensym)) (x1 (gensym)) (y1 (gensym))) ...)) ~~~ 这样的定义可以通过使用 `with-gensyms` 得以简化，后者将整个变量列表绑定到 `gensym` 上。借助这个新的宏，我们只需写成： ~~~ (defmacro with-redraw ((var objs) &body body) (with-gensyms (gob x0 y0 x1 y1) ...)) ~~~ 这个新的宏将被广泛用于后续的章节中。 如果我们需要绑定某些变量，然后依据某些条件，来求值一组表达式中的一个，我们只需在 `let` 里使用一个条件判断： ~~~ (let ((sun-place 'park) (rain-place 'library)) (if (sunny) (visit sun-place) (visit rain-place))) ~~~ 不幸的是，对于相反的情形没有简便的写法，就是说我们总是想要求值相同的代码，但在绑定的那里必须随某些条件而变。 [示例代码 11.3] 包含一个处理类似情况的宏。从它的名字就能看出，`condlet` 行为就好像它是`cond` 和 `let` 的后代一样。它接受一个绑定语句的列表，接着是一个代码主体。每个绑定语句是否生效都要视其对应的测试表达式而定；第一个测试表达式为真的绑定语句所构造的绑定环境将会胜出，代码主体将在这个绑定环境中被求值。有的变量只出现在某些语句中，却在其它语句里没有出现，如果最后被选中的语句里没有为它们指定绑定的话，它们将会被绑定到 `nil` 上： * * * **[示例代码 11.3] `cond` 与 `let` 的组合** ~~~ (defmacro condlet (clauses &body body) (let ((bodfn (gensym)) (vars (mapcar #'(lambda (v) (cons v (gensym))) (remove-duplicates (mapcar #'car (mappend #'cdr clauses)))))) '(labels ((,bodfn ,(mapcar #'car vars) ,@body)) (cond ,@(mapcar #'(lambda (cl) (condlet-clause vars cl bodfn)) clauses))))) (defun condlet-clause (vars cl bodfn) '(,(car cl) (let ,(mapcar #'cdr vars) (let ,(condlet-binds vars cl) (,bodfn ,@(mapcar #'cdr vars)))))) (defun condlet-binds (vars cl) (mapcar #'(lambda (bindform) (if (consp bindform) (cons (cdr (assoc (car bindform) vars)) (cdr bindform)))) (cdr cl))) ~~~ * * * ~~~ > (condlet (((= 1 2) (x (princ 'a)) (y (princ 'b))) ((= 1 1) (y (princ 'c)) (x (princ 'd))) (t (x (princ 'e)) (z (princ 'f)))) (list x y z)) CD (D C NIL) ~~~ 可以把 `condlet` 的定义理解成为 `our-let` 定义的一般化。后者将其主体做成一个函数，然后被应用到初值 (initial value) 形式的求值结果上。`condlet` 展开后的代码用 `labels` 定义了一个本地函数，然后一个 cond 语句来决定哪一组初值将被求值并传给该函数。 注意到展开器使用 `mappend` 代替 `mapcan` 来从绑定语句中解出变量名。这是因为 `mapcan` 是破坏性的，根据第 10.3 节里的警告，它比较危险，会修改参数列表结构。 ### 11.2 `with-` 宏 除了词法环境以外还有另一种上下文。广义上来讲，上下文是世界的状态，包括特殊变量的值，数据结构的内容，以及 Lisp 之外事物的状态。构造这种类型上下文的操作符也必须被定义成宏，除非它们的代码主体要被打包进闭包里。 构造上下文的宏的名字经常以 `with-` 开始。这类宏中，用得最多恐怕要算 `with-open-file` 了。它的主体和一个新打开的文件一起求值，其时，该文件已经绑定到了用户给定的变量： ~~~ (with-open-file (s "dump" :direction :output) (princ 99 s)) ~~~ 该表达式求值完毕以后，文件 "dump" 将自动关闭，它的内容将是两个字符 "99"。 很明显，这个操作符应该定义成宏，因为它绑定了 `s` 。其实，只要一个操作符需要让 `form` 在新的上下文中进行求值，那就应当把它定义为宏。在 **CLTL2** 中新加入的 `ignore-errors` 宏，使它的参数就像在一个 `progn` 里求值一样。不管什么地方出了错，整个 `ignore-errors form` 会直接返回`nil` 。(在读取用户的输入时，可能就有这种需要。所以这还是有点用的。) 尽管 `ignore-errors` 没有创建任何变量，但它还是必须定义成宏，因为它的参数是在一个新的上下文里求值的。 一般而言，创建上下文的宏将被展开成一个代码块；附加的表达式可能被放在主体之前、之后，或者前后都有。如果是出现在主体之后，其目的可能是为了在结束时，让系统的状态保持一致 去做某些清理工作。 例如，`with-open-file` 必须关闭它打开的文件。在这种情况下，典型的方法是将上下文创建的宏展开进一个 `unwind-protect` 里。`unwind-protect` 的目的是确保特定表达式被求值，甚至当执行被中断时。它接受一个或更多参数，这些参数按顺序执行。如果一切正常的话它将返回第一个参数的值，就像 `prog1` 。区别在于，即使当出现错误，或者抛出的异常中断了第一个参数的求值，其余的参数也一样会被求值。 ~~~ > (setq x 'a) A > (unwind-protect (progn (princ "What error?") (error "This error.")) (setq x 'b)) What error? >>Error: This error. ~~~ `unwind-protect` 产生了一个错误。但是在返回到 `toplevel` 之后，我们注意到它的第二个参作为整体，`form toplevel` 数仍然被求值了： ~~~ > x B ~~~ 因为 `with-open-file` 展开成了一个 `unwind-protect` ，所以即使对 `with-open-file` 的 `body` 求值时发生了错误，它打开的文件还是会一如既往地被关闭。 上下文创建宏多数是为特定应用而写的。举个例子，假设我们在写一个程序，它会和多个远程数据库打交道。程序在同一时刻只和一个数据库通信，这个数据库由全局变量 *db* 指定。在使用数据库之前，我们必须对它加锁，以确保没有其他程序能同时使用它。完成操作后需要对其解锁。如果想对数据库 `db` 查询 `q` 的值，或许会这样说： ~~~ (let ((temp *db*)) (setq *db* db) (lock *db*) (prog1 (eval-query q) (release *db*) (setq *db* temp))) ~~~ 我们可以通过宏把所有这些维护操作都藏起来。[示例代码 11.4] 定义了一个宏，它让我们在更高的抽象层面上管理数据库。使用 `with-db` ，我们只需说： ~~~ (with-db db (eval-query q)) ~~~ 而且调用 `with-db` 也更安全，因为它会展开成 `unwind-protect` 而不是简单的 `prog1` 。 [示例代码 11.4] 中的两个定义阐述了编写此类宏的两种可能方式。第一种是完全用宏，第二种把函数和宏结合起来。当 `with-` 宏变得愈发复杂时，第二种方法更有实践意义。 在 CLTL2 Common Lisp 中，`dynamic-extent` 声明使得在为含主体的闭包分配空间时，可以更高效一些( **CLTL1** 实现会忽略该声明)。我们只有在 `with-db-fn` 调用期间才需要这个闭包，该声明也正合乎这个要求，它允许编译器从栈上为其分配空间。这些空间将在let 表达式退出时自动回收，而不是之后由垃圾收集器回收。 * * * **[示例代码 11.4] 一个典型的 `with-` 宏** 完全使用宏： ~~~ (defmacro with-db (db &body body) (let ((temp (gensym))) '(let ((,temp *db*)) (unwind-protect (progn (setq *db* ,db) (lock *db*) ,@body) (progn (release *db*) (setq *db* ,temp)))))) ~~~ 宏和函数结合使用： ~~~ (defmacro with-db (db &body body) (let ((gbod (gensym))) '(let ((,gbod #'(lambda () ,@body))) (declare (dynamic-extent ,gbod)) (with-db-fn *db* ,db ,gbod)))) (defun with-db-fn (old-db new-db body) (unwind-protect (progn (setq *db* new-db) (lock *db*) (funcall body)) (progn (release *db*) (setq *db* old-db)))) ~~~ * * * ### 11.3 条件求值 有时我们需要让宏调用中的某个参数仅在特定条件下才被求值。这超出了函数的能力，因为函数总是会对它所有的参数进行求值。不过诸如 `if`、`and` 和 `cond` 这样内置的操作符能够使某些参数免于求值，除非其它参数返回某些特定的值。例如在下式中 ~~~ (if t 'phew (/ x 0)) ~~~ 第三个参数如果被求值的话将导致一个除零错误。但由于只有前两个参数将被求值，`if` 从整体上将总是安全地返回 `phew` 。 我们可以通过编写宏，将调用展开到已有的操作符上来创造这类新操作符。[示例代码 11.5] 中的两个宏是许多可能的 `if` 变形中的两个。`if3` 的定义显示了应如何定义一个三值逻辑的条件选择。这个宏不再将 `nil` 当成假，把除此之外的都作为真，而是考虑了三种真值类型：真，假，以及不确定，表示为 `?`。它可能用于下面关于五岁小孩的描述： ~~~ (while (not sick) (if3 (cake-permitted) (eat-cake) (throw 'tantrum nil) (plead-insistently))) ~~~ * * * ** [示例代码 11.5] 做条件求值的宏** ~~~ (defmacro if3 (test t-case nil-case ?-case) '(case ,test ((nil) ,nil-case) (? ,?-case) (t ,t-case))) (defmacro nif (expr pos zero neg) (let ((g (gensym))) '(let ((,g ,expr)) (cond ((plusp ,g) ,pos) ((zerop ,g) ,zero) (t ,neg))))) ~~~ * * * 这个新的条件选择展开成一个 `case`。(那个 `nil` 键必须封装在列表里，原因是单独的 `nil` 键会有歧义。) 最后三个参数中只有一个会被求值，至于是哪一个，这取决于第一个参数的值。 nif 的意思是 "numericif" 。该宏的另一种实现出现在 7.2 节上。它接受数值表达式作为第一个参数，并根据这个表达式的符号来求值接下来三个参数中的一个。 ~~~ > (mapcar #'(lambda (x) (nif x 'p 'z 'n)) '(0 1 -1)) (Z P N) ~~~ [示例代码 11.6] 包含了另外几个使用条件求值的宏。宏 `in` 用来高效地测试集合的成员关系。要是你想要测试一个对象是否属于某备选对象的集合，可以把这个查询表达式表示成逻辑或： ~~~ (let ((x (foo))) (or (eql x (bar)) (eql x (baz)))) ~~~ 或者你也可以用集合的成员关系来表达： ~~~ (member (foo) (list (bar) (baz))) ~~~ 后者更抽象，但效率要差些。该 `member` 表达式在两个地方导致了毫无必要的开销。它需要构造点对，因为它必须将所有备选对象连结成一个列表以便 `member` 进行查找。并且为了把备选项做成列表形式它们全都要被求值，尽管某些值可能根本不需要。如果 `(foo)` 和 `(bar)` 的值相等，那么就不需要求值 `(baz)` 了。不管它在建模上多么抽象，使用 `member` 都不是好方法。我们可以通过宏来得到更有效率的抽象：`in` 把 `member` 的抽象与 `or` 的效率结合在了一起。等价的 `in` 表达式: ~~~ (in (foo) (bar) (baz)) ~~~ 跟 `member` 表达式的形态相同，但却可以展开成： ~~~ (let ((#:g25 (foo))) (or (eql #:g25 (bar)) (eql #:g25 (baz)))) ~~~ 情况经常是这样，当需要在简洁和高效两种习惯用法之间择一而从时，我们取中庸之道，方法是编写宏将前者变换成为后者。 发音为 "inqueue" 的 `inq` 是 `in` 的引用变形，类似 `setq` 之于 `set`。表达式： ~~~ (inq operator + - *) ~~~ 展开成： ~~~ (in operator '+ '- '*) ~~~ * * * **[示例代码 11.6] 使用条件求值的宏** ~~~ (defmacro in (obj &rest choices) (let ((insym (gensym))) '(let ((,insym ,obj)) (or ,@(mapcar #'(lambda (c) '(eql ,insym ,c)) choices))))) (defmacro inq (obj &rest args) '(in ,obj ,@(mapcar #'(lambda (a) '',a) args))) (defmacro in-if (fn &rest choices) (let ((fnsym (gensym))) '(let ((,fnsym ,fn)) (or ,@(mapcar #'(lambda (c) '(funcall ,fnsym ,c)) choices))))) (defmacro >case (expr &rest clauses) (let ((g (gensym))) '(let ((,g ,expr)) (cond ,@(mapcar #'(lambda (cl) (>casex g cl)) clauses))))) (defmacro >casex (g cl) (let ((key (car cl)) (rest (cdr cl))) (cond ((consp key) '((in ,g ,@key) ,@rest)) ((inq key t otherwise) '(t ,@rest)) (t (error "bad >case clause"))))) ~~~ * * * 和 `member` 的缺省行为一样，`in` 和 `inq` 用 `eql` 来测试等价性。如果你想要使用其他的测试条件，或者某个一元函数来进行测试，那么可以改用更一般的 `in-if`。`in-if` 之于 `same` 好比是 `in`对 `member` 的关系。表达式: ~~~ (member x (list a b) :test #'equal) ~~~ 也可以写作: ~~~ (in-if #'(lambda (y) (equal x y)) a b) ~~~ 而: ~~~ (some #'oddp (list a b)) ~~~ 就变成: ~~~ (in-if #'oddp a b) ~~~ 把 `cond` 和 `in` 一起用的话，我们还能定义出一个有用的 `case` 变形。Common Lisp 的 `case` 宏假定它的键值都是常量。但有时可能需要 `case` 的行为，同时又希望求值其中的键。针对这类情况我们定义了 `>case` ，除了它会在比较之前先对每个子句里的键进行求值以外，其行为和 `case` 相同。(名字中的 > 意指通常用来表示求值过程的那个箭头符号。) 因为 `>case` 使用了 in，只有它需要的那个键才会被求值。 由于键可以是 Lisp 表达式，无法判断 `(x y)` 到底是个函数调用还是由两个键组成的列表。为了避免这种二义性，键 (除了 `t` 和 `otherwise` ) 必须总是放在列表里给出，哪怕是只有一个。在 `case` 表达式里，由于会产生歧义，nil 不能作为子句的 car 出现。在 `>case` 表达式里，`nil` 作为子句的`car` 就不再有歧义了，但它的含义是该子句的其余部分将不会被求值。 为清晰起见，生成每一个 `>case` 子句展开式的代码被定义在一个单独的函数 `>casex` 里。注意到`>casex` 本身还用到了 `inq`。 ### 11.4 迭代 有时，函数的麻烦之处并非在于它们的参数总是被求值，而是它们只能求值一次。因为函数的每个参数都将被求值刚好一次，如果我们想要定义一个操作符，它接受一些表达式体，并且在这些表达式上进行迭代操作，那唯一的办法就是把它定义成宏。 最简单的例子就是一个能够按顺序永无休止地求值其参数的宏： ~~~ (defmacro forever (&body body) '(do () (nil) ,@body)) ~~~ 这不过是当你不给它任何循环关键字时，`loop` 宏的本分。你可能认为无限循环毫无用处(或者说用处不大)。但当它和 `block` 和 `return-from` 组合起来使用时，这类宏就变成了表达某种循环最自然的方式。这种循环只会在一些突发情况下才停下来。 * * * **[示例代码 11.7] 简单的迭代宏** ~~~ (defmacro while (test &body body) '(do () ((not ,test)) ,@body)) (defmacro till (test &body body) '(do () (,test) ,@body)) (defmacro for ((var start stop) &body body) (let ((gstop (gensym))) '(do ((,var ,start (1+ ,var)) (,gstop ,stop)) ((> ,var ,gstop)) ,@body))) ~~~ * * * [示例代码 11.7] 中给出了一些最简单的迭代宏。其中，`while` 我们之前已经见过了 (7.4 节)，其主体将在测试表达式返回真时求值。与之对应的是 `till` ，它是在测试表达式返回假时求值。最后是for ，同样，在前面也有过一面之缘( 9.6 节)，它在给定的数字区间上做迭代操作。 我们定义这些宏，让它们展开成 `do` ，用这个办法，使得在宏的主体里能使用 `go` 和 `return` 。正如 `do` 从 `block` 和 `tagbody` 那里继承了这些权力，`do` 也把这种权利传给了 `while`、`till` 和`for`。正如 9.7 节上解释的，`do` 内部隐含 `block` 里的 `nil` 标签将被 [示例代码 11.7] 中的宏所捕捉。虽然与其说这是个 bug，不如说它是个特性，但至少应该明确提出来。 当你需要定义更强大的迭代结构时，宏是必不可少的。[示例代码 11.8] 里包括了两个 `dolist` 的一般化；两者都在求值主体时绑定一组变量到一个列表中相继的子序列上。例如，给定两个参数，`do-tuples/o` 将成对迭代： ~~~ > (do-tuples/o (x y) '(a b c d) (princ (list x y))) (A B)(B C)(C D) NIL ~~~ 给定相同的参数，`do-tuples/c` 将会做同样的事，然后折回到列表的开头： * * * **[示例代码 11.8] 迭代子序列的宏** ~~~ (defmacro do-tuples/o (parms source &body body) (if parms (let ((src (gensym))) '(prog ((,src ,source)) (mapc #'(lambda ,parms ,@body) ,@(map0-n #'(lambda (n) '(nthcdr ,n ,src)) (- (length source) (length parms)))))))) (defmacro do-tuples/c (parms source &body body) (if parms (with-gensyms (src rest bodfn) (let ((len (length parms))) '(let ((,src ,source)) (when (nthcdr ,(1- len) ,src) (labels ((,bodfn ,parms ,@body)) (do ((,rest ,src (cdr ,rest))) ((not (nthcdr ,(1- len) ,rest)) ,@(mapcar #'(lambda (args) '(,bodfn ,@args)) (dt-args len rest src)) nil) (,bodfn ,@(map1-n #'(lambda (n) '(nth ,(1- n) ,rest)) len)))))))))) (defun dt-args (len rest src) (map0-n #'(lambda (m) (map1-n #'(lambda (n) (let ((x (+ m n))) (if (>= x len) '(nth ,(- x len) ,src) '(nth ,(1- x) ,rest)))) len)) (- len 2))) ~~~ * * * ~~~ > (do-tuples/c (x y) '(a b c d) (princ (list x y))) (A B)(B C)(C D)(D A) NIL ~~~ 两个宏都返回 `nil` ，除非在主体中有显式的 `return` 。 在需要处理某种路径表示的程序里，会经常用到这类迭代结构。后缀 `/o` 和 `/c` 被用来表明这两个版本的迭代控制结构是分别用于遍历开放和封闭的路径的。举个例子，如果`points` 是一个点的列表而 `(drawline x y)` 在 `x` 和 `y` 之间画线，那么画一条从起点到终点的路径我们写成: ~~~ (do-tuples/o (x y) points (drawline x y)) ~~~ 假如 `points` 是一个多边形的节点列表，为了画出它的轮廓，我们这样写: ~~~ (do-tuples/c (x y) points (drawline x y)) ~~~ 作为第一个实参给出的形参列表的长度是任意的，相应的迭代就会按照那个长度的组合进行。如果只给一个参数，两者都会退化成 `dolist` ： ~~~ > (do-tuples/o (x) '(a b c) (princ x)) ABC NIL > (do-tuples/c (x) '(a b c) (princ x)) ABC NIL ~~~ `do-tuples/c` 的定义比 `do-tuples/o` 更复杂一些，因为它要在搜索到列表结尾时折返回来。如果有`n` 个参数，`do-tuples/c` 必须在返回之前多做 `n-1` 次迭代： ~~~ > (do-tuples/c (x y z) '(a b c d) (princ (list x y z))) (A B C)(B C D)(C D A)(D A B) NIL > (do-tuples/c (w x y z) '(a b c d) (princ (list w x y z))) (A B C D)(B C D A)(C D A B)(D A B C) NIL ~~~ 前一个对 `do-tuples/c` 调用的展开式显示在 [示例代码 11.9] 中。生成过程的困难之处是那些展示折返到列表开头的调用序列。这些调用 (在本例中有两个) 由 `dt-args` 生成。 * * * **[示例代码 11.9] 一个 `do-tuples/c` 调用的展开** ~~~ (do-tuples/c (x y z) '(a b c d) (princ (list x y z))) ~~~ 展开成： ~~~ (let ((#:g2 '(a b c d))) (when (nthcdr 2 #:g2) (labels ((#:g4 (x y z) (princ (list x y z)))) (do ((#:g3 #:g2 (cdr #:g3))) ((not (nthcdr 2 #:g3)) (#:g4 (nth 0 #:g3) (nth 1 #:g3) (nth 0 #:g2)) (#:g4 (nth 1 #:g3) (nth 0 #:g2) (nth 1 #:g2)) nil) (#:g4 (nth 0 #:g3) (nth 1 #:g3) (nth 2 #:g3)))))) ~~~ * * * ### 11.5 多值迭代 内置 `do` 宏早在多重返回值之前就已经有了。幸运的是，`do` 可以继续进化以适应新的形势，因为`Lisp` 的进化掌握在程序员的手中。[示例代码 11.10] 包含一个支持多值的 `do*` 版本。在 `mvdo*`里，每个初值语句可绑定多个变量： ~~~ > (mvdo* ((x 1 (1+ x)) ((y z) (values 0 0) (values z x))) ((> x 5) (list x y z)) (princ (list x y z))) (1 0 0)(2 0 2)(3 2 3)(4 3 4)(5 4 5) (6 5 6) ~~~ 这类迭代非常有用，例如，在交互式图形程序里经常需要处理诸如坐标和区域这样的多值数据。 * * * **[示例代码 11.10] `do*` 的多值绑定版本** ~~~ (defmacro mvdo* (parm-cl test-cl &body body) (mvdo-gen parm-cl parm-cl test-cl body)) (defun mvdo-gen (binds rebinds test body) (if (null binds) (let ((label (gensym))) '(prog nil ,label (if ,(car test) (return (progn ,@(cdr test)))) ,@body ,@(mvdo-rebind-gen rebinds) (go ,label))) (let ((rec (mvdo-gen (cdr binds) rebinds test body))) (let ((var/s (caar binds)) (expr (cadar binds))) (if (atom var/s) '(let ((,var/s ,expr)) ,rec) '(multiple-value-bind ,var/s ,expr ,rec)))))) (defun mvdo-rebind-gen (rebinds) (cond ((null rebinds) nil) ((< (length (car rebinds)) 3) (mvdo-rebind-gen (cdr rebinds))) (t (cons (list (if (atom (caar rebinds)) 'setq 'multiple-value-setq) (caar rebinds) (third (car rebinds))) (mvdo-rebind-gen (cdr rebinds)))))) ~~~ * * * 假设我们想要写一个简单的交互式游戏，游戏的目标是避免被两个追踪者挤成碎片。如果两个追踪者同时碰到你，那么你就输了；如果它们自己撞到一起，你就是赢家。[示例代码 11.11] 显示了该游戏的主循环是如何用 `mvdo*` 写成的。 也有可能写出一个 `mvdo` ，并行绑定其局部变量： ~~~ > (mvdo ((x 1 (1+ x)) ((y z) (values 0 0) (values z x))) ((> x 5) (list x y z)) (princ (list x y z))) (1 0 0)(2 0 1)(3 1 2)(4 2 3)(5 3 4) (6 4 5) ~~~ `do` 的定义中需要用到 `psetq` 的原因在第 7.7 节里曾解释过。为了定义 `mvdo` ，需要一个多值版本的 `psetq` 。 由于 Common Lisp 没有提供这种操作符，所以我们必须自己写一个，如 [示例代码 11.12] 所示。新的宏的工作方式如下： * * * **[示例代码 11.11]：一个碰撞游戏** ~~~ > (let ((w 0) (x 1) (y 2) (z 3)) (mvpsetq (w x) (values 'a 'b) (y z) (values w x)) (list w x y z)) (A B 0 1) (mvdo* (((px py) (pos player) (move player mx my)) ((x1 y1) (pos obj1) (move obj1 (- px x1) (- py y1))) ((x2 y2) (pos obj2) (move obj2 (- px x2) (- py y2))) ((mx my) (mouse-vector) (mouse-vector)) (win nil (touch obj1 obj2)) (lose nil (and (touch obj1 player) (touch obj2 player)))) ((or win lose) (if win 'win 'lose)) (clear) (draw obj1) (draw obj2) (draw player)) ~~~ > `(pos obj)` 返回代表 `obj` 位置的两个值 `x` ，`y` 。开始的时候三个对象的位置是随机的。 > > `(move obj dx dy)` 根据类型和向量 `<dx, dy>` 来移动对象 `obj`。返回的两个值 `x` ，`y` 代表其新位置。 > > `(mouse-vector)` 返回代表当前鼠标移动位置的两个值 `mx`，`my` 。 > > `(touch obj1 obj2)` 返回真，如果 `obj1` 碰上了 `obj2`。 > > `(clear)` 清空游戏区域。 > > `(draw obj)` 在当前位置绘制 `obj`。 * * * `mvpsetq` 的定义依赖于三个工具函数：`mklist` ( 4.3 节)，`group` (4.3 节)，以及在这里定义的`shuffle` ，用来交错两个列表： ~~~ > (shuffle '(a b c) '(1 2 3 4)) (A 1 B 2 C 3 4) ~~~ 借助 `mvpsetq` ，我们就可以定义 `mvdo` 了，如 [示例代码 11.13] 所示。和 `condlet` 一样，这个宏使用了 `mappend` 来代替 `mapcan` 以避免修改最初的宏调用。【注 1】这种 `mappend-mklist` 写法可以把一棵树压扁一层： ~~~ > (mappend #'mklist '((a b c) d (e (f g) h) ((i)) j)) (A B C D E (F G) H (I) J) ~~~ 为了有助于理解这个相当长的宏，[示例代码 11.14] 中含有一个展开示例。 ### 11.6 需要宏的原因 宏并不是保护参数免于求值的唯一方式。另一种方法是把它封装在闭包里。条件求值和重复求值的相似之处在于这两个问题在本质上都不需要宏。例如，我们可以将 `if` 写成函数： ~~~ (defun fnif (test then &optional else) (if test (funcall then) (if else (funcall else)))) ~~~ 我们可以把 `then` 和 `else` 参数表达成闭包，通过这种方式来保护它们，所以下面的表达式： ~~~ (if (rich) (go-sailing) (rob-bank)) ~~~ 可以改成： ~~~ (fnif (rich) #'(lambda () (go-sailing)) #'(lambda () (rob-bank))) ~~~ * * * **[示例代码 11.12] psetq 的多值版本** ~~~ (defmacro mvpsetq (&rest args) (let* ((pairs (group args 2)) (syms (mapcar #'(lambda (p) (mapcar #'(lambda (x) (gensym)) (mklist (car p)))) pairs))) (labels ((rec (ps ss) (if (null ps) '(setq ,@(mapcan #'(lambda (p s) (shuffle (mklist (car p)) s)) pairs syms)) (let ((body (rec (cdr ps) (cdr ss)))) (let ((var/s (caar ps)) (expr (cadar ps))) (if (consp var/s) '(multiple-value-bind ,(car ss) ,expr ,body) '(let ((,@(car ss) ,expr)) ,body))))))) (rec pairs syms)))) (defun shuffle (x y) (cond ((null x) y) ((null y) x) (t (list* (car x) (car y) (shuffle (cdr x) (cdr y)))))) ~~~ * * * 如果我们要的只是条件求值，那么不用宏也一样可以。它们只是让程序更清晰罢了。不过，当我们需要拆开参数 `form`，或者为作为参数传入的变量绑定值时，就只能靠宏了。 同样的道理也适用于那些用于迭代的宏。尽管只有宏才提供唯一的手段，可以用来定义带有表达式体的迭代控制结构，其实用函数来做迭代也是可能的，只要循环体被包装在那个函数里。【注 2】例如内置函数 `mapc` 就是与 `dolist` 对应的函数式版本。表达式: ~~~ (dolist (b bananas) (peel b) (eat b)) ~~~ 和: ~~~ (mapc #'(lambda (b) (peel b) (eat b)) bananas) ~~~ 有相同的副作用。(尽管前者返回 nil ，而后者返回 bananas 列表)。或者，我们也可以把 `forever`实现成函数: ~~~ (defun forever (fn) (do () (nil) (funcall fn))) ~~~ * * * **[示例代码 11.13] do 的多值绑定版本** ~~~ (defmacro mvdo (binds (test &rest result) &body body) (let ((label (gensym)) (temps (mapcar #'(lambda (b) (if (listp (car b)) (mapcar #'(lambda (x) (gensym)) (car b)) (gensym))) binds))) '(let ,(mappend #'mklist temps) (mvpsetq ,@(mapcan #'(lambda (b var) (list var (cadr b))) binds temps)) (prog ,(mapcar #'(lambda (b var) (list b var)) (mappend #'mklist (mapcar #'car binds)) (mappend #'mklist temps)) ,label (if ,test (return (progn ,@result))) ,@body (mvpsetq ,@(mapcan #'(lambda (b) (if (third b) (list (car b) (third b)))) binds)) (go ,label))))) ~~~ * * * **[示例代码 11.14] mvdo 调用的展开** (mvdo ((x 1 (1+ x)) ((y z) (values 0 0) (values z x))) ((> x 5) (list x y z)) (princ (list x y z))) 展开成： ~~~ (let (#:g2 #:g3 #:g4) (mvpsetq #:g2 1 (#:g3 #:g4) (values 0 0)) (prog ((x #:g2) (y #:g3) (z #:g4)) #:g1 (if (> x 5) (return (progn (list x y z)))) (princ (list x y z)) (mvpsetq x (1+ x) (y z) (values z x)) (go #:g1))) ~~~ * * * 不过，前提是我们愿意传给它闭包而非表达式体。 然而，迭代控制结构通常要做的工作会比简单的迭代更多，也就是比 `forever` 更复杂：它们通常会把绑定和迭代合二为一。使用函数的话，绑定操作会很有局限。如果想把变量绑定到列表的后继元素上，那么用某种映射函数就可以。但如果需求比这个更复杂，你就不得不写一个宏了。 备注： 【注1】译者注：原文为 `mapcar`，按照 `condlet` 来看应该是一个错误。 【注2】写一个不需要其参数封装在函数里的迭代函数也并非不可能。我们可以写一个函数在作为其参数传递的表达式上调用 `eval` 。对于 "为什么调用 `eval` 通常是有问题的"，可参见 21.2 节的解释。

## 第 10 章 其他的宏陷阱 编写宏需要格外小心。函数被隔离在它自己的词法世界中，但是宏就另当别论了，因为它要被展开成进调用方的代码，所以除非仔细编写，否则它将会给用户带来意料之外的不便。第 9 章详细说明了变量捕捉，它是这些不速之客中最常见的一个。本章将讨论在编写宏时需要避免的另外四个问题。 ### 10.1 求值的次数 * * * **[示例代码 10.1] 控制参数求值** 正确的版本： ~~~ (defmacro for ((var start stop) &body body) (let ((gstop (gensym))) '(do ((,var ,start (1+ ,var)) (,gstop ,stop)) ((> ,var ,gstop)) ,@body))) ~~~ 导致多重求值： ~~~ (defmacro for ((var start stop) &body body) '(do ((,var ,start (1+ ,var))) ((> ,var ,stop)) ,@body)) ~~~ 错误的求值顺序： ~~~ (defmacro for ((var start stop) &body body) (let ((gstop (gensym))) '(do ((,gstop ,stop) (,var ,start (1+ ,var))) ((> ,var ,gstop)) ,@body))) ~~~ * * * 在上一章中出现了几种错误的 `for`版本。[示例代码 10.1] 给出了另外两个，同时还带有一个正确的版本方便对比。 尽管第二个 `for`并不那么容易发生变量捕捉，但是它还是有个 bug。它将生成一个展开式，在这个展开式里，作为 `stop` 传递的 `form` 在每次迭代时都会被求值。在最理想的情况下，这只会让宏变得低效，重复做一些它本来可以只做一次的操作。如果 `stop` 有副作用，那么宏可能就会出人意料地产生错误的结果。例如，这个循环将永不终止，因为目标在每次迭代时都会倒退： ~~~ > (let ((x 2)) (for (i 1 (incf x)) (princ i))) 12345678910111213... ~~~ 在编写类似 `for`的宏的时候，必须牢记：宏的参数是 `form`，而非值。取决于它们出现在表达式中位置的不同，它们可能会被求值多次。在这种情况下，解决的办法是把变量绑定到 `stop form` 的返回值上，并在循环过程中引用这个变量。 除非是为了迭代而有意为之，否则编写宏的时候，应该确保表达式在宏调用里出现的次数和表达式求值的次数一致。很明显，这个规则对有些情况并不适用：倘若参数总会被求值的话，Common Lisp 的 `or` 的用处就会大打折扣（那就成 Pascal 的 `or` 了）。但是在这种情况下用户知道他们期望的求值次数。对于第二个版本的 `for`v来说就不是这样了：用户没有理由会想要 `stop form` 被求值一次以上，而且事实上也不应该这样做。一个宏要是写成第二个版本的 `for`v那样，十有八九就是弄错了。 对基于 `setf` 的宏来说，无意的多重求值尤其难以处理。Common Lisp 提供了几个实用工具以便编写这样的宏。具体的问题，以及解决方案，将在第 12 章里讨论。 ### 10.2 求值的顺序 表达式求值的顺序，虽然不像它们的求值次数那样重要，但有时先后次序也会成为问题。在 Common Lisp 的函数调用中，参数是从左到右求值的： ~~~ > (setq x 10) 10 > (+ (setq x 3) x) 6 ~~~ 对于宏来说，最好也这样处理。宏通常应该确保表达式求值的顺序和它们在宏调用中出现的顺序一致。 在 [示例代码 10.1] 中，第三个版本的 `for`同样有个难以觉察的 bug。参数 `stop` 将会在 `start` 前被求值，尽管它们在宏调用中出现的顺序和求值的顺序是相反的： ~~~ > (let ((x 1)) (for (i x (setq x 13)) (princ i))) 13 NIL ~~~ 这个宏给人一种莫名其妙的错觉，就好像时间会倒退一样。尽管 `start form` 在代码里面出现在先，但 `stop form` 的求值操作却能影响 `start form` 的返回值。 正确版本的 `for`会确保其参数以它们出现的顺序被求值： ~~~ > (let ((x 1)) (for (i x (setq x 13)) (princ i))) 12345678910111213 NIL ~~~ 这里，在 `stop form` 里设置 `x` 的值就不会影响到前一个参数的返回值了。 尽管上面的例子是杜撰的，但是这类问题确实还会时有发生，而且这种 bug 很难找出来。或许很少有人会写出这样的代码，让宏一个参数的求值影响到另一个参数的返回值，但是人们在无意中做的事情，有可能并非出自本心。尽管在有意这样用时，应当正常工作，但是这不是让 bug 藏身于实用工具的理由。如果有人写出的代码和前例相似，它很可能是误写成的，但 `for` 的正确版本将使错误更容易检测出来。 ### 10.3 非函数式的展开器 Lisp 期望那些生成宏展开式的代码都是纯函数式的，就像第 3 章里说的那样。展开器代码除了作为参数传给它的 `form` 之外不应该有其他依赖，并且它影响外界的唯一渠道只能是它的返回值。 如 CLTL2（685 页）所述，可以确信，在编译代码中的宏调用将不会在运行期重新展开。另一方面，Common Lisp 对宏调用展开的时机，和展开的次数并没有作出保证。如果一个宏的展开式会因上面的两个因素而不同的话，那么就可以认为这个宏是有问题的。例如，假设我们想要统计某个宏的使用次数。我们不能直接对源文件搜索一遍了事，因为在由程序生成的代码里也可能会调用这个宏。所以，我们可能会这样定义这个宏： ~~~ (defmacro nil! (x) ; wrong (incf *nil!s*) '(setf ,x nil)) ~~~ 使用这个定义，使得每次展开 `nil!` 的调用时，全局的 `\*nil!s\*` 的值都会递增。然而，如果我们认为这个变量的值能告诉我们 `nil!` 被调用的次数，那就大错特错了。一个宏调用可以，并且经常会被展开不只一次。 例如，一个对你代码进行变换的预处理器在它决定是否变换代码之前，可能不得不展开表达式中的宏调用。 这是一条普适的规则，即：展开器代码除其参数外不应依赖其他任何东西。所以任何宏，比如说通过字符串来构造展开式的那种，应当小心不要对宏展开时所在的包作任何假设。下面的这个例子虽说简单，但相当有代表性， ~~~ (defmacro string-call (opstring &rest args) ; wrong '(,(intern opstring) ,@args)) ~~~ 它定义了一个宏，这个宏接受一个操作符的打印名称，并把它展开成对该操作符的调用： ~~~ > (defun our+ (x y) (+ x y)) OUR+ > (string-call "OUR+" 2 3) 5 ~~~ 对 `intern` 的调用接受一个字符串，并返回对应的符号。尽管如此，如果我们省略了可选的包参数，它将在当前包里寻找符号。该展开式将因此依赖于展开式生成时所在的包，并且除非 `our+` 在那个包里可见，否则展开式将是一个对未知符号的调用。 展开式代码中的副作用有时会带来一些问题，Miller 和 Benson 在 `<<Lisp Style`and`Design>>` 一书中就为之举了一个非常丑陋的例子。CLTL2（78 页）提到，Common Lisp 并不保证绑定在`&rest` 形参上的列表是新生成的。 它们可能会和程序其他地方的列表共享数据结构。后果就是，你不能破坏性地修改 `&rest` 形参，因为你不知道你将会改掉其他什么东西。 这种可能性对于函数和宏都有影响。对于函数来说，问题出在使用 `apply` 的时候。在合格的 Common Lisp 实现中，将发生下面的事情。假设我们定义一个函数 `et-al` ，它会在它的参数列表末尾加上 `'et 'al` ，再返回它： ~~~ (defun et-al (&rest args) (nconc args (list 'et 'al))) ~~~ 如果我们像平时那样调用这个函数，它看起来工作正常： ~~~ > (et-al 'smith 'jones) (SMITH JONES ET AL) ~~~ 然而，要是我们通过 `apply` 调用它，就会改动已有的数据： ~~~ > (setq greats '(leonardo michelangelo)) (LEONARDO MICHELANGELO) > (apply #'et-al greats) (LEONARDO MICHELANGELO ET AL) > greats (LEONARDO MICHELANGELO ET AL) ~~~ 至少 Common Lisp 的正确实现应该会这样反应，虽然到目前为止没有一个是这样做的。 对宏来说就更危险了。如果一个宏会修改它的 `&rest` 形参，那它可能会因此改掉整个宏调用。这就是说，最终你可能写出一个难以察觉的自我重写的程序。这种危险也更有现实意义 -- 它实实在在地发生在现有的实现中。如果我们定义一个宏，它将某些东西 `nconc` 到它的 `&rest` 参数里: 【注 1】 ~~~ (defmacro echo (&rest args) '',(nconc args (list 'amen))) ~~~ 然后定义一个函数来调用它： ~~~ (defun foo () (echo x)) ~~~ 在一个广泛使用的 Common Lisp 中，则会观察到下面的现象： ~~~ > (foo) (X AMEN AMEN) > (foo) (X AMEN AMEN AMEN) ~~~ 不只是 `foo` 返回了错误的结果，它甚至每次返回的结果都不一样，因为每一次宏展开都替换了 `foo`的定义。 这个例子同时也阐述了之前提到的一个观点：一个宏可能会被展开多次。在这个实现里，第一次调用`foo` 返回的是含有两个 `amen` 的列表。出于某种原因，该实现在 `foo` 被定义时就做了一次宏展开，然后接下来每次调用时都会再展开一次。 将 `foo` 定义成这样会更安全一些： ~~~ (defmacro echo (&rest args) ''(,@args amen)) ~~~ 因为 `comma-at` 等价于 `append` 而非 `nconc` 。在重定义这个宏之后，`foo` 也需要重新定义一下，就算它没有编译也是一样，因为 `echo` 的前一个版本导致它把自己重写了。 对宏来说，受到这种危险威胁的不单单是 &rest 参数。任何宏参数只要是列表就应该单独对待。如果我们定义了一个会修改其参数的宏，以及一个调用该宏的函数， ~~~ (defmacro crazy (expr) (nconc expr (list t))) (defun foo () (crazy (list))) ~~~ 那么主调函数的源代码就有可能被修改，正如在一个实现里，我们首次调用时所看到的： ~~~ > (foo) (T T) ~~~ 和解释代码一样，这种情况在编译的代码里也会发生。 结论是，不要试图通过破坏性修改参数列表结构，来避免构造 `consing` 。这样得到的程序就算可以工作也将是不可移植的。如果你真想在接受变长参数的函数中避免`consing` ，一种解决方案是使用宏，由此将 `consing` 切换到编译期。对于宏的这种应用，可见第 13 章。 宏展开器返回的表达式含有引用列表的话，就应该避免对它进行破坏性的操作。就其本身而言，这不只是对于宏的限制，而是第 3.3 节中提出原则的一个实例。 ### 10.4 递归 有时会自然而然地把一个函数定义成递归的。而有些函数天生就是递归的，如下： ~~~ (defun our-length (x) (if (null x) 0 (1+ (our-length (cdr x))))) ~~~ 这样定义从某种程度来说，比等价的迭代形式看起来更自然一些（尽管可能也更慢一些）： ~~~ (defun our-length (x) (do ((len 0 (1+ len)) (y x (cdr y))) ((null y) len))) ~~~ 一个既不递归，也不属于某个多重递归函数集合的函数，可以通过第 7.10 节描述的简单技术被转换为一个宏。然而，仅是插入反引用和逗号对递归函数是无效的。让我们以内置的 `nth` 为例。（为简单起见，这个版本的 `nth` 将不做错误检查。）[示例代码 10.2] 给出了一个将 `nth` 定义成宏的错误尝试。表面上看 `nthb` 似乎和 `ntha` 等价，但是一个包含对 `nthb` 调用的程序将不能编译，因为对该调用的展开过程无法终止。 * * * **[示例代码 10.2] 对递归函数的错误类比** 这个可以工作： ~~~ (defun ntha (n lst) (if (= n 0) (car lst) (ntha (- n 1) (cdr lst)))) ~~~ 这个不能编译： ~~~ (defmacro nthb (n lst) '(if (= ,n 0) (car ,lst) (nthb (- ,n 1) (cdr ,lst)))) ~~~ * * * 一般而言，是允许宏里含有对另一个宏的引用的，只要展开过程会最终停止就可以。`nthb` 的麻烦之处在于每次的展开都含有一个对其本身的引用。函数版本，`ntha` ，之所以会终止因为它在 `n` 的值上递归，这个值在每次递归中减小。但是宏展开式只能访问到 `form`，而不是它们的值。当编译器试图宏展开，比如说，`(nthb x y)` 时，第一次展开将得到: ~~~ (if (= x 0) (car y) (nthb (- x 1) (cdr y))) ~~~ 然后又会被展开成: ~~~ (if (= x 0) (car y) (if (= (- x 1) 0) (car (cdr y)) (nthb (- (- x 1) 1) (cdr (cdr y))))) ~~~ 如此这般地进入无限循环。一个宏展开成对自身的调用是可以的，但不是这么用的。 像 `nthb` 这样的递归宏，其真正危险之处在于它们通常在解释器里工作正常。而当你最终将程序跑起来，接着想编译它的时候，它甚至无法通过编译。非但如此，常常还没有提示，告诉我们问题出自一个递归的宏； 相反，编译器只会陷入无限循环，让你来找出究竟哪里搞错了。 在本例中，`ntha` 是尾递归的。尾递归函数可以轻易转换成与之等价的迭代形式，然后用作宏的模型。一个像 `nthb` 的宏可以写成: ~~~ (defmacro nthc (n lst) '(do ((n2 ,n (1- n2)) (lst2 ,lst (cdr lst2))) ((= n2 0) (car lst2)))) ~~~ 所以从理论上说，把递归函数改造成宏也并非不可能。但是，要转换更复杂的递归函数可能会比较困难，甚至无法做到。 这取决于你要宏做什么，有时候你可能会发现改成宏和函数的组合就够用了。[示例代码 10.3] 给出了两种方式，可用来生成表面上似乎递归的宏。第一种策略就在 `nthd` 里面，它直接让宏展开成为一个对递归函数的调用。 举个例子，如果你使用宏的目的，仅仅是希望帮助用户避免引用参数的麻烦，那么这种方法就可以胜任了。 * * * **[示例代码 10.3] 解决问题的两个办法** ~~~ (defmacro nthd (n lst) '(nth-fn ,n ,lst)) (defun nth-fn (n lst) (if (= n 0) (car lst) (nth-fn (- n 1) (cdr lst)))) (defmacro nthe (n lst) '(labels ((nth-fn (n lst) (if (= n 0) (car lst) (nth-fn (- n 1) (cdr lst))))) (nth-fn ,n ,lst))) ~~~ * * * 如果你使用宏的目的，是想要将其展开式嵌入到宏调用的词法环境中，那么你更可能会采用 `nthe` 一例中的方案。其中，内置的 `labels special form` （见 2.7 节） 会创建一个局部函数定义。和`nthd` 每次展开都会调用全局定义的函数 `nth-fn` 不同，`nthe` 每个展开式里的函数都用的是该展开式自己定制的版本。 尽管你无法将递归函数直接转化成宏，你却可以写出一个宏，让它的展开式是递归生成的。宏的展开函数就是普通的 Lisp 函数，理所当然也是可以递归的。例如，如果我们想自己定义内置 `or` ，那么就会用到一个递归展开的函数。 * * * **[示例代码 10.4] 递归的展开函数** ~~~ (defmacro ora (&rest args) (or-expand args)) (defun or-expand (args) (if (null args) nil (let ((sym (gensym))) '(let ((,sym ,(car args))) (if ,sym ,sym ,(or-expand (cdr args))))))) (defmacro orb (&rest args) (if (null args) nil (let ((sym (gensym))) '(let ((,sym ,(car args))) (if ,sym ,sym (orb ,@(cdr args))))))) ~~~ * * * [示例代码 10.4] 给出的两个 `or` 定义，它们的内部实现都是递归地展开函数。宏 `ora` 调用递归函数`or-expand` 来生成展开式。这个宏能正常工作，并且与之等价的 `orb` 也一样可以完成任务。尽管`orb` 是递归的，但它是在宏的参数个数上做递归（这在宏展开期可以得到），而不依赖于它们的值（这在宏展开期无法得到）。也许，初看之下它的展开式里应该有一个对 `orb` 自己的引用，其实不然，`orb` 宏的展开，将会需要多步才能完成。【注 2】 每一步宏展开都会生成一个对 `orb` 的调用，这个调用将在下一步展开时替换成一个 `let` ，最后表达式里得到的则是一层套一层的 `let;(orb x y)` 展开成的代码和下式等价： ~~~ (let ((g2 x)) (if g2 g2 (let ((g3 y)) (if g3 g3 nil)))) ~~~ 事实上，`ora` 和 `orb` 是等价的，具体使用哪种风格不过是个人的喜好。 备注： 【注 1】'',(foo) 和 '(quote ,(foo)) 等价。 【注 2】译者注：这里改掉一个原书错误，`nthc` 应为 `nthd` 。

## 第 9 章 变量捕捉 宏很容易遇到一类被称为**变量捕捉**的问题。变量捕捉发生在宏展开导致名字冲突的时候，名字冲突指：某些符号结果出乎意料地引用了来自另一个上下文中的变量。无意的变量捕捉可能会造成极难发觉的 bug。 本章将介绍预见和避免它们的办法。不过，有意的变量捕捉却也是一种有用的编程技术，而且第 14 章的宏都是靠这种技术实现的。 ### 9.1 宏参数捕捉 如果一个宏对无意识的变量捕捉毫无防备，那么它就是有 bug 的宏。为了避免写出这样的宏，我们必须确切地知道捕捉发生的时机。变量捕捉可以分为两类情况： > **宏参数捕捉**和**自由符号捕捉**。 所谓宏参数捕捉，就是在宏调用中作为参数传递的符号无意地引用到了宏展开式本身建立的变量。考虑下面这个 `for` 宏的定义，它像 `Pascal` 的 `for` 在一系列表达式上循环操作： ~~~ (defmacro `for` ((var start stop) &body body) '(do ((,var ,start (1+ ,var)) (limit ,stop)) ((> ,var limit)) ,@body)) ~~~ 这个宏乍看之下没有问题。它甚至似乎也可以正常工作： ~~~ > (for (x 1 5) (princ x)) 12345 NIL ~~~ 确实，这个错误如此隐蔽，可能用上这个版本的宏数百次，都毫无问题。但如果我们这样调用它，问题就出来了： ~~~ (for (limit 1 5) (princ limit)) ~~~ 我们可能会认为这个表达式和之前的结果相同。但它却没有任何输出：它产生了一个错误。为了找到原因，我们仔细观察它的展开式： ~~~ (do ((limit 1 (1+ limit)) (limit 5)) ((> limit limit)) (print limit)) ~~~ 现在错误的地方就很明显了。在宏展开式本身的符号和作为参数传递给宏的符号之间出现了名字冲突。宏展开*捕捉*了 `limit`。这导致它在同一个 `do` 里出现了两次，而这是非法的。 由变量捕捉导致的错误比较罕见，但频率越低其性质就越恶劣。上个捕捉相对还比较温和， 至少这次我们得到了一个错误。更普遍的情况是，捕捉了变量的宏只是产生错误的结果，却没有给出任何迹象显示问题的源头。在下面的例子中： ~~~ > (let ((limit 5)) (for (i 1 10) (when (> i limit) (princ i)))) NIL ~~~ 产生的代码静悄悄地什么也不做。 ### 9.2 自由符号捕捉 偶尔会出现这样的情况，宏定义本身有这么一些符号，它们在宏展开时无意中却引用到了其所在环境中的绑定。假设有个程序，它希望把运行中产生的警告信息保存在一个列表里供事后检查，而不是在问题发生时直接打印输出给用户。于是有人写了一个宏 `gripe` ，它接受一个警告信息，并把它加入全局列表 `w` ： ~~~ (defvar w nil) (defmacro gripe (warning) ; wrong '(progn (setq w (nconc w (list ,warning))) nil)) ~~~ 之后，另一个人希望写个函数 `sample-ratio` ，用来返回两个列表的长度比。如果任何一个列表中的元素少于两个，函数就改为返回 nil ，同时产生一个警告说明这个函数处理的是一个统计学上没有意义的样本。（实际的警告本可以带有更多的信息，但它们的内容与本例无关。） ~~~ (defun sample-ratio (v w) (let ((vn (length v)) (wn (length w))) (if (or (< vn 2) (< wn 2)) (gripe "sample < 2") (/ vn wn)))) ~~~ 如果用 `w = (b)` 来调用 `sample-ratio` ，那么它将会警告说它有个参数只含一个元素，因而得出的结果从统计上来讲是无意义的。但是当对 gripe 的调用被展开时，sample-ratio 就好像被定义成： ~~~ (defun sample-ratio (v w) (let ((vn (length v)) (wn (length w))) (if (or (< vn 2) (< wn 2)) (progn (setq w (nconc w (list "sample < 2"))) nil) (/ vn wn)))) ~~~ 这里的问题是，使用 gripe 时的上下文含有 w 自己的局部绑定。所以，产生的警告没能保存到全局的警告列表里，而是被 nconc 连接到了 sample-ratio 的一个参数的结尾。不但警告丢失了，而且列表 `(b)` 也加上了一个多余的字符串，而程序的其他地方可能还会把它作为数据继续使用： ~~~ > (let ((lst '(b))) (sample-ratio nil lst) lst) (B "sample < 2") > w NIL ~~~ ### 9.3 捕捉发生的时机 许多宏的编写者都希望通过查看宏的定义，就可以预见到所有可能来自上述两种捕捉类型的问题。变量捕捉有些难以捉摸，需要一些经验才能预料到那些被捕捉的变量在程序中所有捣乱的伎俩。幸运的是，还是有办法在你的宏定义中找出那些可能被捕捉的符号，并排除它们的，而无需操心这些符号捕捉如何搞砸你的程序。本节将介绍一套直接了当的检测原则，用它就可以找出可捕捉的符号。本章的其余部分则解释了避免出现变量捕捉的相关技术。 我们接下来提出的方法可以用来定义可捕捉的变量，但是它基于几个从属的概念，所以在继续之前必须首先给这些概念下个定义： > 自由(free)：我们认为表达式中的符号 s 是自由的，当且仅当它被用作表达式中的变量，但表达式却没有为它创建一个绑定。 在下列表达式里: ~~~ (let ((x y) (z 10)) (list w x z)) ~~~ w ，x 和 z 在 list 表达式中看上去都是自由的，因为这个表达式没有建立任何绑定。不过，外围的 let 表达式为 x 和 z 创建了绑定，从整体上说，在 let 里面，只有 y 和 w 是自由的。注意到在: ~~~ (let ((x x)) x) ~~~ 里 x 的第二个实例是自由的。因为它并不在为 x 创建的新绑定的作用域内。 > 框架（skeleton）: 宏展开式的框架是整个展开式，并且去掉任何在宏调用中作为实参的部分。 如果 foo 的定义是： ~~~ (defmacro foo (x y) '(/ (+ ,x 1) ,y)) ~~~ 并且被这样调用： ~~~ (foo (- 5 2) 6) ~~~ 那么它就会产生如下的展开式： ~~~ (/ (+ (- 5 2) 1) 6) ~~~ 这一展开式的框架就是上面这个表达式在把形参 x 和 y 拿走，留下空白后的样子： ~~~ (/ (+ 1) ) ~~~ 有了这两个概念，就可以把判断可捕捉符号的方法简单表述如下： > 可捕捉(capturable)：如果一个符号满足下面条件之一，那就可以认为它在某些宏展开里是可捕捉的 > > > （a） 它作为自由符号出现在宏展开式的框架里，或者 （b） 它被绑定到框架的一部分，而该框架中含有传递给宏的参数，这些参数被绑定或被求值。 用些例子可以明确这个标准的含义。在最简单的情况下： ~~~ (defmacro cap1 () '(+ x 1)) ~~~ x 可被捕捉是因为它作为自由符号出现在框架里。这就是导致 `gripe` 中 bug 的原因。在这个宏里： ~~~ (defmacro cap2 (var) '(let ((x ...) (,var ...)) ...)) ~~~ `x` 可被捕捉是因为它被绑定在一个表达式里，而同时也有一个宏调用的参数被绑定了。（这就是for 中出现的错误。）同样对于下面两个宏： ~~~ (defmacro cap3 (var) '(let ((x ...)) (let ((,var ...)) ...))) (defmacro cap4 (var) '(let ((,var ...)) (let ((x ...)) ...))) ~~~ x 在两个宏里都是可捕捉的。然而，如果 x 的绑定和作为参数传递的变量没有这样一个上下文，在这个上下文中，两者是同时可见的，就像在这个宏里： ~~~ (defmacro safe1 (var) '(progn (let ((x 1)) (print x)) (let ((,var 1)) (print ,var)))) ~~~ 那么 x 将不会被捕捉到。并非所有绑定在框架里的变量都是有风险的。尽管如此，如果宏调用的参数在一个由框架建立的绑定里被求值: ~~~ (defmacro cap5 (&body body) '(let ((x ...)) ,@body)) ~~~ 那么，这样绑定的变量就有被捕捉的风险：在 `cap5` 中，x 是可捕捉的。不过对于下面这种情况: ~~~ (defmacro safe2 (expr) '(let ((x ,expr)) (cons x 1))) ~~~ x 是不可捕捉的，因为当传给 `expr` 的参数被求值时，x 的新绑定将是不可见的。同时，请注意我们只需关心那些框架变量的绑定。在这个宏里: ~~~ (defmacro safe3 (var &body body) '(let ((,var ...)) ,@body)) ~~~ 没有符号会因没有防备而被捕捉（假设第一个参数的绑定是用户有意为之）。 现在让我们来检查一下 `for` 最初的定义，看看使用新的规则是否能发现可捕捉的符号： ~~~ (defmacro for ((var start stop) &body body) ; wrong '(do ((,var ,start (1+ ,var)) (limit ,stop)) ((> ,var limit)) ,@body)) ~~~ 现在可以看出 `for` 的这一定义可能遭受两种方式的捕捉：limit 可能会被作为第一个参数传给 `for`，就像在最早的例子里那样： ~~~ (for (limit 1 5) (princ limit)) ~~~ 但是，如果 limit 出现在循环体里，也同样危险： ~~~ (let ((limit 0)) (for (x 1 10) (incf limit x)) limit) ~~~ 这样用 `for` 的人，可能会期望他自己的 limit 绑定就是在循环里递增的那个，最后整个表达式返回`55`；事实上，只有那个由展开式框架生成的 `limit` 绑定会递增： ~~~ (do ((x 1 (1+ x)) (limit 10)) ((> x limit)) (incf limit x)) ~~~ 并且，由于迭代过程是由这个变量控制的，所以循环甚至将无法终止。 本节中介绍的这些规则不过是个参考，在实际编程中仅仅具有指导意义。它们甚至不是形式化定义的，更不能完全保证其正确性。捕捉是一个不能明确定义的问题，它依赖于你期望的行为。例如，在下面的表达式里: ~~~ (let ((x 1)) (list x)) ~~~ x 在 （list x）被求值时，会指向新的变量，不过我们不会把它视为错误。这正是 let 要做的事。检测捕捉的规则也含混不清。你可以写出通过这些测试的宏，而这样的宏却仍然有可能会遭受意料之外的捕捉。例如: ~~~ (defmacro pathological (&body body) ; wrong (let* ((syms (remove-if (complement #'symbolp) (flatten body))) (var (nth (random (length syms)) syms))) '(let ((,var 99)) ,@body))) ~~~ 当调用这个宏的时候，宏主体中的表达式就像是在一个 `progn` 中被求值 但是主体中有一个随机选出的变量将带有一个不同的值。这很明显是一个捕捉，但它通过了我们的测试，因为这个变量并没有出现在框架里。然而，实践表明该规则在绝大多数时候都是正确的：很少有人（如果真有的话）会想写出类似上面那个例子的宏。 ### 9.4 取更好的名字避免捕捉 前两节将变量捕捉分为两类：参数捕捉，在这种情况下，由宏框架建立的绑定会捕捉参数中用到的符号；和自由符号捕捉，而在这里，宏展开处的绑定会捕捉到宏展开式中的自由符号。常常可以通过给全局变量取个明显的名字来解决后一类问题。在 Common Lisp 中，习惯上会给全局变量取一个两头都是星号的名字。 例如，定义当前包的变量叫做 package 。（这样的名字可以发音为 "star-package-star" 来强调它不是普通的变量。） 所以 gripe 的作者的的确确有责任把那些警告保存在一个名字类似 *warnings* 而非 w 的变量中。如果 sample-ratio 的作者执意要用 *warnings* 做函数参数，那他碰到的每个 bug 都是咎由自取，但如果他觉得用 w 作为参数的名字应该比较保险，就不应该再怪他了。 ### 9.5 通过预先求值避免捕捉 有时，如果不在任何宏展开创建的绑定里求值那些有危险的参数，就可以轻松消除参数捕捉。最简单的情况可以这样处理：让宏以 let 表达式开头。[示例代码 9.1] 包含宏 before 的两个版本，该宏接受两个对象和一个序列，当且仅当第一个对象在序列中出现于第二个对象之前时返回真【注1】。第一个定义是不正确的。它开始的 let 确保了作为 seq 传递的 form 只求值一次，但是它不能有效地避免下面这个问题： * * * **[示例代码 9.1] 用 let 避免捕捉** 易于被捕捉的： ~~~ (defmacro before (x y seq) '(let ((seq ,seq)) (< (position ,x seq) (position ,y seq)))) ~~~ 一个正确的版本： ~~~ (defmacro before (x y seq) '(let ((xval ,x) (yval ,y) (seq ,seq)) (< (position xval seq) (position yval seq)))) ~~~ * * * ~~~ > (before (progn (setq seq '(b a)) 'a) 'b '(a b)) NIL ~~~ 这相当于问 "(a b) 中的 a 是否在 b 前面？" 如果 before 是正确的，它将返回真。宏展开式揭示了真相：对 `<` 的第一个参数的求值重新排列了那个将在第二个参数里被搜索的列表。 ~~~ (let ((seq '(a b))) (< (position (progn (setq seq '(b a)) 'a) seq) (position 'b seq))) ~~~ 要想避免这个问题，只要在一个巨大的 `let` 里求值所有参数就行了。这样 [示例代码 9.1] 中的第二个定义对于捕捉就是安全的了。 不幸的是，这种 let 技术只能在很有限的一类情况下才可行： 1. 所有可能被捕捉的参数都只求值一次，并且 2. 没有一个参数需要在宏框架建立的绑定下被求值。 这个规则排除了相当多的宏。我们比较赞成的 `for` 宏就同时违反了这两个限制。然而，我们可以把这个技术加以变化，使类似 `for` 的宏免于发生捕捉，即将其 body forms 包装在一个 λ表达式里，同时让这个 λ表达式位于任何局部创建的绑定之外。 有些宏（其中包括用于迭代的宏），如果宏调用里面有表达式出现，那么在宏展开后，这些表达式将会在一个新建的绑定中求值。例如在 `for` 的定义中，循环体必须在一个由宏创建的 `do` 中进行求值。因此，`do` 创建的变量绑定会很容易就捕捉到循环里的变量。我们可以把循环体包在一个闭包里，同时在循环里，不再把直接插入表达式，而只是简单地 `funcall` 这个闭包。通过这种办法来保护循环中的变量不被捕捉。 [示例代码 9.2] 给出了一个 `for` 的实现，它使用的就是这种技术。由于闭包是 `for` 展开时生成的第一个东西，因此，所有出现在宏体内的自由符号将全部指向宏调用环境中的变量。现在 `do` 通过闭包的参数跟宏体通信。闭包需要从 `do` 知道的全部就是当前迭代的数字，所以它只有一个参数，也就是宏调用中作为索引指定的那个符号。 这种将表达式包装进 lambda 的方法也不是万金油。虽然你可以用它来保护代码体，但闭包有时也起不到任何作用，例如，当存在同一变量在同一个 let 或 `do` 里被绑定两次的风险时（就像开始的那个有缺陷的for 那样）。幸运的是，在这种情况下，通过重写 `for` 将其主体包装在一个闭包里，我们同时也消除了do 为 var 参数建立绑定的需要。原先那个 `for` 中的 var 参数变成了闭包的参数并且在 `do` 里面可以被一个实际的符号 count 替换掉。所以这个for 的新定义对于捕捉是完全免疫的，就像 9.3 节里的测试所显示的那样。 * * * **[示例代码 9.2] 用闭包避免捕捉** 易于被捕捉的： ~~~ (defmacro for ((var start stop) &body body) '(do ((,var ,start (1+ ,var)) (limit ,stop)) ((> ,var limit)) ,@body)) ~~~ 正确的版本： ~~~ (defmacro for ((var start stop) &body body) '(do ((b #'(lambda (,var) ,@body)) (count ,start (1+ count)) (limit ,stop)) ((> count limit)) (funcall b count))) ~~~ * * * 闭包的缺点在于，它们的效率可能不大理想。我们可能会因此造成又一次函数调用。更糟糕的是，如果编译器没有给闭包分配动态作用域（dynamicextent），那么一等到运行期，闭包所需的空间将不得不从堆里分配。【注2】 ### 9.6 通过 gensym 避免捕捉 这里有一种切实可行的方法可供避免宏参数捕捉：把可捕捉的符号换成 gensym。在 `for` 的最初版本中，当两个符号意外地重名时，就会出问题。如果我们想要避免这种情况：宏框架里含有的符号也同时出现在了调用方代码里，我们也许会给宏定义里的符号取个怪异的名字，寄希望以此来摆脱参数捕捉的魔爪： ~~~ (defmacro for ((var start stop) &body body) ; wrong '(do ((,var ,start (1+ ,var)) (xsf2jsh ,stop)) ((> ,var xsf2jsh)) ,@body)) ~~~ 但是这治标不治本。它并没有消除 bug，只是降低了出问题的可能性。并且还有一个可能性不那么小的问题悬而未决 不难想象，如果把同一个宏嵌套使用的话，仍会出现名字冲突。 我们需要一个办法来确保符号都是唯一的。Common Lisp 函数 gensym 的意义正是在于此。它返回的符号称为 gensym ，这个符号可以保证不和任何手工输入或者由程序生成的符号相等（eq）。 那 Lisp 是如何保证这一点的呢？在 Common Lisp 中，每个包都维护着一个列表，用于保存这个包知道的所有符号。【注3】 一个符号，只要出现在这个列表上，我们就说它被约束（intern）在这个包里。每次调用 gensym 都会返回唯一的，未约束的符号。而 read 每见到一个符号，都会把它约束，所以没人能输入和 gensym 相同的东西。也就是说，如果你有个表达式是这样开头的： ~~~ (eq (gensym) ... ~~~ 那么将无法让这个表达式返回真。 让 gensym 为你构造符号，这个办法其实和 "选个怪名字" 的方法异曲同工，而且更进一步 gensym 给你的名字甚至在电话薄里也找不到。如果 Lisp 不得不显示 gensym， ~~~ > (gensym) #:G47 ~~~ 它打印出来的东西基本上就相当于 Lisp 的 "张三"，即为那种名字无关紧要的东西编造出来的毫无意义的名字。并且为了确保我们不会对此有任何误会，gensym 在显示时候，前面加了一个井号和一个冒号，这是一种特殊的读取宏（read-macro），其目的是为了让我们在试图第二次读取该 gensym 时报错。 在 CLSH2 Common Lisp 里，gensym 的打印形式中的数字来自 *gensym-counter* ，这个全局变量总是绑定到某个整数。如果重置这个计数器，我们就可以让两个 gensym 的打印输出一模一样: ~~~ > (setq x (gensym)) #:G48 > (setq *gensym-counter* 48 y (gensym)) #:G48 > (eq x y) NIL ~~~ 但它们不是一回事。 * * * **[示例代码 9.3] 用 gensym 避免捕捉** 易于被捕捉的： ~~~ (defmacro for ((var start stop) &body body) '(do ((,var ,start (1+ ,var)) (limit ,stop)) ((> ,var limit)) ,@body)) ~~~ 一个正确的版本： ~~~ (defmacro for ((var start stop) &body body) (let ((gstop (gensym))) '(do ((,var ,start (1+ ,var)) (,gstop ,stop)) ((> ,var ,gstop)) ,@body))) ~~~ * * * [示例代码 9.3] 中有一个使用 gensym 的 `for` 的正确定义。现在就没有 limit 可以和传进宏的 form 里的符号有冲突了。它已经被换成一个在现场生成的符号。宏每次展开的时候，limit 都会被一个在展开期创建的唯一符号取代。 初次就把 `for` 定义得完美无缺，还是很难的。完成后的代码，如同一个完成了的定理，精巧漂亮的证明的背后是一次次的尝试和失败。所以不要担心你可能会对一个宏写好几个版本。在开始写类似`for` 这样的宏时，你可以在不考虑变量捕捉问题的情况下，先把第一个版本写出来，然后再回过头来为那些可能卷入捕捉的符号制作 gensym。 ### 9.7 通过包避免捕捉 从某种程度上说，如果把宏定义在它们自己的包里，就有可能避免捕捉。倘若你创建一个 macros 包，并且在其中定义 `for` ，那么你甚至可以使用最初给出的定义 ~~~ (defmacro for ((var start stop) &body body) '(do ((,var ,start (1+ ,var)) (limit ,stop)) ((> ,var limit)) ,@body)) ~~~ 这样，就可以毫无顾虑地从其他任何包调用它。如果你从另一个包，比方说 mycode，里调用 for，就算把 limit 作为第一个参数，它也是 mycode::limit 这和 macros::limit 是两回事，后者才是出现在宏框架中的符号。 然而，包还是没能为捕捉问题提供面面俱到的通用解决方案。首先，宏是某些程序不可或缺的组成部分，将它们从自己的包里分离出来会很不方便。其次，这种方法无法为 macros 包里的其他代码提供任何捕捉保护。 ### 9.8 其他名字空间里的捕捉 前面几节都把捕捉说成是一种仅影响变量的问题。尽管多数捕捉都是变量捕捉，但是 Common Lisp 的其他名字空间里也同样会有这种问题。 函数也可能在局部被绑定，因而，函数绑定也会因无意的捕捉而导致问题。例如， ~~~ > (defun fn (x) (+ x 1)) FN > (defmacro mac (x) '(fn ,x)) MAC > (mac 10) 11 > (labels ((fn (y) (- y 1))) (mac 10)) 9 ~~~ 正如捕捉规则预料的那样，以自由之身出现在 mac 框架中的 fn 带来了被捕捉的风险。如果 fn 在局部被重新绑定的话，那么 mac 的返回值将和平时不一样。 对于这种情况，该如何应对呢？当有捕捉风险的符号与内置函数或宏重名时，那么听之任之应该是上策。CLTL2（260 页） 说，如果任何内置的名字被用作局部函数或宏绑定，"后果是未定义的。" 所以你的宏无论做了什么都没关系 -- 任何人，如果重新绑定内置函数，那么他将来碰到的问题会比你的这个宏更多。 另一方面，保护变量名的方法同样可以用来帮助函数名免于宏参数捕捉：通过使用 gensym 作为宏框架局部定义的任何函数的名字。但是，如果要避免像上面这种情况中的自由符号捕捉，就会稍微麻烦一点。要让变量免受自由符号捕捉，采用的保护方法是使用一目了然的全局名称：例如把 w 换成 *warnings* 。 然而，这个解决方案对函数有些不切实际，因为没有把全局函数的名字区分出来的习惯 大多数函数都是全局的。如果你担心发生这种情况，一个宏使用了另一个函数，而调用这个宏的环境可能会重定义这个函数，那么最佳的解决方案或许就是把你的代码放在一个单独的包里。 代码块名字（block-name） 同样可以被捕捉，比如说那些被 `go` 和 `throw` 使用的标签（tag）。当你的宏需要这些符号时，你应该像 7.8 节的 `our-do` 的定义那样，使用 gensym。 还需要注意的是像 `do` 这样的操作符隐式封装在一个名为 `nil` 的块里。这样在 `do` 里面的一个`return` 或 `return-from nil` 将从 `do` 本身而非包含这个 `do` 的表达式里返回： ~~~ > (block nil (list 'a (do ((x 1 (1+ x))) (nil) (if (> x 5) (return-from nil x) (princ x))))) 12345 (A 6) ~~~ 如果 `do` 没有创建一个名为 `nil` 的块，这个例子将只返回 6 ，而不是`(A 6)`。 `do` 里面的隐式块不是问题，因为 `do` 的这种工作方式广为人知。尽管如此，如果你写一个展开到`do` 的宏，它将捕捉 nil 这个块名称。在一个类似 `for` 的宏里， `return` 或 return-from nil 将从`for` 表达式而非封装这个 `for` 表达式的块中返回。 ### 9.9 为何要庸人自扰 前面举的例子中有些非常牵强做作。看着它们，有人可能会说，"变量捕捉既然这么少见 为什么还要操心它呢？" 回答这个问题有两个方法。一个是用另一个问题反诘道：要是你写得出没有 bug 的程序，为什么还要写有小 bug 的程序呢？ 更长的答案是指出在现实应用程序中，对你代码的使用方式做任何假设都是危险的。任何 Lisp 程序都具备现在被称之为 "开放式架构" 的特征。如果你正在写的代码以后会为他人所用，很可能他们调用你代码的方式是出乎你预料的。而且你要担心的不光是人。程序也能编写程序。可能没人会写这样的代码 ~~~ (before (progn (setq seq '(b a)) 'a) 'b '(a b)) ~~~ 但是程序生成的代码看起来经常就像这样。即使单个的宏生成的是简单合理的展开式，一旦你开始把宏嵌套着调用，展开式就可能变成巨大的，而且看上去没人能写得出来的程序。在这个前提下，就有必要去预防那些可能使你的宏不正确地展开的情况，就算这种情况像是有意设计出来的。 最后，避免变量捕捉不管怎么说，并非难于上青天。它很快会成为你的第二直觉。Common Lisp 中经典的 defmacro 好比厨子手中的菜刀：美妙的想法看上去会有些危险，但是这件利器一到了专家那里，就如入庖丁之手，游刃有余。 【注1】 这个宏只是个例子。实际编程中，它既不应当实现成宏，也不该用这种低效的算法。若需要正确的定义，可见 4.4 节。 【注2】 译者注：dynamicextent 是一种Lisp 编译器优化技术，详情请见 Common Lisp Hyper Spec 的有关内容。 【注3】 关于包（package） 的介绍，可见**附录**。

## 第 8 章 何时使用宏 我们如何知道一个给定的函数是否真的应该是函数，而不是宏呢？多数时候，会很容易分清楚在哪种情况下需要用到宏，哪种情况不需要。缺省情况下，我们应该用函数，因为如果函数能解决问题，而偏要用上宏的话，会让程序变得不优雅。我们应当只有在宏能带来特别的好处时才使用它们。 什么情况下，宏能给我们带来优势呢？这就是本章的主题。通常这不是锦上添花，而是一种必须。大多数我们用宏可以做到的事情，函数都无法完成。第 8.1 节列出了只能用宏来实现的几种操作符。尽管如此，也有一小类（但很有意思的） 情况介于两者之间，对它们来说，不管把操作符实现成函数还是宏似乎都言之有理。对于这种情况，第 8.2 节给出了关于宏的正反两方面考量。最后，在充分考察了宏的能力后，我们在第 8.3 节里转向一个相关问题：人们都用宏干什么？ ### 8.1 当别无他法时 优秀设计的一个通用原则就是：当你发现在程序中的几处都出现了相似的代码时，就应该写一个子例程，并把那些相似的语句换成对这个子例程的调用。如果也把这条原则用到 Lisp 程序上，就必须先决定这个 "子例程" 应该是函数还是宏。 有时，可以很容易确定应当写一个宏而不是函数，因为只有宏才能满足需求。一个像 1+ 这样的函数或许既可以写成函数也可以写成宏： ~~~ (defun 1+ (x) (+ 1 x)) (defmacro 1+ (x) '(+ 1 ,x)) ~~~ 但是来自第 7.3 节的 `while` ，则只能被定义成宏： ~~~ (defmacro while (test &body body) '(do () ((not ,test)) ,@body)) ~~~ 无法用函数来重现这个宏的行为。`while` 的定义里拼接了一个作为 `body` 传入 `do` 的主体里的表达式，它只有当 `test` 表达式返回 `nil` 时才会被求值。没有函数可以做到这一点；是因为在函数调用里，所有的参数在函数调用开始之前就会被求值。 当你需要用宏时，你看中了它哪一点呢？宏有两点是函数无法做到的：宏可以控制（或阻止） 对其参数的求值，并且它可以展开进入到主调方的上下文中。任何需要宏的应用，归根到底都是要用上述两个属性中的至少一个。 "宏不对其参数进行求值"，这个非正式的说法不太准确。更确切的说法应该是，"宏能控制宏调用中参数的求值"。取决于参数在宏展开式中的位置，它们可以被求值一次，多次，或者根本不求值。宏的这种控制主要体现在四个方面： #### 1\. 变换 Common Lisp 的 setf 宏就是这类宏中的一员，它们在求值前都会对传入的参数严加检查。内置的访问函数（access function） 通常都有一个对应的逆操作，其作用是对该访问函数所获取的对象赋值。car 的逆操作是 rplaca ，对于 cdr 来说是 rplacd ，等等。有了 setf ，我们就可以把对这些访问函数的调用当成变量赋值。`(setf (car x) 'a)` 就是个例子，这个表达式可以展开成 `(progn (rplaca x 'a) 'a)`. 为了有这样的效果，setf 必须非常了解它的第一个参数。如果要知道上述的情况需要用到 `rplaca` ， `setf` 就得清楚它的第一个参数是个以 car 开始的表达式。这样的话，setf 以及其他修改参数的操作符，就必须被写成宏。 #### 2\. 绑定 词法变量必须在源代码中直接出现。例如，由于 setq 的第一个参数是不求值的，所以，所有在setq 之上构建的东西都必须是展开到setq 的宏，而不能是调用它的函数。对于 let 这样的操作符也是如此，它的实参必须作为 lambda 表达式的形参出现，还有类似 do 这样展开到 let 的宏也是这样，等等。任何新操作符，只要它修改了参数的词法绑定，那么它就必须写成宏。 #### 3\. 条件求值 函数的所有参数都会被求值。在像 when 这样的结构里，我们希望一些参数仅在特定条件下才被求值。只有通过宏才可能获得这种灵活性。 #### 4\. 多重求值 函数的所有参数不但都会被求值，而且求值的次数都正好是一次。我们需要用宏来定义像 do 这样的结构，这样子，就可以对特定的参数多次求值。 也有几种方式可以利用宏产生的内联展开式带来的优势。这里必须强调一点，宏展开后生成的展开式将会出现在宏调用所在的词法环境之中，因为下列三种用法有两种都基于这个事实。它们是： #### 5\. 利用调用方环境 宏生成的展开式可以含有这样的变量，变量的绑定来自宏调用的上下文环境。下面这个宏： ~~~ (defmacro foo (x) '(+ ,x y)) ~~~ 的行为将因 foo 被调用时 y 的绑定而不同。 这种词法交流通常更多地被视为瘟疫的传染源，而非快乐之源。一般来说，写这样的宏不是什么好习惯。函数式编程的思想对于宏也同样适用：与一个宏交流的最佳方式就是通过它的参数。事实上，需要用到调用方环境的情况极少，因此，如果出现了这样的用法，那十有八九就是什么地方出了问题。（见第9 章） 纵观本书中的所有宏，只有续延传递（continuation-passing）宏（第 20 章）和 ATN 编译器（第23 章）的一部分以这种方式利用了调用方环境。 #### 6\. 包装新环境 宏也可以使其参数在一个新的词法环境下被求值。最经典的例子就是let ，它可以用lambda 实现成宏的形式（见 11.1 节）。在一个 `(let ((y 2)) (+ x y))` 这样的表达式里，y 将指向一个新的变量。 #### 7\. 减少函数调用 宏展开后，展开式内联地插入展开环境。这个设计的第三个结果是宏调用在编译后的代码中没有额外开销。到了运行期，宏调用已经替换成了它的展开式。（这个说法对于声明成inline 的函数也一样成立。） 很明显，如果不是有意为之，情形 5 和 6 将产生变量捕捉上的问题，这可能是宏的编写者所有担心的事情里面最头疼的一件。变量捕捉将在第 9 章讨论。 与其说有七种使用宏的方式，不如说有六个半。在理想的世界里，所有 Common Lisp 编译器都会遵守 inline 声明，所以减少函数调用将是内联函数的职责，而不是宏的。这个建立理想世界的重任就作为练习留给读者吧。 ### 8.2 宏还是函数？ 上一节解决了较简单的一类问题。一个操作符，倘若在参数被求值前就需要访问它，那么这个操作符就应该写成宏，因为别无他法。那么，如果有操作符用两种写法都能实现，那该怎么办呢？ 比如说操作符 `avg` 。它返回参数的平均值。它可以定义成函数： ~~~ (defun avg (&rest args) (/ (apply #'+ args) (length args))) ~~~ 但把它定义成宏也不错： ~~~ (defmacro avg (&rest args) '(/ (+ ,@args) ,(length args))) ~~~ 因为每次调用 avg 的函数版本时，都毫无必要地调用了一次 length。在编译期我们可能不清楚这些参数的值，但却知道参数的个数，所以那是调用 length 最佳的时机。当我们面临这样的选择时，可以考虑下列几点： ### 利: 1. 编译期计算。宏调用共有两次参与计算，分别是：宏展开的时候，以及展开式被求值的时候。一旦程序编译好，Lisp 程序中所有的宏展开也就完成了，而在编译期每进行一次计算，都帮助程序在运行的时候卸掉了一个包袱。如果在编写操作符时，可以让它在宏展开的阶段就完成一部分工作，那么把它写成宏将会让程序更加高效。因为只要是聪明的编译器无法自己完成的工作，函数就只能把这些事情拖到运行期做。第13章介绍一些类似avg 的宏，这些宏能在宏展开的阶段就完成一部分工作。 2. 和Lisp 的集成。有时，用宏代替函数可以令程序和Lisp 集成得更紧密。解决一个特定问题的方法，可以是专门写一个程序，你也可以用宏把这个问题变换成另一个Lisp 已经知道解决办法的问题。如果可行的话，这种方法常常可以使程序变得更短小，也更高效：更小是因为Lisp 代劳了一部分工作，更高效则是因为产品级Lisp 系统通常比用户程序做了更多的优化。这一优势大多时候会出现在嵌入式语言里，而我们从第19章起会全面转向嵌入式语言。 3. 免除函数调用。宏调用在它出现的地方直接展开成代码。所以，如果你把常用的代码片段写成宏，那么就可以每次在使用它的时候免去一次函数调用。在Lisp 的早期方言中，程序员借助宏的这个属性在运行期避免函数调用。而在Common Lisp 里，这个差事应该由声明成 inline 类型的函数接手了。 通过将函数声明成inline，你要求把这个函数就像宏一样，直接编译进调用方的代码。不过，理想和现实还是有距离的； 2（229 页） 说 "编译器可以随意地忽略该声明"，而且某些 Common Lisp 编译器确实也是这样做的。 在某些情况下，效率因素和跟Lisp 之间紧密集成的组合优势可以充分证实使用宏的必要性。在第19章的查询编译器里，可以转移到编译期的计算量相当可观，这使我们有理由把整个程序变成一个独立的巨型宏。尽管效率是初衷，这一转移同时也让程序和Lisp 走得更近：在新版本里，能更容易地使用Lisp 表达式，比如说可以在查询的时候用Lisp 的算术表达式。 ### 弊: 1. 函数即数据，而宏在编译器看来，更像是一些指令。函数可以当成参数传递（例如用 apply），被函数返回，或者保存在数据结构里。但这些宏都做不到。 有的情况下，你可以通过将宏调用封装在 lambda 表达式里来达到目的。如果你想用 apply 或 funcall 来调用某些的宏，这样是可行的，例如： ~~~ > (funcall #'(lambda (x y) (avg x y)) 1 3) 2 ~~~ 不过这样做还是有些麻烦。而且它有时还无法正常工作：如果这个宏带有&rest 形参，那么就无法给它传递可变数量的实参，avg 就是个例子。 1. 源代码清晰。宏定义和等价的函数定义相比更难阅读。所以如果将某个功能写成宏只能稍微改善程序，那么最好还是改成使用函数。 2. 运行期清晰。宏有时比函数更难调试。如果你在含有许多宏的代码里碰到运行期错误，那么你在 backtrace 里看到的代码将包含所有这些宏调用的展开式，而它们和你最初写的代码看起来可能会大相径庭。 并且由于宏展开以后就消失了，所以它们在运行时是看不到的。你不是总能使用 trace 来分析一个宏的调用过程。如果 trace 真的奏效的话，它展示给你的只是对宏展开函数的调用，而非宏调用本身的调用。 1. 递归。在宏里使用递归不像在函数里那么简单。尽管展开一个宏里的展开函数可能是递归的，但展开式本身可能不是。第 10.4 节将处理跟宏里的递归有关的主题。 在决定何时使用宏的时候需要权衡利弊，综合考虑所有这些因素。只有靠经验才能知道哪一个因素在起主导作用。尽管如此，出现在后续章节里的宏的示例涵盖了大多数对宏有利的情形。如果一个潜在的宏符合这里给出的条件，那么把它写成这样可能就是合适的。 最后，应该注意运行期清晰（观点 6） 很少成为障碍。调试那种用很多宏写成的代码并不像你想象的那样困难。如果一个宏的定义长达数百行，在运行期调试它的展开式的确是件苦差事。但至少实用工具往往出现在小而可靠的程序层次中。通常它们的定义长度不超过 15 行。所以就算你最终只得仔细检查一系列的 backtrace ，这种宏也不会让你云遮雾绕，摸不着头脑。 ### 8.3 宏的应用场合 在了解了宏的十八般武艺之后，下一个问题是：我们可以把宏用在哪一类程序里？关于宏的用途，最正式的表述可能是：它们主要用于句法转换（syntactic transformations）。这并不是要严格限制宏的使用范围。由于 Lisp 程序从列表中生成，而列表是 Lisp 数据结构，"句法转换" 的确有很大的发挥空间。第 19-24 章展示的整个程序，其目的就可以说成 "句法转换"，而且从效果上看，所有宏莫不是如此。 宏的种种应用一起织成了一条缎带，这些应用涵盖了从像 while 这样小型通用的宏，直到后面章节定义的大型、特殊用途的宏。缎带的一端是实用工具，它们和每个 Lisp 都内置的那些宏是一样的。它们通常短小、通用，而且相互独立。尽管如此，你也可以为一些特别类型的程序编写实用工具，然后当你有一组宏用于，比如说，图形程序的时候，它们看起来就像是一种专门用于图形编程的语言。在缎带的远端，宏允许你用一种和 Lisp 截然不同的语言来编写整个程序。以这种方式使用宏的做法被称为实现嵌入式语言。 实用工具是自底向上风格的首批成果。甚至当一个程序规模很小而不必分层构建时，它也仍然能够对程序的最底层，即 Lisp 本身加以扩充，并从中获益。nil! 将其参数设置为 nil ，这个实用工具只能定义成宏： ~~~ (defmacro nil! (x) '(setf ,x nil)) ~~~ 看到 nil! ，可能有人会说它什么都做不了，无非可以让我们少输入几个字罢了。是的，但是充其量，宏所能做的也就是让你少打些字而已。如果有人非要这样想的话，那么其实编译器的工作也不过是让人们用机器语言编程的时候可以少些。不可低估实用工具的价值，因为它们的功用会积少成多：几层简单的宏拉开了一个优雅的程序和一个晦涩的程序之间的差距。 多数实用工具都含有模式。当你注意到代码中存在模式时，不妨考虑把它写成实用工具。模式是计算机最擅长的。为什么有程序可以代劳，还要自己动手呢？假设在写某个程序的时候，你发现自己以同样的通用形式在很多地方做循环操作： ~~~ (do () ((not <condition>)) . <body of code>) ~~~ 从列表中生成，是指列表作为编译器的输入。函数不再从列表中生成，虽然在一些早期的方言里的确是这样处理的。 当你在自己的代码里发现一个重复的模式时，这个模式经常会有一个名字。这里，模式的名字是 while 。如果我们想把它作为实用工具提供出来，那么只能以宏的形式，因为需要用到带条件判断的求值，和重复求值。倘若用第 7.4 节的定义实现 while ，如下： ~~~ (defmacro while (test &body body) '(do () ((not ,test)) ,@body)) ~~~ 就可以将该模式的所有实例替换成： ~~~ (while <condition> . <body of code>) ~~~ 这样做使得代码更简短，同时也更清晰地表明了程序的意图。 宏的这种变换参数的能力使得它在编写接口时特别有用。适当的宏可以在本应需要输入冗长复杂表达式的地方只输入简短的表达式。尽管图形界面减少了为最终用户编写这类宏的需要，程序员却一直使用这种类型的宏。最普通的例子是 defun ，在表面上，它创建的函数绑定类似用 Pascal 或 C 这样的语言定义的函数。第 2 章提到下面两个表达式差不多具有相同的效果： ~~~ (defun foo (x) (* x 2)) (setf (symbol-function 'foo) #'(lambda (x) (* x 2))) ~~~ 这样 defun 就可以实现成一个将前者转换成后者的宏。我们可以想象它会这样写： ~~~ (defmacro our-defun (name parms &body body) '(progn (setf (symbol-function ',name) #'(lambda ,parms (block ,name ,@body))) ',name)) ~~~ 像 while 和 nil! 这样的宏可以被视为通用的实用工具。任何 Lisp 程序都可以使用它们。但是特定的领 域同样也可以有它们自己的实用工具。没有理由认为扩展编程语言的唯一平台只能是原始的 Lisp。举个例子，如果你正在编写一个  程序，有时，最佳的实现可能会把它写成两层：一门专用于 CAD 程序的语言 （或者如果你偏爱更现代的说法，一个工具箱（toolkit）），以及在这层之上的，你的特定应用。 Lisp 模糊了许多对其他语言来说理所当然的差异。在其他语言里，在编译期和运行期，程序和数据，以及语言和程序之间具有根本意义上的差异。而在 Lisp 里，这些差异就退化成了口头约定。例如，在语言和程序之间就没有明确的界限。你可以根据手头程序的情况自行界定。因而，是把底层代码称作工具箱，还是称之为语言，确实不过是个说法而已。将其视为语言的一个好处是，它暗示着你可以扩展这门语言，就像你通过实用工具来扩展 Lisp 一样。 设想我们正在编写一个交互式的 2D 绘图程序。为了简单起见，我们将假定程序处理的对象只有线段，每条线段都表示成一个起点 和一个向量 。并且我们的绘图程序的任务之一是平移一组对象。 这正是 [示例代码 8.1] 中函数 move-objs 的任务。出于效率考虑，我们不想在每个操作结束后重绘整个屏幕 只画那些改变了的部分。因此两次调用了函数 bounds ，它返回表示一组对象的矩形边界的四个坐标（最小x ，最小y ，最大x ，最大y）。move-objs 的操作部分被夹在了两次对 bounds 调用的中间，它们分别找到平移前后的矩形边界，然后重绘整个区域。 函数 scale-objs 被用来改变一组对象的大小。由于区域边界可能随缩放因子的不同而放大或者缩小，这个函数也必须在两次 bounds 调用之间发生作用。随着我们绘图程序开发进度的不断推进，这个模式一次又一次地出现在我们眼前：在旋转，翻转，转置等函数里。 通过一个宏，我们可以把这些函数中相同的代码抽象出来。[示例代码 8.2] 中的宏with-redraw 给出了一个框架， 它是图 8.1 中几个函数所共有的。 这样的话，这些函数每一个的定义都缩减到了四行代码，如图 8.2 末尾 * * * **[示例代码 8.1] 最初的平移和缩放** ~~~ (defun move-objs (objs dx dy) (multiple-value-bind (x0 y0 x1 y1) (bounds objs) (dolist (o objs) (incf (obj-x o) dx) (incf (obj-y o) dy)) (multiple-value-bind (xa ya xb yb) (bounds objs) (redraw (min x0 xa) (min y0 ya) (max x1 xb) (max y1 yb))))) (defun scale-objs (objs factor) (multiple-value-bind (x0 y0 x1 y1) (bounds objs) (dolist (o objs) (setf (obj-dx o) (* (obj-dx o) factor) (obj-dy o) (* (obj-dy o) factor))) (multiple-value-bind (xa ya xb yb) (bounds objs) (redraw (min x0 xa) (min y0 ya) (max x1 xb) (max y1 yb))))) ~~~ * * * **[示例代码 8.2] 骨肉分离后的平移和缩放** ~~~ (defmacro with-redraw ((var objs) &body body) (let ((gob (gensym)) (x0 (gensym)) (y0 (gensym)) (x1 (gensym)) (y1 (gensym))) '(let ((,gob ,objs)) (multiple-value-bind (,x0 ,y0 ,x1 ,y1) (bounds ,gob) (dolist (,var ,gob) ,@body) (multiple-value-bind (xa ya xb yb) (bounds ,gob) (redraw (min ,x0 xa) (min ,y0 ya) (max ,x1 xb) (max ,y1 yb))))))) (defun move-objs (objs dx dy) (with-redraw (o objs) (incf (obj-x o) dx) (incf (obj-y o) dy))) (defun scale-objs (objs factor) (with-redraw (o objs) (setf (obj-dx o) (* (obj-dx o) factor) (obj-dy o) (* (obj-dy o) factor)))) ~~~ * * * 所示。通过这两个函数，这个新写的宏在简洁性方面作出的贡献证明了它是物有所值的。并且，一旦把屏幕重绘的细节部分抽象出来，这两个函数就变得清爽多了。 对 with-redraw ，有一种看法是把它视为一种语言的控制结构，这种语言专门用于编写交互式的绘图程序。 随着我们开发出更多这样的宏，它们不管从名义上，还是在实际上都会构成一门专用的编程语言，并且我们的程序也将开始表现出其不俗之处，这正是我们用特制的语言撰写程序所期望的效果。 宏的另一主要用途就是实现嵌入式语言。Lisp 在编写编程语言方面是一种特别优秀的语言，因为Lisp 程序可以表达成列表，而且Lisp 还有内置的解析器（read） 和编译器（compile） 可以用在以这种方式表达的程序中。多数时候甚至不用调用 compile ；你可以通过编译那些用来做转换的代码（第 2.9 节），让你的嵌入式语言在无形中完成编译。 这个宏的定义使用了下一章才出现的 gensym 。它的作用接下来就会说明。 与其说嵌入式语言是构建于 Lisp 之上的语言，不如说它是和Lisp 融为一体的，这使得其语法成为了一个 Lisp 和新语言中特有结构的混合体。实现嵌入式语言的初级方式是用Lisp 给它写一个解释器。有可能的话，一个更好的方法是通过语法转换实现这种语言：将每个表达式转换成 Lisp 代码，然后让解释器可以通过求值的方式来运行它。这就是宏大展身手的时候了。宏的工作恰恰是将一种类型的表达式转换成另一种类型，所以在编写嵌入式语言时，宏是最佳人选。 一般而言，嵌入式语言可以通过转换实现的部分越多越好。主要原因是可以节省工作量。举个例子，如果新语言里含有数值计算，那你就无需面对表示和处理数值量的所有细枝末节。如果 Lisp 的计算功能可以满足你的需要，那么你可以简单地将你的算术表达式转换成等价的Lisp 表达式，然后将其余的留给 Lisp 处理。 代码转换通常都会提高你的嵌入式语言的效率。而解释器在速度方面却一直处于劣势。当代码里出现循环时，通常每次迭代解释器都必须重新解释代码，而编译器却只需做一次编译。因此，就算解释器本身是编译的，使用解释器的嵌入式语言也会很慢。但如果新语言里的表达式被转换成了 Lisp，那么 Lisp 编译器就会编译这些转换出来的代码。这样实现的语言不需要在运行期承受解释的开销。要是你还没有为你的语言编写一个真正编译器，宏会帮助你获得最优的性能。事实上，转换新语言的宏可以看作该语言的编译器 -- 只不过它的大部分工作是由已有的 Lisp 编译器完成的。 这里我们暂时不会考虑任何嵌入式语言的例子，第19-25 章都是关于该主题的。第 19 章专门讲述了解释与转换嵌入式语言之间的区别，并且同时用这两种方法实现了同一种语言。 有一本 Common Lisp 的书断言宏的作用域是有限的，依据是：在所有 CLTL1 里定义的操作符中，只有少于 10% 的操作符是宏。这就好比是说因为我们的房子是用砖砌成的，我们的家具也必须得是。宏在一个 Common Lisp 程序中所占的比例多少完全要看这个程序想干什么。有的程序里可能根本没有宏，而有的程序可能全是宏。

## 第 7 章 宏 Lisp 中，宏的特性让你能用变换的方式定义操作符。宏定义在本质上，是能生成 Lisp 代码的函数 -- 一个能写程序的程序。这一小小开端引发了巨大的可能性，同时也伴随着难以预料的风险。 第 7-10 章将带你走入宏的世界。本章会解释宏如何工作，介绍编写和调试它们的技术，然后分析一些宏风格中存在的问题。 ### 7.1 宏是如何工作的 由于我们可以调用宏并得到它的返回值，因此宏往往被人们和函数联系在一起。宏定义有时和函数定义相似，而且不严谨地说，被人们称为 "内置函数" 的 `do` 其实就是一个宏。但如果把两者过于混为一谈，就会造成很多困惑。宏和常规函数的工作方式截然不同，并且只有知道宏为何不同，以及怎样不同, 才是用好它们的关键。一个函数只产生结果，而宏却产生表达式。当它被求值时，才会产生结果。 要入门，最好的办法就是直接看个例子。假设我们想要写一个宏 `nil!`，它把实参设置为 `nil`。让`(nil! x)` 和 `(setq x nil)` 的效果一样。我们完成这个功能的方法是：把 `nil!` 定义成宏，让它来把前一种形式的实例变成后一种形式的实例: ~~~ > (defmacro nil! (var) (list 'setq var nil)) NIL! ~~~ 用汉语转述的话，这个定义相当于告诉 Lisp： "无论何时，只要看到形如 `(nil!)` 的表达式，请在求值之前先把它转化成 `(setq nil)` 的形式。" 宏产生的表达式将在调用宏的位置求值。宏调用是一个列表，列表的第一个元素是宏的名称。当我们把宏调用 `(nil! x)` 输入到 `toplevel` 的时候发生了什么? Lisp 首先会发觉 `nil!` 是个宏的名字，然后: > 1. 按照上述定义的要求构造表达式，接着， > > > 2. 在调用宏的地方求值该表达式。 构造新表达式的那一步被称为宏展开（macro expansion）。Lisp 查找 `nil!` 的定义，其定义展示了如何为宏调用构建一个即将取代它的表达式。和函数一样，`nil!` 的定义也应用到了宏调用传给它的表达式参数上。 它返回一个三元素列表，这三个元素分别是： `setq`、作为参数传递给宏的那个表达式，以及 `nil`。在本例中，`nil!` 的参数是 `x` ，宏展开式是 `(setq x nil)`。 宏展开之后是第二步：求值（evaluation）。Lisp 求值宏展开式 `(setq x nil)` 时就好像是你原本就写在那儿的一样。求值并不总是立即发生在展开之后，不过在 `toplevel` 下的确是这样的。一个发生在函数定义里的宏调用将在函数编译时展开，但展开式 或者说它产生的对象代码, 要等到函数被调用时才会求值。 如果把宏的展开和求值分清楚，你遇到的和宏有关的困难，或许有很多就能避免。当编写宏的时候，要清楚哪些操作是在宏展开期进行的，而哪些操作是在求值期进行的，通常，这两步操作的对象截然不同。宏展开步骤处理的是表达式，而求值步骤处理的则是它们的值。 有些宏的展开过程比 `nil!` 的情况更复杂。`nil!` 的展开式只是调用了一下内置的 `special form`，但往往一个宏的展开式可能会是另一个宏调用，就好像是一层套一层的俄罗斯套娃。在这种情况下，宏展开就会继续抽丝剥茧直到获得一个没有宏的表达式。这一步骤中可以经过任意多次的展开操作，一直到最终停下来。 尽管有许多语言也提供了某种形式的宏，但 Lisp 宏却格外强大。在编译 Lisp 文件时，解析器先读取源代码，然后将其输出送给编译器。这里有个天才的手笔：解析器的输出由 Lisp 对象的列表组成。通过使用宏，我们可以操作这种处于解析器和编译器之间的中间状态的程序。如果必要的话，这些操作可以无所不包。一个生成展开式的宏拥有 Lisp 的全部威力，可任其驱驰。事实上，宏是货真价实的 Lisp 函数 那种能返回表达式的函数。虽然 `nil!` 的定义中只是调用了一下 `list` ，但其他宏里可能会驱动整个子程序来生成其展开式。 有能力改变编译器所看到的东西，差不多等同于能够对代码进行重写。所以我们就可以为语言增加任何构造，只要用变换的方法把它定义成已有的构造。 ### 7.2 反引用（backquote） 反引用（backquote）是引用（quote）的特别版本，它可以用来创建 Lisp 表达式的模板。反引用最常见的用途之一是用在**宏定义**里。 反引用字符 ` 得名的原因是：它和通常的引号 `'` 相似，只不过方向相反。当单独把反引用作为表达式前缀的时候，它的行为和引号一样： ~~~ `(a b c) 等价于 '(a b c) ~~~ 只有在反引用和逗号 `,` 以及 comma-at `,@` 一同出现时才变得有用。如果说反引用创建了一个模板，那么逗号就在反引用中创建了一个槽(slot) 。一个反引用列表等价于将其元素引用起来，调用一次 `list`。也就是: ~~~ `(a b c) 等价于 (list 'a 'b 'c). ~~~ 在反引用的作用域里，逗号要求 Lisp： "把引用关掉" 。当逗号出现在列表元素前面时，它的效果就相当于取消引用，让 Lisp 把那个元素按原样放在那里。所以: ~~~ `(a ,b c ,d) 等价于 (list 'a b 'c d) ~~~ 插入到结果列表里的不再是符号 b ，取而代之的是它的值。无论逗号在嵌套列表里的层次有多深，它都仍然有效: ~~~ > (setq a 1 b 2 c 3) 3 > `(a ,b c) (A 2 C) > `(a (,b c)) (A (2 C)) ~~~ 而且它们也可以出现在引用的列表里，或者引用的子列表里： ~~~ > `(a b ,c (',(+ a b c)) (+ a b) 'c '((,a 'b))) (A B 3 ('6) (+ A B) 'C '((1 'B))) ~~~ 一个逗号能抵消一个反引用的效果，所以逗号在数量上必须和反引用匹配。如果某个操作符出现在逗号的外层，或者出现在包含逗号的那个表达式的外层，那么我们说该操作符包围了这个逗号。例如在```(,a ,(b ',c))`` 中，最后一个逗号就被前一个逗号和两个反引号所包围。通行的规则是：一个被`n` 个逗号包围的逗号必须被至少 `n + 1` 个反引号所包围。很明显，由此可知：逗号不能出现在反引用的表达式的外面。只要遵守上述规则，就可以嵌套使用反引用和逗号。下面的任何一个表达式如果输入到 toplevel 下都将造成错误： ~~~ ,x `(a ,,b c) `(a ,(b ,c) d) `(,,'a) ~~~ 嵌套的反引用只有在宏定义的宏里才可能会用到。第 16 章将讨论这两个主题。 反引用通常被用来创建列表【注 1】。任何用反引用生成的列表也都可以用 `list` 和普通的引用来实现。使用反引用的好处只是在于它改进了表达式的可读性，因为反引用的表达式和它将生成的表达式很相似。在前一章里我们把 `nil!` 定义成： ~~~ (defmacro nil! (var) (list 'setq var nil)) ~~~ 借助反引用，这个宏可以定义成： ~~~ (defmacro nil! (var) `(setq ,var nil)) ~~~ 在本例中，是否使用反引用的差别还不算太大。不过，随着宏定义长度的增加，反引用也会变得愈加重要。 [示例代码 7.1] 包含了两个 `nif` 可能的定义，这个宏实现了三路数值条件选择。【注 2】 * * * **[示例代码 7.1] 一个使用和不使用反引用的宏定义** 使用反引用： ~~~ (defmacro nif (expr pos zero neg) `(case (truncate (signum ,expr)) (1 ,pos) (0 ,zero) (-1 ,neg))) ~~~ 不使用反引用： ~~~ (defmacro nif (expr pos zero neg) (list 'case (list 'truncate (list 'signum expr)) (list 1 pos) (list 0 zero) (list -1 neg))) ~~~ * * * 首先，第一个参数会被求值成数字。然后会根据这个数字的正负、是否为零，来决定第二、第三和第四个参数中哪一个将被求值： ~~~ > (mapcar #'(lambda (x) (nif x 'p 'z 'n)) '(0 2.5 -8)) (Z P N) ~~~ [示例代码 7.1] 中的两个定义分别定义了同一个宏，但是前者使用的是反引用，而后者则通过显式调用 `list` 来构造它的展开式。以 `(nif x 'p 'z 'n)` 为例，从第一个定义中很容易就能看出来，这个表达式会展开成: ~~~ (case (truncate (signum x)) (1 'p) (0 'z) (-1 'n)) ~~~ 因为这个宏定义体的模样就和它生成的宏展开式差不多。要想理解不使用反引用的第二个版本，你将不得不在脑海中重演一遍展开式的构造过程。 `comma-at`，即 `,@`，是逗号的变形，其行为和逗号相似，但有一点不同：`comma-at` 不像逗号那样仅仅把表达式的值插入到所在的位置，而是把表达式拼接进去。拼接这个操作可以这样理解：在插入的同时，剥去被插入对象最外层的括号： ~~~ > (setq b '(1 2 3)) (1 2 3) > `(a ,b c) (A (1 2 3) C) > `(a ,@b c) (A 1 2 3 C) ~~~ 逗号导致列表 `(1 2 3)` 被插入到 `b` 所在的位置，而 `comma-at` 把列表中的元素插入到那里。对于`comma-at` 的使用，还另有限制： 1. 为了确保其参数可以被拼接，`comma-at` 必须出现在序列（sequence）【注 3】 中。形如`',@b` 的写法是错误的，因为无处可供 `b` 的值进行拼接。 2. 要进行拼接的对象必须是个列表，除非它出现在列表最后。表达式 `'(a ,@1)` 将被求值成 `(a . 1)`，但如果尝试将原子【注 4】(atom) 拼接到列表的中间位置，例如 `'(a ,@1 b)`，将导致一个错误。 `comma-at` 一般用在接受不确定数量参数的宏里，以及将这些参数传给同样接受不确定数量参数的函数和宏里。这一情况通常广泛用于实现隐式的块（block）。Common Lisp 提供几种将代码分组到块的操作符，包括 `block`、`tagbody`，以及 `progn` 。这些操作符很少直接出现在源代码里；它们一般不显山露水，而是藏身在宏的背后。 隐式块出现在任何一个带有表达式体的内置宏里。例如 `let` 和 `cond` 里都有隐式的 `progn` 存在。做这种事情的内建宏里，最简单的一个可能要算 `when` 了： ~~~ (when (eligible obj) (do-this) (do-that) obj) ~~~ 如果 `(eligible obj)` 返回真，那么其余的表达式将会被求值，并且整个 `when` 表达式会返回其中最后一个表达式的值。下面是一个使用 `comma-at` 的示例，它是 `when` 的一种可能的实现： ~~~ (defmacro our-when (test &body body) `(if ,test (progn ,@body))) ~~~ 这一定义使用了一个 `&body` 参数（它和 `&rest` 功能相同，只有美观输出的时候不太一样）来接受可变数量的参数，然后一个 `comma-at` 将它们拼接到一个 `progn` 表达式里。在上述调用的宏展开式里，宏调用体里面的三个表达式将出现在单个 `progn` 中： ~~~ (if (eligible obj) (progn (do-this) (do-that) obj)) ~~~ 多数需要迭代处理其参数的宏都采用类似方式拼接它们。 `comma-at` 的效果也可以不用反引用实现。例如，表达式: ~~~ `(a ,@b c) ~~~ 就和: ~~~ (cons 'a (append b (list 'c))) ~~~ 等价。之所以用上 `comma-at`，只是为了改进这种由表达式生成的表达式的可读性。 宏定义（通常）生成列表。尽管宏展开式可以用函数 `list` 来生成，但反引用的列表模板可以令这一任务更为简单。用 `defmacro` 和反引用定义的宏，在形式上和用 `defun` 定义的函数非常相似。只要不被这种相似性误导，反引用就能让宏定义既容易书写也方便阅读。 由于反引用经常出现在宏定义里，以致于人们有时误以为反引用是 `defmacro` 的一部分。关于反引用的最后一件要记住的事情，是它有自己存在的意义，这跟它在宏定义中的角色无关。你可以在任何需要构造序列的场合使用反引用： ~~~ (defun greet (name) `(hello ,name)) ~~~ ### 7.3 定义简单的宏 在编程领域，最快的学习方式通常是尽快地开始实践。完全理论上的理解可以稍后再说。因此本章介绍一种可以立即开始编写宏的方法。虽然该方法的适用范围很窄，但在这个范围内却可以高度机械化地实现。 > (如果你以前写过宏,可以跳过本节。) 下面举个例子，让我们考虑一下如何写出 Common Lisp 内置函数 `member` 的变形。`member` 缺省用 `eql` 来判断等价与否。如果你想要用 `eq` 来判断是否等价，你就必须显式写成这样： ~~~ (member x choices :test #'eq) ~~~ 如果常常这样做，那我们可能会想要写一个 `member` 的变形，让它总是使用 `eq` 。有些早期的 Lisp 方言就有这样的一个函数，叫做 `memq`： ~~~ (memq x choices) ~~~ 通常应该将 `memq` 定义为内联（inline） 函数，但为了举例子，我们会让它以宏的面目出现。 * * * **[示例代码 7.2] 用于写 memq 的图示** 调用： ~~~ (memq x choices) ~~~ 展开： ~~~ (member x choices :test #'eq) ~~~ * * * 方法如下：从你想要定义的这个宏的一次典型调用开始。先把它写在纸上，然后下面写上它应该展开成的表达式。[示例代码 7.2] 给出了两个这样的表达式。通过宏调用，构造出你这个宏的参数列表，同时给每个参数命名。这个例子中有两个实参，所以我们将会有两个形参，把它们叫做 obj 和 lst ： ~~~ (defmacro memq (obj lst) ~~~ 现在回到之前写下的两个表达式。对于宏调用中的每个参数，画一条线把它和它在展开式里出现的位置连起来。[示例代码 7.2] 中有两条并行线。为了写出宏的实体，把你的注意力转移到展开式。让主体以反引用开头。 现在，开始逐个表达式地阅读展开式。每当发现一个括号，如果它不是宏调用中实参的一部分，就把它放在宏定义里。所以紧接着反引用会有一个左括号。对于展开式里的每个表达式 1. 如果没有线将它和宏调用相连，那么就把表达式本身写下来。 2. 如果存在一条跟宏调用中某个参数的连接，就把出现在宏参数列表的对应位置的那个符号写下来，前置一个逗号。 由于第一个元素 `member` 上没有连接，所以我们照原样使用 `member` ： ~~~ (defmacro memq (obj lst) '(member ~~~ 不过，`x` 上有一条线指向源表达式中的第一个实参，所以我们在宏的主体中使用第一个参数，带一个逗号： ~~~ (defmacro memq (obj lst) '(member ,obj ~~~ 以这种方式继续进行，最后完成的宏定义是： * * * **[示例代码 7.3] 用于写 while 的图示** ~~~ (defmacro memq (obj lst) `(member ,obj ,lst :test #'eq)) (while hungry (stare-intently) (meow) (rub-against-legs)) (do () ((not hungry)) (stare-intently) (meow) (rub-against-legs)) ~~~ * * * 到目前为止，我们写出的宏，其参数个数只能是固定的。现在假设我们打算写一个 `while` 宏，它接受一个条件表达式和一个代码体，然后循环执行代码直到条件表达式返回真。[示例代码 7.3] 含有一个描述猫的行为的 `while` 循环示例。 要写出这样的宏，我们需要对我们的技术稍加修改。和前面一样，先写一个宏调用作为毛坯。然后，以它为基础，构造宏的形参列表，其中，在想要接受任意多个参数的地方，以一个 `&rest` 或 `&body`形参作结： ~~~ (defmacro while (test &body body) ~~~ 现在，在宏调用的下面写出目标展开式，并且和之前一样，画线把宏调用的形参和它们在展开式中的位置连起来。然而，当你碰到一个系列形参，而且它们会被 `&rest` 或 `&body` 实参吸收时，就要把它们当成一组处理，并只用一条线来连接整个参数序列。[示例代码 7.3] 给出了最后的展示。 为了写出宏定义的主体，按之前的步骤处理表达式。在前面给出的两条规则之外，我们还要加上一条： 1. 如果在一系列展开式中的表达式和宏调用里的一系列形参之间存在联系，那么就把对应的 `&rest`或 `&body` 实参记下来，在前面加上 `comma-at`。 于是宏定义的结果将是： ~~~ (defmacro while (test &body body) `(do () ((not ,test)) ,@body)) ~~~ 要想构造带有表达式体的宏，就必须有参数充当打包装箱的角色。这里宏调用中的多个参数被串起来放到 `body`里，然后在 `body` 被拼接进展开式时，再把它拆散开。 用本章所述的这个方法，我们能写出最简单的宏 这种宏只能在参数位置上做文章。但是宏可以比这做的多得多。第 7.7 节将会举一个例子，这个例子无法用简单的反引用列表表达，并且为了生成展开式，例子中的宏成为了真正意义上的程序。 ### 7.4 测试宏展开 宏写好了，那我们怎么测试它呢？像 `memq` 这样的宏，它的结构较简单，只消看看它的代码就能弄清其行为方式。而当编写结构更复杂的宏时，我们必须有办法检查它们展开之后正确与否。 [示例代码 7.4] 给出了一个宏定义和用来查看其展开式的两个方法。内置函数 `macroexpand` 的参数是个表达式，它返回这个表达式的宏展开式。把一个宏调用传给 `macroexpand` ，就能看到宏调用在求值之前最终展开的样子，但是当你测试宏的时候，并不是总想看到彻底展开后的展开式。如果有宏依赖于其他宏，被依赖的宏也会一并展开，所以完全展开后的宏有时是不利于阅读的。 从[示例代码 7.4] 给出的第一个表达式，很难看出 `while` 是否如愿展开，因为不仅内置的宏 do 被展开了，而且它里面的 `prog` 宏也展开了。我们需要一种方法，通过它能看到只展开过一层宏的展开结果。这就是内置函数 `macroexpand-1` 的目的，正如第二个例子所示。就算展开后，得到的结果仍然是宏调用，`macroexpand-1` 也只做一次宏展开就停手。 * * * **[示例代码 7.4] 一个宏和它的两级展开** ~~~ > (defmacro while (test &body body) `(do () ((not ,test)) ,@body)) WHILE > (pprint (macroexpand '(while (able) (laugh)))) (BLOCK NIL (LET NIL (TAGBODY #:G61 (IF (NOT (ABLE)) (RETURN NIL)) (LAUGH) (GO #:G61)))) T > (pprint (macroexpand-1 '(while (able) (laugh)))) (DO NIL ((NOT (ABLE))) (LAUGH)) T ~~~ * * * **[示例代码 7.5] 一个用于测试宏展开的宏** ~~~ (defmacro mac (expr) `(pprint (macroexpand-1 ',expr))) ~~~ * * * 如果每次查看宏调用的展开式都得输入如下的表达式，这会让人很头痛： ~~~ (pprint (macroexpand-1 '(or x y))) ~~~ [示例代码 7.5] 定义了一个新的宏，它让我们有一个简单的替代方法： ~~~ (mac (or x y)) ~~~ 调试函数的典型方法是调用它们，同样的道理，对于宏来说就是展开它们。不过由于宏调用涉及了两次计算，所以它也就有两处可能会出问题。如果一个宏行为不正常，大多数时候你只要检查它的展开式，就能找出有错的地方。不过也有一些时候，展开式看起来是对的，所以你想对它进行求值以便找出问题所在。 如果展开式里含有自由变量，你可能需要先设置一些变量。在某些系统里，你可以复制展开式，把它粘贴到 toplevel 环境里，或者选择它然后在菜单里选 eval。在最坏的情况下你也可以把 macroexpand-1 返回的列表设置在一个变量里，然后对它调用 eval ： ~~~ > (setq exp (macroexpand-1 '(memq 'a '(a b c)))) (MEMBER (QUOTE A) (QUOTE (A B C)) :TEST (FUNCTION EQ)) > (eval exp) (A B C) ~~~ 最后，宏展开不只是调试的辅助手段，它也是一种学习如何编写宏的方式。Common Lisp 带有超过一百个内置宏，其中一些还颇为复杂。通过查看这些宏的展开过程你经常能了解它们是怎样写出来的。 ### 7.5 参数列表的解构 解构（destructuring） 是用在处理函数调用中的一种赋值操作【注 5】的推广形式。如果你定义的函数带有多个形参： ~~~ (defun foo (x y z) (+ x y z)) ~~~ 当调用该函数时： ~~~ (foo 1 2 3) ~~~ 函数调用中实参会按照参数位置的对应关系，赋值给函数的形参：`1` 赋给 `x` ，`2` 赋给 `y` ，`3` 赋给 `z` 。和本例中扁平列表 `(x y z)` 的情形类似，解构（destructuring） 同样也指定了按位置赋值的方式，不过它能按照任意一种列表结构来进行赋值。 Common Lisp 的 `destructuring-bind` 宏（CLTL2 新增） 接受一个匹配模式，一个求值到列表的实参，以及一个表达式体，然后在求值表达式时将模式中的参数绑定到列表的对应元素上： ~~~ > (destructuring-bind (x (y) . z) '(a (b) c d) (list x y z)) (A B (C D)) ~~~ 这一新操作符和其它类似的操作符构成了第 18 章的主题。 在宏参数列表里进行解构也是可能的。Common Lisp 的 `defmacro` 宏允许任意列表结构作为参数列表。当宏调用被展开时，宏调用中的各部分将会以类似 destructuring-bind 的方式被赋值到宏的参数上面。内置的 `dolist` 宏就利用了这种参数列表的解构技术。在一个像这样的调用里： ~~~ (dolist (x '(a b c)) (print x)) ~~~ 展开函数必须把 `x` 和 `'(a b c)` 从作为第一个参数给出的列表里抽取出来。这个任务可以通过给`dolist` 适当的参数列表隐式地完成【注 6】： ~~~ (defmacro our-dolist ((var list &optional result) &body body) '(progn (mapc #'(lambda (,var) ,@body) ,list) (let ((,var nil)) ,result))) ~~~ 在 Common Lisp 中，类似 `dolist` 这样的宏通常把参数包在一个列表里面，而后者不属于宏体。由于 `dolist` 接受一个可选的 `result` 参数，所以它无论如何都必须把它参数的第一部分塞进一个单独的列表。但就算这个多余的列表结构是画蛇添足，它也可以让 `dolist` 调用更易于阅读。假设我们想要定义一个宏 `when-bind` ，它的功能和 `when` 差不多，除此之外它还能绑定一些变量到测试表达式返回的值上。这个宏最好的实现办法可能会用到一个嵌套的参数表： ~~~ (defmacro when-bind ((var expr) &body body) '(let ((,var ,expr)) (when ,var ,@body))) ~~~ 然后这样调用： ~~~ (when-bind (input (get-user-input)) (process input)) ~~~ 而不是原本这样调用： ~~~ (let ((input (get-user-input))) (when input (process input))) ~~~ 审慎地使用它，参数列表解构技术可以带来更加清晰的代码。最起码，它可以用在诸如 `when-bind`和 `dolist` 这样的宏里，它们接受两个或更多的实参，和一个表达式体。 ### 7.6 宏的工作模式 关于 "宏究竟做了什么" 的形式化描述将是既拖沓冗长，又让人不得要领的。就算有经验的程序员也记不住这样让人头晕的描述。想象一下 `defmacro` 是怎样定义的，通过这种方式来记忆它的行为会更容易些。 * * * **[示例代码 7.6] 一个 `defmacro` 的草稿** ~~~ (defmacro our-expander (name) '(get ,name 'expander)) (defmacro our-defmacro (name parms &body body) (let ((g (gensym))) `(progn (setf (our-expander ',name) #'(lambda (,g) (block ,name (destructuring-bind ,parms (cdr ,g) ,@body)))) ',name))) (defun our-macroexpand-1 (expr) (if (and (consp expr) (our-expander (car expr))) (funcall (our-expander (car expr)) expr) expr)) ~~~ * * * 在 Lisp 里用这种方法解释概念已由来已久。早在1962年首次出版的 `Lisp 1.5 Programmer's Manual` ，就在书中给出了一个用 Lisp 写的 `eval` 函数的定义作为参考。由于 `defmacro` 自身也是宏，所以我们可以依法炮制，如 [示例代码 7.6] 所示。这个定义里使用了几种我们尚未提及的技术，所以某些读者可能需要稍后再回过头来读懂它。 [示例代码 7.6] 中的定义相当准确地再现了宏的行为，但就像任何草稿一样，它远非十全十美。它不能正确地处理 `&whole` 关键字。而且，真正的 `defmacro` 为它第一个参数的 `macro-function` 保存的是一个有两个参数的函数，两个参数分别为：宏调用本身，和其发生时的词法环境。还好，只有最刁钻的宏才会用到这些特性。 就算你以为宏就是像 [示例代码 7.6] 那样实现的，在实际使用宏的时候，也基本上不会出错。例如，在这个实现下，本书定义的每一个宏都能正常运行。 [示例代码 7.6] 的定义里产生的展开函数是个被井号引用过的 λ表达式。那将使它成为一个闭包：宏定义中的任何自由符号应该指向 `defmacro` 发生时所在环境里的变量。所以下列代码是可行的： ~~~ (let ((op 'setq)) (defmacro our-setq (var val) (list op var val))) ~~~ 上述代码对 **CLTL2** 来说没有问题。但在 **CLTL1** 里，宏展开器是在空词法环境里定义的【注 7】，所以在一些老的 Common Lisp 实现里，这个 `our-setq` 的定义将不会正常工作。 ### 7.7 作为程序的宏 宏定义并不一定非得是个反引用列表。宏的本质是函数，它把一个表达式转换成另一个表达式。这个函数可以调用 `list` 来生成结果，但是同样也可以调用一整个长达数百行代码的子程序达到这个目的。 第 7.3 节给出了一个编写宏的简易方案。借助这一技术，我们可以写出这样的宏，让它的展开式包含的子表达式和宏调用中的相同。不幸的是，只有最简单的宏才能满足这一条件。现在举个复杂一些的例子，让我们来看看内置的宏 `do` 。要把 `do` 实现成那种只是把参数重新排列一下的宏是不可能的。在展开过程中，必须构造出一些在宏调用中没有出现过的复杂表达式。 关于编写宏，有个更通用的方法：先想想你想要使用的是哪种表达式，再设想一下它应该展开成的模样，最后写出能把前者变换成后者的程序。可以试着手工展开一个例子，分析在表达式从一种形式变换到另一种形式的过程中，究竟发生了什么。从实例出发，你就可以大致明白在你将要写的宏里将需要做些什么工作。 * * * **[示例代码 7.7] do 的预期展开过程** ~~~ (do ((w 3) (x 1 (1+ x)) (y 2 (1+ y)) (z)) ((> x 10) (princ z) y) (princ x) (princ y)) ~~~ 应该被展开成如下的样子： ~~~ (prog ((w 3) (x 1) (y 2) (z nil)) foo (if (> x 10) (return (progn (princ z) y))) (princ x) (princ y) (psetq x (1+ x) y (1+ y)) (go foo)) ~~~ * * * [示例代码 7.7] 显示了 `do` 的一个实例，以及它应该展开成的表达式。手工进行展开有助于理清你对于宏工作方式的认识。例如，在试着写展开式时，你就不得不使用 `psetq` 来更新局部变量，如果没有手工写过展开式，说不定就会忽视这一点。 内置的宏 `psetq` （因 "parallel setq" 而得名） 在行为上和 `setq` 相似，不同之处在于：在做任何赋值操作之前，它所有的（第偶数个） 参数都会被求值。如果是普通的 `setq` ，而且在调用时有两个以上的参数，那么在求值第四个参数的时候，第一个参数的新值将是可见的。 ~~~ > (let ((a 1)) (setq a 2 b a) (list a b)) (2 2) ~~~ 这里，因为先设置的是 `a` ，所以 `b` 得到了它的新值，即 `2` 。而调用 `psetq` 时，应该就好像参数的赋值操作是并行的一样： ~~~ > (let ((a 1)) (psetq a 2 b a) (list a b)) (2 1) ~~~ 所以这里的 `b` 得到的是 `a` 原来的值。这个 `psetq` 宏是特别为支持类似 `do` 这样的宏而提供的，后者需要并行地对它们的一些参数进行求值。（如果这里使用的是`setq` ，而非 `psetq` ，那么最后定义出来的就不是 `do` 而是 `do*` 了。） 仔细观察展开式，还可以看出另一个问题，我们不能真的把 `foo` 作为循环标签使用。如果 `do` 宏里的循环标签也是 `foo` 呢？第 9 章将会具体解决这个问题；至于现在，只要在宏展开里面，用`gensym` 生成一个专门的匿名符号，然后把 `foo` 换成这个符号就行了。 * * * **[示例代码 7.8] 实现 do** ~~~ (defmacro our-do (bindforms (test &rest result) &body body) (let ((label (gensym))) `(prog ,(make-initforms bindforms) ,label (if ,test (return (progn ,@result))) ,@body (psetq ,@(make-stepforms bindforms)) (go ,label)))) (defun make-initforms (bindforms) (mapcar #'(lambda (b) (if (consp b) (list (car b) (cadr b)) (list b nil))) bindforms)) (defun make-stepforms (bindforms) (mapcan #'(lambda (b) (if (and (consp b) (third b)) (list (car b) (third b)) nil)) bindforms)) ~~~ * * * 为了写出 `do` ，我们接下来考虑一下需要做哪些工作，才能把 [示例代码 7.7] 中的第一个表达式变换成第二个。要完成这种变换，如果只是像以前那样，把宏的参数放在某个反引用列表中的适当位置，是不可能的了，我们要更进一步。紧跟着最开始的prog 应该是一个由符号和它们的初始绑定构成的列表，而这些信息需要从传给 `do` 的第二个参数里拆解出来。[示例代码 7.8] 中的函数`make-initforms` 将返回这样的一个列表。我们还需要为 `psetq` 构造一个参数列表，但本例中的情况要复杂一些，因为并非所有的符号都需要更新。在[示例代码 7.8] 中，`make-stepforms` 会返回 `psetq`需要的参数。有了这两个函数，定义的其它部分就易如反掌了。 [示例代码 7.8] 中的代码并不完全是 `do` 在真正的实现里的写法。为了强调在宏展开过程中完成的计算，`make-initforms` 和 `make-stepforms` 被分离出来，成为了单独的函数。在将来，这样的代码通常会留在 `defmacro` 表达式里。 通过这个宏的定义，我们开始领教到宏的能耐了。宏在构造表达式时，可以使用Lisp 所有的功能。而用来生成展开式的代码，其自身就可以是一个程序。 ### 7.8 宏风格 对于宏来说，良好的风格有着不同的含义。风格既体现在阅读代码的时候，也体现在 Lisp 求值代码的时候。宏的引入，使阅读和求值在稍有些不一样的场合下发生了。 一个宏定义牵涉到两类不同的代码，分别是：展开器代码，宏用它来生成其展开式，以及展开式代码，它出现在展开式本身的代码中。编写这两类代码所遵循的准则各不相同。通常，好的编码风格要求程序清晰并且高效。两类宏代码在这两点上侧重的方面截然相反：展开器代码更重视代码的结构清晰可读，而展开式代码对效率的要求更高一些。 效率，只有在编译了的代码里才是最重要的，而在编译了的代码里宏调用已经被展开了。就算展开器代码很高效，它也只会使得代码的编译过程稍微快一些，但这对程序运行的效率没有任何影响。 由于宏调用的展开只是编译器工作中很小的一部分，那些可以高效展开的宏通常甚至不会在编译速度上产生明显的差异。 所以大多数时候，你大可不必字句斟酌，只要像写一个程序的快速初版那样，编写宏展开代码就可以了。如果展开器代码做了一些不必要的工作或者做了很多 `cons`，那又能怎样呢？你的时间最好花在改进程序的其他部分上面。如果在展开器代码里，要在可读性和速度两者之间作一个选择，可读性当然应该胜出。 宏定义通常比函数定义更难以阅读，因为宏定义里含有两种表达式的混合体，它们将在不同的时刻求值。 如果可以牺牲展开器代码的效率，让宏定义更容易读懂，那这笔买卖还是合算的。 * * * **[示例代码 7.9] 两个等价于 and 的宏** ~~~ (defmacro our-and (&rest args) (case (length args) (0 t) (1 (car args)) (t '(if ,(car args) (our-and ,@(cdr args)))))) (defmacro our-andb (&rest args) (if (null args) t (labels ((expander (rest) (if (cdr rest) '(if ,(car rest) ,(expander (cdr rest))) (car rest)))) (expander args)))) ~~~ * * * 举个例子，假设我们想要把一个版本的and 定义成宏。由于: ~~~ (and a b c) ~~~ 等价于: ~~~ (if a (if b c)) ~~~ 我们可以像 [示例代码 7.9] 中的第一个定义那样，用 `if` 来实现 `and` 。根据我们评判普通代码的标准，`our-and` 写得并不好。因为它的展开器代码是递归的，而且在每次递归里都要需要计算同一个列表的每个后继 `cdr` 的长度。 如果这个代码希望在运行期求值，最好像 `our-andb` 那样定义这个宏，它没有做任何多余的计算，就生成了同样的展开式。虽然如此，作为一个宏定义来说，`our-and` 即使算不上好，至少还过得去。尽管每次递归都调用 `length` ，这样可能会比较没效率，但是其代码的组织方式更加清晰地说明了其展开式跟 `and` 的连接词数量之间的依赖关系。 凡事都有例外。在 Lisp 里，对编译期和运行期的区分是人为的，所以任何依赖于此的规则同样也是人为的。 在某些程序里，编译期也就是运行期。如果你在编写一个程序，它的主要目的就是进行代码变换，并且它使用宏来实现这个功能，那么一切就都变了：展开器代码成为了你的程序，而展开式是程序的输出。很明显，在这种情况下，展开器代码应该写得尽可能高效。尽管如此，还是可以说大多数展开器代码: > (a) 只会影响编译速度，而且 > > (b) 也不会影响太多 换句话说，代码的可读性几乎总是应该放在第一位。 对于展开式代码来说，正好相反。对宏展开式来说，代码可读与否不太重要，因为很少有人会去读它，而别人读这种代码的可能性更是微乎其微。平时严禁使用的 `goto` 在展开式里可以网开一面，备受冷眼的 `setq` 也可以稍微抬起头来。 结构化编程的拥护者不喜欢源代码里的 `goto`。他们心目中的洪水猛兽并非机器语言里的跳转指令 前提是这些跳转指令是通过更抽象的控制结构隐藏在源代码里的。在 Lisp 里，`goto` 之所以备受责难，其实是因为很容易把它藏起来：你可以改用 `do` ，而且就算你没有 `do` 可用，还可以自己写一个。很明显，如果你打算在 `goto` 的基础上构建新抽象，`goto` 一定会存在于某些地方。因而，在新的宏定义中使用 `goto` 未必不好，前提是它不能用现成的宏来写。 类似地，不推荐使用 `setq` 的理由是：它让我们很难弄清楚一个给定变量的值是在哪里获得的。虽然这样，但是考虑到会去读宏展开式代码的人不是很多，所以对宏展开式里创建的变量使用 `setq` 也问题不大。如果你查看一些内置宏的展开式，你会看到许多 `setq`。 在某些场合下，展开式代码的清晰性更重要一些。如果你在编写一个复杂的宏，你可能最后还是得阅读它的展开式，至少在调试的时候。 同样，在简单的宏里，只有一个反引用用来把展开器代码和展开式代码分开，所以，如果这样的宏生成了难看的展开式，那么这种惨不忍睹的代码在你的源代码里将会一览无余。 尽管如此，就算对展开式代码的可读性有了要求，效率仍然应该放在第一位。效率于大多数运行时代码都至关重要。而对宏展开来说尤为如此，这里有两个原因：宏的普遍性和不可见性。 宏通常用于实现通用的实用工具，这些工具会出现在程序的每个角落。如此频繁使用的代码是无法忍受低效的。一个宏，虽然看上去小小的，安全无害，但是在所有对它的调用都展开之后，可能会占据你程序的相当篇幅。 这样的宏得到的重视应当比因为它们的长度所获得的重视更多才对。 特别是要避免 `cons`。一个实用工具，如果做了不必要的 `cons`，那就会毁掉一个原本高效的程序。 关注展开式代码效率的另一个原因就是它非常容易被忽视。倘若一个函数实现得不好，那么每次查看其定义时，它都会向你坦陈这一事实。宏就不是这样了。展开式代码的低效率在宏的定义里可能并不显而易见，这也就是需要更加关注它的全部原因。 ### 7.9 宏的依赖关系 如果你重定义了一个函数，调用它的函数会自动用上新的版本【注 8】。 不过，这个说法对宏来说可就不一定成立了。当函数被编译时，函数定义中的宏调用就会替换成它的展开式。如果我们在主调函数编译以后，重定义那个宏会发生什么呢？由于对最初的宏调用的无迹可寻，所以函数里的展开式无法更新。该函数的行为将继续反映出宏的原来的定义： ~~~ > (defmacro mac (x) '(1+ ,x)) MAC > (setq fn (compile nil '(lambda (y) (mac y)))) #<Compiled-Function BF7E7E> > (defmacro mac (x) '(+ ,x 100)) MAC > (funcall fn 1) 2 ~~~ 如果在定义宏之前，就已经编译了宏的调用代码，也会发生类似的问题。**CLTL2** 这样要求，"宏定义必须在其首次使用之前被编译器看到"。各家实现对违反这个规则的反应各自不同。幸运的是，这两类问题都能很容易地避免。如果能满足下面两个条件，你就永远不会因为过时或者不存在的宏定义而烦心： 1. 在调用宏之前，先定义它。 2. 一旦重定义一个宏，就重新编译所有直接（或通过宏间接） 调用它的函数（或宏）。 有些人建议将程序中所有的宏都放在一个单独的文件里，以便保证宏定义被首先编译。这样有点过头了。 我们建议把类似 `while` 的通用宏放在单独的文件里，不过无论如何，通用的实用工具都应该和程序其余的部分分开，不论它们是函数还是宏。 某些宏只是为了用在程序的某个特定部分而写的，自然，这种宏应该跟使用它们的代码放在一起。只要保证每个宏的定义都出现在任何对它们的调用之前，你的程序就可以正确无误地编译。仅仅因为它们是宏，所以就把所有的宏集中写在一起，这样做不会有任何好处，只会让你的代码更难以阅读。 ### 7.10 来自函数的宏 本节将说明把函数转化成宏的方法。将函数转化为宏的第一步是问问你自己是否真的需要这么做。难道，你就不能干脆把函数声明成 `inline` （第 2.9 节） 吗？ 话又说回来，"如何将函数转化为宏" 这个问题还是有其意义的。当你刚开始写宏的时候，假想自己写的是个函数，希望有助于思考，这样做有时会有用 而用这种办法编出来的宏一般多少会有些问题，但这至少可以帮助你起步。关注宏与函数之间关系的另一个原因是为了了解它们究竟有何不同。最后，Lisp 程序员有时确实需要把函数改造成宏。 函数转化为宏的难度取决于该函数的一些特性。最容易转化的一类函数有下面几个特点： 1. 其函数体只有一个表达式。 2. 其参数列表只由参数名组成。 3. 不创建任何新变量（参数除外）。 4. 不是递归的（也不属于任何相互递归的函数组）。 5. 每个参数在函数体里只出现一次。 6. 没有一个参数，它的值会在其参数列表之前的另一个参数出现之前被用到。 ### 7\. 无自由变量。 有一个函数满足这些规定，它是 Common Lisp 的内置函数 `second` ，`second` 返回列表的第二个元素。它可以定义成： ~~~ (defun second (x) (cadr x)) ~~~ 如此这般，可见它满足上述的所有条件，因而可以轻而易举地把它转化成等价的宏定义。只要把一个反引用放在函数体的前面，再把逗号放在每一个出现在参数列表里的符号前面就大功告成了： ~~~ (defmacro second (x) '(cadr ,x)) ~~~ 当然，这个宏也不是在所有相同条件下都可以使用。它不能作为 `apply` 或者 `funcall` 的第一个参数，而且被它调用的函数不能拥有局部绑定。不过，对于普通的内联调用，`second` 宏应该能胜任`second` 函数的工作。 倘若函数体里的表达式不止一个，就要把这个技术稍加变通，因为宏必须展开成单独的表达式。所以无法满足条件1，你必须加上一个 `progn` 。 函数 `noisy-second` ： ~~~ (defun noisy-second (x) (princ "Someone is taking a cadr!") (cadr x)) ~~~ 的功能也可以用下面的宏来完成： ~~~ (defmacro noisy-second (x) '(progn (princ "Someone is taking a cadr!") (cadr ,x))) ~~~ 如果函数没能满足条件 2 的原因是，因为它有 `&rest` 或者 `&body` 参数，那么道理是一样的，除了参数的处理有所不同，这次不能只是把逗号放在前面，而是必须把参数拼接到一个 `list` 调用里。照此办理的话: ~~~ (defun sum (&rest args) (apply #'+ args)) ~~~ 就变成了: ~~~ (defmacro sum (&rest args) '(apply #'+ (list ,@args))) ~~~ 不过上面的宏如果改成这样写会更好些： ~~~ (defmacro sum (&rest args) '(+ ,@args)) ~~~ 当条件 3 无法满足，即在函数体里创建了新变量时，插入逗号的步骤必须改一下。这时不能在参数列表里的所有符号前面放逗号了，取而代之，我们只把逗号加在那些引用了参数的符号前面。例如在： ~~~ (defun foo (x y z) (list x (let ((x y)) (list x z)))) ~~~ 最后两个 x 的实例都没有指向参数 x 。第二个实例根本就不求值，而第三个实例引用的是由 let 建立的新变量。所以只有第一个实例才会有逗号： ~~~ (defmacro foo (x y z) '(list ,x (let ((x ,y)) (list x ,z)))) ~~~ 有时无法满足条件 4，5 和 6 的函数也能转化为宏。不过，这些话题将在以后的章节里分别讨论。其中，第 10.4 节会解决宏里递归引出的问题，而第 10.1 节和 10.2 节将会分别化解多重求值和求值顺序不一致造成的危险。 至于条件 7，用宏模拟闭包并非痴人说梦，有种技术或许可以做到，它类似 3.4 节中提到的错误。但是由于这个办法有些取巧，和本书中名门正派的作风不大协调，因此我们就此点到为止。 ### 7.11 符号宏（symbol-macro） CLTL2 为 Common Lisp 引入了一种新型宏，即符号宏（symbol-macro）。普通的宏调用看起来好像函数调用，而符号宏 "调用" 看起来则像一个符号。 符号宏只能在局部定义。`symbol-macrolet` 的 `special form` 可以在其体内，让一个孤立符号的行为表现和表达式相似： ~~~ > (symbol-macrolet ((hi (progn (print "Howdy") 1))) (+ hi 2)) "Howdy" 3 ~~~ symbol-macrolet 主体中的表达式在求值的时候，效果就像每一个参数位置的 `hi` 在之前都替换成了 `(progn (print "Howdy") 1)` 。 从理论上讲，符号宏就像不带参数的宏。在没有参数的时候，宏就成为了简单的字面上的缩写。不过，这并非是说符号宏一无是处。它们在第 15 章和第 18 章都用到了，而且在以后的例子中同样不可或缺。 ### 备注： +【注 1】反引用也可以用于创建向量（vector），不过这个用法很少在宏定义里出现。 +【注 2】这个宏的定义稍微有些不自然，这是为了避免使用 gensym 。在第 11.3 节上有一个更好的定义。 +【注 3】译者注：序列 (sequence) 是 Common Lisp 标准定义的数据类型，它的两个子类型分别是列表（list）和向量（vector）。 +【注 4】译者注：原子（atom） 也是 Common Lisp 标准定义的数据类型，所有不是列表的 Lisp 对象都是原子，包括向量（vector） 在内。 +【注 5】解构通常用在创建变量绑定，而非do 那样的操作符里。尽管如此，概念上来讲解构也是一种赋值的方式，如果你把列表解构到已有的变量而非新变量上是完全可行的。就是说，没有什么可以阻止你用解构的方法来做类似setq 这样的事情。 +【注 6】该版本用一种奇怪的方式来写以避免使用 gensym ，这个操作符以后会详细介绍。 +【注 7】关于这一区别实际有影响的例子，请参见第 4 章的注释。 +【注 8】编译时内联（inline） 的函数除外，它们和宏的重定义受到相同的约束。