第 13 章 编译期计算

## 第 13 章 编译期计算 前面的章节描述了几类只能用宏实现的操作符。本章将介绍用函数可以解决，但用宏能更高效的一类问题。第 8.2 节列出了在给定情形下使用宏的利弊。有利的一面包括 "在编译期完成计算"。有时，如果把操作符实现成宏，就可以在展开时完成部分工作。本章会着眼于那些充分利用这种可能性的宏。 ### 13.1 新的实用工具 * * * **[示例代码 13.1] 求平均值时转移计算** ~~~ (defun avg (&rest args) (/ (apply #'+ args) (length args))) (defmacro avg (&rest args) '(/ (+ ,@args) ,(length args))) ~~~ * * * 第 8.2 节里提出，通过宏就可能把计算转移到编译期完成。在那里，我们曾经把宏 `avg` 作为例子，它会返回其参数的平均值： ~~~ > (avg pi 4 5) 4.047... ~~~ 在 [示例代码 13.1] 中先把 `avg` 定义成函数，然后又用宏实现它。当把 `avg` 定义成宏时，对`length` 的调用可以在编译期完成。在宏版本里我们也避免了在运行期处理 `&rest` 参数的开销。所以在许多实现里，写成宏的 `avg` 会更快。 * * * **[示例代码 13.2] 转移和避开计算** ~~~ (defun most-of (&rest args) (let ((all 0) (hits 0)) (dolist (a args) (incf all) (if a (incf hits))) (> hits (/ all 2)))) (defmacro most-of (&rest args) (let ((need (floor (/ (length args) 2))) (hits (gensym))) '(let ((,hits 0)) (or ,@(mapcar #'(lambda (a) '(and ,a (> (incf ,hits) ,need))) args))))) ~~~ * * * 这种优化省去了不必要的计算，它的实现归功于在展开期就知道参数的数量。它还可以和我们在 `in`(11.3 节) 中进行的另一类优化结合起来，后者甚至可以避免求值一些参数。[示例代码 13.2] 中有两个版本的 `most-of` ，它在多数参数都为真的时候返回真： ~~~ > (most-of t t t nil) T ~~~ 和 `in` 一样，宏版本展开成的代码只求值它需要数量的参数。例如: ~~~ (most-of (a) (b) (c)) ~~~ 展开的等价代码： ~~~ (let ((count 0)) (or (and (a) (> (incf count) 1)) (and (b) (> (incf count) 1)) (and (c) (> (incf count) 1)))) ~~~ 在最理想的情况下，只对刚过半的参数求值。 * * * **[示例代码 13.3] 使用编译期知道的参数** ~~~ (defun nthmost (n lst) (nth n (sort (copy-list lst) #'>))) (defmacro nthmost (n lst) (if (and (integerp n) (< n 20)) (with-gensyms (glst gi) (let ((syms (map0-n #'(lambda (x) (gensym)) n))) '(let ((,glst ,lst)) (unless (< (length ,glst) ,(1+ n)) ,@(gen-start glst syms) (dolist (,gi ,glst) ,(nthmost-gen gi syms t)) ,(car (last syms)))))) '(nth ,n (sort (copy-list ,lst) #'>)))) (defun gen-start (glst syms) (reverse (maplist #'(lambda (syms) (let ((var (gensym))) '(let ((,var (pop ,glst))) ,(nthmost-gen var (reverse syms))))) (reverse syms)))) (defun nthmost-gen (var vars &optional long?) (if (null vars) nil (let ((else (nthmost-gen var (cdr vars) long?))) (if (and (not long?) (null else)) '(setq ,(car vars) ,var) '(if (> ,var ,(car vars)) (setq ,@(mapcan #'list (reverse vars) (cdr (reverse vars))) ,(car vars) ,var) ,else))))) ~~~ * * * 如果仅仅知道宏的部分参数值，也一样有可能把计算工作转移到编译期进行。图 13.3 就给出了这样的一个宏。函数 `nthmost` 接受一个数 `n` 以及一个数列，并返回数列中第 `n` 大的数；和其他序列函数一样，它是从零开始索引的： ~~~ > (nthmost 2 '(2 6 1 5 3 4)) 4 ~~~ 函数版本写得非常简单。它对列表排序，然后对排序的结果调用 `nth` 。由于 `sort` 是破坏性的，`nthmost` 在排序之前先复制列表。这样实现，使得 `nthmost` 在两方面影响效率：它构造新的点对，而且对整个参数列表排序，尽管我们只关心前 个。 如果我们在编译期知道 `n` 的值，就可以从另一个角度分析这个问题了。[示例代码 13.3] 中的其余代码定义了一个宏版本的 `nthmost` 。这个宏做的第一件事是去检查它的第一个参数。如果第一个参数字面上不是一个数，它就被展开成和我们上面看到的相同的代码。如果第一个参数是一个数的话，我们可以采用另一个办法。 比方说，如果你想要找到一个盘子里第三大的那块饼干，那么你可以依次查看每一块饼干同时保持手里总是拿着已知最大的三块，用这个办法达到目的。当你检查完所有的饼干之后，你手里最小的那块饼干就是你要找的了。如果 是一个小常数，并且这个数字远小于饼干的总数，那么和 "先对它们的全部进行排序" 的方法相比，用这种技术可以让你更方便地得到想找的那块饼干。 * * * **[示例代码 13.4] nthmost 的展开式** ~~~ (nthmost 2 nums) ~~~ 展开成： ~~~ (let ((#:g7 nums)) (unless (< (length #:g7) 3) (let ((#:g6 (pop #:g7))) (setq #:g1 #:g6)) (let ((#:g5 (pop #:g7))) (if (> #:g5 #:g1) (setq #:g2 #:g1 #:g1 #:g5) (setq #:g2 #:g5))) (let ((#:g4 (pop #:g7))) (if (> #:g4 #:g1) (setq #:g3 #:g2 #:g2 #:g1 #:g1 #:g4) (if (> #:g4 #:g2) (setq #:g3 #:g2 #:g2 #:g4) (setq #:g3 #:g4)))) (dolist (#:g8 #:g7) (if (> #:g8 #:g1) (setq #:g3 #:g2 #:g2 #:g1 #:g1 #:g8) (if (> #:g8 #:g2) (setq #:g3 #:g2 #:g2 #:g8) (if (> #:g8 #:g3) (setq #:g3 #:g8) nil)))) #:g3)) ~~~ * * * 这是一种当在编译期已知时采取的策略。在它的展开式里，宏创建了 个变量，然后调用 `nthmost-gen` 来生成那些求值成查看每一块饼干的代码。[ 示例代码 13.4] 给出了一个示例的宏展开。除了不能作为 apply 的参数传递以外，宏 `nthmost` 在行为上和原来的函数一样。这里使用宏的理由完全是出于效率：宏版本不在运行期构造新点对，并且如果是一个小的常数，那么比较的次数可以更少。 难道为了写出高效的程序，就必须兴师动众，编这么长的宏么？对于本例来说，答案可能是否定的。这里之所以给出两个版本的 `nthmost` ，主要的原因是想举个例子，它揭示了一个普遍的原则：当某些参数在编译期已知时，你可以用宏来生成更高效的代码。是否利用这种可能性取决于你想获得多少好处，以及你可以另外付出多少努力来编写一个高效的宏版本。由于 `nthmost` 的宏版本既长又繁，它可能只有在极端场合才值得去写。尽管如此，就算你宁愿不利用它，编译期已知的信息总还是一个值得考虑的因素。 ### 13.2 举例：贝塞尔曲线 就像 `with-` 宏(第 11.2 节)，用于编译期计算的宏更像是为特定应用而写的，而不是为通用目的设计的实用工具。通用的实用工具在编译期能了解多少信息？它的参数个数，可能还有某些参数的值。但如果我们想要利用其他的约束条件，这些条件也许就只能是程序自己才懂得使用的信息了。 本节将作为一个实例，展示宏是如何加速贝塞尔曲线的生成的。如果对曲线的操作是交互式的话，那么它们的生成速度必须得非常快才行。可以看出，如果曲线的分段数是已知的，那么大多数计算就可以在编译期完成。把曲线生成器写成一个宏，我们就可以将预先算好的值嵌入到代码中。这应该比把它们保存在数组里，这种更常规的优化方式甚至还要快。 一条贝塞尔曲线由四个点确定 — 两个端点和两个控制点。在两维平面上，这些点定义了曲线上所有点的 和 坐标的参数方程。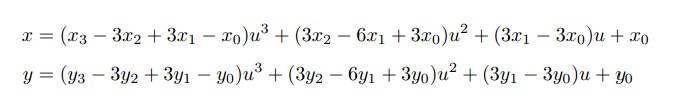如果两个端点是 (x0, y0) 和 (x3, y3)，以及两个控制点 (x1, y1) 和 (x2, y2)，那么曲线上点的方程就是：  如果我们用 `u` 在 `0` 和 `1` 之间的 `n` 个值来求值这个方程，我们就得到曲线上的 `n` 个点。举个例子，如果我们想把曲线画成 `20` 条线段，那么我们将用 `u = .05, .1, ..., .95` 来求值方程。对于`u` 在 `0` 或 `1` 上的求值是不需要的，因为如果 `u = 0` 它们将生成第一个端点 `(x0, y0)`，而当 `u = 1` 时它们将生成第二个端点 。 有个显而易见的优化方法是令 `n` 为定值，并提前计算 `n` 的指数，然后将它们存在一个 `(n - 1) x 3` 的数组里。通过把曲线生成器定义成一个宏，我们甚至可以做得更好。如果 `n` 在展开时已知，程序可以简单地展开成 `n` 条画线指令。那些预先计算好的 `n` 的指数，可以直接作为字面上的值插入到宏展开式里，而不必再保存在数组里了。 [示例代码 13.5] 中有一个实现了这一策略的曲线生成宏。它抛弃了立即画线的策略，而是将生成的点保存在数组里。当交互式地移动一条曲线时，每一个实例必须画两次：一次显示它，还有一次是在画下一个实例之前清除它。在两次画线之间，这些点必须保存在某个地方。 当 `n = 20` 时，`genbez` 展开成 21 个 `setf`。由于 的指数直接出现在代码里，我们省下了在运行期查找它们的开销，以及在启动时计算它们的开销。和 `u` 的指数一样，数组的索引以常量的形式出现在展开式中，所以对那些 `(setf aref)` 的边界检查也可以在编译期完成。 ### 13.3 应用 后面的章节将会提到其它一些宏，它们也使用了编译期的已知信息。其中一个很好的例子是 `if-match` (第 18.4 节)。在这个例子里，模式匹配器会比较两个序列，序列中可能含有变量，在比较的过程中，模式匹配器会分析是否存在某种给这些变量赋值的方式，可以让两个序列相等。`if-match`的设计显示：如果序列中的一个在编译期已知，并且只有这个序列里含有变量，那么匹配可以做得更高效。一个办法是在运行期比较两个序列，并构造列表来保存这个过程中建立的变量绑定，不过我们可以改成用宏，让宏生成的代码严格按照已知的序列来一一对照比较，同时可以在真正的 Lisp 变量里保存绑定。 第 19-24 章里描述的嵌入式语言，也在很大程度上利用了这些可在编译期获得的信息。由于嵌入式语言就是编译器，利用这些信息是其唯一自然的工作方式。这是一个普遍规律：越是精心设计的宏，它对其参数的约束也就越多，并且你利用这些约束来产生高效的代码的机会也就越好。 * * * **[示例代码 13.5] 生成贝塞尔曲线的宏** ~~~ (defconstant *segs* 20) (defconstant *du* (/ 1.0 *segs*)) (defconstant *pts* (make-array (list (1+ *segs*) 2))) (defmacro genbez (x0 y0 x1 y1 x2 y2 x3 y3) (with-gensyms (gx0 gx1 gy0 gy1 gx3 gy3) '(let ((,gx0 ,x0) (,gy0 ,y0) (,gx1 ,x1) (,gy1 ,y1) (,gx3 ,x3) (,gy3 ,y3)) (let ((cx (* (- ,gx1 ,gx0) 3)) (cy (* (- ,gy1 ,gy0) 3)) (px (* (- ,x2 ,gx1) 3)) (py (* (- ,y2 ,gy1) 3))) (let ((bx (- px cx)) (by (- py cy)) (ax (- ,gx3 px ,gx0)) (ay (- ,gy3 py ,gy0))) (setf (aref *pts* 0 0) ,gx0 (aref *pts* 0 1) ,gy0) ,@(map1-n #'(lambda (n) (let* ((u (* n *du*)) (u2 (* u u)) (u3 (expt u 3))) '(setf (aref *pts* ,n 0) (+ (* ax ,u3) (* bx ,u2) (* cx ,u) ,gx0) (aref *pts* ,n 1) (+ (* ay ,u3) (* by ,u2) (* cy ,u) ,gy0)))) (1- *segs*)) (setf (aref *pts* *segs* 0) ,gx3 (aref *pts* *segs* 1) ,gy3)))))) ~~~ `<span class="str" style="color: rgb(128, 0, 0);"> </span>`