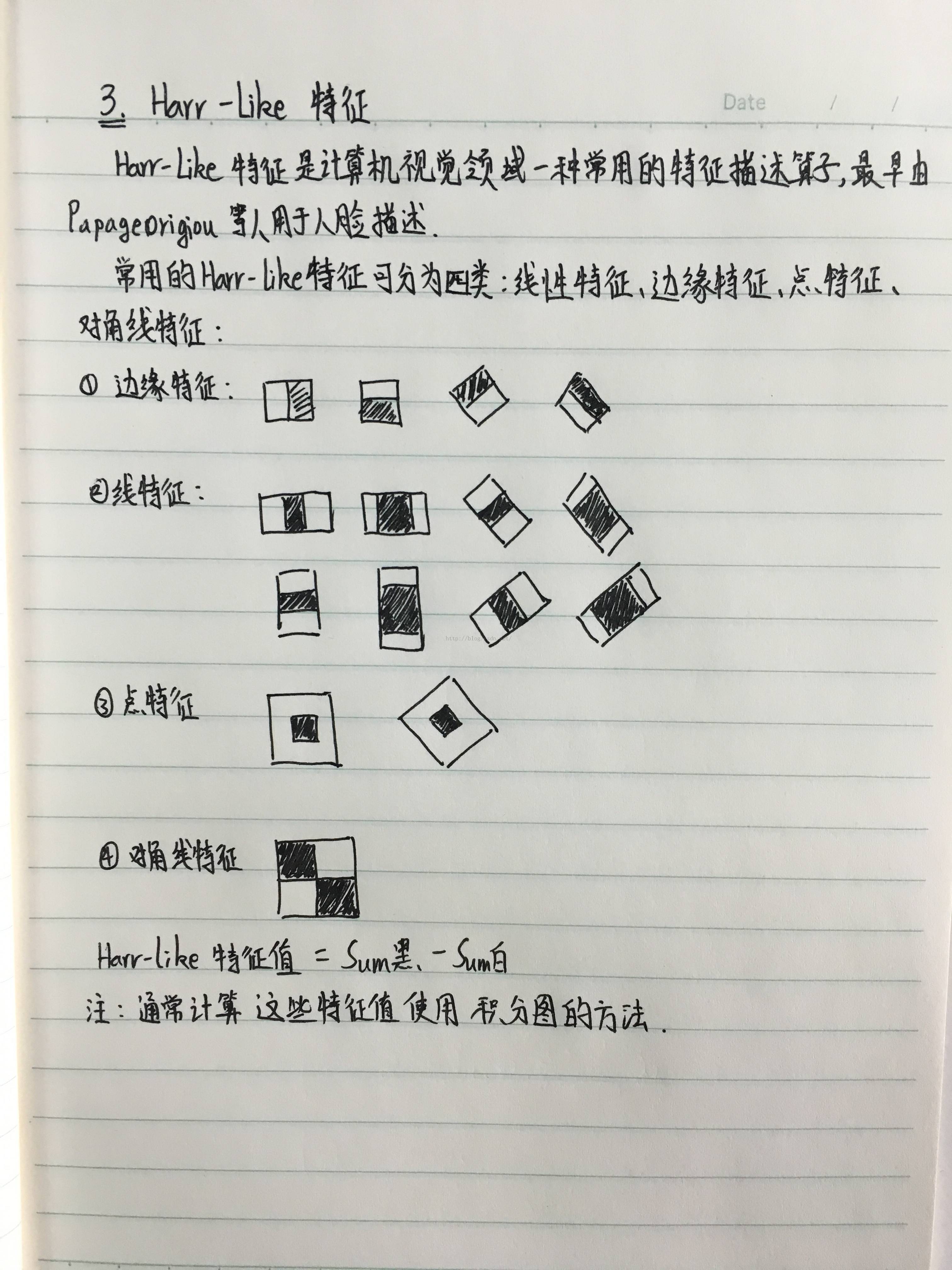
这里懒得写了，直接粘贴一张笔记照片好了，这个HarrLike很简单，相信大家一看就明白： 

> 本篇文章先介绍了提升放法和AdaBoost算法。已经了解的可以直接跳过。后面给出了AdaBoost算法的两个例子，附有详细计算过程。 ## 1、提升方法（来源于统计学习方法）   提升方法是一种常用的统计学习方法，应用十分广泛且有效。在分类问题中，它通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。提升算法基于这样一种思路：对于一个复杂任务来说，将多个专家的判断进行适当的综合所得出的判断，要比其中任何一个专家单独的判断好。实际上，就是“三个臭皮匠顶个诸葛亮”的道理。    历史上，Kearns和Valiant首先提出了“强可学习（strongly learnable）”和“弱可学习（weakly learnable）”的概念。指出：在概率近似正确（probably approximately correct，PAC）学习框架中，一个概念（一个分类），如果存在一个多项式的学习算法能够学习它，并且正确率很高，那么就称这个概念是强可学习的；一个概念，如果存在一个多项式的学习算法能够学习它，学习的正确率仅比随机猜测略好，那么就称这个概念是弱可学习的。非常有趣的是Schapire后来证明强可学习与弱可学习是等价的，也就是说，在PAC学习的框架下，一个概念是强可学习的充分必要条件是这个概念是弱可学习的。    这样一来，问题便成为，在学习中，如果已经发现了“弱学习算法”，那么能否将它提升（boost）为“强学习算法”。大家知道，发现弱学习算法通常要比发现强学习算法容易得多。那么如何具体实施提升，便成为开发提升方法时所要解决的问题。关于提升方法的研究很多，有很多算法被提出。最具代表性的是AdaBoost算法（AdaBoost algorithm）。    对于分类问题而言，给定一个训练样本集，求比较粗糙的分类规则（弱分类器）要比求精确的分类规则（强分类器）容易得多。提升方法就是从弱学习算法出发，反复学习，得到一系列弱分类器，然后组合这些分类器，构成一个强分类器。    这样。对于提升算法来说，有两个问题需要回答：一是在每一轮如何改变训练数据的权值分布；二是如何将弱分类器组合成为一个强分类器。 ## 2、AdaBoost算法   对于上一小节末尾提出的提升方法的两个问题，AdaBoost算法的做法是：1、提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。2、采用加权多数表决的方法。具体的，加大分类误差率小的弱分类器的权值，使其在表决中起较大的作用，减小分类误差大的弱分类器的权值，使其在表决中起较小的作用。    下面给出AdaBoost算法的公式： > 输入：训练数据集T={（x1,y1）,（x2,y2）,...（xN,yN）},其中xi∈X⊆Rn,yi∈Y={−1,+1};弱学习算法。  > 输出：最终分类器G(x)。  > （1）初始化训练数据的权值分布  >     > > D1=(w11,...,w1i,...,w1N),w1i=1N,i=1,2,...,N > >    注：第一次训练弱分类器时各个样本的权值是相等的。  > （2）对m=1,2，…,M     注：这里是个循环  > （a）使用具有权值分布Dm的训练数据集学习，得到基本分类器 > > Gm:X→{−1,+1} > > （b）计算Gm(x)在训练集上的分类误差率 > > em=P(Gm(xi)≠yi)=∑i=1nwmiI(Gm(xi)≠yi) > > 注：I(Gm(xi)≠yi)：不等函数I值为1.相等函数值为0。  > （c）计算Gm(x)的系数 > > αm=12log1−emem > > 这里的对数是自然对数。注：显然αm是em的调单减函数，这里就解释了为什么对于没有正确分类的数据要加大权值。  > （d）更新训练数据集的权值分布  > > > Dm+1=(wm+1,1,...,wm+1,i,...,wm+1,N) > > > > wm+1,i=wmiZmexp(−αmyiGm(xi))i=1,2,...,N > > 这里，Zm是规范化因子  > > > Zm=∑i=1Nwmiexp(−αmyiGm(xi)) > > 它使Dm+1成为一个概率分布。  > 注：自已比较Zm与wm+1,i的表达式，会发现这里的Zm就是在对wm+1,i进行归一化工作。  > （3）构建基本分类器的线性组合 > > f(x)=∑m=1MαmGm(x) > > 得到最终分类器 > > G(x)=sign(f(x))=sign(∑m=1MαmGm(x)) 注：对于增大分类错误数据的权值和分类误差计算的说明： > 1、Gm(x)的系数 > > αm=12log1−emem > > αm表示Gm(x)在最终分类器中的重要性。由αm的表达式可知，当em⩽12时，αm⩾0 ,并且αm随着em的减小而增大，所以分类误差越小的基本分类器在最终分类器中的作用越大。  > 2、计算基本分类器Gm(x)在加权训练数据集上的分类误差率： > > em=P(Gm(xi)≠yi)=∑Gm(xi)≠yiwmi > > ,这里，wmi表示第m轮中第i个实例的权值，∑Ni=1=1（因为权值利用Zm进行了归一化）。这表明，Gm(x)在加权的训练数据集上的分类误差是被Gm(x)误分类杨蓓的权值之和，由此可以看出数据权值分布Dm与基本分类器Gm(x)的分类误差率的关系。 ## 3、AdaBoost算法实例 下面提供一个例子帮助大家理解上面的概念。  给定如下表所示的训练数据。假设弱分类器由xv或x>v产生，其阈值使该分类器在 训练数据集上分类误差率最低。试用AdaBoost算法学习一个强分类器 | 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | | --- | :-: | --: | --- | --- | --- | --- | --- | --- | --- | --- | | x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | y | 1 | 1 | 1 | -1 | -1 | -1 | 1 | 1 | 1 | -1 | 解：初始化数据权值分布 D1=(w11,w12,...,w110) w1i=0.1,i=1,2,...,10 对m=1，  （a）在权值分布为D1的训练数据上，阈值v取2.5时分类误差率最低，故基本分类器为 G1(x)={1,x2.5−1,x>2.5 （b）显然序号为7、8、9数据产生了错误。G1(x)在训练数据集上的误差率等于将这3个数据的权值相加，即 e1=P(G1(xi)≠yi)=∑i=1nw1iI(G1(xi)≠yi)=0.3 注：I(G1(xi)≠yi)表示当G1(xi)不等于yi时 函数I()的值为1，等于时值为0。这里只有i=7,8,9时函数I值为1，其余为0。  （c）计算G1(x)的系数 α1=12log1−e1e1=12log1−e1e1=0.4236 （d）更新训练数据的权值分布： D2=(w21,...,w2i,...,w210) w2i=w1iZ1exp(−α1yiG1(xi)),i=1,2,...,10 Z1=∑i=1Nw1iexp(−α1yiG1(xi))=∑i=11−6,10110exp(−0.4236∗1)+∑i=79110exp(−0.4236∗−1)=0.4583+0.4582=0.9165 w2i=w1iZ1exp(−α1yiG1(xi))=1100.9165exp(−0.4236∗1)=0.07143,i=1,2,...,6,10 w2i=w1iZ1exp(−α1yiG1(xi))=1100.9165exp(−0.4236∗−1)=0.16667,i=7,8,9 D2=(w21,...,w2i,...,w210)=(0.07143,0.07143,0.07143,0.07143,0.07143,0.07143,0.16667,0.16667,0.16667,0.07143,) f1(x)=α1G1(x)=0.4236G1(x) 分类器sign[f1(x)]在训练数据集上有3个误分点。  对m=2，  （a）在权值分布为D2的训练数据上，阈值v取8.5时分类误差率最低，故基本分类器为 G2(x)={1,x8.5−1,x>8.5 （b）显然序号为4、5、6数据产生了错误。G2(x)在训练数据集上的误差率等于将这3个数据的权值相加，即 e2=P(G2(xi)≠yi)=∑i=1nw2iI(G2(xi)≠yi)=0.07143∗3=0.2143 注：I(G2(xi)≠yi)表示当G2(xi)不等于yi时 函数I()的值为1，等于时值为0。这里只有i=4,5,6时函数I值为1，其余为0。  （c）计算G2(x)的系数 α2=12log1−e2e2=12log1−e2e2=0.6496 （d）更新训练数据的权值分布： D3=(w31,...,w3i,...,w310) w3i=w2iZ2exp(−α2yiG2(xi)),i=1,2,...,10 Z2=∑i=1Nw2iexp(−α2yiG2(xi))=∑i=11−3,100.07143exp(−0.6496∗1)+∑i=790.16667exp(−0.4236∗1)+∑i=460.07143exp(−0.4236∗−1)=0.14922+0.26113+0.41032=0.82067 w3i=w2iZ2exp(−α2yiG2(xi))=0.071430.82067exp(−0.6496∗1)=0.0455,i=1,2,3,10 w3i=w2iZ2exp(−α2yiG2(xi))=0.071430.82067exp(−0.6496∗−1)=0.1667,i=4,5,6 w3i=w2iZ2exp(−α2yiG2(xi))=0.166670.82067exp(−0.6496∗1)=0.1060,i=7，8，9 D3=(w31,...,w3i,...,w310)=(0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455) f2(x)=α1G1(x)+α2G2(x)=0.4236G1(x)+0.6496G2(x) 分类器sign[f2(x)]在训练数据集上有3个误分点。  对m=3，  （a）在权值分布为D3的训练数据上，阈值v取5.5时分类误差率最低，故基本分类器为 G3(x)={1,x>5.5−1,x5.5 （b）显然序号为1、2、3、10的数据产生了错误。G3(x)在训练数据集上的误差率等于将这4个数据的权值相加，即 e3=P(G3(xi)≠yi)=∑i=1nw3iI(G2(xi)≠yi)=0.0445∗4=0.1820 注：I(G3(xi)≠yi)表示当G3(xi)不等于yi时 函数I()的值为1，等于时值为0。这里只有i=1,2,3,10时函数I值为1，其余为0。  （c）计算G3(x)的系数 α3=12log1−e3e3=12log1−e3e3=0.7514 （d）更新训练数据的权值分布： D4=(w41,...,w4i,...,w410) w4i=w3iZ3exp(−α3yiG3(xi)),i=1,2,...,10 Z3=∑i=1Nw3iexp(−α3yiG3(xi))=∑i=11−3,100.0455exp(−0.7514∗−1)+∑i=790.1060exp(−0.7514∗1)+∑i=460.1667exp(−0.7514∗1)=0.38593+0.15000+0.23590=0.77183 w4i=w3iZ3exp(−α3yiG3(xi))=0.04550.77183exp(−0.7514∗−1)=0.125,i=1,2,3,10 w4i=w3iZ3exp(−α3yiG3(xi))=0.16670.77183exp(−0.7514∗1)=0.102,i=4,5,6 w4i=w3iZ3exp(−α3yiG3(xi))=0.10600.77183exp(−0.7514∗1)=0.065,i=7，8，9 D4=(w41,...,w4i,...,w410)=(0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125) f3(x)=α1G1(x)+α2G2(x)+α3G3(x)=0.4236G1(x)+0.6496G2(x)+0.7514G3(x) 分类器sign[f3(x)]在训练数据集上有0个误分点。  于是最终分类器为：

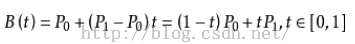
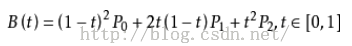
“[贝赛尔曲线](http://baike.baidu.com/view/4019466.htm)”是由法国数学家Pierre Bézier所发明，由此为计算机矢量图形学奠定了基础。它的主要意义在于无论是直线或曲线都能在数学上予以描述。贝塞尔曲线就是这样的一条曲线，它是依据四个位置任意的点坐标绘制出的一条[光滑曲线](http://baike.baidu.com/view/1981214.htm)。 线性公式 给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。这条线由下式给出：  且其等同于线性插值。 ##二次方公式 二次方贝兹曲线的路径由给定点P0、P1、P2的函数B（t）追踪：  TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。 ## 三次方公式 P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。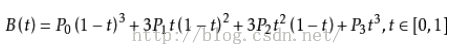 曲线的参数形式为：  现代的成象系统，如PostScript、Asymptote和Metafont，运用了以贝兹样条组成的三次贝兹曲线，用来描绘曲线轮廓。 ## 一般参数公式 阶贝兹曲线可如下推断。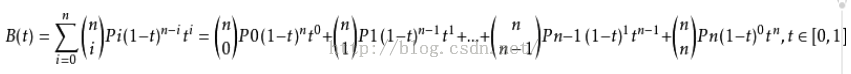给定点P0、P1、…、Pn，其贝兹曲线即：  如上公式可如下递归表达： 用表示由点P0、P1、…、Pn所决定的贝兹曲线。 用平常话来说，阶的贝兹曲线，即双阶贝兹曲线之间的插值。 ## 公式说明 1.开始于P0并结束于Pn的曲线，即所谓的端点插值法属性。 2.曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的，贝塞尔曲线是直线的充分必要条件是控制点共线。 3.曲线的起始点（结束点）相切于贝塞尔多边形的第一节（最后一节）。 4.一条曲线可在任意点切割成两条或任意多条子曲线，每一条子曲线仍是贝塞尔曲线。 5.一些看似简单的曲线（如圆）无法以贝塞尔曲线精确的描述，或分段成贝塞尔曲线（虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时，分成四段的贝兹曲线，可以小于千分之一的最大半径误差近似于圆）。 6.位于固定偏移量的曲线（来自给定的贝塞尔曲线），又称作偏移曲线（假平行于原来的曲线，如两条铁轨之间的偏移）无法以贝兹曲线精确的形成（某些琐屑实例除外）。无论如何，现存的启发法通常可为实际用途中给出近似值。 上述是百度百科中关于贝塞尔曲线的详细描述，对于它的应用，最直观的，就像PS里的钢笔工具，今天，我将给出它的代码实现： 1，贝塞尔类 ~~~ using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Drawing; using System.Drawing.Imaging; namespace TestDemo { unsafe class Bezier { Point PointCubicBezier(Point[] cp, float t) { float ax, bx, cx, ay, by, cy, tS, tC; cx = 1.0f * (cp[1].X - cp[0].X); bx = 3.0f * (cp[2].X - cp[1].X) - cx; ax = cp[3].X - cp[0].X - cx - bx; cy = 1.0f * (cp[1].Y - cp[0].Y); by = 3.0f * (cp[2].Y - cp[1].Y) - cy; ay = cp[3].X - cp[0].Y - cx - by; tS = t * t; tC = tS * t; int x = (int)((ax * tC) + (bx * tS) + (cx * t) + cp[0].X); int y = (int)((ay * tC) + (by * tS) + (cy * t) + cp[0].Y); return new Point(x, y); } public Bitmap DrawBezier(Bitmap src, Point[] cp) { Bitmap a = new Bitmap(src); int w = a.Width; int h = a.Height; BitmapData srcData = a.LockBits(new Rectangle(0, 0, w, h), ImageLockMode.ReadWrite, PixelFormat.Format24bppRgb); byte* p = (byte*)srcData.Scan0; float k = 0; k = 1.0f / (w - 1); Point temp; for (int i = 0; i < w; i++) { temp = PointCubicBezier(cp, (float)i * k); p[temp.X * 3 + temp.Y * srcData.Stride] = 0; p[temp.X * 3 + 1 + temp.Y * srcData.Stride] = 0; p[temp.X * 3 + 2 + temp.Y * srcData.Stride] = 0; } a.UnlockBits(srcData); return a; } } } ~~~ 2，主界面代码 ~~~ using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Windows.Forms; using System.Drawing.Imaging; namespace TestDemo { unsafe public partial class Form1 : Form { public Form1() { InitializeComponent(); string startupPath = System.Windows.Forms.Application.StartupPath; curBitmap = new Bitmap(startupPath + @"\mask.png"); //初始化 pa = new Point(button1.Location.X - pictureBox1.Location.X + 13, button1.Location.Y - pictureBox1.Location.Y + 11); pb = new Point(button2.Location.X - pictureBox1.Location.X + 13, button2.Location.Y - pictureBox1.Location.Y + 11); pc = new Point(button3.Location.X - pictureBox1.Location.X + 13, button3.Location.Y - pictureBox1.Location.Y + 11); pd = new Point(button4.Location.X - pictureBox1.Location.X + 13, button4.Location.Y - pictureBox1.Location.Y + 11); pictureBox1.Image = (Image)bezier.DrawBezier(curBitmap, new Point[] { pa, pb, pc, pd }); } #region 变量声明 //当前图像变量 private Bitmap curBitmap = null; private bool pointMoveStart = false; private Point movePoint; private Point pa; private Point pb; private Point pc; private Point pd; private Bezier bezier = new Bezier(); #endregion #region Response #endregion #region MouseClick private void pictureBox1_MouseMove(object sender, MouseEventArgs e) { if (pictureBox1.Image != null) { label1.Text = "X:" + e.X; label2.Text = "Y:" + e.Y; } } private void button1_MouseDown(object sender, MouseEventArgs e) { pointMoveStart = true; if (e.Button == MouseButtons.Left) movePoint = e.Location; } private void button1_MouseMove(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left && pointMoveStart) { button1.Location = new Point(button1.Location.X + e.X - movePoint.X, button1.Location.Y + e.Y - movePoint.Y); } } private void button1_MouseUp(object sender, MouseEventArgs e) { pointMoveStart = false; pa = new Point(button1.Location.X - pictureBox1.Location.X + 13, button1.Location.Y - pictureBox1.Location.Y + 11); pb = new Point(button2.Location.X - pictureBox1.Location.X + 13, button2.Location.Y - pictureBox1.Location.Y + 11); pc = new Point(button3.Location.X - pictureBox1.Location.X + 13, button3.Location.Y - pictureBox1.Location.Y + 11); pd = new Point(button4.Location.X - pictureBox1.Location.X + 13, button4.Location.Y - pictureBox1.Location.Y + 11); pictureBox1.Image = (Image)bezier.DrawBezier(curBitmap, new Point[] {pa, pb, pc, pd }); } private void button2_MouseDown(object sender, MouseEventArgs e) { pointMoveStart = true; if (e.Button == MouseButtons.Left) movePoint = e.Location; } private void button2_MouseMove(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left && pointMoveStart) { button2.Location = new Point(button2.Location.X + e.X - movePoint.X, button2.Location.Y + e.Y - movePoint.Y); } } private void button2_MouseUp(object sender, MouseEventArgs e) { pointMoveStart = false; pa = new Point(button1.Location.X - pictureBox1.Location.X + 13, button1.Location.Y - pictureBox1.Location.Y + 11); pb = new Point(button2.Location.X - pictureBox1.Location.X + 13, button2.Location.Y - pictureBox1.Location.Y + 11); pc = new Point(button3.Location.X - pictureBox1.Location.X + 13, button3.Location.Y - pictureBox1.Location.Y + 11); pd = new Point(button4.Location.X - pictureBox1.Location.X + 13, button4.Location.Y - pictureBox1.Location.Y + 11); pictureBox1.Image = (Image)bezier.DrawBezier(curBitmap, new Point[] { pa, pb, pc, pd }); } private void button3_MouseDown(object sender, MouseEventArgs e) { pointMoveStart = true; if (e.Button == MouseButtons.Left) movePoint = e.Location; } private void button3_MouseMove(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left && pointMoveStart) { button3.Location = new Point(button3.Location.X + e.X - movePoint.X, button3.Location.Y + e.Y - movePoint.Y); } } private void button3_MouseUp(object sender, MouseEventArgs e) { pointMoveStart = false; pa = new Point(button1.Location.X - pictureBox1.Location.X + 13, button1.Location.Y - pictureBox1.Location.Y + 11); pb = new Point(button2.Location.X - pictureBox1.Location.X + 13, button2.Location.Y - pictureBox1.Location.Y + 11); pc = new Point(button3.Location.X - pictureBox1.Location.X + 13, button3.Location.Y - pictureBox1.Location.Y + 11); pd = new Point(button4.Location.X - pictureBox1.Location.X + 13, button4.Location.Y - pictureBox1.Location.Y + 11); pictureBox1.Image = (Image)bezier.DrawBezier(curBitmap, new Point[] { pa, pb, pc, pd }); } private void button4_MouseDown(object sender, MouseEventArgs e) { pointMoveStart = true; if (e.Button == MouseButtons.Left) movePoint = e.Location; } private void button4_MouseMove(object sender, MouseEventArgs e) { if (e.Button == MouseButtons.Left && pointMoveStart) { button4.Location = new Point(button4.Location.X + e.X - movePoint.X, button4.Location.Y + e.Y - movePoint.Y); } } private void button4_MouseUp(object sender, MouseEventArgs e) { pointMoveStart = false; pa = new Point(button1.Location.X - pictureBox1.Location.X + 13, button1.Location.Y - pictureBox1.Location.Y + 11); pb = new Point(button2.Location.X - pictureBox1.Location.X + 13, button2.Location.Y - pictureBox1.Location.Y + 11); pc = new Point(button3.Location.X - pictureBox1.Location.X + 13, button3.Location.Y - pictureBox1.Location.Y + 11); pd = new Point(button4.Location.X - pictureBox1.Location.X + 13, button4.Location.Y - pictureBox1.Location.Y + 11); pictureBox1.Image = (Image)bezier.DrawBezier(curBitmap, new Point[] { pa, pb, pc, pd }); } #endregion } } ~~~ 结果图如下：   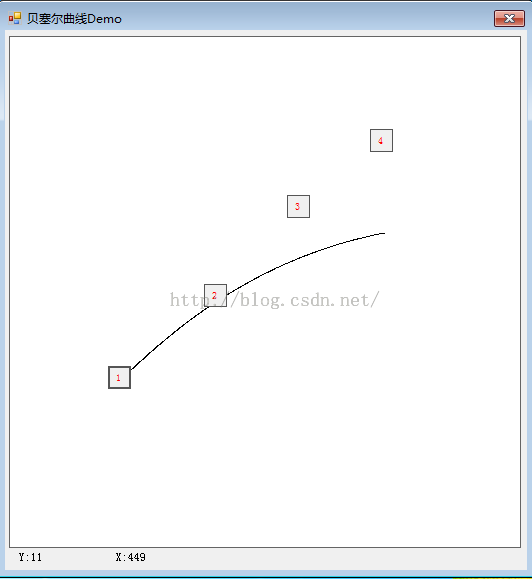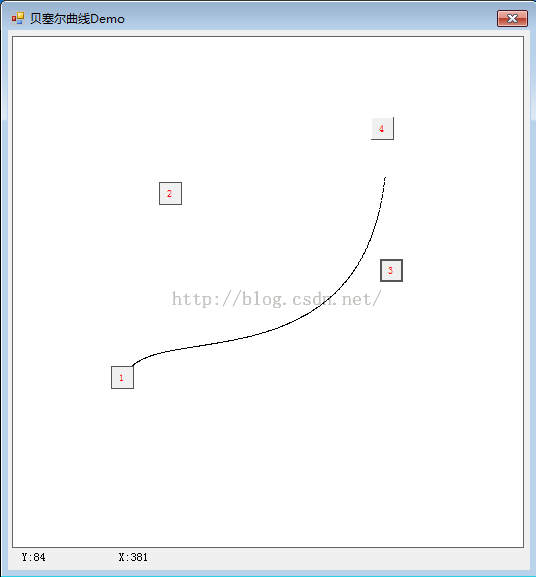最后给出完整C#代码DEMO：[点击打开链接](http://www.zealpixel.com/portal.php?mod=view&aid=134)        跟大家分享一下，希望大家喜欢！

PS中有个表面模糊的功能，这个功能可以在保留边缘的情况下对图像平坦区域进行模糊滤波，这个功能可以实现很好的磨皮效果，它的算法如下：  这个算法很简单，设置半径r，得到一个边长为(2r+1)的正方形窗口，那么窗口中心像素的像素值即为x，当然，对于像素的RGB三个分量，是需要分别计算的，因此这个算法的时间消耗比较大。 类似的算法还有双边滤波等，不过这类滤波普遍都比较耗时，虽然双边滤波已经可以在PC上实时，但是，在手机端还存在较大问题。 下面给出一些对比效果图：  原图                                                                                                                       表面模糊(r=20,y=28)  双边滤波(r=20) 可以看出，表面模糊的效果要比双边滤波效果更好一些！

一直以来，都有个想法，想要做一个属于自己的图像算法库，这个想法，在经过了几个月的努力之后，终于诞生了，这就是ZPhotoEngine算法库。  这个算法库目前包含两个模块：基础图像算法模块+滤镜模块，使用C语言实现，现在免费分享给大家，可以适用于PC/Android/Ios三大平台。 **1,基础图像算法模块** 这个模块，本人以Photoshop基础算法为原形，模拟出了PS大部分的基础算法。 为什么选择Photoshop算法？这个也是我的算法库一个优势，目前开源算法库多如牦牛，但是，能和PS媲美的，少之又少。毕竟现在从摄影照相，到工业设计等等，都在使用Photoshop，试想一下，对于一个图像特效团队来说，如果产品设计人员使用PS设计了一种图像特效，而特效团队又拥有PS的图像算法库，那么，实现这种特效岂不是SO EASY？这不单单是提高效率的问题，更是提高产品的质量，提高产能的事情！ 目前，基础算法模块都包含在ZPhotoEngine里面，其中包含了如下功能： **1.1，基础功能** ZPHOTO_SaturationAdjust饱和度调节 ZPHOTO_HueAndSaturationAdjust色相 饱和度调节 ZPHOTO_LightnessAdjust明度调节 ZPHOTO_LinearBrightContrastAdjust线性对比度亮度调节 ZPHOTO_NLinearBrightContrastAdjust非线性对比度亮度调节 ZPHOTO_AutoContrastAdjust自动对比度调节 ZPHOTO_AutoColorGradationAdjust自动色阶调节 ZPHOTO_CurveAdjust曲线调节调节 ZPHOTO_ColorLevelAdjust色阶调节 ZPHOTO_Posterize色调分离 ZPHOTO_OverExposure多度曝光 ZPHOTO_Invert反相 ZPHOTO_HistagramEqualize色调均化 ZPHOTO_Desaturate去色 ZPHOTO_Blackwhite黑白 ZPHOTO_Threshold阈值 ZPHOTO_FastGaussFilter高斯模糊 ZPHOTO_HighPass高反差保留 ZPHOTO_USM USM锐化 ZPHOTO_FindEdges查找边缘 ZPHOTO_ChannelMixProcess通道混合器 ZPHOTO_Fragment  碎片                              ZPHOTO_MotionBlur  运动模糊                          ZPHOTO_SurfaceBlur  表面模糊        ZPHOTO_RadialBlur旋转模糊 ZPHOTO_ZoomBlur缩放模糊 ZPHOTO_Relief浮雕 ZPHOTO_Mean平均 ZPHOTO_Mosaic马赛克 ZPHOTO_ColorBalance色彩平衡 ZPHOTO_Diffusion扩散                  **1.2，扩展功能** ZPHOTO_ColorTemperatureAdjust色温调节 ZPHOTO_ShadowAdjust阴影调节 ZPHOTO_HighlightAdjust高光调节 ZPHOTO_ExposureAdjust曝光调节 ZPHOTO_FastMeanFilter均值模糊 ZPHOTO_LSNBlur LSN模糊 ZPHOTO_SobelFilter Sobel边缘检测 ZPHOTO_ImageTransformation图像变换(缩放，旋转，镜像，翻转，仿射变换) ZPHOTO_RGBA2BGRA 图像RGBA转BGRA(Android定制) ZPHOTO_BGRA2RGBA 图像BGRA转RGBA(Android定制) **1.3，图层混合算法** ZPHOTO_ImageBlendEffect双图层混合接口 ZPHOTO_ModeDarken变暗图层混合模式 ZPHOTO_ModeMultiply正片叠底图层混合模式 ZPHOTO_ModeColorBurn颜色加深图层混合模式 ZPHOTO_ModeLinearBurn线性渐变图层混合模式 ZPHOTO_ModeDarkness深色图层混合模式 ZPHOTO_ModeLighten变亮图层混合模式 ZPHOTO_ModeScreen滤色图层混合模式 ZPHOTO_ModeColorDodge颜色减淡图层混合模式 ZPHOTO_ModeColorLinearDodge颜色线性减淡图层混合模式 ZPHOTO_ModeColorDodge浅色图层混合模式 ZPHOTO_ModeOverlay叠加图层混合模式 ZPHOTO_ModeSoftLight柔光图层混合模式 ZPHOTO_ModeHardLight强光图层混合模式 ZPHOTO_ModeVividLight亮光图层混合模式 ZPHOTO_ModeLinearLight线性光图层混合模式 ZPHOTO_ModePinLight点光图层混合模式 ZPHOTO_ModeSolidColorMixing实色图层混合模式 ZPHOTO_ModeDifference差值图层混合模式 ZPHOTO_ModeExclusion排除图层混合模式 ZPHOTO_ModeSubtraction减去图层混合模式 ZPHOTO_ModeDivide划分图层混合模式 ZPHOTO_ModeDesaturate去色模式 ZPHOTO_ModeColorInvert反相模式 **1.4，颜色空间转换** 包含RGB与YUV、YCbCr、XYZ、HSL、HSV、CMYK、YDbDr、YIQ、LAB等颜色空间的相互转换接口 **2,滤镜模块ZEffectEngine** 滤镜模块ZEffectEngine，也是我们算法库的一个特色。目前市面上的滤镜特效可谓是层出不穷，以Instagram/Camera360/美图秀秀+美颜相机等为代表，他们的滤镜几乎涵盖了我们的日常生活使用的一大半，而我们的ZEffectEngine，主要是参考借鉴他们的特效，取长补短，实现了差不多上百款滤镜，这些滤镜算法不仅效果不错，而且速度快，调用简单，极大方便了图像应用app的开发。 现在主要包含的滤镜如下： //////////////////////////模拟实现Instagram滤镜////////////////////////// FILTER_IDA_NONE            FILTER_IDA_1977            FILTER_IDA_INKWELL         FILTER_IDA_KELVIN          FILTER_IDA_NASHVILLE       FILTER_IDA_VALENCIA        FILTER_IDA_XPROII          FILTER_IDA_BRANNAN         FILTER_IDA_WALDEN          FILTER_IDA_ADEN            FILTER_IDA_ASHBY           FILTER_IDA_BROOKLYN        FILTER_IDA_CHARMES         FILTER_IDA_CLARENDON       FILTER_IDA_CREMA           FILTER_IDA_DOGPACH         FILTER_IDA_GINGHAM         FILTER_IDA_GINZA           FILTER_IDA_HEFE            FILTER_IDA_HELENA          FILTER_IDA_JUNO            FILTER_IDA_LARK            FILTER_IDA_LUDWIG          FILTER_IDA_MAVEN           FILTER_IDA_MOON            FILTER_IDA_REYES           FILTER_IDA_SKYLINE         FILTER_IDA_SLUMBER         FILTER_IDA_STINSON         FILTER_IDA_VESPER          //////////////////////////模拟实现美图滤镜////////////////////////// FILTER_IDB_WARMER                                       //一键美颜_暖暖 FILTER_IDB_CLEAR                                        //一键美颜_清晰 FILTER_IDB_WHITESKINNED                                 //一键美颜_白皙 FILTER_IDB_COOL                                         //一键美颜_冷艳 FILTER_IDB_ELEGANT                                      //LOMO_淡雅 FILTER_IDB_ANCIENT                                      //LOMO_复古 FILTER_IDB_GETE                                         //LOMO_哥特风 FILTER_IDB_BRONZE                                       //LOMO_古铜色 FILTER_IDB_LAKECOLOR                                    //LOMO_湖水 FILTER_IDB_SLLY                                         //LOMO_深蓝泪雨 FILTER_IDB_SLIVER                                       //格调_银色 FILTER_IDB_FILM                                         //格调_胶片 FILTER_IDB_SUNNY                                        //格调_丽日 FILTER_IDB_WWOZ                                         //格调_绿野仙踪 FILTER_IDB_LOVERS                                       //格调_迷情 FILTER_IDB_LATTE                                        //格调_拿铁 FILTER_IDB_JAPANESE                                     //格调_日系 FILTER_IDB_SANDGLASS                                    //格调_沙漏 FILTER_IDB_AFTEA                                        //格调_午茶 FILTER_IDB_SHEEPSCROLL                                  //格调_羊皮卷 FILTER_IDB_PICNIC                                       //格调_野餐 FILTER_IDB_ICESPIRIT                                    //美颜_冰灵 FILTER_IDB_REFINED                                      //美颜_典雅 FILTER_IDB_BLUESTYLE                                    //美颜_蓝调 FILTER_IDB_LOLITA                                       //美颜_萝莉 FILTER_IDB_LKK                                          //美颜_洛可可 FILTER_IDB_NUANHUANG                                    //美颜_暖黄 FILTER_IDB_RCOOL                                        //美颜_清凉 FILTER_IDB_JSTYLE                                       //美颜_日系人像 FILTER_IDB_SOFTLIGHT                                    //美颜_柔光 FILTER_IDB_TIANMEI                                      //美颜_甜美可人 FILTER_IDB_WEIMEI                                       //美颜_唯美 FILTER_IDB_PURPLEDREAM                                  //美颜_紫色幻想 FILTER_IDB_FOOD                                         //智能_美食           //////////////////////////模拟实现Camera360滤镜效果////////////////////////// FILTER_IDC_MOVIE                                        //LOMO_电影 FILTER_IDC_MAPLELEAF                                    //LOMO_枫叶 FILTER_IDC_COOLFLAME                                    //LOMO_冷焰 FILTER_IDC_WARMAUTUMN                                   //LOMO_暖秋 FILTER_IDC_CYAN                                         //LOMO_青色 FILTER_IDC_ZEAL                                         //LOMO_热情 FILTER_IDC_FASHION                                      //LOMO_时尚 FILTER_IDC_EKTAR                                        //弗莱胶片 -- Ektar FILTER_IDC_GOLD                                         //弗莱胶片 -- Gold FILTER_IDC_VISTA                                        //弗莱胶片 -- Vista FILTER_IDC_XTAR                                         //弗莱胶片 -- Xtra FILTER_IDC_RUDDY                                        //魔法美肤 -- 红润 FILTER_IDC_SUNSHINE                                     //魔法美肤 -- 暖暖阳光 FILTER_IDC_FRESH                                        //魔法美肤 -- 清新丽人 FILTER_IDC_SWEET                                        //魔法美肤 -- 甜美可人 FILTER_IDC_BLACKWHITE                                   //魔法美肤 -- 艺术黑白 FILTER_IDC_WHITENING                                    //魔法美肤 -- 自然美白 FILTER_IDC_JPELEGANT                                    //日系 -- 淡雅 FILTER_IDC_JPJELLY                                      //日系 -- 果冻 FILTER_IDC_JPFRESH                                      //日系 -- 清新 FILTER_IDC_JPSWEET                                      //日系 -- 甜美 FILTER_IDC_JPAESTHETICISM                               //日系 -- 唯美 FILTER_IDC_JPWARM                                       //日系 -- 温暖       //////////////////////////其他滤镜效果////////////////////////// FILTER_IDD_CARTOON                                      //卡通 FILTER_IDD_DARK                                         //暗调 FILTER_IDD_GLOW                                         //Glow FILTER_IDD_LOMO                                         //LOMO FILTER_IDD_NEON                                         //霓虹 FILTER_IDD_OILPAINT                                     //油画 FILTER_IDD_PUNCH                                        //冲印 FILTER_IDD_REMINISCENT                                  //怀旧 FILTER_IDD_SKETCH                                       //素描 FILTER_IDD_GRAPHIC                                      //连环画 FILTER_IDD_ABAOSE                                       //阿宝色 具体效果，简单分享几个：  原图  Instagram 1977滤镜效果  Instagram Kelvin滤镜效果  Instagram Nashville滤镜效果  Camera360  电影 滤镜效果  美图秀秀 紫色幻想 滤镜效果 以上就是目前ZPhotoEngine的主要功能，未来我们还将实现美颜等模块，来跟大家分享一下！ 最后，我给个下载连接： PC版DEMO下载连接：[点击打开链接](http://download.csdn.net/detail/trent1985/9247631) ZPhotoEngine库下载连接(包含PC版+Android版)：[点击打开链接](http://download.csdn.net/detail/trent1985/9237423) 注意：接口说明文档包含在下载连接中，大家有兴趣的可以根据说明文档来调用，实现自己的美图秀秀和PS！

最近在做头发检测的算法研究，在此做个总结。 发色检测目前主要的方法有：1，基于颜色空间统计的发色检测；2，基于概率模型、高斯模型的发色检测；3，基于神经网络机器学习的发色检测； 这三种方法中，最稳定的是第3种，但是该方法实现起来比较复杂，样本量大；最简单的是第1种，但是不精确； 说实在的，这三种方法，都没办法完美检测发色，也就是没办法避开同色的干扰，不过，今天本人还是要介绍一种，相对来讲，比较实用的方法： 本文的算法使用最简单的颜色空间模型和概率模型，参考文献为：《Hair color modeling and head detection》，在此文献基础上修改而成。 为了便于理解，本文直接介绍算法实现过程，相信大家对于没用的也不太想看呵呵，因此，对于理论，大家没兴趣的可以跳过。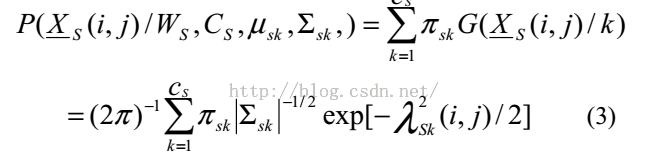 理论基础： 1，基于YCbCr颜色空间，对N个头发区域像素进行 采样统计，结果如下图：  2，将统计结果投影在Cb-Cr平面，结果如下：  3，采用高斯混合概率模型对发色的色度概率分布进行描述：   4，根据Cb和Cr的取值范围对当前像素进行肤色判断：                                                    if(Cb=115&&Cr>=115&&Cr<=143)                                                                             P(i,j)为发色                                                    else                                                                             P(i,j)非发色 上面1-4的过程即论文《Hair color modeling and head detection》中所介绍的方法，测试效果如下：   经过我的测试，论文中的方法检测准确率很低，这里简单放上两张测试图，大家可以看到，误检率很高，把较多的背景和肤色都检测成了发色。 因此，本人对这个算法进行了改进，添加了一个约束条件： 由于发色主要是黑色为主，偏黄或者偏白，这几种情况都跟RGB三分量中的R分量关系最密切，因此，本人添加了R约束：R<Th Th是经验值，这里我们实际使用中可以使用Th=60，这个值是我测试N张图的到的经验值，同时，也可以使用动态调节Th来获取发色区域，这里我 给出几张测试效果：  大家可以从效果上看出，改进的方法效果很不错，呵呵，最后改进后的判断条件如下：                                                    if(Cb=115&&Cr>=115&&Cr<=143&&R<Th)                                                                             P(i,j)为发色                                                    else                                                                             P(i,j)非发色                                                     默认值Th = 60 这里，给出C#代码如下： ~~~ public Bitmap HairD(Bitmap src, int k ) { Bitmap a = new Bitmap(src); Rectangle rect = new Rectangle(0, 0, a.Width, a.Height); System.Drawing.Imaging.BitmapData bmpData = a.LockBits(rect, System.Drawing.Imaging.ImageLockMode.ReadWrite, System.Drawing.Imaging.PixelFormat.Format24bppRgb); int stride = bmpData.Stride; unsafe { byte* pIn = (byte*)bmpData.Scan0.ToPointer(); byte* p; int R, G, B; double Cr, Cb, BrightV; for (int y = 0; y < a.Height; y++) { for (int x = 0; x < a.Width; x++) { p = pIn; R = p[2]; G = p[1]; B = p[0]; Cb = 128 - 37.797 * R / 255 - 74.203 * G / 255 + 112 * B / 255; Cr = 128 + 112 * R / 255 - 93.768 * G / 255 - 18.214 * B / 255; if (!(Cb >= 115 && Cb <= 141 && Cr >= 115 && Cr <= 143&&R<k)) { pIn[0] = (byte)255; pIn[1] = (byte)255; pIn[2] = (byte)255; } pIn += 3; } pIn += stride - a.Width * 3; } } a.UnlockBits(bmpData); return a; } ~~~ 最后，放上一个DEMO，下载地址：[点击打开链接](http://download.csdn.net/detail/trent1985/9217947)

本文转载wzwxiaozheng的白平衡算法，主要包括两部分：色温曲线和色温计算。原文http://blog.csdn.net/wzwxiaozheng/article/details/38434391 1，白平衡算法---色温曲线 本文大体讲解了白平衡的算法流程,适用于想了解和学习白平衡原理的筒子们. 一般情况下要实现AWB算法需要专业的图像和算法基础,本文力图通过多图的方式,深入浅出,降低初学者理解上的门槛,让大家都理解到白平衡算法流程. 看到这里还在继续往下瞄的同学,一定知道了色温的概念,并且知道sensor原始图像中的白色如果不经AWB处理,在高色温(如阴天)下偏蓝,低色温下偏黄,如宾馆里的床头灯(WHY!OTZ) (如下图).   下面这个T恤的图片非常经典,怎么个经典后续再说,不过大体可以看出有偏黄和偏蓝的情况.虽然如此,却已经是AWB矫正以后的效果.   所以,为了眼前的女神白富美在镜头里不变成阿凡达和黄脸婆,这时就需要白平衡来工作了. 流程原理很简单: 1,在各个色温下(2500~7500)拍几张白纸照片,假设拍6张(2500,3500…7500),可以称作色温照. 2,把色温照进行矫正,具体是对R/G/B通道进行轿正,让偏色的白纸照变成白色,并记录各个通道的矫正参数.    实际上只矫正R和B通道就可以,这样就得到了6组矫正参数(Rgain,Bgain). 3,上面是做前期工作,爱思考的小明发现,只要知道当前场景是什么色温,再轿正一下就可以了.事实上也就是如此. 所以,AWB算法的核心就是判断图像的色温,是在白天,晚上,室内,室外,是烈日还是夕阳,还是在阳光下的沙滩上.或者是在卧室里”暖味”的床头灯下. 之前拍了6张色温照以及6组矫正参数.可是6够么,当然不够, 插值一下可以得到无数个值,我们把点连成线, 得到了一个神奇的曲线------色温曲线.大概是下面这个样子.   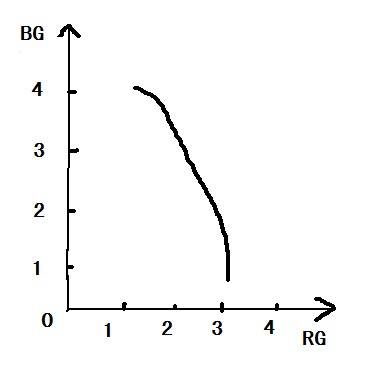上面提到了三个值(RG,BG,色温),这应该是个三维的.没关系,我们再来一条RG跟色温的曲线,这样只要知道色温,就知道RG,知道RG,就知道BG,知道RG,BG就能轿正了,yes!   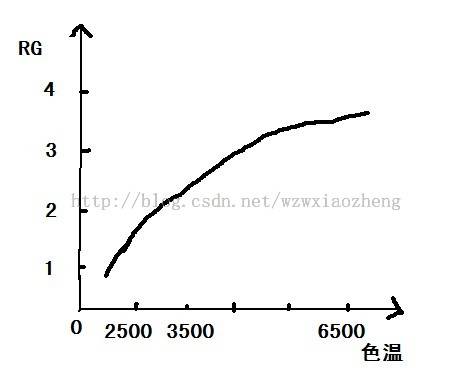至此,我们的前期工作已经全部做完了, 并得到了AWB的色温曲线,下一步只要计算得到当前色温,顺藤摸瓜就能得到当前的矫正参数(Rgain,Bgain),那白平衡的工作就作完了.(放心,当然没这么简单) 2，色温计算 本文主要讲解了白平衡算法中估算当前场景色温的流程. 色温计算的原理并不复杂,但是要做好,还是要细心做好每一步工作,这需要大量的测试,并对算法不断完善. 首先简单说一下流程: 1, 取一帧图像数据,并分成MxN块,假设是25x25,并统计每一块的基本信息(,白色像素的数量及R/G/B通道的分量的均值).  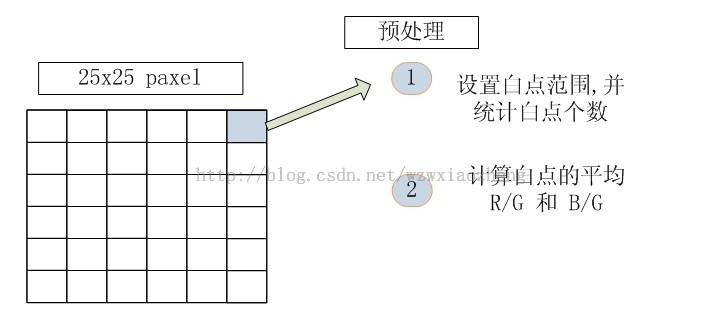2, 根据第1步中的统计值, 找出图像中所有的白色块,并根据色温曲线判断色温. 3, 至此,我们得出来了图像中所有的可能色温,如果是单一光源的话,可以取色温最多的,当作当前色温.    比如25x25=625 个块中,一共找出了100个有效白色块, 里面又有80个白色块代表了色温4500左右, 那当前色温基本就是4500.    根据4500色温得出的Rgain,Bgain来调整当前图像,就不会差(很多!).  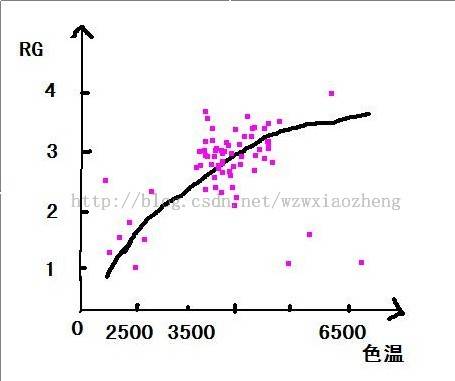下面我们再详细讲解一下,每一步中需要做的工作: 第1步, 计算每一块的基本信息.    关于白色像素统计,大家知道sensor原始图像是偏色的,怎么统计块中的白色点呢,那只有设置一个颜色范围,只要在范围中,就可以认为是白色像素,范围见下图:  统计白色像素个数的用处是,1,如果块中的白色像素太少,可以抛弃掉. 2,如果白色像素太多,多到每一个像素点都是,那也要抛弃掉,因为很可能在该区域过曝了    接着把统计到的白色像素点R/G/B取均值, 并得到该block 的R/G,  B/G值    至此,我们得到了每一块的白点数目及R/G,B/G的值. (请自动对应第1部分中色温曲线). 第二步 计算当前色温    这个比较复杂, 大自然绚丽多彩,景色万千. 上一步中统计的”白色点”难免会有失误的地方,比较常见的如黄色皮肤容易被误判为低色温下的白点,淡蓝色的窗帘,容易被误判为高色温下的白点,一张图中既有白色,也有黄色,也有蓝色的时候,是不是感觉情况有点复杂,其它的大家可继续脑补.    这时我们需要一定的策略来正确的判断出到哪个才是真的白.    通常我们会把取到的白色块,计算一下到曲线的距离,再设置相应的权重.话不多说,上个图大家就都明白了.  假设有上面这样一幅图,该图是在没有开AWB的前提下截取的,可以看到左边白色地方略有偏绿,当前色温是室内白炽灯,大概4000~5000k左右.(请忽略颜色不正的问题,我们在讨论白平衡) 下面我们就根据之前的统计信息和测量好的色温曲线进行白平衡矫正. 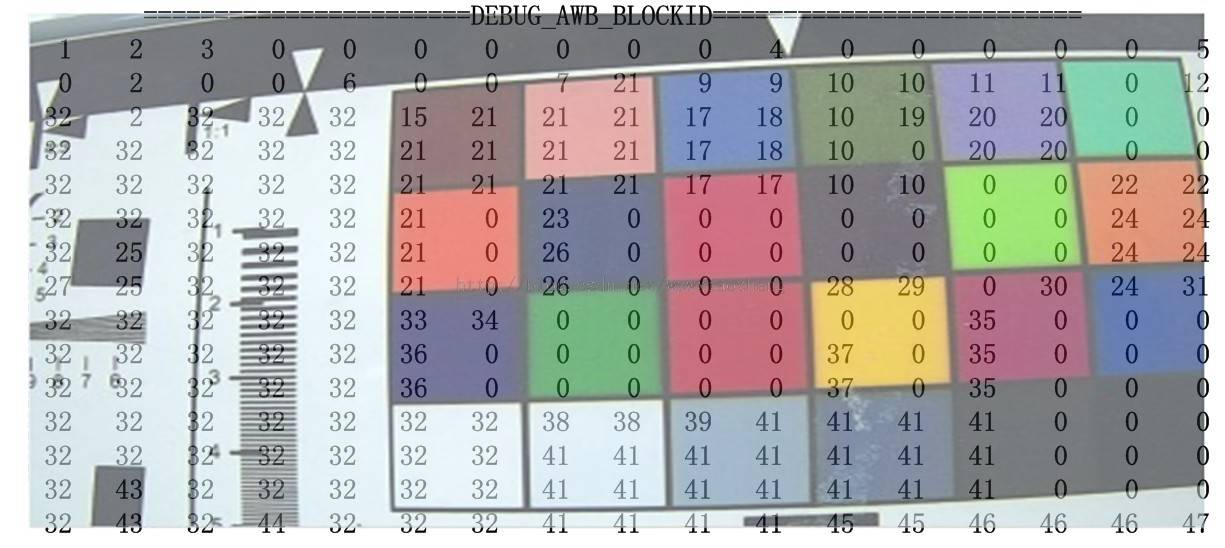首先要找出白区,如下图:  上面这个图中的数字标示出了检测到的白色区域,数字相同的表示一个白区,根据统计信息(白点数,rg/bg值)来区分的.可以看到有误判的地方,比如色卡左上第二块的肤色块.还有最右边从上面数第二块也是容易被判断成低色温白块的情况. 针对这种误判的情况,对不同块根据统计信息进行权重设置,以求让误判的区域对最终结果影响小一些.  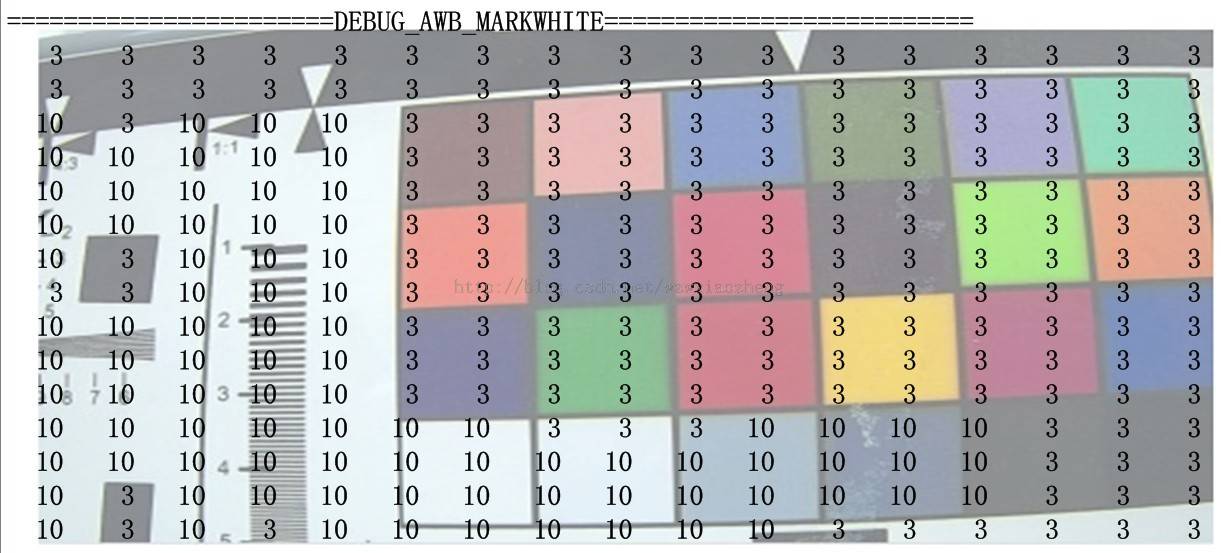上面这个图标注了权重,基本是根据统计信息中白点数来确定的.可以看到图中一片白色被标识了高权重.其它情况被标识了低权重. 权重高低一是看块中白色点数量,二是看rg/bg到色温曲线的距离.    通过上面两个图,大家就可以明显的找到白色区,并根据曲线来矫正,即使不通过曲线矫正,把白色区的r/g,b/g值向1趋近,让r=g=b,也会得到非常好的白平衡效果.如下图所示:  至此,白平衡的基本流程就讲完了,有图有真相,大家一定看着也方便. 总结一下:第一次做白平衡,感觉理论很简单,不用什么基础也能看懂.实际算法调试时,可谓差之毫厘,失之千里.总是感觉不由自主就走上歪路.中间参考了大量资料,比如网上有许多基于色温/灰度世界/白点检测的白平衡算法,实际个人感觉应该把它们都结合起来,让算法强壮,健康才是我们想要的. 还记得第一章中开始的那两张白色T恤的图么,算了,我再贴一下:  这张图可以理解为在多光源下的白平衡调整.阴影色温比阳光下色温要高一些,如果阳光下是5000k,阴影可能是7000k.有光就有影,它们经常出现在一个镜头里,对着其中一个色温调,另一边就会偏色.为了整体效果好,要把翘翘板平衡起来,可以加一些策略在里面。

以DZ论坛验证码识别为例： 对于比较复杂的验证码，比如DZ论坛最新的验证码，处理起来相对麻烦一些，但是原理还是和普通的识别一样的，无非多了个背景处理的方案，看如下对DZ论坛的验证码的识别的思路。  首先我们要去除它的背景，对于这样稍微复杂的背景，用过去的方法很难做到，上图的例子还不是很明显，我发现很多图片背景色和字母色近似，而且字母颜色是不断变化的，背景也是不断变化的。      那我初始的想法是找到图片中使用颜色最多的方法，于是我们用HSL表示各点颜色，接着进行统计，得到最大的几个峰值，这里便是图片中几个最丰富的颜色的L值得累加值。  其余的都可以认为是噪音，我们对每个峰值进行分割，得到如下图片  你看这样就把单个颜色图片分割出来了，接下来就是找到图片中除去黑色和白色后的图片：  然后进行灰化处理，阀值处理，降噪，得到：  接着根据边界检测出来的最左侧x位置，来排序字母顺序：  接下来的事情就轻车熟路了，把图片转成标准模板，通过少量学习就达到了95%以上的识别率： c:15 j:8 8:7 t:9 9:4 x:7 4:6 2:4 h:7 f:8 e:18 b:5 y:3 k:4 w:3 g:5 3:5 7:6 r:2 m:3 q:4 v:2 p:3 6:2 以上数据表示 c学习15次 j学习8次…  只要字符不粘连，大部分验证码干扰技术都是可以有办法，所以为什么google验证码看起来很简单，但是没有人能够很好的破解它得原因。 补充， 有一些字符加入杂点的问题，由于这种验证码不是很普遍，稍微做了研究  CY3E 这个图片3字中有杂点，其他没有，按照文章中介绍的办法，怎么知道这个3不是像其他颜色杂点一样的图片呢？  我觉得需要加入一个步骤，就是对每次过滤颜色生成出来的图片，进行填充 找到3的杂点原图：  然后我们进行[算法](http://cpro.baidu.com/cpro/ui/uijs.php?adclass=0&app_id=0&c=news&cf=1001&ch=0&di=128&fv=18&is_app=0&jk=ca709a7c2cee8241&k=%CB%E3%B7%A8&k0=%CB%E3%B7%A8&kdi0=0&luki=1&n=10&p=baidu&q=67051059_cpr&rb=0&rs=1&seller_id=1&sid=4182ee2c7c9a70ca&ssp2=1&stid=0&t=tpclicked3_hc&td=1740074&tu=u1740074&u=http%3A%2F%2Fwww%2Eeducity%2Ecn%2Flabs%2F649007%2Ehtml&urlid=0)填充：  这个图片与其他全部是杂点的图片之间的差别进行过滤，我考虑可以通过以下方法： 1、连贯点的宽度 2、连贯点的个数 这样剩下的就只剩下CY3E的过滤后的图片了。 至于字符倾斜的问题，我觉得完全可以在[机器学习](http://cpro.baidu.com/cpro/ui/uijs.php?adclass=0&app_id=0&c=news&cf=1001&ch=0&di=128&fv=18&is_app=0&jk=ca709a7c2cee8241&k=%BB%FA%C6%F7%D1%A7%CF%B0&k0=%BB%FA%C6%F7%D1%A7%CF%B0&kdi0=0&luki=2&n=10&p=baidu&q=67051059_cpr&rb=0&rs=1&seller_id=1&sid=4182ee2c7c9a70ca&ssp2=1&stid=0&t=tpclicked3_hc&td=1740074&tu=u1740074&u=http%3A%2F%2Fwww%2Eeducity%2Ecn%2Flabs%2F649007%2Ehtml&urlid=0)过程中，我们自己旋转正在学习的图片一定角度，例如从-10到+10度，只不过这样的学习库会大一些，但是就10个数字的验证码来说，这点性能损失应该可以忽略不计。

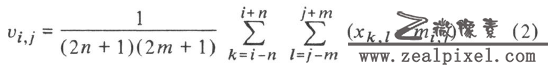图像锐化算法是图像处理中经常用到的基础算法，在Photoshop中，使用的是USM锐化，但是这种锐化速度比较慢，今天，介绍一种很简单的锐化算法：基于均值滤波的锐化算法。 本文要介绍的这个算法，来源于论文《Digital image enhancement and noise fitering by using local statistics》。 算法过程如下： 1，计算窗口范围内的均值： [](http://www.zealpixel.com/data/attachment/portal/201509/20/194532aj17ujsh7pj7u2j2.png) [](http://www.zealpixel.com/data/attachment/portal/201509/20/194532zdqb934lttwggb3u.png) 其中公式(1)为均值计算公式 ，公式(2)为方差计算公式，公式(2)暂时没有用到。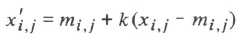 2，锐化公式： 2.1 锐化算法(1)： [](http://www.zealpixel.com/data/attachment/portal/201509/20/194532k75x97y05x99740z.png)   这个公式中x(i,j)表示(i,j)位置像素的锐化值，m(i,j)表示均值。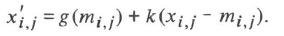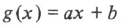 当k=0时，该算法表示均值滤波； 当0<k<1时，该算法表示低通滤波； 当k = 1时，该算法表示原图不变； 当k>1时，该算法表示高通滤波，即锐化算法； 2.2锐化算法(2)： [](http://www.zealpixel.com/data/attachment/portal/201509/20/194532dq85ts6873rvjsqq.png) [](http://www.zealpixel.com/data/attachment/portal/201509/20/194532hcsqth5yhlhq4ohx.png) 其中，g(x)表示一个线性变换，比如a=0.9,b=13,表示一个对比度增强。 当k=0时，该算法表示均值滤波； 当0<k<1时，该算法表示低通滤波； 当k = 1时，该算法表示原图不变； 当k>1时，该算法表示高通滤波，即锐化算法； 以上就是这个基于均值滤波的锐化算法，算法相当简单，易于实现，这里给出效果图： [](http://www.zealpixel.com/data/attachment/portal/201509/20/195613wl4zcod1sofyssl0.jpg) 原图 [](http://www.zealpixel.com/data/attachment/portal/201509/20/195612rrpzsswrwu0m8vax.png) 窗口半径radius=10,k=0.5效果图 [](http://www.zealpixel.com/data/attachment/portal/201509/20/195745ws585bcznsplsccc.png) 窗口半径radius=10,k=2效果图 最后，给出一个简单的DEMO：[基于均值滤波的锐化算法DEMO.zip](http://www.zealpixel.com/portal.php?mod=attachment&id=326)  跟大家分享一下！

# 人脸美妆之唇色检测算法研究 目前，随着人脸检测识别技术的日趋成熟，人脸美化技术的竞争也愈演愈烈，诸如移动设备应用类中的美咖相机，美图秀秀，Perfect 365，天天P图等等，这些应用无疑都在给人们的感官生活带来新的乐趣与新的体验，今天，我在这里给大家介绍一下，这些人脸美妆技术中一个必不可少的内容—-唇彩。 # 唇彩的实现分为以下几个步骤： * **嘴唇粗略检测** * **嘴唇精确检测** * **嘴唇涂色** * * * ##嘴唇粗略检测 嘴唇粗略检测的方法包括两种：  - 1\. 手动标记  手动标记往往是让用户自己移动特征点来定位嘴唇区域。这种方式略繁琐。  - 2\. 自动标记  自动标记往往是通过人脸识别技术，获取嘴唇的大概位置。人脸识别的技术目前已经日趋成熟，市面上诸如Face++等等，我们可以直接调用。  一般而言，目前的美妆软件中，首先使用自动标记，得到嘴唇的大概位置，如果无法检测到人脸，那么，会进一步让用户手动标记，这样给用户一种友好的用户体验。 ##嘴唇精确检测 嘴唇精确位置检测，关系到唇彩的准确度，进而影响美妆的整体效果。这里我介绍两种简单的嘴唇检测算法：  - 1\. 基于YIQ颜色空间的唇色检测算法  -参考论文：基于肤色和唇色信息的人脸检测方法的研究 ~~~ 算法原理：在YIQ颜色空间中，Y表示亮度信号，I和Q表示色度信号，Q分量代表的颜色变化正好覆盖了嘴唇的颜色范围，因此，通过对嘴唇样本的分析，得到嘴唇区域在YIQ颜色空间中的分布范围，以此来判断唇色。 YIQ颜色空间与RGB颜色空间对应关系如下： Y = 0.299 * r + 0.587 * g + 0.114 * b; I = 0.596 * r - 0.275 * g - 0.321 * b; Q = 0.212 * r - 0.523 * g + 0.311 * b; ~~~ 唇色统计的分布结果： | 分量 | 范围 | | --- | --- | | Y | [80,220] | | I | [12,78] | | Q | [7,25] | 对于当前像素P(x,y)，先转换为YIQ，然后分辨判断YIQ分量是否符合上述唇色分布结果，如果符合，则该像素为唇色像素。  -2\. 基于R,G分量分析的唇色检测算法  -参考文献：一种快速鲁棒的唇部检测方法  这个算法主要是提出了一个唇色判断公式：  logG(B0.391∗R0.609)T 这个公式的由来，是作者根据另外一篇文献TW Lewis.Lip feature extraction using ed exclusion.改进而来，至于原因什么的我们不用关心，我们关心的是如何最简单的理解与实现效果呵呵。  这篇论文中并没有给出T的取值，这里我给一个经验值:T= - 0.15;  公式中的B,R自然就是RGB颜色空间的对应分量了，对应于某个像素P(x,y)，如果符合这个公式，那么，这个像素就是唇色像素了。  -3\. 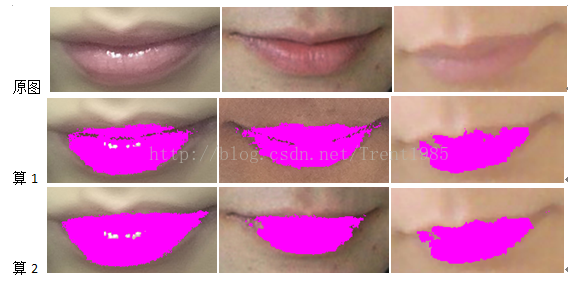算法效果  以上两种算法的效果如下所示：    以上两种方法是基于颜色空间唇色统计的方法，具有速度快，计算简单的特点，但是，由于统计的结果只代表大多数，并非全部，因此，这两种像素都不可能完全判断各种条件下的唇色像素，尤其是不同环境光条件下，容易出现误判。对于这个缺点，一般，我们会在人脸识别后，得到嘴唇的大概位置，在这个大概位置中，使用这些算法，这样一般就可以检测到相对准确的嘴唇区域了，后期在结合一些形态学算子，就可以得到准确的嘴唇区域了，对于唇彩涂色，也就完成了关键的一步了。 ##嘴唇涂色 嘴唇涂色就是根据嘴唇检测得到的准确区域，结合颜色Color的RGB值对其进行上色的过程。  嘴唇涂色一般使用YUV颜色空间，Y表示灰度值，UV表示颜色特征。假设嘴唇区域某像素P(x,y)，涂色值Color(R,G,B),我们先计算P的Y值，然后计算Color的UV值，这样我们就得到了涂色之后的目标YUV，在将这个YUV映射到RGB即可。 ##主要代码 这里放上嘴唇检测的代码程序，供大家参考： ~~~ public Bitmap LipsDetectBmp(Bitmap src) { Bitmap a = new Bitmap(src); int w = a.Width; int h = a.Height; BitmapData srcData = a.LockBits(new Rectangle(0, 0, a.Width, a.Height), ImageLockMode.ReadWrite, PixelFormat.Format32bppArgb); byte* p = (byte*)srcData.Scan0; int r = 0, g = 0, b = 0, offset = srcData.Stride - w * 4; double Y = 0, I = 0, Q = 0; double k = 0; for (int j = 0; j < h; j++) { for (int i = 0; i < w; i++) { b = p[0]; g = p[1]; r = p[2]; ////////////////Process image... //算法1 Y = 0.299 * r + 0.587 * g + 0.114 * b; I = 0.596 * r - 0.275 * g - 0.321 * b; Q = 0.212 * r - 0.523 * g + 0.311 * b; if ((Y >= 80 && Y <= 220 && I >= 12 && I <= 78 && Q >= 7 && Q <= 25)) { p[0] = (byte)255; p[1] = 0; p[2] = (byte)255; } //算法2 //k = Math.Log((double)g / (Math.Pow((double)b, 0.391) * Math.Pow((double)r, 0.609)));//使用算法 ////2时把算法1注释掉即可 //if (k < -0.15) //{ // p[0] = (byte)255; // p[1] = 0; // p[2] = (byte)255; //} p += 4; } p += offset; } a.UnlockBits(srcData); return a; } ~~~ ## 总结 以上就是美妆算法中的唇彩算法过程了，跟大家分享一下，共勉！有什么不明白的可以给我留言或邮件dongtingyue@163.com  最后，分享一个专业的图像处理网站，里面有很多源代码下载：  [http://www.zealpixel.com/portal.php](http://www.zealpixel.com/portal.php)

图像处理中的微分主要应用的是一阶微分和二阶微分两种。这里我们介绍一下图像中微分(求导)的概念。 1，高数中的导数  2，图像中的导数    上面针对一二阶导数进行了详细讲解，希望对大家有所帮助！ 最后，分享一个专业的图像处理网站，里面有很多源代码下载：http://www.zealpixel.com/portal.php [点击打开链接](http://http//www.zealpixel.com/portal.php)

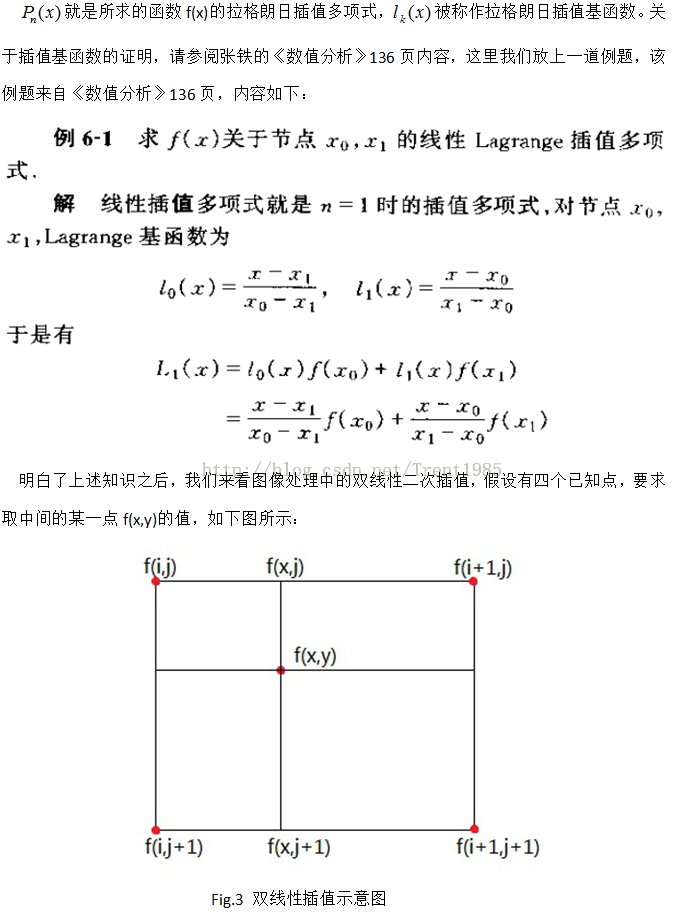
**[研究内容]** 目前比较常用的几种插值算法 **[正文]** 目前比较常用的插值算法有这么几种：最邻近插值，双线性二次插值，三次插值， Lanczos插值等等，今天我们来对比一下这几种插值效果的优劣。 **1，最邻近插值**     最邻近插值算法也叫做零阶插值算法，主要原理是让输出像素的像素值等于邻域内 离它距离最近的像素值。例如下图中所示，P1距离0灰度值像素的距离小于100灰度值的 距离，因此，P1位置的插值像素为0。这个算法的优点是计算简单方便，缺点是图像容 易出现锯齿。  **2，双线性二次插值**     在介绍双线性插值前，我们先介绍一下拉格朗日插值多项式。本文参考引用均来自 张铁的《数值分析》一书。       我们的方法是这样的，根据水平方向上的双线性二次插值，由f(I,j)和f(i+1,j)求取f(x,j)，由 f(I,j+1)和f(i+1,j+1)求取f(x,j+1)，然后再根据这两点的二次插值求取f(x,y)。   根据前面的例题，我们可以很容易的求取各点插值如下：                         f(x,j)=(i+1-x)f(I,j)+(x-i)f(i+1,j)               公式1-(4)                       f(x,j+1)=(i+1-x)f(I,j+1)+(x-i)f(i+1,j+1)           公式1-(5)                        f(x,y)=(i+1-y)f(x,j)+(y-j)f(x,j+1)               公式1-(6)   以上三式综合可以得到：   f(x,y)=(j+1-y)(i+1-x)f(I,j)+(j+1-y)(x-i)f(i+1,j)+(y-j)(i+1-x)f(I,j+1)+(y-j)(x-i)f(i+1,j+1)     公式1-(7)   我们令x=i+p,y=j+q得：   f(i+p,j+q)=(1-q)(1-p)f(I,j)+p(1-q)f(i+1,j)+q(1-p)f(I,j+1)+pqf(i+1,j+1)                公式1-(8)   上式即为数字图像处理中的双线性二次插值公式。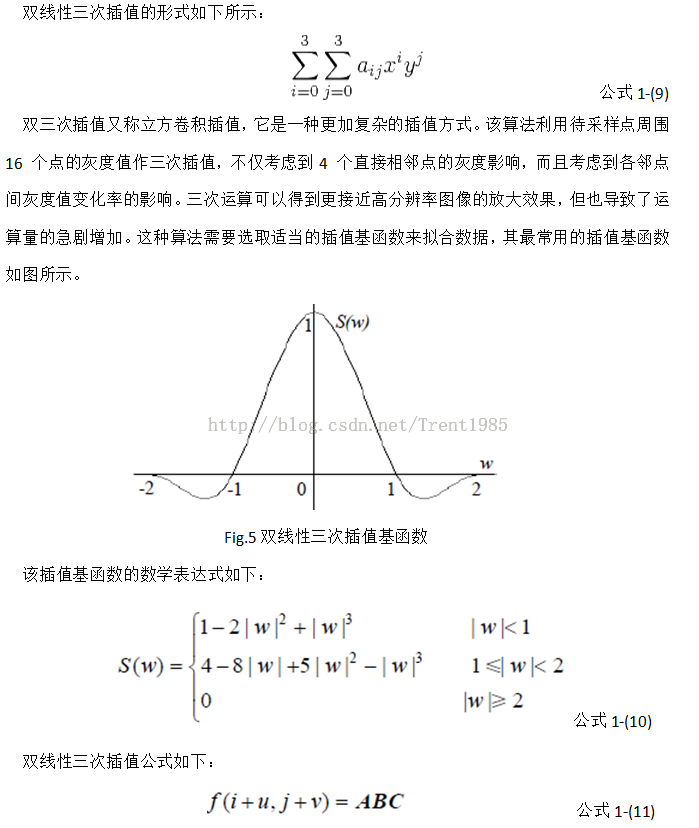 **3，双线性三次插值**  **4，Lanczos插值算法** 该算法的主要原理介绍地址：[http://en.wikipedia.org/wiki/Lanczos_resampling](http://en.wikipedia.org/wiki/Lanczos_resampling) 这里我大概介绍一下算法的流程： 这个算法也是一个模板算法，主要内容是计算模板中的权重信息。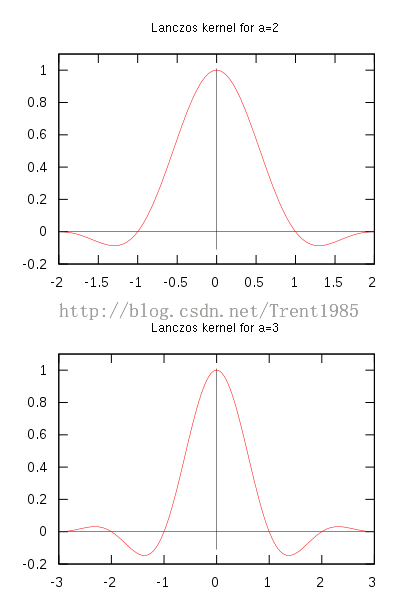 对于一维信息，假如我们输入点集为X，那么，Lanczos对应有个窗口模板Window，这个窗口中每个位置的权重计算如下：                          1-(12)                   Fig.6 Lanczos 通常，这个a取2或者3，a=2时，该算法适用于图像缩小插值；a=3时，该算法适用于放大插值；对应不同a值得Lanczos插值曲线如上图6所示；上述的公式分别为连续和离散的公式。我们根据输入点X的位置，确定对应window中不同位置的权重L(x)，然后对模板中的点值取加权平均，公式如下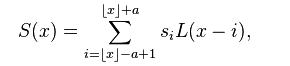：                                                     1-(13) 这个S(x)即为X处的插值结果。 根据上述一维插值，推广得到多维插值公式如下(这里以二维为例)：  1-(14) 上述内容是对不同插值算法简单的进行了介绍，如果不明白可以查找相关知识。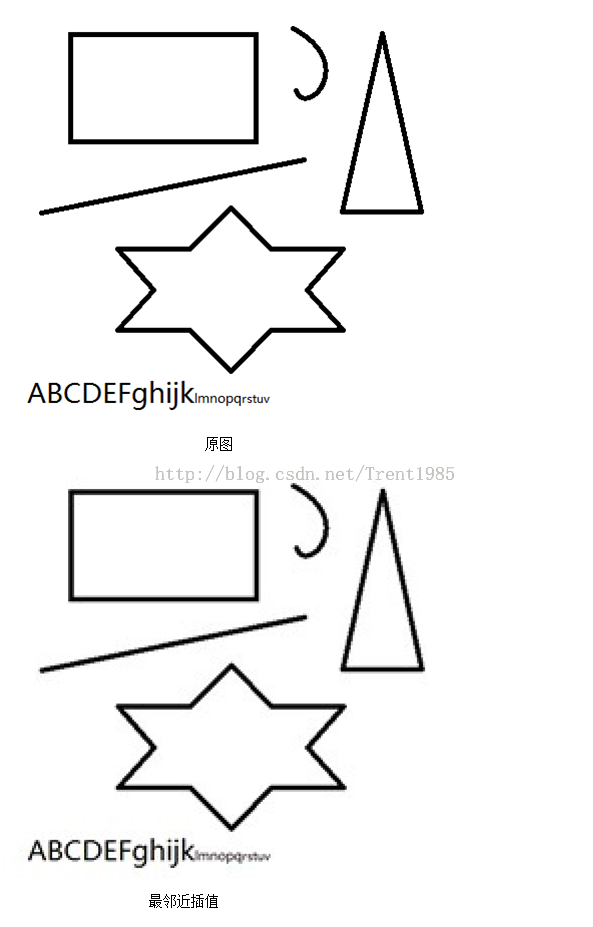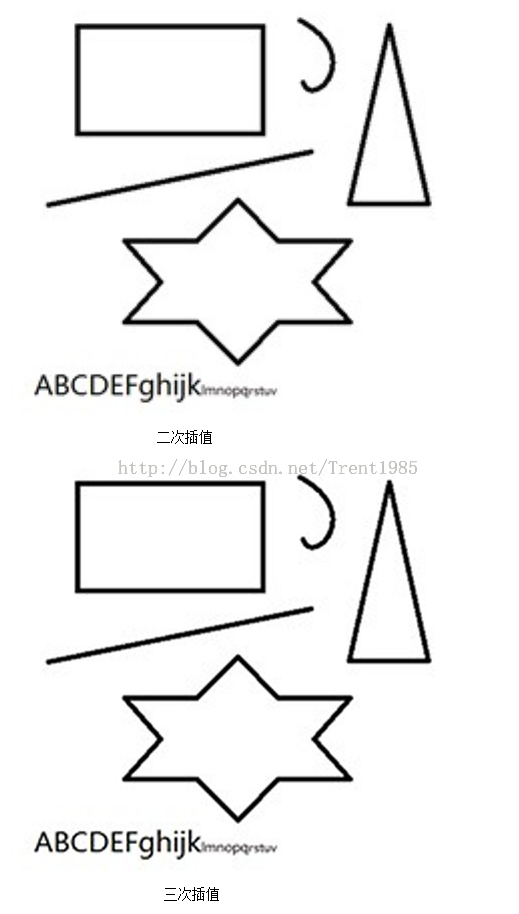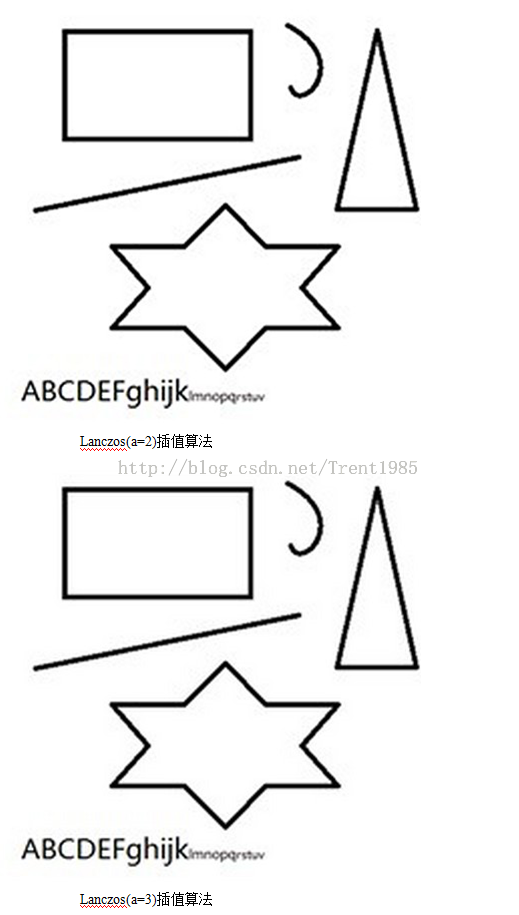 现在我们来看下相应的效果图：    上面的一组效果图均是先将原图缩小50%，然后使用不同算法放大到原图大小得到的。由上面这组图我们可以发现，效果最差的是最邻近插值算法，效果最好的是双线性三次插值，Lanczos算法跟三次插值大致一致； 由于编程语言不同，可能会造成耗时的差距，但是，对于同一种语言，统计得出：最邻近插值速度最快，三次插值速度最慢，而Lanczos算法与二次插值相仿。 综上，Lanczos插值具有速度快，效果好，性价比最高的优点，这也是目前此算法比较流行的原因。 最后，给出一个本人使用C#写的Lanczos代码，代码未经优化，仅供测试，这里的NP是对权重计算构建的映射表： ~~~ private Bitmap ZoomLanczos2Apply(Bitmap srcBitmap, double k) { Bitmap src = new Bitmap(srcBitmap); int width = src.Width; int height = src.Height; BitmapData srcData = src.LockBits(new Rectangle(0, 0, width, height), ImageLockMode.ReadWrite, PixelFormat.Format32bppArgb); byte* pS = (byte*)srcData.Scan0; int w = (int)((double)width * k); int h = (int)((double)height * k); Bitmap dst = new Bitmap(w, h, PixelFormat.Format32bppArgb); BitmapData dstData = dst.LockBits(new Rectangle(0, 0, w, h), ImageLockMode.ReadWrite, PixelFormat.Format32bppArgb); byte* d = (byte*)dstData.Scan0; int offset = dstData.Stride - w * 4; int x = 0, y = 0; double p = 0, q = 0; double n1 = 0, n2 = 0, n3 = 0, n4 = 0, nSum = 0; int p0 = 0, p1 = 0, p2 = 0, p3 = 0, p4 = 0, gray = 0; byte* temp = null; double[] NP1 = new double[] { -0.00623896218505032, -0.0122238956025722, -0.0179556611741633, -0.0234353793884155, -0.028664425422539, -0.0336444239814841, -0.0383772438642046, -0.0428649922670393, -0.0471100088344975, -0.0511148594680326, -0.0548823299036605, -0.0584154190695433, -0.0617173322348938, -0.0647914739617815, -0.0676414408716196, -0.0702710142382982, -0.0726841524200902, -0.0748849831426012, -0.0768777956451566, -0.0786670327031274, -0.0802572825387739, -0.0816532706332581, -0.0828598514525135, -0.0838820000996894, -0.0847248039068906, -0.0853934539789171, -0.0858932367016755, -0.0862295252278804, -0.0864077709525887, -0.0864334949910196, -0.086312279671003, -0.0860497600522689, -0.0856516154846428, -0.0851235612170509, -0.0844713400690516, -0.0837007141764163, -0.0828174568220629, -0.0818273443634177, -0.0807361482670294, -0.0795496272610035, -0.0782735196155422, -0.0769135355615895, -0.0754753498572731, -0.0739645945115212, -0.0723868516738999, -0.0707476466993797, -0.0690524413963838, -0.0673066274661114, -0.0655155201407567, -0.0636843520278618, -0.0618182671676555, -0.0599223153098279, -0.0580014464157926, -0.0560605053920726, -0.0541042270600343, -0.0521372313667693, -0.0501640188415028, -0.048188966301476, -0.0462163228108206, -0.0442502058955092, -0.0422945980170336, -0.0403533433070252, -0.0384301445645995, -0.0365285605177724, -0.0346520033498648, -0.0328037364913793, -0.0309868726774121, -0.0292043722702325, -0.0274590418462525, -0.0257535330461864, -0.0240903416868009, -0.0224718071322479, -0.0209001119225812, -0.0193772816566703, -0.0179051851263444, -0.0164855346982315, -0.015119886939392, -0.013809643482501, -0.0125560521259855, -0.0113602081641975, -0.0102230559423803, -0.00914539063088284, -0.00812786021277406, -0.00717096767873418, -0.00627507342282205, -0.00544039783246632, -0.00466702406578012, -0.00395490100907222, -0.00330384640720963, -0.00271355015928674, -0.00218357777186753, -0.00171337396189679, -0.00130226640121749, -0.000949469594490465, -0.00065408888218426, -0.000415124560192089, -0.000231476107535702, -0.000101946513534946, -0 }; double[] NP2 = new double[] { 0.999794398630316, 0.999177779156011, 0.998150695261436, 0.996714069021198, 0.994869189802256, 0.992617712728975, 0.989961656713271, 0.986903402052547, 0.983445687598761, 0.979591607502511, 0.975344607536654, 0.9707084810045, 0.965687364238256, 0.960285731693901, 0.954508390649264, 0.948360475512591, 0.941847441749449, 0.934975059436304, 0.927749406449645, 0.920176861299994, 0.912264095620641, 0.904018066321406, 0.895446007418168, 0.886555421549337, 0.877354071190877, 0.867849969581877, 0.858051371373022, 0.847966763010743, 0.83760485287009, 0.826974561149762, 0.816085009542993, 0.804945510698284, 0.793565557484247, 0.781954812073053, 0.770123094857198, 0.758080373214511, 0.745836750136481, 0.733402452735159, 0.720787820644003, 0.708003294328147, 0.695059403319663, 0.68196675439345, 0.668736019699406, 0.655377924866579, 0.641903237094975, 0.628322753250659, 0.614647287979759, 0.600887661856885, 0.587054689583387, 0.573159168250756, 0.559211865684328, 0.545223508882287, 0.531204772564777, 0.517166267847729, 0.503118531055783, 0.489072012688425, 0.47503706655321, 0.461023939079635, 0.447042758826945, 0.433103526198797, 0.419216103377392, 0.405390204489315, 0.391635386014941, 0.37796103745288, 0.364376372250524, 0.350890419011333, 0.33751201298905, 0.324249787878619, 0.311112167913061, 0.298107360275149, 0.285243347832182, 0.272527882201696, 0.259968477155437, 0.247572402368387, 0.235346677519141, 0.223298066747373, 0.211433073473617, 0.199757935586031, 0.188278620998268, 0.177000823582037, 0.165929959477376, 0.155071163783102, 0.144429287629353, 0.13400889563358, 0.123814263740785, 0.113849377448258, 0.104117930414501, 0.0946233234514916, 0.0853686638988765, 0.0763567653781721, 0.0675901479244855, 0.059071038492763, 0.050801371835042, 0.0427827917446759, 0.0350166526629909, 0.0275040216433488, 0.0202456806670952, 0.0132421293054104, 0.00649358772061002 }; double[] NP3 = new double[] { 0.00649358772061002, 0.0132421293054104, 0.0202456806670952, 0.0275040216433488, 0.0350166526629909, 0.0427827917446759, 0.0508013718350421, 0.059071038492763, 0.0675901479244855, 0.0763567653781721, 0.0853686638988765, 0.0946233234514916, 0.104117930414501, 0.113849377448258, 0.123814263740785, 0.13400889563358, 0.144429287629353, 0.155071163783102, 0.165929959477376, 0.177000823582037, 0.188278620998268, 0.199757935586031, 0.211433073473617, 0.223298066747373, 0.235346677519141, 0.247572402368387, 0.259968477155437, 0.272527882201696, 0.285243347832182, 0.298107360275149, 0.311112167913061, 0.324249787878619, 0.33751201298905, 0.350890419011333, 0.364376372250524, 0.37796103745288, 0.391635386014941, 0.405390204489315, 0.419216103377392, 0.433103526198797, 0.447042758826944, 0.461023939079634, 0.475037066553209, 0.489072012688425, 0.503118531055783, 0.517166267847729, 0.531204772564777, 0.545223508882287, 0.559211865684328, 0.573159168250756, 0.587054689583387, 0.600887661856885, 0.614647287979759, 0.628322753250659, 0.641903237094975, 0.655377924866579, 0.668736019699406, 0.68196675439345, 0.695059403319663, 0.708003294328147, 0.720787820644003, 0.733402452735159, 0.745836750136481, 0.758080373214511, 0.770123094857198, 0.781954812073053, 0.793565557484247, 0.804945510698284, 0.816085009542993, 0.826974561149762, 0.837604852870089, 0.847966763010743, 0.858051371373022, 0.867849969581877, 0.877354071190877, 0.886555421549337, 0.895446007418168, 0.904018066321406, 0.912264095620641, 0.920176861299994, 0.927749406449646, 0.934975059436304, 0.941847441749449, 0.948360475512591, 0.954508390649264, 0.960285731693901, 0.965687364238256, 0.9707084810045, 0.975344607536654, 0.979591607502512, 0.983445687598761, 0.986903402052547, 0.989961656713271, 0.992617712728975, 0.994869189802256, 0.996714069021198, 0.998150695261436, 0.999177779156011, 0.999794398630316 }; double[] NP4 = new double[] { -0, -0.000101946513534946, -0.000231476107535702, -0.000415124560192089, -0.00065408888218426, -0.000949469594490465, -0.0013022664012175, -0.00171337396189679, -0.00218357777186754, -0.00271355015928674, -0.00330384640720965, -0.00395490100907222, -0.00466702406578012, -0.00544039783246632, -0.00627507342282205, -0.00717096767873415, -0.00812786021277406, -0.00914539063088281, -0.0102230559423803, -0.0113602081641975, -0.0125560521259855, -0.013809643482501, -0.015119886939392, -0.0164855346982315, -0.0179051851263444, -0.0193772816566703, -0.0209001119225812, -0.0224718071322479, -0.0240903416868009, -0.0257535330461864, -0.0274590418462525, -0.0292043722702326, -0.0309868726774121, -0.0328037364913794, -0.0346520033498648, -0.0365285605177724, -0.0384301445645995, -0.0403533433070252, -0.0422945980170336, -0.0442502058955092, -0.0462163228108205, -0.048188966301476, -0.0501640188415028, -0.0521372313667693, -0.0541042270600343, -0.0560605053920726, -0.0580014464157926, -0.0599223153098279, -0.0618182671676555, -0.0636843520278618, -0.0655155201407567, -0.0673066274661114, -0.0690524413963838, -0.0707476466993797, -0.0723868516738999, -0.0739645945115212, -0.0754753498572731, -0.0769135355615895, -0.0782735196155421, -0.0795496272610035, -0.0807361482670294, -0.0818273443634177, -0.0828174568220629, -0.0837007141764163, -0.0844713400690516, -0.0851235612170509, -0.0856516154846428, -0.0860497600522689, -0.086312279671003, -0.0864334949910196, -0.0864077709525887, -0.0862295252278804, -0.0858932367016755, -0.0853934539789171, -0.0847248039068906, -0.0838820000996894, -0.0828598514525135, -0.0816532706332581, -0.0802572825387739, -0.0786670327031274, -0.0768777956451566, -0.0748849831426012, -0.0726841524200902, -0.0702710142382982, -0.0676414408716196, -0.0647914739617815, -0.0617173322348938, -0.0584154190695433, -0.0548823299036604, -0.0511148594680326, -0.0471100088344975, -0.0428649922670393, -0.0383772438642045, -0.0336444239814841, -0.028664425422539, -0.0234353793884155, -0.0179556611741633, -0.0122238956025722, -0.00623896218505032 }; for (int j = 0; j < h; j++) { q = (double)j / (double)k; y = (int)q; q = Math.Abs(q - (double)y); p0 = y * srcData.Stride; y = y >= height ? height - 1 : y; for (int i = 0; i < w; i++) { p = (double)i / (double)k; x = (int)p; p = Math.Abs(p - (double)x); temp = d + i * 4 + j * dstData.Stride; if (p != 0) { x = (x >= width - 3 ? width - 3 : x); x = x < 1 ? 1 : x; gray = (int)(p * 100.0) - 1; gray = Math.Max(0, gray); n1 = NP1[gray]; n2 = NP2[gray]; n3 = NP3[gray]; n4 = 1.0 - n1 - n2 - n3;// NP4[gray]; p2 = x * 4 + p0; p1 = p2 - 4; p3 = p2 + 4; p4 = p2 + 8; nSum = n1 + n2 + n3 + n4; gray = (int)((n1 * (double)((pS + p1)[0]) + n2 * (double)((pS + p2)[0]) + n3 * (double)((pS + p3)[0]) + n4 * (double)((pS + p4)[0]))); gray = Math.Max(0, Math.Min(255, gray)); temp[0] = (byte)gray; gray = (int)((n1 * (double)((pS + p1)[1]) + n2 * (double)((pS + p2)[1]) + n3 * (double)((pS + p3)[1]) + n4 * (double)((pS + p4)[1]))); gray = Math.Max(0, Math.Min(255, gray)); temp[1] = (byte)gray; gray = (int)((n1 * (double)((pS + p1)[2]) + n2 * (double)((pS + p2)[2]) + n3 * (double)((pS + p3)[2]) + n4 * (double)((pS + p4)[2]))); gray = Math.Max(0, Math.Min(255, gray)); temp[2] = (byte)gray; } else { x = x >= width ? width - 1 : x; gray = x * 4 + y * srcData.Stride; temp[0] = (byte)(pS + gray)[0]; temp[1] = (byte)(pS + gray)[1]; temp[2] = (byte)(pS + gray)[2]; } temp[3] = (byte)255; } } for (int i = 0; i < w; i++) { p = (double)i / (double)k; x = (int)p; p = Math.Abs(p - (double)x); x = x >= width ? width - 1 : x; for (int j = 0; j < h; j++) { q = (double)j / (double)k; y = (int)q; q = Math.Abs(q - (double)y); p0 = y * srcData.Stride; temp = d + i * 4 + j * dstData.Stride; if (q != 0) { y = y >= height - 3 ? height - 3 : y; y = y < 1 ? 1 : y; gray = (int)(q * 100.0) - 1; gray = Math.Max(0, gray); n1 = NP1[gray]; n2 = NP2[gray]; n3 = NP3[gray]; n4 = 1.0 - n1 - n2 - n3;// NP4[gray]; nSum = n1 + n2 + n3 + n4; p2 = x * 4 + y * srcData.Stride; p1 = p2 - srcData.Stride; p3 = p2 + srcData.Stride; p4 = p3 + srcData.Stride; gray = (int)((n1 * (double)((pS + p1)[0]) + n2 * (double)((pS + p2)[0]) + n3 * (double)((pS + p3)[0]) + n4 * (double)((pS + p4)[0]))); gray = Math.Max(0, Math.Min(255, gray)); temp[0] = (byte)gray; gray = (int)((n1 * (double)((pS + p1)[1]) + n2 * (double)((pS + p2)[1]) + n3 * (double)((pS + p3)[1]) + n4 * (double)((pS + p4)[1]))); gray = Math.Max(0, Math.Min(255, gray)); temp[1] = (byte)gray; gray = (int)((n1 * (double)((pS + p1)[2]) + n2 * (double)((pS + p2)[2]) + n3 * (double)((pS + p3)[2]) + n4 * (double)((pS + p4)[2]))); gray = Math.Max(0, Math.Min(255, gray)); temp[2] = (byte)gray; } else { y = y >= height ? height - 1 : y; gray = x * 4 + y * srcData.Stride; temp[0] = (byte)(pS + gray)[0]; temp[1] = (byte)(pS + gray)[1]; temp[2] = (byte)(pS + gray)[2]; } temp[3] = (byte)255; } } src.UnlockBits(srcData); dst.UnlockBits(dstData); return dst; } ~~~ 最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载： http://www.zealpixel.com/portal.php [点击打开链接](http://http//www.zealpixel.com/portal.php)

所谓滤镜，最初是指安装在相机镜头前过滤自然光的附加镜头，用来实现调色和添加效果。我们做的滤镜算法又叫做软件滤镜，是对大部分镜头滤镜进行的模拟，当然，误差也就再所难免，我们的宗旨只是无限逼近。也是这个原因，我们无法再现真实的拍摄场景，无法复原照片中未包含的信息，进而也难以实现某些特殊滤镜效果，诸如偏光镜和紫外线滤色镜（UV）的效果等等。     目前滤镜已经成为各种图像处理软件中必备功能，不同的滤镜效果，让我们的娱乐生活更加丰富多彩，对于任何一款软件滤镜效果的实现，我们可以归结为以下几个部分：     1，基本变换     这是滤镜效果的第一步，我们可以根据喜好，设计各种图像效果，这里所有的图像效果可以统一使用如下公式表示：     F(r,g,b,a)=f(r,g,b,a);     这个公式包含四个变换，即RGB颜色空间中RGB三个分量的变换以及透明度Alhpa的变换，这里我们简写为A的变换。     举个灰度变换的例子，它对应的F——f变换如下：     F(r) = b * 0.114 + g * 0.587 + r * 0.299;     F(g) = b * 0.114 + g * 0.587 + r * 0.299;     F(b) = b * 0.114 + g * 0.587 + r * 0.299;     F(a) = a;     这个灰度化也就是一个基本变换。有了这个基本变换，图像也就达到了一定的效果，但是，一些复杂的滤镜，并非简单的基本变换，而是一些复杂的效果叠加，因而也就有了 下面几个步骤。     2，晕影材质模板叠加     打开Instagram应用，我们会发现好多效果都有一些晕影，主要表现为图像四个角偏暗，中间正常或者偏亮，这个其实就是叠加了一定的材质的原因，这里我们介绍Instagram中经典的晕角材质模板，如下图所示：       像这样的材质我们如何叠加呢？这里就会使用一些叠加的算法，其中最常用的还是Photoshop中的混合图层算法，这些混合算法我在前面开始的博客中已经介绍，大家可以仔细研究，这一步主要是使用这些混合图层算法将材质模板和我们第一步基本变换得到的效果图进行混合，从而得出各种晕角效果。当然，这些混合算法并非唯一 ，你完全可自己尝试设计自己喜欢的混合图层算法。     这里给出Photoshop混合图层算法的链接[http://blog.csdn.net/trent1985/article/details/40891661](http://blog.csdn.net/trent1985/article/details/40891661)     3，风格模板叠加     这里的风格叠加与2中的材质叠加算法差不多，这里是说主要是个步骤问题，举个例子，为了实现老照片这个效果，我们第一步通过颜色基本变换，可以达到老照片的泛黄效果，但是还不逼真，因为老照片往往还有一些图像噪声，以及裂纹裂痕，这些效果如果你的算法无法实现，那么，你可以把这些通过PS做成一个模板，在这一步中叠加到图像上面，这样也就实现了更为逼真的效果。这里放上一个Instagram滤镜的风格模板图像如下所示：          4，相框模板叠加     有了1-3的步骤，一款滤镜效果就已经基本完成了，但有时候，你还会想要更加美观，那么你可以使用PS制作一些 精美的相框模板，叠加到滤镜效果上面，岂不是更加美观呢？     上面4个步骤也就是一款滤镜开发的步骤，当然这几个步骤不一定是一款滤镜必须的，可以是其中一个步骤，或者多个步骤，但是，归根结底，任何一款软件 滤镜的实现，应该都逃不出这几个步骤了吧。 只要我们掌握了这 几个步骤 ，那么多次尝试之后 ，总会开发出你 所 喜欢的滤镜效果的。     5，针对第一个步骤，介绍个快速实现方法：     对于任何一款滤镜，如果有基本变换这个步骤，那么我们都可以通过颜色映射构建一个映射表，然后通过查表来快速实现该变换效果，这样可以大大提高滤镜的速度，提升用户的体验。     颜色映射查表法的基本原理：在一张表中为每种颜色记录一个对应的映射目标颜色，当用查表法对一张照片做颜色映射时，只需要遍历照片的每个像素点，然后在表中找到该像素颜色对应的目标颜色，最后将该像素设置为目标颜色即可。查表法实现的前提是颜色的映射与周围的颜色无关，即一种颜色无论周围的颜色为何、无论其位于照片的哪个位置，其目标颜色都应该是相同的。     比如，RGB 可以表示的颜色数量为 `<span style="font-family: NSimsun;">256*256*256 = 16,777,216</span>`，如果要记录每种颜色的映射结果，那么颜色表需要 一千六百多万条记录，这显然无法应用到实际的工程中。为了简化起见，[Lev Zelensky](https://plus.google.com/105075060804712942346/posts)发表了一个基准颜色表，将每相近的 4 种颜色采用一条记录存储，这样颜色表只需要`<span style="font-family: NSimsun;">64 * 64 * 64 = 262,144</span>` 条记录。这个表如下：          注意：上表将 262,144 种颜色分为 8 个块，每块 `<span style="font-family: NSimsun;">64 * 64</span>` 格，每一格的颜色都不同。进行颜色映射时，首先使用数字图像处理软件对该基准颜色表应用要模拟的滤镜来生成映射表（如下图），然后对要处理的照片的每个像素，从基准颜色表中找到该像素颜色的位置，然后在映射表的相应位置就可以得到目的颜色。          使用这种方法，你的滤镜速度可以大大提升。     以上5个步骤就是我结合网络资源和个人总结的部分，喜欢滤镜开发的朋友们可以试试。     最后，介绍一个万能滤镜破解方法：     对于一款滤镜，我们构建一个模板，这个模板大小自定，可以看到滤镜效果即可，比如Instagram，它指定的图像大小是530*530，那么我们构建一个530*530大小的空白模板图像，假如我们要破解Hudson效果，那么，经过 我们分析，这个效果不仅包括基本变换，而且还有 晕影 ，甚至有 与位置相关的梯度模板，这个是破解的 难点，如何 破解，我们可以使用如下步骤：     1，构建256个530*530大小的模板，分别填充0-255种颜色，即灰度颜色；     2，将每个模板 进行Hudson效果处理，得到相应的映射模板库，这个库也就记录了所有的Hudson效果设置，包括基本变换，晕影，梯度等；     3，对于任何一张530*530大小的原始图像，我们只要从2中的模板库中找到对应颜色，对应位置的像素值，那么 这个值就是Hudson的效果；     这1-3步，示意图如下所示：           大家仔细想一下是不是这个道理，有得必有失，这话一点不错，这个方法可以破解 任何 一款滤镜，但是，牺牲的却是滤镜的效率，想一下，是不是呢？     好了 ，今天的介绍就到此结束了，大家有什么疑问可以联系我 ：     本人邮箱[dongtingyueh@163.com](mailto:dongtingyueh@163.com), QQ: 1358009172 **最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载：** [http://www.zealpixel.com/portal.php](http://www.zealpixel.com/portal.php)

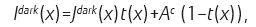
 对于图像去雾，这个研究内容，CSDN 中[33184777](http://my.csdn.net/laviewpbt)博友曾做了大量的研究，也写出了很多不错的博文，比如：[http://blog.csdn.net/laviewpbt/article/details/38711727](http://blog.csdn.net/laviewpbt/article/details/38711727) 令人深受启发。今天在网络上闲逛的时候，发现了一篇2014年的论文Fast Single-Image Defogging,基本上是暗通道的理论，不过算法比较简单，效果还行，特分享一下！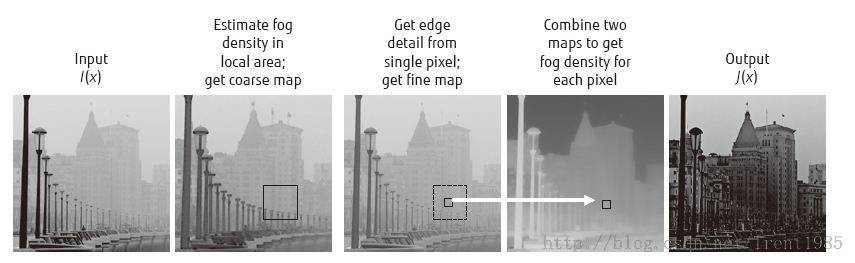     这篇论文中描述的具体过程如下：     1，去雾模型：          这个模型应该不用过多介绍了，目前大部分去雾算法都是根据这个模型进行的，这里依旧是基于暗通道理论，已知原始图像I(x)，求取清晰图像J(x)，未知参数A和t(x)     2，去雾过程图解：      当然这个图解是论文中的，至于效果的实现，本人并没有看到这么好的效果，不知作者做了什么优化。     3，实现2的具体步骤：     3.1 估计大气光A     大气光A的计算，这篇论文依然采用的是何凯明《[Single Image Haze Removal Using Dark Channel Prior](http://files.cnblogs.com/Imageshop/SingleImageHazeRemovalUsingDarkChannelPrior.rar)》中的计算方法，这里不再累赘。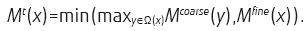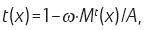    3.2计算Transmission map       这个y实际上就是一个局部窗口欧米伽内的像素，假设窗口半径为r，那么，min I(y)实际上就是用以r为半径的窗口，对R,G,B通道分别进行最小值滤波，然后选择R,G,B通道的滤波结果的最小值作为Mcoarse(x)；     3.3计算Fine map     这一步实际上是为了保留图像边缘，也就是保边滤波作用，比如双边滤波之类，为了达到保边作用，又要兼顾速度问题，作者直接使用了原始图像R,G,B通道的最小值          3.4计算M(x)     这一步，实际上是对Mcoarse进行了重定义，或者是修正：          对Mcoarse重新进行了一定半径窗口内的最大值滤波，然后取结果和Mfine(x)的最小值；     3.5计算t(x)          其中w是一个0到1之间的数值；     3.6计算清晰图像J(x)          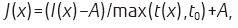其中t0是个很小的常量，防止分母为0； 以上就是整个论文的计算过程了，看起来很简单，对于最小值最大值滤波，已有实时算法，这里不再累赘，大家可以到[33184777](http://my.csdn.net/laviewpbt)的主页看一下，介绍的相当详细。       对于基本没有雾的图像，本人也做了测试（分别是原图和效果图）：   上面所有效果图，测试参数都是：滤波半径9，w=0.8，最后放上本人的代码，由于代码未进行优化，也没有使用实时滤波算法，因此，速度较慢，本人只是为了看下去雾效果而已，有兴趣的可以自己优化。 总体来看，效果还可以，没有发生颜色偏色，过渡失真之类，对于其他算法的效果，大家可以参考[33184777](http://my.csdn.net/laviewpbt)的博文。 代码地址：[http://download.csdn.net/detail/trent1985/7851061](http://download.csdn.net/detail/trent1985/7851061) 最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载： [http://www.zealpixel.com/portal.php](http://www.zealpixel.com/portal.php)

**[研究内容]** 二值图像距离变换 **[正文]** 二值图像距离变换的概念由Rosenfeld和Pfaltz于1966年在论文[1]中提出，目前广泛应用于计算机图形学，目标识别及GIS空间分析等领域，其主要思想是通过表识空间点(目标点与背景点)距离的过程，最终将二值图像转换为灰度图像。 距离变换按照距离的类型可以分为欧式距离变换(Eudlidean Distance Transfrom)和非欧式距离变换两种，其中，非欧式距离变换又包括棋盘距离变换(Chessboard Distance Transform)，城市街区距离变换(Cityblock Distance Transform)，倒角距离变换(Chamfer Distance Transform)等； 距离变换的主要过程： 假设一幅二值图像I，包含一个连通区域S，其中有目标集O和背景集B，距离图为D，则距离变换的定义如公式1-(1)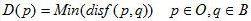：                                         1-(1) 具体步骤如下： 1，将图像中的目标像素点分类，分为内部点，外部点和孤立点。 以中心像素的四邻域为例，如果中心像素为目标像素(值为1)且四邻域都为目标像素(值为1)，则该点为内部点。如果该中心像素为目标像素，四邻域为背景像素(值为0)，则该中心点为孤立点，如下图Fig.1所示。除了内部点和孤立点之外的目标区域点为边界点。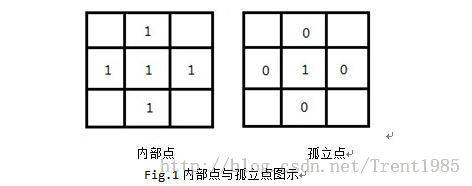  2，计算图像中所有的内部点和非内部点，点集分别为S1，S2。 3，对于S1中的每一个内部点(x,y)，使用距离公式disf()计算骑在S2中的最小距离，这些最小距离构成集合S3。 4，计算S3中的最大最小值Max,Min。 5，对于每一个内部点，转换后的灰度值G计算如下公式1-(2)所示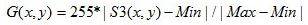：     1-(2) 其中，S3(x,y)表示S1中的点(x,y)在S2中的最短距离 6，对于孤立点保持不变。 在以上距离变换的过程中，距离函数disf()的选取如果是欧式距离，则该距离变换称为欧式距离变换，依次类推。对于距离的求取，目前主要的距离公式如下： 欧式距离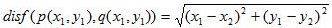：      1-(3) 棋盘距离：                1-(4) 城市街区距离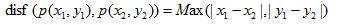：   1-(5) 对于欧式距离变换，由于其结果准确，而计算相比非欧式距离变换较为复杂，因此，出现了较多的快速欧式距离变换算法，这里笔者介绍一种基于3*3模板的快速欧式距离变换算法(文献2)，具体过程如下：  1，按照从上到下，从左到右的顺序，使用模板如图Fig.2，依次循环遍历图像I，此过程称为前向循环。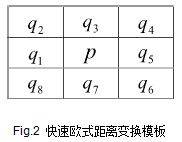  对于p对应的像素(x,y)，我们计算五个距离：d0,d1,d2,d3,d4：     d0=p(x,y)     d1=p(x-1,y)+disf((x-1,y),(x,y))     d2=p(x-1,y-1)+disf((x-1,y-1),(x,y))     d3=p(x,y-1)+disf((x,y-1),(x,y))     d4=p(x+1,y-1)+disf((x-1,y-1),(x,y))     则p(x,y)变换后的像素值为：     p(x,y)=Min(d0,d1,d2,d3,d4);     使用上述算法得到图像I'。     2，按照从下到上，从右到左的顺序，使用Fig.2所示模板依次循环遍历图像I’，此过程称为后向循环。 对于p对应的像素(x,y)，我们计算五个距离：d0,d5,d6,d7,d8：     d0=p(x,y)     d5=p(x+1,y)+disf((x+1,y),(x,y))     d6=p(x+1,y+1)+disf((x+1,y+1),(x,y))     d7=p(x,y+1)+disf((x,y+1),(x,y))     d8=p(x-1,y+1)+disf((x-1,y+1),(x,y))     则p(x,y)后向变换后的像素值为：     p(x,y)=Min(d0,d5,d6,d7,d8);     使用上述算法得到的图像即为距离变换得到的灰度图像。     以上过程即文献2所示快速欧式距离变换算法。如果我们需要非欧氏距离变换的快速算法，只需要修改文献2算法中的欧式距离公式disf()为非欧式距离公式，如棋盘距离，城市街区距离等，过程依次类推。 对于欧式距离变换算法，相关学者研究了速度更快的倒角距离变换算法，来近似欧式距离变换的效果。具体过程如下：     1，使用前向模板如图Fig.3中左边3*3模板，对图像从上到下，从左到右进行扫描，模板中心0点对应的像素值如果为0则跳过，如果为1则计算模板中每个元素与其对应的像素值的和，分别为Sum1,Sum2,Sum3,Sum4，Sum5，而中心像素值为这五个和值中的最小值。     2，使用后向模板如图Fig.3中右边的3*3模板，对图像从下到上，从右到左进行扫描，方法同上。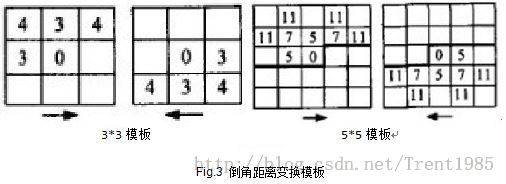     3，一般我们使用的倒角距离变换模板为3*3和5*5，分别如下图所示：  [实验结果]     实验采用512*512大小的图像进行测试，测试PC为64位，Intel(R) Core(TM) i5-3230 CPU, 2.6GHz, 4G RAM，运行环境为VS2008，C#。     实验结果如下：                                                                       (a)原图                                              (b)Euclidean Distance Transfrom                                                     (c) Cityblock  Distance Transfrom                                                (d) Chessboard Distance Transform                                                (e) Chamfer Distance Transform 对于以上欧式距离变换与非欧式距离变换，我们做了时间分析，结果如下：   对于Table 1的数据，是通过计算50张512*512大小的图像得到的平均结果，代码未曾优化，距离变换结果均做了均衡化处理，对于不同配置，不同程序语言可能存在一定差异，总体而言，基于3*3模板的倒角距离变换速度最快，大概是欧氏距离快速算法的一半。 [参考文献] [1] Rosenfeld A,PfaltzJ.L, Sequential operations in digital pic ture processing. Journal of ACM,1966, 13(4):471-494. [2] Frank Y.Shih,Yi-Ta Wu, Fast Euclidean distance transformation in two scans using a 3*3 neighborhood. Journal of Computer Vision and Image Understanding 2004,195–205. 附录 本人使用C#编写的代码如下： 本人的完整demo，包含参考文献，测试图像，地址：[http://download.csdn.net/detail/trent1985/6841125](http://download.csdn.net/detail/trent1985/6841125) ~~~ /// <summary> /// Distance transform for binary image. /// </summary> /// <param name="src">The source image.</param> /// <param name="distanceMode">One parameter to choose the mode of distance transform from 1 to 3, 1 means Euclidean Distance, 2 means CityBlock Distance, 3 means ChessBoard Distance.</param> /// <returns>The result image.</returns> public Bitmap DistanceTransformer(Bitmap src, int distanceMode) { int w = src.Width; int h = src.Height; double p0 = 0, p1 = 0, p2 = 0, p3 = 0, p4 = 0, p5 = 0, p6 = 0, p7 = 0, p8 = 0, min = 0; int mMax = 0, mMin = 255; System.Drawing.Imaging.BitmapData srcData = src.LockBits(new Rectangle(0, 0, w, h), System.Drawing.Imaging.ImageLockMode.ReadOnly, System.Drawing.Imaging.PixelFormat.Format24bppRgb); unsafe { byte* p = (byte*)srcData.Scan0.ToPointer(); int stride = srcData.Stride; byte* pTemp; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x - 1) * 3 + (y - 1) * stride; p2 = pTemp[0] + GetDistance(x, y, x - 1, y - 1, distanceMode); pTemp = p + x * 3 + (y - 1) * stride; p3 = pTemp[0] + GetDistance(x, y, x, y - 1, distanceMode); pTemp = p + (x + 1) * 3 + (y - 1) * stride; p4 = pTemp[0] + GetDistance(x, y, x + 1, y - 1, distanceMode); pTemp = p + (x - 1) * 3 + y * stride; p1 = pTemp[0] + GetDistance(x, y, x - 1, y, distanceMode); min = GetMin(p0, p1, p2, p3, p4); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } for (int y = h - 1; y > 0; y--) { for (int x = w - 1; x > 0; x--) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x + 1) * 3 + y * stride; p5 = pTemp[0] + GetDistance(x, y, x + 1, y, distanceMode); pTemp = p + (x + 1) * 3 + (y + 1) * stride; p6 = pTemp[0] + GetDistance(x, y, x + 1, y + 1, distanceMode); pTemp = p + x * 3 + (y + 1) * stride; p7 = pTemp[0] + GetDistance(x, y, x, y + 1, distanceMode); pTemp = p + (x - 1) * 3 + (y + 1) * stride; p8 = pTemp[0] + GetDistance(x, y, x - 1, y + 1, distanceMode); min = GetMin(p0, p5, p6, p7, p8); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); mMax = (int)Math.Max(min, mMax); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } mMin = 0; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { pTemp = p + x * 3 + y * stride; if (pTemp[0] != 0) { int temp = pTemp[0]; pTemp[0] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[1] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[2] = (byte)((temp - mMin) * 255 / (mMax - mMin)); } } } src.UnlockBits(srcData); return src; } } /// <summary> /// Chamfer distance transform(using two 3*3 windows:forward window434 300 000;backward window 000 003 434). /// </summary> /// <param name="src">The source image.</param> /// <returns>The result image.</returns> public Bitmap ChamferDistancetransfrom(Bitmap src) { int w = src.Width; int h = src.Height; double p0 = 0, p1 = 0, p2 = 0, p3 = 0, p4 = 0, p5 = 0, p6 = 0, p7 = 0, p8 = 0, min = 0; int mMax = 0, mMin = 255; System.Drawing.Imaging.BitmapData srcData = src.LockBits(new Rectangle(0, 0, w, h), System.Drawing.Imaging.ImageLockMode.ReadOnly, System.Drawing.Imaging.PixelFormat.Format24bppRgb); unsafe { byte* p = (byte*)srcData.Scan0.ToPointer(); int stride = srcData.Stride; byte* pTemp; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x - 1) * 3 + (y - 1) * stride; p2 = pTemp[0] + 4; pTemp = p + x * 3 + (y - 1) * stride; p3 = pTemp[0] + 3; pTemp = p + (x + 1) * 3 + (y - 1) * stride; p4 = pTemp[0] + 4; pTemp = p + (x - 1) * 3 + y * stride; p1 = pTemp[0] + 3; min = GetMin(p0, p1, p2, p3, p4); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } for (int y = h - 1; y > 0; y--) { for (int x = w - 1; x > 0; x--) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x + 1) * 3 + y * stride; p5 = pTemp[0] + 3; pTemp = p + (x + 1) * 3 + (y + 1) * stride; p6 = pTemp[0] + 4; pTemp = p + x * 3 + (y + 1) * stride; p7 = pTemp[0] + 3; pTemp = p + (x - 1) * 3 + (y + 1) * stride; p8 = pTemp[0] + 4; min = GetMin(p0, p5, p6, p7, p8); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); mMax = (int)Math.Max(min, mMax); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } mMin = 0; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { pTemp = p + x * 3 + y * stride; if (pTemp[0] != 0) { int temp = pTemp[0]; pTemp[0] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[1] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[2] = (byte)((temp - mMin) * 255 / (mMax - mMin)); } } } src.UnlockBits(srcData); return src; } } private double GetDistance(int x, int y, int dx, int dy, int mode) { double result = 0; switch (mode) { case 1: result = EuclideanDistance(x, y, dx, dy); break; case 2: result = CityblockDistance(x, y, dx, dy); break; case 3: result = ChessboardDistance(x, y, dx, dy); break; } return result; } private double EuclideanDistance(int x, int y, int dx, int dy) { return Math.Sqrt((x - dx) * (x - dx) + (y - dy) * (y - dy)); } private double CityblockDistance(int x, int y, int dx, int dy) { return Math.Abs(x - dx) + Math.Abs(y - dy); } private double ChessboardDistance(int x, int y, int dx, int dy) { return Math.Max(Math.Abs(x - dx), Math.Abs(y - dy)); } private double GetMin(double a, double b, double c, double d, double e) { return Math.Min(Math.Min(Math.Min(a, b), Math.Min(c, d)), e); } ~~~ 最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载： [http://www.zealpixel.com/portal.php](http://www.zealpixel.com/portal.php)

最近，3D影片盛行，3D电视技术也层出不穷，3D技术在带给大家非凡的视觉冲击同时，也在告诉大家这背后隐藏了太多的商机。     目前的3D技术大体分为两种：软件技术和硬件技术。所谓硬件技术就是在拍摄影片时采用多摄像头及各种3D相关设备来拍摄片源；所谓软件技术就是将2D片源通过一定的软件转换为3D格式。     如何使用软件技术将2D转为3D呢？今天我们来研究一种基于单幅图像的3D转换算法。     首先，我们要了解一种最简单的红蓝3D技术，所谓的2D图像转3D图像，它需要两幅有视差的图像来合成一张具有3D信息的效果图，实际上就是用一幅图像包含两张图像的信息。如何实现这一点呢？我们知道在RGB颜色空间中，图像中的每个像素都可以都包含R,G,B三个颜色分量，比如：纯红色(255,0，0)，纯绿色(0,255,0)，纯蓝色(0,0,255)等。     纯红色(255,0,0)的补色为青色(0,255,255)，这两种颜色互不包含，是互补的关系，也就是说，基于这种补色关系，我们有如下结果：     假设图像A的像素M(x,y)的RBG为(R1,G1,B1)，图像B的像素N(x,y)的RGB为(R2,G2,B2)，我们所需要的3D图像S对应像素O(x,y)的RGB值可计算如下(红蓝模式)：                       O(R,G,B) = (R1,G2,B2) 或                       O(R,G,B) = (R2,G1,B1)     以上两个公式中，任何一个，都包含了其中一张图像的R信息，和另一张图像的G,B信息，由于红色的补色是青色，这两个是互不包含的关系，因此，以上公式得到的结果中就包含了两张图像的信息了。     对于红蓝眼镜，其中两个镜片的颜色正是红色和青色，这样，图像经过镜片进入我们眼睛时，实际上就包含了两幅图像信息(一幅图像的R信息，另一幅图像的G,B信息)，从而产生了立体感觉。     基于以上原理，我们可以用PS，方便的将如下两张有视差的图像转换为一张红蓝3D图像：   注：以上原始图1,2像来自于网络     有了上面的理解，我们明白，我们需要2张2D的有视差的图像，才能转换为1张3D图像，但是，我们如何将1张原始图像直接转换为3D图像呢？     一个基本思想，我们通过原始图像，获取图像的深度，视差等3D信息，来构建3D效果图。     这个思想的实现，是个关键问题，经过本人研究，这里，介绍一个思路：     假设有原始图像A，我们要得到的红蓝3D图像为S，算法过程如下：     1，滤波算法           使用一定的滤波算法去除A中的噪声，比如：高斯滤波算法，均值滤波算法，中值滤波算法等等。     2，锐化算法           使用一定的锐化算法恢复并增强A中的细节，比如：Sobel,Laplace，Robert等等。     3，添加深度信息           经过1-2之后，我们得到图像B，这个图像与A已经有了一定的差异，但是，我们如果将B和A作为两张有视差的原始图像来得到S，那么效果并不好，我们还要添加一定的深度信息，构成图像C，这个深度信息获取的算法，可以参考论文(Rapid 2D to 3D Conversion)，这样我们就可以得到图像C了。      4，按照前文所述红蓝3D原理，将图像A,C转为S，S就是一副3D图像了。      这里附上我自己的效果图：    最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载： [http://www.zealpixel.com/portal.php](http://http//www.zealpixel.com/portal.php)

灰度图像彩色化这个课题，一直以来都有不少相关人员在研究，也算是个热门话题，能否把一张灰度图按照我们的意愿，准确的彩色化，成为成败的关键。最近一直在研究这个灰度图像彩色化算法，看了不少论文，做了不少实验，于是，在这里做个总结跟大家分享一下，希望能跟对于这个算法有兴趣高手们能共同讨论一下，也算是抛砖引玉吧！ 目前灰度图像彩色化的算法主要有以下几种： 1，基于优化扩展的彩色化算法 2，基于最短距离和色度混合的彩色化算法 3，基于颜色转移的彩色化算法 相关参考文献举例如下： 1，Colorization using Optimization  这篇是最经典的论文 2，Fast Digital Image Colorization Technique        Fast Colorization Using Edge and Gradient Constrains        Natural Image Colorization 3，Transferring Color to Grayscale Image        Example-based Multiple Local Color Transfer by Strokes        Affective Image  Colorization        Color Transfer Based on Normalized Cumulative Hue Histograms        Color Transfer in Correlated Color Space        Colorization by Example        Color Transfer between Images 以上文献均为举例，有兴趣的可以自行搜索。 现在说一下以上三种方法的优缺点：     对于基于优化扩展的彩色化算法，这种算法主要是基于一种图像分割算法，设立优化条件，寻求最优的图像分割，然后进行着色；这个算法是半自动的算法，所谓半自动算法就是说需要我们人为的在一副灰度图像上画出自己想要添加的颜色线条，根据我们确定的这个颜色线条，结合分割算法，进行着色。这个算法相对于最短距离彩色化算法要准确，但是时间复杂度太高，过于耗时，不适合大规模彩色化。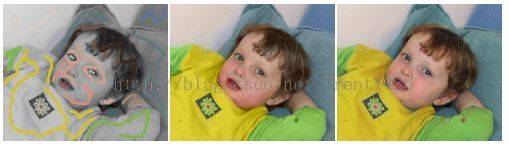     效果图举例：                                                                         Fig.1     对于基于距离和色度混合的彩色化算法，这种算法最大的优点是速度快，属于快速算法，缺点是单纯考虑了距离的影响，忽略了颜色聚类的影响，也属于半自动算法，其主要思想是：用户设定颜色线条，然后根据某种距离公式计算每一个像素到颜色线条的距离，则距离最近的线条颜色即为该像素的颜色。     效果图举例：                                                  Fig.2     对于基于颜色转移的彩色化算法，这种算法最大的优点是：自动化，不需要人为干涉，只需要你提供一张与目标灰度图像内容相近的彩色图像，主要思想是：研究某种颜色匹配算法，将彩色图像中的颜色信息匹配到目标灰度图像中，从而完成灰度图的彩色化。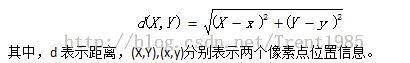这种算法的缺点是：1，在彩色图像中不一定可以找到灰度图中完美匹配的点，因此，对于这些点，效果较差；2，不能按照我们需要的颜色进行彩色化；     效果图举例：                                                                                                                           Fig.3 本文结合以上三种算法的优缺点，介绍本人认为的最简单的最适用的第二种算法：基于最短距离和颜色混合的灰度图像彩色化距离 这个算法过程如下： 1，寻找最短距离算法，图像中的距离算法有很多，比如：欧式距离，Dijkstra距离等，这里我们使用欧式距离，公式如下：  2，对于灰度图A，人为的设定颜色区域S[i]，其中i表示颜色线条的个数，每一个颜色线条，我们使用集合S[i]表示，如图Fig.1中左边灰度图所示，有人为添加的许多颜色线条； 3，对于图像A，包含两个集合，一个是没有着色的像素点集合M，一个是被颜色线条覆盖的像素点集合N，对于N中的每个像素，实际上对应的颜色就是颜色线条的颜色，对于M中的每一个像素点，由于是灰度图像，因此，它只有灰度信息，也就是亮度信息Y（这里我们使用YCbCr颜色空间），我们需要做的就是确定这个像素对应的Cb,Cr色度值。     首先，我们计算M中的每一个像素P(x,y)到每一个颜色线条S[i]的距离，记为D[i]，那么，我们寻找D[i]的最小值，也就是到P距离最短的颜色线条，那么P的颜色就是具有最短距离D[i]的颜色i，这样就可以求出对应的Cb,Cr值了。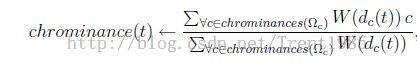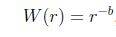     其次，这样的算法有可能得到的图像边缘过度不自然，因此，采取了一种颜色混合的算法，我们把P点的颜色看作是不同颜色线条i距离D[i]的加权，公式如下：  其中d表示欧式距离，c表示色度Cb,Cr，chrominance表示相应的结果色度，W表示一种加权公式 对于W，公式如下：  其中， b一般取4，范围为(0,6] 这样整个彩色化过程就完成了，放上我自己的效果图：     我的效果图是针对以上算法进行了改进之后得到的，有兴趣的图像处理爱好者们可以研究一下，期待跟大侠们交流！我的QQ1358009172，博客http://dongtingyueh.blog.163.com/ 最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载： [http://www.zealpixel.com/portal.php](http://http//www.zealpixel.com/portal.php)

> 原文出处：[数字图像处理课题研究](http://blog.csdn.net/column/details/imagesharp.html) > 作者：[Trent](http://blog.csdn.net/Trent1985) **本系列文章经作者授权在看云整理发布，未经作者允许，请勿转载！** # 数字图像处理课题研究 > 基于图像处理基础知识，对某个图像处理领域的问题进行研究，包括相关资料结果对比，结论等等,并提供相关代码Demo，与大家共同探讨，一起进步。