二值图像的距离变换研究

**[研究内容]** 二值图像距离变换 **[正文]** 二值图像距离变换的概念由Rosenfeld和Pfaltz于1966年在论文[1]中提出，目前广泛应用于计算机图形学，目标识别及GIS空间分析等领域，其主要思想是通过表识空间点(目标点与背景点)距离的过程，最终将二值图像转换为灰度图像。 距离变换按照距离的类型可以分为欧式距离变换(Eudlidean Distance Transfrom)和非欧式距离变换两种，其中，非欧式距离变换又包括棋盘距离变换(Chessboard Distance Transform)，城市街区距离变换(Cityblock Distance Transform)，倒角距离变换(Chamfer Distance Transform)等； 距离变换的主要过程： 假设一幅二值图像I，包含一个连通区域S，其中有目标集O和背景集B，距离图为D，则距离变换的定义如公式1-(1)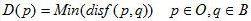：                                         1-(1) 具体步骤如下： 1，将图像中的目标像素点分类，分为内部点，外部点和孤立点。 以中心像素的四邻域为例，如果中心像素为目标像素(值为1)且四邻域都为目标像素(值为1)，则该点为内部点。如果该中心像素为目标像素，四邻域为背景像素(值为0)，则该中心点为孤立点，如下图Fig.1所示。除了内部点和孤立点之外的目标区域点为边界点。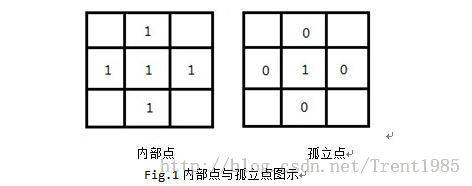  2，计算图像中所有的内部点和非内部点，点集分别为S1，S2。 3，对于S1中的每一个内部点(x,y)，使用距离公式disf()计算骑在S2中的最小距离，这些最小距离构成集合S3。 4，计算S3中的最大最小值Max,Min。 5，对于每一个内部点，转换后的灰度值G计算如下公式1-(2)所示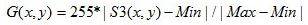：     1-(2) 其中，S3(x,y)表示S1中的点(x,y)在S2中的最短距离 6，对于孤立点保持不变。 在以上距离变换的过程中，距离函数disf()的选取如果是欧式距离，则该距离变换称为欧式距离变换，依次类推。对于距离的求取，目前主要的距离公式如下： 欧式距离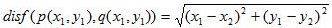：      1-(3) 棋盘距离：                1-(4) 城市街区距离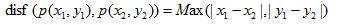：   1-(5) 对于欧式距离变换，由于其结果准确，而计算相比非欧式距离变换较为复杂，因此，出现了较多的快速欧式距离变换算法，这里笔者介绍一种基于3*3模板的快速欧式距离变换算法(文献2)，具体过程如下：  1，按照从上到下，从左到右的顺序，使用模板如图Fig.2，依次循环遍历图像I，此过程称为前向循环。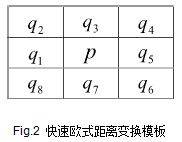  对于p对应的像素(x,y)，我们计算五个距离：d0,d1,d2,d3,d4：     d0=p(x,y)     d1=p(x-1,y)+disf((x-1,y),(x,y))     d2=p(x-1,y-1)+disf((x-1,y-1),(x,y))     d3=p(x,y-1)+disf((x,y-1),(x,y))     d4=p(x+1,y-1)+disf((x-1,y-1),(x,y))     则p(x,y)变换后的像素值为：     p(x,y)=Min(d0,d1,d2,d3,d4);     使用上述算法得到图像I'。     2，按照从下到上，从右到左的顺序，使用Fig.2所示模板依次循环遍历图像I’，此过程称为后向循环。 对于p对应的像素(x,y)，我们计算五个距离：d0,d5,d6,d7,d8：     d0=p(x,y)     d5=p(x+1,y)+disf((x+1,y),(x,y))     d6=p(x+1,y+1)+disf((x+1,y+1),(x,y))     d7=p(x,y+1)+disf((x,y+1),(x,y))     d8=p(x-1,y+1)+disf((x-1,y+1),(x,y))     则p(x,y)后向变换后的像素值为：     p(x,y)=Min(d0,d5,d6,d7,d8);     使用上述算法得到的图像即为距离变换得到的灰度图像。     以上过程即文献2所示快速欧式距离变换算法。如果我们需要非欧氏距离变换的快速算法，只需要修改文献2算法中的欧式距离公式disf()为非欧式距离公式，如棋盘距离，城市街区距离等，过程依次类推。 对于欧式距离变换算法，相关学者研究了速度更快的倒角距离变换算法，来近似欧式距离变换的效果。具体过程如下：     1，使用前向模板如图Fig.3中左边3*3模板，对图像从上到下，从左到右进行扫描，模板中心0点对应的像素值如果为0则跳过，如果为1则计算模板中每个元素与其对应的像素值的和，分别为Sum1,Sum2,Sum3,Sum4，Sum5，而中心像素值为这五个和值中的最小值。     2，使用后向模板如图Fig.3中右边的3*3模板，对图像从下到上，从右到左进行扫描，方法同上。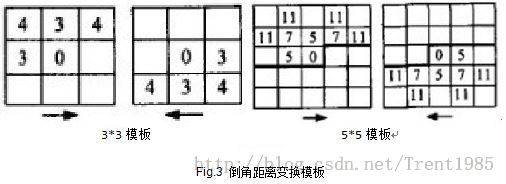     3，一般我们使用的倒角距离变换模板为3*3和5*5，分别如下图所示：  [实验结果]     实验采用512*512大小的图像进行测试，测试PC为64位，Intel(R) Core(TM) i5-3230 CPU, 2.6GHz, 4G RAM，运行环境为VS2008，C#。     实验结果如下：                                                                       (a)原图                                              (b)Euclidean Distance Transfrom                                                     (c) Cityblock  Distance Transfrom                                                (d) Chessboard Distance Transform                                                (e) Chamfer Distance Transform 对于以上欧式距离变换与非欧式距离变换，我们做了时间分析，结果如下：   对于Table 1的数据，是通过计算50张512*512大小的图像得到的平均结果，代码未曾优化，距离变换结果均做了均衡化处理，对于不同配置，不同程序语言可能存在一定差异，总体而言，基于3*3模板的倒角距离变换速度最快，大概是欧氏距离快速算法的一半。 [参考文献] [1] Rosenfeld A,PfaltzJ.L, Sequential operations in digital pic ture processing. Journal of ACM,1966, 13(4):471-494. [2] Frank Y.Shih,Yi-Ta Wu, Fast Euclidean distance transformation in two scans using a 3*3 neighborhood. Journal of Computer Vision and Image Understanding 2004,195–205. 附录 本人使用C#编写的代码如下： 本人的完整demo，包含参考文献，测试图像，地址：[http://download.csdn.net/detail/trent1985/6841125](http://download.csdn.net/detail/trent1985/6841125) ~~~ /// <summary> /// Distance transform for binary image. /// </summary> /// <param name="src">The source image.</param> /// <param name="distanceMode">One parameter to choose the mode of distance transform from 1 to 3, 1 means Euclidean Distance, 2 means CityBlock Distance, 3 means ChessBoard Distance.</param> /// <returns>The result image.</returns> public Bitmap DistanceTransformer(Bitmap src, int distanceMode) { int w = src.Width; int h = src.Height; double p0 = 0, p1 = 0, p2 = 0, p3 = 0, p4 = 0, p5 = 0, p6 = 0, p7 = 0, p8 = 0, min = 0; int mMax = 0, mMin = 255; System.Drawing.Imaging.BitmapData srcData = src.LockBits(new Rectangle(0, 0, w, h), System.Drawing.Imaging.ImageLockMode.ReadOnly, System.Drawing.Imaging.PixelFormat.Format24bppRgb); unsafe { byte* p = (byte*)srcData.Scan0.ToPointer(); int stride = srcData.Stride; byte* pTemp; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x - 1) * 3 + (y - 1) * stride; p2 = pTemp[0] + GetDistance(x, y, x - 1, y - 1, distanceMode); pTemp = p + x * 3 + (y - 1) * stride; p3 = pTemp[0] + GetDistance(x, y, x, y - 1, distanceMode); pTemp = p + (x + 1) * 3 + (y - 1) * stride; p4 = pTemp[0] + GetDistance(x, y, x + 1, y - 1, distanceMode); pTemp = p + (x - 1) * 3 + y * stride; p1 = pTemp[0] + GetDistance(x, y, x - 1, y, distanceMode); min = GetMin(p0, p1, p2, p3, p4); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } for (int y = h - 1; y > 0; y--) { for (int x = w - 1; x > 0; x--) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x + 1) * 3 + y * stride; p5 = pTemp[0] + GetDistance(x, y, x + 1, y, distanceMode); pTemp = p + (x + 1) * 3 + (y + 1) * stride; p6 = pTemp[0] + GetDistance(x, y, x + 1, y + 1, distanceMode); pTemp = p + x * 3 + (y + 1) * stride; p7 = pTemp[0] + GetDistance(x, y, x, y + 1, distanceMode); pTemp = p + (x - 1) * 3 + (y + 1) * stride; p8 = pTemp[0] + GetDistance(x, y, x - 1, y + 1, distanceMode); min = GetMin(p0, p5, p6, p7, p8); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); mMax = (int)Math.Max(min, mMax); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } mMin = 0; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { pTemp = p + x * 3 + y * stride; if (pTemp[0] != 0) { int temp = pTemp[0]; pTemp[0] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[1] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[2] = (byte)((temp - mMin) * 255 / (mMax - mMin)); } } } src.UnlockBits(srcData); return src; } } /// <summary> /// Chamfer distance transform(using two 3*3 windows:forward window434 300 000;backward window 000 003 434). /// </summary> /// <param name="src">The source image.</param> /// <returns>The result image.</returns> public Bitmap ChamferDistancetransfrom(Bitmap src) { int w = src.Width; int h = src.Height; double p0 = 0, p1 = 0, p2 = 0, p3 = 0, p4 = 0, p5 = 0, p6 = 0, p7 = 0, p8 = 0, min = 0; int mMax = 0, mMin = 255; System.Drawing.Imaging.BitmapData srcData = src.LockBits(new Rectangle(0, 0, w, h), System.Drawing.Imaging.ImageLockMode.ReadOnly, System.Drawing.Imaging.PixelFormat.Format24bppRgb); unsafe { byte* p = (byte*)srcData.Scan0.ToPointer(); int stride = srcData.Stride; byte* pTemp; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x - 1) * 3 + (y - 1) * stride; p2 = pTemp[0] + 4; pTemp = p + x * 3 + (y - 1) * stride; p3 = pTemp[0] + 3; pTemp = p + (x + 1) * 3 + (y - 1) * stride; p4 = pTemp[0] + 4; pTemp = p + (x - 1) * 3 + y * stride; p1 = pTemp[0] + 3; min = GetMin(p0, p1, p2, p3, p4); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } for (int y = h - 1; y > 0; y--) { for (int x = w - 1; x > 0; x--) { if (x > 0 && x < w - 1 && y > 0 && y < h - 1) { p0 = (p + x * 3 + y * stride)[0]; if (p0 != 0) { pTemp = p + (x + 1) * 3 + y * stride; p5 = pTemp[0] + 3; pTemp = p + (x + 1) * 3 + (y + 1) * stride; p6 = pTemp[0] + 4; pTemp = p + x * 3 + (y + 1) * stride; p7 = pTemp[0] + 3; pTemp = p + (x - 1) * 3 + (y + 1) * stride; p8 = pTemp[0] + 4; min = GetMin(p0, p5, p6, p7, p8); pTemp = p + x * 3 + y * stride; pTemp[0] = (byte)Math.Min(min, 255); pTemp[1] = (byte)Math.Min(min, 255); pTemp[2] = (byte)Math.Min(min, 255); mMax = (int)Math.Max(min, mMax); } } else { pTemp = p + x * 3 + y * stride; pTemp[0] = 0; pTemp[1] = 0; pTemp[2] = 0; } } } mMin = 0; for (int y = 0; y < h; y++) { for (int x = 0; x < w; x++) { pTemp = p + x * 3 + y * stride; if (pTemp[0] != 0) { int temp = pTemp[0]; pTemp[0] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[1] = (byte)((temp - mMin) * 255 / (mMax - mMin)); pTemp[2] = (byte)((temp - mMin) * 255 / (mMax - mMin)); } } } src.UnlockBits(srcData); return src; } } private double GetDistance(int x, int y, int dx, int dy, int mode) { double result = 0; switch (mode) { case 1: result = EuclideanDistance(x, y, dx, dy); break; case 2: result = CityblockDistance(x, y, dx, dy); break; case 3: result = ChessboardDistance(x, y, dx, dy); break; } return result; } private double EuclideanDistance(int x, int y, int dx, int dy) { return Math.Sqrt((x - dx) * (x - dx) + (y - dy) * (y - dy)); } private double CityblockDistance(int x, int y, int dx, int dy) { return Math.Abs(x - dx) + Math.Abs(y - dy); } private double ChessboardDistance(int x, int y, int dx, int dy) { return Math.Max(Math.Abs(x - dx), Math.Abs(y - dy)); } private double GetMin(double a, double b, double c, double d, double e) { return Math.Min(Math.Min(Math.Min(a, b), Math.Min(c, d)), e); } ~~~ 最后，分享一个专业的图像处理网站（微像素），里面有很多源代码下载： [http://www.zealpixel.com/portal.php](http://www.zealpixel.com/portal.php)