Maxima 的基本微积分操作
最后更新于:2022-04-01 07:31:37
Maxima 对各种微积分的运算提供了强有力的支持。
可以这么说,在基本微积分运算能力上,Maxima 不输给任何商业软件。
### 求极限
求极限是微积分中最基本的运算。在Maxima 中用 limit 函数完成求极限的工作。
limit (expr, x, val)
计算 x 趋近于 val 时 expr 的极限。
如果极限不存在,范围值可能为 und (极限不存在),ind (极限不存在但是有界),infinity(发散)
limit (expr, x, val, dir)
计算 x 从 dir 方向趋近于 val 时 expr 的极限。
dir 为 plus 时求的是右极限,为 minus 时求的是左极限。
'limit(sin(x)/x,x,0);
limit(sin(x)/x,x,0);
'limit((1+1/x)^x,x,inf);
limit((1+1/x)^x,x,inf);
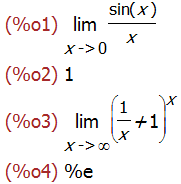
limit((2^(1/x)+1)/(2^(1/x)-1),x,0);
'limit((2^(1/x)+1)/(2^(1/x)-1),x,0,minus);
limit((2^(1/x)+1)/(2^(1/x)-1),x,0,minus);
'limit((2^(1/x)+1)/(2^(1/x)-1),x,0,plus);
limit((2^(1/x)+1)/(2^(1/x)-1),x,0,plus);
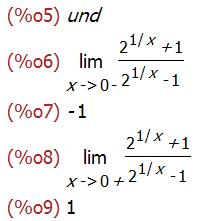
'limit((2*x^2+x)/(x^2-2),x,inf);
limit((2*x^2+x)/(x^2-2),x,inf);

### 微分运算
diff 函数可以实现微分运算,有四种基本形式,最基本的形式是:
diff (expr, x) 求表达式 expr 对 x 的微分。
diff(sin(x)*x^3,x);
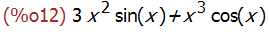
diff(u(x)*v(x),x);
diff(u(x)*v,x);
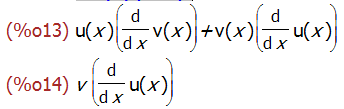
从上面的例子可以看到,一个函数如果不明确表明自变量,diff 函数是不会对其求导的。
diff (expr, x, n)
求表达式 expr 对 x 的 n 次微分。
diff(y^3*exp(-y^2),y,2);
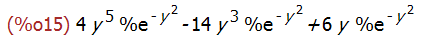
diff (expr, x_1, n_1, …, x_m, n_m) 求的是混合偏导数。
diff(f(x,y),x,2,y,1);
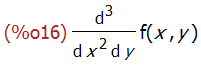
diff (expr) 计算的是全微分。
diff(f(x,y));
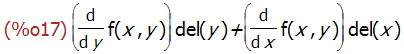
### taylor 级数展开
函数f(x)的在x = a附近的幂级数可以通过powerseries (f(x), x, a)获得。
powerseries (f(x), x, a);
powerseries(1/(1-x^2), x, 0);
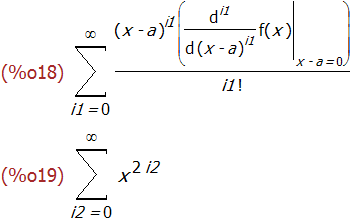
上面得到的结果中的求和指数 i2 看起来显得不那么专业,可以用 niceindices 函数将其变的看起来更专业些。
niceindices(powerseries(1/(1-x^2), x, 0));
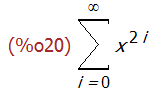
很多时候我们无法得到级数的解析表示,这时候可以用 taylor (f(x), x, a, n)得到函数f(x)在x = a附近第 n 阶项((x - a)^n)以下各项的泰勒级数
taylor(sin(x), x, 0, 8);
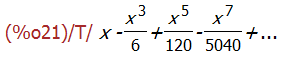
同样,对多元函数也可以进行 taylor 展开。
taylor (sin (y + x), x, 0, 3, y, 0, 3);
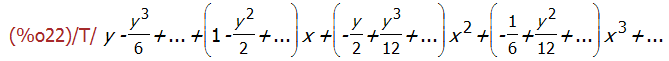
利用 pade 近似可以将 taylor 级数转化为多项式函数。比如下面的例子
taylor(sin(x), x, 0, 8);
pade(%,5,5);
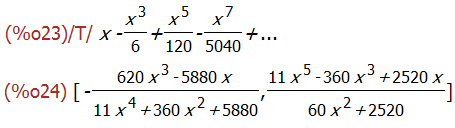
### 积分运算
integrate(expr, x)
计算不定积分。
integrate(expr, x, a, b)
计算定积分,积分上下限分别为 a b。
integrate(1/(1+x^2),x);
integrate(1/(1+x^2),x, minf, inf);
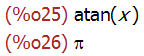
risch (expr, x)
采用 Risch 方法计算不定积分。
risch (x^2*erf(x), x),ratsimp;
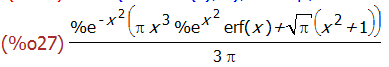
changevar 函数利用变量替换,对待积分函数进行换元。这个功能对学习换元法求积分还是蛮有用的。
'integrate(x^2/(1+x^2),x,0,2);
changevar(%,x=tan(theta),theta,x);
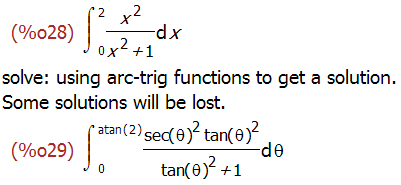
### 求和与求积运算
sum (expr, i, i_0, i_1)
计算求和。
product (expr, i, i_0, i_1)
计算求积。
sum (i^2, i, 1, 7);
sum (a[i], i, 1, 7);
sum(1/k^2,k,0,inf);
sum (1/3^i, i, 1, inf), simpsum;
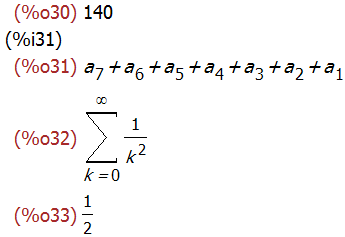
product (x + i*(i+1)/2, i, 1, 4);
product (a(i), i, 1, n);
product (k, k, 1, n), simpproduct;
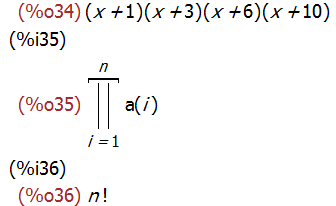
### laplace 变换
Maxima 中提供了两个函数用来计算 laplace 变换和反变换。
laplace (expr, t, s) 对表达式 expr 进行 laplace 变换,积分变量为 t,变换后的参数为 s.
ilt (expr, s, t) 对表达式进行反变换。
需要说明的是这两个函数进行的都是单边 laplace 变换,Maxima 中还没有对双边拉式变换的支持。
laplace (exp (2*t + a) * sin(t) * t, t, s);
laplace ('diff (f (x), x), x, s);
ilt(1/(s+1),s,t);
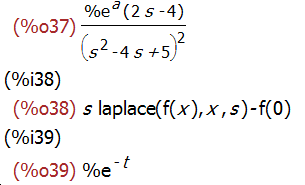
提到 laplace 变换就不能不提提部分分式展开。
在大多数介绍 laplace 变换的初级课本中都只介绍利用部分分式展开的方式进行反变换。
Maxima 提供了 partfrac 函数来完成部分分式展开的工作。下面用一个例子来说明:
x/(x^3+4*x^2+5*x+2);
partfrac (x/(x^3+4*x^2+5*x+2), x);
