源码下载
最后更新于:2022-04-02 01:28:39
## 源码下载
链接: [https://pan.baidu.com/s/1kU53X1l](https://pan.baidu.com/s/1kU53X1l) 密码: itfu
';
坐标旋转和斜面反弹
最后更新于:2022-04-02 01:28:37
## 坐标旋转和斜面反弹
坐标旋转,顾名思义,就是说围绕着某个点旋转坐标系。这一章就来介绍一下如何实现坐标旋转和坐标旋转的作用。
内容如下:
- 坐标旋转
- 斜面反弹
**1、坐标旋转**
**1.1 简单旋转**
在前面的三角函数一章中的实例“指红针”中,我们已经使用过坐标旋转技术。只需一个中心点,一个物体,还有半径和角度(弧度制),通过增减这个角度,然后用基本的三角函数计算位置,就能使物体围绕着中心点旋转。
初始化参数:
```
vr = 0.1; //角度增量
angle = 0;
radius = 100;
centerX = 0;
centerY = 0;
```
在动画循环中做下列计算:
```
object.x = centerX + Math.cos(angle) * radius;
object.y = centerY + Math.sin(angle) * radius;
angle += vr;
```
实例: canvas-demo/rotate.html
每次旋转角度vr设置为0.05,根据上面的公式计算小球旋转后的位置。
如果只知道物体的位置和中心点,如何做旋转呢?其实也不难,我们只需根据两个点来计算出当前角度和半径即可:
```
var dx = ball.x - centerX;
var dy = ball.y - centerY;
var angle = Math.atan2(dy,dx);
var radius = Math.sqrt(dx * dx + dy * dy);
```
得到角度和半径,我们就可以像上面那样旋转了。
上面的方法比较适合单个物体旋转,对于多个物体的旋转,这种方法不是很高效,当然,我们有更好的方法。
**1.2 高级坐标旋转**
如果物体(x,y)围绕着一个点(x2,y2)旋转,而我们只知道物体的坐标和点的坐标,那如何计算旋转后物体的坐标呢?下面有一个很适合这种场景的公式:
```
x1 = (x - x2) * cos(rotation) - (y - y2) * sin(rotation);
y1 = (y - y2) * cos(rotation) + (x - x2) * sin(rotation);
```
我们可以认为(x-x2)、(y-y2)是物体相对于旋转点的坐标,rotation是旋转角度(旋转量,指当前角度和旋转后的角度的差值),x1、y1是物体旋转后的位置坐标。
注意:这里采取的依旧是弧度制。
这条公式是不是看的有点糊里糊涂的,不知道怎么来的,下面我们将介绍它是如何得出的。
先看图:
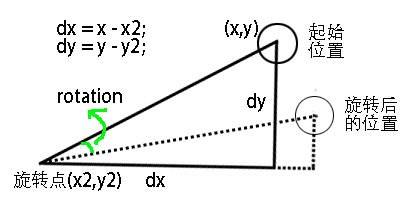
```
/*物体当前的坐标*/
x = radius * cos(angle);
y = radius * sin(angle);
/*物体旋转rotation后的坐标*/
x1 = radius * cos(angle + rotation);
y1 = radius * sin(angle + rotation);
```
下面又来介绍一个两个关于三角函数的数学公式了。
两角之和的余弦值:
```
cos(a + b) = cos(a) * cos(b) - sin(a) * sin(b);
```
两角之和的正弦值:
```
sin(a + b) = sin(a) * cos(b) + cos(a) * sin(b);
```
基于这两条推导公式,我们将x1和y1的公式展开:
```
x1 = radius * cos(angle) * cos(rotation) - radius * sin(angle) *sin(rotation);
y1 = radius * sin(angle) * cos(rotation) + radius * cos(angle) * sin(rotation);
```
最后将x、y变量代入公式,就会得到最初那条公式:
```
x1 = x * cos(rotation) - y * sin(rotation);
y1 = y * cos(rotation) + x * sin(rotation);
```
注意:这里的x、y是相对于旋转点的x、y坐标,也就是上面的(x-x2)、(y-y2),而不是相对于坐标系的坐标。
使用这个公式,我们不需要知道起始角度和旋转后的角度,只需要知道旋转角度即可。
**(1)旋转单个物体**
有了公式,当然要实践一下,我们先来试试旋转单个物体
这里的vr依旧是0.05,然后计算这个角度的正弦和余弦值,然后根据小球相对于中心点的位置计算出x1、y1,接着利用公式计算出小球旋转后的坐标。
```
sin = Math.sin(angle);
cos = Math.cos(angle);
var x1 = ball.x - centerX;
var y1 = ball.y - centerY;
ball.x = centerX + (x1 * cos - y1 * sin);
ball.y = centerY + (y1 * cos + x1 * sin);
```
还是要强制一句,这个公式传入的x、y是物体相对于旋转点的坐标,不是旋转点的坐标,也不是物体的坐标。
你可能会疑惑,这不是跟第一个例子的效果一样吗?为什么要用这个公式呢?不要急,接着看下面的旋转多个物体,看完后你就会明白这条公式的好处了。
**(2)旋转多个物体**
假如要旋转多个物体,我们将小球保存在变量balles的数组中,旋转代码如下:
```
balles.forEach(function(ball){
var dx = ball.x - centerX;
var dy = ball.y - centerY;
var angle = Math.atan2(dy,dx);
var dist = Math.sqrt(dx * dx + dy * dy);
angle += vr;
ball.x = centerX + Math.cos(angle) * dist;
ball.y = centerY + Math.sin(angle) * dist;
});
```
使用高级坐标旋转是这样的:
```
var cos = Math.cos(vr);
var sin = Math.sin(vr);
balles.forEach(function(ball){
var x1 = ball.x - centerX;
var y1 = ball.y - centerY;
var x2 = x1 * cos - y1 * sin;
var y2 = y2 * cos + x1 * sin;
ball.x = centerX + x2;
ball.y = centerY + y2;
});
```
我们来对比一下这两种方式,在第一种方式中,每次循环都调用了4次Math函数,也就是说,旋转每一个小球都要调用4次Math函数,而第二种方式,只调用了两次Math函数,而且都位于循环之外,不管增加多少小球,它们都只会执行一次。
实例:canvas-demo/rotate3.htmll
我们用鼠标来控制多个球的旋转速度,如果鼠标位置在canvas的中央,那么它们都静止不动,如果鼠标向左移动,这些小球就沿逆时针方向旋转,如果向右移动,小球就沿顺时针方法越转越快。
**2、斜面反弹**
前面我们学习了如何让物体反弹,不过都是基于垂直或水平的反弹面,如果是一个斜面,我们该如何反弹呢?
处理斜面反弹,我们要做的是:旋转整个系统使反弹面水平,然后做反弹,最后再旋转回来,这意味着反弹面、物体的坐标位置和速度向量都发生了旋转。
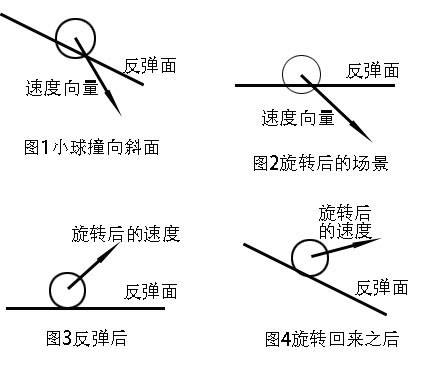
图1是小球撞向斜面,向量箭头表示小球的方向
图2中,整个场景旋转了,反弹面处于水平位置,就像前面碰撞示例中的底部障碍一样。在这里,速度向量也随着整个场景向右旋转了。
图3中,我们就可以实现反弹了,也就是改变y轴上的速度
图4中,就是整个场景旋转回到最初的角度。
什么,你还看不明白,那我再给你画个图吧:
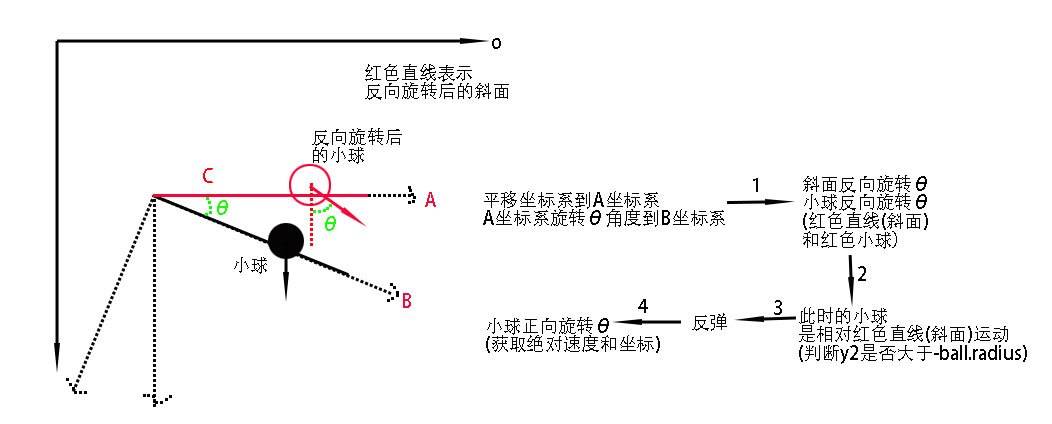
斜面和小球的旋转都是相对于(x,y)。
经历了上图,你应该明白,如果还不明白,请自己画图看看,画出每一步。
**2.1 旋转起来**
为了斜面反弹的真实性,我们需要创建一个斜面,在canvas中,我们只需画一条斜线,这样我们就可以看到小球在哪里反弹了。
相信画直线对你来说不难,下面创建一个Line类:
```
function Line(x1, y1, x2, y2) {
this.x = 0;
this.y = 0;
this.x1 = (x1 === undefined) ? 0 : x1;
this.y1 = (y1 === undefined) ? 0 : y1;
this.x2 = (x2 === undefined) ? 0 : x2;
this.y2 = (y2 === undefined) ? 0 : y2;
this.rotation = 0;
this.scaleX = 1;
this.scaleY = 1;
this.lineWidth = 1;
};
/*绘制直线*/
Line.prototype.draw = function(context) {
context.save();
context.translate(this.x, this.y); //平移
context.rotate(this.rotation); // 旋转
context.scale(this.scaleX, this.scaleY);
context.lineWidth = this.lineWidth;
context.beginPath();
context.moveTo(this.x1, this.y1);
context.lineTo(this.x2, this.y2);
context.closePath();
context.stroke();
context.restore();
};
```
先看实例(点击一下按钮看看):canvas-demo/rotateBevel.html
在上面的例子中,我创建的小球是随机位置的,不过都位于斜线的上方。
一开始,我们首先声明ball、line、gravity和bounce,然后初始化ball和line的位置,接着计算直线旋转角度的cos和sin值
```
line = new Line(0, 0, 300, 0);
line.x = 50;
line.y = 200;
line.rotation = (10 * Math.PI / 180); //设置线的倾斜角度
cos = Math.cos(line.rotation);
sin = Math.sin(line.rotation);
```
接下来,用小球的位置减去直线的位置(50,100),就会得到小球相对于直线的位置:
```
var x1 = ball.x - line.x;
var y1 = ball.y - line.y;
```
完成了上面这些,我们现在可以开始旋转,获取旋转后的位置和速度:
```
var x2 = x1 * cos + y1 * sin;
var y2 = y1 * cos - x1 * sin;
```
如果你够仔细,可能你也发现了,这里的代码好像和坐标旋转公式有点区别:
```
x1 = x * cos(rotation) - y * sin(rotation);
y1 = y * cos(rotation) + x * sin(rotation);
```
加号变减号,减号变加号了,写错了吗?其实没有,这是因为现在直线的斜度是10,那要将它旋转成水平的话,就不是旋转10,而是-10才对:
```
sin(-10) = - sin(10)
cos(-10) = cos(10)
```
当你旋转后获得相对于直线的坐标和速度后,你就可以使用位置x2、y2和速度vx1、vy1来执行反弹了,根据什么来判断球碰撞直线呢?用y2,因为此时y2是相对直线的位置的,所以“底边”就是line自己,也就是0,还要考虑小球的大小,需要判断y2是否大于0-ball.radius:
```
if(y2 > -ball.radius) {
y2 = -ball.radius;
vy1 *= bounce;
};
```
最后,你还要将整个系统旋转归位,计算原始角度的正余弦值:
```
x1 = x2 * cos - y2 * sin;
y1 = y2 * cos + x2 * sin;
```
求得ball实例的绝对位置:
```
ball.x = line.x + x1;
ball.y = line.y + y1;
```
**2.2 优化代码**
在上面的例子中,有些代码在反弹之前是没必要执行的,所以我们可以将它们放到if语句中:
```
if(y2 > -ball.radius) {
var x2 = x1 * cos + y1 * sin;
var vx1 = ball.vx * cos + ball.vy * sin;
var vy1 = ball.vy * cos - ball.vx * sin;
y2 = -ball.radius;
vy1 *= bounce;
//旋转回来,计算坐标和速度
x1 = x2 * cos - y2 * sin;
y1 = y2 * cos + x2 * sin;
ball.vx = vx1 * cos - vy1 * sin;
ball.vy = vy1 * cos + vx1 * sin;
ball.x = line.x + x1;
ball.y = line.y + y1;
};
```
**2.3 修复“不从边缘落下”的问题**
如果你试过上面的例子,现在你也看到了,即使小球到了直线的边缘,它还是会沿着直线方向滚动,这不科学,原因在于我们是模拟,并不是真实的碰撞,小球并不知道线的起点和终点在哪里。
**2.3.1 碰撞检测**
在前面的碰撞检测中,我们介绍过一个方法tool.intersects(),可用来检测直线的边界框是否与小球的边界框重叠。
当然,我们还需要获得直线的边界框,这里给Line类添加一个方法getBound:
```
Line.prototype.getBound = function() {
if(this.rotation === 0) {
var minX = Math.min(this.x1, this.x2);
var minY = Math.min(this.y1, this.y2);
var maxX = Math.max(this.x1, this.x2);
var maxY = Math.max(this.y1, this.y2);
return {
x: this.x + minX,
y: this.y + minY,
width: maxX - minX,
height: maxY - minY
};
} else {
//基于坐标系原点旋转
var sin = Math.sin(this.rotation);
var cos = Math.cos(this.rotation);
var x1r = cos * this.x1 + sin * this.y1;
var x2r = cos * this.x2 + sin * this.y2;
var y1r = cos * this.y1 + sin * this.x1;
var y2r = cos * this.y2 + sin * this.x2;
return {
x: this.x + Math.min(x1r, x2r),
y: this.y + Math.min(y1r, y2r),
width: Math.max(x1r, x2r) - Math.min(x1r, x2r),
height: Math.max(y1r, y2r) - Math.min(y1r, y2r)
};
}
};
```
返回一个包含有x、y、width和height属性的矩形对象。
使用如下:
```
if(tool.intersects(ball.getBound(), line.getBound()){
}
```
下面介绍一个更精确的方法。
**2.3.2 边界检查**
```
var bounds = line.getBound();
if(ball.x + ball.radius > bounds.x && ball.x - ball.radius -ball.radius){}
```
上面的代码也是导致2.4中例子没有掉落到下面的原因,因为当小球从第二个斜面掉落下,却是落到了第一个斜面的下面,也就会触发第一个斜面和小球的反弹,这不是我们想要的,如何解决呢?先看下图:

左边小球在y轴上的速度大于它与直线的相对距离,这表示它刚刚从直线上穿越下来;右边小球的速度向量小于它与直线的相对距离,这表示,它在这一帧和上一帧都位于线下,因此它此时只是在线下运动,所以我们需要的是在小球穿过直线的那一瞬间才执行反弹。
也就是:比较vy1和y2,仅当vy1大于y2时才执行反弹:
```
if(y2 > -ball.radius && y2 < vy1) {}
```
看看修复后的例子:canvas-demo/rotateBevel3.html
**总结**
这一章,我们介绍了坐标旋转和斜面反弹,其中不遗余力的分析了坐标旋转公式,并且修复了“不从边缘落下”和“线下”两个问题,一定要掌握坐标旋转,后面我们还将多处用到。
**附录**
重要公式:
(1)坐标旋转
```
x1 = x * Math.cos(rotation) - y * Math.sin(rotation);
y1 = y * Math.cos(rotation) + x * Math.sin(rotation);
```
(2)反向坐标旋转
```
x1 = x * Math.cos(rotation) + y * Math.sin(rotation);
y1 = y * Math.cos(rotation) - x * Math.sin(rotation);
```
';
碰撞检测
最后更新于:2022-04-02 01:28:35
## 碰撞检测
碰撞检测是物体与物体之间的交互,其实在前面的边界检测也是一种碰撞检测,只不过检测的对象是物体与边界之间。在本章中,我们将介绍更多的碰撞检测,比如:两个物体间的碰撞检测、一个物体与一个点的碰撞检测、基于距离的碰撞检测等等碰撞检测方法。
**什么是碰撞检测呢?**
简单来说,碰撞检测就是判定两个物体是否在同一时间内占用一块空间,用数学的角度来看,就是两个物体有没有交集。
检测碰撞的方法有很多,一般我们使用如下两种:
从几何图形的角度来检测,就是判断一个物体是否与另一个有重叠,我们可以用物体的矩形边界来判断。
检测距离,就是判断两个物体是否足够近到发生碰撞,需要计算距离和判断两个物体是否足够近。
**1、基于几何图形的碰撞检测**
基于几何图形的碰撞检测,一般情况下是检查一个矩形是否与其他矩形相交,或者某一个坐标点是否落在矩形内。
**1.1 两个物体间的碰撞检测(矩形边界检测法)**
在上一章中,我们介绍了一个 getBound() 方法,参数为球对象,返回矩形对象。
```
function getBound(body){
return {
x: (body.x - body.radius),
y: (body.y - body.radius),
width: body.radius * 2,
height: body.radius * 2
};
}
```
现在我们已经知道如何获取物体的矩形边界,那么只需检测两个对象的边界框是否相交,就可以判断两个物体是否碰撞了。我们在 tool.js 工具类中添加一个工具函数 tool.intersects :
```
tool.intersects = function(bodyA,bodyB){
return !(bodyA.x + bodyA.width < bodyB.x ||
bodyB.x + bodyB.width < bodyA.x ||
bodyA.y + bodyA.height < bodyB.y ||
bodyB.y + bodyB.height < bodyA.y);
};
```
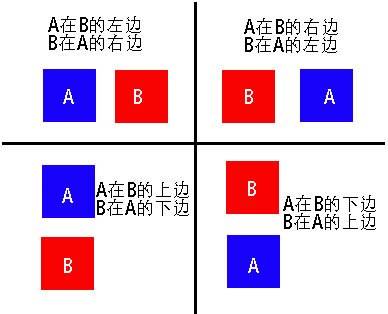
这个函数传入两个矩形对象,如果返回true,表示两个矩形相交了;否则,返回false。(如果你看不明白这段代码,请看下图,让一个矩形分别位于另一个矩形的上下左右位置):
检测函数已经知道了,当要检测两个物体是否相交时,就可以做如下判断:
```
if (tool.intersects(objectA,objectB)) {
console.log('撞上了');
}
```
注意:这里传入的必须是矩形对象。如果是球,可调用getBound()方法返回矩形对象。如果已经是矩形对象,就直接传入。
这里有一个需要注意的问题,有些时候,我们的物体是不规则的,如果我们采取矩形边界检测,有时候会不精确(只有真正的矩形才是精确的):
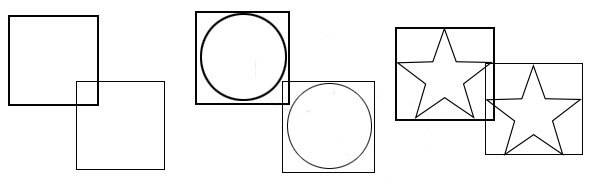
在上面的图中,有矩形、圆形和五角形,我们都可以采取矩形边界检测法,不过,你会发现,当物体是不规则的形状时,虽然通过上面的 tool.intesects() 方法判断两个物体已经碰撞,但实际上并没有,所以矩形边界检测法对不规则的图形来说,这只是一种不精确的检测方法,如果你要精确检测,那就要做更多的检测了。当然,矩形边界检测法对于大多数情况下已经足够了。
实例又来了(用iframe插入会导致页面卡,所以放在单独页面中,点击可看):http://ghmagical.com/Iframe/show/code/intersect
```
if(activeRect !== rect && tool.intersects(activeRect, rect)) {
activeRect.y = rect.y - activeRect.height;
activeRect = createRect();
};
```
这个例子是不是有点像俄罗斯方块呢,每一次只有一个活动物体,然后循环检测它是否与已经存在的物体碰撞,如果碰撞,则将活动物体放在与它碰撞物体的上面,然后创建一个新的方块。
**1.2 物体与点的碰撞检测**
在前面我们在 tool工具类中添加了一个工具函数 tool.containsPoint,它接受三个参数,第一个是矩形对象,后面两个是一个点的x和y的坐标,返回值是true或false:
```
tool.containsPoint = function(body, x, y){
return !(x < body.x || x > (body.x + body.width)
|| y < body.y || y > (body.y + body.height));
};
```
其实,tool.containsPoint()函数就是在检测点与矩形是否碰撞。
比如,要检测点(50,50)是否在一个矩形内:
```
if(tool.containsPoint(body,50,50)){
console.log('在矩形内');
}
```
tool.intesects()和tool.containsPoint()方法都会遇到精确问题,对矩形最精确,越不规则,精确率就越小。大多数情况下,都会采取这两种方法。当然,如果你要对不规则图形采取更精确的方法,那你就要写更多的代码去执行精确的检测了。
**2、基于距离的碰撞检测**
距离就是指两个物体间的距离,当然,物体总是有高宽的,这就还要考虑高宽。一般我们会先确定两个物体的最小距离,然后计算当前距离,最后进行比较,如果当前距离比最小距离小,那肯定发生了碰撞。
这种距离检测法,对圆来说是最精确的,而对于其他图形,或多或少会有一些精确问题。
**2.1 基于距离的简单碰撞检测**
基于距离的碰撞检测的最理想的情况是:有两个正圆形要进行碰撞检测,从圆的中心点开始计算。
要检测两个圆是否碰撞,其实就是比较两个圆的中心点的距离与两个圆的半径和的大小关系。
```
dx = ballB.x - ballA.x;
dy = ballB.y - ballA.y;
dist = Math.sqrt(dx * dx + dy * dy);
if(dist < ballA.radius + ballB.radius){
console.log('碰撞了');
}
```
实例:canvas-demo/distanceIntersect.html
在上面的例子中,碰撞距离就是一个球的半径加上另一个球的半径,也是碰撞的最小距离,而两者真正的距离就是圆心与圆心的距离。
```
var dx = ballB.x - ballA.x;
var dy = ballB.y - ballA.y;
var dist = Math.sqrt(dx * dx + dy * dy);
if(ball != ballB && dist < ballA.radius + ballB.radius){
ctx.strokeStyle = 'red';
var txt = '你压着我了';
var tx = ballA.x - ctx.measureText(txt).width / 2;
ctx.font = '30px Arial'
ctx.strokeText(txt,tx,ballA.y);
};
```
**2.2 弹性碰撞**
就像2.1节里的例子一样,当两个球碰撞时,我们加入了文字提示,当然,我们还可以做更多操作,比如这节要讲的弹性碰撞。
实例:canvas-demo/springIntersect.html
首先我们加入一个放在canvas中心的圆球ballA,然后加入多个随机大小和随机速度的圆球,让它们做匀速运动,遇到墙就反弹,最后在每一帧使用基于距离的方法检测小球是否与中央的圆球ballA发生了碰撞,如果发生了碰撞,则计算弹动目标点和两球间的最小距离来避免小球完全撞上圆球ballA。
对于小球和圆球ballA的碰撞,我们可以这样理解,我们在ballA外设置了目标点,然后让小球向目标点弹动,一旦小球到达目标点,就不再继续碰撞,弹性运动就结束了,继续做匀速运动。
下面的效果就像一群小气泡在大气泡上反弹,小气泡撞入大气泡一点距离,这个距离取决于小气泡的速度,然后被弹出来。
如果你看不懂它如何反弹的,那你就要回到上一章看看《缓动和弹动》是如何实现的了。
**3、多物体的碰撞检测策略**
这一节并不会介绍新的碰撞检测方法,而是介绍如何优化多物体碰撞代码。
如果你用过二维数组,那么你肯定知道如何去遍历数组元素,通常的方法是使用两个循环函数,而多物体的碰撞检测,也类似二维数组:
```
for(var i = 0; i < objects.length; i++){
var objectA = objects[i];
for(var j = 0; j < objects.length; j++){
var objectB = objects[j];
if(tool.intersects(objectA,objectB){}
}
};
```
上面的方法的语法是没错的,不过这段代码有两个效率问题:
**(1)多余的自身碰撞检测**
它检测了同一个物体是否自身碰撞,比如:第一个物体(i=0)是objects[0],在第二次循环中,第一个物体(j=0)也是objects[0],是不是完全没必要的检测,我们可以这样避免:
```
if(i != j && tool.intersects(objectA,objectB){}
```
这样会节省了i次碰撞检测
**(2)重复碰撞检测**
第一次(i=0)循环时,我们检测了objects[0](i=0)和objects[1](j=1)的碰撞;第二次(i=1)循环时,代码似乎又检测了objects[1](i=1)和objects[0](j=0)的碰撞,这岂不是多余的吗?
我们应该做如下的避免:
```
for(var i = 0; i < objects.length; i++){
var objectA = objects[i];
for(var j = i + 1; j < objects.length; j++){
var objectB = objects[j];
if(tool.intersects(objectA,objectB){}
}
};
```
这样处理后,不仅避免了自身碰撞检测,而且减少了重复碰撞检测。
实例:canvas-demo/collision.html
在上面的例子中,两个球在碰撞后的弹动代码并没有太大的区别,只不过这里将ballB当成了中央位置的圆球而已:
```
function checkCollision(ballA, ballB) {
var dx = ballA.x - ballB.x;
var dy = ballA.y - ballB.y;
var dist = Math.sqrt(dx * dx + dy * dy);
var min_dist = ballB.radius + ballA.radius;
if(dist < min_dist) {
var angle = Math.atan2(dy, dx);
var tx = ballB.x + Math.cos(angle) * min_dist;
var ty = ballB.y + Math.sin(angle) * min_dist;
var ax = (tx - ballA.x) * spring * 0.5;
var ay = (ty - ballA.y) * spring * 0.5;
ballA.vx += ax;
ballA.vy += ay;
ballB.vx += (-ax);
ballB.vy += (-ay);
};
};
```
上面代码最后四行的意思是:不仅ballB要从ballA弹开,而且ballA要从ballB弹出,它们的加速度的绝对值是相同的,方向相反。
不知道你有没有注意到,ax和ay的计算都乘以0.5,这是因为当ballA移动ax时,ballB也反向移动ax,那么就造成了 ax 变成 2ax ,所以要乘以0.5,才是真正的加速度。当然,你也可以将spring减小成原来的一半。
**总结**
碰撞检测是很多动画中必不可少的,你必须掌握基于几何图形的碰撞检测、基于距离的碰撞检测方法,以及如何更有效的的检测多物体间的碰撞。
**附录**
**重要公式:**
(1)矩形边界碰撞检测
```
tool.intersects = function(bodyA,bodyB){
return !(bodyA.x + bodyA.width < bodyB.x ||
bodyB.x + bodyB.width < bodyA.x ||
bodyA.y + bodyA.height < bodyB.y ||
bodyB.y + bodyB.height < bodyA.y);
};
```
(2)基于距离的碰撞检测
```
dx = objectB.x - objectA.x;
dy = objectB.y - objectA.y;
dist = Math.sqrt(dx * dx + dy * dy);
if(dist < objectA.radius + objectB.radius){}
```
(3)多物体碰撞检测
```
for(var i = 0; i < objects.length; i++){
var objectA = objects[i];
for(var j = i + 1; j < objects.length; j++){
var objectB = objects[j];
if(tool.intersects(objectA,objectB){}
}
};
```
';
缓动与弹动
最后更新于:2022-04-02 01:28:32
## 缓动与弹动
这一章主要讲解缓动(比例速度)和弹动(比例加速度)。
**1、比例运动**
比例运动 是指运动与距离成比例的运动。
缓动和弹动都是比例运动,两者关系紧密,都是将对象从已有位置移动到目标位置的方法。缓动是指物体滑动到目标点就停下来了。弹动是指物体来回地反弹一会儿,最终停在目标点的运动。
两者的共同点:
- 有一个目标点
- 确定物体到目标点的距离
- 运动与距离是成正比的----距离越远,运动的程度越大
两者的不同点:
- 运动和距离成正比的方式不一样。缓动是指 速度 与 距离 成正比(物体离目标越远,物体运动的速度越快,当物体运动到很接近目标点时,物体几乎就停下来了);而弹动是指 加速度 与 距离 成正比(物体离目标点越远,加速度就快速增大,当物体很接近目标点时,加速度变得很小,但它还是在加速;当它越过目标点之后,随着距离的变大,反向加速度也随之变大,就会把它拉回了,最终在摩擦力的作用下停住。)
**2、缓动**
缓动的类型不止一种,我们可以“缓入”(ease in)到一个位置,也可以从一个位置“缓出”(ease out)。
在现实生活中,相信大家都坐过公交(自动过滤土豪),在宽敞的马路上时,公交会高速前进,特别是车少的道路,司机会开的尽可能快(限速之内),当快要达到一个站点时,司机就会适当的减速。当公交还有几米就要停下来的时候,速度已经很慢很慢了。这就是一种缓动。
**如何实现缓动呢?**
一般来说,我们会如下处理:
- 为运动确定一个小于1且大于0的小数作为比例系数(easing)
- 确定目标点
- 计算物体与目标点的距离
- 计算速度,速度=距离 * 比例系数
- 用当前位置加上速度来计算新的位置
- 不断重复第3步到第5步,直到物体到达目标点
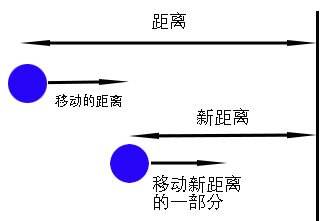
缓动的整个过程并不复杂,我们需要知道距离(物体与目标点(target)之间,变化值)、比例系数(easing,速度除以距离)。
```
dx = targetX - ball.x;
dy = targetY - ball.y;
easing = vx / dx; => vx = dx * easing;
easing = vy / dy; => vy = dy * easing;
```
根据《速度与加速度》那一章的公式:
```
ball.x += vx; => ball.x += dx*easing; => ball.x += (targetX - ball.x) * easing;
ball.y += vy; => ball.y += dy*easing; => ball.y += (targetY - ball.y) * easing;
```
最终缓动公式:
```
ball.x += (targetX - ball.x) * easing;
ball.y += (targetY - ball.y) * easing;
```
实例:canvas-demo/easing.html
关键代码:
```
var easing = 0.05;
var targetX = canvas.width - 10;
var targetY = canvas.height - 10;
```
在上面的例子中,我们将比例系数设为0.05,用变量easing表示,然后在循环中调用下面的代码:
```
ball.x += (targetX- ball.x)*easing; //每次循环中调用
```
这样简单的处理,就能实现刹车模式,这就是缓动的一种效果,你可以改变easing看看。
上面的例子中的目标点是canvas边界,其实,目标点是可以 变动 的,因为我们每次都会重新计算距离,所以只须在播放每一帧的时候知道目标点的位置,然后就可以计算距离和速度了。比如:将鼠标位置(mouse.x和mouse.y)作为目标点,你可以试试,会发现鼠标里的越远,小球就运动的越快。
这里还有一个关键性问题:**何时停止缓动**
不是到达目标点就停止缓动吗?估计这是你看到这的第一想法,你还可能立即想到下面判断公式:
```
if(ball.x === targetX && ball.y === targetY){
//到达目标点
}
```
这是理论上的判断,但是从数学的角度来看,下面的公式永远不会相等:
```
(ball.x + (targetX - ball.x) * easing) !== targetX
```
这是为什么呢?
这就涉及了 芝诺饽论 ,简单的理解是这样:为了把一个物体从A点移到B点,就必须把它先移到到A和B的中间点C,然后再移到C和B的中间点,然后再折半,不断地重复下去,每次移到到物体到距离目标点的一半,这样就会进入无穷循环下去,物体永远不会到达目标点。
我们来看看数学例子:物体从0的位置,要将它移到100,比例系数easing设为0.,5,然后将它每次移动距离的一半,过程如下:
- 从原点开始,在第一帧后,它移到到50
- 在第二帧后,移动到75
- 在第三帧后,移动到87.5
- 就这样循环下去,物体位置变化是93.75、96.875等,经过20帧后,它的位置是99.999809265
看到没有,它会离目标点越来越近,可是理论上是永远不会到达目标点的,所以上面的判断公式是永远不会返回true的。
但毕竟肉眼是无法分辨这么精确的位置变化的,有时候当ball.x 等于99的时候,我们在canvas上看就已经是到达终点了,所以这就产生了一个问题:多近才是足够近呢?
这就需要我们人为的指定一个特定值,判断物体到目标点的距离是否小于特定值,如果小于特定值,那我们就认为它到达终点了。
```
/*二维坐标*/
distance = Math.sqrt(dx * dx + dy * dy);
/*一维坐标*/
distance = Math.abs(dx)
if(distance < 1){
console.log('到达终点');
cancelAnimationFrame(requestID);
}
```
一般采取是否小于1来判断是否到达目标点,是为了停止动画,避免资源的浪费。
在tool.js工具类中,我们已经封装了停止` requestAnimaitonFrame` 动画的方法,就是 `cancelRequestAnimationFrame` ,参数是requestID。
```
var cancelAnimationFrame = function() {
return window.cancelAnimationFrame || window.webkitCancelAnimationFrame || window.mozCancelAnimationFrame || function(id) {
clearTimeout(id);
};
}();
```
当然,缓动并不仅仅适用于运动,它还可以应用很多属性:
**(1)旋转**
定义起始角度:
```
var rotation = 0;
var targetRotation = 360;
```
然后缓动:
```
rotation += (targetRotation - rotation) * easing;
object.rotation = rotation * Math.PI / 180;
```
别忘了弧度与角度的转换。
**(2)透明度**
设置起始透明度
```
var alpha = 0;
var targetAlpha = 1;
```
设置缓动:
```
alpha += (targetAlpha - alpha) * easing;
object.color = 'rgba(255,0,0,' + alpha + ')';
```
**2、弹动**
前面提到过,在弹动中,物体的 加速度 与它到目标点的 距离 成正比。
现实中的弹动例子:在橡皮筋的一头系上一个小球(悬空,静止时的点就是目标点),另一头固定起来。当我们用力(力足够大)去拉小球然后松开,我们会看到小球反复的上下运动几次后,速度逐渐慢下来,停在目标点上。(没玩过橡皮筋的,可以去实践一下)
**2.1 一维坐标上的弹动**
实现弹动的代码和缓动类似,只不过将速度换成了加速度(spring)。
```
var spring = 0.1;
var targetX = canvas.width / 2;
var vx = 0;
```
计算小球到目标点的距离:
```
var dx = targetX - ball.x;
```
计算加速度,与距离是成比例的:
```
var ax = dx * spring;
```
将加速度加在速度上,然后添加到小球的位置上:
```
vx += ax;
ball.x += vx;
```
我们先模拟一下整个弹动过程,假设小球的x是0,vx也是0,目标点的x是100,spring变量的值为0.1:
- 用距离(100)乘以spring,得到10,将它加在vx上,vx变为10,把vx加在小球的位置上,小球的x为10
- 下一帧,距离(100-10)为90,加速度为90乘以0.1,等于9,加在vx上,vx就变为19,小球的x变为了29
- 再下一帧,距离是71,加速度是7.1,vx是26.1,小球的x为55.1
重复几次后,随着小球一帧一帧的靠近目标,加速度变得越来越小,速度越来越快,虽然增加的幅度在减小,但还是在增加。
当小球越过了目标点,到底了x轴上的117点时,与目标点的距离是-17(100-117)了,也就是加速度会是-1.7,当速度加上这个加速度时,小球就会减速运动。
这就是弹动的过程。
看看实例(目标点定在canvas的中心点,相当于将球从中心点拉到左边,然后松开):canvas-demo/spring.html
上面的例子中,小球是不是有种被弹簧拉扯的效果,但是,由于小球的摆动幅度不变,它现在貌似停不下来,这不科学,现实中,它的摆动幅度应该是越来越小(由于阻力),弹动的越来越慢,直到停下来,所以为了更真实,我们应该给它添加一个摩擦力friction:
```
var friction = 0.95;
```
然后改变速度:
```
vx += ax;
vx *= friction;
ball.x += vx;
```
当小球停止时,我们就不需去执行动画了,所以我们还需要判断是否停止:
```
if(Math.abs(vx) < 0.001){
vx += ax;
vx *= friction;
ball.x += vx;
};
```
注意:当你的初始速度vx为0时,这样是无法进入弹动的,对我来说,我会加入一个变量判断是否开始弹动:
```
var isBegin = false;
if(!isBegin || Math.abs(vx) < 0.001){
vx += ax;
vx *= friction;
ball.x += vx;
isBegin = true;
};
```
**2.2 二维坐标上的弹动**
二维坐标上的弹动与一维坐标上的弹动并没有大区别,只不过前者多了y轴上的弹动。
初始化变量:
```
var vx = 0;
var ax = 0;
var vy = 0;
var ay = 0;
var dx = 0;
var dy = 0;
```
设置x、y轴上的弹动:
```
if(Math.abs(vx) > 0.001){
dx = targetX - ball.x;
ax = dx * spring;
vx += ax;
vx *= friction;
ball.x += vx;
dy = targetY - ball.y;
ay = dy * spring;
vy += ay;
vy *= friction;
ball.y += vy;
};
```
例子(将canvas的中心点作为目标点,相当于一开始将球从中心点拉到左上角,然后松开):canvas-demo/spring2.html
上面的例子依旧是一个直线弹动,你可以试试将vx或vy的初始值增大一点,设为50,会有意想不到的动画。
**2.3 向移动的目标点弹动**
在缓动中也说过,目标点不一定是固定,而对于弹动也一样,目标点可以是移动的,只需在每一帧改变目标点的坐标值即可,比如:鼠标坐标是目标点:
```
dx = targetX - ball.x;
dy = targetY - ball.y;
/*改成如下*/
dx = mouse.x - ball.x;
dy = mouse.y - ball.y;
```
**2.4 绘制弹簧**
在上面的几个例子中,虽然有了弹簧的效果,可是始终还是没看到橡皮筋所在,所以我们有必要来将橡皮筋绘画出来:
```
ctx.beginPath();
ctx.moveTo(ball.x,ball.y);
ctx.lineTo(mouse.x,mouse.y);
ctx.stroke();
```
实例:canvas-demo/spring3.html
为了更真实,你还可以加上重力加速度:
```
var gravity = 2;
vy += gravity;
```
注意:在物理学中,重力是一个常数,只由你所在星球的质量来决定的。理论上,应该保持gravity值不变,比如0.5,然后给物体增加一个mass(质量)属性,比如10,然后用mass乘以gravity得到5(依旧用gravity变量表示)。
**2.5 链式弹动**
链式运动是指物体A以物体B为目标点,物体B又以物体C为目标点,诸如此类的运动。
看看例子,然后再来分析:canvas-demo/spring4.html
在上面的例子中,我们创建了四个球,每个球都有自己的属性 vx 和 vy ,初始为0。在动画函数 animation 里,我们使用Array.forEach()方法来绘制每一个球,然后连线。在 connect 方法中,你可以看到第一个球的目标点是鼠标位置,剩余的球都是以上一个球(balles[i-1])的坐标位置为目标点来弹动。
我还给球添加了重力:
```
ball.vy += gravity;
```
运动结束时,四个球会连成一串。
**2.6 目标偏移量**
在上面的所有例子中,我们使用的都是模拟橡皮筋,如果我们模拟的是一个弹性金属材料制作的弹簧会怎样呢?是不是球还可以这样自由的运动呢?
答案是否定,在现实中,你无法让物体顶着弹簧从一头运动到另一头,还不明白?看下图:

假设上面的图中连接球和固定点是金属弹簧,那么球是永远都到不了固定点的位置的,因为弹簧是有体积的,会把球挡住,而且一旦弹簧收缩到它正常的长度,它就不会对小球施加拉力了,所以,真正的目标点,其实是弹簧处于松弛(拉伸)状态时,系着小球那一端的那个点(这个点是变化的)。
那如何确定目标点呢?
其实,从我上面的图你就应该想到,要用三角函数,因为我们知道球的位置、固定点的位置,那我们就可以获得球与固定点之间的夹角 θ ,当然,我们还需要定义一个弹簧的长度(springLength),比如:100。
计算目标点的代码如下:
```
dx = ball.x - fixedX;
dy = ball.y -fixedY;
angle = Math.atan2(dy,dx);
targetX = fixedX + Math.cos(angle) * springLength;
targetY = fixedY + Math.sin(angle) * springLength;
```
又到了例子时刻(以canvas的中心点为固定点,弹簧长度为100,小球可拖动):canvas-demo/spring5.html
试过上面例子了吗?我们再来看看上面的图:

图中的A点相当于例子中的固定点(也就是canvas的中心点),B点是弹簧(无压缩无拉伸)正常情况下的位置(也是弹动的目标点),C点就是你拖动小球然后松开鼠标的位置,那么AB之间的距离就是弹簧的长度100,而BC之间的距离就是小球弹动的距离了,同时,基于直角三角形,我们也很容易求得 θ 的值。
我们还定义了一个 getBound() 方法,传入球对象,返回一个矩形对象,也就是球的矩形边界。
例子的部分代码:
```
dx = ballA.x - mouse.x;
dy = ballA.y - mouse.y;
angle = Math.atan2(dy, dx); // 获取鼠标与球之间的夹角θ
//计算目标点坐标
targetX = mouse.x + Math.cos(angle) * springLength;
targetY = mouse.y + Math.sin(angle) * springLength;
ballA.vx += (targetX - ballA.x) * spring;
ballA.vy += (targetY - ballA.y) * spring;
ballA.vx *= friction;
ballA.vy *= friction;
ballA.x += ballA.vx;
ballA.y += ballA.vy;
```
**2.7 用弹簧连接多个物体**
我们还可以用弹簧连接多个物体,先从连接两个物体开始,让它们互相向对方弹动,移动其中一个,另一个就要跟随弹动过去:
上例子:canvas-demo/spring6.html
在上面的例子中,我们创建了两个Ball实例 ball0 和 ball1 ,都是可拖动的,ball0向ball1弹动,ball1向ball0弹动,而且它们之间有一定的偏移量,两者用弹簧连接。
springTo() 方法接受两个参数,第一个参数是移动物体,第二个参数是目标点。还要引入两个变量: ball0_dragging 和 ball1_dragging ,作为是否拖动小球的标志。
```
if(!ball0_dragging) {
springTo(ball0, ball1);
};
if(!ball1_dragging) {
springTo(ball1, ball0);
};
```
下面让我们加入第三个球ball2:canvas-demo/spring7.html
**总结**
本章主要介绍了两个比例运动:缓动和弹动
缓动是指 速度 与 距离 成正比(物体离目标越远,物体运动的速度越快,当物体运动到很接近目标点时,物体几乎就停下来了);
弹动是指 加速度 与 距离 成正比(物体离目标点越远,加速度就快速增大,当物体很接近目标点时,加速度变得很小,但它还是在加速;当它越过目标点之后,随着距离的变大,反向加速度也随之变大,就会把它拉回了,最终在摩擦力的作用下停住。)
**附录**
**重要公式:**
(1)简单缓动
```
dx = targetX - object.x;
dy = targetY - object.y;
vx = dx * easing;
vy = dy * easing;
object.x += vx;
object.y += vy;
```
可精简:
```
vx = (targetX - object.x) * easing;
vy = (targetY - object.y) * easing;
object.x += vx;
object.y += vy;
```
再精简:
```
object.x += (targetX - object.x) * easing;
object.y += (targetY - object.y) * easing;
```
(2)简单弹动
```
ax = (targetX - object.x) * spring;
ay = (targetY - object.y) * spring;
vx += ax;
vy += ay;
vx *= friction;
vy *= friction;
object.x += vx;
object.y += vy;
```
可精简:
```
vx += (targetX - object.x) * spring;
vy += (targetY - object.y) * spring;
vx *= friction;
vy *= friction;
object.x += vx;
object.y += vy;
```
再精简:
```
vx += (targetX - object.x) * spring;
vy += (targetY - object.y) * spring;
object.x += (vx *= friction);
object.y += (vy *= friction);
```
(3)有偏移的弹动
```
dx = object.x - fixedX;
dy = object.y - fixedY;
targetX = fixedX + Math.cos(angle) * springLength;
targetY = fixedY + Math.sin(angle) * springLength;
```
';
移动物体
最后更新于:2022-04-02 01:28:30
## 移动物体
在第二章《用户交互》中,介绍过鼠标事件和触摸事件,可是到目前为止,我们用到鼠标事件和触摸事件还比较少,在本章中,我们将真正的进入交互动画中,主要介绍下面的内容:
- 如何判断鼠标是否落在某一个物体上
- 拖曳物体
- 投掷物体
**1、鼠标事件和触摸事件**
在介绍三种交互动画前,我们先来回顾一下鼠标事件和触摸事件。
**1.1 鼠标事件**
要触发鼠标事件,当然得有触发它的设备,不能光用眼睛盯着屏幕, 而触发鼠标事件的设备当然是鼠标,它会检测自身的移动以及按钮是否单击,随后计算机会触发一系列的事情:追踪鼠标指针的位置,确定鼠标按钮被按下时指针的位置,计算鼠标的移动速度以及确定何时发生双击事件等等。
简单的来说,鼠标要做的事就是 单击 和 移动 。
单击事件又可分解为两个事件: 鼠标键按下 的事件及 按键弹起 的事件,大多数情况下,这两个事件是同时发生的,但鼠标要做的例外一个事 移动 时,在这两个事件之间还会多了一个事件: 按下、移动、再释放 。
在《用户交互》这一章曾经说过,我们无法捕捉到canvas上的任何绘制图形、线等,所以我们只能将事件绑定到canvas元素上,然后通过计算鼠标相对于canvas元素的坐标来判断鼠标落在哪个绘制到canvas上的物体上。
下面我们就来讲解一下如何判断鼠标是否落在某一个物体(比如前面我们多次绘制的ball)上。
还是用图来分析:

如上图所示,一般情况下,当要检测鼠标是否落在物体上时,我们会将物体放置在一个矩形区域(图中的红框)内,该矩形区域也称为物体的边界,然后通过获取鼠标位置,判断是否落在矩形区域内即可。
当然,你要捕捉的物体必须有x、y、width与height属性(不管是直接获取还是计算得出),前面我们已经知道如何获取鼠标相对canvas的坐标了,接下来往tool对象中添加一个方法 containsPoint() ,该函数接受三个参数,第一个是物体(body)对象(包括x、y、width与height属性),第二个和第三个参数则分别代表鼠标位置,返回值为true或false,判断一个指定的坐标位置是否位于矩形边界内。
```
tool.containsPoint = function(body, x, y){
return !(x < body.x || x > (body.x + body.width)
|| y < body.y || y > (body.y + body.height));
};
```
containsPoint()方法返回false表示不在矩形边界内,否则在矩形边界内。
将物体包裹在一个矩形之内,这是我们大多数情况下采取的方法,如果你想更加精确,那就要进行更加精确的计算了,比如:物体是圆形,那你就要使用三角函数来计算鼠标位置和圆心的距离:
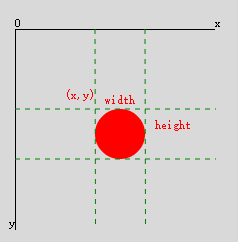
```
dx = point.x -body.x;
dy = point.y - body.y;
dist = Math.sqrt(dx*dx + dy*dy)
if(dist < body.radius){
console.log('鼠标移到物体上');
}
```
实例:canvas-demo/containsPoint.html
**1.2 触摸事件**
捕获触摸事件与捕获鼠标事件并没有太大的区别,在tool.captureMT()方法中,我已经将触摸事件和鼠标事件封装在了一起。
与鼠标事件不同的是,要触发触摸事件的不是鼠标,而是手指、触摸笔等等,而且鼠标会一直都在,而手指却不是一直处在触摸状态,所以添加一个isPressed属性,用于判断屏幕上是否有手指在触摸。
```
var isPressed = false;
function touchstart(event){
isPressed = true; //
};
function touchend(event){
isPressed = false;
};
```
**2、移动物体**
**2.1. 拖曳物体**
拖曳物体其实就是通过不断更新物体的坐标位置使其追随鼠标指针的位置。
拖曳圆球看看:canvas-demo/drag.html
关键代码:
```
ball.x = event.point.x;
ball.y = event.point.y;
```
**2.2 投掷物体**
投掷物体就是用鼠标选中一个物体,拖曳着它向某个方向移动,松开鼠标后,物体沿着拖曳的方向继续移动。
在投掷物体时,必须在拖曳物体的过程中计算物体的速度向量,并在释放物体时将这速度向量赋给物体。比如,如果你以每帧10个像素的速度向左拖曳小球,那么在你释放球时,它的速度向量应该是vx = -10。
那么如何计算出物体被拖曳时的速度向量,只需按照如下计算:
```
速度向量 = 新的位置 - 旧的位置。
```
在动画中,我们以帧为单位,所以时间也可以说是帧数。在拖曳物体时,它会在每一帧拥有一个新的位置,用当前帧的位置减去上一帧的位置,就可以计算出这一帧所移动的距离,这也就是每帧移动像素的速度向量值。
实例:拖曳物体,然后松开鼠标看看效果:canvas-demo/hurl.html
关键代码:
```
ball.speed.x = ball.x - oldX;
ball.speed.y = ball.y - oldY;
oldX = ball.x;
oldY = ball.y;
```
用小球当前的x、y轴坐标分别减去oldX与oldY,从而获得小球当前的速度向量,并将它们保存在球的速度中,最后将oldX与oldY变量更新为小球当前的位置。
**总结**
在这一章中,我们进一步了解了动画中的交互行为。掌握上面这些内容,你就可以在动画中实现对物体的拖曳、释放以及投资。
到目前为止,《canvas动画包教不包会》系列已经进行了七章,分别介绍了用户交互、三角函数、速度与加速度、边界和摩擦力、移动物体,这些是动画的基础知识,要想轻松的实现丰富的动画,就必须好好掌握这些。
';
边界与摩擦力
最后更新于:2022-04-02 01:28:28
## 边界与摩擦力
在前面的几章中,我们已经介绍了如何实现用户交互、利用三角函数实现物体旋转、给物体加上速度和加速度,利用这些知识,我们已经能够实现很丰富的动画效果,不过,似乎动画还不够真实,比如:物体可以无限的向左或向右移动、运动没有阻力,这就是这一章要处理的问题:边界和摩擦力。
**1、边界**
在一个游戏中,很少会让物体可以无限的向左或向右的移动,这就出现了“活动范围”这一词,我们在这里称为“边界”,边界也可以认为是我们用墙将物体围住,限制它的移动位置。
在canvas中,我们一般会设置三种边界:
- 整个canvas元素
- 大于canvas的区域,比如有一张大地图,物体可以在里面任意移动,移到边界时地图也跟着移动变化
- 小于canvas的区域,比如给物体设置了一个小房间,限制它的活动范围
**1.1 设置边界**
设置边界其实也是一种碰撞检测,只不过物体的碰撞对象变成了边界。
当我们将整个canvas大小作为边界时,我们可以很容易检测:
```
if(ball.x > canvas.width){
console.log('超出了右边界');
}else if(ball.x < 0){
console.log('超出了左边界');
};
if(ball.y > canvas.height){
console.log('超出了下边界');
}else if(ball.y < 0){
console.log('超出了上边界');
};
```
这里为什么是 ball.y < 0 是超出了上边界,请回想一下canvas的坐标是怎样的。
那么,如果不是基于整个canvas元素内,怎么做呢?一般以两个点作为范围点,看下图:
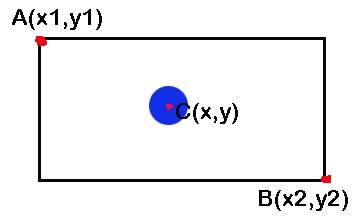
如何检测物体在这个范围内,代码如下:
```
if( ball.x < x1 ){
console.log('物体超出了左边界');
}else if( ball.x > x2){
console.log('物体超出了右边界');
};
if( ball.y < y1 ){
console.log('物体超出了上边界');
}else if( ball.y > y2){
console.log('物体超出了下边界');
};
```
当然,上面这段代码是检测物体的中心点是否越界,如果要检测是否完全越界,就需要加或减物体的高宽了:比如检测物体是否完全越出了左边界:
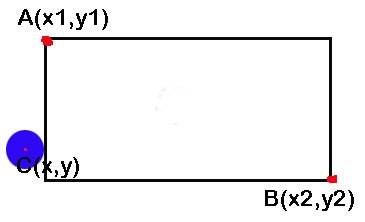
```
if( ball.x < (x1 - ball.radius)){
console.log('物体完全越出了左边界');
};
```
大多数情况下,我们不是单纯的检测物体是否越界,而是为了在物体越界后进行某些操作,当然,你也可以在物体越界后不做任何操作,不过这不是我们所推荐的。
当物体越界时,一般我们会进行以下4中选择操作:
- 移除物体
- 重置物体,也就是让物体所有状态恢复到原始位置
- 屏幕环绕:让同一个物体出现在边界内的另一个位置
- 物体反弹,也就是向反方向运动
**1.2 移除物体**
移除物体多用在多个物体在canvas上移动时,这时,我们一般将它们的引用保存到一个数组中,再通过遍历整个数组的来移动它们(前面的例子,我都是采取这种方式),这样,我们就可以使用 Array.splice 方法来移除数组中的某个物体了。
```
var balls = []; // 存放多个物体的数组
var ball = balls[i];
if(ball.x < x1 || ball.x > x2 || ball.y < y1 || ball.y > y2){
balls.splice(balls.indexof(ball),1);
i -= 1;
}
```
上面的检测越界条件是和检测在边界内的条件是不一样的。
注意:当你使用 Array.splice 方法在循环中移除元素后,需要加上 i -= 1,不然后续循环会出问题。当然,你也可以使用反向遍历,就不会存在这问题:
```
var i = balls.length;
while( i-- ){
if(ball.x < x1 || ball.x > x2 || ball.y < y1 || ball.y > y2){
balls.splice(balls.indexof(ball),1);
}
}
```
**1.3 重置物体**
重置物体其实就是重新设置物体的位置坐标。
在下面的例子,你会看到一个物体从上向下落下,当它离开canvas后,又有一个物体在同一个位置开始从上向下落下,看起来是不同的物体,其实是同一个,只不过每次它离开canvas后,都将它的 ball.y 设置为原始值,在这里是0。
实例:canvas-demo/animationResetObject.html
**1.4 屏幕环绕**
屏幕环绕的意思是当物体从屏幕左边移出,它就会在屏幕右边再次出现;当物体从屏幕上方移出,它又会出现在屏幕下方,反之亦然。
屏幕环绕和重置物体类似,都遵循着同一个物体的原则,只不过屏幕环绕是让其从一边出再从相反的一边进而已。
**1.5 反弹**
在让物体反弹之前,你需要检测物体何时离开屏幕,当它刚要离开时,要保持它的位置不变而仅改变它的速度向量,也可以说是速度值取反。
在检测何时反弹时,有一点需要注意,我们不能等到物体完全移出canvas才开始反弹,这显然和现实不符合,不知道你有没有玩过足球,当你将足球踢向墙壁时,你会看到球在撞墙后,停在那里并很快反弹回来。
当物体移到如下图位置,物体就要开始反弹:
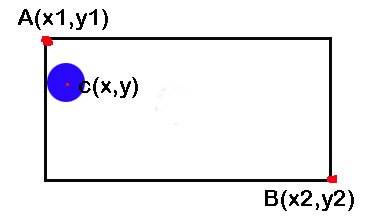
```
if( ball.x <= (x1 + ball.radius)){
ball.x = x1 + ball.width;
ball.speed.x *= -1;
}
```
在上面的代码中,我们将 -1 作为反弹系数,不过在现实中,反弹的速度总是会有所减小,这是因为能量损失,所以为了模拟更真实的动画,你可以将 -1 乘以一个百分比来实现能量损耗的效果。
```
ball.speed.x *= -0.8;
```
反弹的步骤如下:
- 检测物体是否越界
- 如果发生越界,立即将物体置回边界
- 反转物体的速度向量的方向,也可以说是速度取反。
实例: canvas-demo/oneDirection.html
**2、摩擦力(friction)**
摩擦力,又一物理概念,也可称为阻力,指两个互相接触的物体,当它们要发生或已经发生相对运动时,就会在接触面上产生一种阻碍相对运动的力。
上面是概念式的说法,简单的讲,摩擦力就是阻止你运动的力,它并不会改变你运动的方向,而只会让你慢慢减速,直至速度为0。
如果想让动画更加真实,很多时候我们都需要考虑摩擦力,那如何用代码实现呢?
**(1)精确方法**
上面也说到,摩擦力是阻止你运动的力,这就意味着,可以用速度向量减去摩擦力。更准确地说,只能沿着速度向量的方向减去与摩擦力相等的大小,而不能分别在x、y轴上减小速度向量,也可以这样理解,摩擦力必须与合速度相减,然后再根据减后的合速度分别求出x、y轴上的最终速度。
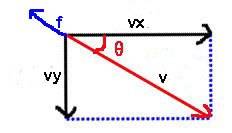
如下方式:
```
var v = Math.sqrt( vx * vx + vy * vy );
var angle = Math.atan2(vy,vx);
if(v > f){
v -= f;
}else{
v = 0;
};
vx = Math.cos(angle) * v;
vy = Math.sin(angle) * v;
```
**(2)约等方法**
约等方法是指将x、y轴上的速度向量乘以一个百分数,一个接近0.9的系数能很好的模拟出摩擦力的效果。
```
vx *= f;
vy *= f;
```
使用这种方法的好处就是不必去做条件判断,但它只能无限接近于0,不过由于JavaScript的精度约束,最后的结果也会变为0。
在上面的反弹中,反弹系数也是用这种方法。
**总结**
介绍了如何检测是否越界
越界后的处理方式:移除物体、重置物体、屏幕环绕、反弹
实现摩擦力的两种方法:精度方法、约等方法
**附录**
**重要公式:**
**(1)检测是否越界**
```
if( object.x - object.width / 2 > right ||
object.x + object.width / 2 < left ||
object.y - object.height / 2 > bottom ||
object.y + object.height / 2 < top){}
```
**(2)摩擦力(精度方法)**
```
var v = Math.sqrt( vx * vx + vy * vy );
var angle = Math.atan2(vy,vx);
if(v > f){
v -= f;
}else{
v = 0;
};
vx = Math.cos(angle) * v;
vy = Math.sin(angle) * v;
```
**(3)摩擦力(约等方法)**
```
vx *= friction;
vy *= friction;
```
';
速度与加速度
最后更新于:2022-04-02 01:28:25
## 速度与加速度
在上两章中,我们介绍了数学中三角函数的概念和使用,在这一章中,我们将介绍物理知识:速度向量与加速度。
真是坑爹!学完数学又要学习物理,真的是回到了初中......,不过你放心,这里介绍的都不是深奥的物理知识。
这一章的内容包括:
- 速度向量
- 加速度
- 附录:重要公式
**1、速度向量**
速度向量和速度并不等同,后者仅仅是前者的一部分,前者还包括了一个重要因素:方向,因此,速度向量也可以说是某个方向上的速度。
方向在动画中是极其重要的,就比如说,你做一个赛车游戏,要是连方向都搞不清楚,那岂不是常常发生连环车祸。
我们可以将速度向量分为两种:单轴上的速度向量和双轴上的速度向量
**1.1 单轴上的速度向量**
单轴上的速度向量也就是把速度向量只放到X轴(水平运动)或Y轴(垂直运动)上。

如上图所示,单轴上的速度向量可以有四个方向:
```
var vx = 1; //定义x轴速度
var vy = 1; //定义y轴速度
沿x轴正方向:ball.x += vx;
沿x轴反方向:ball.x -= vx;
沿y轴正方向:ball.y += vy;
沿y轴反方向:ball.y -= vy;
```
接下来我们模拟四个方向的运动(点击增加球按钮,随机生成四个方向运动圆球,在碰到边界时,会将速度 v 变为速度的负值 -v ,让其反方向运动):
实例:canvas-demo/oneDirection.html
关键代码:
```
ball.x += ball.speed.x;
// 或
ball.y += ball.speed.y;
```
这段代码就是让圆球沿着x轴或y轴运动。
边界检测(下一章会讲到)和反方向运动:
```
if(ball.x >= (canvas.width-ball.radius*2) || ball.x <= 0){
ball.speed.x = -ball.speed.x;
};
```
注意:canvas上的Y坐标轴的方向是和普通坐标轴的方向相反,如不清楚,可到三角函数那一章看坐标图,这里就不贴出了。
**1.2 双轴上的速度向量**
我们也可以将双轴上的速度向量看做是任意方向上运动。

下面做一个实例,就好像发射炮弹一样:
实例:canvas-demo/twoDirection.html
重要代码:
```
ball.x += 5;
ball.y += 4;
```
x轴的速度定为5,y轴的速度定为4。
当然,像上面这样直接在x方向和y方向上增加速度的情况比较少见,更多时候,我们都是知道物体在某个方向上以一定速度运动,这时,我们就需要求x方向和y方向上的速度了,怎么求呢?
接下来就要用到之前介绍的三角函数了。
举个例子:一个物体以每帧1像素的速度向45°(θ = 45°,v = 1)的方向移动

就像上图一样,我们可以将速度v分解成vx和vy,这恰好就是x方向和y方向。我们已经知道一个角θ=45°,还有一条斜边v = 1,那利用Math.cos与Math.sin函数就可以很简单的求到vx和vy了。
```
vx = Math.cos(45 * Math.PI / 180) *1;
vy = Math.sin(45 * Math.PI / 180)*1;
```
获得了vx和vy,我们就可以像单轴上的速度一样分别给x方向和y方向添加速度了。
注意:一个物体隐含了许多可供调整的属性,并不仅仅局限于速度,还有旋转速度、颜色深浅等等,要想让物体做更多的动画效果,就必须学会将速度变化的原理应用到其他属性上,俗称举一反三。
**2、加速度**
加速度也是向量,包括了方向,一般用a来表示加速度。
讲到加速度,在生活中最明显的就是汽车启动了,当你启动汽车,踩下油门,汽车的速度就会增加,从0开始,过一两秒后,速度将提升到每小时5~6公里,随后又变成10公里每小时等。
从计算的角度来看,加速度就是增加到速度向量上的数值。
加速度也可分为:单轴加速度和双轴加速度
**2.1 单轴加速度**
单轴加速度和单轴上的速度向量类似,也是只沿着x轴或y轴运动,同样有四个方向。

看例子(你可以按键盘左键和右键看看):
当你按左键时,你会发现速度越来越慢,多度减速时甚至反方向运动了,当你按右键时,速度回越来越快,最后飞出了canvas。
```
ball.speed.x += ax;
ball.x += ball.speed.x;
function keyLeft(){
ax += (-0.01);
};
function keyRight(){
ax += 0.02;
};
window.tool.captureKeyDown({"37":keyLeft,"39":keyRight}); // 这事件在用户交互一章中已封装的
```
**2.2 双轴加速度**
双轴加速度和双轴上的速度是同一个道理,通过加速度分解,你可以得到x轴上的加速度和y轴上的加速度,这里就不出例子了,你可以试着改变上面的例子,给物体加入一个任何角度的加速度。
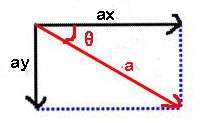
**2.3 重力加速度(g)**
我想大家对重力加速度并不陌生,这是我们在生活中感觉最明显,比如你往上跳一跳,随后便会自然落下,这就是给你添加了一个重力加速度。
重力加速度简单来说就是y轴上的一个加速度,在计算加速度时,我们只需将重力加速度g添加到每一帧的vy(y轴上的加速度和)属性上就可以了。
我们来模拟一下重力加速度(点击按钮):
原理:小球从空中自由降落至地面,然后弹起,循环往复,直到它最终速度为零停留在地面。
代码解析:
```
var g = 0.3; //重力加速度
var bounce = -0.7; //反弹系数
//边界检测
if(ball.y >= (canvas.height - ball.radius * 2)) {
ball.y = canvas.height - ball.radius * 2;
ball.speed.y *= bounce; //反复相乘,最后趋近于0
};
ball.speed.y += g;
ball.y += ball.speed.y;
```
**总结**
速度和加速度是动画的基础元素,其中两者都是向量,包括了一个重要因素:方向。
要学会应用 分解 和 合成 ,将速度或加速度分解到x、y轴上,然后将每条轴上的加速度或速度相加,然后再分别与物体的位置坐标相加。
**附录:**
**总要公式:**
(1)将角速度分解为x、y轴上的速度向量
```
vx = speed * Math.cos(angle)
vy = spedd * Math.sin(angle)
```
(2)将角加速度分解为x、y轴上的加速度
```
ax = force * Math.cos(angle)
ay = force * Math.sin(angle)
```
(3)将加速度加入速度向量
```
vx += ax;
vy += ay;
```
(4)将速度向量加入位置坐标
```
object.x += vx;
object.y += vy;
```
';
三角函数(二)
最后更新于:2022-04-02 01:28:23
## 三角函数(二)
这一章依旧是关于三角函数的,让我们来看看使用三角函数能做些什么,内容如下:
波形(平滑的上下运动、线性运动、脉冲运动)
圆周运动与椭圆运动
两点间的距离(勾股定律)
**1、波形**
看到下面这张邪恶的波形图,我们又要感慨一声:初中的回忆

没错,这就是正弦波,也就是正弦曲线(sin()),上面的图只是正弦函数的一个周期[0,2π],对应正弦值范围是:[-1,1]。如果你要取sin()在[0,2π]之间的值,我们可以这样获取:
```
for(var angle = 0; angle < Math.PI*2; angle += 0.1){
console.log(Math.sin(angle));
}
```
上面的值并没有包括-1、1和0,因为以0.1的步长是不会出现π或π/2的整数倍。
再次提醒,Math对象中所有关于三角函数的计算都是基于 弧度 的。
还是那句话,不要纸上谈兵,下面还是用例子说话:
**(1)平滑的上下运动**
实例:canvas-demo/sin.html
在上面的例子中,我们通过 angle+=0.1 改变angle的值,然后传递给Math.sin(),它会根据angle值的变化,返回从0到1再变到-1最后回到0的值,最终就产生了跟正弦波轨迹一样的平滑运动,如下代码:
```
ball.x += 1;
ball.y += Math.sin(ball.angle) * 10;
ball.angle += 0.1;
```
**(2)线性运动**
线性运动也可称为匀速运动,也就是物体朝着一个方向做匀速(等速度)运动。对于线性运动,这里就不给例子了,你只需将上面平滑运动中的例子内这段代码注释掉就是线性运动:
ball.angle += 0.1;
**(3)脉冲运动**
我们都知道,动画并不仅仅局限于坐标的变化,还有很多,比如:物体颜色、物体大小等等。而脉冲运动就是通过改变物体的大小(比例)而形成的。
实例:canvas-demo/pulsingMotion.html
在这个例子中,给Ball类添加了一个scale属性,表示Ball的大小比例,通过下面的代码改变比例:
```
ball.scale = 1 + Math.sin(ball.angle);
ball.angle += 0.1;
ball.radius = 10 * ball.scale;
```
特别强调,不要让上面的这些例子限制了你的思维,你可以利用正弦波进行任何属性的改变,相信你会得到各种有趣酷炫的视觉效果。
**2、圆周运动与椭圆运动**
**(1)圆周运动**
圆周运动是指绕着一个完整的圆形轨迹做运动,也可以这样理解,物体离圆心的距离不变的运动。
表达式:
```
sin(θ) = x1 / R => x1 = R * sin(θ)
cos(θ) = y1 / R => y1 = R * cos(θ)
```
实例:
主要计算公式(radius为50):
```
ball.x = centerX + Math.sin(ball.angle)*radius;
ball.y = centerY + Math.cos(ball.angle)*radius;
```
**(2)椭圆运动**
我们将椭圆的长轴和短轴分别设为2a和2b。
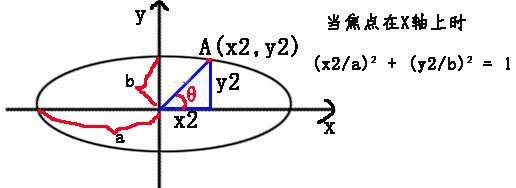
表达式:
```
x2 = a * cosθ
y2 = b * sinθ
```
椭圆和正圆的唯一区别就是,正圆上任何一个点到圆心的距离都是一样的,而椭圆却不一样。
实例:canvas-demo/ellipseMotion.html
与正圆运动不一样的是,椭圆运动是根据两个半径值来计算的(radiusX为100,radiusY为50):
```
ball.x = centerX + Math.sin(ball.angle)*radiusX;
ball.y = centerY + Math.cos(ball.angle)*radiusY;
```
**3、两点间的距离(勾股定律)**
很多时候,我们需要知道两个物体间的距离(对于后面的碰撞检测很重要),这时我们又要用到数学了,那就是勾股定律(要知道详情,请百度)。
假设有点A(x1,y1)和点B(x2,y2),要求它们的距离很简单:
```
var dx = x2 - x1;
var dy = y2 - y1;
var dist = Math.sqrt(dx * dx + dy * dy);
```
dist就是两点间的距离了。其实在上面我们用到了很多,比如圆的半径,就是这样计算来的,只不过它有一个特殊点(原点(0,0)),就相等于 x1 = 0, y1 = 0 。
**附录:**
**(1)角度与弧度互转**
```
radians = degrees * Math.PI /180
degrees = radians * 180 / Math.PI
```
**(2)旋转(弧度)**
```
dx = point.x - object.x;
dy = point.y - object.y;
boject.rotation = Math.atan2(dy, dx);
```
**(3)平滑运动**
```
value = center + Math.sin(angle) * range;
angle += speed;
```
**(4)圆形运动**
```
xposition = centerX + Math.cos(angle) * radius;
yposition = centerY + Math.sin(angle) * radius;
angle += speed;
```
**(5)椭圆运动**
```
xposition = centerX + Math.cos(angle) * radiusX;
yposition = centerY + Math.sin(angle) * radiusY;
angle += speed;
```
**(6)两点间的距离**
```
var dx = x2 - x1;
var dy = y2 - y1;
var dist = Math.sqrt(dx * dx + dy * dy);
```
';
三角函数(一)
最后更新于:2022-04-02 01:28:21
## 三角函数
三角函数、勾股定理、两点间的距离,还有sin、cos、tan,是不是感觉这些很是熟悉,恍惚间回到了初中时代,想起了数学课本上那一道道让人头疼的三角函数。今天就让我们来回顾一下!
对于三角函数,我会分为两章来讲,这一章主要讲三角函数和反三角函数的基本公式:
- 角度与弧度的转换
- Math对象中的三角函数
- 实例:指红针
在下一章主要讲我们能利用三角函数做些什么:
波形(平滑的上下运动、线性运动、脉冲运动)
圆周运动与椭圆运动
两点间的距离(勾股定律)
现在我们就进入这一章的内容!
**1、三角函数**
**(1)角度和弧度**
角度和弧度都是角的度量单位,一弧度约等于57.2958°,反向计算可得360°(一个完整圆的角度)等于6.2832弧度(也就是2*PI),所以弧度(radians)和角度(degrees)的转换公式如下:
```
1弧度 = degrees * PI / 180;
1度 = radians * 180 / PI;
```
在JavaScript中是这样:
```
1弧度 = degrees * Math.PI / 180;
1度 = radians * 180 / Math.PI;
```
在后面,我们会经常用到这公式,如果记不住,可以写在纸上。
**(2)坐标系**
数学上的坐标系(下图左边)和网页坐标系(下图右边)是有所区别的:
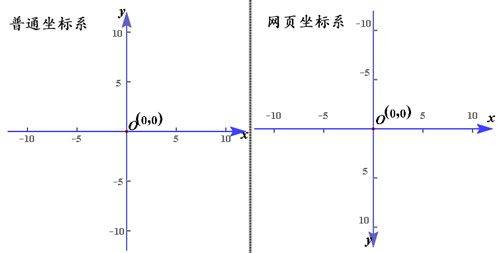
从上图可以看到,网页坐标系相当于普通坐标系绕着x轴旋转180度得来的,两者y轴的正方向相反,而且网页是以左上角为坐标原点的,也就是o点,当然,就像上图一样,网页上也会有负方向。
也正是因为y轴正方向的不同,所以导致角度测量也是不同的,如下图:
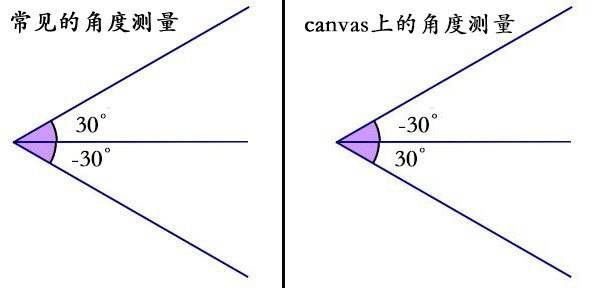
实质就是绕着X轴旋转180度后得到canvas上的坐标,角度的正负很重要。
**(3)直角三角形**
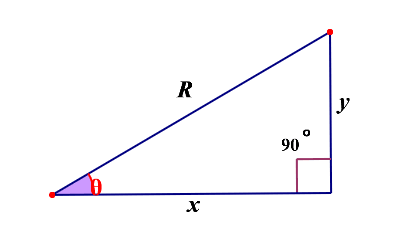
相信大家对直角三角形并不会陌生(留意这张图:x是邻边,y是对边,R是斜边,θ是角度),在数学上,有如下三角函数:
```
正弦:sin(θ) = y / R
余弦:cos(θ) = x / R
正切:tan(θ) = y / x
/*反三角函数*/
反正弦:arcsin(y/R) = θ
反余弦:arccos(x/R) = θ
反正切:arctan(y/x) = θ
```
看得是不是有点晕晕的,如果你还想完整的了解三角函数,建议百度。
在JavaScript的Math对象中,已经给我们封装好了这些方法,我们只需如下调用:
```
Math.sin(θ*Math.PI/180)
Math.cos(θ*Math.PI/180)
Math.tan(θ*Math.PI/180)
/*反三角函数*/
Math.asin(y/R)*(180/Math.PI) = θ
Math.acos(x/R)*(180/Math.PI) = θ
Math.atan(y/x)*(180/Math.PI) = θ
```
我想你应该也注意到了,在使用Math对象中的三角函数时,并不是直接的传入 θ 角度值,而是使用 `θ*180/Math.PI `得到的值,这是因为Math对象中的三角函数采用的弧度制,也就是说,传入的值是弧度,而不是角度,反三角函数得到的值也是弧度,而不是角度。
注意:使用Math对象的三角函数时,一定要留意角度和弧度的转换。
在这里,还要额外的说一个常用(可能你会一直用它,而忽略Math.atan())的方法:
```
Math.atan2(y,x)
```
Math.atan2()也是一个反正切函数,不过它接受两个参数:对边和邻边的长度,一般是X坐标和Y坐标。
**Math.atan()和Math.atan2()的区别**:
Math.atan(θ)和Math.atan2(x,y)两个方法除了传入参数不一样外,它们的返回值也会有所不同:
Math.atan2()返回值的范围是-PI到PI之间(不包括-PI)的值,而Math.atan()返回的值范围是-PI/2到PI/2(不包括-PI/2和PI/2)之间。
我们再用一个例子来看一下区别:
下面使用 Math.atan() ,结果如下:
```
A: Math.atan(-1/2) -0.5 => Math.atan(-1/2)*180/Math.PI -26.57°
B: Math.atan(1/2) 0.5 => Math.atan(1/2)*180/Math.PI 26.57°
C: Math.atan(1/-2) -0.5 => Math.atan(1/-2)*180/Math.PI -26.57°
D: Math.atan(-1/-2) 0.5 => Math.atan(-1/-2)*180/Math.PI 26.57°
```
光是从上面得到的值,我们无法判断到底是三角形A还是C或B还是D。
而使用 Math.atan2() :
```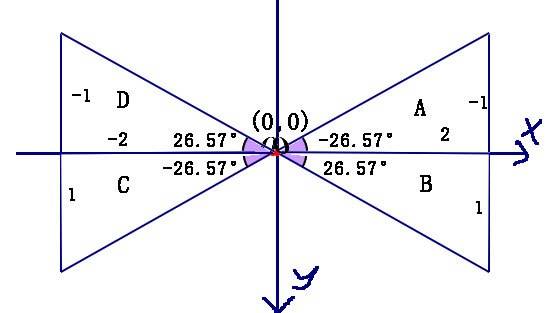
A: Math.atan2(-1,2) -0.5 => Math.atan2(-1,2)*180/Math.PI -26.57
B: Math.atan2(1,2) 0.5 => Math.atan2(1,2)*180/Math.PI 26.57
C: Math.atan2(1,-2) 2.7 => Math.atan2(1,-2)*180/Math.PI 153.43
D: Math.atan2(-1,-2) -2.7 => Math.atan2(-1,-2)*180/Math.PI -153.43
```
显然,使用Math.atan2()得到的值都是不一样的,这样我们就可以很容易的知道第一个是A三角形,第二个是B三角形,第三个是C三角形,第四个是D三角形。
注意:这里不需记住具体值,只需记住正负号,还有大于90还是小于90。
同一个三角形得到不同的值是因为两个方法测量角的方式不一样(下面是两种方法对D三角形的测量):
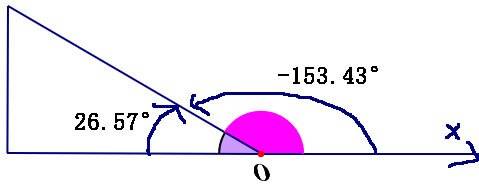
注意:这个函数很有用。
光说不练这肯定不符合TG法则,所以下面我们来搞一个例子,相信大家都玩过指南针吧,当然,这里我们不会搞出一个指南针,而是搞出一个“指红针”。
canvas-demo/disk.html
对这里例子,还是直接上图:
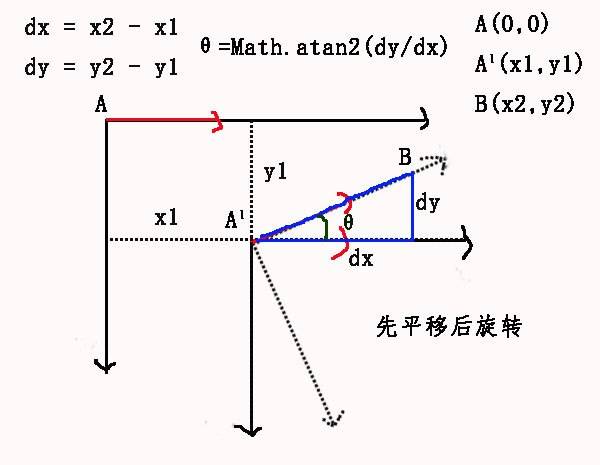
在上面的图中,红色代表了三角磁铁的指向,先平移,A1是向右平移x1,向下平移y1后的A,B是鼠标点坐标,根据鼠标坐标和三角磁铁的中心点计算出需要旋转的角度,也就是上面的θ,然后旋转cavnas。
注意:每次绘制不同的三角磁铁时,必须先使用save()保存状态,再绘制完一个三角磁铁后,再用restore()恢复上一次的状态,不然的话,每次旋转平移都会在上一次的基础上平移旋转,而不是以(0,0)点平移,后旋转了。如果不明白,可以试试不用save()和restore(),看看会发生什么。
**总结**
常用的三角函数有:`Math.sin()、Math.cos()、Math.tan()`
常用的反三角函数有:`Math.asin()、Math.acos()、Math.atan()、Math.atan2()`(用的频率很高)
一般情况下,对canvas做变形(平移、旋转、缩放等)操作时,都要使用`save()`和`restore()`来保存和恢复状态。
';
用户交互
最后更新于:2022-04-02 01:28:18
## 用户交互
没有用户交互的动画就跟电视上的动画片一样,不管谁看,都是一个样,千年不变。显然,这不是我们想要的,很多时候,我们需要用户参与进来,这样才能产生丰富的动画效果,这就是专门用一章来了解用户交互的原因。
用户交互是基于用户事件的,这些事件通常包括鼠标事件、键盘事件以及触摸事件。
**1、事件绑定和事件取消**
在这里,并不会对JavaScript事件做过多的解析,如需详细了解,可看这里:《[JavaScript学习笔记整理(10):Event事件](http://ghmagical.com/article/page/id/nXCnaSLsuyWd)》。
由于我们无法获取到canvas上绘制的线和形状,所以只能在canvas上绑定事件,然后根据鼠标相对canvas的位置而确定在哪个线或形状上,比如要为canvas绑定鼠标点击(mousedown)事件:
```
function MClick(event){
console.log('鼠标点击了canvas');
};
canvas.addEventListener('mousedown',MClick,false);
```
当鼠标在canvas上点击时,每次都会在控制台打印出"鼠标点击了canvas"。
我们使用removeEventListener()还可以取消鼠标点击事件:
```
canvas.removeEventListener('mousedown',MClick,false);
```
上面的代码就取消了canvas上的鼠标点击事件,不过要注意的是,这里传入的只能是函数名,而不能传入函数体,而且只是取消了鼠标点击事件中的MClick事件处理函数,如果还绑定了其他的鼠标点击事件,依然有效。
**2、鼠标事件**
鼠标事件有很多种,常见的有下面这些:
```
mousedown
mouseup
click
dblclick
mousewheel
mousemove
mouseover
mouseout
```
当为元素注册一个鼠标事件处理函数时,它还会为函数传入一个MouseEvent对象,这个对象包含了多个属性,比如我们接下来要用的`pageX`和`pageY`。
`pageX` 和 `pageY` 分别是触点相对HTML文档左边沿的X坐标和触点相对HTML文档上边沿的Y坐标。只读属性。
注意:当存在滚动的偏移时,pageX包含了水平滚动的偏移,pageY包含了垂直滚动的偏移。
显然,通过pageX和pageY获取到的只是相对于HTML文档的鼠标位置,并不是我们想要的,我们需要的是相对于canvas的鼠标位置,如何得到呢?
只需用pageX和pageY分别减去canvas元素的左偏移和上偏移距离就可得到相对canvas的鼠标位置:
```
canvas.addEventListener('mousedown',function(event){
var x = (event.pageX || event.clientX + document.body.scrollLeft +document.documentElement.scrollLeft) - canvas.offsetLeft;
var y = (event.pageY || event.clientY + document.body.scrollTop +document.documentElement.scrollTop) - canvas.offsetTop;
},false);
```
在上面的代码中,还使用了clientX和clientY,这是为了兼容不同的浏览器。
注意:这里的canvas偏移位置是相对HTML文档的。
为了避免后面重复写代码,我们先来造个轮子,创建一个tool.js文件(后续都会用到),在里面创建一个全局对象tool,然后将需要的方法传入进去:
```
window.tool = {};
window.tool.captureMouse = function(element,mousedown,mousemove,mouseup){
/*传入Event对象*/
function getPoint(event){
event = event || window.event; /*为了兼容IE*/
/*将当前的鼠标坐标值减去元素的偏移位置,返回鼠标相对于element的坐标值*/
var x = (event.pageX || event.clientX + document.body.scrollLeft + document.documentElement.scrollLeft);
x -= element.offsetLeft;
var y = (event.pageY || event.clientY + document.body.scrollTop + document.documentElement.scrollTop);
y -= element.offsetTop;
return {x:x,y:y};
};
if(!element) return;
/*为element元素绑定mousedown事件*/
element.addEventListener('mousedown',function(event){
event.point = getPoint(event);
mousedown && mousedown.call(this,event);
},false);
/*为element元素绑定mousemove事件*/
element.addEventListener('mousemove',function(event){
event.point = getPoint(event);
mousemove && mousemove.call(this,event);
},false);
/*为element元素绑定mouseup事件*/
element.addEventListener('mouseup',function(event){
event.point = getPoint(event);
mouseup && mouseup.call(this,event);
},false);
};
```
轮子已经造好了,使用方法也很简单:
```
/*回调函数会传入一个event对象,event.point中包含了x和y属性,分别对应鼠标相对element的X坐标和Y坐标,函数内的this指向绑定元素element*/
function mousedown(event) {
console.log(event.point.x,event.ponit.y);
console.log(this);
document.querySelector('.pointX').innerHTML = event.point.x;
document.querySelector('.pointY').innerHTML = event.point.y;
};
function mousemove(event) {
console.log(event.point);
document.querySelector('.pointX1').innerHTML = event.point.x;
document.querySelector('.pointY1').innerHTML = event.point.y;
var x = event.point.x;
var y = event.point.y;
var radius = 5;
/*清除整个canvas画布*/
ctx.clearRect(0,0,canvas.width,canvas.height);
ctx.fillStyle = 'red';
ctx.beginPath();
/*绘制一个跟随鼠标的圆*/
ctx.arc(x,y,radius,0,2*Math.PI,true);
ctx.fill();
ctx.closePath();
};
function mouseup(event) {
console.log(event.point);
document.querySelector('.pointX2').innerHTML = event.point.x;
document.querySelector('.pointY2').innerHTML = event.point.y;
};
/*传入canvas元素,后面是传入三个函数,分别对应mousedown、mousemove和mouseup事件的事件处理函数*/
tool.captureMouse(canvas, mousedown, mousemove, mouseup);
```
上面代码中的mousedown、mousemove和mouseup三个方法都是自定义的,三个回调函数都会传入一个event对象(element当前绑定事件的event对象), event.point 是我定义的,它包含了 x 和 y 属性,分别对应鼠标相对element(也就是元素左上角)的X坐标和Y坐标,函数内的 this 指向绑定元素element。
实例(获取鼠标坐标):canvas-demo/captureMousePoint.html
**3、触摸事件**
常用触摸事件:
touchstart
touchmove
touchend
触摸事件和鼠标事件最大的区别在于,触摸有可能会在同一时间有多个触摸点,而鼠标永远都是只有一个触摸点。
要获取触摸点相对canvas的坐标,同样是根据event对象中的pageX和pageY,还有canvas相对于HTML文档的偏移位置来确定,不过由于触摸点可能有多个,它传递给事件处理函数的是TouchEvent对象,使用方法稍微有一点区别:
```
canvas.addEventListener('touchstart',function(event){
var touchEvnet = event.changedTouches[0];
var x = (touchEvent.pageX || touchEvent.clientX + document.body.scrollLeft+ document.documentElement.scrollLeft );
x -= canvas.offsetLeft;
var y = (touchEvent.pageY || touchEvent.clientY + document.body.scrollTop + document.documentElement.scrollTop );
y -= canvas.offsetTop;
});
```
注意上面代码中的 event.changedTouches[0] ,这是获取当前触摸事件引发的所有Touch对象中第一个触摸点的Touch对象,当然还有 event.touches[0] 也可以获取到,它是获取所有仍然处于活动状态的触摸点中的第一个。
对于触摸事件,我们也可以在tool这个轮子里添加一个captureTouch方法,你可以用手机或者打开浏览器控制台模拟手机模式看看这个例子:触摸例子(canvas-demo/captureTouchPoint.html)
```
window.tool.captureTouch = function(element,touchstart,touchmove,touchend){
/*传入Event对象*/
function getPoint(event){
event = event || window.event;
var touchEvent = event.changedTouches[0];
/*将当前的鼠标坐标值减去元素的偏移位置,返回鼠标相对于element的坐标值*/
var x = (touchEvent.pageX || touchEvent.clientX + document.body.scrollLeft + document.documentElement.scrollLeft);
x -= element.offsetLeft;
var y = (touchEvent.pageY || touchEvent.clientY + document.body.scrollTop + document.documentElement.scrollTop);
y -= element.offsetTop;
return {x:x,y:y};
};
if(!element) return;
/*为element元素绑定touchstart事件*/
element.addEventListener('touchstart',function(event){
event.point = getPoint(event);
touchstart && touchstart.call(this,event);
},false);
/*为element元素绑定touchmove事件*/
element.addEventListener('touchmove',function(event){
event.point = getPoint(event);
touchmove && touchmove.call(this,event);
},false);
/*为element元素绑定touchend事件*/
element.addEventListener('touchend',function(event){
event.point = getPoint(event);
touchend && touchend.call(this,event);
},false);
};
```
下面我会将鼠标事件和触摸事件结合在一起,添加一个captureMT方法:
```
window.tool.captureMT = function(element, touchStartEvent, touchMoveEvent, touchEndEvent) {
'use strict';
var isTouch = ('ontouchend' in document);
var touchstart = null;
var touchmove = null
var touchend = null;
if(isTouch){
touchstart = 'touchstart';
touchmove = 'touchmove';
touchend = 'touchend';
}else{
touchstart = 'mousedown';
touchmove = 'mousemove';
touchend = 'mouseup';
};
/*传入Event对象*/
function getPoint(event) {
/*将当前的触摸点坐标值减去元素的偏移位置,返回触摸点相对于element的坐标值*/ event = event || window.event;
var touchEvent = isTouch ? event.changedTouches[0]:event;
var x = (touchEvent.pageX || touchEvent.clientX + document.body.scrollLeft + document.documentElement.scrollLeft);
x -= element.offsetLeft;
var y = (touchEvent.pageY || touchEvent.clientY + document.body.scrollTop + document.documentElement.scrollTop);
y -= element.offsetTop;
return {x: x,y: y};
};
if(!element) return;
/*为element元素绑定touchstart事件*/
element.addEventListener(touchstart, function(event) {
event.point = getPoint(event);
touchStartEvent && touchStartEvent.call(this, event);
}, false);
/*为element元素绑定touchmove事件*/
element.addEventListener(touchmove, function(event) {
event.point = getPoint(event);
touchMoveEvent && touchMoveEvent.call(this, event);
}, false);
/*为element元素绑定touchend事件*/
element.addEventListener(touchend, function(event) {
event.point = getPoint(event);
touchEndEvent && touchEndEvent.call(this, event);
}, false);
};
```
在上面的代码中,我们先检测是移动还是PC('ontouchend' in document),然后将布尔值传给变量 isTouch ,然后定义使用mouse事件还是touch事件,获取坐标点时,也是根据 isTouch的值来绝对直接用 event还是用 event.changedTouches[0] 。
**4、键盘事件**
键盘事件只有三个:
keydown 按下键盘时触发该事件。
keyup 松开键盘时触发该事件。
keypress 只要按下的键并非Ctrl、Alt、Shift和Meta,就接着触发keypress事件(较少用到)。
只要用户一直按键不松开,就会连续触发键盘事件,触发顺序如下:
```
keydown
keypress
keydown
keypress
(重复以上过程)
keyup
```
在这里,我们只来了解keydown和keyup就足够了。
我们会将事件绑定到window上,而不是canvas上,因为如果将键盘事件绑定到某个元素上,那么该元素只有在获取到焦点时才会触发键盘事件,而绑定到window上时,我们可以任何时候监听到。
一般来说,我们比较关心键盘上的箭头按钮(上下左右):
```
function keyEvent(event){
switch (event.keyCode){
case 38:
keybox.innerHTML = '你点击了向上箭头(↑)';
break;
case 40:
keybox.innerHTML = '你点击了向下箭头(↓)';
break;
case 37:
keybox.innerHTML = '你点击了向左箭头(←)';
break;
case 39:
keybox.innerHTML = '你点击了向右箭头(→)';
break;
default:
keybox.innerHTML = '你点击了其他按钮';
};
};
window.addEventListener('keydown',keyEvent,false);
```
String.fromCharCode(e.keyCode);
为了便利,我将keydown和keyup事件封装成这样:
```
window.tool.captureKeyDown = function(params) {
function keyEvent(event) {
params[event.keyCode]();
};
window.addEventListener('keydown', keyEvent, false);
};
window.tool.captureKeyUp = function(params) {
function keyEvent(event) {
params[event.keyCode]();
};
window.addEventListener('keyup', keyEvent, false);
};
```
需要时只需如下调用:
```
function keyLeft(){
keybox.innerHTML = '你点击了向左箭头(←)';
};
function keyRight(){
keybox.innerHTML = '你点击了向右箭头(→)';
};
window.tool.captureKeyEvent({"37":keyLeft,"39":keyRight});
```
传入一个键值对形式的对象,键名是键码,键值是调用函数。
实例(先点击下面,让其获取到焦点):
canvas-demo/keyboard.html
在后面会有个附录,有完整的键码值对应表。不过,我们不需要去死记硬背,你可以使用到再去查或者使用插件 keycode.js(可到这里下载:https://github.com/lamberta/html5-animation):
```
```
其实keycode.js里定义了一个全局变量keycode,然后以键值对的形式定义键名和键名值。
**总结**
用户交互在游戏动画中是很重要的一步,所以掌握用户交互的各种事件是必须的,而且特别强调一点是,要学会制造轮子,避免重复的编写相同的代码,不过,初学者建议多敲 。
附录:
';
基础动画
最后更新于:2022-04-02 01:28:16
## 基础动画
实现动画,我们首先想到的肯定是`setTimeout`和`setInterval`,这两个在这里就不细说了。
除了这两个外,我们还可以使用`requestAnimationFrame()`这个方法。
`requestAnimationFrame` 是专门为实现高性能的帧动画而设计的一个API
`requestAnimationFrame()`这个方法是用来在页面重绘之前,通知浏览器调用一个指定的函数,以满足开发者操作动画的需求。这个方法接受一个函数为参,该函数会在重绘前调用。
注意: 如果想得到连贯的逐帧动画,函数中必须重新调用 `requestAnimationFrame()`。
如果你想做逐帧动画的时候,你应该用这个方法。这就要求你的动画函数执行会先于浏览器重绘动作。通常来说,被调用的频率是每秒60次,但是一般会遵循W3C标准规定的频率。如果是后台标签页面,重绘频率则会大大降低。
回调函数只会被传入一个DOMHighResTimeStamp参数,这个参数指示当前被 requestAnimationFrame 序列化的函数队列被触发的时间。因为很多个函数在这一帧被执行,所以每个函数都将被传入一个相同的时间戳,尽管经过了之前很多的计算工作。这个数值是一个小数,单位毫秒,精确度在 10 µs。
参数 callback 在每次需要重新绘制动画时,会调用这个参数所指定的函数。这个回调函数会收到一个参数,这个 DOMHighResTimeStamp 类型的参数指示当前时间距离开始触发 `requestAnimationFrame` 的回调的时间。 返回值 requestID 是一个长整型非零值,作为一个唯一的标识符.你可以将该值作为参数传给 `cancelAnimationFrame()` 来取消这个回调函数。
```
if (!window.requestAnimationFrame) {
window.requestAnimationFrame = (window.webkitRequestAnimationFrame ||
window.mozRequestAnimationFrame ||
window.msRequestAnimationFrame ||
window.oRequestAnimationFrame ||
function (callback) {
return window.setTimeout(callback, 1000 / 60 );
});
}
if (!window.cancelAnimationFrame) {
window.cancelAnimationFrame = (window.cancelRequestAnimationFrame ||
window.webkitCancelAnimationFrame || window.webkitCancelRequestAnimationFrame ||
window.mozCancelAnimationFrame || window.mozCancelRequestAnimationFrame ||
window.msCancelAnimationFrame || window.msCancelRequestAnimationFrame ||
window.oCancelAnimationFrame || window.oCancelRequestAnimationFrame ||
window.clearTimeout);
}
```
实例:canvas-demo/requestAnimationFrame.html:
```
```
';
截图保存
最后更新于:2022-04-02 01:28:14
## 截图保存
在canvas中绘出的图片只是`canvas`标签而已,并非是真正的图片,我们并不能保存,不过我们可以利用`canvas.toDataURL()`这个方法把canvas绘制的图形生成一幅图片,生成图片后,就能对图片进行相应的操作了。
首先我们定义用一个a标签定义下载的链接,然后再给a设置下载的链接。
```
下载
var imageURL=canvas.toDataURL("image/jpeg")
```
当然,你也可以动态的设置下载的文件名
```
document.getElementById("download")setAttribute("download","abc.png");
document.getElementById("download").href=imageURL;
```
当然,我们也可以保存为另外的图片格式:image/png
注意:
- toDataURL() 是canvas的方法
- a的download属性只有 Firefox 和 Chrome 支持 download 属性。
';
合成与裁剪
最后更新于:2022-04-02 01:28:12
## 合成与裁剪
在我们绘制图形时,不同的图形会因为绘制的先后而有了层级关系。如果新绘制的图形和原有内容有重叠部分,在默认情况下,新绘制的图形是会覆盖在原有内容之上。
在HTML中,我们会添加z-index来修改层级关系,那么,在canvas里,我们如何修改呢?
我们可以利用 `globalCompositeOperation` 属性来改变。
```
globalCompositeOperation
```
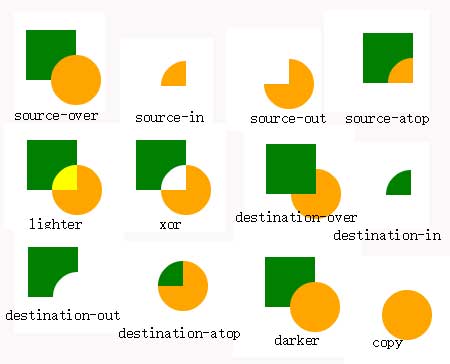
它共有12个可选值:
| 属性值 | 描述 |
| :---: | :---: |
| source-over | (默认值) 新图形会覆盖在原有内容之上 |
| source-in | 新图形仅仅会出现与原有内容重叠的部分,其他区域都变成透明的。 |
| source-out | 只有新图形中与原有内容不重叠的部分会被绘制出来 |
| source-atop | 新图形中与原有内容重叠部分会被绘制,并覆盖于原有内容之上。 |
| lighter | 两图形中重叠部分作加色处理 |
| xor | 重叠部分会变成透明 |
| destination-over | 会在原有内容之上绘制新图形 |
| destination-in | 原有内容与新图形重叠的部分会被保留,其他部分变成透明的 |
| destination-out | 原有内容中与新图形不重叠的部分会被保留 |
| destination-atop | 原有内容中与新图形重叠部分会被保留,并会在原有内容之上绘制新图形 |
| darker | 两图形重叠部分作减色处理 |
| copy | 只有新图形会被保留,其他都被清除掉 |
**裁切路径**
裁切路径和普通的 canvas 图形差不多,不同的是它的作用是遮罩,用来隐藏没有遮罩的部分。
如果和上面介绍的 `globalCompositeOperation` 属性作一比较,它可以实现与 source-in 和 source-atop 差不多的效果。最重要的区别是裁切路径不会在 canvas 上绘制东西,而且它永远不受新图形的影响。
我们用 `clip()` 方法来创建一个新的裁切路径。默认情况下,canvas 有一个与它自身一样大的裁切路径(也就是没有裁切效果)。
例子:
在这里,用` clip()` 方法创建一个圆形的裁切路径,裁切路径创建之后所有出现在它里面的东西才会画出来。
```
var img=new Image();
img.src="canvas_girl.jpg";
img.onload=function(){
cxt.beginPath();
cxt.arc(120,100,50,0,Math.PI*2,true);
cxt.clip();
cxt.drawImage(img,10,10);
}
```

';
坐标变换
最后更新于:2022-04-02 01:28:09
## 坐标变换
在Canvas中,变形包括移动、旋转、缩放、变形,跟CSS3中的2D转换类似。
(注意:原有内容不会受变形的影响,变形只是坐标变换,新绘制的图形就是在变换后的坐标轴里绘制的。)
下面我们来逐一的认识。
**一、移动(translate)**
canvas的移动是指移动 canvas 和它的原点到一个不同的位置。
```
translate(x, y)
```
translate 方法接受两个参数。x 是左右偏移量,y 是上下偏移量,如右图所示。
实例:canvas-demo/translate.html:
```
cxt.fillRect(0,0,100,100);
cxt.save();
cxt.translate(60,60);
cxt.fillStyle="red";
cxt.fillRect(0,0,100,100);
cxt.restore();
```
**二、旋转(rotate)**
用于以原点为中心旋转 canvas。
```
rotate(angle)
```
这个方法只接受一个参数:旋转的角度(angle),它是顺时针方向的,以弧度为单位的值。
实例:canvas-demo/tranform-rotate.html:
```
cxt.beginPath();
cxt.moveTo(0,50);
cxt.lineTo(100,50);
cxt.stroke();
cxt.save();
cxt.rotate(Math.PI/12);
cxt.strokeStyle="red";
cxt.beginPath();
cxt.moveTo(0,50);
cxt.lineTo(100,50);
cxt.stroke();
cxt.restore();
```
**三、缩放(scale)**
```
scale(x, y)
```
scale 方法接受两个参数。x,y 分别是横轴和纵轴的缩放因子,它们都必须是正值。值比 1.0 小表示缩小,比 1.0 大则表示放大,值为 1.0 时什么效果都没有。
实例:canvas-demo/scale.html:
```
cxt.fillRect(20,20,50,50);
cxt.save();
cxt.scale(.5,.5);
cxt.fillStyle="red";
cxt.fillRect(20,20,50,50);
```
**四、变形**
区别: transform()方法的行为相对于由 rotate(),scale(), translate(), or transform() 完成的其他变换。例如:如果我们已经将绘图设置为放到两倍,则 transform() 方法会把绘图放大两倍,那么我们的绘图最终将放大四倍。这一点和之前的变换是一样的。 但是setTransform()不会相对于其他变换来发生行为。它的参数也是六个,context.setTransform(a,b,c,d,e,f),与transform()一样。
```
transform(m11, m12, m21, m22, dx, dy)
```
参数:
m11 水平缩放绘图。 默认值1
m12 水平倾斜绘图。 默认值0
m21 垂直倾斜绘图。 默认值0
m22 垂直缩放绘图。 默认值1
dx 水平移动绘图。 默认值0
dy 垂直移动绘图。 默认值0
这个方法必须将当前的变形矩阵乘上下面的矩阵:
```
m11 m21 dx
m12 m22 dy
0 0 1
```
注意:该变换只会影响 transform() 方法调用之后的绘图。
```
setTransform(m11, m12, m21, m22, dx, dy)
```
参数: m11 水平缩放绘图。 默认值1 m12 水平倾斜绘图。 默认值0 m21 垂直倾斜绘图。 默认值0 m22 垂直缩放绘图。 默认值1 dx 水平移动绘图。 默认值0 dy 垂直移动绘图。 默认值0
**五、transform和translate、scale、rotate**
**5.1 translate**
```
cxt.translate(dx,dy)
```
cxt.transform (1,0,0,1,dx,dy)代替cxt.translate(dx,dy)。 也可以使用 cxt.transform(0,1,1,0.dx,dy)代替。
**5.2 scale**
```
cxt.scale(m11, m22):
```
也即是说可以使用 cxt.transform(m11,0,0,m22,0,0)代替cxt.scale(m11,m22); 也可以使用cxt.transform (0,m22,m11,0, 0,0);
**5.3 rotate**
```
rotate(θ)
```
也即是说可以用
- `cxt.transform(Math.cos(θ*Math.PI/180),Math.sin(θ*Math.PI/180)`
- `Math.sin(θ*Math.PI/180),Math.cos(θ*Math.PI/180),0,0)`可以替代`context.rotate(θ)`。
- 也可以使用 cxt.transform(-Math.sin(θ*Math.PI/180),Math.cos(θ*Math.PI/180), Math.cos(θ*Math.PI/180),Math.sin(θ*Math.PI/180), 0,0)替代。
';
保存和恢复
最后更新于:2022-04-02 01:28:07
在了解变形之前,我先介绍一下两个在你开始绘制复杂图形就必不可少的方法。
- save()方法用于保存canvas状态。
- restore()方法用于恢复到canvas的上一个状态。
Canvas 的状态就是当前画面应用的所有样式和变形的一个快照。
Canvas 状态是以堆(stack)的方式保存的。每一次调用` save()` 方法,当前的状态就会被保存进堆中(类似数组的push());而每一次调用`restore()`方法,就会将当前状态从堆中移除(类似数组的pop())。这种状态包括:
- 当前应用的变形(即移动,旋转和缩放)
- 当前的裁切路径(使用clip()方法裁切)
- strokeStyle, fillStyle, globalAlpha, lineWidth, lineCap, lineJoin, miterLimit, shadowOffsetX, shadowOffsetY, shadowBlur, shadowColor, globalCompositeOperation,font,textAlgin和textBaseline的值.
你可以调用任意多次 save ()方法。 每一次调用 restore() 方法,上一个保存的状态就从堆中弹出,所有设定都恢复。
实例:canvas-demo/save.html:
```
cxt.fillStyle="red";
cxt.fillRect(10,10,50,50);
cxt.save();
cxt.fillStyle="blue";
cxt.fillRect(20,20,30,30);
cxt.restore();
cxt.fillRect(30,30,10,10);
```
我们第一步先设置了填充色为红色,画了一个大正方形,然后保存状态;第二步将填充色设置为蓝色,画了一个小一点正方形;跟着调用restore()恢复状态,也就是恢复填充色为红色的状态,再画了一个更小的正方形。
到目前为止所做的动作和前面章节的都很类似。不过一旦我们调用 restore,状态堆中最后的状态会弹出,并恢复所有设置。如果不是之前用 save 保存了状态,那么我们就需要手动改变设置来回到前一个状态,这个对于两三个属性的时候还是适用的,一旦多了,我们的代码将会猛涨。
';
像素操作
最后更新于:2022-04-02 01:28:05
## 像素操作
**一、ImageData对象**
ImageData对象中存储着canvas对象真实的像素数据,它包含以下几个只读属性: width 图片宽度,单位是像素 height 图片高度,单位是像素 data 包含着RGBA格式的整型数据,范围在0至255之间(包括255)。
我们具体来看看`data`属性:
`data` 属性返回一个对象,该对象包含指定的 ImageData 对象的图像数据。
对于 ImageData 对象中的每个像素,都存在着四方面的信息,即 RGBA 值:
R - 红色(0-255)
G - 绿色(0-255)
B - 蓝色(0-255)
A - alpha 通道(0-255; 0 是透明的,255 是完全可见的)
color/alpha 信息以数组形式存在,并存储于 ImageData 对象的 data 属性中。
**二、 创建一个ImageData对像**
有两个版本的 `createImageData()` 方法:
**2.1 以指定的尺寸(以像素计)创建新的 ImageData 对象**
```
var imgData=cxt.createImageData(width,height);
```
一个新的具体特定尺寸的ImageData对像。所有像素被预设为透明黑。
实例:canvas-demo/createImageData.html:
下面的代码中,我创建了一个`100*100`像素的 ImageData 对象,然后为每个像素添加颜色
```
var imgData=cxt.createImageData(100,100);
for(var i=0;i
';
图像与视频
最后更新于:2022-04-02 01:28:03
## 图像与视频
基础语法:
```
drawImage(image, sx, sy, sWidth, sHeight, dx, dy, dWidth, dHeight)
```
参数:
- image:绘制到上下文的元素。允许任何的 canvas 图像源。例如:HTMLImageElement,HTMLVideoElement,或者 HTMLCanvasElement。
- dx:目标画布的左上角在目标canvas上 X 轴的位置。
- dy:目标画布的左上角在目标canvas上 Y 轴的位置。
- dWidth:在目标画布上绘制图像的宽度。 允许对绘制的图像进行缩放。 如果不说明, 在绘制时图片宽度不会缩放。
- dHeight:在目标画布上绘制图像的高度。 允许对绘制的图像进行缩放。 如果不说明, 在绘制时图片高度不会缩放。
- sx:需要绘制到目标上下文中的,源图像的矩形选择框的左上角 X 坐标。
- sy:需要绘制到目标上下文中的,源图像的矩形选择框的左上角 Y 坐标。
- sWidth:需要绘制到目标上下文中的,源图像的矩形选择框的宽度。如果不说明,整个矩形从坐标的sx和sy开始,到图像的右下角结束。
- sHeight:需要绘制到目标上下文中的,源图像的矩形选择框的高度。
要绘制图像,我们首先要获得图像:
**第一种:直接获取**
```
 ```
**第二种:动态创建**
```
```
获得了源图对象,我们就可以使用 `drawImage()` 方法将它渲染到 canvas 里。
`drawImage()` 方法有三种形态:
**(1) 绘制图片默认大小**
```
drawImage(image, x, y)
```
image 是 image 或者 canvas 对象或video对象,x 和 y 是其在目标 canvas 里的起始坐标。
实例:canvas-demo/drawImage1.html:
```
```
会将图片完整的绘制在画布上。
**(2) 绘制并设置大小**
```
drawImage(image, x, y, width, height)
```
前面三个参数和第一种使用方式的参数含义一样,不过,这个方法多了2个参数:width 和 height,这两个参数用来控制 当图像画入时绘制的大小。
实例:canvas-demo/drawImage2.html:
```
```
**(3) 切片**
```
drawImage(image, sx, sy, sWidth, sHeight, dx, dy, dWidth, dHeight)
```
第一个参数和其它的是相同的,都是一个图像或者另一个 canvas 的引用。其它8个参数中,前4个是定义图像源的切片位置和大小,后4个则是定义切片的目标在canvas上显示的位置和大小。
实例:canvas-demo/drawImage3.html:
```
```
**视频截图**
除了将图像、canvas绘制到canvas上外,drawImage()方法的第一个参数还可以是video对象,这也是我们可以实现播放视频的关键。
实例:canvas-demo/video.html:
```
```
注意:出于安全考虑,HTML5 Canvas 规范不允许我们保存和修改其他域中的图像。
```
**第二种:动态创建**
```
```
获得了源图对象,我们就可以使用 `drawImage()` 方法将它渲染到 canvas 里。
`drawImage()` 方法有三种形态:
**(1) 绘制图片默认大小**
```
drawImage(image, x, y)
```
image 是 image 或者 canvas 对象或video对象,x 和 y 是其在目标 canvas 里的起始坐标。
实例:canvas-demo/drawImage1.html:
```
```
会将图片完整的绘制在画布上。
**(2) 绘制并设置大小**
```
drawImage(image, x, y, width, height)
```
前面三个参数和第一种使用方式的参数含义一样,不过,这个方法多了2个参数:width 和 height,这两个参数用来控制 当图像画入时绘制的大小。
实例:canvas-demo/drawImage2.html:
```
```
**(3) 切片**
```
drawImage(image, sx, sy, sWidth, sHeight, dx, dy, dWidth, dHeight)
```
第一个参数和其它的是相同的,都是一个图像或者另一个 canvas 的引用。其它8个参数中,前4个是定义图像源的切片位置和大小,后4个则是定义切片的目标在canvas上显示的位置和大小。
实例:canvas-demo/drawImage3.html:
```
```
**视频截图**
除了将图像、canvas绘制到canvas上外,drawImage()方法的第一个参数还可以是video对象,这也是我们可以实现播放视频的关键。
实例:canvas-demo/video.html:
```
```
注意:出于安全考虑,HTML5 Canvas 规范不允许我们保存和修改其他域中的图像。
';
文本
最后更新于:2022-04-02 01:28:00
## 文本
canvas 提供了两种方法来渲染文本:
```
fillText(text, x, y [, maxWidth])
```
在指定的(x,y)位置填充指定的文本,绘制的最大宽度是可选的:
```
strokeText(text, x, y [, maxWidth])
```
在指定的(x,y)位置绘制文本边框,绘制的最大宽度是可选的。
当然,我们也可以改变文本的样式:
| 属性 | 描述 | 范例 |
| :---: | :---: | :---: |
| font | 当前我们用来绘制文本的样式. 这个字符串使用和 CSS font 属性相同的语法. 默认的字体是 10px sans-serif。 | ctx.font="30px Arial"; |
| textAlign | 文本对齐选项. 可选的值包括:start, end, left, right, center. 默认值是 start。 | ctx.textAlign = 'end' |
| textBaseline | 基线对齐选项. 可选的值包括:top, hanging, middle, alphabetic, ideographic, bottom。默认值是 alphabetic。 | ctx.textBaseline = 'top' |
| direction | 文本方向。可能的值包括:ltr, rtl, inherit。默认值是 inherit。 | ctx.direction = 'ltr' |
font属性的语法:
```
font = 'style variant weight size/line-height family'
```
- style(font-style):字体样式,可选值:normal, italic, oblique
- variant(font-variant):字体变体,可选值:normal, small-caps
- weight(font-weight):字体粗细,可选值:normal, bold, bolder, lighter, 100 - 900
- size/line-height:字号和行高
- family(font-family):字体
**文本测量**
canvas提供了一个方法:
```
measureText()
```
`measureText()`方法返回的对象中,包含一个名为`width`的属性,它的值代表你传递给该方法的文本所占据的宽度。
';
圆形与圆弧
最后更新于:2022-04-02 01:27:58
## 圆形与圆弧
**arc()**
绘制圆弧或者圆,我们使用`arc()`方法
```
arc(x, y, radius, startAngle, endAngle, anticlockwise)
```
- x:圆弧中心(圆心)的 x 轴坐标。
- y:圆弧中心(圆心)的 y 轴坐标。
- radius:圆弧的半径。
- startAngle:圆弧的起始点, x轴方向开始计算,单位以弧度表示。
- endAngle:圆弧的终点, 单位以弧度表示。
- anticlockwise 可选:可选的Boolean值 ,如果为 true,逆时针绘制圆弧,反之,顺时针绘制。
注意:`arc()`函数中的角度单位是弧度,不是度数。角度与弧度的js表达式:
```
radians=(Math.PI/180)*degrees。
```
实例:canvas-demo/arc.html:
```
cxt.beginPath();
cxt.arc(70,70,50,0,Math.PI/2,true);
cxt.stroke();
cxt.beginPath();
cxt.arc(180,70,50,0,Math.PI/2,false);
cxt.stroke();
cxt.beginPath();
cxt.arc(300,70,50,0,Math.PI/2,true);
cxt.fill();
cxt.beginPath();
cxt.arc(400,70,50,0,Math.PI/2,false);
cxt.fill();
```
**arcTo()**
`arcTo()`方法用于在画布上创建介于两个切线之间的弧/曲线。
```
arcTo(x1, y1, x2, y2, radius)
```
- x1:第一个控制点的 x 轴坐标。
- y1:第一个控制点的 y 轴坐标。
- x2:第二个控制点的 x 轴坐标。
- y2:第二个控制点的 y 轴坐标。
- radius:圆弧的半径。
实例:canvas-demo/arcTo.html:
```
```
';
路径
最后更新于:2022-04-02 01:27:56
## 路径
路径是通过不同颜色和宽度的线段或曲线相连形成的不同形状的点的集合。一个路径,甚至一个子路径,都是闭合的。利用路径绘制,我们可以绘制出任意图形。
路径绘制的步骤:
- 需要创建路径起始点。
- 使用画图命令去画出路径。
- 把路径封闭。
- 一旦路径生成,就能通过描边或填充路径区域来渲染图形。
以下是所要用到的函数:
新建一条路径,生成之后,图形绘制命令被指向到路径上生成路径。
```
beginPath()
```
闭合路径之后图形绘制命令又重新指向到上下文中。
```
closePath()
```
这个方法会通过绘制一条从当前点到开始点的直线来闭合图形。如果图形是已经闭合了的,即当前点为开始点,该函数什么也不做。
通过线条来绘制图形轮廓。
```
stroke()
```
通过填充路径的内容区域生成实心的图形。
```
fill()
```
注意:当你调用fill()函数时,所有没有闭合的形状都会自动闭合,所以你不需要调用closePath()函数。但是调用stroke()时不会自动闭合。
**移动笔触**
将笔触移动到指定的坐标x以及y上
```
moveTo(x,y)
```
绘制一条从当前位置到指定x以及y位置的直线
```
lineTo(x,y)
```
例子:
```
cxt.beginPath();
cxt.moveTo(150,150);
cxt.lineTo(150,250);
cxt.lineTo(300,250);
cxt.stroke();
cxt.closePath();
```

```
cxt.beginPath();
cxt.moveTo(400,400);
cxt.lineTo(400,500);
cxt.lineTo(500,500);
cxt.fill();
```

**pointInPath()**
pointInPath()方法用来判断一个点是否在当前路径上。如果在,则返回true。
';