三角函数(一)
最后更新于:2022-04-02 01:28:21
## 三角函数
三角函数、勾股定理、两点间的距离,还有sin、cos、tan,是不是感觉这些很是熟悉,恍惚间回到了初中时代,想起了数学课本上那一道道让人头疼的三角函数。今天就让我们来回顾一下!
对于三角函数,我会分为两章来讲,这一章主要讲三角函数和反三角函数的基本公式:
- 角度与弧度的转换
- Math对象中的三角函数
- 实例:指红针
在下一章主要讲我们能利用三角函数做些什么:
波形(平滑的上下运动、线性运动、脉冲运动)
圆周运动与椭圆运动
两点间的距离(勾股定律)
现在我们就进入这一章的内容!
**1、三角函数**
**(1)角度和弧度**
角度和弧度都是角的度量单位,一弧度约等于57.2958°,反向计算可得360°(一个完整圆的角度)等于6.2832弧度(也就是2*PI),所以弧度(radians)和角度(degrees)的转换公式如下:
```
1弧度 = degrees * PI / 180;
1度 = radians * 180 / PI;
```
在JavaScript中是这样:
```
1弧度 = degrees * Math.PI / 180;
1度 = radians * 180 / Math.PI;
```
在后面,我们会经常用到这公式,如果记不住,可以写在纸上。
**(2)坐标系**
数学上的坐标系(下图左边)和网页坐标系(下图右边)是有所区别的:
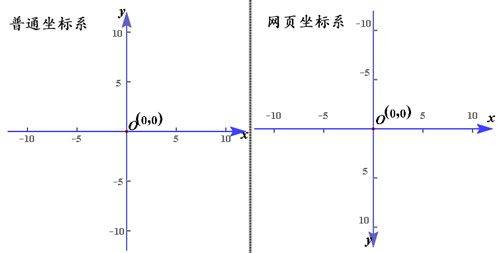
从上图可以看到,网页坐标系相当于普通坐标系绕着x轴旋转180度得来的,两者y轴的正方向相反,而且网页是以左上角为坐标原点的,也就是o点,当然,就像上图一样,网页上也会有负方向。
也正是因为y轴正方向的不同,所以导致角度测量也是不同的,如下图:
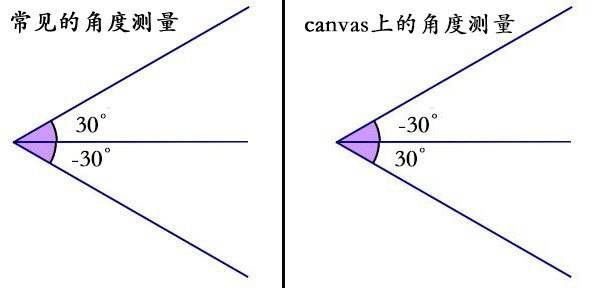
实质就是绕着X轴旋转180度后得到canvas上的坐标,角度的正负很重要。
**(3)直角三角形**
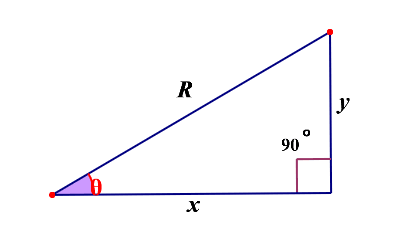
相信大家对直角三角形并不会陌生(留意这张图:x是邻边,y是对边,R是斜边,θ是角度),在数学上,有如下三角函数:
```
正弦:sin(θ) = y / R
余弦:cos(θ) = x / R
正切:tan(θ) = y / x
/*反三角函数*/
反正弦:arcsin(y/R) = θ
反余弦:arccos(x/R) = θ
反正切:arctan(y/x) = θ
```
看得是不是有点晕晕的,如果你还想完整的了解三角函数,建议百度。
在JavaScript的Math对象中,已经给我们封装好了这些方法,我们只需如下调用:
```
Math.sin(θ*Math.PI/180)
Math.cos(θ*Math.PI/180)
Math.tan(θ*Math.PI/180)
/*反三角函数*/
Math.asin(y/R)*(180/Math.PI) = θ
Math.acos(x/R)*(180/Math.PI) = θ
Math.atan(y/x)*(180/Math.PI) = θ
```
我想你应该也注意到了,在使用Math对象中的三角函数时,并不是直接的传入 θ 角度值,而是使用 `θ*180/Math.PI `得到的值,这是因为Math对象中的三角函数采用的弧度制,也就是说,传入的值是弧度,而不是角度,反三角函数得到的值也是弧度,而不是角度。
注意:使用Math对象的三角函数时,一定要留意角度和弧度的转换。
在这里,还要额外的说一个常用(可能你会一直用它,而忽略Math.atan())的方法:
```
Math.atan2(y,x)
```
Math.atan2()也是一个反正切函数,不过它接受两个参数:对边和邻边的长度,一般是X坐标和Y坐标。
**Math.atan()和Math.atan2()的区别**:
Math.atan(θ)和Math.atan2(x,y)两个方法除了传入参数不一样外,它们的返回值也会有所不同:
Math.atan2()返回值的范围是-PI到PI之间(不包括-PI)的值,而Math.atan()返回的值范围是-PI/2到PI/2(不包括-PI/2和PI/2)之间。
我们再用一个例子来看一下区别:
下面使用 Math.atan() ,结果如下:
```
A: Math.atan(-1/2) -0.5 => Math.atan(-1/2)*180/Math.PI -26.57°
B: Math.atan(1/2) 0.5 => Math.atan(1/2)*180/Math.PI 26.57°
C: Math.atan(1/-2) -0.5 => Math.atan(1/-2)*180/Math.PI -26.57°
D: Math.atan(-1/-2) 0.5 => Math.atan(-1/-2)*180/Math.PI 26.57°
```
光是从上面得到的值,我们无法判断到底是三角形A还是C或B还是D。
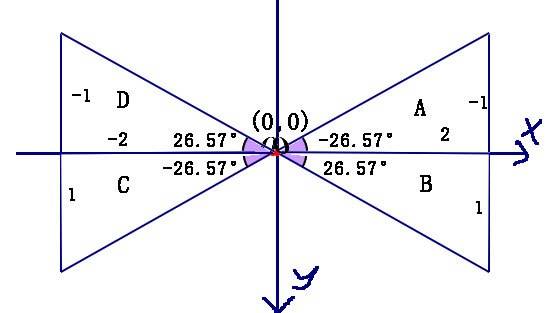
而使用 Math.atan2() :
```
A: Math.atan2(-1,2) -0.5 => Math.atan2(-1,2)*180/Math.PI -26.57
B: Math.atan2(1,2) 0.5 => Math.atan2(1,2)*180/Math.PI 26.57
C: Math.atan2(1,-2) 2.7 => Math.atan2(1,-2)*180/Math.PI 153.43
D: Math.atan2(-1,-2) -2.7 => Math.atan2(-1,-2)*180/Math.PI -153.43
```
显然,使用Math.atan2()得到的值都是不一样的,这样我们就可以很容易的知道第一个是A三角形,第二个是B三角形,第三个是C三角形,第四个是D三角形。
注意:这里不需记住具体值,只需记住正负号,还有大于90还是小于90。
同一个三角形得到不同的值是因为两个方法测量角的方式不一样(下面是两种方法对D三角形的测量):
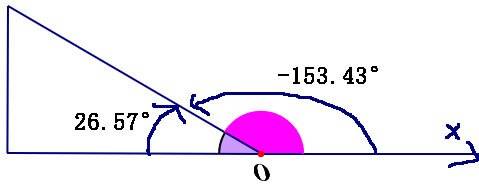
注意:这个函数很有用。
光说不练这肯定不符合TG法则,所以下面我们来搞一个例子,相信大家都玩过指南针吧,当然,这里我们不会搞出一个指南针,而是搞出一个“指红针”。
canvas-demo/disk.html
对这里例子,还是直接上图:
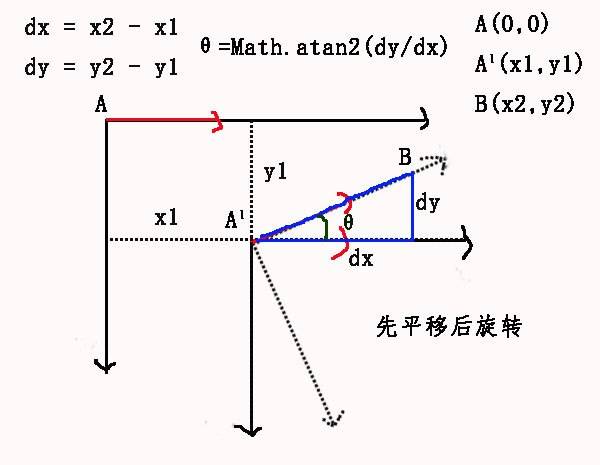
在上面的图中,红色代表了三角磁铁的指向,先平移,A1是向右平移x1,向下平移y1后的A,B是鼠标点坐标,根据鼠标坐标和三角磁铁的中心点计算出需要旋转的角度,也就是上面的θ,然后旋转cavnas。
注意:每次绘制不同的三角磁铁时,必须先使用save()保存状态,再绘制完一个三角磁铁后,再用restore()恢复上一次的状态,不然的话,每次旋转平移都会在上一次的基础上平移旋转,而不是以(0,0)点平移,后旋转了。如果不明白,可以试试不用save()和restore(),看看会发生什么。
**总结**
常用的三角函数有:`Math.sin()、Math.cos()、Math.tan()`
常用的反三角函数有:`Math.asin()、Math.acos()、Math.atan()、Math.atan2()`(用的频率很高)
一般情况下,对canvas做变形(平移、旋转、缩放等)操作时,都要使用`save()`和`restore()`来保存和恢复状态。
';