第十八课: Billboard和粒子
最后更新于:2022-04-01 04:37:53
# 第十八课:Billbard和粒子
公告板是3D世界中的2D元素。它既不是最顶层的2D菜单,也不是可以随意转动的3D平面,而是介于两者之间的一种元素,比如游戏中的血条。
公告板的独特之处在于:它位于某个特定位置,朝向是自动计算的,这样它就能始终面向相机(观察者)。
## 方案1:2D法
2D法十分简单。只需计算出点在屏幕空间的坐标,然后在该处显示2D文本(参见第十一课)即可。
~~~
// Everything here is explained in Tutorial 3 ! There's nothing new.
glm::vec4 BillboardPos_worldspace(x,y,z, 1.0f);
glm::vec4 BillboardPos_screenspace = ProjectionMatrix * ViewMatrix * BillboardPos_worldspace;
BillboardPos_screenspace /= BillboardPos_screenspace.w;
if (BillboardPos_screenspace.z < 0.0f){
// Object is behind the camera, don't display it.
}
~~~
就这么搞定了!
2D法优点是简单易行,无论点与相机距离远近,公告板始终保持大小不变。但此法总是把文本显示在最顶层,有可能会遮挡其他物体,影响渲染效果。
## 方案2:3D法
与2D法相比,3D法常常效果更好,也没复杂多少。我们的目的就是无论相机如何移动,都要让公告板网格正对着相机:

可将此视为模型矩阵的构造问题之简化版。基本思路是将公告板的各角落置于 (存疑待查)The idea is that each corner of the billboard is at the center position, displaced by the camera’s up and right vectors :
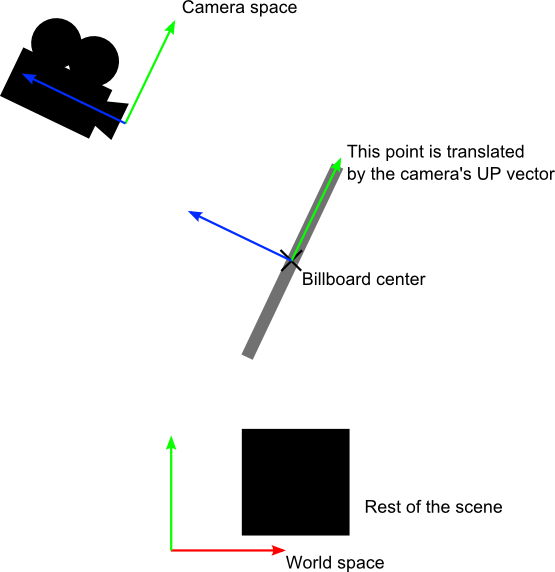
当然,我们仅仅知道世界空间中的公告板中心位置,因此还需要相机在世界空间中的up/right向量。
在相机空间,相机的up向量为(0,1,0)。要把up向量变换到世界空间,只需乘以观察矩阵的逆矩阵(由相机空间变换至世界空间的矩阵)。
用数学公式表示即:
CameraRight_worldspace = {ViewMatrix[0][0], ViewMatrix[1][0], ViewMatrix[2][0]}CameraUp_worldspace = {ViewMatrix[0][1], ViewMatrix[1][1], ViewMatrix[2][1]}
接下来,顶点坐标的计算就很简单了:
~~~
vec3 vertexPosition_worldspace =
particleCenter_wordspace
+ CameraRight_worldspace * squareVertices.x * BillboardSize.x
+ CameraUp_worldspace * squareVertices.y * BillboardSize.y;
~~~
- `particleCenter_worldspace`顾名思义即公告板的中心位置,以vec3类型的uniform变量表示。
- `squareVertices`是原始的网格。左顶点的`squareVertices.x`为-0.5(存疑待查),which are thus moved towars the left of the camera (because of the *CameraRight_worldspace)
- `BillboardSize`是公告板大小,以世界单位为单位,uniform变量。
效果如下。怎么样,是不是很简单?

为了保证内容完整性,这里给出`squareVertices`的数据:
~~~
// The VBO containing the 4 vertices of the particles.
static const GLfloat g_vertex_buffer_data[] = {
-0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
-0.5f, 0.5f, 0.0f,
0.5f, 0.5f, 0.0f,
};
~~~
## 方案3:固定大小3D法
正如上面所看到的,公告板大小随着相机与之的距离变化。有些情况下的确需要这样的效果,但血条这类公告板则需要保持大小不变。
~~~
vertexPosition_worldspace = particleCenter_wordspace;
// Get the screen-space position of the particle's center
gl_Position = VP * vec4(vertexPosition_worldspace, 1.0f);
// Here we have to do the perspective division ourselves.
gl_Position /= gl_Position.w;
// Move the vertex in directly screen space. No need for CameraUp/Right_worlspace here.
gl_Position.xy += squareVertices.xy * vec2(0.2, 0.05);
~~~

## 方案4:限制垂直旋转法
一些引擎以公告板表示远处的树和灯。不过,这些树可不能任意转向,**必须**是竖直的。So you need an hybrid system that rotates only around one axis.(存疑待查)
这个方案作为练习留给读者。
# 粒子(Particles)与实例(Instancing)
粒子与3D公告板很类似。不过,粒子有如下四个特点:
- 数量较大
- 可以运动
- 有生有死
- 半透明
伴随这些特点而来的是一系列问题。本课仅介绍**其中一种**解决方案,其他解决方案还多着呢……
## 一大波粒子正在接近中……
首先想到的思路就是套用上一课的代码,调用`glDrawArrays`逐个绘制粒子。这可不是个好办法。因为这种思路意味着你那锃光瓦亮的GTX 512显卡一次只能绘制**一个**四边形(很明显,性能损失高达99%)。就这么一个接一个地绘制公告板。
显然,我们得一次性绘制所有的粒子。
方法有很多种,如下是其中三种:
- 生成一个VBO,将所有粒子置于其中。简单,有效,在各种平台上均可行。
- 使用geometry shader。这不在本教程范围内,主要是因为50%的机器不支持该特性。
- 使用实例(instancing)。大部分机器都支持该特性。
本课将采用第三种方法。这种方法兼具性能优势和普适性,更重要的是,如果此法行得通,那第一种方法也就轻而易举了。
## 实例
“实例”的意思是以一个网格(比如本课中由两个三角形组成的四边形)为蓝本,创建多个该网格的实例。
具体地讲,我们通过如下一些buffer实现instancing:
- 一部分用于描述原始网格
- 一部分用于描述各实例的特性
这些buffer的内容可自行选择。在我们这个简单的例子包含了:
- 一个网格顶点buffer。没有index buffer,因此一共有6个`vec3`变量,构成两个三角形,进而组合成一个四边形。
- 一个buffer存储粒子的中心。
- 一个buffer存储粒子的颜色。
这些buffer都是标准buffer。创建方式如下:
~~~
// The VBO containing the 4 vertices of the particles.
// Thanks to instancing, they will be shared by all particles.
static const GLfloat g_vertex_buffer_data[] = {
-0.5f, -0.5f, 0.0f,
0.5f, -0.5f, 0.0f,
-0.5f, 0.5f, 0.0f,
0.5f, 0.5f, 0.0f,
};
GLuint billboard_vertex_buffer;
glGenBuffers(1, &billboard_vertex_buffer);
glBindBuffer(GL_ARRAY_BUFFER, billboard_vertex_buffer);
glBufferData(GL_ARRAY_BUFFER, sizeof(g_vertex_buffer_data), g_vertex_buffer_data, GL_STATIC_DRAW);
// The VBO containing the positions and sizes of the particles
GLuint particles_position_buffer;
glGenBuffers(1, &particles_position_buffer);
glBindBuffer(GL_ARRAY_BUFFER, particles_position_buffer);
// Initialize with empty (NULL) buffer : it will be updated later, each frame.
glBufferData(GL_ARRAY_BUFFER, MaxParticles * 4 * sizeof(GLfloat), NULL, GL_STREAM_DRAW);
// The VBO containing the colors of the particles
GLuint particles_color_buffer;
glGenBuffers(1, &particles_color_buffer);
glBindBuffer(GL_ARRAY_BUFFER, particles_color_buffer);
// Initialize with empty (NULL) buffer : it will be updated later, each frame.
glBufferData(GL_ARRAY_BUFFER, MaxParticles * 4 * sizeof(GLubyte), NULL, GL_STREAM_DRAW);
~~~
粒子更新方法如下:
~~~
// Update the buffers that OpenGL uses for rendering.
// There are much more sophisticated means to stream data from the CPU to the GPU,
// but this is outside the scope of this tutorial.
// http://www.opengl.org/wiki/Buffer_Object_Streaming
glBindBuffer(GL_ARRAY_BUFFER, particles_position_buffer);
glBufferData(GL_ARRAY_BUFFER, MaxParticles * 4 * sizeof(GLfloat), NULL, GL_STREAM_DRAW); // Buffer orphaning, a common way to improve streaming perf. See above link for details.
glBufferSubData(GL_ARRAY_BUFFER, 0, ParticlesCount * sizeof(GLfloat) * 4, g_particule_position_size_data);
glBindBuffer(GL_ARRAY_BUFFER, particles_color_buffer);
glBufferData(GL_ARRAY_BUFFER, MaxParticles * 4 * sizeof(GLubyte), NULL, GL_STREAM_DRAW); // Buffer orphaning, a common way to improve streaming perf. See above link for details.
glBufferSubData(GL_ARRAY_BUFFER, 0, ParticlesCount * sizeof(GLubyte) * 4, g_particule_color_data);
~~~
绘制之前还需绑定buffer。绑定方法如下:
~~~
// 1rst attribute buffer : vertices
glEnableVertexAttribArray(0);
glBindBuffer(GL_ARRAY_BUFFER, billboard_vertex_buffer);
glVertexAttribPointer(
0, // attribute. No particular reason for 0, but must match the layout in the shader.
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// 2nd attribute buffer : positions of particles' centers
glEnableVertexAttribArray(1);
glBindBuffer(GL_ARRAY_BUFFER, particles_position_buffer);
glVertexAttribPointer(
1, // attribute. No particular reason for 1, but must match the layout in the shader.
4, // size : x + y + z + size => 4
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// 3rd attribute buffer : particles' colors
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, particles_color_buffer);
glVertexAttribPointer(
2, // attribute. No particular reason for 1, but must match the layout in the shader.
4, // size : r + g + b + a => 4
GL_UNSIGNED_BYTE, // type
GL_TRUE, // normalized? *** YES, this means that the unsigned char[4] will be accessible with a vec4 (floats) in the shader ***
0, // stride
(void*)0 // array buffer offset
);
~~~
绘制方法与以往有所不同。这次不使用`glDrawArrays`或者`glDrawElements`(如果原始网格有index buffer的话)。这次用的是`glDrawArraysInstanced`或者`glDrawElementsInstanced`,效果等同于调用`glDrawArrays`N次(N是最后一个参数,此例中即`ParticlesCount`)。
~~~
glDrawArraysInstanced(GL_TRIANGLE_STRIP, 0, 4, ParticlesCount);
~~~
有件事差点忘了。我们还没告诉OpenGL哪个buffer是原始网格,哪些buffer是各实例的特性。调用`glVertexAttribDivisor`即可完成。有完整注释的代码如下:
~~~
// These functions are specific to glDrawArrays*Instanced*.
// The first parameter is the attribute buffer we're talking about.
// The second parameter is the "rate at which generic vertex attributes advance when rendering multiple instances"
// http://www.opengl.org/sdk/docs/man/xhtml/glVertexAttribDivisor.xml
glVertexAttribDivisor(0, 0); // particles vertices : always reuse the same 4 vertices -> 0
glVertexAttribDivisor(1, 1); // positions : one per quad (its center) -> 1
glVertexAttribDivisor(2, 1); // color : one per quad -> 1
// Draw the particules !
// This draws many times a small triangle_strip (which looks like a quad).
// This is equivalent to :
// for(i in ParticlesCount) : glDrawArrays(GL_TRIANGLE_STRIP, 0, 4),
// but faster.
glDrawArraysInstanced(GL_TRIANGLE_STRIP, 0, 4, ParticlesCount);
~~~
如你所见,instancing是很灵活的,你可以将`AttribDivisor`设为任意整数。例如,'glVertexAttribDivisor(2, 10)'即设置后续10个实例都拥有相同的颜色。
## 意义何在?
意义在于如今我们只需在每帧中更新一个很小的buffer(粒子中心位置),而非整个网格。如此一来,带宽利用效率提升了4倍。
## 生与死
于场景中其它对象不同的是,粒子的生死更替十分频繁。我们得用一种速度相当快的方式来创建新粒子,抛弃旧粒子。`new Particle()`这种办法显然不够好。
## 创建新粒子
首先得创建一个大的粒子容器:
~~~
// CPU representation of a particle
struct Particle{
glm::vec3 pos, speed;
unsigned char r,g,b,a; // Color
float size, angle, weight;
float life; // Remaining life of the particle. if < 0 : dead and unused.
};
const int MaxParticles = 100000;
Particle ParticlesContainer[MaxParticles];
~~~
接下来,我们得想办法创建新粒子。如下的函数在`ParticleContainer`中线性搜索(听起来有些暴力)新粒子。不过,它是从上次已知位置开始搜索的,因此一般很快就返回了。
~~~
int LastUsedParticle = 0;
// Finds a Particle in ParticlesContainer which isn't used yet.
// (i.e. life < 0);
int FindUnusedParticle(){
for(int i=LastUsedParticle; i<MaxParticles; i++){
if (ParticlesContainer[i].life < 0){
LastUsedParticle = i;
return i;
}
}
for(int i=0; i<LastUsedParticle; i++){
if (ParticlesContainer[i].life < 0){
LastUsedParticle = i;
return i;
}
}
return 0; // All particles are taken, override the first one
}
~~~
现在我们可以把`ParticlesContainer[particleIndex]`当中的`life`、`color`、`speed`和`position`设置成一些有趣的值。欲知详情请看代码,此处大有文章可作。我们比较关心的是每一帧中要生成多少粒子。这跟具体的应用有关,我们就设为每秒10000个(噢噢,略多啊)新粒子好了:
~~~
int newparticles = (int)(deltaTime*10000.0);
~~~
记得把个数限定在一个固定范围内:
~~~
// Generate 10 new particule each millisecond,
// but limit this to 16 ms (60 fps), or if you have 1 long frame (1sec),
// newparticles will be huge and the next frame even longer.
int newparticles = (int)(deltaTime*10000.0);
if (newparticles > (int)(0.016f*10000.0))
newparticles = (int)(0.016f*10000.0);
~~~
## 删除旧粒子
这个需要一些技巧,参见下文=)
## 仿真主循环
`ParticlesContainer`同时容纳了“活着的”和“死亡的”粒子,但发送到GPU的buffer仅含活着的粒子。
所以,我们要遍历每个粒子,看它是否是活着的,是否应该“处死”。如果一切正常,那就添加重力,最后将其拷贝到GPU上相应的buffer中。
~~~
// Simulate all particles
int ParticlesCount = 0;
for(int i=0; i<MaxParticles; i++){
Particle& p = ParticlesContainer[i]; // shortcut
if(p.life > 0.0f){
// Decrease life
p.life -= delta;
if (p.life > 0.0f){
// Simulate simple physics : gravity only, no collisions
p.speed += glm::vec3(0.0f,-9.81f, 0.0f) * (float)delta * 0.5f;
p.pos += p.speed * (float)delta;
p.cameradistance = glm::length2( p.pos - CameraPosition );
//ParticlesContainer[i].pos += glm::vec3(0.0f,10.0f, 0.0f) * (float)delta;
// Fill the GPU buffer
g_particule_position_size_data[4*ParticlesCount+0] = p.pos.x;
g_particule_position_size_data[4*ParticlesCount+1] = p.pos.y;
g_particule_position_size_data[4*ParticlesCount+2] = p.pos.z;
g_particule_position_size_data[4*ParticlesCount+3] = p.size;
g_particule_color_data[4*ParticlesCount+0] = p.r;
g_particule_color_data[4*ParticlesCount+1] = p.g;
g_particule_color_data[4*ParticlesCount+2] = p.b;
g_particule_color_data[4*ParticlesCount+3] = p.a;
}else{
// Particles that just died will be put at the end of the buffer in SortParticles();
p.cameradistance = -1.0f;
}
ParticlesCount++;
}
}
~~~
如下所示,效果看上去差不多了,不过还有一个问题……

## 排序
正如[第十课][1]中所讲,你必须按从后往前的顺序对半透明对象排序,方可获得正确的混合效果。
~~~
void SortParticles(){
std::sort(&ParticlesContainer[0], &ParticlesContainer[MaxParticles]);
}
~~~
`std::sort`需要一个函数判断粒子的在容器中的先后顺序。重载`Particle::operator<`即可:
~~~
// CPU representation of a particle
struct Particle{
...
bool operator<(Particle& that){
// Sort in reverse order : far particles drawn first.
return this->cameradistance > that.cameradistance;
}
};
~~~
这样`ParticleContainer`中的粒子就是排好序的了,显示效果已经变正确了:
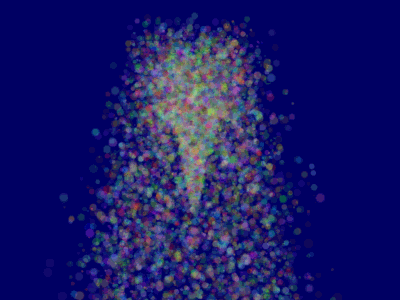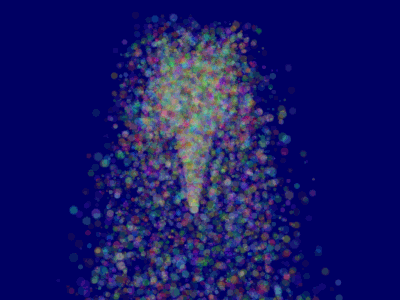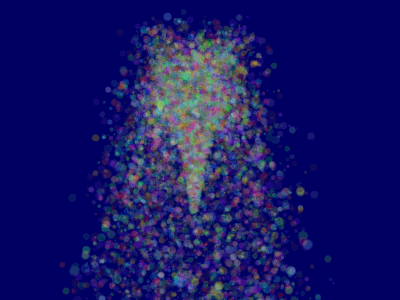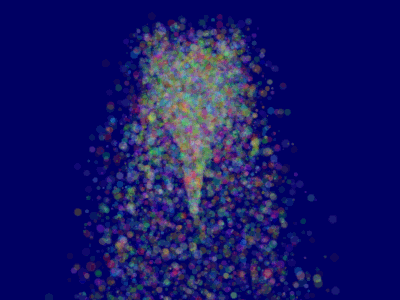
## 延伸课题
## 动画粒子
你可以用纹理图集(texture atlas)实现粒子的动画效果。将各粒子的年龄和位置发送到GPU,按照[2D字体一课][2]的方法在shader中计算UV坐标,纹理图集是这样的:

## 处理多个粒子系统
如果你需要多个粒子系统,有两种方案可选:要么仅用一个粒子容器,要么每个粒子系统一个。
如果选择将**所有**粒子放在一个容器中,那么就能很好地对粒子进行排序。主要缺陷是所有的粒子都得使用同一个纹理。这个问题可借助纹理图集加以解决。纹理图集是一张包含所有纹理的大纹理,可通过UV坐标访问各纹理,其使用和编辑并不是很方便。
如果为每个粒子系统设置一个粒子容器,那么只能在各容器内部对粒子进行排序。这就导致一个问题:如果两粒子系统相互重叠,我们就会看到瑕疵。不过,如果你的应用中不会出现两粒子系统重叠的情况,那这就不是问题。
当然,你也可以采用一种混合系统:若干个粒子系统,各自配备纹理图集(足够小,易于管理)。
## 平滑粒子
你很快就能发现一个常见的瑕疵:当粒子和几何体相交时,粒子的边界变得很明显,十分难看:

(image from [http://www.gamerendering.com/2009/09/16/soft-particles/](http://www.gamerendering.com/2009/09/16/soft-particles/) )
一个通常采用的解决方法是测试当前绘制的片断的深度值。如果该片断的深度值是“较近”的,就将其淡出。
然而,这就需要对Z-Buffer进行采样。这在“正常”的Z-Buffer中是不可行的。你得将场景渲染到一个[渲染目标][3]。或者,你可以用`glBlitFrameBuffer`把Z-Buffer内容从一个帧缓冲拷贝到另一个。
[http://developer.download.nvidia.com/whitepapers/2007/SDK10/SoftParticles_hi.pdf](http://developer.download.nvidia.com/whitepapers/2007/SDK10/SoftParticles_hi.pdf)
## 提高填充率
当前GPU的一个主要限制因素就是填充率:在16.6ms内可写片段(像素)数量要足够多,以达到60FPS。
这是一个大问题。由于粒子一般需要**很高**的填充率,同一个片段要重复绘制10多次,每次都是不同的粒子。如果不这么做,最终效果就会出现上述瑕疵。
在所有写入的的片段中,很多都是毫无用处的:比如位于边界上的片段。你的粒子纹理在边界上通常是完全透明的,但粒子的网格却仍然得绘制这些无用的片段,然后用与之前完全相同的值更新颜色缓冲。
这个小工具能够计算纹理的紧凑包围网格(这个也就是用`glDrawArraysInstanced()`渲染的那个网格):

[[http://www.humus.name/index.php?page=Cool&ID=8][4]。Emil](http://www.humus.name/index.php?page=Cool&ID=8][4]。Emil) Person的网站上也有很多精彩的文章。
## 粒子物理效果
有些应用中,你可能想让粒子和世界产生一些交互。比如,粒子可以在撞到地面时反弹。
比较简单的做法是为每个粒子做光线投射(raycasting),投射方向为当前位置与未来位置形成的向量。我们将在[拾取教程][5]。但这种做法开销太大了,你没法做到在每一帧中为每个粒子做光线投射。
根据你的具体应用,可以用一系列平面来近似几何体(译注:k-DOP),然后 对这些平面做光线投射。你也可以采用真正的光线投射,将结果缓存起来,然后据此近似计算附近的碰撞(也可以兼用两种方法)。
另一种迥异的技术是将现有的Z-Buffer作为几何体的粗略近似,在此之上进行粒子碰撞。这种方法效果“足够好”,速度快。不过由于无法在CPU端访问Z-Buffer(至少速度不够快),你得完全在GPU上进行仿真。因此,这种方法更加复杂。
如下是一些相关文章:[[http://www.altdevblogaday.com/2012/06/19/hack-day-report/][6](http://www.altdevblogaday.com/2012/06/19/hack-day-report/][6)]
[[http://www.gdcvault.com/search.php#&category=free&firstfocus=&keyword=Chris+Tchou’s%2BHalo%2BReach%2BEffects&conference_id=][7](http://www.gdcvault.com/search.php#&category=free&firstfocus=&keyword=Chris+Tchou’s%2BHalo%2BReach%2BEffects&conference_id=][7)]
## GPU仿真
如上所述,你可以完全在GPU上模拟粒子的运动。你还是得在CPU端管理粒子的生命周期——至少在创建粒子时。
可选方案很多,不过都不属于本课程讨论范围。这里仅给出一些指引。
- 采用变换反馈(Transform Feedback)机制。Transform Feedback让你能够将顶点着色器的输出结果存储到GPU端的VBO中。把新位置存储到这个VBO,然后在下一帧以这个VBO为起点,然后再将更新的位置存储到前一个VBO中。原理相同但无需Transform Feedback的方法:将粒子的位置编码到一张纹理中,然后利用渲染到纹理(Render-To-Texture)更新之。
- 采用通用GPU计算库:CUDA或OpenCL。这些库具有与OpenGL互操作的函数。
- 采用计算着色器Compute Shader。这是最漂亮的解决方案,不过只在较新的GPU上可用。
> 请注意,为了简化问题,在本课的实现中`ParticleContainer`是在GPU buffer都更新之后再排序的。这使得粒子的排序变得不准确了(有一帧的延迟),不过不是太明显。你可以把主循环拆分成仿真、排序两部分,然后再更新,就可以解决这个问题。
第十七课: 旋转
最后更新于:2022-04-01 04:37:51
# 第十七课:旋转
虽然本课有些超出OpenGL的范围,但是解决了一个常见问题:怎样表示旋转?
《第三课:矩阵》中,我们了解到矩阵可以让点绕某个轴旋转。矩阵可以简洁地表示顶点的变换,但使用难度较大:例如,从最终结果中获取旋转轴就很麻烦。
本课将展示两种最常见的表示旋转的方法:欧拉角(Euler angles)和四元数(Quaternion)。最重要的是,本课将详细解释为何要尽量使用四元数。
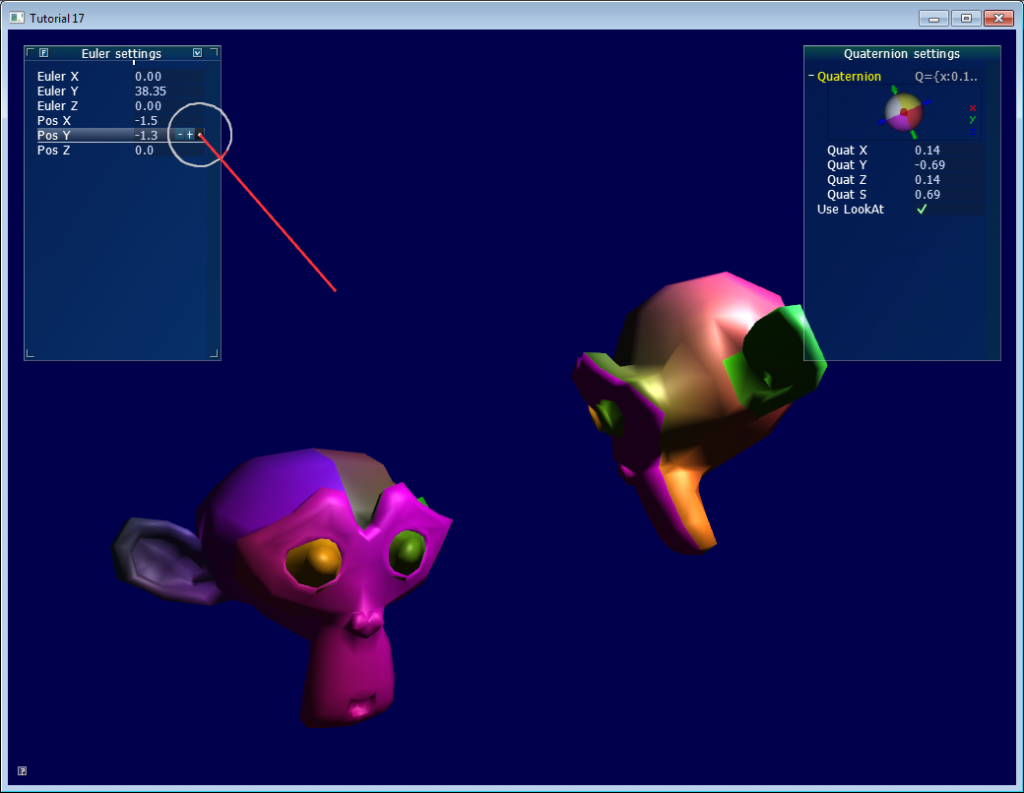
## 旋转与朝向(orientation)
阅读有关旋转的文献时,你可能会为其中的术语感到困惑。本课中:
-
“朝向”是状态:该物体的朝向为……
-
“旋转”是操作:旋转该物体
也就是说,当实施旋转操作时,就改变了物体的朝向。 两者形式相同,因此容易混淆。闲话少叙,开始进入正题……
## 欧拉角
欧拉角是表示朝向的最简方法,只需存储绕X、Y、Z轴旋转的角度,非常容易理解。你可以用vec3来存储一个欧拉角:
~~~
vec3 EulerAngles( RotationAroundXInRadians, RotationAroundYInRadians, RotationAroundZInRadians);
~~~
这三个旋转是依次施加的,通常的顺序是:Y-Z-X(但并非一定要按照这种顺序)。顺序不同,产生的结果也不同。
一个欧拉角的简单应用就是用于设置角色的朝向。通常,游戏角色不会绕X和Z轴旋转,仅仅绕竖直的Y轴旋转。因此,无需处理三个朝向,只需用一个float型变量表示方向即可。
另外一个使用欧拉角的例子是FPS相机:用一个角度表示头部朝向(绕Y轴),一个角度表示俯仰(绕X轴)。参见`common/controls.cpp`的示例。
不过,面对更加复杂的情况时,欧拉角就显得力不从心了。例如:
- 对两个朝向进行插值比较困难。简单地对X、Y、Z角度进行插值得到的结果不太理想。
- 实施多次旋转很复杂且不精确:必须计算出最终的旋转矩阵,然后据此推测书欧拉角。
- “臭名昭著”的“万向节死锁”(Gimbal Lock)问题有时会让旋转“卡死”。其他一些奇异状态还会导致模型方向翻转。
- 不同的角度可产生同样的旋转(例如-180°和180°)
- 容易出错——如上所述,一般的旋转顺序是YZX,如果用了非YZX顺序的库,就有麻烦了。
- 某些操作很复杂:如绕指定的轴旋转N角度。
四元数是表示旋转的好工具,可解决上述问题。
## 四元数
四元数由4个数[x y z w]构成,表示了如下的旋转:
~~~
// RotationAngle is in radians
x = RotationAxis.x * sin(RotationAngle / 2)
y = RotationAxis.y * sin(RotationAngle / 2)
z = RotationAxis.z * sin(RotationAngle / 2)
w = cos(RotationAngle / 2)
~~~
`RotationAxis`,顾名思义即旋转轴。`RotationAngle`是旋转的角度。
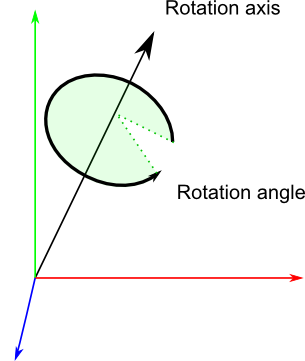
因此,四元数实际上存储了一个旋转轴和一个旋转角度。这让旋转的组合变简单了。
## 解读四元数
四元数的形式当然不如欧拉角直观,不过还是能看懂的:xyz分量大致代表了各个轴上的旋转分量,而w=acos(旋转角度/2)。举个例子,假设你在调试器中看到了这样的值[ 0.7 0 0 0.7 ]。x=0.7,比y、z的大,因此主要是在绕X轴旋转;而2*acos(0.7) = 1.59弧度,所以旋转角度应该是90°。
同理,[0 0 0 1] (w=1)表示旋转角度 = 2*acos(1) = 0,因此这是一个*单位四元数*(unit quaternion),表示没有旋转。
## 基本操作
不必理解四元数的数学原理:这种表示方式太晦涩了,因此我们一般通过一些工具函数进行计算。如果对这些数学原理感兴趣,可以参考[实用工具和链接](http://www.opengl-tutorial.org/miscellaneous/useful-tools-links/)中的数学书籍。
### 怎样用C++创建四元数?
~~~
// Don't forget to #include <glm/gtc/quaternion.hpp> and <glm/gtx/quaternion.hpp>
// Creates an identity quaternion (no rotation)
quat MyQuaternion;
// Direct specification of the 4 components
// You almost never use this directly
MyQuaternion = quat(w,x,y,z);
// Conversion from Euler angles (in radians) to Quaternion
vec3 EulerAngles(90, 45, 0);
MyQuaternion = quat(EulerAngles);
// Conversion from axis-angle
// In GLM the angle must be in degrees here, so convert it.
MyQuaternion = gtx::quaternion::angleAxis(degrees(RotationAngle), RotationAxis);
~~~
### 怎样用GLSL创建四元数?
不要在shader中创建四元数。应该把四元数转换为旋转矩阵,用于模型矩阵中。顶点会一如既往地随着MVP矩阵的变化而旋转。
某些情况下,你可能确实需要在shader中使用四元数。例如,GPU骨骼动画。GLSL中没有四元数类型,但是可以将四元数存在vec4变量中,然后在shader中计算。
### 怎样把四元数转换为矩阵?
~~~
mat4 RotationMatrix = quaternion::toMat4(quaternion);
~~~
这下可以像往常一样建立模型矩阵了:
~~~
mat4 RotationMatrix = quaternion::toMat4(quaternion);
...
mat4 ModelMatrix = TranslationMatrix * RotationMatrix * ScaleMatrix;
// You can now use ModelMatrix to build the MVP matrix
~~~
## 那究竟该用哪一个呢?
在欧拉角和四元数之间作选择还真不容易。欧拉角对于美工来说显得很直观,因此如果要做一款3D编辑器,请选用欧拉角。但对程序员来说,四元数却是最方便的。所以在写3D引擎内核时应该选用四元数。
一个普遍的共识是:在程序内部使用四元数,在需要和用户交互的地方就用欧拉角。
这样,在处理各种问题时,你才能得心应手(至少会轻松一点)。如果确有必要(如上文所述的FPS相机,设置角色朝向等情况),不妨就用欧拉角,附加一些转换工作。
## 其他资源
1. [实用工具和链接](http://www.opengl-tutorial.org/miscellaneous/useful-tools-links/)中的书籍
1.
老是老了点,《游戏编程精粹1》(Game Programming Gems I)有几篇关于四元数的好文章。也许网络上就有这份资料。
1.
一个关于旋转的[GDC报告][http://www.essentialmath.com/GDC2012/GDC2012_JMV_Rotations.pdf](http://www.essentialmath.com/GDC2012/GDC2012_JMV_Rotations.pdf)
1. The Game Programing Wiki [Quaternion tutorial](http://content.gpwiki.org/index.php/OpenGL:Tutorials:Using_Quaternions_to_represent_rotation)
1. Ogre3D [FAQ on quaternions](http://www.ogre3d.org/tikiwiki/Quaternion+and+Rotation+Primer)。 第二部分大多是针对OGRE的。
1. Ogre3D [Vector3D.h](https://bitbucket.org/sinbad/ogre/src/3cbd67467fab3fef44d1b32bc42ccf4fb1ccfdd0/OgreMain/include/OgreVector3.h?at=default)和[Quaternion.cpp](https://bitbucket.org/sinbad/ogre/src/3cbd67467fab3fef44d1b32bc42ccf4fb1ccfdd0/OgreMain/src/OgreQuaternion.cpp?at=default)
## 速查手册
## 怎样判断两个四元数是否相同?
向量点积是两向量夹角的余弦值。若该值为1,那么这两个向量同向。判断两个四元数是否相同的方法与之十分相似:
~~~
float matching = quaternion::dot(q1, q2);
if ( abs(matching-1.0) < 0.001 ){
// q1 and q2 are similar
}
~~~
由点积的acos值还可以得到q1和q2间的夹角。
## 怎样旋转一个点?
方法如下:
~~~
rotated_point = orientation_quaternion * point;
~~~
……但如果想计算模型矩阵,你得先将其转换为矩阵。注意,旋转的中心始终是原点。如果想绕别的点旋转:
~~~
rotated_point = origin + (orientation_quaternion * (point-origin));
~~~
## 怎样对两个四元数插值?
SLERP意为球面线性插值(Spherical Linear intERPolation)、可以用GLM中的`mix`函数进行SLERP:
~~~
glm::quat interpolatedquat = quaternion::mix(quat1, quat2, 0.5f); // or whatever factor
~~~
## 怎样累积两个旋转?
只需将两个四元数相乘即可。顺序和矩阵乘法一致。亦即逆序相乘:
~~~
quat combined_rotation = second_rotation * first_rotation;
~~~
## 怎样计算两向量之间的旋转?
(也就是说,四元数得把v1旋转到v2)
基本思路很简单:
- 两向量间的夹角很好找:由点积可知其cos值。
- 旋转轴很好找:两向量的叉乘积。
如下的算法就是依照上述思路实现的,此外还处理了一些特例:
~~~
quat RotationBetweenVectors(vec3 start, vec3 dest){
start = normalize(start);
dest = normalize(dest);
float cosTheta = dot(start, dest);
vec3 rotationAxis;
if (cosTheta < -1 + 0.001f){
// special case when vectors in opposite directions:
// there is no "ideal" rotation axis
// So guess one; any will do as long as it's perpendicular to start
rotationAxis = cross(vec3(0.0f, 0.0f, 1.0f), start);
if (gtx::norm::length2(rotationAxis) < 0.01 ) // bad luck, they were parallel, try again!
rotationAxis = cross(vec3(1.0f, 0.0f, 0.0f), start);
rotationAxis = normalize(rotationAxis);
return gtx::quaternion::angleAxis(180.0f, rotationAxis);
}
rotationAxis = cross(start, dest);
float s = sqrt( (1+cosTheta)*2 );
float invs = 1 / s;
return quat(
s * 0.5f,
rotationAxis.x * invs,
rotationAxis.y * invs,
rotationAxis.z * invs
);
}
~~~
(可在`common/quaternion_utils.cpp`中找到该函数)
## 我需要一个类似gluLookAt的函数。怎样旋转物体使之朝向某点?
调用`RotationBetweenVectors`函数!
~~~
// Find the rotation between the front of the object (that we assume towards +Z,
// but this depends on your model) and the desired direction
quat rot1 = RotationBetweenVectors(vec3(0.0f, 0.0f, 1.0f), direction);
~~~
现在,你也许想让物体保持竖直:
~~~
// Recompute desiredUp so that it's perpendicular to the direction
// You can skip that part if you really want to force desiredUp
vec3 right = cross(direction, desiredUp);
desiredUp = cross(right, direction);
// Because of the 1rst rotation, the up is probably completely screwed up.
// Find the rotation between the "up" of the rotated object, and the desired up
vec3 newUp = rot1 * vec3(0.0f, 1.0f, 0.0f);
quat rot2 = RotationBetweenVectors(newUp, desiredUp);
~~~
组合到一起:
~~~
quat targetOrientation = rot2 * rot1; // remember, in reverse order.
~~~
注意,“direction”仅仅是方向,并非目标位置!你可以轻松计算出方向:`targetPos – currentPos`。
得到目标朝向后,你很可能想对`startOrientation`和`targetOrientation`进行插值
(可在`common/quaternion_utils.cpp`中找到此函数。)
## 怎样使用LookAt且限制旋转速度?
基本思想是采用SLERP(用`glm::mix`函数),但要控制插值的幅度,避免角度偏大。
~~~
float mixFactor = maxAllowedAngle / angleBetweenQuaternions;
quat result = glm::gtc::quaternion::mix(q1, q2, mixFactor);
~~~
如下是更为复杂的实现。该实现处理了许多特例。注意,出于优化的目的,代码中并未使用`mix`函数。
~~~
quat RotateTowards(quat q1, quat q2, float maxAngle){
if( maxAngle < 0.001f ){
// No rotation allowed. Prevent dividing by 0 later.
return q1;
}
float cosTheta = dot(q1, q2);
// q1 and q2 are already equal.
// Force q2 just to be sure
if(cosTheta > 0.9999f){
return q2;
}
// Avoid taking the long path around the sphere
if (cosTheta < 0){
q1 = q1*-1.0f;
cosTheta *= -1.0f;
}
float angle = acos(cosTheta);
// If there is only a 2° difference, and we are allowed 5°,
// then we arrived.
if (angle < maxAngle){
return q2;
}
float fT = maxAngle / angle;
angle = maxAngle;
quat res = (sin((1.0f - fT) * angle) * q1 + sin(fT * angle) * q2) / sin(angle);
res = normalize(res);
return res;
}
~~~
可以这样用`RotateTowards`函数:
~~~
CurrentOrientation = RotateTowards(CurrentOrientation, TargetOrientation, 3.14f * deltaTime );
~~~
(可在`common/quaternion_utils.cpp`中找到此函数)
## 怎样……
第十六课: 阴影贴图
最后更新于:2022-04-01 04:37:48
# 第十六课:阴影贴图(Shadow mapping)
第十五课中已经学习了如何创建光照贴图。光照贴图可用于静态对象的光照,其阴影效果也很不错,但无法处理运动的对象。
阴影贴图是目前(截止2012年)最好的生成动态阴影的方法。此法最大的优点是易于实现,缺点是想完全**正确**地实现不大容易。
本课首先介绍基本算法,探究其缺陷,然后实现一些优化。由于撰写本文时(2012),阴影贴图技术还在被广泛地研究;我们将提供一些指导,以便你根据自身需要,进一步改善你的阴影贴图。
## 基本的阴影贴图
基本的阴影贴图算法包含两个步骤。首先,从光源的视角将场景渲染一次,只计算每个片断的深度。接着从正常的视角把场景再渲染一次,渲染时要测试当前片断是否位于阴影中。
“是否在阴影中”的测试实际上非常简单。如果当前采样点比阴影贴图中的同一点离光源更远,那说明场景中有一个物体比当前采样点离光源更近;即当前片断位于阴影中。
下图可以帮你理解上述原理:
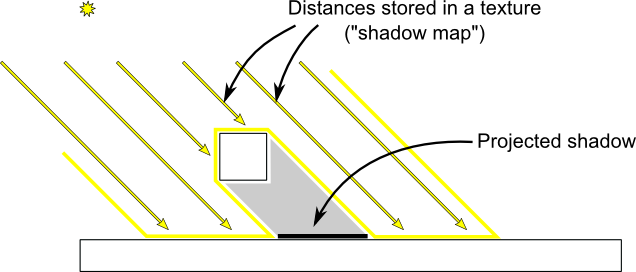
## 渲染阴影贴图
本课只考虑平行光——一种位于无限远处,其光线可视为相互平行的光源。故可用正交投影矩阵来渲染阴影贴图。正交投影矩阵和一般的透视投影矩阵差不多,只不过未考虑透视——因此无论距离相机多远,物体的大小看起来都是一样的。
## 设置渲染目标和MVP矩阵
十四课中,大家学习了把场景渲染到纹理,以便稍后从shader中访问的方法。
这里采用了一幅1024x1024、16位深度的纹理来存储阴影贴图。对于阴影贴图来说,通常16位绰绰有余;你可以自由地试试别的数值。注意,这里采用的是深度纹理,而非深度渲染缓冲区(这个要留到后面进行采样)。
~~~
// The framebuffer, which regroups 0, 1, or more textures, and 0 or 1 depth buffer.
GLuint FramebufferName = 0;
glGenFramebuffers(1, &FramebufferName);
glBindFramebuffer(GL_FRAMEBUFFER, FramebufferName);
// Depth texture. Slower than a depth buffer, but you can sample it later in your shader
GLuint depthTexture;
glGenTextures(1, &depthTexture);
glBindTexture(GL_TEXTURE_2D, depthTexture);
glTexImage2D(GL_TEXTURE_2D, 0,GL_DEPTH_COMPONENT16, 1024, 1024, 0,GL_DEPTH_COMPONENT, GL_FLOAT, 0);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthTexture, 0);
glDrawBuffer(GL_NONE); // No color buffer is drawn to.
// Always check that our framebuffer is ok
if(glCheckFramebufferStatus(GL_FRAMEBUFFER) != GL_FRAMEBUFFER_COMPLETE)
return false;
~~~
MVP矩阵用于从光源的视角绘制场景,其计算过程如下:
- 投影矩阵是正交矩阵,可将整个场景包含到一个AABB(axis-aligned box, 轴向包围盒)里,该包围盒在X、Y、Z轴上的坐标范围分别为(-10,10)、(-10,10)、(-10,20)。这样做是为了让整个场景始终可见,这一点在“再进一步”小节还会讲到。
- 视图矩阵对场景做了旋转,这样在观察坐标系中,光源的方向就是-Z方向(需要温习[第三课]
-
模型矩阵可设为任意值。
~~~
glm::vec3 lightInvDir = glm::vec3(0.5f,2,2);
// Compute the MVP matrix from the light's point of view
glm::mat4 depthProjectionMatrix = glm::ortho<float>(-10,10,-10,10,-10,20);
glm::mat4 depthViewMatrix = glm::lookAt(lightInvDir, glm::vec3(0,0,0), glm::vec3(0,1,0));
glm::mat4 depthModelMatrix = glm::mat4(1.0);
glm::mat4 depthMVP = depthProjectionMatrix * depthViewMatrix * depthModelMatrix;
// Send our transformation to the currently bound shader,
// in the "MVP" uniform
glUniformMatrix4fv(depthMatrixID, 1, GL_FALSE, &depthMVP[0][0])
~~~
## Shaders
这一次渲染中所用的着色器很简单。顶点着色器仅仅简单地计算一下顶点的齐次坐标:
~~~
#version 330 core
// Input vertex data, different for all executions of this shader.
layout(location = 0) in vec3 vertexPosition_modelspace;
// Values that stay constant for the whole mesh.
uniform mat4 depthMVP;
void main(){
gl_Position = depthMVP * vec4(vertexPosition_modelspace,1);
}
~~~
fragment shader同样简单:只需将片断的深度值写到location 0(即写入深度纹理)。
~~~
#version 330 core
// Ouput data
layout(location = 0) out float fragmentdepth;
void main(){
// Not really needed, OpenGL does it anyway
fragmentdepth = gl_FragCoord.z;
}
~~~
渲染阴影贴图比渲染一般的场景要快一倍多,因为只需写入低精度的深度值,不需要同时写深度值和颜色值。显存带宽往往是影响GPU性能的关键因素。
## 结果
渲染出的纹理如下所示:

颜色越深表示z值越小;故墙面的右上角离相机更近。相反地,白色表示z=1(齐次坐标系中的值),离相机十分遥远。
## 使用阴影贴图
## 基本shader
现在回到普通的着色器。对于每一个计算出的fragment,都要测试其是否位于阴影贴图之“后”。
为了做这个测试,需要计算:**在创建阴影贴图所用的坐标系中**,当前片断的坐标。因此要依次用通常的`MVP`矩阵和`depthMVP`矩阵对其做变换。
不过还需要一些技巧。将depthMVP与顶点坐标相乘得到的是齐次坐标,坐标范围为[-1,1],而纹理采样的取值范围却是[0,1]。
举个例子,位于屏幕中央的fragment的齐次坐标应该是(0,0);但要对纹理中心进行采样,UV坐标就应该是(0.5,0.5)。
这个问题可以通过在片断着色器中调整采样坐标来修正,但用下面这个矩阵去乘齐次坐标则更为高效。这个矩阵将坐标除以2(主对角线上[-1,1] -> [-0.5, 0.5]),然后平移(最后一行[-0.5, 0.5] -> [0,1])。
~~~
glm::mat4 biasMatrix(
0.5, 0.0, 0.0, 0.0,
0.0, 0.5, 0.0, 0.0,
0.0, 0.0, 0.5, 0.0,
0.5, 0.5, 0.5, 1.0
);
glm::mat4 depthBiasMVP = biasMatrix*depthMVP;
~~~
终于可以写vertex shader了。和之前的差不多,不过这次要输出两个坐标。
- `gl_Position`是当前相机所在坐标系下的顶点坐标
- `ShadowCoord`是上一个相机(光源)所在坐标系下的顶点坐标
~~~
// Output position of the vertex, in clip space : MVP * position
gl_Position = MVP * vec4(vertexPosition_modelspace,1);
// Same, but with the light's view matrix
ShadowCoord = DepthBiasMVP * vec4(vertexPosition_modelspace,1);
~~~
fragment shader就很简单了:
- `texture2D( shadowMap, ShadowCoord.xy ).z` 是光源到距离最近的遮挡物之间的距离。
- `ShadowCoord.z`是光源和当前片断之间的距离
……因此,若当前fragment比最近的遮挡物还远,那意味着这个片断位于(这个最近的遮挡物的)阴影中
~~~
float visibility = 1.0;
if ( texture2D( shadowMap, ShadowCoord.xy ).z < ShadowCoord.z){
visibility = 0.5;
}
~~~
我们只需把这个原理加到光照计算中。当然,环境光分量无需改动,毕竟这只分量是个为了模拟一些光亮,让即使处在阴影或黑暗中的物体也能显出轮廓来(否则就会是纯黑色)。
~~~
color =
// Ambiant : simulates indirect lighting
MaterialAmbiantColor +
// Diffuse : "color" of the object
visibility * MaterialDiffuseColor * LightColor * LightPower * cosTheta+
// Specular : reflective highlight, like a mirror
visibility * MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5);
~~~
## 结果——阴影瑕疵(Shadow acne)
这是目前的代码渲染的结果。很明显,大体的思想是实现了,不过质量不尽如人意。
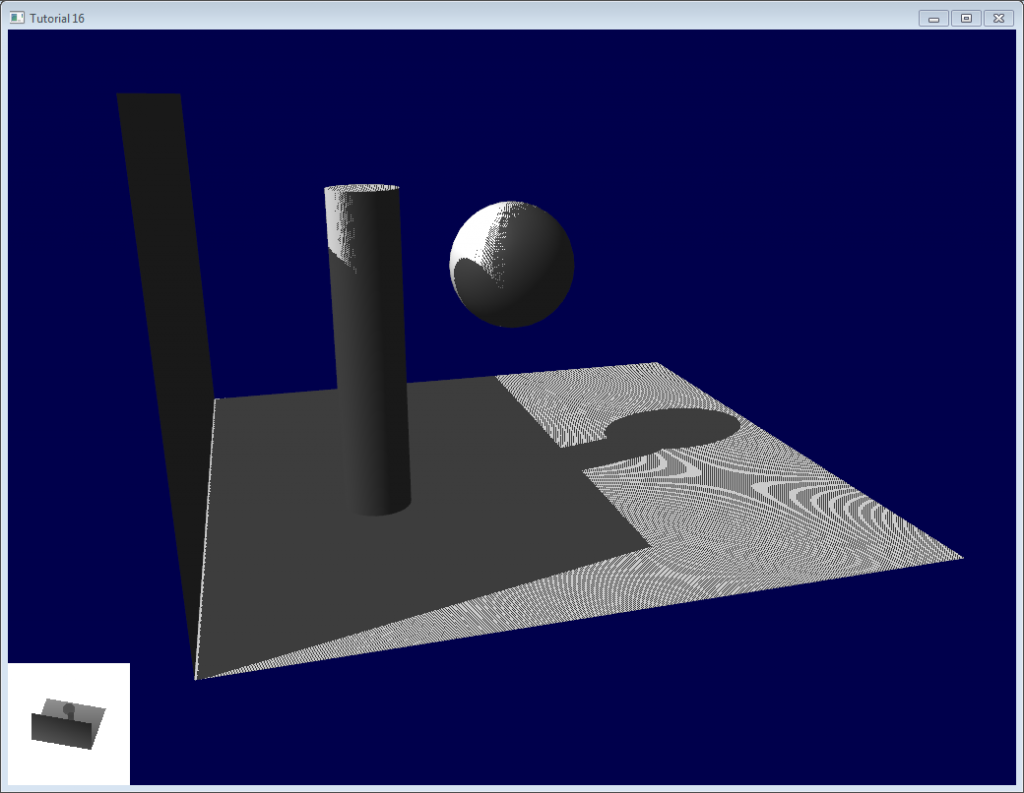
逐一检查图中的问题。代码有两个工程:`shadowmaps`和`shadowmaps_simple`,任选一项。simple版的效果和上图一样糟糕,但代码比较容易理解。
## 问题
## 阴影瑕疵
最明显的问题就是**阴影瑕疵**:

这种现象可用下面这张简单的图解释:
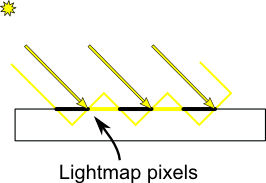
通常的“补救措施”是加上一个误差容限(error margin):仅当当前fragment的深度(再次提醒,这里指的是从光源的坐标系得到的深度值)确实比光照贴图像素的深度要大时,才将其判定为阴影。这可以通过添加一个偏差(bias)来办到:
~~~
float bias = 0.005;
float visibility = 1.0;
if ( texture2D( shadowMap, ShadowCoord.xy ).z < ShadowCoord.z-bias){
visibility = 0.5;
}
~~~
效果好多了::

不过,您也许注意到了,由于加入了偏差,墙面与地面之间的瑕疵显得更加明显了。更糟糕的是,0.005的偏差对地面来说太大了,但对曲面来说又太小了:圆柱体和球体上的瑕疵依然可见。
一个通常的解决方案是根据斜率调整偏差:
~~~
float bias = 0.005*tan(acos(cosTheta)); // cosTheta is dot( n,l ), clamped between 0 and 1
bias = clamp(bias, 0,0.01);
~~~
阴影瑕疵消失了,即使在曲面上也看不到了。

还有一个技巧,不过这个技巧灵不灵得看具体的几何形状。此技巧只渲染阴影中的背面。这就对厚墙的几何形状提出了硬性要求(请看下一节——阴影悬空(Peter Panning),不过即使有瑕疵,也只会出现在阴影遮蔽下的表面上。【译者注:在迪斯尼经典动画[《小飞侠》](http://movie.douban.com/subject/1296538/)中,小飞侠彼得·潘的影子和身体分开了,小仙女温蒂又给他缝好了。】

渲染阴影贴图时剔除正面的三角形:
~~~
// We don't use bias in the shader, but instead we draw back faces,
// which are already separated from the front faces by a small distance
// (if your geometry is made this way)
glCullFace(GL_FRONT); // Cull front-facing triangles -> draw only back-facing triangles
~~~
渲染场景时正常地渲染(剔除背面)
~~~
glCullFace(GL_BACK); // Cull back-facing triangles -> draw only front-facing triangles
~~~
代码中也用了这个方法,和“加入偏差”联合使用。
## 阴影悬空(Peter Panning)
现在没有阴影瑕疵了,但地面的光照效果还是不对,看上去墙面好像悬在半空(因此术语称为“阴影悬空”)。实际上,加上偏差会加剧阴影悬空。

这个问题很好修正:避免使用薄的几何形体就行了。这样做有两个好处:
- 首先,(把物体增厚)解决了阴影悬空问题:物体比偏差值要大得多,于是一切麻烦烟消云散了
- 其次,可在渲染光照贴图时启用背面剔除,因为现在,墙壁上有一个面面对光源,就可以遮挡住墙壁的另一面,而这另一面恰好作为背面被剔除了,无需渲染。
缺点就是要渲染的三角形增多了(每帧多了一倍的三角形!)

## 走样
即使是使用了这些技巧,你还是会发现阴影的边缘上有一些走样。换句话说,就是一个像素点是白的,邻近的一个像素点是黑的,中间缺少平滑过渡。

## PCF(percentage closer filtering,百分比渐近滤波)
一个最简单的改善方法是把阴影贴图的`sampler`类型改为**`sampler2DShadow`**。这么做的结果是,每当对阴影贴图进行一次采样时,硬件就会对相邻的纹素进行采样,并对它们全部进行比较,对比较的结果做双线性滤波后返回一个[0,1]之间的float值。
例如,0.5即表示有两个采样点在阴影中,两个采样点在光明中。
注意,它和对滤波后深度图做单次采样有区别!一次“比较”,返回的是true或false;PCF返回的是4个“true或false”值的插值结果

可以看到,阴影边界平滑了,但阴影贴图的纹素依然可见。
## 泊松采样(Poisson Sampling)
一个简易的解决办法是对阴影贴图做N次采样(而不是只做一次)。并且要和PCF一起使用,这样即使采样次数不多,也可以得到较好的效果。下面是四次采样的代码:
~~~
for (int i=0;i<4;i++){
if ( texture2D( shadowMap, ShadowCoord.xy + poissonDisk[i]/700.0 ).z < ShadowCoord.z-bias ){
visibility-=0.2;
}
}
~~~
`poissonDisk`是一个常量数组,其定义看起来像这样:
~~~
vec2 poissonDisk[4] = vec2[](
vec2( -0.94201624, -0.39906216 ),
vec2( 0.94558609, -0.76890725 ),
vec2( -0.094184101, -0.92938870 ),
vec2( 0.34495938, 0.29387760 )
);
~~~
这样,根据阴影贴图采样点个数的多少,生成的fragment会随之变明或变暗。

常量700.0确定了采样点的“分散”程度。散得太密,还是会发生走样;散得太开,会出现**条带**(截图中未使用PCF,以便让条带现象更明显;其中做了16次采样)


## 分层泊松采样(Stratified Poisson Sampling)
通过为每个像素分配不同采样点个数,我们可以消除这一问题。主要有两种方法:分层泊松法(Stratified Poisson)和旋转泊松法(Rotated Poisson)。分层泊松法选择不同的采样点数;旋转泊松法采样点数保持一致,但会做随机的旋转以使采样点的分布发生变化。本课仅对分层泊松法作介绍。
与之前版本唯一不同的是,这里用了一个随机数来索引`poissonDisk`:
~~~
for (int i=0;i<4;i++) {
int index = // A random number between 0 and 15, different for each pixel (and each i !)
visibility -= 0.2*(1.0-texture( shadowMap, vec3(ShadowCoord.xy + poissonDisk[index]/700.0, (ShadowCoord.z-bias)/ShadowCoord.w) ));
}
~~~
可用如下代码(返回一个[0,1]间的随机数)产生随机数
~~~
float dot_product = dot(seed4, vec4(12.9898,78.233,45.164,94.673));
return fract(sin(dot_product) * 43758.5453);
~~~
本例中,`seed4`是参数`i`和`seed`的组成的vec4向量(这样才会是在4个位置做采样)。参数seed的值可以选用`gl_FragCoord`(像素的屏幕坐标),或者`Position_worldspace`:
~~~
// - A random sample, based on the pixel's screen location.
// No banding, but the shadow moves with the camera, which looks weird.
int index = int(16.0*random(gl_FragCoord.xyy, i))%16;
// - A random sample, based on the pixel's position in world space.
// The position is rounded to the millimeter to avoid too much aliasing
//int index = int(16.0*random(floor(Position_worldspace.xyz*1000.0), i))%16;
~~~
这样做之后,上图中的那种条带就消失了,不过噪点却显现出来了。不过,一些“漂亮的”噪点可比上面那些条带“好看”多了。
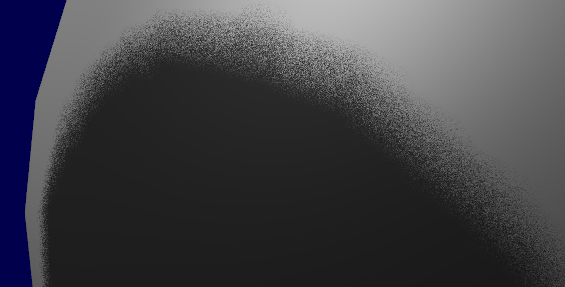
上述三个例子的实现请参见tutorial16/ShadowMapping.fragmentshader。
## 深入研究
即使把这些技巧都用上,仍有很多方法可以提升阴影质量。下面是最常见的一些方法:
## 早优化(Early bailing)
不要把采样次数设为16,太大了,四次采样足矣。若这四个点都在光明或都在阴影中,那就算做16次采样效果也一样:这就叫过早优化。若这些采样点明暗各异,那你很可能位于阴影边界上,这时候进行16次采样才是合情理的。
## 聚光灯(Spot lights)
处理聚光灯这种光源时,不需要多大的改动。最主要的是:把正交投影矩阵换成透视投影矩阵:
~~~
glm::vec3 lightPos(5, 20, 20);
glm::mat4 depthProjectionMatrix = glm::perspective<float>(45.0f, 1.0f, 2.0f, 50.0f);
glm::mat4 depthViewMatrix = glm::lookAt(lightPos, lightPos-lightInvDir, glm::vec3(0,1,0));
~~~
大部分都一样,只不过用的不是正交视域四棱锥,而是透视视域四棱锥。考虑到透视除法,采用了texture2Dproj。(见“第四课——矩阵”的脚注)
第二步,在shader中,把透视考虑在内。(见“第四课——矩阵”的脚注。简而言之,透视投影矩阵根本就没做什么透视。这一步是由硬件完成的,只是把投影的坐标除以了w。这里在着色器中模拟这一步操作,因此得自己做透视除法。顺便说一句,正交矩阵产生的齐次向量w始终为1,这就是为什么正交矩阵没有任何透视效果。)
用GLSL完成此操作主要有两种方法。第二种方法利用了内置的`textureProj`函数,但两种方法得出的效果是一样的。
~~~
if ( texture( shadowMap, (ShadowCoord.xy/ShadowCoord.w) ).z < (ShadowCoord.z-bias)/ShadowCoord.w )
if ( textureProj( shadowMap, ShadowCoord.xyw ).z < (ShadowCoord.z-bias)/ShadowCoord.w )
~~~
## 点光源(Point lights)
大部分是一样的,不过要做深度立方体贴图(cubemap)。立方体贴图包含一组6个纹理,每个纹理位于立方体的一面,无法用标准的UV坐标访问,只能用一个代表方向的三维向量来访问。
空间各个方向的深度都保存着,保证点光源各方向都能投射影子。T
## 多个光源组合
该算法可以处理多个光源,但别忘了,每个光源都要做一次渲染,以生成其阴影贴图。这些计算极大地消耗了显存,也许很快你的显卡带宽就吃紧了。
## 自动光源四棱锥(Automatic light frustum)
本课中,囊括整个场景的光源四棱锥是手动算出来的。虽然在本课的限定条件下,这么做还行得通,但应该避免这样的做法。如果你的地图大小是1Km x 1Km,你的阴影贴图大小为1024x1024,则每个纹素代表的面积为1平方米。这么做太蹩脚了。光源的投影矩阵应尽量紧包整个场景。
对于聚光灯来说,只需调整一下范围就行了。
对于太阳这样的方向光源,情况就复杂一些:光源**确实**照亮了整个场景。以下是计算方向光源视域四棱锥的一种方法:
潜在阴影接收者(Potential Shadow Receiver,PSR)。PSR是这样一种物体——它们同时在【光源视域四棱锥,观察视域四棱锥,以及场景包围盒】这三者之内。顾名思义,PSR都有可能位于阴影中:相机和光源都能“看”到它。
潜在阴影投射者(Potential Shadow Caster,PSC)= PSR + 所有位于PSR和光源之间的物体(一个物体可能不可见但仍然会投射出一条可见的阴影)。
因此,要计算光源的投影矩阵,可以用所有可见的物体,“减去”那些离得太远的物体,再计算其包围盒;然后“加上”位于包围盒与广元之间的物体,再次计算新的包围盒(不过这次是沿着光源的方向)。
这些集合的精确计算涉及凸包体的求交计算,但这个方法(计算包围盒)实现起来简单多了。
此法在物体离开视域四棱锥时,计算量会陡增,原因在于阴影贴图的分辨率陡然增加了。你可以通过多次平滑插值来弥补。CSM(Cascaded Shadow Map,层叠阴影贴图法)无此问题,但实现起来较难。
## 指数阴影贴图(Exponential shadow map)
指数阴影贴图法试图借助“位于阴影中的、但离光源较近的片断实际上处于‘某个中间位置’”这一假设来减少走样。这个方法涉及到偏差,不过测试已不再是二元的:片断离明亮曲面的距离越远,则其越显得黑暗。
显然,这纯粹是一种障眼法,两物体重叠时,瑕疵就会显露出来。
## LiSPSM(Light-space perspective Shadow Map,光源空间透视阴影贴图)
LiSPSM调整了光源投影矩阵,从而在离相机很近时获取更高的精度。这一点在“duelling frustra”现象发生时显得尤为重要。所谓“duelling frustra”是指:点光源与你(相机)距离远,『视线』方向又恰好与你的视线方向相反。离光源近的地方(即离你远的地方),阴影贴图精度高;离光源远的地方(即离你近的地方,你最需要精确阴影贴图的地方),阴影贴图的精度又不够了。
不过LiSPSM实现起来很难。详细的实现方法请看参考文献。
CSM(Cascaded shadow map,层叠阴影贴图)CSM和LiSPSM解决的问题一模一样,但方式不同。CSM仅对观察视域四棱锥的各部分使用了2~4个标准阴影贴图。第一个阴影贴图处理近处的物体,所以在近处这块小区域内,你可以获得很高的精度。随后几个阴影贴图处理远一些的物体。最后一个阴影贴图处理场景中的很大一部分,但由于透视效应,视觉感官上没有近处区域那么明显。
撰写本文时,CSM是复杂度/质量比最好的方法。很多案例都选用了这一解决方案。
## 总结
正如您所看到的,阴影贴图技术是个很复杂的课题。每年都有新的方法和改进方案发表。但目前为止尚无完美的解决方案。
幸运的是,大部分方法都可以混合使用:在LiSPSM中使用CSM,再加PCF平滑等等是完全可行的。尽情地实验吧。
总结一句,我建议您坚持尽可能使用预计算的光照贴图,只为动态物体使用阴影贴图。并且要确保两者的视觉效果协调一致,任何一者效果太好/太坏都不合适。
第十五课: 光照贴图
最后更新于:2022-04-01 04:37:46
# 第十五课:光照贴图(Lightmap)
## 简介
这堂课是视频课程,没有介绍新的OpenGL相关技术/语法。不过,大家会学习如何利用现有知识,生成高质量的阴影。
本课介绍了用Blender创建简单场景的方法;还介绍了如何烘培(bake)光照贴图(lightmap),以便在你的项目中使用。

无需Blender预备知识,我会讲解包括快捷键的所有内容
## 关于光照贴图
光照图是永久、一次性地烘焙好的。也就是说光照图是完全静态的,你不能在运行时移动光源,连删除都不行。
但对于阳光这种光源来说,光照图还是大有用武之地的;在不会打碎灯泡的室内场景中,也是可以的。2009年发布的《镜之边缘》(*Mirror Edge*)室内、室外场景中大量采用了光照图。
更重要的是,光照图很容易配置,速度无可匹敌。
## 视频
这是个1024x768 高清视频。
[Youku 标清含中文字幕](http://v.youku.com/v_show/id_XNDg5MjYzMzk2.html)[Vimeo 高清原版视频](http://player.vimeo.com/video/24359223?title=0&byline=0&portrait=0)
## 附录
用OpenGL渲染时,你大概会注意到一些瑕疵(这里故意把瑕疵放大了):

这是由mipmap造成的。从远处观察时,mipmap对纹素做了混合。纹理背景中的黑色像素点和光照图中的像素点混合在了一起。为了避免这一点,可以采取如下措施:
- 让Blender在UV图的limits上生成一个margin。这个margin参数位于bake面板。要想效果更好,可以把margin值设为20个纹素。
-
获取纹理时,加上一个偏离(bias):
~~~
color = texture2D( myTextureSampler, UV, -2.0 ).rgb;
~~~
-2是偏离量。这个值是通过不断尝试得出的。上面的截图中bias值为+2,也就是说OpenGL将在原本的mipmap层次上再加两层(因此,纹素大小变为原来的1/16,瑕疵也随之变小了)。-
-
后期处理中可将背景填充为黑色,这一点我后面还会再讲。
第十四课: 渲染到纹理
最后更新于:2022-04-01 04:37:44
# 第十四课:渲染到纹理
“渲染到纹理”是一系列特效方法之一。基本思想是:像通常那样渲染一个场景——只是这次是渲染到可以重用的纹理中。
应用包括:游戏(in-game)相机、后期处理(post-processing)以及你能想象到一切.
## 渲染到纹理
我们有三个任务:创建要渲染的纹理对象;将纹理渲染到对象上;使用生成的纹理。
## 创建渲染目标(Render Target)
我们要渲染的对象叫做帧缓存。它像一个容器,用来存纹理和一个可选的深度缓冲区(depth buffer)。在OpenGL中我们可以像创建其他对象一样创建它:
~~~
// The framebuffer, which regroups 0, 1, or more textures, and 0 or 1 depth buffer.
GLuint FramebufferName = 0;
glGenFramebuffers(1, &FramebufferName);
glBindFramebuffer(GL_FRAMEBUFFER, FramebufferName);
~~~
现在需要创建纹理,纹理中包含着色器的RGB输出。这段代码非常的经典:
~~~
// The texture we're going to render to
GLuint renderedTexture;
glGenTextures(1, &renderedTexture);
// "Bind" the newly created texture : all future texture functions will modify this texture
glBindTexture(GL_TEXTURE_2D, renderedTexture);
// Give an empty image to OpenGL ( the last "0" )
glTexImage2D(GL_TEXTURE_2D, 0,GL_RGB, 1024, 768, 0,GL_RGB, GL_UNSIGNED_BYTE, 0);
// Poor filtering. Needed !
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
~~~
同时还需要一个深度缓冲区(depth buffer)。这是可选的,取决于纹理中实际需要画的东西;由于我们渲染的是小猴Suzanne,所以需要深度测试。
~~~
// The depth buffer
GLuint depthrenderbuffer;
glGenRenderbuffers(1, &depthrenderbuffer);
glBindRenderbuffer(GL_RENDERBUFFER, depthrenderbuffer);
glRenderbufferStorage(GL_RENDERBUFFER, GL_DEPTH_COMPONENT, 1024, 768);
glFramebufferRenderbuffer(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, GL_RENDERBUFFER, depthrenderbuffer);
~~~
最后,配置frameBuffer。
~~~
// Set "renderedTexture" as our colour attachement #0
glFramebufferTexture(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, renderedTexture, 0);
// Set the list of draw buffers.
GLenum DrawBuffers[2] = {GL_COLOR_ATTACHMENT0};
glDrawBuffers(1, DrawBuffers); // "1" is the size of DrawBuffers
~~~
这个过程中可能出现一些错误,取决于GPU的性能;下面是检查的方法:
~~~
// Always check that our framebuffer is ok
if(glCheckFramebufferStatus(GL_FRAMEBUFFER) != GL_FRAMEBUFFER_COMPLETE)
return false;
~~~
## 渲染到纹理
渲染到纹理很直观。简单地绑定帧缓存,然后像往常一样画场景。轻松搞定!
~~~
// Render to our framebuffer
glBindFramebuffer(GL_FRAMEBUFFER, FramebufferName);
glViewport(0,0,1024,768); // Render on the whole framebuffer, complete from the lower left corner to the upper right
~~~
fragment shader只需稍作调整:
~~~
layout(location = 0) out vec3 color;
~~~
这意味着每当修改变量“color”时,实际修改了0号渲染目标;这是因为之前调用了`glFramebufferTexture(GL_FRAMEBUFFER, GL_COLOR_ATTACHMENT0, renderedTexture, 0);
注意:最后一个参数表示mipmap的级别,这个0和GL_COLOR_ATTACHMENT0没有任何关系。
## 使用渲染出的纹理
我们将画一个简单的铺满屏幕的四边形。需要buffer、shader、ID……
~~~
// The fullscreen quad's FBO
GLuint quad_VertexArrayID;
glGenVertexArrays(1, &quad_VertexArrayID);
glBindVertexArray(quad_VertexArrayID);
static const GLfloat g_quad_vertex_buffer_data[] = {
-1.0f, -1.0f, 0.0f,
1.0f, -1.0f, 0.0f,
-1.0f, 1.0f, 0.0f,
-1.0f, 1.0f, 0.0f,
1.0f, -1.0f, 0.0f,
1.0f, 1.0f, 0.0f,
};
GLuint quad_vertexbuffer;
glGenBuffers(1, &quad_vertexbuffer);
glBindBuffer(GL_ARRAY_BUFFER, quad_vertexbuffer);
glBufferData(GL_ARRAY_BUFFER, sizeof(g_quad_vertex_buffer_data), g_quad_vertex_buffer_data, GL_STATIC_DRAW);
// Create and compile our GLSL program from the shaders
GLuint quad_programID = LoadShaders( "Passthrough.vertexshader", "SimpleTexture.fragmentshader" );
GLuint texID = glGetUniformLocation(quad_programID, "renderedTexture");
GLuint timeID = glGetUniformLocation(quad_programID, "time");
~~~
现在想渲染到屏幕上的话,必须把glBindFramebuffer的第二个参数设为0。
~~~
// Render to the screen
glBindFramebuffer(GL_FRAMEBUFFER, 0);
glViewport(0,0,1024,768); // Render on the whole framebuffer, complete from the lower left corner to the upper right
~~~
我们用下面这个shader来画全屏的四边形:
~~~
#version 330 core
in vec2 UV;
out vec3 color;
uniform sampler2D renderedTexture;
uniform float time;
void main(){
color = texture( renderedTexture, UV + 0.005*vec2( sin(time+1024.0*UV.x),cos(time+768.0*UV.y)) ).xyz;
}
~~~
这段代码只是简单地采样纹理,加上一个随时间变化的微小偏移。
## 结果

## 进一步探索
## 使用深度
在一些情况下,使用已渲染的纹理可能需要深度。本例中,像下面这样,简单地渲染到纹理中:
~~~
glTexImage2D(GL_TEXTURE_2D, 0,GL_DEPTH_COMPONENT24, 1024, 768, 0,GL_DEPTH_COMPONENT, GL_FLOAT, 0);
~~~
(“24”是精度。你可以按需从16,24,32中选。通常24刚好)
上面这些已经足够您起步了。课程源码中有完整的实现。
运行可能有点慢,因为驱动无法使用[Hi-Z](http://developer.amd.com/media/gpu_assets/Depth_in-depth.pdf)这类优化。
下图的深度层次已经经过手动“优化”。通常,深度纹理不会这么清晰。深度纹理中,近 = Z接近0 = 颜色深; 远 = Z接近1 = 颜色浅。

## 多重采样
能够用多重采样纹理来替代基础纹理:只需要在C++代码中将glTexImage2D替换为[glTexImage2DMultisample](http://www.opengl.org/sdk/docs/man3/xhtml/glTexImage2DMultisample.xml),在fragment shader中将`sampler2D/texture`替换为`sampler2DMS/texelFetch`。
但要注意:`texelFetch`多出了一个参数,表示采样的数量。换句话说,就是没有自动“滤波”(在多重采样中,正确的术语是“分辨率(resolution)”)功能。
所以需要你自己解决多重采样的纹理,另外,非多重采样纹理,是多亏另一个着色器。
没有什么难点,只是体积庞大。
## 多重渲染目标
你可能需要同时写多个纹理。
简单地创建若干纹理(都要有正确、一致的大小!),调用glFramebufferTexture,为每一个纹理设置一个不同的color attachement,用更新的参数(如`(2,{GL_COLOR_ATTACHMENT0,GL_COLOR_ATTACHMENT1,GL_DEPTH_ATTACHMENT})`一样)调用glDrawBuffers,然后在片断着色器中多添加一个输出变量:
~~~
layout(location = 1) out vec3 normal_tangentspace; // or whatever
~~~
提示1:如果真需要在纹理中输出向量,浮点纹理也是有的,可以用16或32位精度代替8位……看看[glTexImage2D](http://www.opengl.org/sdk/docs/man/xhtml/glTexImage2D.xml)的参考手册(搜GL_FLOAT)。提示2:对于以前版本的OpenGL,请使用glFragData[1] = myvalue。
## 练习
- 试使用`glViewport(0,0,512,768)`代替`glViewport(0,0,1024,768)`;(帧缓存、屏幕两种情况都试试)
- 在最后一个fragment shader中尝试一下用其他UV坐标
- 试用一个真正的变换矩阵变换四边形。首先用硬编码方式。然后尝试使用`controls.hpp`里面的函数,观察到了什么现象?
> © [http://www.opengl-tutorial.org/](http://www.opengl-tutorial.org/)
> Written with [StackEdit](https://stackedit.io/).
第十三课:法线贴图
最后更新于:2022-04-01 04:37:42
# 第十三课:法线贴图
欢迎来到第十三课!今天讲法线贴图(normal mapping)。
学完[第八课:基本光照模型](http://www.opengl-tutorial.org/beginners-tutorials/tutorial-8-basic-shading/)后,我们知道了如何用三角形法线得到不错的光照效果。需要注意的是,截至目前,每个顶点仅有一个法线:在三角形三个顶点间,法线是平滑过渡的;而颜色(纹理的采样)恰与此相反。
## 法线纹理
法线纹理看起来像这样:

每个纹素的RGB值实际上表示的是XYZ向量:颜色的分量取值范围为0到1,而向量的分量取值范围是-1到1;可以建立从纹素到法线的简单映射:
~~~
normal = (2*color)-1 // on each component
~~~
法线纹理整体呈蓝色,因为法线基本是朝上的(上方即Z轴正向。OpenGL中Y轴=上,有所不同。这种不兼容很蠢,但没人想为此重写现有的工具,我们将就用吧。后面介绍详情。)
法线纹理的映射方式和颜色纹理相似。麻烦的是如何将法线从各三角形局部坐标系(切线坐标系tangent space,亦称图像坐标系image space)变换到模型坐标系(计算光照采用的坐标系)。
## 切线和双切线(Tangent and Bitangent)
想必大家对矩阵已经十分熟悉了;大家知道,定义一个坐标系(本例是切线坐标系)需要三个向量。现在Up向量已经有了,即法线:可用Blender计算,或做一个简单的叉乘。下图中蓝色箭头代表法线(法线贴图整体颜色也恰好是蓝色)。

然后是切线T:垂直于平面的向量。切线有很多个:

这么多切线中该选哪一个呢?理论上,任何一个都可以。不过我们得和相邻顶点保持一致,以免导致边缘出现瑕疵。一个通行的办法是将切线方向和纹理坐标系对齐:
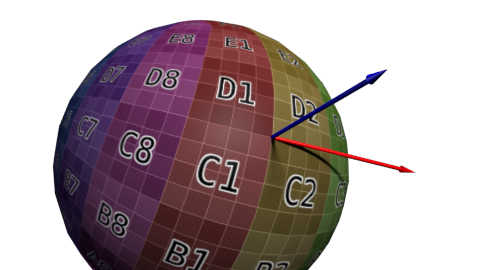
定义一组基需要三个向量,因此我们还得计算双切线B(本来可以随便选一条切线,但选定垂直于其他两条轴的切线,计算会方便些)。
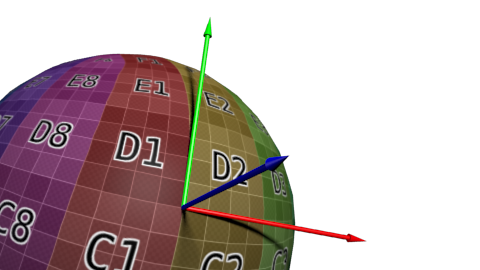
算法如下:若把三角形的两条边记为`deltaPos1`和`deltaPos2`,`deltaUV1`和`deltaUV2`是对应的UV坐标下的差值;此问题可用如下方程表示:
~~~
deltaPos1 = deltaUV1.x * T + deltaUV1.y * B
deltaPos2 = deltaUV2.x * T + deltaUV2.y * B
~~~
求解T和B就得到了切线和双切线!(代码见下文)
已知T、B、N向量之后,即可得下面这个漂亮的矩阵,完成从模型坐标系到切线坐标系的变换:
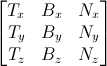
有了TBN矩阵,我们就能把法线(从法线纹理中提取而来)变换到模型坐标系。
可我们需要的却是与之相反的变换:从切线坐标系到模型坐标系,法线保持不变。所有计算均在切线坐标系中进行,不会对其他计算产生影响。
既然要进行逆向的变换,那只需对以上矩阵求逆即可。这个矩阵(正交阵,即各向量相互正交,请看后面“延伸阅读”小节)的逆矩阵恰好也就是其转置矩阵,计算十分简单:
~~~
invTBN = transpose(TBN)
~~~
亦即:
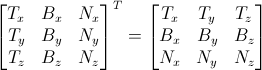
## 准备VBO
## 计算切线和双切线
我们需要为整个模型计算切线、双切线和法线。用一个单独的函数完成这项工作:
~~~
void computeTangentBasis(
// inputs
std::vector<glm::vec3> & vertices,
std::vector<glm::vec2> & uvs,
std::vector<glm::vec3> & normals,
// outputs
std::vector<glm::vec3> & tangents,
std::vector<glm::vec3> & bitangents
){
~~~
为每个三角形计算边(`deltaPos`)和`deltaUV`
~~~
for ( int i=0; i<vertices.size(); i+=3){
// Shortcuts for vertices
glm::vec3 & v0 = vertices[i+0];
glm::vec3 & v1 = vertices[i+1];
glm::vec3 & v2 = vertices[i+2];
// Shortcuts for UVs
glm::vec2 & uv0 = uvs[i+0];
glm::vec2 & uv1 = uvs[i+1];
glm::vec2 & uv2 = uvs[i+2];
// Edges of the triangle : postion delta
glm::vec3 deltaPos1 = v1-v0;
glm::vec3 deltaPos2 = v2-v0;
// UV delta
glm::vec2 deltaUV1 = uv1-uv0;
glm::vec2 deltaUV2 = uv2-uv0;
~~~
现在用公式来算切线和双切线:
~~~
float r = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV1.y * deltaUV2.x);
glm::vec3 tangent = (deltaPos1 * deltaUV2.y - deltaPos2 * deltaUV1.y)*r;
glm::vec3 bitangent = (deltaPos2 * deltaUV1.x - deltaPos1 * deltaUV2.x)*r;
~~~
最后,把这些*切线*和*双切线*缓存到数组。记住,还没为这些缓存的数据生成索引,因此每个顶点都有一份拷贝。
~~~
// Set the same tangent for all three vertices of the triangle.
// They will be merged later, in vboindexer.cpp
tangents.push_back(tangent);
tangents.push_back(tangent);
tangents.push_back(tangent);
// Same thing for binormals
bitangents.push_back(bitangent);
bitangents.push_back(bitangent);
bitangents.push_back(bitangent);
}
~~~
## 生成索引
索引VBO的方法和之前类似,仅有些许不同。
若找到一个相似顶点(相同的坐标、法线、纹理坐标),我们不使用它的切线、次法线;反而要取其均值。因此,只需把旧代码修改一下:
~~~
// Try to find a similar vertex in out_XXXX
unsigned int index;
bool found = getSimilarVertexIndex(in_vertices[i], in_uvs[i], in_normals[i], out_vertices, out_uvs, out_normals, index);
if ( found ){ // A similar vertex is already in the VBO, use it instead !
out_indices.push_back( index );
// Average the tangents and the bitangents
out_tangents[index] += in_tangents[i];
out_bitangents[index] += in_bitangents[i];
}else{ // If not, it needs to be added in the output data.
// Do as usual
[...]
}
~~~
注意,这里没做规范化。这样做很讨巧,因为小三角形的切线、双切线向量也小;相对于大三角形(对最终形状影响较大),对最终结果的影响力也就小。
## Shader
## 新增的缓冲区和uniform变量
新加上两个缓冲区:分别存放切线和双切线:
~~~
GLuint tangentbuffer;
glGenBuffers(1, &tangentbuffer);
glBindBuffer(GL_ARRAY_BUFFER, tangentbuffer);
glBufferData(GL_ARRAY_BUFFER, indexed_tangents.size() * sizeof(glm::vec3), &indexed_tangents[0], GL_STATIC_DRAW);
GLuint bitangentbuffer;
glGenBuffers(1, &bitangentbuffer);
glBindBuffer(GL_ARRAY_BUFFER, bitangentbuffer);
glBufferData(GL_ARRAY_BUFFER, indexed_bitangents.size() * sizeof(glm::vec3), &indexed_bitangents[0], GL_STATIC_DRAW);
~~~
还需要一个uniform变量存储新的法线纹理:
~~~
[...]
GLuint NormalTexture = loadTGA_glfw("normal.tga");
[...]
GLuint NormalTextureID = glGetUniformLocation(programID, "NormalTextureSampler");
~~~
另外一个uniform变量存储3x3的模型视图矩阵。严格地讲,这个矩阵不必要,但有它更方便;详见后文。由于仅仅计算旋转,不需要位移,因此只需矩阵左上角3x3的部分。
~~~
GLuint ModelView3x3MatrixID = glGetUniformLocation(programID, "MV3x3");
~~~
完整的绘制代码如下:
~~~
// Clear the screen
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// Use our shader
glUseProgram(programID);
// Compute the MVP matrix from keyboard and mouse input
computeMatricesFromInputs();
glm::mat4 ProjectionMatrix = getProjectionMatrix();
glm::mat4 ViewMatrix = getViewMatrix();
glm::mat4 ModelMatrix = glm::mat4(1.0);
glm::mat4 ModelViewMatrix = ViewMatrix * ModelMatrix;
glm::mat3 ModelView3x3Matrix = glm::mat3(ModelViewMatrix); // Take the upper-left part of ModelViewMatrix
glm::mat4 MVP = ProjectionMatrix * ViewMatrix * ModelMatrix;
// Send our transformation to the currently bound shader,
// in the "MVP" uniform
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);
glUniformMatrix4fv(ModelMatrixID, 1, GL_FALSE, &ModelMatrix[0][0]);
glUniformMatrix4fv(ViewMatrixID, 1, GL_FALSE, &ViewMatrix[0][0]);
glUniformMatrix4fv(ViewMatrixID, 1, GL_FALSE, &ViewMatrix[0][0]);
glUniformMatrix3fv(ModelView3x3MatrixID, 1, GL_FALSE, &ModelView3x3Matrix[0][0]);
glm::vec3 lightPos = glm::vec3(0,0,4);
glUniform3f(LightID, lightPos.x, lightPos.y, lightPos.z);
// Bind our diffuse texture in Texture Unit 0
glActiveTexture(GL_TEXTURE0);
glBindTexture(GL_TEXTURE_2D, DiffuseTexture);
// Set our "DiffuseTextureSampler" sampler to user Texture Unit 0
glUniform1i(DiffuseTextureID, 0);
// Bind our normal texture in Texture Unit 1
glActiveTexture(GL_TEXTURE1);
glBindTexture(GL_TEXTURE_2D, NormalTexture);
// Set our "Normal TextureSampler" sampler to user Texture Unit 0
glUniform1i(NormalTextureID, 1);
// 1rst attribute buffer : vertices
glEnableVertexAttribArray(0);
glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer);
glVertexAttribPointer(
0, // attribute
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// 2nd attribute buffer : UVs
glEnableVertexAttribArray(1);
glBindBuffer(GL_ARRAY_BUFFER, uvbuffer);
glVertexAttribPointer(
1, // attribute
2, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// 3rd attribute buffer : normals
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glVertexAttribPointer(
2, // attribute
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// 4th attribute buffer : tangents
glEnableVertexAttribArray(3);
glBindBuffer(GL_ARRAY_BUFFER, tangentbuffer);
glVertexAttribPointer(
3, // attribute
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// 5th attribute buffer : bitangents
glEnableVertexAttribArray(4);
glBindBuffer(GL_ARRAY_BUFFER, bitangentbuffer);
glVertexAttribPointer(
4, // attribute
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// Index buffer
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, elementbuffer);
// Draw the triangles !
glDrawElements(
GL_TRIANGLES, // mode
indices.size(), // count
GL_UNSIGNED_INT, // type
(void*)0 // element array buffer offset
);
glDisableVertexAttribArray(0);
glDisableVertexAttribArray(1);
glDisableVertexAttribArray(2);
glDisableVertexAttribArray(3);
glDisableVertexAttribArray(4);
// Swap buffers
glfwSwapBuffers();
~~~
## Vertex shader
和前面讲的一样,所有计算都在观察坐标系中做,因为在这获取片断坐标更容易。这就是为什么要用模型视图矩阵乘T、B、N向量。
~~~
vertexNormal_cameraspace = MV3x3 * normalize(vertexNormal_modelspace);
vertexTangent_cameraspace = MV3x3 * normalize(vertexTangent_modelspace);
vertexBitangent_cameraspace = MV3x3 * normalize(vertexBitangent_modelspace);
~~~
这三个向量确定了TBN矩阵,其创建方式如下:
~~~
mat3 TBN = transpose(mat3(
vertexTangent_cameraspace,
vertexBitangent_cameraspace,
vertexNormal_cameraspace
)); // You can use dot products instead of building this matrix and transposing it. See References for details.
~~~
此矩阵是从观察坐标系到切线坐标系的变换(若有一矩阵名为`XXX_modelspace`,则它执行的是从模型坐标系到切线坐标系的变换)。可以利用它计算切线坐标系中的光线方向和视线方向。
~~~
LightDirection_tangentspace = TBN * LightDirection_cameraspace;
EyeDirection_tangentspace = TBN * EyeDirection_cameraspace;
~~~
## Fragment shader
切线坐标系中的法线很容易获取:就在纹理中:
~~~
// Local normal, in tangent space
vec3 TextureNormal_tangentspace = normalize(texture2D( NormalTextureSampler, UV ).rgb*2.0 - 1.0);
~~~
一切准备就绪。漫反射光的值由切线坐标系中的n和l计算得来(在哪个坐标系中计算并不重要,重要的是n和l必须位于同一坐标系中),再用*clamp( dot( n,l ), 0,1 )*截断。镜面光用*clamp( dot( E,R ), 0,1 )*截断,E和R也必须位于同一坐标系中。搞定!S
## 结果
这是目前得到的结果,可以看到:
- 砖块看上去凹凸不平,这是因为砖块表面法线变化比较剧烈
- 水泥部分看上去很平整,这是因为这部分的法线纹理都是整齐的蓝色

## 延伸阅读
## 正交化(Orthogonalization)
Vertex shader中,为了计算得更快,我们没有用矩阵求逆,而是进行了转置。这只有当矩阵表示的坐标系是正交的时候才成立,而眼前这个矩阵还不是正交的。幸运的是这个问题很容易解决:只需在`computeTangentBasis()`末尾让切线与法线垂直。I
~~~
t = glm::normalize(t - n * glm::dot(n, t));
~~~
这个公式有点难理解,来看看图:
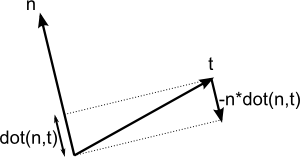
n和t差不多是相互垂直的,只要把`t`沿`-n`方向稍微“压”一下,这个幅度是`dot(n,t)`。[这里](http://www.cse.illinois.edu/iem/least_squares/gram_schmidt/)有一个applet也讲得很清楚(仅含两个向量)
## 左手坐标系还是右手坐标系?
一般不必担心这个问题。但在某些情况下,比如使用对称模型时,UV坐标方向是错的,导致切线T方向错误。
检查是否需要翻转这些方向很容易:TBN必须形成一个右手坐标系,即,向量`cross(n,t)`应该和b同向。
用数学术语讲,“向量A和向量B同向”就是“`dot(A,B)>0`”;故只需检查`dot( cross(n,t) , b )`是否大于0。
若`dot( cross(n,t) , b ) < 0`,就要翻转`t`:
~~~
if (glm::dot(glm::cross(n, t), b) < 0.0f){
t = t * -1.0f;
}
~~~
在`computeTangentBasis()`末对每个顶点都做这个操作。
## 高光纹理(Specular texture)
纯粹出于乐趣,我在代码里加上了高光纹理;取代了原先作为高光颜色的灰色`vec3(0.3,0.3,0.3)`,现在看起来像这样:

注意,现在水泥部分始终是黑色的:因为高光纹理中,其高光分量为0。
## 用立即模式进行调试
本站的初衷是让大家**不再**使用过时、缓慢、问题频出的立即模式。
不过,用立即模式进行调试却十分方便:
这里,我们在立即模式下画了一些线条表示切线坐标系。
要进入立即模式,得关闭3.3 Core Profile:
~~~
glfwOpenWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_COMPAT_PROFILE);
~~~
然后把矩阵传给旧式的OpenGL流水线(你也可以另写一个着色器,不过这样做更简单,反正都是在hacking):
~~~
glMatrixMode(GL_PROJECTION);
glLoadMatrixf((const GLfloat*)&ProjectionMatrix[0]);
glMatrixMode(GL_MODELVIEW);
glm::mat4 MV = ViewMatrix * ModelMatrix;
glLoadMatrixf((const GLfloat*)&MV[0]);
~~~
禁用着色器:
~~~
glUseProgram(0);
~~~
然后画线条(本例中法线都已被归一化,乘了0.1,放到了对应顶点上):
~~~
glColor3f(0,0,1);
glBegin(GL_LINES);
for (int i=0; i<indices.size(); i++){
glm::vec3 p = indexed_vertices[indices[i]];
glVertex3fv(&p.x);
glm::vec3 o = glm::normalize(indexed_normals[indices[i]]);
p+=o*0.1f;
glVertex3fv(&p.x);
}
glEnd();
~~~
记住:实际项目中不要用立即模式!只在调试时用!别忘了之后恢复到Core Profile,它可以保证不会启用立即模式!
## 用颜色进行调试
调试时,将向量的值可视化很有用。最简单的方法是把向量都写到帧缓冲区。举个例子,我们把`LightDirection_tangentspace`可视化一下试试
~~~
color.xyz = LightDirection_tangentspace;
~~~
这说明:
-
在圆柱体的右侧,光线(如白色线条所示)是朝上(在切线坐标系中)的。也就是说,光线和三角形的法线同向。
-
在圆柱体的中间部分,光线和切线方向(指向+X)同向。
友情提示:
- 可视化前,变量是否需要规范化?这取决于具体情况。
- 如果结果不好看懂,就逐分量地可视化。比如,只观察红色,而将绿色和蓝色分量强制设为0。
- 别折腾alpha值,太复杂了
>
- 若想将一个负值可视化,可以采用和处理法线纹理一样的技巧:转而把`(v+1.0)/2.0`可视化,于是黑色就代表-1,而白色代表+1。只不过这样做有点绕弯子。
## 用变量名进行调试
前面已经讲过了,搞清楚向量所处的坐标系至关重要。千万别把一个观察坐标系里的向量和一个模型坐标系里的向量做点乘。
给向量名称添加后缀“_modelspace”可以有效地避免这类计算错误。
## 怎样制作法线贴图
作者James O’Hare。点击图片放大。

## 练习
- 在`indexVBO_TBN`函数中,在做加法前把向量归一化,看看结果。
- 用颜色可视化其他向量(如`instance`、`EyeDirection_tangentspace`),试着解释你看到的结果。
## 工具和链接
- [Crazybump](http://www.crazybump.com/) 制作法线纹理的好工具,收费。
- [Nvidia photoshop插件](http://developer.nvidia.com/nvidia-texture-tools-adobe-photoshop)免费,不过Photoshop不免费……
- [用多幅照片制作法线贴图](http://www.zarria.net/nrmphoto/nrmphoto.html)
- [用单幅照片制作法线贴图](http://www.katsbits.com/tutorials/textures/making-normal-maps-from-photographs.php)
- 关于[矩阵转置](http://www.katjaas.nl/transpose/transpose.html)的详细资料
## 参考文献
- [Lengyel, Eric. “Computing Tangent Space Basis Vectors for an Arbitrary Mesh”. Terathon Software 3D Graphics Library, 2001.](http://www.terathon.com/code/tangent.html)
- [Real Time Rendering, third edition](http://www.amazon.com/dp/1568814240)
- [ShaderX4](http://www.amazon.com/dp/1584504250)
第十二课:OpenGL扩展
最后更新于:2022-04-01 04:37:39
# 第十二课:OpenGL扩展
## 扩展
GPU的性能随着更新换代一直在提高,支持渲染更多的三角形和像素点。然而,原始性能不是我们唯一关心的。NVIDIA, AMD和Intel也通过增加功能来改善他们的显卡。来看一些例子。
### ARB_fragment_program
回溯到2002年,GPU都没有顶点着色器或片断着色器:所有的一切都硬编码在芯片中。这被称为固定功能流水线(Fixed-Function Pipeline (FFP))。同样地,当时最新的OpenGL 1.3中也没有接口可以创建、操作和使用所谓的“着色器”,因为它根本不存在。接着NVIDIA决定用实际代码描述渲染过程,来取代数以百计的标记和状态量。这就是ARB_fragment_program的由来。当时还没有GLSL,但你可以写这样的程序:
~~~
!!ARBfp1.0 MOV result.color, fragment.color; END
~~~
但若要显式地令OpenGL使用这些代码,你需要一些还不在OpenGL里的特殊函数。在进行解释前,再举个例子。
### ARB_debug_output
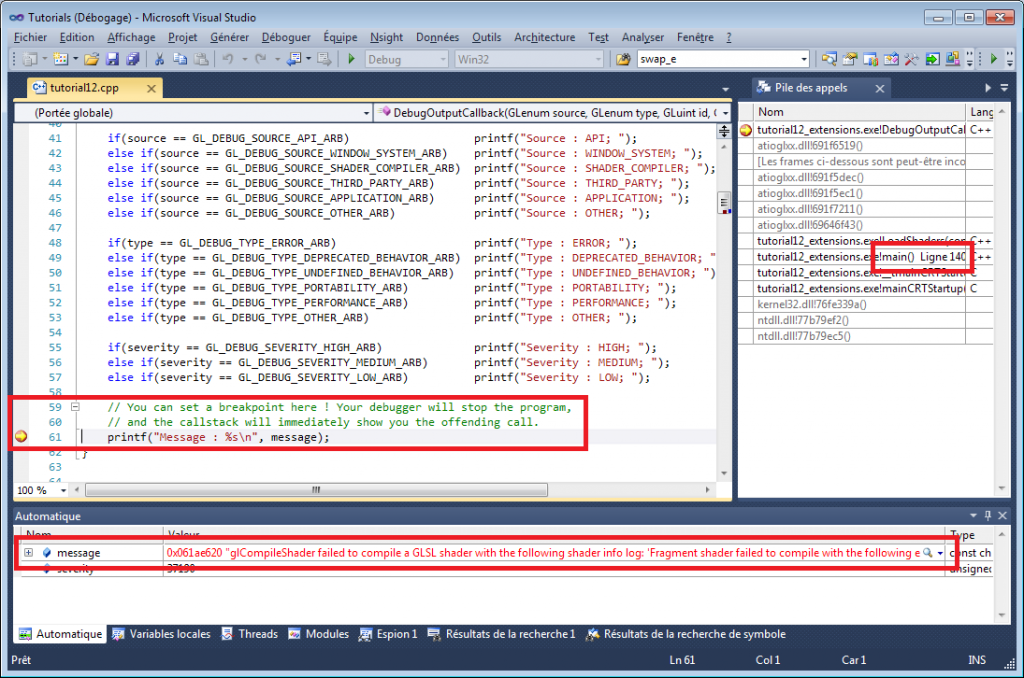
好,你说『ARB_fragment_program太老了,所以我不需要扩展这东西』?其实有不少新的扩展非常方便。其中一个便是ARB_debug_output,它提供了一个不存在于OpenGL 3.3中的,但你可以/应该用到的功能。它定义了像GL_DEBUG_OUTPUT_SYNCHRONOUS_ARB或GL_DEBUG_SEVERITY_MEDIUM_ARB之类的字符串,和DebugMessageCallbackARB这样的函数。这个扩展的伟大之处在于,当你写了一些不正确的代码,例如:
~~~
glEnable(GL_TEXTURE); // Incorrect ! You probably meant GL_TEXTURE_2D !
~~~
你能得到错误消息和错误的精确位置。总结:
- 即便在现在的OpenGL 3.3中,扩展仍旧十分有用。
- 请使用ARB_debug_output !下文有链接。
### 获取扩展 – 复杂的方式
『手动』查找一个扩展的方法是使用以下代码片断 (转自OpenGL.org wiki):
~~~
int NumberOfExtensions;
glGetIntegerv(GL_NUM_EXTENSIONS, &NumberOfExtensions);
for(i=0; i<NumberOfExtensions; i++) {
const GLubyte *ccc=glGetStringi(GL_EXTENSIONS, i);
if ( strcmp(ccc, (const GLubyte *)"GL_ARB_debug_output") == 0 ){
// The extension is supported by our hardware and driver
// Try to get the "glDebugMessageCallbackARB" function :
glDebugMessageCallbackARB = (PFNGLDEBUGMESSAGECALLBACKARBPROC) wglGetProcAddress("glDebugMessageCallbackARB");
}
}
~~~
### 获得所有的扩展 – 简单的方式
上面的方式太复杂。若用GLEW, GLee, gl3w这些库,就简单多了。例如,有了GLEW,你只需要在创建窗口后调用glewInit(),不少方便的变量就创建好了:
~~~
if (GLEW_ARB_debug_output){ // Ta-Dah ! }
~~~
(小心:debug_output是特殊的,因为你需要在上下文创建的时候启用它。在GLFW中,这通过glfwOpenWindowHint(GLFW_OPENGL_DEBUG_CONTEXT, 1)完成。)
### ARB vs EXT vs …
扩展的名字暗示了它的适用范围:
GL*:所有平台;GLX*:只有Linux和Mac下可使用(X11);WGL_:只有Windows下可使用。
EXT:通用的扩展。ARB:已经被OpenGL架构评审委员会的所有成员接受(EXT扩展没多久后就经常被提升为ARB)的扩展。NV/AMD/INTEL:顾名思义 =)
## 设计与扩展
### 问题
比方说,你的OpenGL 3.3应用程序需要渲染一些大型线条。你能够写一个复杂的顶点着色器来完成,或者简单地用[GL_NV_path_rendering](http://www.opengl.org/registry/specs/NV/path_rendering.txt),它能帮你处理所有复杂的事。
因此你可以这样写代码:
~~~
if ( GLEW_NV_path_rendering ){
glPathStringNV( ... ); // Draw the shape. Easy !
}else{
// Else what ? You still have to draw the lines
// on older NVIDIA hardware, on AMD and on INTEL !
// So you have to implement it yourself anyway !
}
~~~
### 均衡考量
当使用扩展的益处(如渲染质量、性能),超过维护两种不同方法(如上面的代码,一种靠你自己实现,一种使用扩展)的代价时,通常就选择用扩展。
例如,在时空幻境(Braid, 一个时空穿越的二维游戏)中,当你干扰时间时,就会有各种各样的图像变形效果,而这种效果在旧硬件上没法渲染。
而在OpenGL 3.3及更高版本中,包含了99%的你可能会用到的工具。一些扩展很有用,比如GL_AMD_pinned_memory,虽然它通常没法像几年前使用GL_ARB_framebuffer_object(用于纹理渲染)那样让你的游戏看起来变好10倍。
如果你不得不兼容老硬件,那么就不能用OpenGL 3+,你需要用OpenGL 2+来代替。你将不再能使用各种神奇的扩展了,你需自行处理那些问题。
更多的细节可以参考例子[OpenGL 2.1版本的第14课 – 纹理渲染](http://code.google.com/p/opengl-tutorial-org/source/browse/tutorial14_render_to_texture/tutorial14.cpp?name=2.1%20branch#152),第152行,需手动检查GL_ARB_framebuffer_object是否存在。常见问题可见FAQ。
## 结论Conclusion
OpenGL扩展提供了一个很好的方式来增强OpenGL的功能,它依赖于你用户的GPU。
虽然现在扩展属于高级用法(因为大部分功能在核心中已经有了),了解扩展如何运作和怎么用它提高软件性能(付出更高的维护代价)还是很重要的。
## 深度阅读
- debug_output tutorial by Aks 因为有GLEW,你可以跳过第一步。
- [The OpenGL extension registry](http://www.opengl.org/registry/) 所有扩展的规格说明。圣经。
- [GLEW](http://glew.sourceforge.net/) OpenGL标准扩展库
- [gl3w](https://github.com/skaslev/gl3w) 简单的OpenGL 3/4核心配置加载
第十一课:2D文本
最后更新于:2022-04-01 04:37:37
# 第十一课:2D文本
本课将学习如何在三维场景之上绘制二维文本。本例是一个简单的计时器:
## API
我们将实现这些简单的接口(位于`common/text2D.h`):
~~~
void initText2D(const char * texturePath);
void printText2D(const char * text, int x, int y, int size);
void cleanupText2D();
~~~
为了让代码在640*480和1080p分辨率下都能正常工作,x和y的范围分别设为[0-800]和[0-600]。顶点着色器将根据实际屏幕大小做对它做调整。
完整的实现代码请参阅`common/text2D.cpp`。
## 纹理
`initText2D`简单地读取一个纹理和一些着色器,很好理解。来看看纹理:
该纹理由[CBFG](http://www.codehead.co.uk/cbfg/)生成。CBFG是诸多从字体生成纹理的工具之一。把纹理加载到Paint.NET,加上红色背景(仅为了观察方便;本教程中的红色背景,都代表透明)。
`printText2D()`在屏幕的适当位置,生成一个纹理坐标正确的四边形。
## 绘制
首先,填充这些缓冲区:
~~~
std::vector<glm::vec2> vertices;
std::vector<glm::vec2> UVs;
~~~
文本中的每个字母,都要计算其四边形包围盒的顶点坐标,然后添加两个三角形(组成一个四边形):
~~~
for ( unsigned int i=0 ; i<length ; i++ ){
glm::vec2 vertex_up_left??? = glm::vec2( x+i*size???? , y+size );
glm::vec2 vertex_up_right?? = glm::vec2( x+i*size+size, y+size );
glm::vec2 vertex_down_right = glm::vec2( x+i*size+size, y????? );
glm::vec2 vertex_down_left? = glm::vec2( x+i*size???? , y????? );
vertices.push_back(vertex_up_left?? );
vertices.push_back(vertex_down_left );
vertices.push_back(vertex_up_right? );
vertices.push_back(vertex_down_right);
vertices.push_back(vertex_up_right);
vertices.push_back(vertex_down_left);
~~~
轮到UV坐标了。计算左上角的坐标:
~~~
char character = text[i];
float uv_x = (character%16)/16.0f;
float uv_y = (character/16)/16.0f;
~~~
这样做是可行的(基本可行,详见下文),因为[A的ASCII值](http://www.asciitable.com/)为65。65%16 = 1,因此A位于第1列(列号从0开始)。
65/16 = 4,因此A位于第4行(这是整数除法,所以结果不是想象中的4.0625)
两者都除以16.0以使之落于[0.0 - 1.0]区间内,这正是OpenGL纹理所需的。
现在只需对顶点重复相同的操作:
~~~
glm::vec2 uv_up_left = glm::vec2( uv_x , 1.0f - uv_y );
glm::vec2 uv_up_right = glm::vec2( uv_x+1.0f/16.0f, 1.0f - uv_y );
glm::vec2 uv_down_right = glm::vec2( uv_x+1.0f/16.0f, 1.0f - (uv_y + 1.0f/16.0f) );
glm::vec2 uv_down_left = glm::vec2( uv_x , 1.0f - (uv_y + 1.0f/16.0f) );
UVs.push_back(uv_up_left );
UVs.push_back(uv_down_left );
UVs.push_back(uv_up_right );
UVs.push_back(uv_down_right);
UVs.push_back(uv_up_right);
UVs.push_back(uv_down_left);
}
~~~
其余的操作和往常一样:绑定缓冲区,填充,选择着色器程序,绑定纹理,开启、绑定、配置顶点属性,开启混合,调用glDrawArrays。欧也,搞定了。
注意非常重要的一点:这些坐标位于[0,800][0,600]范围内。也就是说,这里**不需要**矩阵。vertex shader只需简单换算就可以把这些坐标转换到[-1,1][-1,1]范围内(也可以在C++代码中完成这一步)。
~~~
void main(){
// Output position of the vertex, in clip space
// map [0..800][0..600] to [-1..1][-1..1]
vec2 vertexPosition_homoneneousspace = vertexPosition_screenspace - vec2(400,300); // [0..800][0..600] -> [-400..400][-300..300]
vertexPosition_homoneneousspace /= vec2(400,300);
gl_Position = vec4(vertexPosition_homoneneousspace,0,1);
// UV of the vertex. No special space for this one.
UV = vertexUV;
}
~~~
fragment shader的工作也很少:
~~~
void main(){
color = texture( myTextureSampler, UV );
}
~~~
顺便说一下,别在工程中使用这些代码,因为它只能处理拉丁字符。否则你的产品在印度、中国、日本(甚至德国,因为纹理上没有ß这个字母)就别想卖了。这幅纹理是我用法语字符集生成的,在法国用用还可以(注意 é, à, ç等字母)。修改其他教程的代码时注意库的使用。其他教程大多使用OpenGL 2,和本教程不兼容。很可惜,我还没找到一个足够好的、能处理UTF-8字符集的库。
顺带提一下,您最好看看Joel Spolsky写的[The Absolute Minimum Every Software Developer Absolutely, Positively Must Know About Unicode and Character Sets (No Excuses!)](http://www.joelonsoftware.com/articles/Unicode.html)。
如果您需要处理大量的文本,可以参考这篇[Valve的文章](http://www.valvesoftware.com/publications/2007/SIGGRAPH2007_AlphaTestedMagnification.pdf)。
第十课:透明
最后更新于:2022-04-01 04:37:35
# 第十课:透明
## alpha通道
alpha通道的概念很简单。之前是写RGB结果,现在改为写RGBA:
~~~
// Ouput data : it's now a vec4
out vec4 color;
~~~
前三个分量仍可以通过混合操作符(swizzle operator).xyz访问,最后一个分量通过.a访问:
~~~
color.a = 0.3;
~~~
不太直观,但alpha = 不透明度;因此alpha = 1代表完全不透明,alpha = 0为完全透明。
这里我们简单地将alpha硬编码为0.3;但更常见的做法是用一个uniform变量表示它,或从RGBA纹理中读取(TGA格式支持alpha通道,而GLFW支持TGA)。
结果如下。既然我们能“看透”模型表面,请确保关闭隐面消除(`glDisable(GL_CULL_FACE)`)。否则就发现模型没有了“背”面。
## 顺序很重要!
上一个截图看上去还行,但这仅仅是运气好罢了。
## 问题所在
这里我画了一红一绿两个alpha值为50%的正方形。从中可以看出顺序的重要性,最终的颜色显著影响了眼睛对深度的感知。
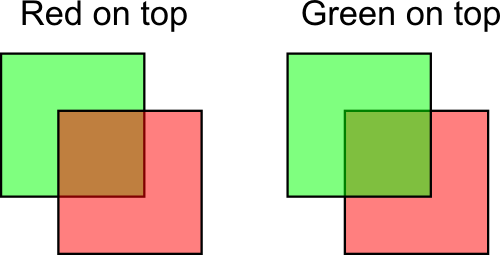
我们的场景中也出现了同样的现象。试着稍稍改变一下视角:
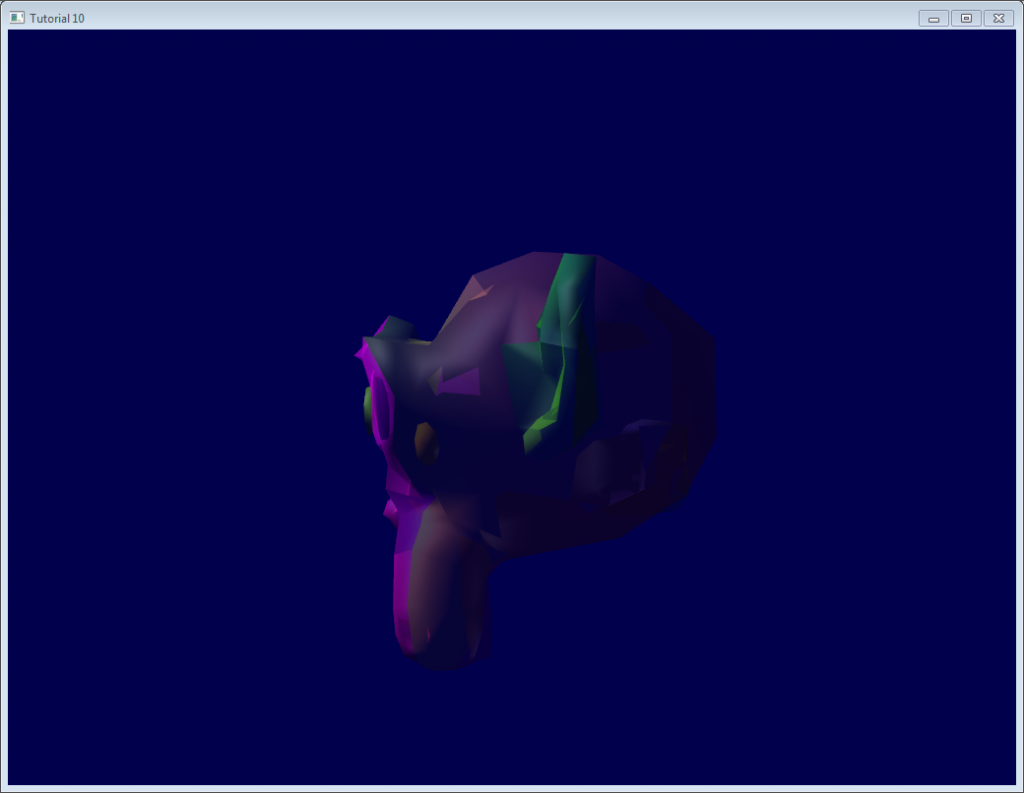
事实证明这个问题十分棘手。游戏中透明的东西不多,对吧?
## 常见解决方案
常见解决方案即对所有的透明三角形排序。是的,所有的透明三角形。
- 绘制场景的不透明部分,让深度缓冲区能丢弃被遮挡的透明三角形。
- 对透明三角形按深度从近到远排序。
- 绘制透明三角形。
可以用C语言的`qsort`函数或者C++的`std::sort`函数来排序。细节就不多说了,因为……
## 警告
这么做可以解决问题(下一节还会介绍它),但:
- 填充速率会被限制,即,每个片断会写10、20次,也许更多。这对力不从心的内存总线来说太沉重了。通常,深度缓冲区可以自动丢弃“远”片断;但这时,我们显式地对片断进行排序,故深度缓冲区实际上没发挥作用。
- 这些操作,每个像素上都会做4遍(我们用了4倍多重采样抗锯齿(MSAA)),除非用了什么高明的优化。
- 透明三角形排序很耗时
- 若要逐个三角形地切换纹理,或者更糟糕地,要切换着色器——性能会大打折扣。别这么干。
一个足够好的解决方案是:
- 限制透明多边形的数量
- 对所有透明多边形使用同一个着色器和纹理
- 若这些透明多边形必须看起来很不同,请用纹理区分!
- 若不排序,效果也还行,那最好别排序。
## 顺序无关透明
如果你的引擎确实需要顶尖的透明效果,这有一些技术值得研究一番:
- [2001年Depth Peeling论文](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.18.9286&rep=rep1&type=pdf):像素级精细度,但速度不快
- ~~[Dual Depth Peeling](http://developer.download.nvidia.com/SDK/10/opengl/src/dual_depth_peeling/doc/DualDepthPeeling.pdf)~~:小幅改进
- 桶排序相关的几篇论文。把fragment存到数组,在shader中进行深度排序。
- [ATI Mecha Demo](http://fr.slideshare.net/hgruen/oit-and-indirect-illumination-using-dx11-linked-lists):又好又快,但实现起来有难度,需要最新的硬件。用链表存储fragment。
- [Cyril Crassin实现的ATI Mecha](http://blog.icare3d.org/2010/07/opengl-40-abuffer-v20-linked-lists-of.html):实现难度更大
注意,即便是《小小大星球》(*Little Big Planet*)这种最新的端游,也只用了一层透明。
## 混合函数
要让之前的代码运行,得设置好混合函数。In order for the previous code to work, you need to setup your blend function.
~~~
// Enable blending
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
~~~
这意味着
~~~
New color in framebuffer =
current alpha in framebuffer * current color in framebuffer +
(1 - current alpha in framebuffer) * shader's output color
~~~
前文所述红色方块居上的例子中:
~~~
new color = 0.5*(0,1,0) + (1-0.5)*(1,0.5,0.5); // (the red was already blended with the white background)
new color = (1, 0.75, 0.25) = the same orange
~~~
第九课:VBO索引
最后更新于:2022-04-01 04:37:32
# 第九课:VBO索引
## 索引的原理
目前为止,建立VBO时我们总是重复存储一些共享的顶点和边。
本课将介绍索引技术。借助索引,我们可以重复使用一个顶点。这是用*索引缓冲区(index buffer)*来实现的。
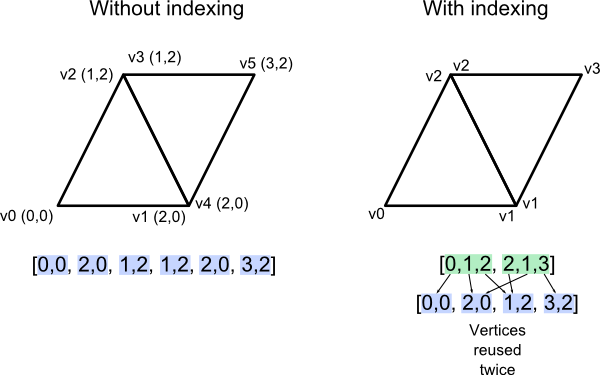
索引缓冲区存储的是整数;每个三角形有三个整数索引,用索引就可以在各种*属性缓冲区*(顶点坐标、颜色、UV坐标、其他UV坐标、法向缓冲区等)中找到顶点的信息。这有点像OBJ文件格式,但有一点相差甚远:索引缓冲区只有一个。这意味着若两个三角形共用一个顶点,那这个顶点的所有属性对两个三角形来说都是一样的。
## 共享vs分开
来看看法向的例子。下图中,艺术家创建了两个三角形,试图模拟一个平滑曲面。可以把两个三角形的法向融合成一个顶点的法向。为方便观看,我画了一条红线表示平滑曲面。
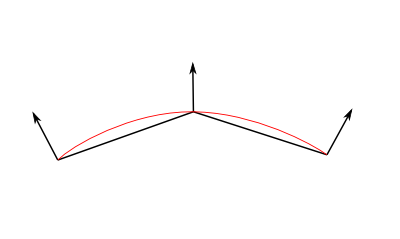
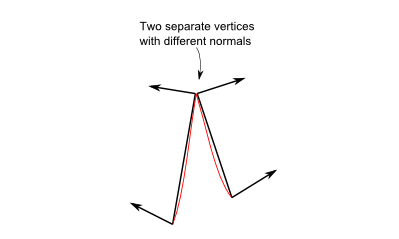
然而在第二幅图中,美工想画的是“缝隙”或“边缘”。若融合了法向,就意味着色器会像前例一样进行平滑插值,生成一个平滑的表面:

因此在这种情况下,把顶点的法向分开存储反而更好;在OpenGL中,唯一实现方法是:把顶点连同其属性完整复制一份。
## OpenGL中的索引VBO
索引的用法很简单。首先,需要创建一个额外的缓冲区存放索引。代码与之前一样,不过参数是`ELEMENT_ARRAY_BUFFER`,而非`ARRAY_BUFFER`。
~~~
std::vector<unsigned int> indices;
// fill "indices" as needed
// Generate a buffer for the indices
GLuint elementbuffer;
glGenBuffers(1, &elementbuffer);
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, elementbuffer);
glBufferData(GL_ELEMENT_ARRAY_BUFFER, indices.size() * sizeof(unsigned int), &indices[0], GL_STATIC_DRAW);
~~~
只需把`glDrawArrays`替换为如下语句,即可绘制模型:
~~~
// Index buffer
glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, elementbuffer);
// Draw the triangles !
glDrawElements(
GL_TRIANGLES, // mode
indices.size(), // count
GL_UNSIGNED_INT, // type
(void*)0 // element array buffer offset
);
~~~
(小提示:最好使用`unsigned short`,不要用`unsigned int`。这样更节省空间,速度也更快。)
## 填充索引缓冲区
现在遇到真正的问题了。如前所述,OpenGL只能使用一个索引缓冲区,而OBJ(及一些其他常用的3D格式,如Collada)每个属性都有一个索引缓冲区。这意味着,必须通过某种方式把若干个索引缓冲区合并成一个。
合并算法如下:
~~~
For each input vertex
Try to find a similar ( = same for all attributes ) vertex between all those we already output
If found :
A similar vertex is already in the VBO, use it instead !
If not found :
No similar vertex found, add it to the VBO
~~~
完整的C++代码位于`common/vboindexer.cpp`,注释很详尽。如果理解了以上算法,读懂代码应该没问题。
若两顶点的坐标、UV坐标和法线都相等,则认为两顶点是同一顶点。若还有其他属性,这一标准得酌情修改。
为了表述的简单,我们采用了蹩脚的线性查找来寻找相似顶点。实际中用`std::map`会更好。
## 补充:FPS计数器
虽然和索引没有直接关系,但现在去看看“FPS计数器”是很合适的——这样我们就能看到,索引究竟能提升多少性能。[“工具——调试器”](http://www.opengl-tutorial.org/miscellaneous/useful-tools-links/#header-4)中还有些其他和性能相关的工具。
OpenGL中级教程
最后更新于:2022-04-01 04:37:30
第八课:基本着色
最后更新于:2022-04-01 04:37:28
# 第八课:基础光照模型
在第八课中,我们将学习光照模型的基础知识。包括:
- 物体离光源越近会越亮
- 直视反射光时会有高亮(镜面反射)
- 当光没有直接照射物体时,物体会更暗(漫反射)
- 用环境光简化计算
不包括:
- 阴影。这是个宽阔的主题,大到需要专题教程了。
- 类镜面反射(包括水)
- 任何复杂的光与物质的相互作用,像次表面散射(比如蜡)
- 各向异性材料(比如拉丝的金属)
- 追求真实感的,基于物理的光照模型
- 环境光遮蔽(在洞穴里会更黑)
- 颜色溢出(一块红色的地毯会映得白色天花板带红色)
- 透明度
- 任何种类的全局光照(它包括了上面的所有)
总而言之:只讲基础。
## 法向
过去的几个教程中我们一直在处理法向,但是并不知道法向到底是什么。
### 三角形法向
一个平面的法向是一个长度为1并且垂直于这个平面的向量。
一个三角形的法向是一个长度为1并且垂直于这个三角形的向量。通过简单地将三角形两条边进行叉乘计算(向量a和b的叉乘结果是一个同时垂直于a和b的向量,记得?),然后归一化:使长度为1。伪代码如下:
~~~
triangle ( v1, v2, v3 )
edge1 = v2-v1
edge2 = v3-v1
triangle.normal = cross(edge1, edge2).normalize()
~~~
不要将法向(normal)和normalize()函数混淆。Normalize()函数是让一个向量(任意向量,不一定必须是normal)除以其长度,从而使新长度为1。法向(normal)则是某一类向量的名字。
### 顶点法向
引申开来:顶点的法向,是包含该顶点的所有三角形的法向的均值。这很方便——因为在顶点着色器中,我们处理顶点,而不是三角形;所以在顶点处有信息是很好的。并且在OpenGL中,我们没有任何办法获得三角形信息。伪代码如下:
~~~
vertex v1, v2, v3, ....
triangle tr1, tr2, tr3 // all share vertex v1
v1.normal = normalize( tr1.normal + tr2.normal + tr3.normal )
~~~
### 在OpenGL中使用顶点法向
在OpenGL中使用法向很简单。法向是顶点的属性,就像位置,颜色,UV坐标等一样;按处理其他属性的方式处理即可。第七课的loadOBJ函数已经将它们从OBJ文件中读出来了。
~~~
GLuint normalbuffer;
glGenBuffers(1, &normalbuffer);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glBufferData(GL_ARRAY_BUFFER, normals.size() * sizeof(glm::vec3), &normals[0], GL_STATIC_DRAW);
~~~
和
~~~
// 3rd attribute buffer : normals
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, normalbuffer);
glVertexAttribPointer(
2, // attribute
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
~~~
有这些准备就可以开始了。
## 漫反射部分
### 表面法向的重要性
当光源照射一个物体,其中重要的一部分光向各个方向反射。这就是“漫反射分量”。(我们不久将会看到光的其他部分去哪里了)
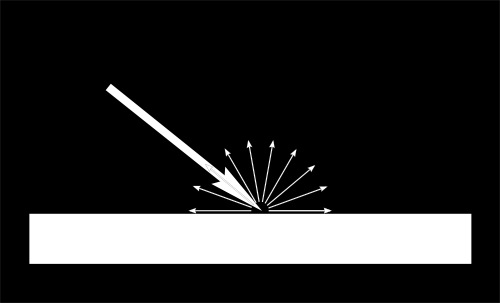
当一定量的光线到达某表面,该表面根据光到达时的角度而不同程度地被照亮。
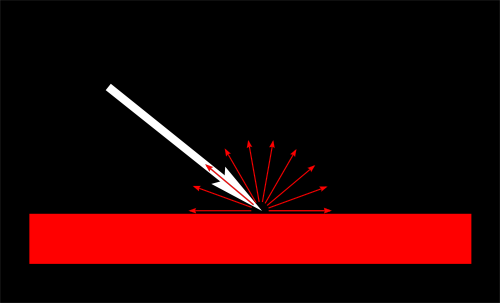
如果光线垂直于表面,它会聚在一小片表面上。如果它以一个倾斜角到达表面,相同的强度光照亮更大一片表面:
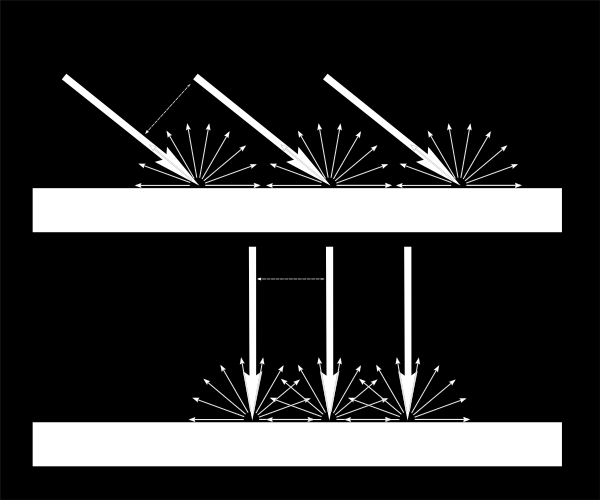
这意味着在斜射下,表面的点会较黑(但是记住,更多的点会被照射到,总光强度仍然是一样的)
也就是说,当计算像素的颜色时,入射光和表面法向的夹角很重要。因此有:
~~~
// Cosine of the angle between the normal and the light direction,
// clamped above 0
// - light is at the vertical of the triangle -> 1
// - light is perpendicular to the triangle -> 0
float cosTheta = dot( n,l );
color = LightColor * cosTheta;
~~~
在这段代码中,n是表面法向,l是从表面到光源的单位向量(和光线方向相反。虽然不直观,但能简化数学计算)。
### 注意正负
求cosTheta的公式有漏洞。如果光源在三角形后面,n和l方向相反,那么n.l是负值。这意味着colour=一个负数,没有意义。因此这种情况须用clamp()将cosTheta赋值为0:
~~~
// Cosine of the angle between the normal and the light direction,
// clamped above 0
// - light is at the vertical of the triangle -> 1
// - light is perpendicular to the triangle -> 0
// - light is behind the triangle -> 0
float cosTheta = clamp( dot( n,l ), 0,1 );
color = LightColor * cosTheta;
~~~
### 材质颜色
当然,输出颜色也依赖于材质颜色。在这幅图像中,白光由绿、红、蓝光组成。当光碰到红色材质时,绿光和蓝光被吸收,只有红光保留着。
我们可以通过一个简单的乘法来模拟:
~~~
color = MaterialDiffuseColor * LightColor * cosTheta;
~~~
### 模拟光源
首先假设在空间中有一个点光源,它向所有方向发射光线,像蜡烛一样。
对于该光源,我们的表面收到的光通量依赖于表面到光源的距离:越远光越少。实际上,光通量与距离的平方成反比:
~~~
color = MaterialDiffuseColor * LightColor * cosTheta / (distance*distance);
~~~
最后,需要另一个参数来控制光的强度。它可以被编码到LightColor中(将在随后的课程中讲到),但是现在暂且只一个颜色值(如白色)和一个强度(如60瓦)。
~~~
color = MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance);
~~~
### 组合在一起
为了让这段代码运行,需要一些参数(各种颜色和强度)和更多代码。
MaterialDiffuseColor简单地从纹理中获取。
LightColor和LightPower通过GLSL的uniform变量在着色器中设置。
cosTheta由n和l决定。我们可以在任意坐标系中表示它们,因为都是一样的。这里选相机坐标系,是因为它计算光源位置简单:
~~~
// Normal of the computed fragment, in camera space
vec3 n = normalize( Normal_cameraspace );
// Direction of the light (from the fragment to the light)
vec3 l = normalize( LightDirection_cameraspace );
~~~
Normal_cameraspace和LightDirection_cameraspace在顶点着色器中计算,然后传给片断着色器:
~~~
// Output position of the vertex, in clip space : MVP * position
gl_Position = MVP * vec4(vertexPosition_modelspace,1);
// Position of the vertex, in worldspace : M * position
Position_worldspace = (M * vec4(vertexPosition_modelspace,1)).xyz;
// Vector that goes from the vertex to the camera, in camera space.
// In camera space, the camera is at the origin (0,0,0).
vec3 vertexPosition_cameraspace = ( V * M * vec4(vertexPosition_modelspace,1)).xyz;
EyeDirection_cameraspace = vec3(0,0,0) - vertexPosition_cameraspace;
// Vector that goes from the vertex to the light, in camera space. M is ommited because it's identity.
vec3 LightPosition_cameraspace = ( V * vec4(LightPosition_worldspace,1)).xyz;
LightDirection_cameraspace = LightPosition_cameraspace + EyeDirection_cameraspace;
// Normal of the the vertex, in camera space
Normal_cameraspace = ( V * M * vec4(vertexNormal_modelspace,0)).xyz; // Only correct if ModelMatrix does not scale the model ! Use its inverse transpose if not.
~~~
这段代码看起来很牛,但它就是在第三课中学到的东西:矩阵。每个向量命名时,都嵌入了所在的空间名,这样在跟踪时更简单。 你也应该这样做。
M和V分别是模型和视图矩阵,并且是用与MVP完全相同的方式传给着色器。
### 运行时间
现在有了编写漫反射光源的一切必要条件。向前吧,刻苦努力地尝试 
### 结果
只包含漫反射分量时,我们得到以下结果(再次为无趣的纹理道歉):

这次结果比之前好,但感觉仍少了一些东西。特别地,Suzanne的背后完全是黑色的,因为我们使用clamp()。
## 环境光分量
环境光分量是最华丽的优化。
我们期望的是Suzanne的背后有一点亮度,因为在现实生活中灯泡会照亮它背后的墙,而墙会反过来(微弱地)照亮物体的背后。
但计算它的代价大得可怕。
因此通常可以简单地做点假光源取巧。实际上,直接让三维模型发光,使它看起来不是完全黑即可。
可这样完成:
~~~
vec3 MaterialAmbientColor = vec3(0.1,0.1,0.1) * MaterialDiffuseColor;
color =
// Ambient : simulates indirect lighting
MaterialAmbientColor +
// Diffuse : "color" of the object
MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
~~~
来看看它的结果
### 结果
好的,效果更好些了。如果要更好的结果,可以调整(0.1, 0.1, 0.1)值。

## 镜面反射分量
反射光的剩余部分就是镜面反射分量。这部分的光在表面有确定的反射方向。

如图所示,它形成一种波瓣。在极端的情况下,漫反射分量可以为零,这样波瓣非常非常窄(所有的光从一个方向反射),这就是镜子。
*(的确可以调整参数值,得到镜面;但这个例子中,镜面唯一反射的只有光源,渲染结果看起来会很奇怪)*
~~~
// Eye vector (towards the camera)
vec3 E = normalize(EyeDirection_cameraspace);
// Direction in which the triangle reflects the light
vec3 R = reflect(-l,n);
// Cosine of the angle between the Eye vector and the Reflect vector,
// clamped to 0
// - Looking into the reflection -> 1
// - Looking elsewhere -> < 1
float cosAlpha = clamp( dot( E,R ), 0,1 );
color =
// Ambient : simulates indirect lighting
MaterialAmbientColor +
// Diffuse : "color" of the object
MaterialDiffuseColor * LightColor * LightPower * cosTheta / (distance*distance) ;
// Specular : reflective highlight, like a mirror
MaterialSpecularColor * LightColor * LightPower * pow(cosAlpha,5) / (distance*distance);
~~~
R是反射光的方向,E是视线的反方向(就像之前对“l”的假设);如果二者夹角很小,意味着视线与反射光线重合。
pow(cosAlpha,5)用来控制镜面反射的波瓣。可以增大5来获得更大的波瓣。
### 最终结果

注意到镜面反射使鼻子和眉毛更亮。
这个光照模型因为简单,已被使用了很多年。但它有一些问题,所以被microfacet BRDF之类的基于物理的模型代替,后面将会讲到。
在下节课中,我们将学习怎么提高VBO的性能。将是第一节中级课程!
第七课:模型加载
最后更新于:2022-04-01 04:37:26
# 第七课:模型加载
目前为止,我们一直在硬编码描述立方体。你一定觉得这样做很笨拙、不方便。
本课将学习从文件中加载3D模型。和加载纹理类似,我们先写一个小的、功能有限的加载器,接着再为大家介绍几个比我们写的更好的、实用的库。
为了让课程尽可能简单,我们将采用简单、常用的OBJ格式。同样也是出于简单原则,我们只处理每个顶点有一个UV坐标和一个法向量的OBJ文件(目前你不需要知道什么是法向量)。
## 加载OBJ模型
加载函数在common/objloader.hpp中声明,在common/objloader.cpp中实现。函数原型如下:
~~~
bool loadOBJ(
const char * path,
std::vector & out_vertices,
std::vector & out_uvs,
std::vector & out_normals
)
~~~
我们让loadOBJ读取文件路径,把数据写入out_vertices/out_uvs/out_normals。如果出错则返回false。std::vector是C++中的数组,可存放glm::vec3类型的数据,数组大小可任意修改,不过std::vector和数学中的向量(vector)是两码事。其实它只是个数组。最后提一点,符号&意思是这个函数将会直接修改这些数组。
### OBJ文件示例
OBJ文件看起来大概像这样:
~~~
# Blender3D v249 OBJ File: untitled.blend
# www.blender3d.org
mtllib cube.mtl
v 1.000000 -1.000000 -1.000000
v 1.000000 -1.000000 1.000000
v -1.000000 -1.000000 1.000000
v -1.000000 -1.000000 -1.000000
v 1.000000 1.000000 -1.000000
v 0.999999 1.000000 1.000001
v -1.000000 1.000000 1.000000
v -1.000000 1.000000 -1.000000
vt 0.748573 0.750412
vt 0.749279 0.501284
vt 0.999110 0.501077
vt 0.999455 0.750380
vt 0.250471 0.500702
vt 0.249682 0.749677
vt 0.001085 0.750380
vt 0.001517 0.499994
vt 0.499422 0.500239
vt 0.500149 0.750166
vt 0.748355 0.998230
vt 0.500193 0.998728
vt 0.498993 0.250415
vt 0.748953 0.250920
vn 0.000000 0.000000 -1.000000
vn -1.000000 -0.000000 -0.000000
vn -0.000000 -0.000000 1.000000
vn -0.000001 0.000000 1.000000
vn 1.000000 -0.000000 0.000000
vn 1.000000 0.000000 0.000001
vn 0.000000 1.000000 -0.000000
vn -0.000000 -1.000000 0.000000
usemtl Material_ray.png
s off
f 5/1/1 1/2/1 4/3/1
f 5/1/1 4/3/1 8/4/1
f 3/5/2 7/6/2 8/7/2
f 3/5/2 8/7/2 4/8/2
f 2/9/3 6/10/3 3/5/3
f 6/10/4 7/6/4 3/5/4
f 1/2/5 5/1/5 2/9/5
f 5/1/6 6/10/6 2/9/6
f 5/1/7 8/11/7 6/10/7
f 8/11/7 7/12/7 6/10/7
f 1/2/8 2/9/8 3/13/8
f 1/2/8 3/13/8 4/14/8
~~~
因此:
-
# 是注释标记,就像C++中的//
- usemtl和mtlib描述了模型的外观。本课用不到。
- v代表顶点
- vt代表顶点的纹理坐标
- vn代表顶点的法向
- f代表面
v vt vn都很好理解。f比较麻烦。例如f 8/11/7 7/12/7 6/10/7:
- 8/11/7描述了三角形的第一个顶点
- 7/12/7描述了三角形的第二个顶点
- 6/10/7描述了三角形的第三个顶点
- 对于第一个顶点,8指向要用的顶点。此例中是-1.000000 1.000000 -1.000000(索引从1开始,和C++中从0开始不同)
- 11指向要用的纹理坐标。此例中是0.748355 0.998230。
- 7指向要用的法向。此例中是0.000000 1.000000 -0.000000。
我们称这些数字为索引。若几个顶点共用同一个坐标,索引就显得很方便,文件中只需保存一个“V”,可以多次引用,节省了存储空间。
不好的地方在于,我们不能让OpenGL混用顶点、纹理和法向索引。因此本课采用的方法是创建一个标准的、未加索引的模型。等第九课时再讨论索引,届时将会介绍如何解决OpenGL的索引问题。
### 用Blender创建OBJ文件
我们写的蹩脚加载器功能实在有限,因此在导出模型时得格外小心。下图展示了在Blender中导出模型的情形:
### 读取OBJ文件
OK,真正开始编码了。需要一些临时变量存储.obj文件的内容。
~~~
std::vector vertexIndices, uvIndices, normalIndices;
std::vector temp_vertices;
std::vector temp_uvs;
std::vector temp_normals;
~~~
学第五课纹理立方体时,你已学会如何打开文件了:
~~~
FILE * file = fopen(path, "r");
if( file == NULL ){
printf("Impossible to open the file !n");
return false;
}
~~~
读文件直到文件末尾:
~~~
while( 1 ){
char lineHeader[128];
// read the first word of the line
int res = fscanf(file, "%s", lineHeader);
if (res == EOF)
break; // EOF = End Of File. Quit the loop.
// else : parse lineHeader
~~~
(注意,我们假设第一行的文字长度不超过128,这样做太愚蠢了。但既然这只是个实验品,就凑合一下吧)
首先处理顶点:
~~~
if ( strcmp( lineHeader, "v" ) == 0 ){
glm::vec3 vertex;
fscanf(file, "%f %f %fn", &vertex.x, &vertex.y, &vertex.z );
temp_vertices.push_back(vertex);
~~~
也就是说,若第一个字是“v”,则后面一定是3个float值,于是以这3个值创建一个glm::vec3变量,将其添加到数组。
~~~
}else if ( strcmp( lineHeader, "vt" ) == 0 ){
glm::vec2 uv;
fscanf(file, "%f %fn", &uv.x, &uv.y );
temp_uvs.push_back(uv);
~~~
也就是说,如果不是“v”而是“vt”,那后面一定是2个float值,于是以这2个值创建一个glm::vec2变量,添加到数组。
以同样的方式处理法向:
~~~
}else if ( strcmp( lineHeader, "vn" ) == 0 ){
glm::vec3 normal;
fscanf(file, "%f %f %fn", &normal.x, &normal.y, &normal.z );
temp_normals.push_back(normal);
~~~
接下来是“f”,略难一些:
~~~
}else if ( strcmp( lineHeader, "f" ) == 0 ){
std::string vertex1, vertex2, vertex3;
unsigned int vertexIndex[3], uvIndex[3], normalIndex[3];
int matches = fscanf(file, "%d/%d/%d %d/%d/%d %d/%d/%dn", &vertexIndex[0], &uvIndex[0], &normalIndex[0], &vertexIndex[1], &uvIndex[1], &normalIndex[1], &vertexIndex[2], &uvIndex[2], &normalIndex[2] );
if (matches != 9){
printf("File can't be read by our simple parser : ( Try exporting with other optionsn");
return false;
}
vertexIndices.push_back(vertexIndex[0]);
vertexIndices.push_back(vertexIndex[1]);
vertexIndices.push_back(vertexIndex[2]);
uvIndices .push_back(uvIndex[0]);
uvIndices .push_back(uvIndex[1]);
uvIndices .push_back(uvIndex[2]);
normalIndices.push_back(normalIndex[0]);
normalIndices.push_back(normalIndex[1]);
normalIndices.push_back(normalIndex[2]);
~~~
代码与前面的类似,只不过读取的数据多一些。
### 处理数据
我们只需改变一下数据的形式。读取的是字符串,现在有了一组数组。这还不够,我们得把数据组织成OpenGL要求的形式。也就是去掉索引,只保留顶点坐标数据。这步操作称为索引。
遍历每个三角形(每个“f”行)的每个顶点(每个 v/vt/vn):
~~~
// For each vertex of each triangle
for( unsigned int i=0; i
~~~
顶点坐标的索引存放到vertexIndices[i]:
~~~
unsigned int vertexIndex = vertexIndices[i];
~~~
因此坐标是temp_vertices[ vertexIndex-1 ](-1是因为C++的下标从0开始,而OBJ的索引从1开始,还记得吗?):
~~~
glm::vec3 vertex = temp_vertices[ vertexIndex-1 ];
~~~
这样就有了一个顶点坐标:
~~~
out_vertices.push_back(vertex);
~~~
UV和法向同理,任务完成!
## 使用加载的数据
到这一步,几乎什么变化都没发生。这次我们不再声明一个static const GLfloat g_vertex_buffer_data[] = {…},而是创建一个顶点数组(UV和法向同理)。用正确的参数调用loadOBJ:
~~~
// Read our .obj file
std::vector vertices;
std::vector uvs;
std::vector normals; // Won't be used at the moment.
bool res = loadOBJ("cube.obj", vertices, uvs, normals);
~~~
把数组传给OpenGL:
~~~
glBufferData(GL_ARRAY_BUFFER, vertices.size() * sizeof(glm::vec3), &vertices[0], GL_STATIC_DRAW);
~~~
结束了!
## 结果
不好意思,纹理不好看。我不太擅长美工。欢迎您来提供一些好的纹理。
## 其他模型格式及加载器
这个小巧的加载器应该比较适合初学,不过别在实际中使用它。参考一下[实用链接和工具](http://www.opengl-tutorial.org/miscellaneous/useful-tools-links/)页面,看看有什么能用的。不过请注意,等到第九课才会真正用到这些工具。
第六课:键盘和鼠标
最后更新于:2022-04-01 04:37:23
# 第六课:键盘和鼠标
欢迎来到第六课!
我们将学习如何通过鼠标和键盘来移动相机,就像在第一人称射击游戏中一样。
## 接口
这段代码在整个课程中多次被使用,因此把它单独放在一个文件中:common/controls.cpp,然后在common/controls.hpp中声明函数接口,这样tutorial06.cpp就能使用它们了。
和前节课比,tutorial06.cpp里的代码变动很小。主要的变化是:每一帧都计算MVP(投影视图矩阵)矩阵,而不像之前那样只算一次。现在把这段代码加到主循环中:
~~~
do{
// ...
// Compute the MVP matrix from keyboard and mouse input
computeMatricesFromInputs();
glm::mat4 ProjectionMatrix = getProjectionMatrix();
glm::mat4 ViewMatrix = getViewMatrix();
glm::mat4 ModelMatrix = glm::mat4(1.0);
glm::mat4 MVP = ProjectionMatrix * ViewMatrix * ModelMatrix;
// ...
}
~~~
这段代码需要3个新函数:
- computeMatricesFromInputs()读键盘和鼠标操作,然后计算投影视图矩阵。这就是奇妙所在。
- getProjectionMatrix()返回计算好的投影矩阵。
- getViewMatrix()返回计算好的视图矩阵。
这只是一种实现方式,当然,如果你不喜欢这些函数,勇敢地去改写它们。
来看看controls.cpp在做什么。
## 实际代码
我们需要几个变量。
~~~
// position
glm::vec3 position = glm::vec3( 0, 0, 5 );
// horizontal angle : toward -Z
float horizontalAngle = 3.14f;
// vertical angle : 0, look at the horizon
float verticalAngle = 0.0f;
// Initial Field of View
float initialFoV = 45.0f;
float speed = 3.0f; // 3 units / second
float mouseSpeed = 0.005f;
FoV is the level of zoom. 80° = very wide angle, huge deformations. 60° – 45° : standard. 20° : big zoom.
~~~
首先根据输入,重新计算位置,水平角,竖直角和视场角(FoV);再由它们算出视图和投影矩阵。
### 方向
读取鼠标位置是容易的:
~~~
// Get mouse position
int xpos, ypos;
glfwGetMousePos(&xpos, &ypos);
~~~
我们需要把光标放到屏幕中心,否则它将很快移到屏幕外,导致无法响应。
~~~
// Reset mouse position for next frame
glfwSetMousePos(1024/2, 768/2);
~~~
注意:这段代码假设窗口大小是1024*768,这不是必须的。你可以用glfwGetWindowSize来设定窗口大小。
计算观察角度:
~~~
// Compute new orientation
horizontalAngle += mouseSpeed * deltaTime * float(1024/2 - xpos );
verticalAngle += mouseSpeed * deltaTime * float( 768/2 - ypos );
~~~
从右往左阅读这几行代码:
- 1024/2 – xpos表示鼠标离窗口中心点的距离。这个值越大,转动角越大。
- float(…)是浮点数转换,使乘法顺利进行
- mouseSpeed用来加速或减慢旋转,可以随你调整或让用户选择。
- += : 如果你没移动鼠标,1024/2-xpos的值为零,horizontalAngle+=0不改变horizontalAngle的值。如果你用的是”=”,每帧视角都被强制转回到原始方向,这就不好了。
现在,在世界坐标系下计算一个向量,代表视线方向。
~~~
// Direction : Spherical coordinates to Cartesian coordinates conversion
glm::vec3 direction(
cos(verticalAngle) * sin(horizontalAngle),
sin(verticalAngle),
cos(verticalAngle) * cos(horizontalAngle)
);
~~~
这是一种标准计算,如果你不了解余弦和正弦,下面有一个简短的解释:
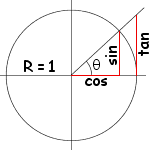
上面的公式,只是上图在三维空间下的推广。
我们想算出相机的『上方向』。『上方向』不一定是Y轴正方向:你俯视时,『上方向』实际上是水平的。这里有一个例子,位置相同,视点相同的相机,却有不同的『上方向』。
本例中,唯一不变的是,『相机的右边』这个方向始终取水平方向。你可以试试:保持手臂水平伸直,向正上方看、向下看;向这之间的任何方向看(译注:『看』立刻产生视线方向)。现在定义『右方向』向量:因为是水平的,故Y坐标为零,X和Z值就像上图中的一样,只是角度旋转了90度,或Pi/2弧度。
~~~
// Right vector
glm::vec3 right = glm::vec3(
sin(horizontalAngle - 3.14f/2.0f),
0,
cos(horizontalAngle - 3.14f/2.0f)
);
~~~
我们有一个『右方向』和一个视线方向,或者说是『前方向』。『上方向』垂直于这两者。一个很有用的数学工具可以让三者的联系变得简单:叉乘。
~~~
// Up vector : perpendicular to both direction and right
glm::vec3 up = glm::cross( right, direction );
~~~
叉乘是在做什么呢?很简单,回忆第三课讲到的右手定则。第一个向量是大拇指;第二个是食指;叉乘的结果就是中指。十分方便。
### 位置
代码十分直观。顺便说下,我用上/下/右/左键而不用wsad;是因为我的azerty键盘中,美式键盘的awsd键位处实际上是zqsd。qwerZ键盘其实又不一样了,更别提韩国键盘了。我甚至不知道韩国人民用的键盘是什么布局,但我猜想肯定很不一样。
~~~
// Move forward
if (glfwGetKey( GLFW_KEY_UP ) == GLFW_PRESS){
position += direction * deltaTime * speed;
}
// Move backward
if (glfwGetKey( GLFW_KEY_DOWN ) == GLFW_PRESS){
position -= direction * deltaTime * speed;
}
// Strafe right
if (glfwGetKey( GLFW_KEY_RIGHT ) == GLFW_PRESS){
position += right * deltaTime * speed;
}
// Strafe left
if (glfwGetKey( GLFW_KEY_LEFT ) == GLFW_PRESS){
position -= right * deltaTime * speed;
}
~~~
这里唯一特别的是deltaTime。你不会希望每帧偏移1单元的,原因很简单:
- 如果你有一台快电脑,每秒能跑60帧,你每秒移动60*speed个单位。
- 如果你有一台慢电脑,每秒能跑20帧,你每秒移动20*speed个单位。
电脑性能不能成为速度不稳的借口;你需要通过“前一帧到现在的时间”或“时间间隔(deltaTime)”来控制移动步长。
- 如果你有一台快电脑,每秒能跑60帧,你每帧移动1/60*speed个单位,每秒移动1*speed个单位。
- 如果你有一台慢电脑,每秒能跑20帧,你每帧移动1/20*speed个单位,每秒移动1*speed个单位。
这就好多了。deltaTime很容易算:
~~~
double currentTime = glfwGetTime();
float deltaTime = float(currentTime - lastTime);
~~~
### 视场角
为了好玩,我们可以把视场角绑定到鼠标滚轮,作为简陋的缩放功能:
~~~
float FoV = initialFoV - 5 * glfwGetMouseWheel();
~~~
### 计算矩阵
计算矩阵已经很直观了。使用和前面几乎一样的函数,仅参数不同。
~~~
// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit <-> 100 units
ProjectionMatrix = glm::perspective(FoV, 4.0f / 3.0f, 0.1f, 100.0f);
// Camera matrix
ViewMatrix = glm::lookAt(
position, // Camera is here
position+direction, // and looks here : at the same position, plus "direction"
up // Head is up (set to 0,-1,0 to look upside-down)
);
~~~
## 结果

### 隐藏面消除
现在可以自由移动鼠标,你会注意到:如果鼠标移动到立方体里面,多边形仍然会被显示。这看起来理所当然,实则可以优化。事实上,在常见应用中,你从来不会处于立方体内。
有一个思路是让GPU检查相机在三角形的后面还是前面。如果在前面,显示该三角形;如果相机在三角形后面,且不在网格(网格必须是封闭的)内部,那么必有其他三角形在相机前面,故不显示该三角形。没有人会注意到什么,除了一切都会变快:三角形平均少了两倍!
更妙的是,检查起来还很简单:GPU计算三角形的法向(用叉乘,记得吧?),然后检查这个法向是否朝向相机。
不幸的是这样做有代价:三角形的方向是隐式的。这意味着如果你在缓冲区中交换两个顶点,可能会产生洞。但一般来说,它值得做一点额外工作。一般你只要在三维建模软件中点击“反转法向”(实际是交换两个顶点,从而反转法向),一切就正常了。
开启隐藏面消除是很轻松的:
~~~
// Cull triangles which normal is not towards the camera
glEnable(GL_CULL_FACE);
~~~
## 练习
- 限制verticalAngle,使之不能颠倒方向
- 创建一个相机,使它绕着物体旋转 ( position = ObjectCenter + ( radius * cos(time), height, radius * sin(time) ) );然后将半径/高度/时间的变化绑定到键盘/鼠标上,诸如此类。
- 玩得开心!
第五课:带纹理的立方体
最后更新于:2022-04-01 04:37:21
# 第五课:纹理立方体
本课学习如下几点:
- 什么是UV坐标
- 怎样自行加载纹理
- 怎样在OpenGL中使用纹理
- 什么是滤波?什么是mipmap?怎样使用?
- 怎样利用GLFW更加有效地加载纹理?
- 什么是alpha通道?
## 关于UV坐标
给一个模型贴纹理时,需要通过某种方式告诉OpenGL用哪一块图像来填充三角形。这是借助UV坐标来实现的。
每个顶点除了位置坐标外还有两个浮点数坐标:U和V。这两个坐标用于获取纹理,如下图所示:

注意纹理是怎样在三角形上扭曲的。
## 自行加载.BMP图片
了解BMP文件格式并不重要:很多库可以帮你做这个。但BMP格式极为简单,可以帮助你理解那些库的工作原理。所以,我们从头开始写一个BMP文件加载器,以便你理解其工作原理,不过(在实际工程中)**千万别再用这个实验品**。
如下是加载函数的声明:
~~~
GLuint loadBMP_custom(const char * imagepath);
~~~
使用方式如下:
~~~
GLuint image = loadBMP_custom("./my_texture.bmp");
~~~
接下来看看如何读取BMP文件。
首先需要一些数据。读取文件时将设置这些变量。
~~~
// Data read from the header of the BMP file
unsigned char header[54]; // Each BMP file begins by a 54-bytes header
unsigned int dataPos; // Position in the file where the actual data begins
unsigned int width, height;
unsigned int imageSize; // = width*height*3
// Actual RGB data
unsigned char * data;
~~~
现在正式开始打开文件。
~~~
// Open the file
FILE * file = fopen(imagepath,"rb");
if (!file) {printf("Image could not be openedn"); return 0;}
~~~
文件一开始是54字节长的文件头,用于标识“这是不是一个BMP文件”、图像大小、像素位等等。来读取文件头吧:
~~~
if ( fread(header, 1, 54, file)!=54 ){ // If not 54 bytes read : problem
printf("Not a correct BMP filen");
return false;
}
~~~
文件头总是以“BM”开头。实际上,如果用十六进制编辑器打开BMP文件,你会看到如下情形:
因此,得检查一下头两个字节是否确为‘B’和‘M’:
~~~
if ( header[0]!='B' || header[1]!='M' ){
printf("Not a correct BMP filen");
return 0;
}
~~~
现在可以读取文件中图像大小、数据位置等信息了:
~~~
// Read ints from the byte array
dataPos = *(int*)&(header[0x0A]);
imageSize = *(int*)&(header[0x22]);
width = *(int*)&(header[0x12]);
height = *(int*)&(header[0x16]);
~~~
如果这些信息缺失得手动补齐:
~~~
// Some BMP files are misformatted, guess missing information
if (imageSize==0) imageSize=width*height*3; // 3 : one byte for each Red, Green and Blue component
if (dataPos==0) dataPos=54; // The BMP header is done that way
~~~
现在我们知道了图像的大小,可以为之分配一些内存,把图像读进去:
~~~
// Create a buffer
data = new unsigned char [imageSize];
// Read the actual data from the file into the buffer
fread(data,1,imageSize,file);
//Everything is in memory now, the file can be closed
fclose(file);
~~~
到了真正的OpenGL部分了。创建纹理和创建顶点缓冲器差不多:创建一个纹理、绑定、填充、配置。
在glTexImage2D函数中,GL_RGB表示颜色由三个分量构成,GL_BGR则说明在内存中颜色值是如何存储的。实际上,BMP存储的并不是RGB,而是BGR,因此得把这个告诉OpenGL。
~~~
// Create one OpenGL texture
GLuint textureID;
glGenTextures(1, &textureID);
// "Bind" the newly created texture : all future texture functions will modify this texture
glBindTexture(GL_TEXTURE_2D, textureID);
// Give the image to OpenGL
glTexImage2D(GL_TEXTURE_2D, 0,GL_RGB, width, height, 0, GL_BGR, GL_UNSIGNED_BYTE, data);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
~~~
稍后再解释最后两行代码。同时,得在C++代码中使用刚写好的函数加载一个纹理:
~~~
GLuint Texture = loadBMP_custom("uvtemplate.bmp");
~~~
另外十分重要的一点: 使用2次幂(power-of-two)的纹理!
- 优质纹理: 128*128*, 256*256, 1024*1024, 2*2…
- 劣质纹理: 127*128, 3*5, …
- 勉强可以但很怪异的纹理: 128*256
## 在OpenGL中使用纹理
先来看看片断着色器。大部分代码一目了然:
~~~
#version 330 core
// Interpolated values from the vertex shaders
in vec2 UV;
// Ouput data
out vec3 color;
// Values that stay constant for the whole mesh.
uniform sampler2D myTextureSampler;
void main(){
// Output color = color of the texture at the specified UV
color = texture( myTextureSampler, UV ).rgb;
}
~~~
注意三个点:
- 片断着色器需要UV坐标。看似合情合理。
- 同时也需要一个“Sampler2D”来获知要加载哪一个纹理(同一个着色器中可以访问多个纹理)
- 最后一点,用texture()访问纹理,该方法返回一个(R,G,B,A)的vec4变量。马上就会了解到分量A。
顶点着色器也很简单,只需把UV坐标传给片断着色器:
~~~
#version 330 core
// Input vertex data, different for all executions of this shader.
layout(location = 0) in vec3 vertexPosition_modelspace;
layout(location = 1) in vec2 vertexUV;
// Output data ; will be interpolated for each fragment.
out vec2 UV;
// Values that stay constant for the whole mesh.
uniform mat4 MVP;
void main(){
// Output position of the vertex, in clip space : MVP * position
gl_Position = MVP * vec4(vertexPosition_modelspace,1);
// UV of the vertex. No special space for this one.
UV = vertexUV;
}
~~~
还记得第四课中的“layout(location = 1) in vec2 vertexUV” 吗?我们得在这儿把相同的事情再做一遍,但这次的缓冲器中放的不是(R,G,B)三元组,而是(U,V)数对。
~~~
// Two UV coordinatesfor each vertex. They were created with Blender. You'll learn shortly how to do this yourself.
static const GLfloat g_uv_buffer_data[] = {
0.000059f, 1.0f-0.000004f,
0.000103f, 1.0f-0.336048f,
0.335973f, 1.0f-0.335903f,
1.000023f, 1.0f-0.000013f,
0.667979f, 1.0f-0.335851f,
0.999958f, 1.0f-0.336064f,
0.667979f, 1.0f-0.335851f,
0.336024f, 1.0f-0.671877f,
0.667969f, 1.0f-0.671889f,
1.000023f, 1.0f-0.000013f,
0.668104f, 1.0f-0.000013f,
0.667979f, 1.0f-0.335851f,
0.000059f, 1.0f-0.000004f,
0.335973f, 1.0f-0.335903f,
0.336098f, 1.0f-0.000071f,
0.667979f, 1.0f-0.335851f,
0.335973f, 1.0f-0.335903f,
0.336024f, 1.0f-0.671877f,
1.000004f, 1.0f-0.671847f,
0.999958f, 1.0f-0.336064f,
0.667979f, 1.0f-0.335851f,
0.668104f, 1.0f-0.000013f,
0.335973f, 1.0f-0.335903f,
0.667979f, 1.0f-0.335851f,
0.335973f, 1.0f-0.335903f,
0.668104f, 1.0f-0.000013f,
0.336098f, 1.0f-0.000071f,
0.000103f, 1.0f-0.336048f,
0.000004f, 1.0f-0.671870f,
0.336024f, 1.0f-0.671877f,
0.000103f, 1.0f-0.336048f,
0.336024f, 1.0f-0.671877f,
0.335973f, 1.0f-0.335903f,
0.667969f, 1.0f-0.671889f,
1.000004f, 1.0f-0.671847f,
0.667979f, 1.0f-0.335851f
};
~~~
上述UV坐标对应于下面的模型:
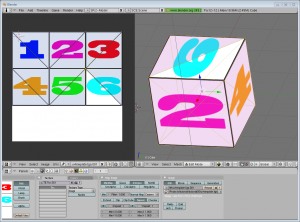
其余的就很清楚了。创建一个缓冲器、绑定、填充、配置,与往常一样绘制顶点缓冲器对象。要注意把glVertexAttribPointer的第二个参数(大小)3改成2。
结果如下:

放大后:
## 什么是滤波和mipmap?怎样使用?
正如在上面截图中看到的,纹理质量不是很好。这是因为在loadBMP_custom函数中,有两行这样写道:
~~~
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
~~~
这意味着在片断着色器中,texture()将直接提取位于(U,V)坐标的纹素(texel)。
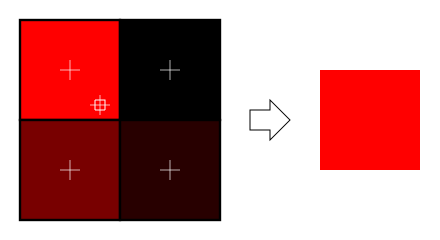
有几种方法可以改善这一状况。
### 线性滤波(Linear filtering)
若采用线性滤波。texture()会查看周围的纹素,然后根据UV坐标距离各纹素中心的距离来混合颜色。这就避免了前面看到的锯齿状边缘。
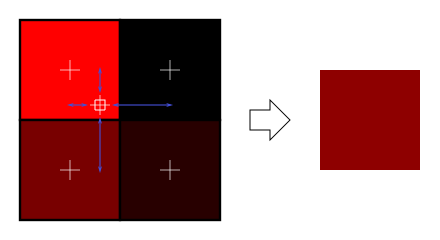
线性滤波可以显著改善纹理质量,应用的也很多。但若想获得更高质量的纹理,可以采用各向异性滤波,不过速度上有些慢。
### 各向异性滤波(Anisotropic filtering)
这种方法逼近了真正片断中的纹素区块。例如下图中稍稍旋转了的纹理,各向异性滤波将沿蓝色矩形框的主方向,作一定数量的采样(即所谓的“各向异性层级”),计算出其内的颜色。
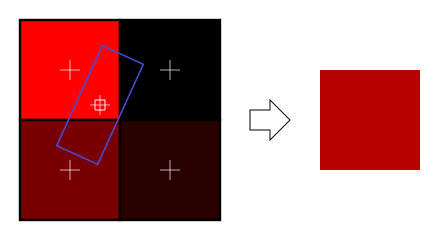
### Mipmaps
线性滤波和各向异性滤波都存在一个共同的问题。那就是如果从远处观察纹理,只对4个纹素作混合显得不够。实际上,如果3D模型位于很远的地方,屏幕上只看得见一个片断(像素),那计算平均值得出最终颜色值时,图像所有的纹素都应该考虑在内。很显然,这样做没有考虑性能问题。相反,人们引入了mipmap这一概念:

- 一开始,把图像缩小到原来的1/2,接着一次做下去,直到图像只有1×1大小(应该是图像所有纹素的平均值)
- 绘制模型时,根据纹素大小选择合适的mipmap。
- 可以选用nearest、linear、anisotropic等任意一种滤波方式来对mipmap采样。
- 要想效果更好,可以对两个mipmap采样然后混合,得出结果。
好在这个比较简单,OpenGL都帮我们做好了,只需一个简单的调用:
~~~
// When MAGnifying the image (no bigger mipmap available), use LINEAR filtering
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
// When MINifying the image, use a LINEAR blend of two mipmaps, each filtered LINEARLY too
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
// Generate mipmaps, by the way.
glGenerateMipmap(GL_TEXTURE_2D);
~~~
## 怎样利用GLFW加载纹理?
我们的loadBMP_custom函数很棒,因为这是我们自己写的!不过用专门的库更好。GLFW就可以加载纹理(仅限TGA文件):
~~~
GLuint loadTGA_glfw(const char * imagepath){
// Create one OpenGL texture
GLuint textureID;
glGenTextures(1, &textureID);
// "Bind" the newly created texture : all future texture functions will modify this texture
glBindTexture(GL_TEXTURE_2D, textureID);
// Read the file, call glTexImage2D with the right parameters
glfwLoadTexture2D(imagepath, 0);
// Nice trilinear filtering.
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR_MIPMAP_LINEAR);
glGenerateMipmap(GL_TEXTURE_2D);
// Return the ID of the texture we just created
return textureID;
}
~~~
## 压缩纹理
学到这儿,你可能会想怎样加载JPEG文件而不是TGA文件呢?
简单的说:别这么干。还有更好的选择。
### 创建压缩纹理
- 下载[The Compressonator](http://developer.amd.com/tools-and-sdks/archive/legacy-cpu-gpu-tools/the-compressonator/),一款ATI工具
- 用它加载一个二次幂纹理
- 将其压缩成DXT1、DXT3或DXT5格式(这些格式之间的差别请参考[Wikipedia](http://en.wikipedia.org/wiki/S3_Texture_Compression)):
- 生成mipmap,这样就不用在运行时生成mipmap了。
- 导出为.DDS文件。
至此,图像已压缩为可被GPU直接使用的格式。在着色中随时调用texture()均可以实时解压。这一过程看似很慢,但由于它节省了很多内存空间,传输的数据量就少了。传输内存数据开销很大;纹理解压缩却几乎不耗时(有专门的硬件负责此事)。一般情况下,才用压缩纹理可使性能提升20%。
### 使用压缩纹理
来看看怎样加载压缩纹理。这和加载BMP的代码很相似,只不过文件头的结构不一样:
~~~
GLuint loadDDS(const char * imagepath){
unsigned char header[124];
FILE *fp;
/* try to open the file */
fp = fopen(imagepath, "rb");
if (fp == NULL)
return 0;
/* verify the type of file */
char filecode[4];
fread(filecode, 1, 4, fp);
if (strncmp(filecode, "DDS ", 4) != 0) {
fclose(fp);
return 0;
}
/* get the surface desc */
fread(&header, 124, 1, fp);
unsigned int height = *(unsigned int*)&(header[8 ]);
unsigned int width = *(unsigned int*)&(header[12]);
unsigned int linearSize = *(unsigned int*)&(header[16]);
unsigned int mipMapCount = *(unsigned int*)&(header[24]);
unsigned int fourCC = *(unsigned int*)&(header[80]);
~~~
文件头之后是真正的数据:紧接着是mipmap层级。可以一次性批量地读取:
~~~
unsigned char * buffer;
unsigned int bufsize;
/* how big is it going to be including all mipmaps? */
bufsize = mipMapCount > 1 ? linearSize * 2 : linearSize;
buffer = (unsigned char*)malloc(bufsize * sizeof(unsigned char));
fread(buffer, 1, bufsize, fp);
/* close the file pointer */
fclose(fp);
~~~
这里要处理三种格式:DXT1、DXT3和DXT5。我们得把“fourCC”标识转换成OpenGL能识别的值。
~~~
unsigned int components = (fourCC == FOURCC_DXT1) ? 3 : 4;
unsigned int format;
switch(fourCC)
{
case FOURCC_DXT1:
format = GL_COMPRESSED_RGBA_S3TC_DXT1_EXT;
break;
case FOURCC_DXT3:
format = GL_COMPRESSED_RGBA_S3TC_DXT3_EXT;
break;
case FOURCC_DXT5:
format = GL_COMPRESSED_RGBA_S3TC_DXT5_EXT;
break;
default:
free(buffer);
return 0;
}
~~~
像往常一样创建纹理:
~~~
// Create one OpenGL texture
GLuint textureID;
glGenTextures(1, &textureID);
// "Bind" the newly created texture : all future texture functions will modify this texture
glBindTexture(GL_TEXTURE_2D, textureID);
~~~
现在只需逐个填充mipmap:
~~~
unsigned int blockSize = (format == GL_COMPRESSED_RGBA_S3TC_DXT1_EXT) ? 8 : 16;
unsigned int offset = 0;
/* load the mipmaps */
for (unsigned int level = 0; level < mipMapCount && (width || height); ++level)
{
unsigned int size = ((width+3)/4)*((height+3)/4)*blockSize;
glCompressedTexImage2D(GL_TEXTURE_2D, level, format, width, height,
0, size, buffer + offset);
offset += size;
width /= 2;
height /= 2;
}
free(buffer);
return textureID;
~~~
### 反转UV坐标
DXT压缩源自DirectX。和OpenGL相比,DirectX中的V纹理坐标是反过来的。所以使用压缩纹理时,得用(coord.v, 1.0-coord.v)来获取正确的纹素。这步操作何时做都可以:可以在导出脚本中做,可以在加载器中做,也可以在着色器中做……
## 总结
刚刚学习的是创建、加载以及在OpenGL中使用纹理。
总的来说,压缩纹理体积小、加载迅速、使用便捷,应该只用压缩纹理;主要的缺点是得用The Compressonator来转换图像格式。
## 练习
- 源代码中实现了DDS加载器,但没有做纹理坐标的改动(译者注:指文中讲述的反转 UV坐标)。在适当的位置添加该功能,以使正方体正确显示。
- 试试各种DDS格式。所得结果有何不同?压缩率呢?
- 试试在The Compressonator不生成mipmap。结果如何?请给出3种方案解决这一问题。
## 参考文献
- [Using texture compression in OpenGL](http://www.oldunreal.com/editing/s3tc/ARB_texture_compression.pdf) , Sébastien Domine, NVIDIA
第四课:彩色立方体
最后更新于:2022-04-01 04:37:19
# 第四课:彩色立方体
欢迎来到第四课!你将学到:
- 画立方体,代替单调的三角形
- 加上绚丽的色彩
- 学习深度缓存(Z-Buffer)
## 画立方体
立方体有六个方形表面,而OpenGL只支持画三角形,因此需要画12个三角形,每面两个。我们用定义三角形顶点的方式来定义这些顶点。
~~~
// Our vertices. Tree consecutive floats give a 3D vertex; Three consecutive vertices give a triangle.
// A cube has 6 faces with 2 triangles each, so this makes 6*2=12 triangles, and 12*3 vertices
static const GLfloat g_vertex_buffer_data[] = {
-1.0f,-1.0f,-1.0f, // triangle 1 : begin
-1.0f,-1.0f, 1.0f,
-1.0f, 1.0f, 1.0f, // triangle 1 : end
1.0f, 1.0f,-1.0f, // triangle 2 : begin
-1.0f,-1.0f,-1.0f,
-1.0f, 1.0f,-1.0f, // triangle 2 : end
1.0f,-1.0f, 1.0f,
-1.0f,-1.0f,-1.0f,
1.0f,-1.0f,-1.0f,
1.0f, 1.0f,-1.0f,
1.0f,-1.0f,-1.0f,
-1.0f,-1.0f,-1.0f,
-1.0f,-1.0f,-1.0f,
-1.0f, 1.0f, 1.0f,
-1.0f, 1.0f,-1.0f,
1.0f,-1.0f, 1.0f,
-1.0f,-1.0f, 1.0f,
-1.0f,-1.0f,-1.0f,
-1.0f, 1.0f, 1.0f,
-1.0f,-1.0f, 1.0f,
1.0f,-1.0f, 1.0f,
1.0f, 1.0f, 1.0f,
1.0f,-1.0f,-1.0f,
1.0f, 1.0f,-1.0f,
1.0f,-1.0f,-1.0f,
1.0f, 1.0f, 1.0f,
1.0f,-1.0f, 1.0f,
1.0f, 1.0f, 1.0f,
1.0f, 1.0f,-1.0f,
-1.0f, 1.0f,-1.0f,
1.0f, 1.0f, 1.0f,
-1.0f, 1.0f,-1.0f,
-1.0f, 1.0f, 1.0f,
1.0f, 1.0f, 1.0f,
-1.0f, 1.0f, 1.0f,
1.0f,-1.0f, 1.0f
};
~~~
OpenGL的缓冲区由一些标准的函数(glGenBuffers, glBindBuffer, glBufferData, glVertexAttribPointer)来创建、绑定、填充和配置;这些可参阅第二课。绘制的函数调用也没变,只需改绘制的点的个数:
~~~
// Draw the triangle !
glDrawArrays(GL_TRIANGLES, 0, 12*3); // 12*3 indices starting at 0 -> 12 triangles -> 6 squares
~~~
这段代码,有几点要解释:
- 现在为止,三维模型都是固定的:要改就要改源码,重新编译,然后祈望不会错。我们将在第七课中学习如何加载动态模型。
- 实际上,每个顶点至少被写了三次(在以上代码中搜索“-1.0f,-1.0f,-1.0f”看看)。这是可怕的内存浪费。我们将在第九课中学习怎样优化。
现在,你有了画一个白色立方体的所有必备条件。让着色器运行起来,至少试试吧:)
## 添加颜色 Adding colors
颜色,从概念上说,像极了位置:它就是数据。OpenGL中,它们都是“属性”。事实上,之前已在glEnableVertexAttribArray()和glVertexAttribPointer()用过属性设置了。现在我们加上颜色属性,代码很相似的。
首先,声明颜色:每个顶点一个RGB(红绿蓝)三元组。这里用随机的方式生成的,所以结果可能看起来不那么好;但你可以调整得更好,例如:把顶点的位置作为颜色值。
~~~
// One color for each vertex. They were generated randomly.
static const GLfloat g_color_buffer_data[] = {
0.583f, 0.771f, 0.014f,
0.609f, 0.115f, 0.436f,
0.327f, 0.483f, 0.844f,
0.822f, 0.569f, 0.201f,
0.435f, 0.602f, 0.223f,
0.310f, 0.747f, 0.185f,
0.597f, 0.770f, 0.761f,
0.559f, 0.436f, 0.730f,
0.359f, 0.583f, 0.152f,
0.483f, 0.596f, 0.789f,
0.559f, 0.861f, 0.639f,
0.195f, 0.548f, 0.859f,
0.014f, 0.184f, 0.576f,
0.771f, 0.328f, 0.970f,
0.406f, 0.615f, 0.116f,
0.676f, 0.977f, 0.133f,
0.971f, 0.572f, 0.833f,
0.140f, 0.616f, 0.489f,
0.997f, 0.513f, 0.064f,
0.945f, 0.719f, 0.592f,
0.543f, 0.021f, 0.978f,
0.279f, 0.317f, 0.505f,
0.167f, 0.620f, 0.077f,
0.347f, 0.857f, 0.137f,
0.055f, 0.953f, 0.042f,
0.714f, 0.505f, 0.345f,
0.783f, 0.290f, 0.734f,
0.722f, 0.645f, 0.174f,
0.302f, 0.455f, 0.848f,
0.225f, 0.587f, 0.040f,
0.517f, 0.713f, 0.338f,
0.053f, 0.959f, 0.120f,
0.393f, 0.621f, 0.362f,
0.673f, 0.211f, 0.457f,
0.820f, 0.883f, 0.371f,
0.982f, 0.099f, 0.879f
};
~~~
缓冲区的创建、绑定和填充方法和之前一样:
~~~
GLuint colorbuffer;
glGenBuffers(1, &colorbuffer);
glBindBuffer(GL_ARRAY_BUFFER, colorbuffer);
glBufferData(GL_ARRAY_BUFFER, sizeof(g_color_buffer_data), g_color_buffer_data, GL_STATIC_DRAW);
~~~
配置也一样:
~~~
// 2nd attribute buffer : colors
glEnableVertexAttribArray(1);
glBindBuffer(GL_ARRAY_BUFFER, colorbuffer);
glVertexAttribPointer(
1, // attribute. No particular reason for 1, but must match the layout in the shader.
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
~~~
现在,顶点着色器中,我们已能访问这个额外的缓冲区:
~~~
// Notice that the "1" here equals the "1" in glVertexAttribPointer
layout(location = 1) in vec3 vertexColor;
~~~
本例将不会在顶点着色器里做花哨的玩意,只是简单地过渡到片断着色器:
~~~
// Output data ; will be interpolated for each fragment.
out vec3 fragmentColor;
void main(){
[...]
// The color of each vertex will be interpolated
// to produce the color of each fragment
fragmentColor = vertexColor;
}
~~~
片断着色器中,要再次声明片断颜色:
~~~
// Interpolated values from the vertex shaders
in vec3 fragmentColor;
~~~
…然后把它的值赋给输出颜色:
~~~
// Output color = color specified in the vertex shader,
// interpolated between all 3 surrounding vertices
color = fragmentColor;
~~~
于是得到:
额,好丑。为了搞清楚,我们先看看各画一个看起来“远”和“近”的三角形,会发生什么:
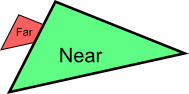
似乎挺好。现在画“远”的三角形:
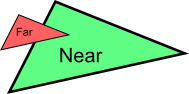
它遮住了“近”三角形!它本应该画在“近”三角形后面的!我们的立方体就有这个问题:一些理应被遮挡的面,因为绘制时间晚,实际可见。我们将用深度缓存(Z-Buffer)算法解决它。
*便签1*: 如果你没发现问题,把相机放到(4,3,-3)试试
*便签2*: 如果“类似于位置,颜色是一种属性”,那为什么颜色要声明 vec3 fragmentColor,而位置不需要?实际上,位置有点特殊:它是唯一必须赋初值的(否则OpenGL不知道在哪画三角形)。所以在顶点着色器里, gl_Position是内置变量。
## 深度缓存(Z-Buffer)The Z-Buffer
该问题的解决方案是:在缓冲区中存储每个片断的深度(即“Z”值);而每次画片断时,先确保当前片断确实比先前画的片断更近。
你可以自己实现,但让硬件自己去做更简单:
~~~
// Enable depth test
glEnable(GL_DEPTH_TEST);
// Accept fragment if it closer to the camera than the former one
glDepthFunc(GL_LESS);
~~~
这就解决之前所有问题了。

## 练习
-
在不同的位置画立方体和三角形。你需要生成两个MVP矩阵,在主循环中做两次绘制调用,但只需一个着色器。
-
自己生成颜色值。一些提示:随机生成,使每次运行颜色都不同;依据顶点的位置;将前二者结合;或其他的创新想法。若你不了解C,参考以下语法:
~~~
static GLfloat g_color_buffer_data[12*3*3];
for (int v = 0; v < 12*3 ; v++){
g_color_buffer_data[3*v+0] = your red color here;
g_color_buffer_data[3*v+1] = your green color here;
g_color_buffer_data[3*v+2] = your blue color here;
}
~~~
- 完成上面习题后,试令颜色在每帧都改变。你需要在每一帧都调用glBufferData。请确保已先绑定(glBindBuffer)了合适的缓冲区!
第三课:矩阵
最后更新于:2022-04-01 04:37:16
# 第三课: 矩阵
引擎完全没有推动飞船。飞船静止在原处,而引擎推动了环绕着飞船的宇宙。
*《飞出个未来》(一部美国科幻动画片)*
> 这一课是所有课程中最重要的。请至少看八遍。
## 齐次坐标(Homogeneous coordinates)
目前为止,我们仍然把三维顶点视为三元组(x, y, z)。现在引入一个新的分量w,得到向量(x, y, z, w)。
请先记住以下两点(稍后我们会给出解释):
若w==1,则向量(x, y, z, 1)为空间中的点。
若w==0,则向量(x, y, z, 0)为方向。
`(事实上,要永远记着。)`
这有什么不同呢?对于旋转,二者没什么不同。当你旋转点和方向时,结果是一样的。但对于平移(将点沿着某个方向移动),情况就不同了。『平移一个方向』是毫无意义的。
齐次坐标使我们能用同一个公式对点和方向作运算。
## 变换矩阵(Transformation matrices)
### 矩阵简介
简而言之,矩阵就是一个行、列数固定的,纵横排列的数表。比如,一个2×3矩阵看起来像这样:

三维图形学中我们只用到4×4矩阵,它能对顶点(x, y, z, w)作变换。这一变换是用矩阵左乘顶点来实现的:
矩阵x顶点(记住顺序!!矩阵左乘顶点,顶点用列向量表示)= 变换后的顶点
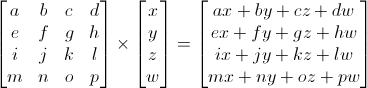
这看上去复杂,实则不然。左手指着a,右手指着x,得到ax。 左手移向右边一个数b,右手移向下一个数y,得到by。依次类推,得到cz、dw。最后求和ax + by + cz + dw,就得到了新的x!每一行都这么算下去,就得到了新的(x, y, z, w)向量。
这种重复无聊的计算就让计算机代劳吧。
**用C++,GLM表示:**
~~~
glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.
~~~
**用GLSL表示:**
~~~
mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM
~~~
`(还没把这些复制到你的代码里跑跑吗?赶紧试试!)`
### 平移矩阵(Translation matrices)
平移矩阵是最简单易懂的变换矩阵。平移矩阵是这样的:
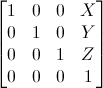
其中,X、Y、Z是点的位移增量。
例如,若想把向量(10, 10, 10, 1)沿X轴方向平移10个单位,可得:
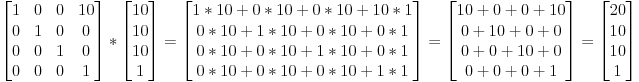
`(算算看!一定要动手算算!!)`
这样就得到了齐次向量(20, 10, 10, 1)!记住,末尾的1表示这是一个点,而不是方向。经过变换计算后,点仍然是点,很合理。
下面来看看,对一个代表Z轴负方向的向量,作上述平移变换会得到什么结果:
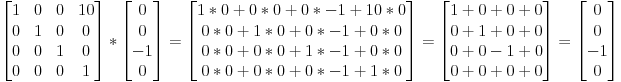
即还是原来的(0, 0, -1, 0)方向,这也很合理,正好印证了前面的结论:“平移一个方向是毫无意义的”。
那怎么用代码表示平移变换呢?
**用C++,GLM表示:**
~~~
#include <glm/transform.hpp> // after <glm/glm.hpp>
glm::mat4 myMatrix = glm::translate(10,0,0);
glm::vec4 myVector(10,10,10,0);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result
~~~
**用GLSL表示:**呃,实际中我们几乎不用GLSL做。大多数情况下在C++代码中用glm::translate()算出矩阵,然后把它传给GLSL。在GLSL中只做一次乘法:
~~~
vec4 transformedVector = myMatrix * myVector;
~~~
### 单位矩阵(Identity matrix)
单位矩阵很特殊,它什么也不做。我提到它是因为,知道它和知道A*1.0=A一样重要。
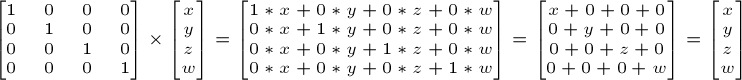
用C++表示:
~~~
glm::mat4 myIdentityMatrix = glm::mat4(1.0);
~~~
### 缩放矩阵(Scaling matrices)
缩放矩阵也很简单:
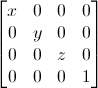
例如把一个向量(点或方向皆可)沿各方向放大2倍:
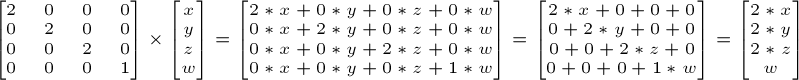
w还是没变。你也许会问:“缩放一个向量”有什么用?嗯,大多数情况下是没什么用,所以一般不会去做;但在某些罕见情况下它就有用了。(顺便说一下,单位矩阵只是缩放矩阵的一个特例,其(X, Y, Z) = (1, 1, 1)。单位矩阵同时也是旋转矩阵的一个特例,其(X, Y, Z)=(0, 0, 0))。
**用C++表示:**
~~~
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2,2,2);
~~~
### 旋转矩阵(Rotation matrices)
旋转矩阵比较复杂。这里略过细节,因为日常应用中,你并不需要知道矩阵的内部构造。想了解更多,请看[矩阵和四元组常见问题](http://www.cs.princeton.edu/~gewang/projects/darth/stuff/quat_faq.html)(这个资源很热门,应该有中文版吧)。
**用C++表示:**
~~~
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );
~~~
### 复合变换
前面已经学习了如何旋转、平移和缩放向量。要是能将它们组合起来就更好了。只需把这些矩阵相乘即可,例如:
~~~
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;
~~~
!!!千万注意!!!这行代码最先执行缩放,接着旋转,最后才是平移。这就是矩阵乘法的工作方式。
变换的顺序不同,得出的结果也不同。体验一下:
- 向前一步(小心别磕着爱机)然后左转;
- 左转,然后向前一步
实际上,上述顺序正是你在变换游戏人物或者其他物体时所需的:先缩放;再调整方向;最后平移。例如,假设有个船的模型(为简化,略去旋转):
`错误做法:`
-
按(10, 0, 0)平移船体。船体中心目前距离原点10个单位。
-
将船体放大2倍。以原点为参照,每个坐标都变成原来的2倍,就出问题了。……最后你是得到一艘放大的船,但其中心位于2*10=20。这可不是你想要的结果。
`正确做法:`
-
将船体放大2倍,得到一艘中心位于原点的大船。
-
平移船体。船大小不变,移动距离也正确。
矩阵-矩阵乘法和矩阵-向量乘法类似,所以这里也会省略一些细节,不清楚的请移步“矩阵和四元数常见问题”。现在,就让计算机来算:
**用C++,GLM表示:**
~~~
glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;
~~~
**用GLSL表示:**
~~~
mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;
~~~
## 模型(Model)、视图(View)和投影(Projection)矩阵
*在接下来的课程中,我们假定已知绘制Blender经典三维模型:小猴Suzanne的方法。*
利用模型、视图和投影矩阵,可以将变换过程清晰地分解为三个阶段。这个方法你可以不用(我们在前两课就没用),但最好要用。我们即将看到,它们把整个流程划分得很清楚,故被广为使用。
### 模型矩阵
这个三维模型,和我们心爱的红色三角形一样,是由一组顶点定义的。顶点的XYZ坐标是相对于物体中心定义的:也就是说,若某顶点位于(0, 0, 0),它就在物体的中心。

也许玩家需要用键鼠控制这个模型,所以我们希望能够移动它。这简单,只需学会:缩放*旋转*平移就行了。在每一帧中,用算出的这个矩阵,去乘(在GLSL中乘,不是C++中!)所有的顶点,物体就动了。唯一不动的就是世界坐标系(World Space)的中心。

现在,物体所有顶点都位于世界坐标系。下图中黑色箭头的意思是:*从模型坐标系(Model Space)(顶点都相对于模型的中心定义)变换到世界坐标系(顶点都相对于世界坐标系中心定义)。*

下图概括了这一过程:
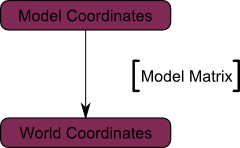
### 视图矩阵
这里再引用一下《飞出个未来》:
引擎完全没有推动飞船。飞船静止在原处,而引擎推动了环绕着飞船的宇宙。
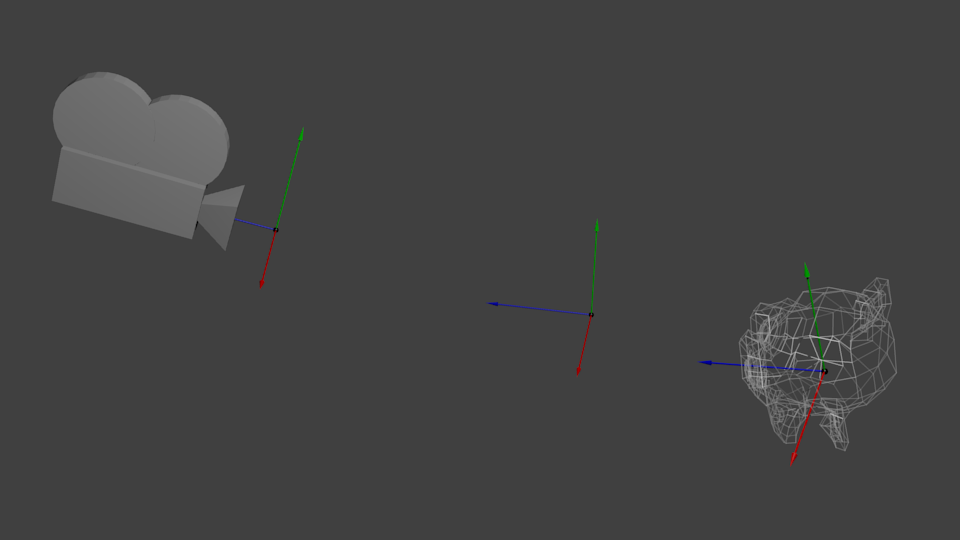
仔细想想,相机的原理也是相通的。如果想换个角度观察一座山,你可以移动相机也可以……移动山。后者在生活中不可行,在计算机图形学中却十分方便。
起初,相机位于世界坐标系的原点。移动世界只需乘上一个矩阵。假如你想把相机向右(X轴正方向)移动3个单位,这和把整个世界(包括网格)向左(X轴负方向)移3个单位是等效的!脑子有点乱?来写代码:
~~~
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(-3,0,0);
~~~
下图展示了:从世界坐标系(顶点都相对于世界坐标系中心定义)到观察坐标系(Camera Space,顶点都相对于相机定义)的变换。

**在脑袋撑爆前,来欣赏一下GLM伟大的glm::LookAt函数吧:**
~~~
glm::mat4 CameraMatrix = glm::LookAt(
cameraPosition, // the position of your camera, in world space
cameraTarget, // where you want to look at, in world space
upVector // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);
~~~
下图解释了上述变换过程:
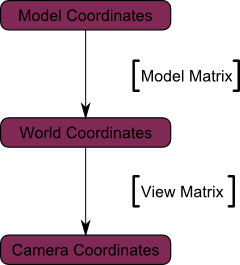
还没完呢。
### 投影矩阵
现在,我们处于观察坐标系中。这意味着,经历了这么多变换后,现在一个坐标为(0,0)的顶点,应该被画在屏幕的中心。但仅有x、y坐标还不足以确定物体是否应该画在屏幕上:它到相机的距离(z)也很重要!两个x、y坐标相同的顶点,z值较大的一个将会最终显示在屏幕上。
这就是所谓的透视投影(perspective projection):

好在用一个4×4矩阵就能表示这个投影¹ :
~~~
// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective(
FoV, // The horizontal Field of View, in degrees : the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)
4.0f / 3.0f, // Aspect Ratio. Depends on the size of your window. Notice that 4/3 == 800/600 == 1280/960, sounds familiar ?
0.1f, // Near clipping plane. Keep as big as possible, or you'll get precision issues.
100.0f // Far clipping plane. Keep as little as possible.
);
~~~
最后一个变换:
*从观察坐标系(顶点都相对于相机定义)到齐次坐标系(Homogeneous Space)(顶点都在一个小立方体中定义。立方体内的物体都会在屏幕上显示)的变换。*
最后一幅图示:
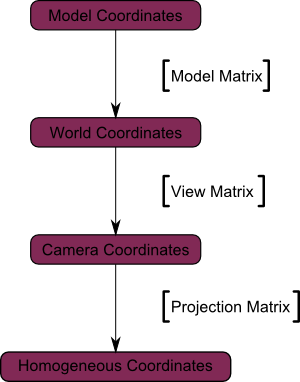
再添几张图,以便大家更好地理解投影变换。投影前,蓝色物体都位于观察坐标系中,红色的东西是相机的视域四棱锥(frustum):这是相机实际能看见的区域。

用投影矩阵去乘前面的结果,得到如下效果:

此图中,视域四棱锥变成了一个正方体(每条棱的范围都是-1到1,图上不太明显),所有的蓝色物体都经过了相同的形变。因此,离相机近的物体就显得大一些,远的显得小一些。和真实生活中一样!
让我们从视域四棱锥的“后面”看看它们的模样:
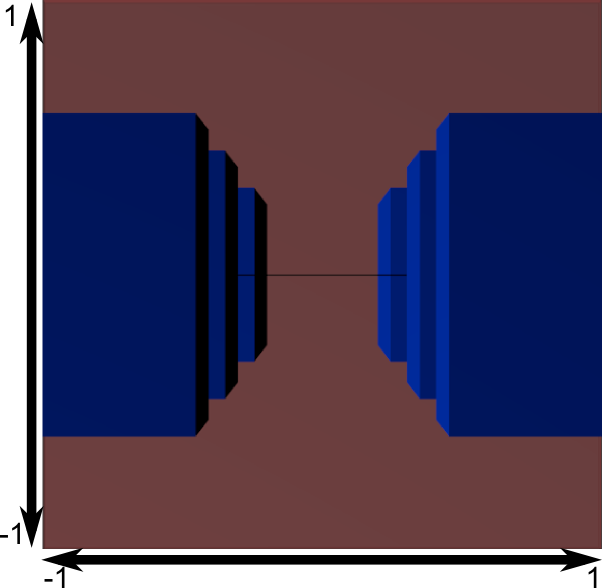
这就是你得出的图像了!看上去太方方正正了,因此,还需要做一次数学变换使之适合实际的窗口大小:

这就是实际渲染的图像啦!
### 复合变换:模型视图投影矩阵(MVP)
… 再来一串亲爱的矩阵乘法:
~~~
// C++ : compute the matrix
glm::mat3 MVPmatrix = projection * view * model; // Remember : inverted !
// GLSL : apply it
transformed_vertex = MVP * in_vertex;
~~~
## 总结
**第一步:创建模型视图投影(MVP)矩阵。任何要渲染的模型都要做这一步。**
~~~
// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit 100 units
glm::mat4 Projection = glm::perspective(45.0f, 4.0f / 3.0f, 0.1f, 100.0f);
// Camera matrix
glm::mat4 View = glm::lookAt(
glm::vec3(4,3,3), // Camera is at (4,3,3), in World Space
glm::vec3(0,0,0), // and looks at the origin
glm::vec3(0,1,0) // Head is up (set to 0,-1,0 to look upside-down)
);
// Model matrix : an identity matrix (model will be at the origin)
glm::mat4 Model = glm::mat4(1.0f); // Changes for each model !
// Our ModelViewProjection : multiplication of our 3 matrices
glm::mat4 MVP = Projection * View * Model; // Remember, matrix multiplication is the other way around
~~~
**第二步:把MVP传给GLSL**
~~~
// Get a handle for our "MVP" uniform.
// Only at initialisation time.
GLuint MatrixID = glGetUniformLocation(programID, "MVP");
// Send our transformation to the currently bound shader,
// in the "MVP" uniform
// For each model you render, since the MVP will be different (at least the M part)
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);
~~~
**第三步:在GLSL中用MVP变换顶点**
~~~
in vec3 vertexPosition_modelspace;
uniform mat4 MVP;
void main(){
// Output position of the vertex, in clip space : MVP * position
vec4 v = vec4(vertexPosition_modelspace,1); // Transform an homogeneous 4D vector, remember ?
gl_Position = MVP * v;
}
~~~
**完成!三角形和第二课的一样,仍然在原点(0, 0, 0),然而是从点(4, 3, 3)透视观察的;相机的上方向为(0, 1, 0),视场角(field of view)45°。**

第6课中你会学到怎样用键鼠动态修改这些值,从而创建一个和游戏中类似的相机。但我们会先学给三维模型上色(第4课)、贴纹理(第5课)。
## 练习
**试着替换glm::perspective**
**不用透视投影,试试正交投影(orthographic projection )(glm::ortho)**
**把ModelMatrix改成先平移,再旋转,最后放缩三角形**
**其他不变,但把模型矩阵运算改成平移-旋转-放缩的顺序,会有什么变化?如果对一个人作变换,你觉得什么顺序最好呢?**
*附注*
*1 : [...]好在用一个4×4矩阵就能表示这个投影:实际上,这句话并不对。透视变换不是仿射(affine)的,因此,透视投影无法完全由一个矩阵表示。向量与投影矩阵相乘之后,它齐次坐标的每个分量都要除以自身的W(透视除法)。W分量恰好是-Z(投影矩阵会保证这一点)。这样,离原点更远的点,被除了较大的Z值;其X、Y坐标变小,点与点之间变紧,物体看起来就小了,这才产生了透视效果。*
第二课:画第一个三角形
最后更新于:2022-04-01 04:37:14
# 第二课: 画第一个三角形
这将又是一篇长教程。
用OpenGL 3实现复杂的东西很方便;为此付出的代价是,画一个简单的三角形变得比较麻烦。
不要忘了,定期复制粘贴,跑一下代码。
> 如果程序启动时崩溃了,很可能是你从错误的目录下运行了它。请仔细地阅读第一课中讲到的如何配置Visual Studio!
## 顶点数组对象(VAO)
你需要创建一个顶点数组对象,并将它设为当前对象(细节暂不深入):
~~~
GLuint VertexArrayID;
glGenVertexArrays(1, &VertexArrayID);
glBindVertexArray(VertexArrayID);
~~~
当窗口创建成功后(即OpenGL上下文创建后),马上做这一步工作;必须在任何其他OpenGL调用前完成。
若想进一步了解顶点数组对象(VAO),可以参考其他教程;但这不是很重要。
## 屏幕坐标系
三点定义一个三角形。当我们在三维图形学中谈论“点(point)”时,我们经常说“顶点(Vertex)”。一个顶点有三个坐标:X,Y和Z。你可以用以下方式来想象这三个坐标:
X 在你的右方Y 在你的上方Z 是你背后的方向(是的,背后,而不是你的前方)这里有一个更形象的方法:使用右手定则
X 是你的拇指Y 是你的食指Z 是你的中指。如果你把你的拇指指向右边,食指指向天空,那么中指将指向你的背后。让Z指往这个方向很奇怪,为什么要这样呢?简单的说:因为基于右手定则的坐标系被广泛使用了100多年,它会给你很多有用的数学工具;而唯一的缺点只是Z方向不直观。
`补充:`注意,你可以自由地移动你的手:你的X,Y和Z轴也将跟着移动(详见后文)。
我们需要三个三维点来组成一个三角形;现在开始:
~~~
// An array of 3 vectors which represents 3 vertices
static const GLfloat g_vertex_buffer_data[] = {
-1.0f, -1.0f, 0.0f,
1.0f, -1.0f, 0.0f,
0.0f,? 1.0f, 0.0f,
};
~~~
第一个顶点是(-1, -1, 0)。
这意味着除非我们以某种方式变换它,否则它将显示在屏幕的(-1, -1)位置。什么意思呢?屏幕的原点在中间,X在右方,Y在上方。屏幕坐标如下图:
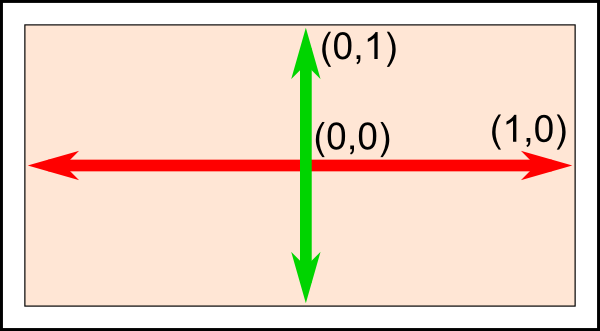
该机制内置于显卡,无法改变。因此(-1, -1)是屏幕的左下角,(1, -1)是右下角,(0, 1)在中上位置。这个三角形应该占满了大部分屏幕。
## 画我们的三角形
下一步把这个三角形传给OpenGL。我们通过创建一个缓冲区完成:
~~~
// This will identify our vertex buffer
GLuint vertexbuffer;
// Generate 1 buffer, put the resulting identifier in vertexbuffer
glGenBuffers(1, &vertexbuffer);
// The following commands will talk about our 'vertexbuffer' buffer
glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer);
// Give our vertices to OpenGL.
glBufferData(GL_ARRAY_BUFFER, sizeof(g_vertex_buffer_data), g_vertex_buffer_data, GL_STATIC_DRAW);
~~~
这只要做一次。
现在,我们的主循环中,那个之前啥都没有的地方,就能画我们宏伟的三角形了:
~~~
// 1rst attribute buffer : vertices
glEnableVertexAttribArray(0);
glBindBuffer(GL_ARRAY_BUFFER, vertexbuffer);
glVertexAttribPointer(
0, // attribute 0. No particular reason for 0, but must match the layout in the shader.
3, // size
GL_FLOAT, // type
GL_FALSE, // normalized?
0, // stride
(void*)0 // array buffer offset
);
// Draw the triangle !
glDrawArrays(GL_TRIANGLES, 0, 3); // Starting from vertex 0; 3 vertices total -> 1 triangle
glDisableVertexAttribArray(0);
~~~
结果如图:

白色略显无聊。让我们来看看怎么把它涂成红色。这就需要用到一个叫『着色器(Shader)』的东西。
## 着色器
### 编译着色器
在最简单的配置下,你将需要两个着色器:一个叫顶点着色器,它将作用于每个顶点上;另一个叫片断(Fragment)着色器,它将作用于每一个采样点。我们使用4倍反走样,因此每像素有四个采样点。
着色器编程使用GLSL(GL Shader Language,GL着色语言),它是OpenGL的一部分。与C或Java不同,GLSL必须在运行时编译,这意味着每次启动程序,所有的着色器将重新编译。
这两个着色器通常放在单独的文件里。本例中,我们有SimpleFragmentShader.fragmentshader和SimpleVertexShader.vertexshader两个着色器。他们的扩展名是无关紧要的,可以是.txt或者.glsl。
以下是代码。完全理解它不是很重要,因为通常一个程序只做一次,看懂注释就够了。所有其他课程代码都用到了这个函数,所以它被放在一个单独的文件中:common/loadShader.cpp。注意,和缓冲区一样,着色器不能直接访问:我们仅仅有一个编号(ID)。真正的实现隐藏在驱动程序中。
~~~
GLuint LoadShaders(const char * vertex_file_path,const char * fragment_file_path){
// Create the shaders
GLuint VertexShaderID = glCreateShader(GL_VERTEX_SHADER);
GLuint FragmentShaderID = glCreateShader(GL_FRAGMENT_SHADER);
// Read the Vertex Shader code from the file
std::string VertexShaderCode;
std::ifstream VertexShaderStream(vertex_file_path, std::ios::in);
if(VertexShaderStream.is_open())
{
std::string Line = "";
while(getline(VertexShaderStream, Line))
VertexShaderCode += "\n" + Line;
VertexShaderStream.close();
}
// Read the Fragment Shader code from the file
std::string FragmentShaderCode;
std::ifstream FragmentShaderStream(fragment_file_path, std::ios::in);
if(FragmentShaderStream.is_open()){
std::string Line = "";
while(getline(FragmentShaderStream, Line))
FragmentShaderCode += "\n" + Line;
FragmentShaderStream.close();
}
GLint Result = GL_FALSE;
int InfoLogLength;
// Compile Vertex Shader
printf("Compiling shader : %s\n", vertex_file_path);
char const * VertexSourcePointer = VertexShaderCode.c_str();
glShaderSource(VertexShaderID, 1, &VertexSourcePointer , NULL);
glCompileShader(VertexShaderID);
// Check Vertex Shader
glGetShaderiv(VertexShaderID, GL_COMPILE_STATUS, &Result);
glGetShaderiv(VertexShaderID, GL_INFO_LOG_LENGTH, &InfoLogLength);
std::vector VertexShaderErrorMessage(InfoLogLength);
glGetShaderInfoLog(VertexShaderID, InfoLogLength, NULL, &VertexShaderErrorMessage[0]);
fprintf(stdout, "%s\n", &VertexShaderErrorMessage[0]);
// Compile Fragment Shader
printf("Compiling shader : %s\n", fragment_file_path);
char const * FragmentSourcePointer = FragmentShaderCode.c_str();
glShaderSource(FragmentShaderID, 1, &FragmentSourcePointer , NULL);
glCompileShader(FragmentShaderID);
// Check Fragment Shader
glGetShaderiv(FragmentShaderID, GL_COMPILE_STATUS, &Result);
glGetShaderiv(FragmentShaderID, GL_INFO_LOG_LENGTH, &InfoLogLength);
std::vector FragmentShaderErrorMessage(InfoLogLength);
glGetShaderInfoLog(FragmentShaderID, InfoLogLength, NULL, &FragmentShaderErrorMessage[0]);
fprintf(stdout, "%s\n", &FragmentShaderErrorMessage[0]);
// Link the program
fprintf(stdout, "Linking programn");
GLuint ProgramID = glCreateProgram();
glAttachShader(ProgramID, VertexShaderID);
glAttachShader(ProgramID, FragmentShaderID);
glLinkProgram(ProgramID);
// Check the program
glGetProgramiv(ProgramID, GL_LINK_STATUS, &Result);
glGetProgramiv(ProgramID, GL_INFO_LOG_LENGTH, &InfoLogLength);
std::vector ProgramErrorMessage( max(InfoLogLength, int(1)) );
glGetProgramInfoLog(ProgramID, InfoLogLength, NULL, &ProgramErrorMessage[0]);
fprintf(stdout, "%s\n", &ProgramErrorMessage[0]);
glDeleteShader(VertexShaderID);
glDeleteShader(FragmentShaderID);
return ProgramID;
}
~~~
### 我们的顶点着色器
我们先写顶点着色器。
第一行告诉编译器我们将用OpenGL 3的语法。
~~~
#version 330 core
~~~
第二行声明输入数据:
~~~
layout(location = 0) in vec3 vertexPosition_modelspace;
~~~
具体解释一下这一行:
“vec3”在GLSL中是一个三维向量。类似于(但不相同)以前我们用来声明三角形的glm::vec3。最重要的是,如果我们在C++中使用三维向量,那么在GLSL中也使用三维向量。
“layout(location = 0)”指我们用来赋给vertexPosition_modelspace这个属性的缓冲区。每个顶点能有多种属性:位置,一种或多种颜色,一个或多个纹理坐标,等等。OpenGL不知道什么是颜色:它只是看到一个vec3。因此我们必须告诉它,哪个缓冲对应哪个输入。通过将glvertexAttribPointer函数的第一个参数值赋给layout,我们就完成了这一点。参数值“0”并不重要,它可以是12(但是不大于glGetIntegerv(GL_MAX_VERTEX_ATTRIBS, &v));重要的是两边参数值保持一致。
“vertexPosition_modelspace”这个变量名你可以任取,它将包含每个顶点着色器运行所需的顶点位置值。
“in”的意思是这是一些输入数据。不久我们将会看到“out”关键词。
每个顶点都会调用main函数(和C语言一样):
~~~
void main(){
~~~
我们的main函数只是将顶点的位置设为缓冲区里的值,无论这值是多少。因此如果我们给出位置(1,1),那么三角形将有一个顶点在屏幕的右上角。在下一课中我们将看到,怎样对输入位置做一些更有趣的计算。
~~~
gl_Position.xyz = vertexPosition_modelspace;
gl_Position.w = 1.0;
}
~~~
gl_Position是为数不多的内置变量之一:你必须赋一个值给它。其他操作都是可选的,我们将在第四课中看到“其他操作”指的是什么。
### 我们的片断着色器
作为我们的第一个片断着色器,我们只做一个简单的事:设置每个片断的颜色为红色。(记住,每像素有4个片断,因为我们用的是4倍反走样)
~~~
out vec3 color;
void main(){
color = vec3(1,0,0);
}
~~~
vec3(1,0,0)代表红色。因为在计算机屏幕上,颜色由红,绿,蓝这个顺序三元组表示。因此(1,0,0)意思是全红,没有绿色,也没有蓝色。
## 把它们组合起来
在main循环前,调用我们的LoadShaders函数:
~~~
// Create and compile our GLSL program from the shaders
GLuint programID = LoadShaders( "SimpleVertexShader.vertexshader", "SimpleFragmentShader.fragmentshader" );
~~~
现在在main循环中,首先清屏:
~~~
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
~~~
然后告诉OpenGL你想用你的着色器:
~~~
// Use our shader
glUseProgram(programID);
// Draw triangle...
~~~
…接着转眼间,这就是你的红色三角形!

下一课中我们将学习变换:如何设置你的相机,移动物体等等。
第一课:新建一个窗口
最后更新于:2022-04-01 04:37:12
# 第一课: 新建一个窗口
## 简介
欢迎来到第一课!
在学习OpenGL之前,我们将先学习如何生成,运行,和玩转(最重要的一点)课程中的代码。
## 预备知识
不需要特别的预备知识。如果你有C、Java、Lisp、Javascript等编程语言的经验,那么理解课程代码会更快;但这不是必需的;如果没有,那么也仅仅是同时学两样东西(编程语言+OpenGL)会稍微复杂点而已。
课程全部用“傻瓜式C++”编写:我费了很大劲尽量让代码简单些。代码里没有模板(template)、类或指针。就是说,即使只懂Java,也能理解所有内容。
## 忘记一切
如前面所说,我们不需要预备知识;但请暂时把『老式OpenGL』先忘了吧(例如glBegin()这类东西)。在这里,你将学习新式OpenGL(OpenGL 3和4),而多数网上教程还在讲『老式OpenGL』(OpenGL 1和2)。所以,在你的脑袋乱成一锅粥之前,把它们都搁在一边吧。
## 生成课程中的代码
所有课程代码都能在Windows、Linux、和Mac上生成,而且过程大体相同:
- 更新驱动 !!赶快更新吧。我可是提醒过你哟。
- 下载C++编译器。
- 安装CMake
- 下载全部课程代码
- 用CMake创建工程
- 编译工程
- 试试这些例子!
各平台的详细代码生成过程将会在后面一一给出,不过具体每个平台可能会有差异。如果你不确定,可以去看看Windows平台的生成说明,然后按照需改动一下来适应你自己的平台。
### 在Windows平台上生成课程代码
1.
更新驱动应该很轻松。直接去NVIDIA或者AMD的官网下载。若不清楚GPU的型号:控制面板->系统和安全->系统->设备管理器->显示适配器。如果是Intel集成显卡,一般由电脑厂商(Dell、HP等)提供驱动。
1.
建议用Visual Studio 2010 Express来编译。 这里可以免费下载。 若喜欢用MinGW,推荐[Qt Creator](http://qt-project.org/)。安装哪个都行。下列步骤是用Visual Studio讲解的,其他IDE也差不多。
1.
从这里下载安装 [CMake](http://www.cmake.org/cmake/resources/software.html) 。
1.
[下载课程源码](http://www.opengl-tutorial.org/?page_id=200) ,解压到例如C:/Users/XYZ/Projects/OpenGLTutorials .
1.
启动CMake。让第一栏路径指向刚才解压缩的文件夹;若不确定,就选包含CMakeLists.txt的文件夹。第二栏,填CMake输出路径 (译者注:这里CMake输出一个可以在Visual Studio中打开和编译的工程)。例如C:/Users/XYZ/Projects/OpenGLTutorials-build-Visual2010-32bits,或者C:/Users/XYZ/Projects/OpenGLTutorials/build/Visual2010-32bits。注意,此处可随便填,不一定要和源码在同一文件夹。
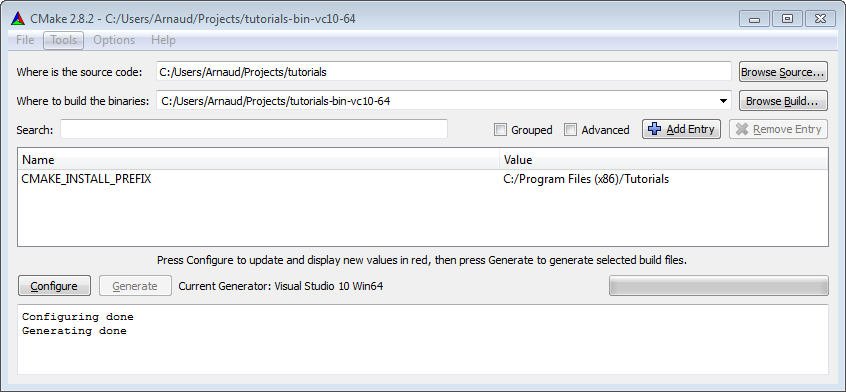
1.
点击Configure。由于是首次configure工程,CMake会让你选择编译器。根据步骤1选择。如果你的Windows是64位的,选64位。不清楚就选32位。\
1.
再点Configure直至红色行全部消失。点Generate。Visual Studio工程创建完毕。Visual Studio工程创建完毕。不再需要CMake了,可以卸载掉。
1.
打开 C:/Users/XYZ/Projects/OpenGL/Tutorials-build-Visual2010-32bits会看到Tutorials.sln文件(译者注:这就是CMake生成的VS项目文件),用Visual Studio打开它。

在 Build 菜单中,点Build All。每个课程代码和依赖项都会被编译。生成的可执行文件会出现在 C:/Users/XYZ/Projects/OpenGLTutorials。但愿不会报错。
1. 打开C:/Users/XYZ/Projects/OpenGLTutorials/playground,运行playground.exe,会弹出一个黑色窗口。
也可以在Visual Studio中运行任意一课的代码,但得先设置工作目录:右键点击Playground,选择Debugging、Working Directory、Browse,设置路径为C:/Users/XYZ/Projects/OpenGLTutorials/playground。验证一下。再次右键点击Playground,“Choose as startup project”。按F5就可以调试了。
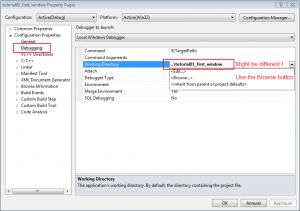
## 在Linux上生成
Linux版本众多,这里不可能列出所有的平台。按需变通一下吧,也不妨看一下发行版文档。
1.
安装最新驱动。强烈推荐闭源的二进制驱动;它们不开源,但好用。如果发行版不提供自动安装,试试[Ubuntu指南](http://help.ubuntu.com/community/BinaryDriverHowto).
1.
安装全部需要的编译器、工具和库。完整清单如下:cmake make g++ libx11-dev libgl1-mesa-dev libglu1-mesa-dev libxrandr-dev libxext-dev 。 用 sudo apt-get install ***** 或者 su && yum install ******。
1.
[下载课程源码](http://www.opengl-tutorial.org/?page_id=200) 并解压到如 ~/Projects/OpenGLTutorials/
1.
接着输入如下命令 :
~~~
cd ~/Projects/OpenGLTutorials/
mkdir build
cd build
cmake ..
~~~
1.
build/目录会创建一个makefile文件。
1.
键入“make all”。每个课程代码和依赖项都会被编译。生成的可执行文件在~/Projects/OpenGLTutorials/。但愿不会报错。
1.
打开~/Projects/OpenGLTutorials/playground,运行./playground会弹出一个黑色窗口。
提示:推荐使用[Qt Creator](http://qt-project.org/)作为IDE。值得一提的是,Qt Creator内置支持CMake,调试起来也顺手。如下是QtCreator使用说明:
1.在QtCreator中打开Tools->Options->Compile-&Execute->CMake
2.设置CMake路径。很可能像这样/usr/bin/cmake
3.File->Open Project;选择 tutorials/CMakeLists.txt
4.选择生成目录,最好选择tutorials文件夹外面
5.还可以在参数栏中设置-DCMAKE_BUILD_TYPE=Debug。验证一下。
6.点击下面的锤子图标。现在教程可以从tutorials/文件夹启动了。
7.要想在QtCreator中运行教程源码,点击Projects->Execution parameters->Working Directory,选择着色器、纹理和模型所在目录。以第二课为例:~/opengl-tutorial/tutorial02_red_triangle/
## 在Mac上生成
Mac OS不支持OpenGL 3.3。最近,搭载MacOS 10.7 Lion和兼容型GPU的Mac电脑可以跑OpenGL 3.2了,但3.3还不行;所以我们用2.1移植版的课程代码。除此外,其他步骤和Windows类似(也支持Makefiles,此处不赘述):
1.从Mac App Store安装XCode
2.下载[CMake](http://www.cmake.org/cmake/resources/software.html),安装.dmg。无需安装命令行工具。
3.下载[课程源码](http://www.opengl-tutorial.org/?page_id=200) (2.1版!!)解压到如~/Projects/OpenGLTutorials/ .
4.启动CMake (Applications->CMake)。让第一栏路径指向刚才解压缩的文件夹,不确定就选包含CMakeLists.txt的文件夹。第二栏,填CMake输出路径。例如~/Projects/OpenGLTutorials_bin_XCode/。注意,这里可以随便填,不一定要和源码在同一文件夹。
5.点击Configure。由于是首次configure工程,CMake会让你选择编译器。选择Xcode。
6.再点Configure直至红色行全部消失。点Generate。Xcode项目创建完毕。不再需要CMake了,可以卸载掉。
7.打开~/Projects/OpenGLTutorials_bin_XCode/会看到Tutorials.xcodeproj文件:打开它。
8.选择一个教程,在Xcode的Scheme面板上运行,点击Run按钮编译和运行:
**在第二课及后续课程中,Run按钮就失效了。下一版本会解决这个bug。目前,请用Cmd-B键运行(双击源码文件夹/tutorialX/tutorialX,或者通过终端)。**
## 关于Code::Blocks的说明
由于C::B和CMake中各有一个bug,你得在Project->Build->Options->Make commands中手动设置编译命令,如下图所示:
同时你还得手动设置工作目录:Project->Properties->Build targets->tutorial N->execution working dir(即src_dir/tutorial_N/)。
## 运行课程例子
一定要在正确的目录下运行课程例子:你可以双击可执行文件;如果爱用命令行,请用cd命令切换到正确的目录。
若想从IDE中运行程序,别忘了看看上面的说明——先正确设置工作目录。
## 如何学习本课程
每课都附有源码和数据,可在tutorialXX/找到。不过,建议您不改动这些工程,将它们作为参考;推荐在playground/playground.cpp中做试验,怎么折腾都行。要是弄乱了,就去粘一段课程代码,一切就会恢复正常。
我们会在整个教程中提供代码片段。不妨在看教程时,直接把它们复制到playground里跑跑看。动手实验才是王道。单纯看别人写好的代码学不了多少。即使仅仅粘贴一下代码,也会碰到不少问题。
## 新建一个窗口
终于!写OpenGL代码的时刻来了!
呃,其实还早着呢。有的教程都会教你以“底层”的方式做事,好让你清楚每一步的原理。但这往往很无聊也无用。所以,我们用一个外部的库——GLFW来帮我们处理窗口、键盘消息等细节。你也可以使用Windows的Win32 API、Linux的X11 API,或Mac的Cocoa API;或者用别的库,比如SFML、FreeGLUT、SDL等,请参见链接页。
我们开始吧。从处理依赖库开始:我们要用一些基本库,在控制台显示消息:
~~~
// Include standard headers
#include <stdio.h>
#include <stdlib.h>
~~~
然后是GLEW库。这东西的原理,我们以后再说。
~~~
// Include GLEW. Always include it before gl.h and glfw.h, since it's a bit magic.
#include <GL/glew.h>
~~~
我们使用GLFW库处理窗口和键盘消息,把它也包含进来:
~~~
// Include GLFW
#include <GL/glfw.h>
~~~
下面的GLM是个很有用的三维数学库,我们暂时没用到,但很快就会用上。GLM库很好用,但没有什么神奇的,你自己也可以写一个。添加“using namespace”是为了不用写“glm::vec3”,直接写“vec3”。
~~~
// Include GLM
#include <glm/glm.hpp>
using namespace glm;
~~~
如果把这些#include都粘贴到playground.cpp,编译器会报错,说缺少main函数。所以我们创建一个 :
~~~
int main(){
~~~
首先初始化GLFW :
~~~
// Initialise GLFW
if( !glfwInit() )
{
fprintf( stderr, "Failed to initialize GLFW\n" );
return -1;
}
~~~
可以创建我们的第一个OpenGL窗口啦!
~~~
glfwOpenWindowHint(GLFW_FSAA_SAMPLES, 4); // 4x antialiasing
glfwOpenWindowHint(GLFW_OPENGL_VERSION_MAJOR, 3); // We want OpenGL 3.3
glfwOpenWindowHint(GLFW_OPENGL_VERSION_MINOR, 3);
glfwOpenWindowHint(GLFW_OPENGL_PROFILE, GLFW_OPENGL_CORE_PROFILE); //We don't want the old OpenGL
// Open a window and create its OpenGL context
if( !glfwOpenWindow( 1024, 768, 0,0,0,0, 32,0, GLFW_WINDOW ) )
{
fprintf( stderr, "Failed to open GLFW window\n" );
glfwTerminate();
return -1;
}
// Initialize GLEW
glewExperimental=true; // Needed in core profile
if (glewInit() != GLEW_OK) {
fprintf(stderr, "Failed to initialize GLEW\n");
return -1;
}
glfwSetWindowTitle( "Tutorial 01" );
~~~
编译并运行。一个窗口弹出后立即关闭了。可不是嘛!还没设置等待用户Esc按键再关闭呢:
~~~
// Ensure we can capture the escape key being pressed below
glfwEnable( GLFW_STICKY_KEYS );
do{
// Draw nothing, see you in tutorial 2 !
// Swap buffers
glfwSwapBuffers();
} // Check if the ESC key was pressed or the window was closed
while( glfwGetKey( GLFW_KEY_ESC ) != GLFW_PRESS &&
glfwGetWindowParam( GLFW_OPENED ) );
~~~
第一课就到这啦!第二课会教大家画三角形。
OpenGL基础知识
最后更新于:2022-04-01 04:37:09