第十七课: 旋转

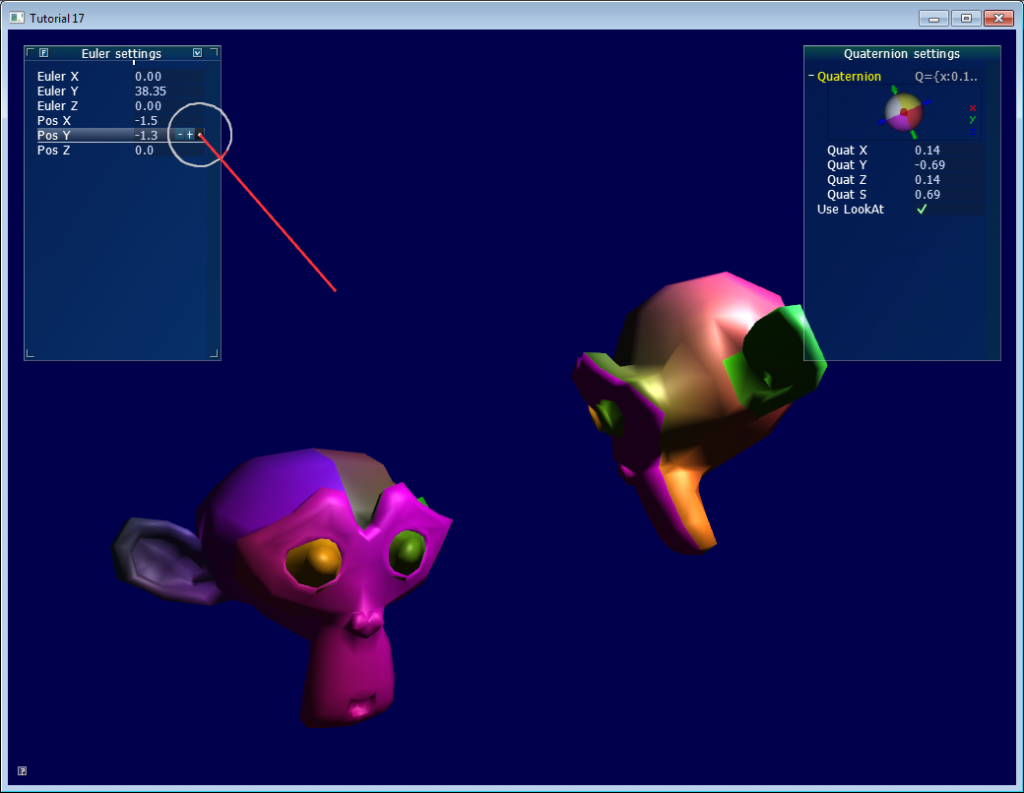
# 第十七课：旋转 虽然本课有些超出OpenGL的范围，但是解决了一个常见问题：怎样表示旋转？ 《第三课：矩阵》中，我们了解到矩阵可以让点绕某个轴旋转。矩阵可以简洁地表示顶点的变换，但使用难度较大：例如，从最终结果中获取旋转轴就很麻烦。 本课将展示两种最常见的表示旋转的方法：欧拉角（Euler angles）和四元数（Quaternion）。最重要的是，本课将详细解释为何要尽量使用四元数。  ## 旋转与朝向（orientation） 阅读有关旋转的文献时，你可能会为其中的术语感到困惑。本课中： - “朝向”是状态：该物体的朝向为…… - “旋转”是操作：旋转该物体 也就是说，当实施旋转操作时，就改变了物体的朝向。 两者形式相同，因此容易混淆。闲话少叙，开始进入正题…… ## 欧拉角 欧拉角是表示朝向的最简方法，只需存储绕X、Y、Z轴旋转的角度，非常容易理解。你可以用vec3来存储一个欧拉角： ~~~ vec3 EulerAngles( RotationAroundXInRadians, RotationAroundYInRadians, RotationAroundZInRadians); ~~~ 这三个旋转是依次施加的，通常的顺序是：Y-Z-X（但并非一定要按照这种顺序）。顺序不同，产生的结果也不同。 一个欧拉角的简单应用就是用于设置角色的朝向。通常，游戏角色不会绕X和Z轴旋转，仅仅绕竖直的Y轴旋转。因此，无需处理三个朝向，只需用一个float型变量表示方向即可。 另外一个使用欧拉角的例子是FPS相机：用一个角度表示头部朝向（绕Y轴），一个角度表示俯仰（绕X轴）。参见`common/controls.cpp`的示例。 不过，面对更加复杂的情况时，欧拉角就显得力不从心了。例如： - 对两个朝向进行插值比较困难。简单地对X、Y、Z角度进行插值得到的结果不太理想。 - 实施多次旋转很复杂且不精确：必须计算出最终的旋转矩阵，然后据此推测书欧拉角。 - “臭名昭著”的“万向节死锁”(Gimbal Lock)问题有时会让旋转“卡死”。其他一些奇异状态还会导致模型方向翻转。 - 不同的角度可产生同样的旋转（例如-180°和180°） - 容易出错——如上所述，一般的旋转顺序是YZX，如果用了非YZX顺序的库，就有麻烦了。 - 某些操作很复杂：如绕指定的轴旋转N角度。 四元数是表示旋转的好工具，可解决上述问题。 ## 四元数 四元数由4个数[x y z w]构成，表示了如下的旋转： ~~~ // RotationAngle is in radians x = RotationAxis.x * sin(RotationAngle / 2) y = RotationAxis.y * sin(RotationAngle / 2) z = RotationAxis.z * sin(RotationAngle / 2) w = cos(RotationAngle / 2) ~~~ `RotationAxis`，顾名思义即旋转轴。`RotationAngle`是旋转的角度。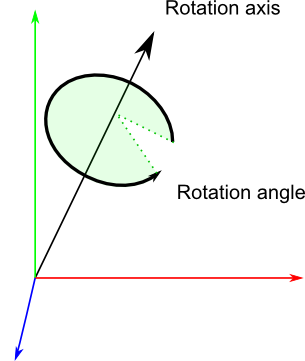  因此，四元数实际上存储了一个旋转轴和一个旋转角度。这让旋转的组合变简单了。 ## 解读四元数 四元数的形式当然不如欧拉角直观，不过还是能看懂的：xyz分量大致代表了各个轴上的旋转分量，而w=acos(旋转角度/2)。举个例子，假设你在调试器中看到了这样的值[ 0.7 0 0 0.7 ]。x=0.7，比y、z的大，因此主要是在绕X轴旋转；而2*acos(0.7) = 1.59弧度，所以旋转角度应该是90°。 同理，[0 0 0 1] (w=1)表示旋转角度 = 2*acos(1) = 0，因此这是一个*单位四元数*（unit quaternion），表示没有旋转。 ## 基本操作 不必理解四元数的数学原理：这种表示方式太晦涩了，因此我们一般通过一些工具函数进行计算。如果对这些数学原理感兴趣，可以参考[实用工具和链接](http://www.opengl-tutorial.org/miscellaneous/useful-tools-links/)中的数学书籍。 ### 怎样用C++创建四元数？ ~~~ // Don't forget to #include <glm/gtc/quaternion.hpp> and <glm/gtx/quaternion.hpp> // Creates an identity quaternion (no rotation) quat MyQuaternion; // Direct specification of the 4 components // You almost never use this directly MyQuaternion = quat(w,x,y,z); // Conversion from Euler angles (in radians) to Quaternion vec3 EulerAngles(90, 45, 0); MyQuaternion = quat(EulerAngles); // Conversion from axis-angle // In GLM the angle must be in degrees here, so convert it. MyQuaternion = gtx::quaternion::angleAxis(degrees(RotationAngle), RotationAxis); ~~~ ### 怎样用GLSL创建四元数？ 不要在shader中创建四元数。应该把四元数转换为旋转矩阵，用于模型矩阵中。顶点会一如既往地随着MVP矩阵的变化而旋转。 某些情况下，你可能确实需要在shader中使用四元数。例如，GPU骨骼动画。GLSL中没有四元数类型，但是可以将四元数存在vec4变量中，然后在shader中计算。 ### 怎样把四元数转换为矩阵？ ~~~ mat4 RotationMatrix = quaternion::toMat4(quaternion); ~~~ 这下可以像往常一样建立模型矩阵了: ~~~ mat4 RotationMatrix = quaternion::toMat4(quaternion); ... mat4 ModelMatrix = TranslationMatrix * RotationMatrix * ScaleMatrix; // You can now use ModelMatrix to build the MVP matrix ~~~ ## 那究竟该用哪一个呢？ 在欧拉角和四元数之间作选择还真不容易。欧拉角对于美工来说显得很直观，因此如果要做一款3D编辑器，请选用欧拉角。但对程序员来说，四元数却是最方便的。所以在写3D引擎内核时应该选用四元数。 一个普遍的共识是：在程序内部使用四元数，在需要和用户交互的地方就用欧拉角。 这样，在处理各种问题时，你才能得心应手（至少会轻松一点）。如果确有必要（如上文所述的FPS相机，设置角色朝向等情况），不妨就用欧拉角，附加一些转换工作。 ## 其他资源 1. [实用工具和链接](http://www.opengl-tutorial.org/miscellaneous/useful-tools-links/)中的书籍 1. 老是老了点，《游戏编程精粹1》（Game Programming Gems I）有几篇关于四元数的好文章。也许网络上就有这份资料。 1. 一个关于旋转的[GDC报告][http://www.essentialmath.com/GDC2012/GDC2012_JMV_Rotations.pdf](http://www.essentialmath.com/GDC2012/GDC2012_JMV_Rotations.pdf) 1. The Game Programing Wiki [Quaternion tutorial](http://content.gpwiki.org/index.php/OpenGL:Tutorials:Using_Quaternions_to_represent_rotation) 1. Ogre3D [FAQ on quaternions](http://www.ogre3d.org/tikiwiki/Quaternion+and+Rotation+Primer)。 第二部分大多是针对OGRE的。 1. Ogre3D [Vector3D.h](https://bitbucket.org/sinbad/ogre/src/3cbd67467fab3fef44d1b32bc42ccf4fb1ccfdd0/OgreMain/include/OgreVector3.h?at=default)和[Quaternion.cpp](https://bitbucket.org/sinbad/ogre/src/3cbd67467fab3fef44d1b32bc42ccf4fb1ccfdd0/OgreMain/src/OgreQuaternion.cpp?at=default) ## 速查手册 ## 怎样判断两个四元数是否相同？ 向量点积是两向量夹角的余弦值。若该值为1，那么这两个向量同向。判断两个四元数是否相同的方法与之十分相似： ~~~ float matching = quaternion::dot(q1, q2); if ( abs(matching-1.0) < 0.001 ){ // q1 and q2 are similar } ~~~ 由点积的acos值还可以得到q1和q2间的夹角。 ## 怎样旋转一个点？ 方法如下： ~~~ rotated_point = orientation_quaternion * point; ~~~ ……但如果想计算模型矩阵，你得先将其转换为矩阵。注意，旋转的中心始终是原点。如果想绕别的点旋转： ~~~ rotated_point = origin + (orientation_quaternion * (point-origin)); ~~~ ## 怎样对两个四元数插值？ SLERP意为球面线性插值（Spherical Linear intERPolation）、可以用GLM中的`mix`函数进行SLERP： ~~~ glm::quat interpolatedquat = quaternion::mix(quat1, quat2, 0.5f); // or whatever factor ~~~ ## 怎样累积两个旋转？ 只需将两个四元数相乘即可。顺序和矩阵乘法一致。亦即逆序相乘： ~~~ quat combined_rotation = second_rotation * first_rotation; ~~~ ## 怎样计算两向量之间的旋转？ （也就是说，四元数得把v1旋转到v2） 基本思路很简单： - 两向量间的夹角很好找：由点积可知其cos值。 - 旋转轴很好找：两向量的叉乘积。 如下的算法就是依照上述思路实现的，此外还处理了一些特例： ~~~ quat RotationBetweenVectors(vec3 start, vec3 dest){ start = normalize(start); dest = normalize(dest); float cosTheta = dot(start, dest); vec3 rotationAxis; if (cosTheta < -1 + 0.001f){ // special case when vectors in opposite directions: // there is no "ideal" rotation axis // So guess one; any will do as long as it's perpendicular to start rotationAxis = cross(vec3(0.0f, 0.0f, 1.0f), start); if (gtx::norm::length2(rotationAxis) < 0.01 ) // bad luck, they were parallel, try again! rotationAxis = cross(vec3(1.0f, 0.0f, 0.0f), start); rotationAxis = normalize(rotationAxis); return gtx::quaternion::angleAxis(180.0f, rotationAxis); } rotationAxis = cross(start, dest); float s = sqrt( (1+cosTheta)*2 ); float invs = 1 / s; return quat( s * 0.5f, rotationAxis.x * invs, rotationAxis.y * invs, rotationAxis.z * invs ); } ~~~ （可在`common/quaternion_utils.cpp`中找到该函数） ## 我需要一个类似gluLookAt的函数。怎样旋转物体使之朝向某点？ 调用`RotationBetweenVectors`函数！ ~~~ // Find the rotation between the front of the object (that we assume towards +Z, // but this depends on your model) and the desired direction quat rot1 = RotationBetweenVectors(vec3(0.0f, 0.0f, 1.0f), direction); ~~~ 现在，你也许想让物体保持竖直： ~~~ // Recompute desiredUp so that it's perpendicular to the direction // You can skip that part if you really want to force desiredUp vec3 right = cross(direction, desiredUp); desiredUp = cross(right, direction); // Because of the 1rst rotation, the up is probably completely screwed up. // Find the rotation between the "up" of the rotated object, and the desired up vec3 newUp = rot1 * vec3(0.0f, 1.0f, 0.0f); quat rot2 = RotationBetweenVectors(newUp, desiredUp); ~~~ 组合到一起： ~~~ quat targetOrientation = rot2 * rot1; // remember, in reverse order. ~~~ 注意，“direction”仅仅是方向，并非目标位置！你可以轻松计算出方向：`targetPos – currentPos`。 得到目标朝向后，你很可能想对`startOrientation`和`targetOrientation`进行插值 （可在`common/quaternion_utils.cpp`中找到此函数。） ## 怎样使用LookAt且限制旋转速度？ 基本思想是采用SLERP（用`glm::mix`函数），但要控制插值的幅度，避免角度偏大。 ~~~ float mixFactor = maxAllowedAngle / angleBetweenQuaternions; quat result = glm::gtc::quaternion::mix(q1, q2, mixFactor); ~~~ 如下是更为复杂的实现。该实现处理了许多特例。注意，出于优化的目的，代码中并未使用`mix`函数。 ~~~ quat RotateTowards(quat q1, quat q2, float maxAngle){ if( maxAngle < 0.001f ){ // No rotation allowed. Prevent dividing by 0 later. return q1; } float cosTheta = dot(q1, q2); // q1 and q2 are already equal. // Force q2 just to be sure if(cosTheta > 0.9999f){ return q2; } // Avoid taking the long path around the sphere if (cosTheta < 0){ q1 = q1*-1.0f; cosTheta *= -1.0f; } float angle = acos(cosTheta); // If there is only a 2° difference, and we are allowed 5°, // then we arrived. if (angle < maxAngle){ return q2; } float fT = maxAngle / angle; angle = maxAngle; quat res = (sin((1.0f - fT) * angle) * q1 + sin(fT * angle) * q2) / sin(angle); res = normalize(res); return res; } ~~~ 可以这样用`RotateTowards`函数： ~~~ CurrentOrientation = RotateTowards(CurrentOrientation, TargetOrientation, 3.14f * deltaTime ); ~~~ （可在`common/quaternion_utils.cpp`中找到此函数） ## 怎样……