第六课:键盘和鼠标
最后更新于:2022-04-01 04:37:23
# 第六课:键盘和鼠标
欢迎来到第六课!
我们将学习如何通过鼠标和键盘来移动相机,就像在第一人称射击游戏中一样。
## 接口
这段代码在整个课程中多次被使用,因此把它单独放在一个文件中:common/controls.cpp,然后在common/controls.hpp中声明函数接口,这样tutorial06.cpp就能使用它们了。
和前节课比,tutorial06.cpp里的代码变动很小。主要的变化是:每一帧都计算MVP(投影视图矩阵)矩阵,而不像之前那样只算一次。现在把这段代码加到主循环中:
~~~
do{
// ...
// Compute the MVP matrix from keyboard and mouse input
computeMatricesFromInputs();
glm::mat4 ProjectionMatrix = getProjectionMatrix();
glm::mat4 ViewMatrix = getViewMatrix();
glm::mat4 ModelMatrix = glm::mat4(1.0);
glm::mat4 MVP = ProjectionMatrix * ViewMatrix * ModelMatrix;
// ...
}
~~~
这段代码需要3个新函数:
- computeMatricesFromInputs()读键盘和鼠标操作,然后计算投影视图矩阵。这就是奇妙所在。
- getProjectionMatrix()返回计算好的投影矩阵。
- getViewMatrix()返回计算好的视图矩阵。
这只是一种实现方式,当然,如果你不喜欢这些函数,勇敢地去改写它们。
来看看controls.cpp在做什么。
## 实际代码
我们需要几个变量。
~~~
// position
glm::vec3 position = glm::vec3( 0, 0, 5 );
// horizontal angle : toward -Z
float horizontalAngle = 3.14f;
// vertical angle : 0, look at the horizon
float verticalAngle = 0.0f;
// Initial Field of View
float initialFoV = 45.0f;
float speed = 3.0f; // 3 units / second
float mouseSpeed = 0.005f;
FoV is the level of zoom. 80° = very wide angle, huge deformations. 60° – 45° : standard. 20° : big zoom.
~~~
首先根据输入,重新计算位置,水平角,竖直角和视场角(FoV);再由它们算出视图和投影矩阵。
### 方向
读取鼠标位置是容易的:
~~~
// Get mouse position
int xpos, ypos;
glfwGetMousePos(&xpos, &ypos);
~~~
我们需要把光标放到屏幕中心,否则它将很快移到屏幕外,导致无法响应。
~~~
// Reset mouse position for next frame
glfwSetMousePos(1024/2, 768/2);
~~~
注意:这段代码假设窗口大小是1024*768,这不是必须的。你可以用glfwGetWindowSize来设定窗口大小。
计算观察角度:
~~~
// Compute new orientation
horizontalAngle += mouseSpeed * deltaTime * float(1024/2 - xpos );
verticalAngle += mouseSpeed * deltaTime * float( 768/2 - ypos );
~~~
从右往左阅读这几行代码:
- 1024/2 – xpos表示鼠标离窗口中心点的距离。这个值越大,转动角越大。
- float(…)是浮点数转换,使乘法顺利进行
- mouseSpeed用来加速或减慢旋转,可以随你调整或让用户选择。
- += : 如果你没移动鼠标,1024/2-xpos的值为零,horizontalAngle+=0不改变horizontalAngle的值。如果你用的是”=”,每帧视角都被强制转回到原始方向,这就不好了。
现在,在世界坐标系下计算一个向量,代表视线方向。
~~~
// Direction : Spherical coordinates to Cartesian coordinates conversion
glm::vec3 direction(
cos(verticalAngle) * sin(horizontalAngle),
sin(verticalAngle),
cos(verticalAngle) * cos(horizontalAngle)
);
~~~
这是一种标准计算,如果你不了解余弦和正弦,下面有一个简短的解释:
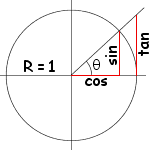
上面的公式,只是上图在三维空间下的推广。
我们想算出相机的『上方向』。『上方向』不一定是Y轴正方向:你俯视时,『上方向』实际上是水平的。这里有一个例子,位置相同,视点相同的相机,却有不同的『上方向』。
本例中,唯一不变的是,『相机的右边』这个方向始终取水平方向。你可以试试:保持手臂水平伸直,向正上方看、向下看;向这之间的任何方向看(译注:『看』立刻产生视线方向)。现在定义『右方向』向量:因为是水平的,故Y坐标为零,X和Z值就像上图中的一样,只是角度旋转了90度,或Pi/2弧度。
~~~
// Right vector
glm::vec3 right = glm::vec3(
sin(horizontalAngle - 3.14f/2.0f),
0,
cos(horizontalAngle - 3.14f/2.0f)
);
~~~
我们有一个『右方向』和一个视线方向,或者说是『前方向』。『上方向』垂直于这两者。一个很有用的数学工具可以让三者的联系变得简单:叉乘。
~~~
// Up vector : perpendicular to both direction and right
glm::vec3 up = glm::cross( right, direction );
~~~
叉乘是在做什么呢?很简单,回忆第三课讲到的右手定则。第一个向量是大拇指;第二个是食指;叉乘的结果就是中指。十分方便。
### 位置
代码十分直观。顺便说下,我用上/下/右/左键而不用wsad;是因为我的azerty键盘中,美式键盘的awsd键位处实际上是zqsd。qwerZ键盘其实又不一样了,更别提韩国键盘了。我甚至不知道韩国人民用的键盘是什么布局,但我猜想肯定很不一样。
~~~
// Move forward
if (glfwGetKey( GLFW_KEY_UP ) == GLFW_PRESS){
position += direction * deltaTime * speed;
}
// Move backward
if (glfwGetKey( GLFW_KEY_DOWN ) == GLFW_PRESS){
position -= direction * deltaTime * speed;
}
// Strafe right
if (glfwGetKey( GLFW_KEY_RIGHT ) == GLFW_PRESS){
position += right * deltaTime * speed;
}
// Strafe left
if (glfwGetKey( GLFW_KEY_LEFT ) == GLFW_PRESS){
position -= right * deltaTime * speed;
}
~~~
这里唯一特别的是deltaTime。你不会希望每帧偏移1单元的,原因很简单:
- 如果你有一台快电脑,每秒能跑60帧,你每秒移动60*speed个单位。
- 如果你有一台慢电脑,每秒能跑20帧,你每秒移动20*speed个单位。
电脑性能不能成为速度不稳的借口;你需要通过“前一帧到现在的时间”或“时间间隔(deltaTime)”来控制移动步长。
- 如果你有一台快电脑,每秒能跑60帧,你每帧移动1/60*speed个单位,每秒移动1*speed个单位。
- 如果你有一台慢电脑,每秒能跑20帧,你每帧移动1/20*speed个单位,每秒移动1*speed个单位。
这就好多了。deltaTime很容易算:
~~~
double currentTime = glfwGetTime();
float deltaTime = float(currentTime - lastTime);
~~~
### 视场角
为了好玩,我们可以把视场角绑定到鼠标滚轮,作为简陋的缩放功能:
~~~
float FoV = initialFoV - 5 * glfwGetMouseWheel();
~~~
### 计算矩阵
计算矩阵已经很直观了。使用和前面几乎一样的函数,仅参数不同。
~~~
// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit <-> 100 units
ProjectionMatrix = glm::perspective(FoV, 4.0f / 3.0f, 0.1f, 100.0f);
// Camera matrix
ViewMatrix = glm::lookAt(
position, // Camera is here
position+direction, // and looks here : at the same position, plus "direction"
up // Head is up (set to 0,-1,0 to look upside-down)
);
~~~
## 结果

### 隐藏面消除
现在可以自由移动鼠标,你会注意到:如果鼠标移动到立方体里面,多边形仍然会被显示。这看起来理所当然,实则可以优化。事实上,在常见应用中,你从来不会处于立方体内。
有一个思路是让GPU检查相机在三角形的后面还是前面。如果在前面,显示该三角形;如果相机在三角形后面,且不在网格(网格必须是封闭的)内部,那么必有其他三角形在相机前面,故不显示该三角形。没有人会注意到什么,除了一切都会变快:三角形平均少了两倍!
更妙的是,检查起来还很简单:GPU计算三角形的法向(用叉乘,记得吧?),然后检查这个法向是否朝向相机。
不幸的是这样做有代价:三角形的方向是隐式的。这意味着如果你在缓冲区中交换两个顶点,可能会产生洞。但一般来说,它值得做一点额外工作。一般你只要在三维建模软件中点击“反转法向”(实际是交换两个顶点,从而反转法向),一切就正常了。
开启隐藏面消除是很轻松的:
~~~
// Cull triangles which normal is not towards the camera
glEnable(GL_CULL_FACE);
~~~
## 练习
- 限制verticalAngle,使之不能颠倒方向
- 创建一个相机,使它绕着物体旋转 ( position = ObjectCenter + ( radius * cos(time), height, radius * sin(time) ) );然后将半径/高度/时间的变化绑定到键盘/鼠标上,诸如此类。
- 玩得开心!