第三课:矩阵
最后更新于:2022-04-01 04:37:16
# 第三课: 矩阵
引擎完全没有推动飞船。飞船静止在原处,而引擎推动了环绕着飞船的宇宙。
*《飞出个未来》(一部美国科幻动画片)*
> 这一课是所有课程中最重要的。请至少看八遍。
## 齐次坐标(Homogeneous coordinates)
目前为止,我们仍然把三维顶点视为三元组(x, y, z)。现在引入一个新的分量w,得到向量(x, y, z, w)。
请先记住以下两点(稍后我们会给出解释):
若w==1,则向量(x, y, z, 1)为空间中的点。
若w==0,则向量(x, y, z, 0)为方向。
`(事实上,要永远记着。)`
这有什么不同呢?对于旋转,二者没什么不同。当你旋转点和方向时,结果是一样的。但对于平移(将点沿着某个方向移动),情况就不同了。『平移一个方向』是毫无意义的。
齐次坐标使我们能用同一个公式对点和方向作运算。
## 变换矩阵(Transformation matrices)
### 矩阵简介
简而言之,矩阵就是一个行、列数固定的,纵横排列的数表。比如,一个2×3矩阵看起来像这样:

三维图形学中我们只用到4×4矩阵,它能对顶点(x, y, z, w)作变换。这一变换是用矩阵左乘顶点来实现的:
矩阵x顶点(记住顺序!!矩阵左乘顶点,顶点用列向量表示)= 变换后的顶点
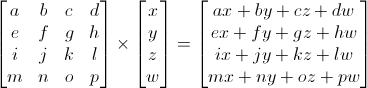
这看上去复杂,实则不然。左手指着a,右手指着x,得到ax。 左手移向右边一个数b,右手移向下一个数y,得到by。依次类推,得到cz、dw。最后求和ax + by + cz + dw,就得到了新的x!每一行都这么算下去,就得到了新的(x, y, z, w)向量。
这种重复无聊的计算就让计算机代劳吧。
**用C++,GLM表示:**
~~~
glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.
~~~
**用GLSL表示:**
~~~
mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM
~~~
`(还没把这些复制到你的代码里跑跑吗?赶紧试试!)`
### 平移矩阵(Translation matrices)
平移矩阵是最简单易懂的变换矩阵。平移矩阵是这样的:
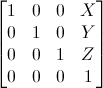
其中,X、Y、Z是点的位移增量。
例如,若想把向量(10, 10, 10, 1)沿X轴方向平移10个单位,可得:
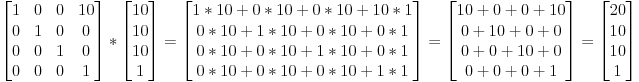
`(算算看!一定要动手算算!!)`
这样就得到了齐次向量(20, 10, 10, 1)!记住,末尾的1表示这是一个点,而不是方向。经过变换计算后,点仍然是点,很合理。
下面来看看,对一个代表Z轴负方向的向量,作上述平移变换会得到什么结果:
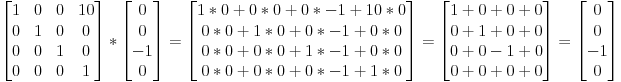
即还是原来的(0, 0, -1, 0)方向,这也很合理,正好印证了前面的结论:“平移一个方向是毫无意义的”。
那怎么用代码表示平移变换呢?
**用C++,GLM表示:**
~~~
#include <glm/transform.hpp> // after <glm/glm.hpp>
glm::mat4 myMatrix = glm::translate(10,0,0);
glm::vec4 myVector(10,10,10,0);
glm::vec4 transformedVector = myMatrix * myVector; // guess the result
~~~
**用GLSL表示:**呃,实际中我们几乎不用GLSL做。大多数情况下在C++代码中用glm::translate()算出矩阵,然后把它传给GLSL。在GLSL中只做一次乘法:
~~~
vec4 transformedVector = myMatrix * myVector;
~~~
### 单位矩阵(Identity matrix)
单位矩阵很特殊,它什么也不做。我提到它是因为,知道它和知道A*1.0=A一样重要。
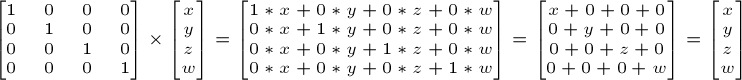
用C++表示:
~~~
glm::mat4 myIdentityMatrix = glm::mat4(1.0);
~~~
### 缩放矩阵(Scaling matrices)
缩放矩阵也很简单:
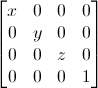
例如把一个向量(点或方向皆可)沿各方向放大2倍:
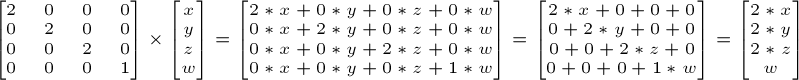
w还是没变。你也许会问:“缩放一个向量”有什么用?嗯,大多数情况下是没什么用,所以一般不会去做;但在某些罕见情况下它就有用了。(顺便说一下,单位矩阵只是缩放矩阵的一个特例,其(X, Y, Z) = (1, 1, 1)。单位矩阵同时也是旋转矩阵的一个特例,其(X, Y, Z)=(0, 0, 0))。
**用C++表示:**
~~~
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 myScalingMatrix = glm::scale(2,2,2);
~~~
### 旋转矩阵(Rotation matrices)
旋转矩阵比较复杂。这里略过细节,因为日常应用中,你并不需要知道矩阵的内部构造。想了解更多,请看[矩阵和四元组常见问题](http://www.cs.princeton.edu/~gewang/projects/darth/stuff/quat_faq.html)(这个资源很热门,应该有中文版吧)。
**用C++表示:**
~~~
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::vec3 myRotationAxis( ??, ??, ??);
glm::rotate( angle_in_degrees, myRotationAxis );
~~~
### 复合变换
前面已经学习了如何旋转、平移和缩放向量。要是能将它们组合起来就更好了。只需把这些矩阵相乘即可,例如:
~~~
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;
~~~
!!!千万注意!!!这行代码最先执行缩放,接着旋转,最后才是平移。这就是矩阵乘法的工作方式。
变换的顺序不同,得出的结果也不同。体验一下:
- 向前一步(小心别磕着爱机)然后左转;
- 左转,然后向前一步
实际上,上述顺序正是你在变换游戏人物或者其他物体时所需的:先缩放;再调整方向;最后平移。例如,假设有个船的模型(为简化,略去旋转):
`错误做法:`
-
按(10, 0, 0)平移船体。船体中心目前距离原点10个单位。
-
将船体放大2倍。以原点为参照,每个坐标都变成原来的2倍,就出问题了。……最后你是得到一艘放大的船,但其中心位于2*10=20。这可不是你想要的结果。
`正确做法:`
-
将船体放大2倍,得到一艘中心位于原点的大船。
-
平移船体。船大小不变,移动距离也正确。
矩阵-矩阵乘法和矩阵-向量乘法类似,所以这里也会省略一些细节,不清楚的请移步“矩阵和四元数常见问题”。现在,就让计算机来算:
**用C++,GLM表示:**
~~~
glm::mat4 myModelMatrix = myTranslationMatrix * myRotationMatrix * myScaleMatrix;
glm::vec4 myTransformedVector = myModelMatrix * myOriginalVector;
~~~
**用GLSL表示:**
~~~
mat4 transform = mat2 * mat1;
vec4 out_vec = transform * in_vec;
~~~
## 模型(Model)、视图(View)和投影(Projection)矩阵
*在接下来的课程中,我们假定已知绘制Blender经典三维模型:小猴Suzanne的方法。*
利用模型、视图和投影矩阵,可以将变换过程清晰地分解为三个阶段。这个方法你可以不用(我们在前两课就没用),但最好要用。我们即将看到,它们把整个流程划分得很清楚,故被广为使用。
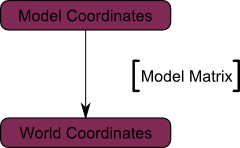
### 模型矩阵
这个三维模型,和我们心爱的红色三角形一样,是由一组顶点定义的。顶点的XYZ坐标是相对于物体中心定义的:也就是说,若某顶点位于(0, 0, 0),它就在物体的中心。

也许玩家需要用键鼠控制这个模型,所以我们希望能够移动它。这简单,只需学会:缩放*旋转*平移就行了。在每一帧中,用算出的这个矩阵,去乘(在GLSL中乘,不是C++中!)所有的顶点,物体就动了。唯一不动的就是世界坐标系(World Space)的中心。

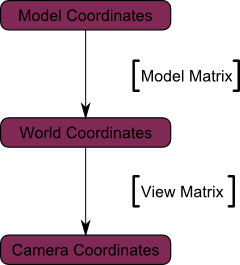
现在,物体所有顶点都位于世界坐标系。下图中黑色箭头的意思是:*从模型坐标系(Model Space)(顶点都相对于模型的中心定义)变换到世界坐标系(顶点都相对于世界坐标系中心定义)。*

下图概括了这一过程:
### 视图矩阵
这里再引用一下《飞出个未来》:
引擎完全没有推动飞船。飞船静止在原处,而引擎推动了环绕着飞船的宇宙。
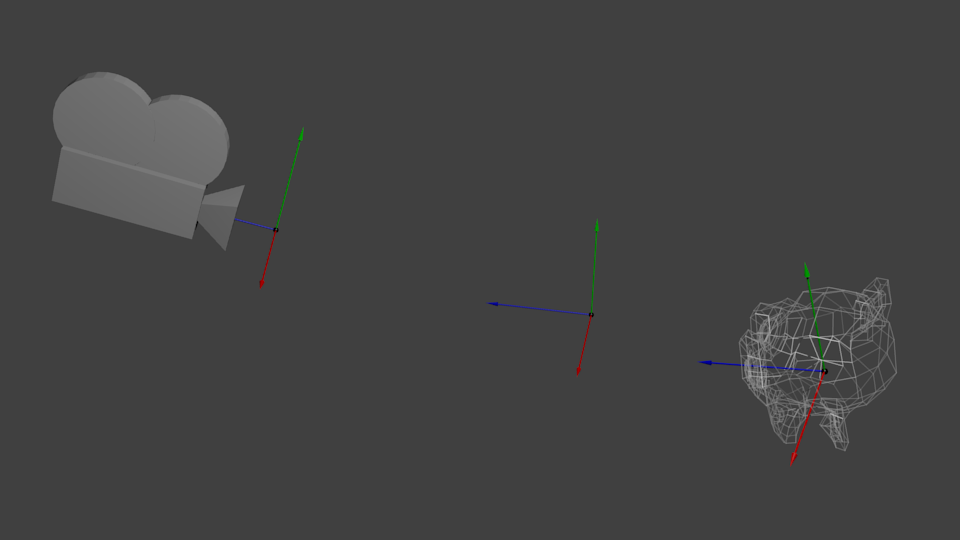
仔细想想,相机的原理也是相通的。如果想换个角度观察一座山,你可以移动相机也可以……移动山。后者在生活中不可行,在计算机图形学中却十分方便。
起初,相机位于世界坐标系的原点。移动世界只需乘上一个矩阵。假如你想把相机向右(X轴正方向)移动3个单位,这和把整个世界(包括网格)向左(X轴负方向)移3个单位是等效的!脑子有点乱?来写代码:
~~~
// Use #include <glm/gtc/matrix_transform.hpp> and #include <glm/gtx/transform.hpp>
glm::mat4 ViewMatrix = glm::translate(-3,0,0);
~~~
下图展示了:从世界坐标系(顶点都相对于世界坐标系中心定义)到观察坐标系(Camera Space,顶点都相对于相机定义)的变换。

**在脑袋撑爆前,来欣赏一下GLM伟大的glm::LookAt函数吧:**
~~~
glm::mat4 CameraMatrix = glm::LookAt(
cameraPosition, // the position of your camera, in world space
cameraTarget, // where you want to look at, in world space
upVector // probably glm::vec3(0,1,0), but (0,-1,0) would make you looking upside-down, which can be great too
);
~~~
下图解释了上述变换过程:
还没完呢。
### 投影矩阵
现在,我们处于观察坐标系中。这意味着,经历了这么多变换后,现在一个坐标为(0,0)的顶点,应该被画在屏幕的中心。但仅有x、y坐标还不足以确定物体是否应该画在屏幕上:它到相机的距离(z)也很重要!两个x、y坐标相同的顶点,z值较大的一个将会最终显示在屏幕上。
这就是所谓的透视投影(perspective projection):

好在用一个4×4矩阵就能表示这个投影¹ :
~~~
// Generates a really hard-to-read matrix, but a normal, standard 4x4 matrix nonetheless
glm::mat4 projectionMatrix = glm::perspective(
FoV, // The horizontal Field of View, in degrees : the amount of "zoom". Think "camera lens". Usually between 90° (extra wide) and 30° (quite zoomed in)
4.0f / 3.0f, // Aspect Ratio. Depends on the size of your window. Notice that 4/3 == 800/600 == 1280/960, sounds familiar ?
0.1f, // Near clipping plane. Keep as big as possible, or you'll get precision issues.
100.0f // Far clipping plane. Keep as little as possible.
);
~~~
最后一个变换:
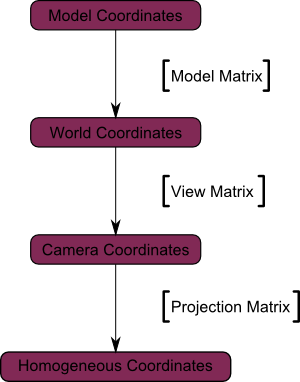
*从观察坐标系(顶点都相对于相机定义)到齐次坐标系(Homogeneous Space)(顶点都在一个小立方体中定义。立方体内的物体都会在屏幕上显示)的变换。*
最后一幅图示:
再添几张图,以便大家更好地理解投影变换。投影前,蓝色物体都位于观察坐标系中,红色的东西是相机的视域四棱锥(frustum):这是相机实际能看见的区域。

用投影矩阵去乘前面的结果,得到如下效果:

此图中,视域四棱锥变成了一个正方体(每条棱的范围都是-1到1,图上不太明显),所有的蓝色物体都经过了相同的形变。因此,离相机近的物体就显得大一些,远的显得小一些。和真实生活中一样!
让我们从视域四棱锥的“后面”看看它们的模样:
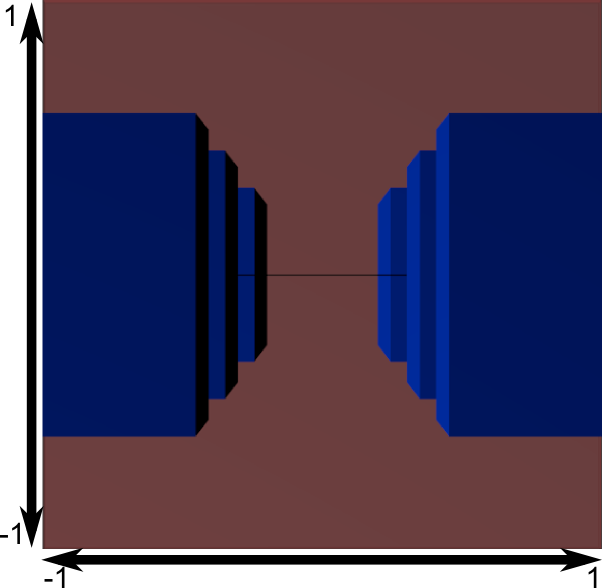
这就是你得出的图像了!看上去太方方正正了,因此,还需要做一次数学变换使之适合实际的窗口大小:

这就是实际渲染的图像啦!
### 复合变换:模型视图投影矩阵(MVP)
… 再来一串亲爱的矩阵乘法:
~~~
// C++ : compute the matrix
glm::mat3 MVPmatrix = projection * view * model; // Remember : inverted !
// GLSL : apply it
transformed_vertex = MVP * in_vertex;
~~~
## 总结
**第一步:创建模型视图投影(MVP)矩阵。任何要渲染的模型都要做这一步。**
~~~
// Projection matrix : 45° Field of View, 4:3 ratio, display range : 0.1 unit 100 units
glm::mat4 Projection = glm::perspective(45.0f, 4.0f / 3.0f, 0.1f, 100.0f);
// Camera matrix
glm::mat4 View = glm::lookAt(
glm::vec3(4,3,3), // Camera is at (4,3,3), in World Space
glm::vec3(0,0,0), // and looks at the origin
glm::vec3(0,1,0) // Head is up (set to 0,-1,0 to look upside-down)
);
// Model matrix : an identity matrix (model will be at the origin)
glm::mat4 Model = glm::mat4(1.0f); // Changes for each model !
// Our ModelViewProjection : multiplication of our 3 matrices
glm::mat4 MVP = Projection * View * Model; // Remember, matrix multiplication is the other way around
~~~
**第二步:把MVP传给GLSL**
~~~
// Get a handle for our "MVP" uniform.
// Only at initialisation time.
GLuint MatrixID = glGetUniformLocation(programID, "MVP");
// Send our transformation to the currently bound shader,
// in the "MVP" uniform
// For each model you render, since the MVP will be different (at least the M part)
glUniformMatrix4fv(MatrixID, 1, GL_FALSE, &MVP[0][0]);
~~~
**第三步:在GLSL中用MVP变换顶点**
~~~
in vec3 vertexPosition_modelspace;
uniform mat4 MVP;
void main(){
// Output position of the vertex, in clip space : MVP * position
vec4 v = vec4(vertexPosition_modelspace,1); // Transform an homogeneous 4D vector, remember ?
gl_Position = MVP * v;
}
~~~
**完成!三角形和第二课的一样,仍然在原点(0, 0, 0),然而是从点(4, 3, 3)透视观察的;相机的上方向为(0, 1, 0),视场角(field of view)45°。**

第6课中你会学到怎样用键鼠动态修改这些值,从而创建一个和游戏中类似的相机。但我们会先学给三维模型上色(第4课)、贴纹理(第5课)。
## 练习
**试着替换glm::perspective**
**不用透视投影,试试正交投影(orthographic projection )(glm::ortho)**
**把ModelMatrix改成先平移,再旋转,最后放缩三角形**
**其他不变,但把模型矩阵运算改成平移-旋转-放缩的顺序,会有什么变化?如果对一个人作变换,你觉得什么顺序最好呢?**
*附注*
*1 : [...]好在用一个4×4矩阵就能表示这个投影:实际上,这句话并不对。透视变换不是仿射(affine)的,因此,透视投影无法完全由一个矩阵表示。向量与投影矩阵相乘之后,它齐次坐标的每个分量都要除以自身的W(透视除法)。W分量恰好是-Z(投影矩阵会保证这一点)。这样,离原点更远的点,被除了较大的Z值;其X、Y坐标变小,点与点之间变紧,物体看起来就小了,这才产生了透视效果。*