[TOC=2] ## 15.1 简介 本章中，我会讲解如何自定义语法。用户定义语法称作**宏（Macro）**。Lisp/Scheme中的宏比C语言中的宏更加强大。宏可以使你的程序优美而紧凑。 宏是代码的变换。代码在被求值或编译前进行变换，and the procedure continues as if the transformed codes are written from the beginning. 你可以在Scheme中通过用符合R5RS规范的`syntax-rules`轻易地定义简单宏，相比之下，在Common Lisp中自定义语法就复杂多了。使用`syntax-rules`可以直接定义宏而不用担心**变量的捕获（Variable Capture）**。On the other hand, defining complicated macros that cannot be defined using the syntax-rules is more difficult than that of the Common Lisp. ## 15.2 实例：简单宏 我将以一个简单的宏作为例子。 [代码片段 1] 一个将变量赋值为’()的宏 ~~~ (define-syntax nil! (syntax-rules () ((_ x) (set! x '())))) ~~~ `syntax-reuls`的第二个参数由是变换前表达式构成的表。`_`代表宏的名字。简言之，**代码片段1**表示表达式`(nil! x)`会变换为`(set! x '())`. 这类过程不能通过函数来实现，这是因为函数的闭包性质限制它不能影响外部变量。让我们来用函数实现**代码片段1**，并观察效果。 ~~~ (define (f-nil! x) (set! x '())) (define a 1) ;Value: a (f-nil! a) ;Value: 1 a ;Value: 1 ; the value of a dose not change (nil! a) ;Value: 1 a ;Value: () ; a becomes '() ~~~ 我会演示另外一个例子。我们编写宏`when`，其语义为：当谓词求值为真时，求值相应语句。 ~~~ (define-syntax when (syntax-rules () ((_ pred b1 ...) (if pred (begin b1 ...))))) ~~~ **代码片段2**中的`...`代表了任意多个数的表达式（包括0个表达式）。**代码片段2**揭示了诸如表达式`(when pred b1 ...)`会变换为`(if pred (begin b1 ...))`。 由于这个宏是将表达式变换为`if`特殊形式，因此它不能使用函数来实现。下面的例子演示了如何使用`when`。 ~~~ (let ((i 0)) (when (= i 0) (display "i == 0") (newline))) i == 0 ;Unspecified return value ~~~ 我会演示两个实宏：`while`和`for`。只要谓词部分求值为真，`while`就会对语句体求值。而数字在指定的范围中，`for`就会对语句体求值。 ~~~ (define-syntax while (syntax-rules () ((_ pred b1 ...) (let loop () (when pred b1 ... (loop)))))) (define-syntax for (syntax-rules () ((_ (i from to) b1 ...) (let loop((i from)) (when (< i to) b1 ... (loop (1+ i))))))) ~~~ 下面演示了如何实用它们： ~~~ define-syntax while (syntax-rules () ((_ pred b1 ...) (let loop () (when pred b1 ... (loop)))))) (define-syntax for (syntax-rules () ((_ (i from to) b1 ...) (let loop((i from)) (when (< i to) b1 ... (loop (1+ i))))))) ~~~ > 练习1 > > 编写一个宏，其语义为：当谓词求值为假时执行相应的表达式。（语义与`when`相对） ## 15.3 syntax-rule的更多细节 ### 15.3.1 多个定义模式

[TOC=2] ## 14.1 简介 本章中，我将讲解向量和结构体。向量是一组通过整数索引的数据。与C语言中的数组不同，一个向量可以储存不同类型的数据。与表相比，向量更加紧凑且存取时间更短。但从另外一方面来说，向量是通过副作用来操作的，这样会造成负担。Scheme中的结构体与C语言中的结构体类似。但Scheme中的结构体比C语言中的更容易使用，这是因为Scheme为结构体自动创建了读取函数和写入函数，这受益于Lisp/Scheme程序设计语言中的宏。 ## 14.2 向量 ### 14.2.1 字面值 向量通过闭合的`#(`和`)`表示，例如`#(1 2 3)`。作为字面值时，它们应该被引用，例如： ~~~ '#(1 2 3) ; 整数向量 '#(a 0 #\a) ; 由符号、整数和字符构成的向量 ~~~ ### 14.2.2 向量函数 下面的函数都是R5RS规定的函数： (vector? obj) 如果obj是一个向量则返回#t。 (make-vector k) (make-vector k fill) 放回一个有k个元素的向量。如果指定了第二个参数fill，那么所有的元素都会被初始化为fill。 (vector obj …) 返回由参数列表构成的向量。 (vector-length vector) 返回向量vector的长度。 (vector-ref vector k) 返回向量vector的索引为k的元素。（译注：和C语言类似，向量从0开始索引。） (vector-set! vector k obj) 将向量vector的索引为k的元素修改为obj。 (vector->list vector) 将vector转换为表。 (list->vector list) 将list转换为向量。 (vector-fill! vector fill) 将向量vector的所有元素设置为fill。 例：一个对向量中元素求和的函数。 ~~~ (define (vector-add v1 v2) (let ((lenv1 (vector-length v1)) (lenv2 (vector-length v2))) (if (= lenv1 lenv2) (let ((v (make-vector lenv1))) (let loop ((i 0)) (if (= i lenv1) v (begin (vector-set! v i (+ (vector-ref v1 i) (vector-ref v2 i))) (loop (1+ i)))))) (error "different dimensions.")))) ~~~ > 练习1 > > 编写一个用于计算两向量内积的函数。 ## 14.3 结构体 ### 14.3.1 大体功能 虽然R5RS中没有定义结构体，但是在很多Scheme实现中，都实现了类似于Common Lisp中的结构体。这些结构体本质上来说都是向量。每一个槽都通过使用一个宏来命名，我将会在下一章（十五章）中讲解这个问题。结构体通过不同的属性清楚地表示数据。定义结构体的宏自动为结构体创建**读取（accessor）函数**和**设置（setter）函数**。你可以通过“程序”来写程序，这被认为是Lisp/Scheme最好之处之一。 ### 14.3.2 MIT-Scheme中的结构体 在MIT-Scheme中，结构体通过函数`define-structure`来定义。为了使你更加容易理解，我会用一个实例来讲解。请考虑书籍。书籍都有下列属性： * 标题 * 作者 * 出版商 * 出版年份 * ISBN号 因此结构体book就可以像下面这样定义： ~~~ (define-structure book title authors publisher year isbn) ~~~ 下面演示了如何注册《大教堂与市集（The Cathedral and Bazaar）》。 ~~~ (define bazaar (make-book "The Cathedral and the Bazaar" "Eric S. Raymond" "O'Reilly" 1999 0596001088)) ~~~ 然而，这样做多多少少有点不便，因为属性与值的关联并不清楚。参量`keyword-constructor`可以用于解决这个问题。下面的代码就是使用这个参量的重写版，这个版本中，属性与值的关联就非常清楚了。更进一步来说，制定这个参量后，参数的顺序就不重要了。 参量`copier`可用于为结构体创建一个拷贝（copier）函数。 ~~~ (define-structure (book keyword-constructor copier) title authors publisher year isbn) (define bazaar (make-book 'title "The Cathedral and the Bazaar" 'authors "Eric S. Raymond" 'publisher "O'Reilly" 'year 1999 'isbn 0596001088)) ~~~ * 一个名字形如`[结构体名称]?`的函数用于检查某对象是否为特定结构体。例如，可使用函数`book?`来检查`bazaar`是否为`book`结构体的一个实例。 ~~~ (book? bazaar) ;Value: #t ~~~ * 一个名字形如`copy-[结构体名称]`的函数用于拷贝结构体。例如，下面的代码演示了将`bazaar`拷贝到`cathedral`。 ~~~ (define cathedral (copy-book bazaar)) ~~~ * 一个名字形如`[结构体名称]-[属性名称]`的函数用于读取结构体某属性的值。例如，下面的代码演示了如何读取`bazaar`的`title`属性。 ~~~ (book-title bazaar) ;Value 18: "The Cathedral and the Bazaar" ~~~ * 一个名字形如`set-[结构体名称]-[属性名称]!`用于将某属性设定为特定值。下面的代码演示了如何将`bazaar`的`year`字段更新到2001（《大教堂与市集》2001年再版）。 ~~~ (set-book-year! bazaar 2001) ;Unspecified return value (book-year bazaar) ;Value: 2001 ~~~ 请参阅[MIT/GNU Scheme Reference: 2.10 Structure Definitions](http://deathking.github.io/yast-cn/www.gnu.org/software/mit-scheme/documentation/scheme_3.html#SEC41)以获得关于结构体的跟多信息。 ## 14.4 The Mastermind — 一个简单的密码破解游戏 作为向量的示例，我会演示一个简单地密码破解游戏。这是一个猜对手密码的游戏。密码是由0到9中四个不同的数组成的四位数。

## 13.1 简介 本章中，我会讲解用于表示数据关联的关联表和哈希表。关联的数据室由键和值组成的序对，值由键唯一定义。表1显示了书籍和作者构成的配对。书籍可以确定作者，反之由作者定义书籍则不可，这是因为一个作者可能会写很多本书。表1中，由于P. Graham和L.Carroll分别写了两本书，因此他们的书无法被作者的名字唯一定义。 表1 Author Book P. Graham On Lisp P. Graham ANSI Common Lisp E. S. Raymond The Cathedral and the Bazaar K. Dybvig The Scheme Programming Language F. P. Brooks, Jr. The Mythical Man-Month L. Carroll Alice’s Adventures in Wonderland L. Carroll Through the Looking-Glass, and What Alice Found There R^5RS定义了关联表，因此它再所有Scheme实现中都可用。

[TOC=2] ## 12.1 简介 我会在本章讲解在Lisp/Scheme程序设计语言中具有字符性质的数据类型——符号。 ## 12.2 有关符号的基本函数 下列都是有关符号的基本函数。 `(symbol? x)` 如果`x`是一个符号则返回`#t`。 `(string->symbol str)` 将`str`转换为符号。`str`应该都是小写的，否则地址系统可能无法正常工作。在MIT-Scheme中，`(string->symbol "Hello")`和`'Hello`是不同的。 ```scheme (eq? (string->symbol "Hello") 'Hello) ;Value: () (eq? (string->symbol "Hello") (string->symbol "Hello")) ;Value: #t (symbol->string (string->symbol "Hello")) ;Value 15: "Hello" ``` `(symbol->string sym)` 将sym转换为字符。 ## 12.3 统计文本中的单词 下面的代码是一段统计文本中单词个数的程序，这也是被经常用作演示符号的例子。这个程序使用了**哈希表（Hash table）**和**关联表（Association list）**，这些都将在下一章中讲解。 ~~~ 01: ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; 02: ;;; wc.scm 03: ;;; a scheme word-count program 04: ;;; 05: ;;; by T.Shido 06: ;;; on August 19, 2005 07: ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; 08: 09: (define (list->symbol ls0) 10: (string->symbol (list->string (reverse! ls0)))) 11: 12: (define (char-in c . ls) 13: (let loop((ls0 ls)) 14: (if (null? ls0) 15: #f 16: (or (char=? c (car ls0)) 17: (loop (cdr ls0)))))) 18: 19: (define (read-words fname) 20: (with-input-from-file fname 21: (lambda () 22: (let loop((w '()) (wls '())) 23: (let ((c (read-char))) 24: (cond 25: ((eof-object? c) 26: (reverse! (if (pair? w) 27: (cons (list->symbol w) wls) 28: wls))) 29: ((char-in c #\Space #\Linefeed #\Tab #\, #\. #\ #\( #\) #\= #\? #\! #\; #\:) 30: (loop '() (if (pair? w) 31: (cons (list->symbol w) wls) 32: wls))) 33: (else 34: (loop (cons (char-downcase c) w) wls)))))))) 35: 36: (define (sort-by-frequency al) 37: (sort al (lambda (x y) (> (cdr x) (cdr y))))) 38: 39: (define (wc fname) 40: (let ((wh (make-eq-hash-table))) 41: (let loop((ls (read-words fname))) 42: (if (null? ls) 43: (sort-by-frequency (hash-table->alist wh)) 44: (begin 45: (hash-table/put! wh (car ls) (1+ (hash-table/get wh (car ls) 0))) 46: (loop (cdr ls))))))) (wc "opensource.txt") ⇒ ((the . 208) (to . 142) (a . 104) (of . 103) (and . 83) (that . 75) (is . 73) (in . 65) (i . 64) (you . 55) (it . 54) (they . 48) (for . 46) (what . 38) (work . 37) (but . 35) (have . 32) (on . 32) (people . 32) (are . 30) (be . 29) (do . 29) (from . 27) (so . 26) (like . 25) (as . 25) (by . 24) (source . 24) (not . 23) (open . 23) (can . 23) (we . 22) (was . 22) (one . 22) (it's . 22) (an . 21) (this . 20) (about . 20) (business . 18) (working . 18) (most . 17) (there . 17) (at . 17) (with . 16) (don't . 16) (just . 16) (their . 16) (something . 15) (than . 15) (has . 15) (if . 15) (when . 14) (because . 14) (more . 14) (were . 13) (office . 13) (own . 13) (or . 12) (online . 12) (now . 12) (blogging . 12) (how . 12) (employees . 11) (them . 11) (think . 11) (time . 11) (company . 11) (lot . 11) (want . 11) (companies . 10) (could . 10) (know . 10) (get . 10) (learn . 10) (better . 10) (some . 10) (who . 10) (even . 9) (thing . 9) (much . 9) (no . 9) (make . 9) (up . 9) (being . 9) (money . 9) (relationship . 9) (that's . 9) (us . 9) (anyone . 8) (average . 8) (bad . 8) (same . 8) ..........) ~~~ 说明： 行号 函数 说明 09 `(list->symbo ls0)` 将一个由字符构成的列表（`ls0`）转换为一个符号 12 `(char-in c . ls)` 检查 ## 12.4 小结 符号是Lisp/Scheme中用于解析分析文段（例如词数统计，解析等）的一种字符式数据类型，有一些速度很快的函数适用于符号。

[TOC=2] ## 11.1 简介 我只介绍了表和数，因为它们在Scheme中最为常用。然而，Scheme也有像**字符（Character）**、**字符串（String）**、**符号（Symbol）**、**向量（Vector）**等的其它数据类型，我将在11到14章节中介绍它们。 ## 11.2 字符 在某个字符前添加`#\`来表明该物是一个字符。例如，`#\a`表示字符a。字符`#\Space`、`#\Tab`、`#\Linefeed`和`#\Return`分别代表空格（Space）、制表符（Tab），Linefeed和返回（Return）。R5RS中定义了下面的与字符相关的函数。 `(char? obj)` 如果obj是一个字符则返回`#t`。 `(char=? c1 c3)` 如果c1和c2是同一个字符的话则返回`#t`。 `(char->integer c)` 将c转化为对应的整数（字符代码，character code）。示例：`(char->integer #\a) => 97` `(integer->char n)` 该函数将一个整数转化为对应的字符。 `(char<? c1 c2)` `(char<= c1 c2)` `(char> c1 c2)` `(char>= c1 c2)` 这些函数用于比较字符。实际上，这些函数比较的是字符代码的大小。例如，`(char<? c1 c2)`等同于`(< (char->integer c1) (char->integer c2))` `(char-ci=? c1 c2)` `(char-ci<? c1 c2)` `(char-ci<=? c1 c2)` `(char-ci>? c1 c2)` `(char-ci>=? c1 c2)` 这些比较函数对大小写不敏感。 `(char-alphabetic? c)` `(char-numeric? c)` `(char-whitespace? c)` `(char-upper-case? c)` `(char-lower-case? c)` 这些函数分别用于检测字符c是否为字母、数字、空白符、大写字母或小写字母。 `(char-upcase c)` `(char-downcase c)` 这些函数分别返回字符C对应的大写或小写。 ## 11.3 字符串 字符串通过两个闭合的双引号表示。例如，”abc”表示字符串abc。R5RS定义了下面的函数。 `(string? s)` 如果`s`是一个字符则返回`#t`。 `(make-string n c)` 返回由`n`个字符`c`组成的字符串。参数`c`可选。 `(string-length s)` 返回字符串`s`的长度。 `(string=? s1 s2)` 如果字符串`s1`和`s2`相同的话则返回`#t`。 `(string-ref s idx)` 返回字符串`s`中索引为`idx`的字符（索引从0开始计数）。 `(string-set! s idx c)` 将字符串`s`中索引为`idx`的字符设置为`c`。 `(substring s start end)` 返回字符串`s`从`start`开始到`end-1`处的子串。例如`(substring "abcdefg" 1 4) => "b c d"` `(string-append s1 s2 ...)` 连接两个字符串`s1`和`s2` `(string->list s)` 将字符串`s`转换为由字符构成的表。 `(list->string ls)` 将一个由字符构成的表转换为字符串。 `(string-copy s)` 复制字符串`s`。 > 练习1 > > 编写一个函数`title-style`，该函数用于将每个单词的首字母大写。 > > > > > > ~~~ > (title-style "the cathedral and the bazaar") > ;⇒ "The Cathedral And The Bazaar" > ~~~ > > > > ## 11.4 小结 本章讲解了字符和字符串。下章我将讲解符号。符号是Lisp/Scheme中的一种字符型数据类型。使用这种数据类型，可以对文本进行快速操作。 ## 11.5 习题解答 ### 11.5.1 练习1 先将字符串转化为表，将空格之后的字符大写，最后将表转换会字符串。【译注：原文似有误。】 ~~~ (define (identity x) x) (define (title-style str) (let loop ((ls (string->list str)) (w #t) (acc '())) (if (null? ls) (list->string (reverse acc)) (let ((c (car ls))) (loop (cdr ls) (char-whitespace? c) (cons ((if w char-upcase identity) c) acc)))))) ;;; Another answer, You can assign caps to the string. (define (title-style str) (let ((n (string-length str))) (let loop ((w #t) (i 0)) (if (= i n) str (let ((c (string-ref str i))) (if w (string-set! str i (char-upcase c))) (loop (char-whitespace? c) (1+ i))))))) (title-style "the cathedral and the bazaar") ;⇒ "The Cathedral And The Bazaar" ~~~

[TOC=2] ## 10.1 简介 因为Scheme是函数式语言，通常来说，你可以编写不使用赋值的语句。然而，如果使用赋值的话，有些算法就可以轻易实现了。尤其是内部状态和**继续（continuations ）**需要赋值。 尽管赋值非常习见并且易于理解，但它有一些本质上的缺陷。参见《计算机程序的构造和解释》的第三章第一节“赋值和局部状态”以及《为什么函数式编程如此重要》 R5RS中规定的用于赋值的特殊形式是`set!`、`set-car!`、`set-cdr!`、`string-set!`、`vector-set!`等。除此之外，有些实现也依赖于赋值。由于赋值改变了参数的值，因此它具有**破坏性（destructive）**。Scheme中，具有破坏性的方法都以`!`结尾，以警示程序员。 ## 10.2 set! `set!`可以为一个参数赋值。与Common Lisp不同，`set!`无法给一个S-表达式赋值。 赋值前参数应被定义。 ~~~ (define var 1) (set! var (* var 10)) var ⇒ 10 (let ((i 1)) (set! i (+ i 3)) i) ⇒ 4 ~~~ ## 10.3 赋值和内部状态 ### 10.3.1 静态作用域（词法闭包） Scheme中变量的作用域被限定在了源码中定义其的那个括号里。作用域与源代码书写方式一致的作用域称为**“词法闭包（Lexical closure）”**或**“静态作用域（Static scope）”**。This way of scope eliminates bags, as you can grasp the scope of parameters quite easily — written on the source code.另一方面，还有一种被称为**“动态作用域（Dynamic scope）”**的作用域。这种作用域仅在程序运行时确定。由于会在调试时带来种种问题，这种作用域现在已经不再使用。 特殊形式`let`、`lambda`、`letrec`生成闭包。lambda表达式的参数仅在函数定义内部有效。`let`只是`lambda`的语法糖，因此二者无异。 ### 10.3.2 使用赋值和词法闭包来实现内部状态 你可以使用词法闭包来实现带有内部状态的过程。例如，用于模拟银行账户的过程可以按如下的方式编写：初始资金是10美元。函数接收一个整形参数。正数表示存入，负数表示取出。为了简单起见，这里允许存款为负数。 ~~~ (define bank-account (let ((balance 10)) (lambda (n) (set! balance (+ balance n)) balance))) ~~~ 该过程将存款赋值为`(+ balance n)`。下面是调用这个过程的结果。 The procedure assigns (+ balance n) to the balance. 
Following is the result of calling this function. ~~~ (bank-account 20) ; donating 20 dollars ;Value: 30 (bank-account -25) ; withdrawing 25 dollars ;Value: 5 ~~~ 因为在Scheme中，你可以编写返回过程的过程，因此你可以编写一个创建银行账户的函数。这个例子喻示着使用函数式程序设计语言可以很容易实现面向对象程序设计语言。实际上，只需要在这个基础上再加一点东西就可以实现一门面向对象程序设计语言了。 ~~~ (define (make-bank-account balance) (lambda (n) (set! balance (+ balance n)) balance)) (define gates-bank-account (make-bank-account 10)) ; Gates makes a bank account by donating 10 dollars ;Value: gates-bank-account (gates-bank-account 50) ; donating 50 dollars ;Value: 60 (gates-bank-account -55) ; withdrawing 55 dollars ;Value: 5 (define torvalds-bank-account (make-bank-account 100)) ; Torvalds makes a bank account by donating 100 dollars ;Value: torvalds-bank-account (torvalds-bank-account -70) ; withdrawing 70 dollars ;Value: 30 (torvalds-bank-account 300) ; donating 300 dollars ;Value: 330 ~~~ ### 10.3.3 副作用 Scheme过程的主要目的是返回一个值，而另一个目的则称为**副作用（Side Effect）**。赋值和IO操作就是副作用。 > 练习 1 > > 修改make-bank-account函数 Modify make-bank-account so that withdrawing more than balance causes error.
> hint: Use begin to group more than one S-expressions. ## 10.4 表的破坏性操作（set-car!，set-cdr!） 函数set-cat!和set-cdr!分别为一个cons单元的car部分和cdr部分赋新值。和set!不同，这两个操作可以为S-表达式赋值。 ~~~ (define tree '((1 2) (3 4 5) (6 7 8 9))) (set-car! (car tree) 100) ; changing 1 to 100 tree ((100 2) (3 4 5) (6 7 8 9)) (set-cdr! (third tree) '(a b c)) ; changing '(7 8 9) to '(a b c) tree ⇒ ((100 2) (3 4 5) (6 a b c)) ~~~ ### 10.4.1 队列 队列可以用set-car!和set-cdr!实现。队列是一种**先进先出(First in first out, FIFO)**的数据结构，表则是**先进后出(First in last out，FILO)**。图表1展示了队列的结构。`cons-cell-top`的car部分指向表（头），而（`cons-cell-top`的）cdr部分指向表末的cons单元（表尾）。 入队操作按如下步骤进行（见图表2）： 1\. 将当前最末的cons单元（可以通过`cons-cell-top`取得）的cdr部分重定向到新的元素。 2\. 将`cons-cell-top`的cdr部分重定向到新的元素 出队操作按如下步骤进行（见图表3） 1\. 将队首元素存放在一个局部变量里。 2\. 将`cons-cell-top`的car部分重定向到表的第二个元素 [代码片段1]展示了如何实现队列。函数enqueue!返回将元素obj添加进队列queue后的队列。函数dequeue!将队列的首元素移出队列并将该元素的值作为返回值。 [代码片段1] 队列的Scheme实现 ~~~ (define (make-queue) (cons '() '())) (define (enqueue! queue obj) (let ((lobj (cons obj '()))) (if (null? (car queue)) (begin (set-car! queue lobj) (set-cdr! queue lobj)) (begin (set-cdr! (cdr queue) lobj) (set-cdr! queue lobj))) (car queue))) (define (dequeue! queue) (let ((obj (car (car queue)))) (set-car! queue (cdr (car queue))) obj)) (define q (make-queue)) ;Value: q (enqueue! q 'a) ;Value 12: (a) (enqueue! q 'b) ;Value 12: (a b) (enqueue! q 'c) ;Value 12: (a b c) (dequeue! q) ;Value: a q ;Value 13: ((b c) c) ~~~ ## 10.5 小结 这一章中，我讲解了赋值和变量的作用域。虽然在Scheme中，赋值并不常用，但它对于某些算法和数据结构来说是必不可少的。滥用赋值会让你的代码丑陋。当万不得已时才使用赋值！在后面的几章里，我会介绍Scheme中的数据结构。 ## 10.6 习题解答 ### 10.6.1 练习1 ~~~ (define (make-bank-account amount) (lambda (n) (let ((m (+ amount n))) (if (negative? m) 'error (begin (set! amount m) amount))))) ~~~

[TOC=2] ## 9.1 简介 通过前面章节的学习，你已经可以在Scheme的交互式前端中编写并执行程序了。在本章中，我讲介绍如何输入和输出。使用这个特性，你可以从文件中读取数据或向文件中写入数据。 ## 9.2 从文件输入 ### open-input-file，read-char和eof-object? 函数`(open-input-file filename)`可以用于打开一个文件。此函数返回一个用于输入的端口。函数`(read-char port)`用于从端口中读取一个字符。当读取到**文件结尾（EOF）**时，此函数返回`eof-object`，你可以使用`eof-object?`来检查。函数`(close-input-port port)`用于关闭输入端口。[代码片段1]展示了一个函数，该函数以字符串形式返回了文件内容。 [代码片段1] 以字符串的形式返回文件内容 ~~~ (define (read-file file-name) (let ((p (open-input-file file-name))) (let loop((ls1 '()) (c (read-char p))) (if (eof-object? c) (begin (close-input-port p) (list->string (reverse ls1))) (loop (cons c ls1) (read-char p)))))) ~~~ 比如，在[范例1]中展示的结果就是将[代码片段1]应用于文件hello.txt。由于换行符是由`'\n'`表示的，这就很容易阅读。然而，像格式化输出[范例2]，我们也可使用`display`函数。 [文件]hello.txt ~~~ Hello world! Scheme is an elegant programming language. ~~~ [范例1] ~~~ (cd "C:\\doc") (read-file "hello.txt") ;Value 14: "Hello world!\nScheme is an elegant programming language.\n" ~~~ [范例2] ~~~ (display (read-file "hello.txt")) Hello world! Scheme is an elegant programming language. ;Unspecified return value ~~~ ### 9.2.2 语法call-with-input-file和with-input-from-file 你通过使用语法`call-with-input-file`和`with-input-from-file`来打开文件以供读取输入。这些语法是非常方便的，因为它们要处理错误。 > `(call-with-input-file filename procedure)` > > 该函数将名为`filename`的文件打开以供读取输入。函数`procedure`接受一个输入端口作为参数。文件有可能再次使用，因此当`procedure`结束时文件不会自动关闭，文件应该显式地关闭。[代码片段1]可以按照[代码片段2]那样用`call-with-input-file`编写。 [代码片段2] call-with-input-file版本 ~~~ (define (read-file file-name) (call-with-input-file file-name (lambda (p) (let loop((ls1 '()) (c (read-char p))) (if (eof-object? c) (begin (close-input-port p) (list->string (reverse ls1))) (loop (cons c ls1) (read-char p))))))) ~~~ > `(with-input-from-file filename procedure)` 该函数将名为`filename`的文件作为标准输入打开。函数`procedure`不接受任何参数。当`procedure`退出时，文件自动被关闭。[代码片段3]展示了如何用`with-input-from-file`来重写[代码片段1]。 [代码片段3] with-input-from-file版本 ~~~ (define (read-file file-name) (with-input-from-file file-name (lambda () (let loop((ls1 '()) (c (read-char))) (if (eof-object? c) (list->string (reverse ls1)) (loop (cons c ls1) (read-char))))))) ~~~ ### 9.2.3 read 函数`(read port)`从端口`port`中读入一个S-表达式。用它来读诸如”paren.txt”中带括号的内容就很方便。 ~~~ '(Hello world! Scheme is an elegant programming language.) '(Lisp is a programming language ready to evolve.) ~~~ [代码片段4] ~~~ (define (s-read file-name) (with-input-from-file file-name (lambda () (let loop ((ls1 '()) (s (read))) (if (eof-object? s) (reverse ls1) (loop (cons s ls1) (read))))))) ~~~ 下面展示了用`s-read`读取”paren.txt”的结果。 ~~~ (s-read "paren.txt") ⇒ ((quote (hello world! scheme is an elegant programming language.)) (quote (lisp is a programming language ready to evolve.))) ~~~ > 练习1 > > 编写函数`(read-lines)`，该函数返回一个由字符串构成的表，分别代表每一行的内容。在Scheme中，换行符是由`#\Linefeed`表示。下面演示了将该函数用于”hello.txt”的结果。 > > `(read-lines "hello.txt") ⇒ ("Hello world!" "Scheme is an elegant programming language.")` ## 9.3 输出至文件 ### 9.3.1 打开一个用于输出的port 输出有和输入类似的函数，比如： `(open-output-file filename)` 该函数打开一个文件用作输出，放回该输出端口。 `(close-output-port port)` 关闭用于输出的端口。 `(call-with-output-file filename procedure)` 打开文件`filename`用于输出，并调用过程`procedure`。该函数以输出端口为参数。 `(with-output-to-file filename procedure)` 打开文件`filename`作为标准输出，并调用过程`procedure`。该过程没有参数。当控制权从过程`procedure`中返回时，文件被关闭。 ### 9.3.2 用于输出的函数 下面的函数可用于输出。如果参数`port`被省略的话，则输出至标准输出。 `(write obj port)` 该函数将`obj`输出至`port`。字符串被双引号括起而字符具有前缀`#\`。 `(display obj port)` 该函数将`obj`输出至`port`。字符串*不被*双引号括起而字符*不*具有前缀`#\`。 `(newline port)` 以新行起始。 `(write-char char port)` 该函数向`port`写入一个字符。 > 练习2 > > 编写函数`(my-copy-file)`实现文件的拷贝。 > 练习3 > > 编写函数`(print-line)`，该函数具有任意多的字符作为参数，并将它们输出至标准输出。输出的字符应该用新行分隔。 ## 9.4 小结 因为Scheme的IO设施非常的小，所以本章也十分短。下一章中，我会讲解赋值。 ## 9.5 习题解答 ### 9.5.1 答案1 ~~~ (define (group-list ls sep) (letrec ((iter (lambda (ls0 ls1) (cond ((null? ls0) (list ls1)) ((eqv? (car ls0) sep) (cons ls1 (iter (cdr ls0) '()))) (else (iter (cdr ls0) (cons (car ls0) ls1))))))) (map reverse (iter ls '())))) (define (read-lines file-name) (with-input-from-file file-name (lambda () (let loop((ls1 '()) (c (read-char))) (if (eof-object? c) (map list->string (group-list (reverse ls1) #\Linefeed)) ; * (loop (cons c ls1) (read-char))))))) ~~~ 示例： ~~~ (group-list '(1 4 0 3 7 2 0 9 5 0 0 1 2 3) 0) ;Value 13: ((1 4) (3 7 2) (9 5) () (1 2 3)) (read-lines "hello.txt") ;Value 14: ("Hello world!" "Scheme is an elegant programming language." "") ~~~ ### 9.5.2 答案2 ~~~ (define (my-copy-file from to) (let ((pfr (open-input-file from)) (pto (open-output-file to))) (let loop((c (read-char pfr))) (if (eof-object? c) (begin (close-input-port pfr) (close-output-port pto)) (begin (write-char c pto) (loop (read-char pfr))))))) ~~~ ### 9.5.3 答案3 ~~~ (define (print-lines . lines) (let loop((ls0 lines)) (if (pair? ls0) (begin (display (car ls0)) (newline) (loop (cdr ls0)))))) ~~~

[TOC=2] ## 8.1 简介 **高阶函数（Higher Order Function）**是一种以函数为参数的函数。它们都被用于**映射（mapping）**、**过滤（filtering）**、**归档（folding）**和**排序（sorting）**表。高阶函数提高了程序的模块性。编写对各种情况都适用的高阶函数与为单一情况编写递归函数相比，可以使程序更具可读性。比如说，使用一个高阶函数来实现排序可以使得我们使用不同的条件来排序，这就将排序条件和排序过程清楚地划分开来。函数`sort`具有两个参数，其一是一个待排序的表，其二是**定序（Ordering）**函数。下面展示了按照大小将一个整数表正序排序。`<`函数就是（本例中的）两数的定序函数。 ~~~ (sort '(7883 9099 6729 2828 7754 4179 5340 2644 2958 2239) <) ;⇒ (2239 2644 2828 2958 4179 5340 6729 7754 7883 9099) ~~~ 另一方面，按照每个数末两位的大小排序可以按下面的方式实现： ~~~ (sort '(7883 9099 6729 2828 7754 4179 5340 2644 2958 2239) (lambda (x y) (< (modulo x 100) (modulo y 100)))) ;⇒ (2828 6729 2239 5340 2644 7754 2958 4179 7883 9099) ~~~ 正如这里所演示的，像**快速排序（Quick Sort）**、**归并排序（Merge Sort）**等排序过程，将定序函数完全分离开来提高了代码的复用性。 在本节中，我将讲解预定义的高阶函数，然后介绍如何定义高阶函数。由于Scheme并不区别过程和其它的数据结构，因此你可以通过将函数当作参数传递轻松的定义自己的高阶函数。 实际上，Scheme中预定义函数的本质就是高阶函数，因为Scheme并没有定义块结构的语法，因此使用`lambda`表达式作为一个块。 ## 8.2 映射 映射是将同样的行为应用于表所有元素的过程。R5RS定义了两个映射过程：其一为返回转化后的表的`map`过程，另一为注重副作用的`for-each`过程。 ### 8.2.1 map `map`过程的格式如下： ~~~ (map procedure list1 list2 ...) ~~~ `procedure`是个与某个过程或`lambda`表达式相绑定的符号。作为参数的表的个数视`procedure`需要的参数而定。 例： ~~~ ; Adding each item of '(1 2 3) and '(4 5 6). (map + '(1 2 3) '(4 5 6)) ;⇒ (5 7 9) ; Squaring each item of '(1 2 3) (map (lambda (x) (* x x)) '(1 2 3)) ;⇒ (1 4 9) ~~~ ### 8.2.2 for-each `for-each`的格式与`map`一致。但`for-each`并不返回一个具体的值，只是用于副作用。 例： ~~~ (define sum 0) (for-each (lambda (x) (set! sum (+ sum x))) '(1 2 3 4)) sum ;⇒ 10 ~~~ > 练习1 > > 用`map`编写下面的函数： > > 1. 一个将表中所有元素翻倍的函数； > 2. 一个将两个表中对应位置元素相减的函数； ## 8.3 过滤 尽管过滤函数并没有在R5RS中定义，但MIT-Scheme实现提供了`keep-matching-items`和`delete-matching-item`两个函数。其它实现中应该有类似的函数。 ~~~ (keep-matching-items '(1 2 -3 -4 5) positive?) ;⇒ (1 2 5) ~~~ > 练习2 > > 编写下列函数： > > 1. **滤取（Filtering Out）**出一个表中的偶数； > 2. 滤取出不满足`10 ≤ x ≤ 100`的数； ## 8.4 归档 尽管在R5RS中没有定义归档函数，但MIT-Scheme提供了`reduce`等函数。 ~~~ (reduce + 0 '(1 2 3 4)) ;⇒ 10 (reduce + 0 '(1 2)) ;⇒ 3 (reduce + 0 '(1)) ;⇒ 1 (reduce + 0 '()) ;⇒ 0 (reduce + 0 '(foo)) ;⇒ foo (reduce list '() '(1 2 3 4)) ;⇒ (((1 2) 3) 4) ~~~ > 练习3 > > 1. 编写一个将表中所有元素平方的函数，然后求取它们的和，最后求和的平方根。 ## 8.5 排序 尽管R5RS中没有定义排序函数，但MIT-Scheme提供了`sort`（实为`merge-sort`实现）和`quick-sort`函数。 ~~~ (sort '(3 5 1 4 -1) <) ;⇒ (-1 1 3 4 5) ~~~ > 练习4 > > 编写下列函数 > > 1. 以`sin(x)`的大小升序排序； > 2. 以表长度降序排序； ## 8.6 apply函数 `apply`函数是将一个过程应用于一个表（译注：将表展开，作为过程的参数）。此函数具有任意多个参数，但首参数和末参数分别应该是一个过程和一个表。虽然乍看之下不然，但这个函数的确非常方便。 ~~~ (apply max '(1 3 2)) ;⇒ 3 (apply + 1 2 '(3 4 5)) ;⇒ 15 (apply - 100 '(5 12 17)) ;⇒ 66 ~~~ > 练习5 > > 用`apply`编写练习3中的函数。 ## 8.7 编写高阶函数 自己编写高阶函数非常容易。这里用`member-if`、`member`和`fractal`演示。 ### 8.7.1 member-if和member `member-if`函数使用一个谓词和一个表作为参数，返回一个子表，该子表的`car`部分即是原列表中首个满足该谓词的元素。`member-if`函数可以像下面这样定义： ~~~ (define (member-if proc ls) (cond ((null? ls) #f) ((proc (car ls)) ls) (else (member-if proc (cdr ls))))) (member-if positive? '(0 -1 -2 3 5 -7)) ;⇒ (3 5 -7) ~~~ 接下来，`member`函数检查特定元素是否在表中，该函数编写如下。函数需要三个参数，其一为用于比较的函数，其二为特定项，其三为待查找表。 ~~~ (define (member proc obj ls) (cond ((null? ls) #f) ((proc obj (car ls)) ls) (else (member proc obj (cdr ls))))) (member string=? "hello" '("hi" "guys" "bye" "hello" "see you")) ;⇒ ("hello" "see you") ~~~ ### 8.7.2 不规则曲线 生成像C曲线、龙曲线等不规则曲线可以通过在两个点中插入一个点来实现 which are generated by inserting a point(s) between two points according to a positioning function can be separated into two parts: a common routine to generate fractal curves and a positioning function. 。代码实现如下： ~~~ ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; ;;; frac.scm ;;; ;;; draw fractal curves ;;; by T.Shido ;;; on August 20, 2005 ;;; ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; ;;; 平面直角坐标系上的点通过序对来表示，其中car部分和cdr部分分别代表 ;;; x坐标和y坐标。 ;;; 函数_x和_y用来取得坐标，point用来建立一个点。 (define _x car) (define _y cdr) (define point cons) ;;; (rappend ls0 ls1) ;;; (rappend '(1 2 3) '(4 5 6)) -> (3 2 1 4 5 6) ;;; ;;; 接受两个表作为参数，将第一个表反转后与第二个表连接起来。 (define (rappend ls0 ls1) (let loop((ls0 ls0) (ls1 ls1)) (if (null? ls0) ls1 (loop (cdr ls0) (cons (car ls0) ls1))))) ;;; (devide p1 p2 r) ;;; dividing p1 and p2 internally by the ratio r. (define (divide p1 p2 r) (point (+ (* r (_x p1)) (* (- 1.0 r) (_x p2))) (+ (* r (_y p1)) (* (- 1.0 r) (_y p2))))) ;;; (print-curve points fout) ;;; 将点输出至文件。将一系列点points按一行一个点得格式输出至fout代 ;;; 表的文件 (define (print-curve points fout) (with-output-to-file fout (lambda () (for-each (lambda (p) (display (_x p)) (display " ") (display (_y p)) (newline)) points)))) ;;; (fractal proc n points fout) ;;; 创建分型图形的高阶函数。其中，proc是定位函数，n是重复次数， ;;; points是初始点构成的表，fout是输出文件的文件名。 ;;; 函数由两个叫做loop和iter的循环构成。loop对数据表做n次插入。 ;;; The iter adds new points to the data list using the positioning function. In short, fractal generates curves by repeating iter for n times. The positioning function proc takes two points as arguments and returns a list of the first point and the interpolated point. (define (fractal proc n points fout) (let loop ((i 0) (points points)) (if (= n i) (print-curve points fout) (loop (1+ i) (let iter ((points points) (acc '())) (if (null? (cdr points)) (reverse! (cons (car points) acc)) (iter (cdr points) (rappend (proc (first points) (second points)) acc))))))) 'done) ;;; (c-curve p1 p2) ;;; C-曲线的定位函数 (define (c-curve p1 p2) (let ((p3 (divide p1 p2 0.5))) (list p1 (point (+ (_x p3) (- (_y p3) (_y p2))) (+ (_y p3) (- (_x p2) (_x p3))))))) ;;; (dragon-curve p1 p2) ;;; 龙曲线的定位函数 (define dragon-curve (let ((n 0)) (lambda (p1 p2) (let ((op (if (even? n) + -)) (p3 (divide p1 p2 0.5))) (set! n (1+ n)) (list p1 (point (op (_x p3) (- (_y p3) (_y p2))) (op (_y p3) (- (_x p2) (_x p3))))))))) ;;; (koch p1 p2) ;;; Koch曲线的定位函数 (define (koch p1 p2) (let ((p3 (divide p1 p2 2/3)) (p4 (divide p1 p2 1/3)) (p5 (divide p1 p2 0.5)) (c (/ (sqrt 3) 2))) (list p1 p3 (point (- (_x p5) (* c (- (_y p4) (_y p3)))) (+ (_y p5) (* c (- (_x p4) (_x p3))))) p4))) ~~~ 下面的代码演示了如何生成分型曲线。源代码在这里。使用之前请先编译，以节省计算时间。 ~~~ (compile-file "frac.scm") (load "frac") ;; C-Curve (fractal c-curve 14 '((0 . 0) (2 . 3)) "c14.dat") ;Value: done ;; Dragon-Curve (fractal dragon-curve 14 '((0 . 0) (1 . 0)) "d14.dat") ;Value: done ;; Koch-Curve (fractal koch 5 '((0 . 0) (1 . 0)) "k5.dat") ;Value: done ~~~ X坐标和Y坐标都存储在名字形如`*.dat`的文件中。你可以使用你喜欢的制图程序来绘制。图表1-3都是用gnuplot绘制的。 > 练习 6 > > 1. 自己实现`keep-matching-items`。 > 2. 自己实现`map`。接受不止一个表作为参数可能有点困难。剩余的参数是通过带点得序对`(.)`来定义的。其`cdr`部分以表的形式传递给函数。 例: my-list `scheme (define (my-list . x) x) `多说一句，你需要`apply`函数。 ## 8.8 小结 本章中，我讲解了高阶函数。正如在生成分形图形体现的那样，高阶函数增强了模块化成都。你可以很容易地定义高阶函数。当你编写函数时，更要在乎将其实现为更抽象的高阶函数，这样可以让你的代码能够**复用（reusable）**。 在下一章节中，我会介绍IO。 ## 8.9 习题解答 ### 8.9.1 答案1 ~~~ ; 1 (define (double ls) (map (lambda (x) (* x 2)) ls)) ; 2 (define (sub ls1 ls2) (map - ls1 ls2)) ~~~ ### 8.9.2 答案2 ~~~ ; 1 (define (filter-even ls) (keep-matching-items ls even?)) ; 2 (define (filter-10-100 ls) (keep-matching-items ls (lambda (x) (<= 10 x 100)))) ~~~ ### 8.9.3 答案3 ~~~ (define (sqrt-sum-sq ls) (sqrt (reduce + 0 (map (lambda (x) (* x x)) ls)))) ~~~ ### 8.9.4 答案4 ~~~ ; 1 (define (sort-sin ls) (sort ls (lambda (x y) (< (sin x) (sin y))))) ; 2 (define (sort-length ls) (sort ls (lambda (x y) (> (length x) (length y))))) ~~~ ### 8.9.5 答案5 ~~~ (define (sqrt-sum-sq-a ls) (sqrt (apply + (map (lambda (x) (* x x)) ls)))) ~~~ ### 8.9.6 答案6 ~~~ ; 1 (define (my-keep-matching-items ls fn) (cond ((null? ls) '()) ((fn (car ls)) (cons (car ls) (my-keep-matching-items (cdr ls) fn))) (else (my-keep-matching-items (cdr ls) fn)))) ; 2 (define (my-map fun . lss) (letrec ((iter (lambda (fun lss) (if (null? lss) '() (cons (fun (car lss)) (iter fun (cdr lss)))))) (map-rec (lambda (fun lss) (if (memq '() lss) '() (cons (apply fun (iter car lss)) (map-rec fun (iter cdr lss))))))) (map-rec fun lss))) (my-map + '(1 2 3) '(10 20 30) '(100 200 300)) ;⇒ (111 222 333) ~~~

[TOC=2] ## 7.1 简介 本章中我会介绍重复。通过重复，你可以编写“通常的”程序。虽然也可以使用`do`表达式，但Scheme中通常通过递归实现重复。 ## 7.2 递归 在自己的定义中调用自己的函数叫做**递归函数（Recursive Function）**。虽然这听起来很奇怪，但是循环的常见方法。If you have an analogy comparing functions to machines, recursion makes no sense. 然而，正因为函数式过程，函数调用自己是有意义的。比如说，让我们来考察一下文献调研吧。你可能需要去阅读你正在阅读的文献所引用的文献（cited-1）。进一步，你可能还需要去阅读文件（cite-1）所引用的其它文献。这样，文献调研就是一个递归的过程，你也可以重复这个调研过程直到满足了特定条件（比如说，你累了）。Thus, an analogy that compares functions in programming languages to some kind of human activities (say, literature survey) is useful to understand recursive functions. 我们通常使用计算阶乘来解释递归。 [代码片段1] 用于计算阶乘的fact函数 ~~~ (define (fact n) (if (= n 1) 1 (* n (fact (- n 1))))) ~~~ `(fact 5)`的计算过程如下： ~~~ (fact 5) ⇒ 5 * (fact 4) ⇒ 5 * 4 * (fact 3) ⇒ 5 * 4 * 3 * (fact 2) ⇒ 5 * 4 * 3 * 2 * (fact 1) ⇒ 5 * 4 * 3 * 2 * 1 ⇒ 5 * 4 * 3 * 2 ⇒ 5 * 4 * 6 ⇒ 5 * 24 ⇒ 120 ~~~ `(fact 5)`调用`(fact 4)`，`(fact 4)`调用`(fact 3)`，最后`(fact 1)`被调用。`(fact 5)`，`(fact 4)`……以及`(fact 1)`都被分配了不同的存储空间，直到`(fact (- i 1))`返回一个值之前，`(fact i)`都会保留在内存中，由于存在函数调用的开销，这通常会占用更多地内存空间和计算时间。 然而，递归函数可以以一种简单的方式表达重复。表是被递归定义的，进而表和递归函数可以很好地配合。例如，一个让表中所有元素翻倍的函数可以像下面这样写。如果参数是空表，那么函数应该停止计算并返回一个空表。 ~~~ (define (list*2 ls) (if (null? ls) '() (cons (* 2 (car ls)) (list*2 (cdr ls))))) ~~~ > 练习1 > > 用递归编写下面的函数。 > > 1. 用于统计表中元素个数的`my-length`函数。（`length`是一个预定义函数）。 > 2. 一个求和表中元素的函数。 > 3. 一个分别接受一个表`ls`和一个对象`x`的函数，该函数返回从`ls`中删除`x`后得到的表。 > 4. 一个分别接受一个表`ls`和一个对象`x`的函数，该函数返回`x`在`ls`中首次出现的位置。索引从`0`开始。如果`x`不在`ls`中，函数返回`#f`。 ## 7.3 尾递归 普通的递归调用并不高效因为它既浪费存储空间又具有函数调用开销。与之相反，尾递归函数包含了计算结果，当计算结束时直接将其返回。特别地，由于Scheme规范要求尾递归调用转化为循环，因此尾递归调用就不存在函数调用开销。 [代码片段2]展示了[代码片段1]中函数`fact`的尾递归版本。 [代码片段2] fact函数的尾递归版本fact-tail ~~~ (define (fact-tail n) (fact-rec n n)) (define (fact-rec n p) (if (= n 1) p (let ((m (- n 1))) (fact-rec m (* p m))))) ~~~ `fact-tail`计算阶乘的过程像这样： ~~~ (fact-tail 5) ⇒ (fact-rec 5 5) ⇒ (fact-rec 4 20) ⇒ (fact-rec 3 60) ⇒ (fact-rec 2 120) ⇒ (fact-rec 1 120) ⇒ 120 ~~~ 因为`fact-rec`并不等待其它函数的计算结果，因此当它计算结束时即从内存中释放。计算通过修改`fact-rec`的参数来演进，这基本上等同于循环。如上文所述，Scheme将尾递归转化为循环，Scheme就无需提供循环的语法来实现重复。 > 练习2 > > 用尾递归编写下面的函数 > > 1. 用于翻转表元素顺序的`my-reverse`函数。（`reverse`函数是预定义函数） > 2. 求和由数构成的表。 > 3. 将一个代表正整数的字符串转化为对应整数。例如，”1232”会被转化为1232。不需要检查不合法的输入。提示，字符到整数的转化是通过将字符#\0……#\9的ASCII减去48，可以使用函数`char->integer`来获得字符的ASCII码。函数`string->list`可以将字符串转化为由字符构成的表。 ## 7.4 命名let 命名`let`（**named let**）可以用来表达循环。[代码片段3]中的函数`fact-let`展示了如何使用命名`let`来计算阶乘。`fact-let`函数使用了一个**命名`let`表达式**`(loop)`，这与在[代码片段2]中展示的`fact-rec`函数是不同的。在被注释为`;1`的那行，代码将参数`n1`和`p`都初始化为`n`。再每次循环后，参数在被注释为`;2`的那行更新：将`n1`减1，而将`p`乘以`(n1 - 1)`。 在Scheme中，用命名`let`来表达循环是俗成的方法。 [代码片段3] fact-let的实现 ~~~ (define (fact-let n) (let loop((n1 n) (p n)) ; 1 (if (= n1 1) p (let ((m (- n1 1))) (loop m (* p m)))))) ; 2 ~~~ > 练习3 > > 用命名`let`编写下面的函数。 > > 1. 练习1的问题3和问题4； > 2. 练习2中的函数； > 3. `range`函数：返回一个从`0`到`n`的表（但不包含`n`）。 ## 7.5 letrec `letrec`类似于`let`，但它允许一个名字递归地调用它自己。语法`letrec`通常用于定义复杂的递归函数。[代码片段4]展示了`fact`函数的`letrec`版本。 [代码片段4] fact函数的letrec版本 ~~~ (define (fact-letrec n) (letrec ((iter (lambda (n1 p) (if (= n1 1) p (let ((m (- n1 1))) (iter m (* p m))))))) ; * (iter n n))) ~~~ 正如被注释为`;*`的那行代码所示，局部变量`iter`可以在它的定义里面引用它自己。语法`letrec`是定义局部变量的俗成方式。 > 练习4 > > 用`letrec`重写练习2。 ## 7.6 do表达式 虽然并不常见，但语法`do`也可用于表达重复。它的格式如下： ~~~ (do binds (predicate value) body) ~~~ 变量在`binds`部分被绑定，而如果`predicate`被求值为真，则函数从循环中**逃逸（escape）**出来，并返回值`value`，否则循环继续进行。 `binds`部分的格式如下所示： ~~~ [binds] → ((p1 i1 u1) (p2 i2 u2) ... ) ~~~ 变量`p1`，`p2`，…被分别初始化为`i1`，`i2`，…并在循环后分别被更新为`u1`，`u2`，…。 [代码片段5]演示了`fact`的`do`表达式版本。 [代码片段5] fact函数的do表达式版本 ~~~ (define (fact-do n) (do ((n1 n (- n1 1)) (p n (* p (- n1 1)))) ((= n1 1) p))) ~~~ 变量`n1`和`p`分别被初始化为`n`和`n`，在每次循环后分别被减去1和乘以`(n1 - 1)`。当`n1`变为`1`时，函数返回`p`。 我认为`do`比命名`let`还要复杂一些。 > 练习5 > > 用`do`表达式重写练习2。 ## 7.7 小结 现在你可以用我讲解过的技巧来编写常见程序了。通常来说，命名`let`用于编写简单的循环，而`letrec`则是用来写复杂的局部递归函数。 下一章中我讲讲解高阶函数。高阶函数使得你的代码更加“Scheme风味”。 ## 7.8 习题解答 ### 7.8.1 练习1 ~~~ ; 1 (define (my-length ls) (if (null? ls) 0 (+ 1 (my-length (cdr ls))))) ; 2 (define (my-sum ls) (if (null? ls) 0 (+ (car ls) (my-sum (cdr ls))))) ; 3 (define (remove x ls) (if (null? ls) '() (let ((h (car ls))) ((if (eqv? x h) (lambda (y) y) (lambda (y) (cons h y))) (remove x (cdr ls)))))) ; 4 (define (position x ls) (position-aux x ls 0)) (define (position-aux x ls i) (cond ((null? ls) #f) ((eqv? x (car ls)) i) (else (position-aux x (cdr ls) (1+ i))))) ~~~ ### 7.8.2 练习2 ~~~ ; 1 (define (my-reverse ls) (my-reverse-rec ls ())) (define (my-reverse-rec ls0 ls1) (if (null? ls0) ls1 (my-reverse-rec (cdr ls0) (cons (car ls0) ls1)))) ;------------------- ; 2 (define (my-sum-tail ls) (my-sum-rec ls 0)) (define (my-sum-rec ls n) (if (null? ls) n (my-sum-rec (cdr ls) (+ n (car ls))))) ;-------------------- ; 3 (define (my-string->integer str) (char2int (string->list str) 0)) (define (char2int ls n) (if (null? ls) n (char2int (cdr ls) (+ (- (char->integer (car ls)) 48) (* n 10)))) ~~~ ### 7.8.3 练习3 ~~~ ; 1 (define (remove x ls) (let loop((ls0 ls) (ls1 ())) (if (null? ls0) (reverse ls1) (loop (cdr ls0) (if (eqv? x (car ls0)) ls1 (cons (car ls0) ls1)))))) ; 2 (define (position x ls) (let loop((ls0 ls) (i 0)) (cond ((null? ls0) #f) ((eqv? x (car ls0)) i) (else (loop (cdr ls0) (1+ i)))))) ; 3 (define (my-reverse-let ls) (let loop((ls0 ls) (ls1 ())) (if (null? ls0) ls1 (loop (cdr ls0) (cons (car ls0) ls1))))) ; 4 (define (my-sum-let ls) (let loop((ls0 ls) (n 0)) (if (null? ls0) n (loop (cdr ls0) (+ (car ls0) n))))) ; 5 (define (my-string->integer-let str) (let loop((ls0 (string->list str)) (n 0)) (if (null? ls0) n (loop (cdr ls0) (+ (- (char->integer (car ls0)) 48) (* n 10)))))) ; 6 (define (range n) (let loop((i 0) (ls1 ())) (if (= i n) (reverse ls1) (loop (1+ i) (cons i ls1))))) ~~~ ### 7.8.4 练习4 ~~~ ; 1 (define (my-reverse-letrec ls) (letrec ((iter (lambda (ls0 ls1) (if (null? ls0) ls1 (iter (cdr ls0) (cons (car ls0) ls1)))))) (iter ls ()))) ; 2 (define (my-sum-letrec ls) (letrec ((iter (lambda (ls0 n) (if (null? ls0) n (iter (cdr ls0) (+ (car ls0) n)))))) (iter ls 0))) ; 3 (define (my-string->integer-letrec str) (letrec ((iter (lambda (ls0 n) (if (null? ls0) n (iter (cdr ls0) (+ (- (char->integer (car ls0)) 48) (* n 10))))))) (iter (string->list str) 0))) ~~~ ### 7.8.5 练习5 ~~~ ; 1 (define (my-reverse-do ls) (do ((ls0 ls (cdr ls0)) (ls1 () (cons (car ls0) ls1))) ((null? ls0) ls1))) ; 2 (define (my-sum-do ls) (do ((ls0 ls (cdr ls0)) (n 0 (+ n (car ls0)))) ((null? ls0) n))) ; 3 (define (my-string->integer-do str) (do ((ls0 (string->list str) (cdr ls0)) (n 0 (+ (- (char->integer (car ls0)) 48) (* n 10)))) ((null? ls0) n))) ~~~

[TOC=2] ## 6.1 简介 在前面的章节中，我已经讲述了如何定义函数。在本节中，我讲介绍局部变量，这将会使定义函数变得更加容易。 ## 6.2 let表达式 使用`let`表达式可以定义局部变量。格式如下： ~~~ (let binds body) ~~~ 变量在`binds`定义的形式中被声明并初始化。`body`由任意多个S-表达式构成。`binds`的格式如下： ~~~ [binds] → ((p1 v1) (p2 v2) ...) ~~~ 声明了变量`p1`、`p2`，并分别为它们赋初值`v1`、`v2`。变量的**作用域（Scope）**为`body`体，也就是说变量只在`body`中有效。 > 例1：声明局部变量`i`和`j`，将它们与`1`、`2`绑定，然后求二者的和。 ~~~ (let ((i 1) (j 2)) (+ i j)) ;Value: 3 ~~~ `let`表达式可以嵌套使用。 > 例2：声明局部变量`i`和`j`，并将分别将它们与`1`和`i+2`绑定，然后求它们的乘积。 ~~~ (let ((i 1)) (let ((j (+ i 2))) (* i j))) ;Value: 3 ~~~ 由于变量的作用域仅在`body`中，下列代码会产生错误，因为在变量`j`的作用域中没有变量`i`的定义。 ~~~ (let ((i 1) (j (+ i 2))) (* i j)) ;Error ~~~ `let*`表达式可以用于引用定义在同一个绑定中的变量。实际上，`let*`只是嵌套的`let`表达式的语法糖而已。 ~~~ (let* ((i 1) (j (+ i 2))) (* i j)) ;Value: 3 ~~~ > 例3：函数`quadric-equation`用于计算二次方程。它需要三个代表系数的参数：`a`、`b`、`c` （`ax^2 + bx + c = 0`），返回一个存放答案的实数表。通过逐步地使用`let`表达式，可以避免不必要的计算。 ~~~ ;;;The scopes of variables d,e, and f are the regions with the same background colors. (define (quadric-equation a b c) (if (zero? a) 'error ; 1 (let ((d (- (* b b) (* 4 a c)))) ; 2 (if (negative? d) '() ; 3 (let ((e (/ b a -2))) ; 4 (if (zero? d) (list e) (let ((f (/ (sqrt d) a 2))) ; 5 (list (+ e f) (- e f))))))))) (quadric-equation 3 5 2) ; solution of 3x^2+5x+2=0 ;Value 12: (-2/3 -1) ~~~ > 这个函数的行为如下： > > 1. 如果二次项系数`a`为`0`，函数返回`'error`。 > 2. 如果`a ≠ 0`，则将变量`d`与判别式`(b^2 - 4ac)`的值绑定。 > 3. 如果`d`为负数，则返回`'()`。 > 4. 如果`d`不为负数，则将变量`e`与`-b/2a`绑定。 > 5. 如果`d`为`0`，则返回一个包含`e`的表。 > 6. 如果`d`是正数，则将变量`f`与`√(d/2a)`绑定，并返回由`(+ e f)`和`(- e f)`> 构成的表。 实际上，`let`表达式只是`lambda`表达式的一个语法糖： ~~~ (let ((p1 v1) (p2 v2) ...) exp1 exp2 ...) ;⇒ ((lambda (p1 p2 ...) exp1 exp2 ...) v1 v2) ~~~ 这是因为`lambda`表达式用于定义函数，它为变量建立了一个作用域。 > 练习1 > > 编写一个解决第四章练习1的函数，该函数旨在通过一个初始速度`v`和与水平面所成夹角`a`来计算飞行距离。 ## 6.3 总结 本节中，我介绍了`let`表达式，`let`表达式是`lambda`表达式的一个语法糖。变量的作用域通过使用`let`表达式或`lambda`表达式来确定。在Scheme中，这个有效域由源代码的编写决定，这叫做**词法闭包（lexical closure）**。 ## 6.4 习题解答 ### 6.4.1 答案1 ~~~ (define (throw v a) (let ((r (/ (* 4 a (atan 1.0)) 180))) (/ (* 2 v v (cos r) (sin r)) 9.8))) ~~~

[TOC=2] ## 5.1 简介 上一章中，我讲解了如何定义函数。本章中，我会讲解如何通过条件编写过程。这个是编写使用程序很重要的一步。 ## 5.2 if表达式 `if`表达式将过程分为两个部分。`if`的格式如下： ~~~ (if predicate then_value else_value) ~~~ 如果`predicate`部分为真，那么`then_value`部分被求值，否则`else_value`部分被求值，并且求得的值会返回给`if`语句的括号外。`true`是除`false`以外的任意值，`true`使用`#t`表示，`false`用`#f`表示。 在R5RS中，`false`（`#f`）和空表`（’()）`是两个不同的对象。然而，在MIT-Scheme中，这两个为同一对象。这个不同可能是历史遗留问题，在以前的标准——R4RS中，`#f`和`’()`被定义为同一对象。 因此，从兼容性角度考虑，你不应该使用表目录作为谓词。使用函数`null?`来判断表是否为空。 ~~~ (null? '()) ;Value: #t (null? '(a b c)) ;Value: () ;#f ~~~ 函数`not`可用于对谓词取反。此函数只有一个参数且如果参数值为`#f`则返回`#t`，反之，参数值为`#t`则返回`#f`。`if`表达式是一个特殊形式，因为它不对所有的参数求值。因为如果`predicate`为真，则只有`then_value`部分被求值。另一方面，如果`predicate`为假，只有`else_value`部分被求值。 例：首项为`a0`，增长率`r`，项数为`n`的几何增长（geometric progression）数列之和 ~~~ (define (sum-gp a0 r n) (* a0 (if (= r 1) n (/ (- 1 (expt r n)) (- 1 r))))) ; !! ~~~ 通常来说，几何增长数列的求和公式如下： ~~~ a0 * (1 - r^n) / (1 - r) (r ≠ 1) a0 * n (r = 1) ~~~ 如果`if`表达式对所有参数求值的话，那么有`;!!`注释的那行就算在`r=1`时也会被求值，这将导致产生一个“除数为0”的错误。 你也可以省去`else_value`项。这样的话，当`predicate`为假时，返回值就没有被指定。如果你希望当`predicate`为假时返回`#f`，那么就要明确地将它写出来。 `then_value`和`else_value`都应该是S-表达式。如果你需要副作用，那么就应该使用`begin`表达式。我们将在下一章讨论`begin`表达式。 > 练习1 > > 编写下面的函数。阅读第五节了解如何编写谓词。 > > * 返回一个实数绝对值的函数。 > * 返回一个实数的倒数的函数。如果参数为`0`，则返回`#f`。 > * 将一个整数转化为ASCII码字符的函数。整数可以被转化为33-126号之间的ASCII码。使用`integer->char`可以将整数转化为字符。如果给定的整数不能够转化为字符，那么就返回`#f`。 ## 5.3 and和or `and`和`or`是用于组合条件的两个特殊形式。Scheme中的`and`和`or`不同于C语言中的约定。它们不返回一个布尔值（`#t`或`#f`），而是返回给定的参数之一。`and`和`or`可以使你的代码更加短小。 ### 5.3.1 and `and`具有任意个数的参数，并从左到右对它们求值。如果某一参数为`#f`，那么它就返回`#f`，而不对剩余参数求值。反过来说，如果所有的参数都不是`#f`，那么就返回最后一个参数的值。 ~~~ (and #f 0) ;Value: () (and 1 2 3) ;Value: 3 (and 1 2 3 #f) ;Value: () ~~~ ### 5.3.2 or `or`具有可变个数的参数，并从左到右对它们求值。它返回第一个不是值`#f`的参数，而余下的参数不会被求值。如果所有的参数的值都是`#f`的话，则返回最后一个参数的值。 ~~~ (or #f 0) ;Value: 0 (or 1 2 3) ;Value: 1 (or #f 1 2 3) ;Value: 1 (or #f #f #f) ;Value: () ~~~ > 练习2 > > 编写下面的函数。 > > * 一个接受三个实数作为参数的函数，若参数皆为正数则返回它们的乘积。 > * 一个接受三个实数作为参数的函数，若参数至少一个为负数则返回它们的乘积。 ## 5.4 cond表达式 尽管所有的分支都可以用`if`表达式表达，但当条件有更多的可能性时，你就需要使用嵌套的`if`表达式了，这将使代码变得复杂。处理这种情况可以使用`cond`表达式。`cond`表达式的格式如下： ~~~ (cond (predicate_1 clauses_1) (predicate_2 clauses_2) ...... (predicate_n clauses_n) (else clauses_else)) ~~~ 在`cond`表达式中，`predicates_i`是按照从上到下的顺序求值，而当`predicates_i`为真时，`clause_i`会被求值并返回。`i`之后的`predicates`和`clauses`不会被求值。如果所有的`predicates_i`都是假的话，则返回`cluase_else`。在一个子句中，你可以写数条S-表达式，而`clause`的值是最后一条S-表达式。 > 例：城市游泳池的收费。 > > Foo市的城市游泳池按照顾客的年龄收费： > > 如果 age ≤ 3 或者 age ≥ 65 则 免费； > 如果 介于 4 ≤ age ≤ 6 则 0.5美元； > 如果 介于 7 ≤ age ≤ 12 则 1.0美元； > 如果 介于 13 ≤ age ≤ 15 则 1.5美元； > 如果 介于 16 ≤ age ≤ 18 则 1.8美元； > 其它 则 2.0美元； > > 那么，一个返回城市游泳池收费的函数如下： ~~~ (define (fee age) (cond ((or (<= age 3) (>= age 65)) 0) ((<= 4 age 6) 0.5) ((<= 7 age 12) 1.0) ((<= 13 age 15) 1.5) ((<= 16 age 18) 1.8) (else 2.0))) ~~~ > 练习 3 > > 编写下列函数。 > > 成绩（A-D）是由分数决定的。编写一个将分数映射为成绩的函数，映射规则如下： > + A 如果 score ≥ 80 > + B 如果 60 ≤ score ≤ 79 > + C 如果 40 ≤ score ≤ 59 > + D 如果 score < 40 ## 5.5 做出判断的函数 我将介绍一些用于做判断的函数。这些函数的名字都以`'?'`结尾。 ### eq?、eqv?和equal? 基本函数`eq?`、`eqv?`、`equal?`具有两个参数，用于检查这两个参数是否“一致”。这三个函数之间略微有些区别。 > `eq?` > 该函数比较两个对象的地址，如果相同的话就返回`#t`。例如，`(eq? str str)`返回`#t`，因为`str`本身的地址是一致的。与此相对的，因为字符串`”hello”`和`”hello”`被储存在了不同的地址中，函数将返回`#f`。不要使用`eq?`来比较数字，因为不仅在R5RS中，甚至在MIT-Scheme实现中，它都没有指定返回值。使用`eqv?`或者`=`替代。 ~~~ (define str "hello") ;Value: str (eq? str str) ;Value: #t (eq? "hello" "hello") ;Value: () ← It should be #f in R5RS ;;; comparing numbers depends on implementations (eq? 1 1) ;Value: #t (eq? 1.0 1.0) ;Value: () ~~~ > `eqv?` > 该函数比较两个存储在内存中的对象的类型和值。如果类型和值都一致的话就返回`#t`。对于过程（`lambda`表达式）的比较依赖于具体的实现。这个函数不能用于类似于表和字符串一类的序列比较，因为尽管这些序列看起来是一致的，但它们的值是存储在不同的地址中。 ~~~ (eqv? 1.0 1.0) ;Value: #t (eqv? 1 1.0) ;Value: () ;;; don't use it to compare sequences (eqv? (list 1 2 3) (list 1 2 3)) ;Value: () (eqv? "hello" "hello") ;Value: () ;;; the following depends on implementations (eqv? (lambda(x) x) (lambda (x) x)) ;Value: () ~~~ > `equal?` > 该函数用于比较类似于表或者字符串一类的序列。 ~~~ (equal? (list 1 2 3) (list 1 2 3)) ;Value: #t (equal? "hello" "hello") ;Value: #t ~~~ ### 5.5.2 用于检查数据类型的函数 下面列举了几个用于检查类型的函数。这些函数都只有一个参数。 * `pair?` 如果对象为序对则返回`#t`； * `list?` 如果对象是一个表则返回`#t`。要小心的是空表`’()`是一个表但是不是一个序对。 * `null?` 如果对象是空表’()的话就返回#t。 * `symbol?` 如果对象是一个符号则返回#t。 * `char?` 如果对象是一个字符则返回#t。 * `string?` 如果对象是一个字符串则返回#t。 * `number?` 如果对象是一个数字则返回#t。 * `complex?` 如果对象是一个复数则返回#t。 * `real?` 如果对象是一个实数则返回#t。 * `rational?` 如果对象是一个有理数则返回#t。 * `integer?` 如果对象是一个整数则返回#t。 * `exact?` 如果对象不是一个浮点数的话则返回#t。 * `inexact?` 如果对象是一个浮点数的话则返回#t。 ### 5.5.3 用于比较数的函数 > `=`、`>`、`<`、`<=`、`>=` > 这些函数都有任意个数的参数。如果参数是按照这些函数的名字排序的话，函数就返回`#t`。 ~~~ (= 1 1 1.0) ;Value: #t (< 1 2 3) ;Value: #t (< 1) ;Value: #t (<) ;Value: #t (= 2 2 2) ;Value: #t (< 2 3 3.1) ;Value: #t (> 4 1 -0.2) ;Value: #t (<= 1 1 1.1) ;Value: #t (>= 2 1 1.0) ;Value: #t (< 3 4 3.9) ;Value: () ~~~ > `odd?`、`even?`、`positive?`、`negative?`、`zero?` > 这些函数仅有一个参数，如果这些参数满足函数名所指示的条件话就返回`#t`。 ### 5.5.4 用于比较符号的函数 在比较字符的时候可以使用`char=?`、`char<?`、`char>?`、`char<=?`以及`char>=?`函数。具体的细节请参见R5RS。 ### 5.5.5 用于比较字符串的函数 比较字符串时，可以使用`string=?`和`string-ci=?`等函数。具体细节请参见R5RS。 ## 5.6 总结 在这一章中，我总结了关于分支的知识点。编写分支程序可以使用`if`表达式和`cond`表达式。 下一章我将讲解局部变量。 ## 5.7 习题解答 ### 5.7.1 答案1 ~~~ ; 1 (define (my-abs n) (* n (if (positive? n) 1 -1))) ; 2 (define (inv n) (if (not (zero? n)) (/ n) #f)) ; 3 (define (i2a n) (if (<= 33 n 126) (integer->char n) #f)) ~~~ ### 5.7.2 答案2 ~~~ ; 1 (define (pro3and a b c) (and (positive? a) (positive? b) (positive? c) (* a b c))) ; 2 (define (pro3or a b c) (if (or (negative? a) (negative? b) (negative? c)) (* a b c))) ~~~ ### 5.7.3 答案3 ~~~ (define (score n) (cond ((>= n 80) 'A) ((<= 60 n 79) 'B) ((<= 40 n 59) 'C) (else 'D))) ~~~

[TOC=2] ## 4.1 简介 在前面的章节中，我已经讲解了： 1. 如何安装MIT-Scheme； 2. Scheme解释器是如何对S-表达式求值； 3. 基本的表操作； 在本章中，我会讲解如何自定义函数。由于Sheme是函数式编程语言，你需要通过编写小型函数来构造程序。因此，明白如何构造并组合这些函数对掌握Scheme尤为关键。在前端定义函数非常不便，因此我们通常需要在文本编辑器中编辑好代码，并在解释器中加载它们。 ## 4.2 如何定义简单函数并加载它们 你可以使用`define`来将一个符号与一个值绑定。你可以通过这个操作符定义例如数、字符、表、函数等任何类型的全局参数。 让我们使用任意一款编辑器（记事本亦可）来编辑代码片段1中展示的代码，并将它们存储为`hello.scm`，放置在类似于`C:\doc\scheme\`的文件夹下。如果可以的话，把这些文件放在你在第一章定义的MIT-Scheme默认文件夹下。 代码片段1（hello.scm） ~~~ ; Hello world as a variable (define vhello "Hello world") ;1 ; Hello world as a function (define fhello (lambda () ;2 "Hello world")) ~~~ 接下来，向Scheme解释器输入下面的命令： ~~~ (cd "C:\\doc\\scheme") ;Value 14: #[pathname 14 "c:\\doc\\scheme\\"] (load "hello.scm") ;Loading "hello.scm" -- done ;Value: fhello ~~~ 通过这些命令，`hello.scm`就被加载到解释器中。如果你的当前目录被设定在了脚本所在目录，那么你就不需要再输入第一行的命令了。然后，向解释器输入下面的命令： ~~~ vhello ;Value 15: "Hello world" fhello ;Value 16: #[compound-procedure 16 fhello] (fhello) ;Value 17: "Hello world" ~~~ 操作符`define`用于声明变量，它接受两个参数。`define`运算符会使用第一个参数作为全局参数，并将其与第二个参数绑定起来。因此，代码片段1的第1行中，我们声明了一个全局参数`vhello`，并将其与`"Hello，World"`绑定起来。 紧接着，在第2行声明了一个返回`“Hello World”`的过程。 特殊形式`lambda`用于定义过程。`lambda`需要至少一个的参数，第一个参数是由定义的过程所需的参数组成的表。因为本例`fhello`没有参数，所以参数表是空表。 在解释器中输入`vhello`，解释器返回“Hello，World”。如果你在解释器中输入`fhello`，它也会返回像下面这样的值：`#[compound-procedure 16 fhello]`，这说明了Scheme解释器把过程和常规数据类型用同样的方式对待。正如我们在前面章节中讲解的那样，Scheme解释器通过内存空间中的数据地址操作所有的数据，因此，所有存在于内存空间中的对象都以同样的方式处理。 如果把`fhello`当过程对待，你应该用括号括住这些符号，比如`(fhello)`。 然后解释器会按照第二章讲述的规则那样对它求值，并返回“Hello World”。 ## 4.3 定义有参数的函数 可以通过在`lambda`后放一个参数表来定义有参数的函数。将代码片段2保存为`farg.scm`并放在同`hello.scm`一致的目录。 代码片段2 (farg.scm) ~~~ ; hello with name (define hello (lambda (name) (string-append "Hello " name "!"))) ; sum of three numbers (define sum3 (lambda (a b c) (+ a b c))) ~~~ 保存文件，并在解释器中载入此文件，然后调用我们定义的函数。 ~~~ (load "farg.scm") ;Loading "farg.scm" -- done ;Value: sum3 (hello "Lucy") ;Value 20: "Hello Lucy!" (sum3 10 20 30) ;Value: 60 Hello ~~~ 函数`hello`有一个参数`(name)`，并会把`“Hello”`、`name的值`、和`"!"`连结在一起并返回。 预定义函数`string-append`可以接受任意多个数的参数，并返回将这些参数连结在一起后的字符串。 `sum3`：此函数有三个参数并返回这三个参数的和。 ## 4.4 一种函数定义的短形式 用`lambda`定义函数是一种规范的方法，但你也可以使用类似于代码片段3中展示的短形式。 代码片段3 ~~~ ; hello with name (define (hello name) (string-append "Hello " name "!")) ; sum of three numbers (define (sum3 a b c) (+ a b c)) ~~~ 在这种形式中，函数按照它们被调用的形式被定义。代码片段2和代码片段3都是相同的。有些人不喜欢这种短形式的函数定义，但是我在教程中使用这种形式，因为它可以使代码更短小。 > 练习1 > > 按照下面的要求编写函数。这些都非常简单但实用。 > > 1. 将参数加1的函数。 > 2. 将参数减1的函数。 > 练习2 > > 让我们按照下面的步骤编写一个用于计算飞行距离的函数。 > > 1. 编写一个将角的单位由度转换为弧度的函数。180度即π弧度。π可以通过下面的式子定义： `(define pi (* 4 (atan 1.0)))`。 > 2. 编写一个用于计算按照一个常量速度（水平分速度）运动的物体，t秒内的位移的函数。 > 3. 编写一个用于计算物体落地前的飞行时间的函数，参数是垂直分速度。忽略空气阻力并取重力加速度`g`为`9.8m/s^2`。提示：设落地时瞬时竖直分速度为`-Vy`，有如下关系。`2 * Vy = g * t` 
> 此处`t`为落地时的时间。 > 4. 使用问题1-3中定义的函数编写一个用于计算一个以初速度`v`和角度`theta`掷出的小球的飞行距离。 > 5. 计算一个初速度为40m/s、与水平方向呈30°的小球飞行距离。这个差不多就是一个臂力强劲的职业棒球手的投掷距离。 > > 提示：首先，将角度的单位转换为弧度（假定转换后的角度为`theta1`）。初始水平、竖直分速度分别表示为：`v*cos(theta1)`和`v*sin(theta1)`。落地时间可以通过问题3中定义的函数计算。由于水平分速度不会改变， 因此可以利用问题2中的函数计算距离。 ## 4.5 关于编辑器 这里，我会推荐一些能非常方便地编辑Scheme代码的编辑器。 ### 4.5.1 Emacs Emacs21的Windows版本可以从http://ftp.gnu.org/gnu/emacs/windows/找到，下载emacs-21.3-bin-i386.tar.gz并解压它。 你会在bin文件夹下发现一个叫runemacs.exe的可执行文件。双击这个程序来启动编辑器。尽管键位布局和Windows的标准相当不同，但是因为有一个菜单栏和鼠标控制器而显得相当用户友好。你也可以通过编辑名为.emacs的配置文件来实现自定义配置。编辑器提供了一种Scheme模式，此模式下能够编辑器能识别预定义单词，以及通过Ctri-i或TAB键来自动缩进。除此之外，当一个输入一个右括号后，编辑器会自动显示与之匹配的左括号。 在Windows系统中，emacs不能够与MIT-Scheme进行交互。你只能手动地储存并加载源代码。但从另一个方面来说，在UNIX和Linux系统下，emacs可以同MIT-Scheme进行交互式地调用，因此编辑代码也可以在交互中完成。 ### 4.5.2 Edwin Edwin是MIT-Scheme配备的编辑器。它有点像emacs18。但它没有菜单栏和鼠标控制，因此显得不太用户友好。只有少数人用这个编辑器，因此网络上可用的说明也很少。虽然如此，你可以使用这个编辑器进行交互式的代码编辑。我在Windows上使用这个编辑器编辑Scheme代码。 #### 如何使用Edwin 双击Edwin的图标以启动Edwin。当Edwin启动后，一个叫`*Scheme*`的默认缓冲区出现在屏幕上，它对应于emacs中的`*scratch*`缓冲区。你可以将`*scheme*`用作解释器前端。按下Ctrl-X Ctrl-e 就可以对S-表达式进行求值。 * 文件的打开与关闭，编辑器的关闭。按下Ctrl-X Ctrl-F来打开一个文件。如果你指定的文件并不存在，则会创建一个新文件。初始路径被设置为了‘C:\’，你在打开文件前应该修改这个路径。按下Ctrl-X Ctrl-S来保存文件，而按下Ctrl-x Ctrl-w则是文件另存为。退出编辑器请按下Ctrl-x Ctrl-c。 * 缩进。按下Ctrl-i或者TAB可以缩进。 * 剪切，复制和粘贴。我们无法使用鼠标，因此复制（剪切）、粘贴起来就会显得不太方便。但你可以像下面这样做： * 首先，通过方向键将光标移动至待选区域的开头，然后按下Ctrl-SPACE。 * 然后移动至结束位置按下Ctrl-w来剪切区域，按下Alt-w来复制区域。 * 最后，移动至你想要复制的区域，按下Ctrl-y。 * 求值S-表达式 * 按键Alt-z用于求值以`define`开头的S-表达式。 * 按键Alt-:用于在一个小型的缓冲区中求值S-表达式。这个通常用在测试用Alt-z求值的函数。 * 按键Ctrl-x Ctrl-e用于求值整个`*scheme*`缓冲区中的S-表达式。 请查阅[Scheme用户手册](http://www-swiss.ai.mit.edu/projects/scheme/documentation/user_8.html)以获得更多关于Edwin的帮助。你下载的MIT-Scheme中也附带了同样的文档。 ## 4.6 小结 本章中，我讲解了如何定义函数。特殊形式`define`用于定义函数和全局参数。我也讲解了用合适的编辑器（比如emacs）来编辑源代码，载入源码文件比在前端直接定义函数方便多了。 下个章节中，我讲介绍分支。 ## 4.7 习题解答 ### 4.7.1 答案1 ~~~ ; 1 (define (1+ x) (+ x 1)) ; 2 (define (1- x) (- x 1)) ~~~ ### 4.7.2 答案2 代码如下所示： ~~~ ; definition of pi (define pi (* 4 (atan 1.0))) ; degree -> radian (define (radian deg) (* deg (/ pi 180.0))) ; free fall time (define (ff-time vy) (/ (* 2.0 vy) 9.8)) ; horizontal distance (define (dx vx t) (* vx t)) ; distance (define (distance v ang) (dx (* v (cos (radian ang))) ; vx (ff-time (* v (sin (radian ang)))))) ; t ~~~ 向解释器中载入后，距离可以像这样计算： ~~~ (distance 40 30) ;Value: 141.39190265868385 ~~~ 函数返回一个合理的值：141.1米，因为忽略了空气阻力，所以这个值略微偏大。

[TOC=2] ## 3.1 简介 作为Lisp语言大家族的一员，Scheme同样擅长于处理表。你应该理解表以及有关表的操作以掌握Scheme。表在在后面章节中的递归函数和高阶函数中扮演重要角色。 在本章中，我会讲解基本的表操作，例如`cons`，`car`，`cdr`，`list`和`quote`。 ## 3.2 Cons单元和表 ### 3.2.1 Cons单元 首先，让我解释一下表的元素：**Cons单元（Cons cells）**。Cons单元是一个存放了两个地址的内存空间。Cons单元可用函数`cons`生成。 在前端输入`(cons 1 2)` ~~~ (cons 1 2) ;Value 11: (1 . 2) ~~~ 系统返回`(1 . 2)`。如图一所示，函数`cons`给两个地址分配了内存空间，并把存放指向`1`的地址放在一个空间，把存放指向`2`的地址放在另一个空间。存放指向`1`的地址的内存空间被称作`car`部分，对应的，存放指向`2`的地址的内存空间被称作`cdr`部分。`car`和`cdr`分别是**寄存器地址部分（Contents of the Address part of the Register）**和**寄存器减量部分（Contents of the Decrement part of the Register）**的简称。这些名字最初来源于Lisp首次被实现所使用的硬件环境中内存空间的名字。这些名字同时也表明Cons单元的本质就是一个内存空间。`cons`这个名字是术语**构造（construction）**的简称。  一个Cons单元 Cons单元也可以被串起来。 ~~~ (cons 3 (cons 1 2)) ;Value 15: (3 1 . 2) ~~~ ·(3 . (1 . 2))·可以更方便地表示为`(3 1 . 2)`。这种情况的内存空间如图2所示。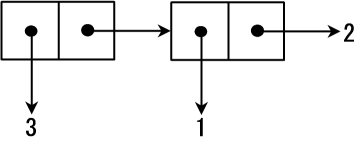  串连Cons单元 Cons单元可以存放不同类型的数据，也可以嵌套。 ~~~ (cons #\a (cons 3 "hello")) ;Value 17: (#\a 3 . "hello") (cons (cons 0 1) (cons 1 2)) ;Value 23: ((0 . 1) 1 . 2) ~~~ 这是因为Scheme可以通过地址操作所有的数据。（`#\c`代表了一个字符`c`。例如，`#\a`就代表字符`a`） ### 3.2.2 表 表是Cons单元通过用`cdr`部分连接到下一个`Cons`单元的开头实现的。表中包含的`’()`被称作空表。就算数据仅由一个Cons单元组成，只要它的`cdr`单元是`’()`，那它就是一个表。图3展示了表`(1 2 3)`的内存结构。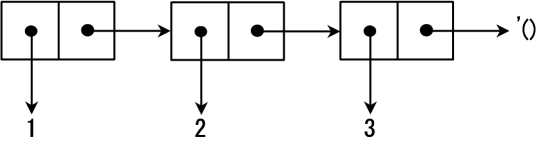  表(1 2 3)的内存结构 事实上，表可以像下面这样递归地定义： 1. `‘()`是一个表 2. 如果`ls`是一个表且`obj`是某种类型的数据，那么`(cons obj ls)`也是一个表 正因为表是一种被递归定义的数据结构，将它用在递归的函数中显然是合理的。 ## 3.3 原子 不使用Cons单元的数据结构称为**原子（atom）**。数字，字符，字符串，向量和空表`’()`都是原子。`’()`既是原子，又是表。 > 练习1 > > 使用`cons`来构建在前端表现为如下形式的数据结构。 > > 1. `("hi" . "everybody")` > 2. `(0)` > 3. `(1 10 . 100)` > 4. `(1 10 100)` > 5. `(#\I "saw" 3 "girls")` > 6. `("Sum of" (1 2 3 4) "is" 10)` ## 3.4 引用 所有的记号都会依据Scheme的求值规则求值：所有记号都会从最内层的括号依次向外层括号求值，且最外层括号返回的值将作为S-表达式的值。一个被称为**引用（quote）**的形式可以用来阻止记号被求值。它是用来将符号或者表原封不动地传递给程序，而不是求值后变成其它的东西。 例如，`(+ 2 3)`会被求值为`5`，然而`(quote (+ 2 3))`则向程序返回`(+ 2 3)`本身。因为`quote`的使用频率很高，他被简写为`’`。 比如： * `’(+ 2 3)`代表列表`(+ 2 3)`本身； * `’+`代表符号`+`本身； 实际上，`’()`是对空表的引用，也就是说，尽管解释器返回`()`代表空表，你也应该用`’()`来表示空表。 ### 3.4.1 特殊形式 Scheme有两种不同类型的操作符：其一是函数。函数会对所有的参数求值并返回值。另一种操作符则是特殊形式。特殊形式不会对所有的参数求值。除了`quote`，`lambda`，`define`，`if`，`set!`，等都是特殊形式。 ## 3.5 car函数和cdr函数 返回一个Cons单元的`car`部分和`cdr`部分的函数分别是`car`和`cdr`函数。如果`cdr`部分串连着Cons单元，解释器会打印出整个`cdr`部分。如果Cons单元的`cdr`部分不是`’()`，那么其值稍后亦会被展示。 ~~~ (car '(1 2 3 4)) ;Value: 1 (cdr '(1 2 3 4)) ;Value 18: (2 3 4) ~~~ > 练习2 > > 求值下列S-表达式。 > > 1. `(car '(0))` > 2. `(cdr '(0))` > 3. `(car '((1 2 3) (4 5 6)))` > 4. `(cdr '(1 2 3 . 4))` > 5. `(cdr (cons 3 (cons 2 (cons 1 '()))))` ## 3.6 list函数 `list`函数使得我们可以构建包含数个元素的表。函数`list`有任意个数的参数，且返回由这些参数构成的表。 ~~~ (list) ;Value: () (list 1) ;Value 24: (1) (list '(1 2) '(3 4)) ;Value 25: ((1 2) (3 4)) (list 0) ;Value 26: (0) (list 1 2) ;Value 27: (1 2) ~~~ ## 3.7 小结 本章讲解了表和表的基本操作。我担心前三章有些无趣。我希望下一章能有趣点，它主要讲述了如何编写函数。我也会讲解如何用编辑器来编辑代码，如何将代码加载到解释器中，以及如何定义函数。 ## 3.8 习题解答 ### 3.8.1 答案1 ~~~ ;1 (cons "hi" "everybody") ;Value 32: ("hi" . "everybody") ;2 (cons 0 '()) ;Value 33: (0) ;3 (cons 1 (cons 10 100)) ;Value 34: (1 10 . 100) ;4 (cons 1 (cons 10 (cons 100 '()))) ;Value 35: (1 10 100) ;5 (cons #\I (cons "saw" (cons 3 (cons "girls" '())))) ;Value 36: (#\I "saw" 3 "girls") ;6 (cons "Sum of" (cons (cons 1 (cons 2 (cons 3 (cons 4 '())))) (cons "is" (cons 10 '())))) ;Value 37: ("Sum of" (1 2 3 4) "is" 10) ~~~ ### 3.8.2 答案2 ~~~ ;1 (car '(0)) ;Value: 0 ;2 (cdr '(0)) ;Value: () ;3 (car '((1 2 3) (4 5 6))) ;Value 28: (1 2 3) ;4 (cdr '(1 2 3 . 4)) ;Value 29: (2 3 . 4) ;5 (cdr (cons 3 (cons 2 (cons 1 '())))) ;Value 31: (2 1) ~~~

[TOC=2] ## 2.1 简介 让我们把Scheme解释器当作计算器来使用。它比Windows附带的计算机方便多了。 ## 2.2 将Scheme作为一个计算器 点击 `开始` → `所有程序` → `MIT Scheme` → `Scheme` 来启动Scheme解释器以及如下图所示的控制台。  首先，让我们计算1加2的值，在提示符中输入`(+ 1 2)`： ~~~ 1 ]=> (+ 1 2) ;Value: 3 1 ]=> ~~~ 解释器返回3作为答案。请注意以下三点： 1. 一对括号代表了一次计算的步骤。本例中，`(+ 1 2)`代表步骤`1+2`。 2. 左括号后紧跟着一个函数的名字，然后是参数。Scheme中大多数的操作符都是函数。在本例中，函数`+`首先出现，然后紧跟两个参数：`1`和`2`. 3. 标记的分隔符是**空格（Space）**、**制表符（Tab）**或者**换行符（Newline）**。逗号和分号不是分隔符。 让我们来详细地分析计算过程。在这个函数中，当所有的参数被求值后，计算开始处理。对参数的求值顺序是没有被规范的，也就是说，参数并不是总是会从左到右求值。 * 符号`+`被求值为加法过程。仅在前端输入`+`，解释器会返回：`[arity-dispatched-procedure 1]` 这表明`+`是代表“过程1”的一个符号 * 对`1`求值得到`1`。通常来说，对布尔值，数字，字符以及字符串求值的结果就是它们本身。另一方面，对符号求值的结果可能是一些它的东西。 * 对`2`求值得到`2`。 * 最后，对`(+ 1 2)`求值得到3并跳出括号。在Scheme中，求得的值会跳出括号外，并且这个值（表达式的最终值）会被打印到前端。 函数`+`可以接受任意多的参数。 ~~~ (+) ;→ 0 (+ 1) ;→ 1 (+ 1 2) ;→ 3 (+ 1 2 3) ;→ 6 ~~~ ## 2.3 四种基本算术操作 Scheme（以及大多数Lisp方言）都可以处理分数。 函数`exact->inexact` 用于把分数转换为浮点数。Scheme也可以处理复数。复数是形如`a+bi`的数，此处`a`称为实部，`b`称为虚部。`+`、`-`、`*`和`/`分别代表加、减、乘、除。这些函数都接受任意多的参数。 例： ~~~ (- 10 3) ;→ 7 (- 10 3 5) ;→ 2 (* 2 3) ;→ 6 (* 2 3 4) ;→ 24 (/ 29 3) ;→ 29/3 (/ 29 3 7) ;→ 29/21 (/ 9 6) ;→ 3/2 (exact->inexact (/ 29 3 7)) ;→ 1.380952380952381 ~~~ 括号可以像下面这样嵌套： ~~~ (* (+ 2 3) (- 5 3)) ;→ 10 (/ (+ 9 1) (+ 2 3)) ;→ 2 ~~~ 形如这些由**括号**、**标记（token）**以及**分隔符**组成的式子，被称为**S-表达式**。 > 练习 1 > > 使用Scheme解释器计算下列式子： > > 1. (1+39) * (53-45) > 2. (1020 / 39) + (45 * 2) > 3. 求和：39, 48, 72, 23, 91 > 4. 求平均值：39, 48, 72, 23, 91（结果取为浮点数） ## 2.4 其它算术操作 ### 2.4.1 quotient，remainder，modulo和sqrt * 函数`quotient`用于求**商数（quotient）**。 * 函数`remainder`和`modulo`用于求**余数（remainder）**。 * 函数`sqrt`用于求参数的**平方根（square root）**。 ~~~ (quotient 7 3) ;→ 2 (modulo 7 3) ;→ 1 (sqrt 8) ;→ 2.8284271247461903 ~~~ ### 2.4.2 三角函数 数学上的三角函数，诸如`sin`，`cos`，`tan`，`asin`，`acos`和`atan`都可以在Scheme中使用。`atan`接受1个或2个参数。如果期望`atan`的结果是1/2 π，就使用第二个参数指明使用弧度制。 ~~~ (atan 1) ;→ 0.7853981633974483 (atan 1 0) ;→ 1.5707963267948966 ~~~ ### 2.4.3 指数和对数 指数通过`exp`函数运算，对数通过`log`函数运算。`a`的`b`次幂可以通过`(expt a b)`来计算。 > 练习2 > > 使用Scheme解释器求解下列式子： > > 1. 圆周率π。 > 2. exp(2/3)。 > 3. 3的4次幂。 > 4. 1000的对数 ## 2.5 小结 本章中，我们已经将Scheme解释器当作计算器来使用。这会让你快速上手Scheme。我会在下个章节讲解Scheme的数据类型‘表’。 ## 2.6 习题解答 ### 2.6.1 答案1 ~~~ ;1 (* (+ 1 39) (- 53 45)) ;⇒ 320 ;2 (+ (/ 1020 39) (* 45 2)) ;⇒ 1510/13 ;3 (+ 39 48 72 23 91) ;⇒ 273 ;4 (exact->inexact (/ (+ 39 48 72 23 91) 5)) ;⇒ 54.6 ~~~ ### 2.6.2 答案2 ~~~ ;1 (* 4 (atan 1.0)) ;⇒ 3.141592653589793 ;2 (exp 2/3) ;⇒ 1.9477340410546757 ;3 (expt 3 4) ;⇒ 81 ;4 (log 1000) ;⇒ 6.907755278982137 ~~~

[TOC=2] ## 1.1 为什么使用Scheme 使用Scheme，你可以： * 编写漂亮的程序。 * 享受编程的乐趣。 这些就是为什么要学习Scheme的原因。在你用Scheme编写一些实用程序的时候会遇到一些困难。 然而，正因为这是一门值得学习的语言，所以许多卓越的黑客钟爱Scheme。事实上，计算机程序的构造和解释（Structure and Interpretation of Computer Programs，SICP）——最好的计算机科学教科书之一——使用Scheme来描述演示程序。GNU也使用Scheme（一种被称作guile的实现）作为其应用软件的通用脚本语言。guild相当于MS-Word或者Excel（原文是Excell，应该是作者的笔误，译者注）中的宏。它被用来通过简单的脚本来操作应用程序。 尽管Common Lisp更加适合构建实用应用程序，但我依然推荐你首先学习Scheme，因为这门语言： * 设计紧凑 * 语法简单 业界大牛提出过“Scheme使你成为更棒的程序员”的看法。即是你很少在商业项目上使用Scheme，但学习Scheme获得的良好感觉将会指导你使用其它的编程语言。 网络上的Scheme教程（真是多如牛毛）总是或多或少的有些困难，因而不太适合初学者。这样来说的话，本教程是面向新手程序员的，他们只需要对编程有一点了解即可。 ## 1.2 目标读者 本教程的目标读者是仅有一点编程经验的PC用户，例如： * 教授使用Scheme授课，无法跟上进度的学生。 * 想要学习编程的人。 Scheme的语法相当地简单，并且可以通过一个简单的方式解释清楚。尽管如此，对初学者来说这种解释还是太困难了。在本教程中，我会循序渐进地讲解。 Scheme代码仅由单词，括号和空格组成，这些最初可能会使你感到烦扰。然而，如果你使用了一个合适的编辑器，它会为你展示配对的括号和自动缩进。因此，你不用担心括号的配对，并且你可以通过缩进来阅读代码。如果缩进看起来很奇怪，你可以用编辑器找出错误的配对。 ## 1.3 安装MIT-Scheme 这节是面向Windows用户的教程。我没有使用Macintosh的经验，因此无法提供给你相关的帮助。如果你是Unix（或者Linux）用户，（如果你无法自己安装）请让管理员安装它。Scheme的使用并不依赖于操作系统。只有安装才会因不同的系统而不同。 Scheme程序设计语言中有一些规范，最新的规范在Revised5 Report on the Algorithmic Language Scheme (R5RS)。 大多数的实现都是（完全或者部分地）基于R5RS。如果你使用的是部分符合R5RS的实现，那么在使用时你就得当心一点。在Windows系统上有很多免费的Scheme实现，比如：ChezScheme, MzScheme, DrScheme, SCM。在本教程中，我使用MIT/GNU Scheme，因为它高效并且非常容易安装。MIT-Scheme的解释器十分快速，除此之外它还能够将你的程序编译为本地代码。MIT-Scheme的问题就是它并不完全符合R5RS规范。稍后我会详细说明这点。事实上，只有MIT-Scheme和DrScheme有安装包。有人推荐DrScheme，但是它太慢了。如果你有手动安装软件的能力，我推荐你安装Petite Chez Scheme。这是一个运行在命令提示符（DOS Windows）下的非常棒的解释器。 《Scheme实现》比较了几种Scheme实现。当你习惯Scheme后，去尝试几种不同的实现将会是很好的主意。或许你需要一台Linux机器，因为大多数Scheme实现都是只能运行在Unix和Linux上的。 ### 1.3.1 如何在Windows上安装MIT-Scheme MIT-Scheme可以简单地通过下载并执行安装包来进行安装。 1. 访问MIT/GNU Scheme的主页，下载适用于Windows的二进制包： mit-scheme-N.N.N-ix86-win32.exe。 2. 双击下载好的安装包。安装包会询问一些事项，按照默认的设置进行即可。 3. 安装完毕后，有4个快捷方式被创建出来，分别是：Scheme，Compiler，Edwin和Documentation。Scheme，Compiler和Edwin都是指向同一个程序的快捷方式，但它们调用程序的参数不同。使用Compiler，你可以把程序编译为本地代码，这样可使你的程序运行时间更短。但反过来说，Compiler会消耗更多的内存。Edwin是一个类Emacs的编辑器，用于编辑Scheme程序。你可以使用这个编辑器或者你最喜欢的编辑器。 4. 你可以通过编辑配置文件scheme.ini来自定义MIT-Scheme。 scheme.ini文件的创建路径是由环境变量`HOMEPATH`决定的。你可以通过在命令提示符（DOS Windows）中输入`>set HOMEPATH`来取得`HOMEPATH`的值。在WinXP中，`HOMEPATH`被预定义为：`\Document and Setting\username` 下面的代码给出了一个scheme.ini文件的例子： ~~~ (cd "C:\\doc\\scheme") (define call/cc call-with-current-continuation) ~~~ 第一行代码代表将工作目录切换到C:\doc\scheme。通过这条代码，MIT-Scheme移动工作路径切换到这个路径，你不需要再敲击程序的绝对路径来载入Scheme程序。第二行是定义`call-with-current-continuation`的缩略词。 ## 1.4 小结 安装非常容易（除了编辑scheme.ini文件），你应该毫无问题。 下一章节是如何与MIT-Scheme前端会话。

# Yet Another Scheme Tutorial ## Scheme入门教程 > 本书出处：http://deathking.github.io/yast-cn/ > Takafumi Shido 著 > DeathKing 译 这是一本面向初学者的温和且循序渐进的Scheme教程。目标读者是仅有些许编程经验的PC用户。 如果你不满意于其它的教程，那么请尝试本书。我们有很多方法去解释像Scheme程序设计语言这样的抽象主题，这之中最好的方法取决于读者的能力以及素养。（没有对任何人来说都绝对完美的方法。）这也正是尽管已经有很多Scheme语言的教程，我还另写一本的原因所在。 本教程的目的在于给读者在Scheme程序设计上提供足够的知识和能力以便能够阅读最好的计算机科学教科书之一的——《计算机程序的构造和解释》（Structure and Interpreter of Computer Program，SICP）。SICP使用Scheme作为授课语言。 > Scheme is comparable to Go, a traditional Chinese board game. The reason is that both of them generate beautiful code/board from extremely simple rules, which are one of the simplest in the areas (programming languages and board games). > > The simple rules and infinite beautiful variation make them attractive to intelligent people. The nature, at the same time, makes them rather difficult to be mastered. > > I wrote the tutorial to provide the key to master the language. I believe the Chinese translation helps many programmers to master Scheme programming language. > > **Takafumi Shido** Scheme恰似中国传统棋盘游戏——围棋。 这是因为它们都可以根据相当简单的规则产生美妙的代码或者棋局，这些规则在它们的领域中都是最简单的。简单的规则，无限的美妙变幻，这些都无比吸引那些聪明的家伙。但同时，大自然却让它们难以掌握。 我编写这份教程以打开掌握Scheme之门。我相信中文译版会帮助更多的程序员掌握Scheme程序设计语言。 **紫藤貴文**