OpenCV2学习笔记(五)
最后更新于:2022-04-01 06:35:56
##图像滤波基础
**一:基本概念**
滤波是数字图像处理中的一个基本操作,在信号处理领域可以说无处不在。图像滤波,即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,通常是数字图像处理中不可缺少的操作,其处理效果的好坏将直接影响到后续运算和分析的效果。简单来说,图像滤波的根本目的是在图像中提取出人类感兴趣的特征。
当我们观察一幅图像时,有两种处理方法:
1\. 观察不同的灰度(或彩色值)在图像中的分布情况,即空间分布。
2\. 观察图像中的灰度(或彩色值)的变化情况,这涉及到频率方面的问题。
因此,图像滤波分为频域和空域滤波,简单来说,空域指用图像的灰度值来描述一幅图像;而频域指用图像灰度值的变化来描述一幅图像。而低通滤波器和高通滤波器的概念就是在频域中产生的。低通滤波器旨在去除图像中的高频成分,而高通滤波器则是去除了图像中的低频成分。
这里简单记录以下低通滤波器中的均值和高斯滤波器(线性滤波器)、中值滤波器(非线性滤波器);高通滤波器中的sobel算子(方向滤波器)和拉普拉斯变换(二阶导数),其中,sobel算子和拉普拉斯变换均可以对图像的边缘进行检测。
**二:低通滤波器**
消除图像中的噪声成分叫作图像的平滑化或低通滤波。信号或图像的能量大部分集中在幅度谱的低频和中频段是很常见的,而在较高频段,感兴趣的信息经常被噪声淹没。因此一个能降低高频成分幅度的滤波器就能够减弱噪声的影响。
图像滤波的目的有两个:一是抽出对象的特征作为图像识别的特征模式;另一个是为适应图像处理的要求,消除图像数字化时所混入的噪声。当然,在设计低通滤波器时,要考虑到滤波对图像造成的细节丢失等问题。
平滑滤波是低频增强的空间域滤波技术。它的目的有两类:一类是图像模糊;另一类是滤除图像噪声。空间域的平滑滤波一般采用简单平均法进行,就是求邻近像元点的平均灰度值或亮度值。邻域的大小与平滑的效果直接相关,邻域越大平滑的效果越好,但邻域过大,平滑会使边缘信息损失的越大,从而使输出的图像变得模糊,因此需合理选择邻域的大小。
关于滤波器,一种形象的比喻法是:我们可以把滤波器想象成一个包含加权系数的窗口,当使用这个滤波器平滑处理图像时,就把这个窗口放到图像之上,透过这个窗口来看我们得到的图像。
滤波器的种类有很多, 在OpenCV中,提供了如下几种常用的图像平滑处理操作方法及函数:
1\. 领域均值滤波:blur函数,将图像的每个像素替换为相邻矩形内像素的平均值(均值滤波)
2\. 高斯低通滤波:GaussianBlur函数
3\. 方框滤波:boxblur函数
4\. 中值滤波:medianBlur函数
5\. 双边滤波:bilateralFilter函数
以下是均值滤波和高斯低通滤波的简单代码,在Qt中新建控制台项目,在.pro文件中添加以下内容:
~~~
INCLUDEPATH+=C:\OpenCV\install\include\opencv\
C:\OpenCV\install\include\opencv2\
C:\OpenCV\install\include
LIBS+=C:\OpenCV\lib\libopencv_calib3d249.dll.a\
C:\OpenCV\lib\libopencv_contrib249.dll.a\
C:\OpenCV\lib\libopencv_core249.dll.a\
C:\OpenCV\lib\libopencv_features2d249.dll.a\
C:\OpenCV\lib\libopencv_flann249.dll.a\
C:\OpenCV\lib\libopencv_gpu249.dll.a\
C:\OpenCV\lib\libopencv_highgui249.dll.a\
C:\OpenCV\lib\libopencv_imgproc249.dll.a\
C:\OpenCV\lib\libopencv_legacy249.dll.a\
C:\OpenCV\lib\libopencv_ml249.dll.a\
C:\OpenCV\lib\libopencv_nonfree249.dll.a\
C:\OpenCV\lib\libopencv_objdetect249.dll.a\
C:\OpenCV\lib\libopencv_ocl249.dll.a\
C:\OpenCV\lib\libopencv_video249.dll.a\
C:\OpenCV\lib\libopencv_photo249.dll.a\
C:\OpenCV\lib\libopencv_stitching249.dll.a\
C:\OpenCV\lib\libopencv_superres249.dll.a\
C:\OpenCV\lib\libopencv_ts249.a\
C:\OpenCV\lib\libopencv_videostab249.dll.a
~~~
然后修改main函数,这里设定卷积核的大小均为5*5:
~~~
#include <QCoreApplication>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <QDebug>
int main(int argc, char *argv[])
{
QCoreApplication a(argc, argv);
// 输入图像
cv::Mat image= cv::imread("c:/peng.jpg",0);
if (!image.data)
return 0;
cv::namedWindow("Original Image");
cv::imshow("Original Image",image);
// 对图像进行高斯低通滤波
cv::Mat result;
cv::GaussianBlur(image,result,cv::Size(5,5),1.5);
cv::namedWindow("Gaussian filtered Image");
cv::imshow("Gaussian filtered Image",result);
// 对图像进行均值滤波
cv::blur(image,result,cv::Size(5,5));
cv::namedWindow("Mean filtered Image");
cv::imshow("Mean filtered Image",result);
return a.exec();
}
~~~
效果:
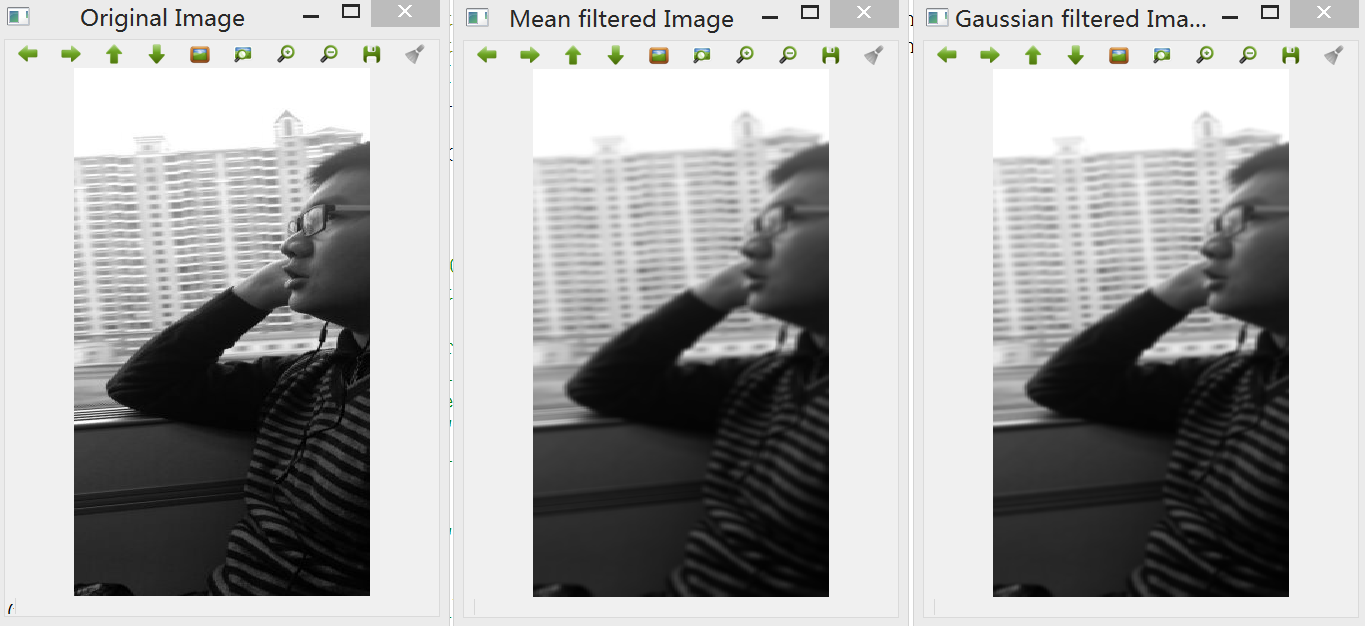
相比均值滤波,高斯低通滤波的主要不同是引入了加权方案,因为在通常情况下,对于图像的一个像素,与越靠近的临近像素有更高的关联性,因此离中心像素近的像素系数应该比远处的像素拥有更多的权重。在高斯滤波器中,像素的全重与它离开中心像素点的距离成正比,一维高斯函数可表示为以下形式:
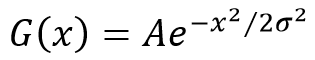
其中,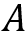为归一化系数,作用是使不同权重之和为1;称为西格玛数值,它的主要作用是控制高斯函数的高度,数值越大则函数越平坦。若要查看高斯滤波器的核,只需选择合适的西格玛数值,然后调用函数cv::getGaussianKernel,返回一个ksize*1的数组,该数组的元素满足高斯公式:
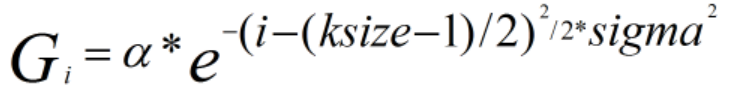
式中的参数分别对应cv::GaussianBlur函数中的参数。以下代码显示出核的值,在main函数中添加:
~~~
// 得到高斯核 (西格玛数值=1.5)
cv::Mat gauss= cv::getGaussianKernel(9,1.5,CV_32F);
// 显示高斯核的值
cv::Mat_<float>::const_iterator it= gauss.begin<float>();
cv::Mat_<float>::const_iterator itend= gauss.end<float>();
qDebug() << "[";
for ( ; it!= itend; ++it)
{
qDebug() << *it << " ";
}
qDebug() << "]";
~~~
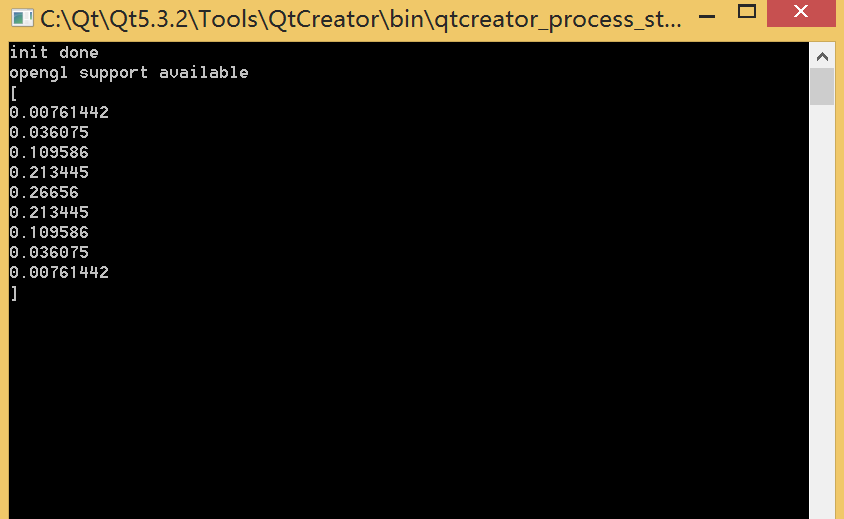
若要对一幅图像使用二维高斯滤波器,根据二维高斯滤波器的可分离特性(即一个二维高斯滤波器可分解为两个一维高斯滤波器),可以先对图像的行使用一维高斯滤波器,再对图像的列使用一维高斯滤波器。在OpenCV中,指定高斯滤波的方法是将系数个数(第三个参数,必须是奇数)以及西格玛数值 (第四个参数)提供给cv::GaussianBlur函数。
关于GaussianBlur函数的源码解析可以参考:[http://www.cnblogs.com/tornadomeet/archive/2012/03/10/2389617.html](http://www.cnblogs.com/tornadomeet/archive/2012/03/10/2389617.html)
以上的均值滤波和高斯低通滤波均属于线性滤波,此外还存在非线性滤波器,中值滤波器就是最常用的其中一种。与均值滤波、高斯低通滤波相似,它是对一个像素的相邻区域进行操作以确定像素的值,不同的是中值滤波器仅仅统计这组数组的中值,并用该中值替换中心像素点的值。中值滤波广泛用于噪声滤除,以下给出简单的实现和效果。
首先需要编写一个简单的图像加噪函数,作用是生成若干椒盐噪声:
~~~
void salt(cv::Mat& image, int n) // 添加椒盐噪声
{
for(int k=0; k<n; k++){
int i = rand()%image.cols;
int j = rand()%image.rows;
if(image.channels() == 1)
{
if(rand() % 2 == 0)
image.at<uchar>(j,i) = 0;
else
image.at<uchar>(j,i) = 255;
}else{
if(rand() % 2 == 0)
{
image.at<cv::Vec3b>(j,i)[0] = 0;
image.at<cv::Vec3b>(j,i)[1] = 0;
image.at<cv::Vec3b>(j,i)[2] = 0;
}
else
{
image.at<cv::Vec3b>(j,i)[0] = 255;
image.at<cv::Vec3b>(j,i)[1] = 255;
image.at<cv::Vec3b>(j,i)[2] = 255;
}
}
}
}
~~~
验证中值滤波法与之前的均值滤波法的效果,修改main函数:
~~~
#include <QCoreApplication>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <QDebug>
int main(int argc, char *argv[])
{
QCoreApplication a(argc, argv);
// 输入图像
image = cv::imread("c:/peng.jpg",0);
if (!image.data)
return 0;
// 给图像添加椒盐噪声
salt(image, 3000);
// 显示加噪图图
cv::namedWindow("Salt&Pepper Image");
cv::imshow("Salt&Pepper Image",image);
// 对图像进行均值滤波
cv::blur(image,result,cv::Size(5,5));
cv::namedWindow("Mean filter");
cv::imshow("Mean filter",result);
// 对图像进行中值滤波
cv::medianBlur(image,result,5);
cv::namedWindow("Median Filter");
cv::imshow("Median Filter",result);
return a.exec();
}
~~~
效果如下:
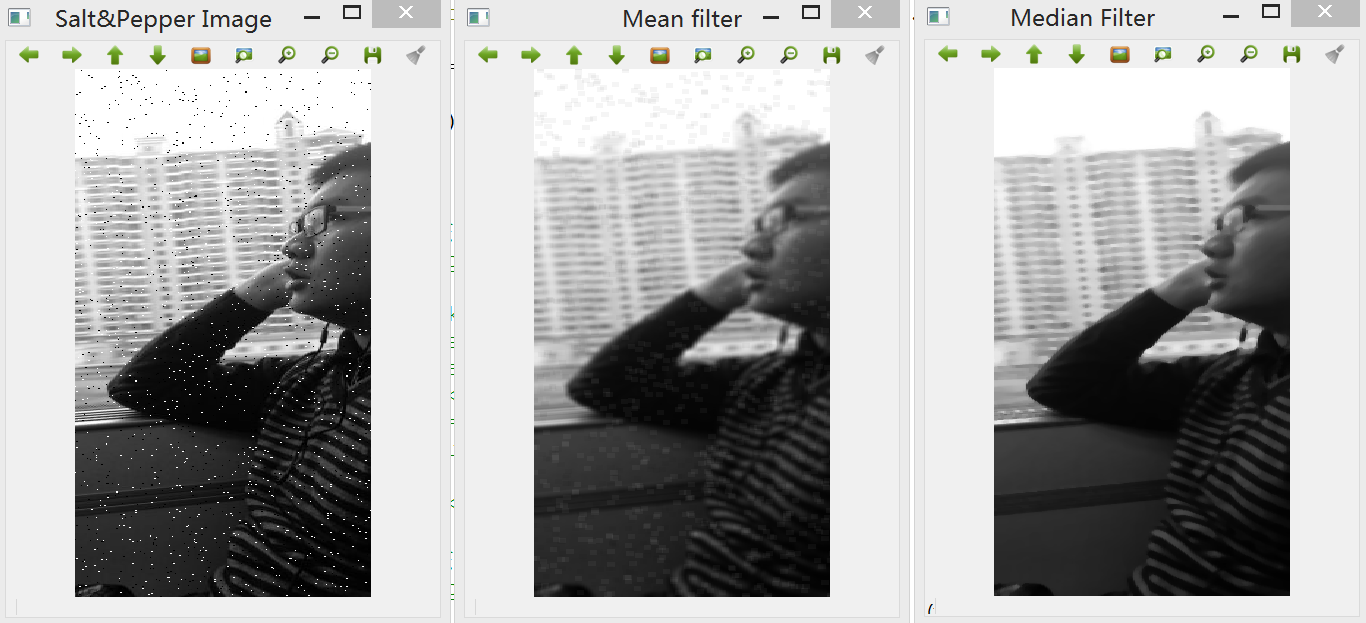

可以看到,中值滤波器对于去除椒盐噪点效果拔群,这是由于一个例外的黑点或白点像素出现在一个相邻区域时,通常不会被选为中值,因为它们代表的是0或255两个极端,因此这些噪声点总会被替换为某个相邻像素的值,而均值滤波和高斯滤波均会引入噪点信息,噪点处的像素值会极大地影响区域的结果,因此无法很好地滤除这一类噪声。
由于中值滤波器是非线性的,因此它无法表示为一个核矩阵。此外,中值滤波器还有保留边缘锐利度的优点。但是缺点是相同区域中的纹理细节也被滤除,如下图中的树木部分。
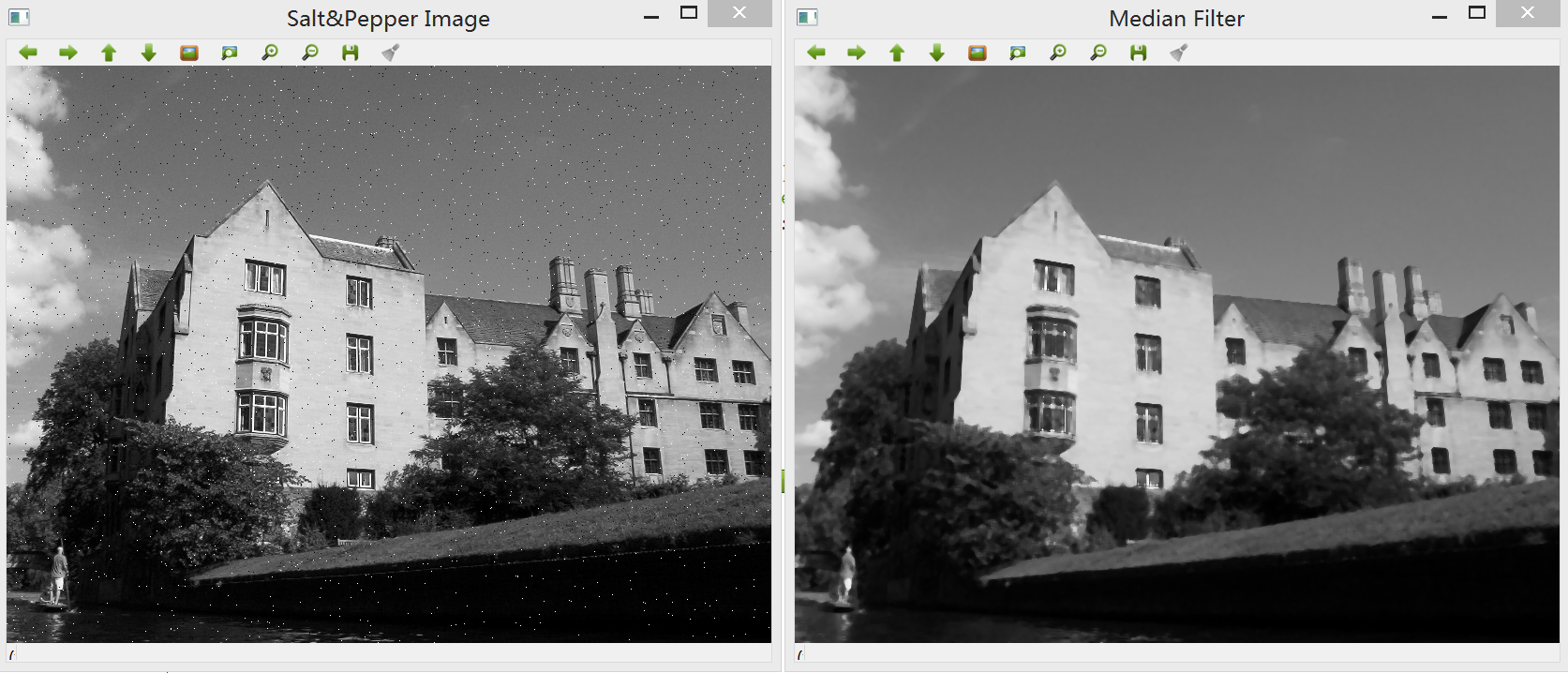
**三:高通滤波器**
前面主要介绍了低通滤波器对图像进行模糊处理,这里进行相反的变换,使用高通滤波器进行图像锐化或边缘检测。Sobel算子就是通过卷积操作来计算图像的一阶导数,由于边缘处图像灰度变化率较大,因此可以用sobel算子来进行边缘检测。提个简单的3*3 Sobel算子的核定义为:

如果将图像视为二维函数,Sobel算子可被认为是在垂直和水平方向变化的测量。这种测量在数学中被成为梯度,通常它被定义为由函数在两个正交方向上的一阶导数组成的二维向量:
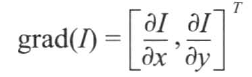
因此,Sobel算子通过在水平和垂直方向下进行像素差分给出图像梯度的近似。它在感兴趣像素的小窗口内运算,这样可减少噪声的影响。OpenCV中提供了函数cv::Sobel使用Sobel核计算图像卷积的结果,其函数的主要参数如下:
~~~
cv::Sobel(image, // 输入图像
sobel, // 输出图像
image_depth, // 图像类型
xorder, yorder, // 核的阶数
kernel_size, // 核的大小
alpha,beta); // 缩放值及偏移值
~~~
现设计算法,使用Sobel方向滤波器。在main函数中添加:
~~~
cv::Mat image= cv::imread("c:/075.png",0); // 输入图像
if (!image.data)
return 0;
cv::namedWindow("Original Image");
cv::imshow("Original Image",image);
// 水平滤波器设置
cv::Mat sobelX;
cv::Sobel(image, sobelX, CV_8U, 1, 0, 3, 0.4, 128);
cv::namedWindow("Sobel X Image");
cv::imshow("Sobel X Image", sobelX);
// 垂直滤波器设置
cv::Mat sobelY;
cv::Sobel(image, sobelY, CV_8U, 0, 1, 3, 0.4, 128);
cv::namedWindow("Sobel Y Image");
cv::imshow("Sobel Y Image", sobelY);
// 计算Sobel范式,滤波器结果保存在16位有符号整数图像中
cv::Sobel(image, sobelX, CV_16S, 1, 0);
cv::Sobel(image, sobelY, CV_16S, 0, 1);
cv::Mat sobel;
// 将水平和垂直方向相加
sobel = abs(sobelX) + abs(sobelY);
// 搜索Sobel的极大值
double sobmin, sobmax;
cv::minMaxLoc(sobel, &sobmin, &sobmax);
// 将图像转换为8位图像
cv::Mat sobelImage;
sobel.convertTo(sobelImage, CV_8U, -255./sobmax, 255);
// 输出图像
cv::namedWindow("Sobel Image");
cv::imshow("Sobel Image", sobelImage);
// 将结果阈值化得到二值图像
cv::Mat ThresholdedImage;
cv::threshold(sobelImage, ThresholdedImage, 225, 255, cv::THRESH_BINARY);
cv::namedWindow("Binary Sobel Image");
cv::imshow("Binary Sobel Image",ThresholdedImage);
~~~
得出水平、垂直方向的边缘检测和融合了两个方向的检测结果:
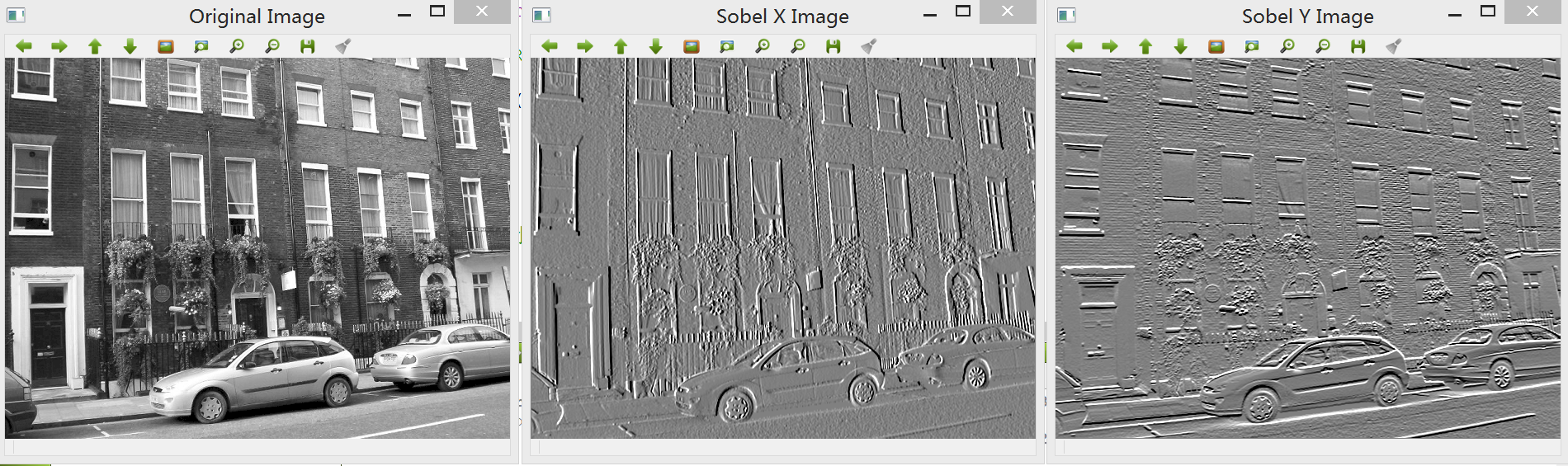
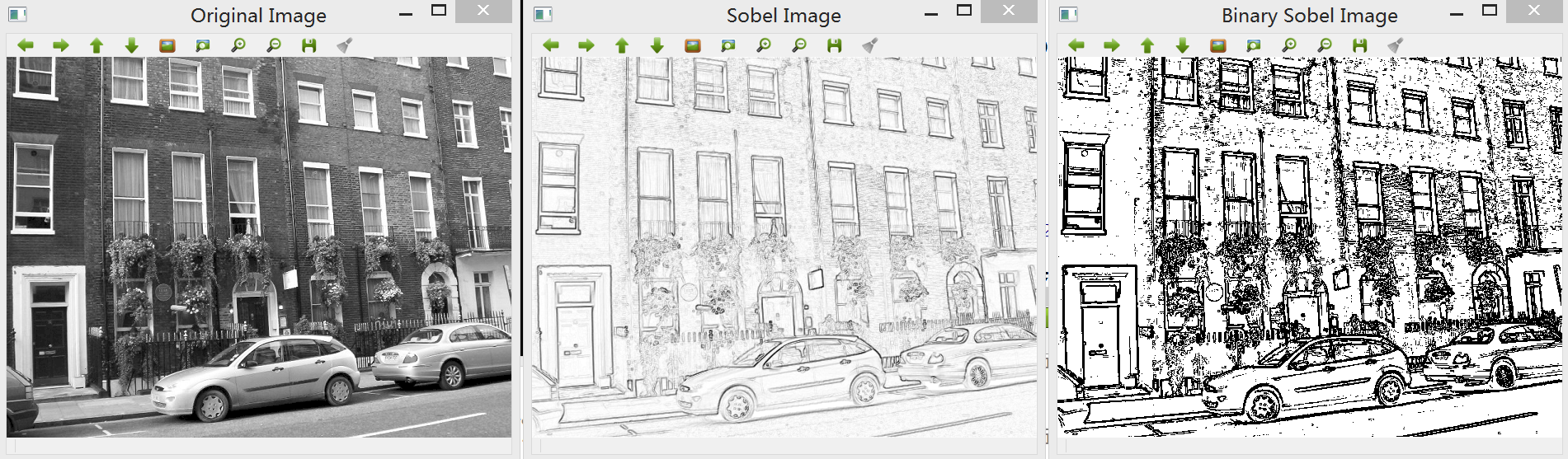
Sobel算子是一种经典的边缘检测线性滤波器,其主要介绍参考:[http://blog.csdn.net/liyuefeilong/article/details/43452711](http://blog.csdn.net/liyuefeilong/article/details/43452711)
拉普拉斯(Laplacian)是另一种基于图像导数的高斯线性滤波器,它计算二阶导数以衡量图像的弯曲度。在OpenCV中,使用cv::Laplacian函数来计算,它与cv::Sobel函数相类似。事实上,拉普拉斯与Sobel法都使用同一个函数cv::getDerivkernels来获取核矩阵。他们的唯一差别是不存在指定导数阶数的参数,因为它们都是二阶导数。,2D函数的拉普拉斯变换定义如下:
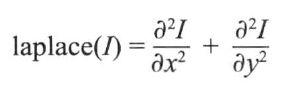
可用一个最简单的3*3核近似:
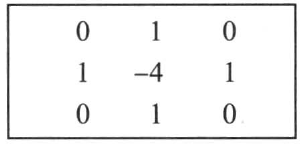
与Sobel算子相同,也能够使用更大的核计算Laplacian,同时由于Laplacian运算对于噪声十分敏感,我们倾向于这么做(除非计算效率更重要)。需要注意Laplacian核的总数为0,这保证了强度不变区域的Laplacian为0。事实上,由于Laplacian度量的是图像函数的曲率,它在平坦区域应该等于0。
拉普拉斯算子的效果可能很难解释。从核的定义来看,很明显,任何孤立的像素值(它与相邻像素值截然不同)将被算子放大。这源于算子对噪点的高灵敏度。但是拉普拉斯算子值在图像边缘处的表现更有趣。边缘的存在是图像中不同灰度区域间快速过渡的结果。沿着图像在一条边上的变化(例如,从暗处到亮处),可以观察到灰度的提升意味着从正曲率(强度值开始上升)到负曲率(当强度即将达到最高至)的渐变。因此,正、负拉普拉斯算子值(或导数)之间的过渡是存在边缘的指示器。另一种表达这个事实的方法是说,边缘位于Laplacian函数的零交叉点。
下图是取一幅图像中的一个观测窗口进行放大得出的个像素点的像素值,可以看到沿着Laplacian的零交叉点,就可以得到一条对应于图像窗口中可见的边缘曲线。

然而,跟随Laplacian图像中零交叉曲线是一件容易出错的事,因此在以下程序中将给出一个简化的算法用于检测近似的零交叉位置,即函数:
~~~
cv::Mat getZeroCrossings(float threshold = 1.0);
cv::Mat getZeroCrossingsWithSobel(float threshold);
~~~
大致的扫描过程是,比较当前像素与左侧像素,如果两者符号不同,那么说明当前像素存在零交叉。如果没有,在正上方位置重复相同的测试。在第二个函数中,还引入Sobel算子来得到零点交叉的二值图像,以下给出Laplacian变换算法的实现过程。
首先,创建一个类Laplacian来实现一些与拉普拉斯变换有关的操作,先在Laplacian.h中添加:
~~~
#ifndef LAPLACIAN_H
#define LAPLACIAN_H
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
class Laplacian
{
public:
Laplacian():aperture(3){}
// 设置卷积核的大小
void setAperture(int a);
// 计算浮点Laplacian
cv::Mat calcLaplacian(const cv::Mat &image);
// 返回8位图像存储的Laplacian结果
cv::Mat getLaplacianImage(double scale = -1.0);
// 以下函数可得到零点交叉的二值图像
cv::Mat getZeroCrossings(float threshold = 1.0);
cv::Mat getZeroCrossingsWithSobel(float threshold);
private:
cv::Mat img; // 原图像
cv::Mat laplace; // 包含Laplacian的32位浮点图像
int aperture; // 卷积核的大小
};
#endif // LAPLACIAN_H
~~~
接着在Laplacian.cpp中定义各个函数:
~~~
#include "laplacian.h"
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
// 设置卷积核的大小
void Laplacian::setAperture(int a)
{
aperture = a;
}
// 计算浮点Laplacian
cv::Mat Laplacian::calcLaplacian(const cv::Mat &image)
{
// 计算Laplacian
cv::Laplacian(image, laplace, CV_32F, aperture);
// 保留图像的局部备份(用于零点交叉)
img = image.clone();
return laplace;
}
// 返回8位图像存储的Laplacian结果
// 零点交叉于灰度值128
// 如果没有指定scale参数,则最大值缩放至强度255
// 必须在调用它之前调用calcLaplacian()
cv::Mat Laplacian::getLaplacianImage(double scale)
{
if (scale<0) {
double lapmin, lapmax;
cv::minMaxLoc(laplace,&lapmin,&lapmax);
scale= 127/ std::max(-lapmin,lapmax);
}
cv::Mat laplaceImage;
laplace.convertTo(laplaceImage,CV_8U,scale,128);
return laplaceImage;
}
// 得到零点交叉的二值图像
// 如果相邻像素的乘积小于threshold
// 则零点交叉被忽略
cv::Mat Laplacian::getZeroCrossings(float threshold)
{
// 创建迭代器
cv::Mat_<float>::const_iterator it= laplace.begin<float>()+laplace.step1();
cv::Mat_<float>::const_iterator itend= laplace.end<float>();
cv::Mat_<float>::const_iterator itup= laplace.begin<float>();
// 初始化为白色的二值图像
cv::Mat binary(laplace.size(),CV_8U,cv::Scalar(255));
cv::Mat_<uchar>::iterator itout= binary.begin<uchar>()+binary.step1();
// 对输入阈值取反
threshold *= -1.0;
for ( ; it!= itend; ++it, ++itup, ++itout)
{
// 如果相邻像素的乘积为负数,则符号发生改变
if (*it * *(it-1) < threshold)
*itout= 0; // 水平方向零点交叉
else if (*it * *itup < threshold)
*itout= 0; // 垂直方向零点交叉
}
return binary;
}
// 使用sobel算子得到零点交叉的二值图像
// 如果相邻的像素的乘积小雨threshold
// 那么零点交叉将被忽略
cv::Mat Laplacian::getZeroCrossingsWithSobel(float threshold)
{
cv::Mat sx;
cv::Sobel(img,sx,CV_32F,1,0,1);
cv::Mat sy;
cv::Sobel(img,sy,CV_32F,0,1,1);
// 创建迭代器
cv::Mat_<float>::const_iterator it= laplace.begin<float>()+laplace.step1();
cv::Mat_<float>::const_iterator itend= laplace.end<float>();
cv::Mat_<float>::const_iterator itup= laplace.begin<float>();
cv::Mat_<float>::const_iterator itx= sx.begin<float>()+sx.step1();
cv::Mat_<float>::const_iterator ity= sy.begin<float>()+sy.step1();
// 初始化为白色的二值图像
cv::Mat binary(laplace.size(),CV_8U,cv::Scalar(255));
cv::Mat_<uchar>::iterator itout= binary.begin<uchar>()+binary.step1();
for ( ; it!= itend; ++it, ++itup, ++itout, ++itx, ++ity) {
// 如果相邻像素的乘积为负数,则符号发生改变
if (*it * *(it-1) < 0.0 && fabs(*ity) > threshold)
*itout= 0; // 水平方向零点交叉
else if (*it * *itup < 0.0 && fabs(*ity) > threshold)
*itout= 0; // 垂直方向零点交叉
}
return binary;
}
~~~
最后修改main函数:
~~~
#include <QCoreApplication>
#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <QDebug>
#include "laplacian.h"
int main(int argc, char *argv[])
{
QCoreApplication a(argc, argv);
cv::Mat image= cv::imread("c:/073.jpg",0); // 输入图像
if (!image.data)
return 0;
// 显示包含感兴趣区域的灰度化原图像
cv::rectangle(image,cv::Point(362,135),cv::Point(374,147),cv::Scalar(255,255,255));
cv::namedWindow("Original Image with ROI");
cv::imshow("Original Image with ROI",image);
// 直接调用函数进行7*7的拉普拉斯变换
cv::Mat laplace;
cv::Laplacian(image,laplace,CV_8U,7,0.01,128);
cv::namedWindow("Laplacian Image");
cv::imshow("Laplacian Image",laplace);
// 使用自建类Laplacian实现拉普拉斯变换
Laplacian laplacian;
laplacian.setAperture(7);
cv::Mat flap= laplacian.calcLaplacian(image);
double lapmin, lapmax;
cv::minMaxLoc(flap,&lapmin,&lapmax);
laplace = laplacian.getLaplacianImage();
cv::namedWindow("Laplacian Image (7x7)");
cv::imshow("Laplacian Image (7x7)",laplace);
// 显示零点交叉
cv::Mat zeros;
zeros= laplacian.getZeroCrossings(lapmax);
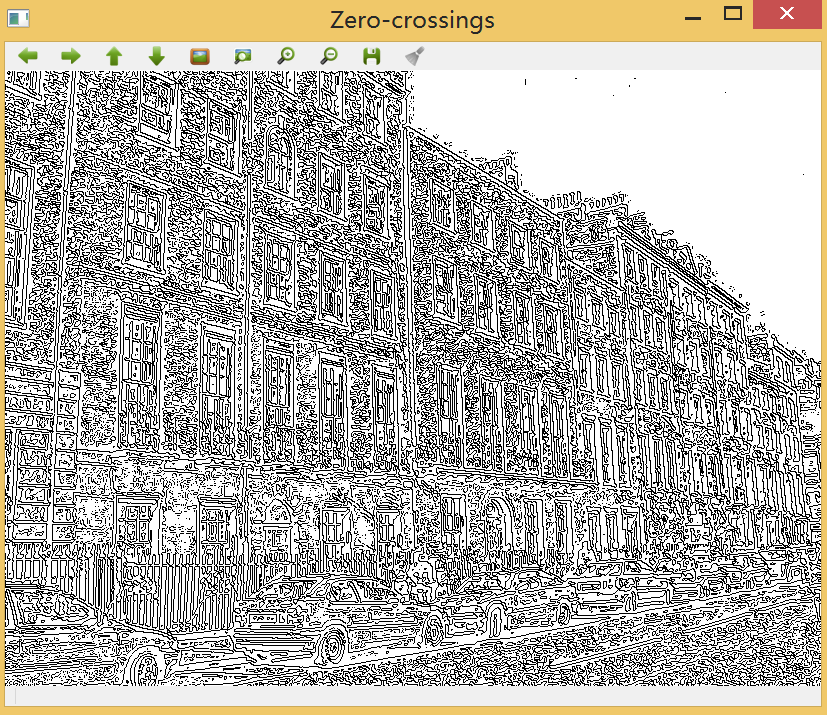
cv::namedWindow("Zero-crossings");
cv::imshow("Zero-crossings",zeros);
// 使用Sobel算子显示零点交叉
zeros= laplacian.getZeroCrossings();
zeros= laplacian.getZeroCrossingsWithSobel(50);
cv::namedWindow("Zero-crossings (2)");
return a.exec();
}
~~~
调用函数(左)、使用自建类实现7*7拉普拉斯变换的效果对比:
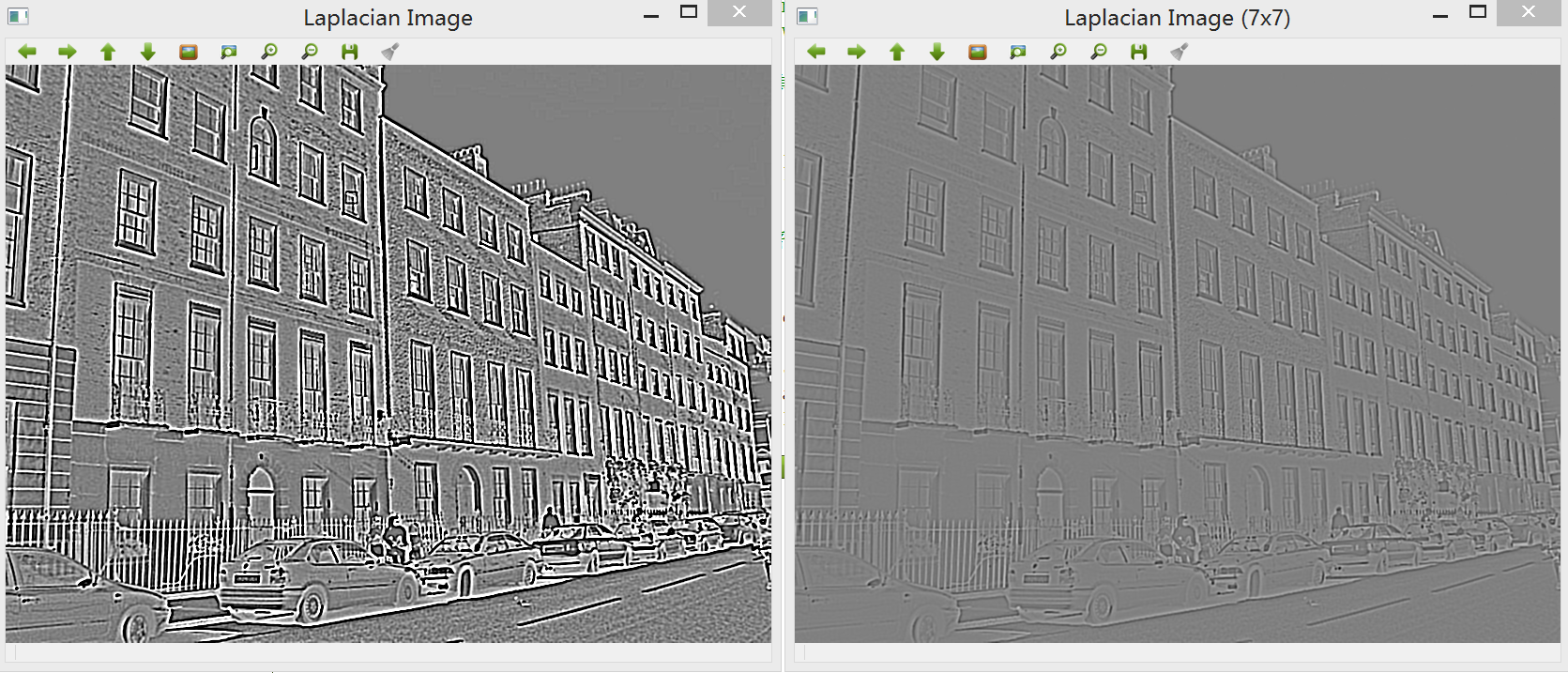
输出零点交叉检测到的所有边缘,由于Laplacian不对强边与弱边作区分,且对噪声十分敏感,因此输出结果检测到很多的边缘。